-
Recent interest in charge exchange nuclear reactions has resulted in new experimental [1] and theoretical [2] challenges. In particular, double charge exchange heavy ion induced reactions (DCE) can be exploited for the production of exotic nuclei [3] and establishing a connection with neutrinoless double beta decay [1, 4]. A heavy ion induced DCE reaction is a process in which the interaction between projectile nucleus a and target nucleus A gives rise to the conversion of two neutrons (protons) belonging to A into two protons (neutrons) without variations in mass. An opposite transition simultaneously occurs in the projectile. We depicted the following isospin transitions:
$ (a,z)+(A,Z) \rightarrow (A,Z \pm 2)+ $ $ (a,z \mp 2) $ , where a and A are the mass numbers and z and Z are the atomic numbers of the projectile and target, respectively. The DCE exit channel can also be the result of two subsequent single charge exchange (SCE) processes, i.e., two isospin transitions of the form$ (a,z)+(A,Z) \rightarrow (A,Z \pm $ $ 1)+(a,z \mp 1) $ . In addition, it can be reached through subsequent multi-nucleon transfer processes such as a two-proton transfer followed by a two-neutron transfer. Hence, two-step SCE reactions and multi-nucleon transfers have to be considered as competing processes for DCE reactions. Current theoretical studies are focused on the interplay between DCE and these processes [2, 5, 6].In this paper, we present preliminary results concerning the calculation of SCE and DCE reaction cross sections by means of a constrained molecular dynamics (CoMD) model [7, 8]. We also calculated the total cross section for the DCE reactions by including the contributions from SCE and multi-nucleon transfers. The choice of CoMD model is motivated by recent results regarding its use in investigating the role of pairing correlations in the one neutron transfer and two neutron transfer processes in heavy ion collisions. CoMD model calculations of the ratios between 1NT and 2NT cross sections were in good agreement with the experimental results [9].
The CoMD approach allows for access to all possible exit channels of a heavy ion collision at fixed incident energy and impact parameter. Furthermore, an event-by-event description of the collision, typical of molecular dynamics models, allows for using the same selection criteria for the calculations as in the experimental data analysis. Nevertheless, with respect to more sophisticated approaches, such as distorted wave Born approximation (DWBA) [10], coupled channel Born approximation (CCBA) [11], and coupled reaction channels [12] calculations, molecular dynamics models do not provide information on the detailed level structure of the colliding nuclei. However, as we are interested in the integrated cross section we consider this to be an acceptable limitation. Future improvements of the model will concern the inclusion of details on the nuclear structure. Such an effort will provide a novel approach to heavy ion collisions, in which the nuclear structure features and collision dynamics can be treated within the same framework.
-
We briefly review the main features of the CoMD model. Within this model, each nucleon is represented by a Gaussian distribution function in the coordinates and momentum space
$ f_{i}({{r}}, {{p}}) = \frac{1}{(2 \pi \sigma_{r} \sigma_{p})^{3}} \exp \left [- \frac{({{r}}- \langle {{r}}_{i} \rangle)^{2}}{2 \sigma_{r}^{2}}- \frac{({{p}}- \langle {{p}}_{i} \rangle)}{2 \sigma_{p}^{2}}^2 \right ], $

(1) where
$\langle {{r}}_{i} \rangle$ and$\langle {{p}}_{i} \rangle$ are the centers of position and momentum of the$i\text{-}{\rm th}$ nucleon, respectively, while$ \sigma_{r} $ and$ \sigma_{p} $ are their related dispersions, which satisfy the minimum uncertainty relation$\sigma_{r} \sigma_{p} = \dfrac{\hbar}{2}$ . The effective interaction has the form,$ V = V^{\rm vol}+V^{(3)}+V^{\rm sym}+V^{\rm surf}+V^{\rm coul}. $

(2) By defining the superposition integral
$ \rho_{ij} \equiv \int {\rm d}^{3}r_{i}{\rm d}^{3}r_{j} \rho_{i}({{r}}_{i}) \rho_{j}({{r}}_{j}) \delta ({{r}}_{i}- {{r}}_{j}), $

(3) $ \rho_{i} \equiv \int {\rm d}^{3}pf_{i}({{r}}, {{p}}), $

(4) the terms of Eq. (2) can be written as
$ V^{\rm vol} = \frac{t_{0}}{2 \rho_{0}} \sum\limits_{i,j \neq i} \rho_{ij}, $

(5) $ V^{(3)} = \frac{t_{3}}{(\mu +1) \rho_{0}^{\mu}} \sum\limits_{i,j \neq i} \rho_{ij}^{\mu}, $

(6) $ V^{\rm sym} = \frac{a_{\rm sym}}{2 \rho_{0}} \sum\limits_{i,j \neq i}(2 \delta_{\tau_{i}, \tau_{j}}-1) \rho_{ij} ,$

(7) $ V^{\rm surf} = \frac{C_{s}}{2 \rho_{0}} \sum\limits_{i,j \neq i} \rho_{ij} \nabla^{2}_{\langle {{r}}_{i} \rangle}(\rho_{ij}), $

(8) $ V^{\rm Coul} = \frac{1}{2} \sum\limits_{i,j \neq i} \frac{e^{2}}{\lvert \langle {{r}}_{i} \rangle - \langle {{r}}_{j} \rangle \rvert}erf \left (\frac{\lvert \langle {{r}}_{i} \rangle - \langle {{r}}_{j} \rangle \rvert}{2 \sigma_{r}} \right ). $

(9) The
$V^{\rm vol}$ and$ V^{(3)} $ terms represent the nucleon-nucleon two- and three-body potentials, respectively, the values of$ t_{0} $ ,$ t_{3} $ μ were fixed to$ -356 \, {\rm{MeV}} $ ,$ 303 \, {\rm{MeV}} $ , and$ \dfrac{7}{6} $ to reproduce saturation density$ \rho_{0} $ and compressibility of symmetric nuclear matter$ K = 200 \, {\rm{MeV}} $ . Eq. (7) represents the symmetry potential,$a_{\rm sym} = 32 \, {\rm{MeV}}$ is the symmetry energy at saturation density and$ \tau_{i} $ is the isospin degree of freedom. Within the CoMD model, similar to transport models [13], the density dependence of the symmetry interaction is treated by employing the form factors given by variational many-body theories [14-16]. For this work, we adopted a form factor for which the symmetry interaction has a linear dependence on the density (for details on the symmetry interaction within the CoMD approach see Ref. [17]). At nuclear matter saturation density,$ \rho_{0} = 0.16 \, {\rm{fm}}^{-3} $ , such parameterization of the symmetry interaction corresponds to a strength of the symmetry energy of$ S(\rho_{0}) = 24.5 \, {\rm{MeV}} $ and a slope of$ L(\rho_{0}) = 61 \, {\rm{MeV}} $ .Coefficient
$ C_{s} $ of the surface potential (8) is used as a free parameter for reproducing the nuclear radii. The Coulomb potential (9) has an error function dependence on the coordinates of the protons. The equations of motion are derived using a time-dependent variational principle, so that$ \langle \dot{{{r}}}_{i} \rangle = \frac{\partial H}{\partial \langle {{p}}_{i} \rangle} \qquad \langle \dot{{{p}}}_{i} \rangle = - \frac{\partial H}{ \partial \langle {{r}}_{i} \rangle}, $

(10) where
$H = \sum\nolimits_{i} \dfrac{\langle {{p}}_{i} \rangle}{2m}+V$ is the Hamiltonian of the system. The main feature of the CoMD model concerns the constraint on the nucleon one-body phase space occupation probability which ensures the fermionic nature of nucleons both in the ground state and during the time evolution of nuclear reactions. The constraint consists in the requirement$ \bar{f}_{i} \leqslant 1, \,\,\, \forall i, $

(11) $ \bar{f}_{i} \equiv \sum\limits_{j} \delta_{s_{i},s_{j}} \delta_{\tau_{i}, \tau_{j}} \int_{h^{3}}f_{j}({{r}}, {{p}}){\rm d}^{3}r {\rm d}^{3}p, $

(12) where
$ s_{i} $ is the spin degree of freedom related to the$ i $ -th nucleon. To calculate the phase space occupation probability of the$ i $ -th nucleon$ \bar{f}_{i} $ the integral is performed in a hypercube of volume$ h^{3} $ centered around point$(\langle {{r}}_{i} \rangle , \langle {{p}}_{i} \rangle)$ in the phase space, with size$ \sqrt{\dfrac{2 \pi \hbar \sigma_{r}}{\sigma_{p}}} $ and$ \sqrt{\dfrac{2 \pi \hbar \sigma_{p}}{\sigma_{r}}} $ , respectively, in the coordinate and momentum spaces. At each time step of integration of the equations of motion, for each nucleon i, quantity$ \bar{f}_{i} $ is checked. If$ \bar{f}_{i}>1 $ an ensemble$ K_{i} $ of nearest particles (including the nucleon i) is determined within the distances of$ 3 \sigma_{r} $ ,$ 3 \sigma_{p} $ in the phase space. The momenta of the particles belonging to the$ K_{i} $ ensemble are randomly changed through a series of two-body elastic scatterings to generate a new sample. This procedure accounts for the conservation of total momentum and total kinetic energy. The new sample is accepted only if the phase space occupation density is reduced, e.g.$ \bar{f}_{i} \leqslant 1 $ . The Pauli blocking in the nucleon-nucleon collision integral is handled straightforward based on the constraint. For each nucleon-nucleon collision we calculate the$ \bar{f}_{i} $ quantities for both particles after the collision. If these functions are lower than 1, the collision is accepted, otherwise it is rejected. This constraint procedure is in the spirit of other, previously released, molecular dynamics models similar to the anti-symmetrized molecular dynamics (AMD) [18] and the fermionic molecular dynamics (FMD) [19], in which the collision is accepted if the final state is a Slater determinant. The calculations of Slater determinants for heavy and super-heavy systems require a huge computational effort in terms of CPU time. The strategy adopted within the CoMD approach has been developed to reduce the CPU time. In contrast with the quantum molecular dynamics (QMD) [20] model, in which Pauli-blocking is uniquely handled in the two-body collision integral, the CoMD approach ensures that the nucleons obey the Pauli principle during the entire duration of a nucleus-nucleus collision. -
Within the CoMD framework, we generated a sample of
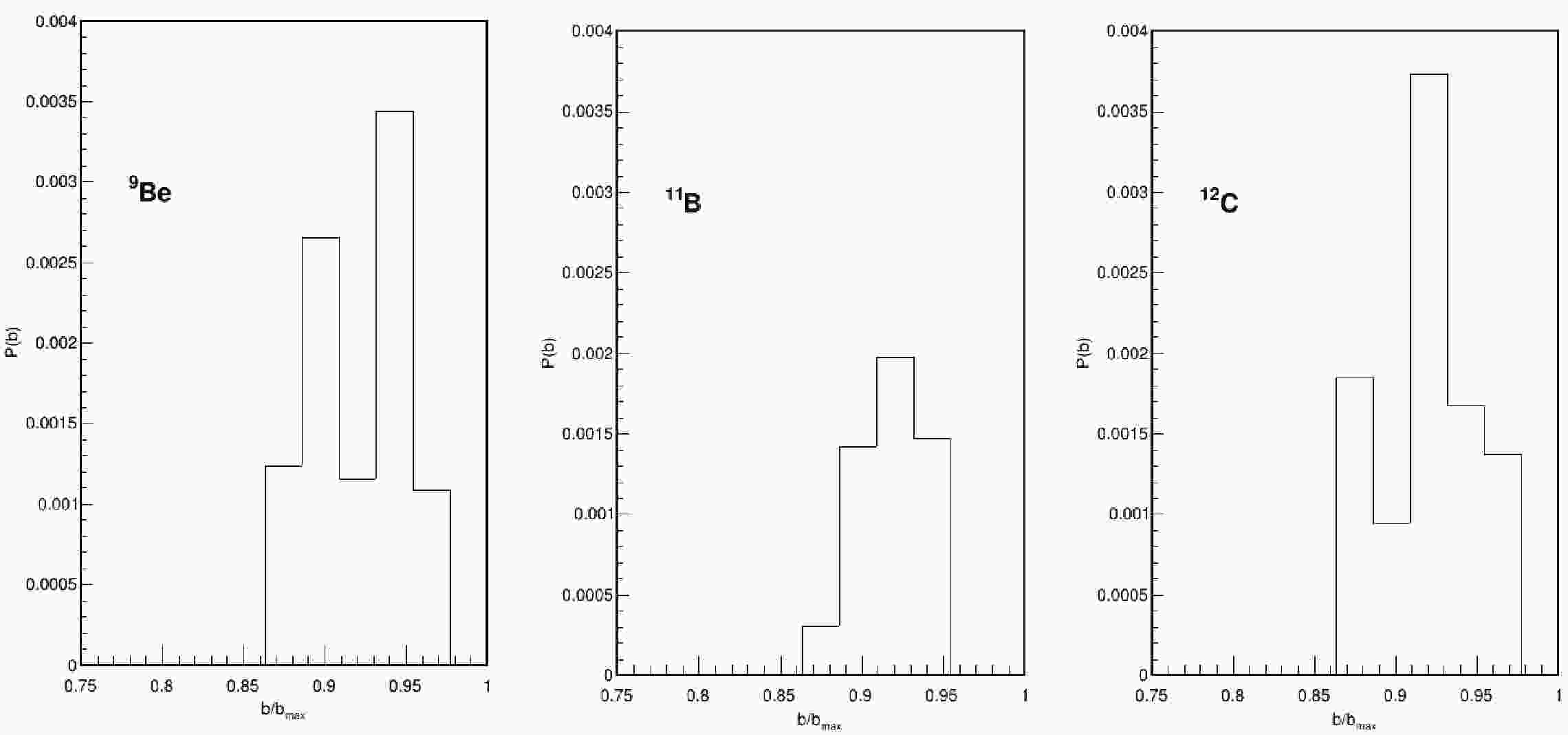
$3 \times 10^{4}$ events for reactions in which an$\rm ^{18}O$ projectile is sent onto the following targets:$^{9}\rm Be$ ,$^{11}\rm B$ , and$^{12}\rm C$ . The projectile has a laboratory incident energy of 84 MeV. Corresponding to this incident energy value, the model provided satisfactory results for neutron transfer processes [9], which is the reason for choosing this incident energy for these reactions. For each colliding system, the events have been generated within an impact parameter interval of$1 \,{\rm fm} \leqslant b \leqslant 9 \, {\rm{fm}}$ . The time evolution of the collisions has been followed up to$ 300 \, \dfrac{fm}{c} $ . We first consider the evaluation of the SCE cross sections. The SCE exit channels correspond to the transitions,$^{18}_{8}{\rm O}+ {{}^{A}_{Z}{\rm X}} \rightarrow $ $ {{}^{18}_{7}{\rm N}}+ {{}^{A}_{Z+1}{\rm Y}}$ ,$^{18}_{8}{\rm O}+ {{}^{A}_{Z}{\rm X}} \rightarrow {{}^{A}_{Z-1}{\rm Y}}+ {{}^{18}_{9}{\rm F}}$ . The former is related to a neutron to proton transition in the target (proton to neutron in the projectile nucleus$^{18}\rm O$ ) while the latter is related to a proton to neutron transition (neutron to proton in the projectile nucleus$^{18}\rm O$ ). Figure 1 shows the probability distributions for SCE reactions as a function of the reduced impact parameter${b}/{b_{\max}}$ for the colliding systems under examination.
Figure 1. Probability distributions as a function of the reduced impact parameter
$b/b_{\max}$ of the SCE exit channels for the reactions$\rm ^{18}O+ {}^{9}Be$ ,$\rm ^{18}O+ {}^{11}B$ ,$\rm ^{18}O+ {}^{12}C$ .SCE processes, therefore, occur in peripheral collisions. The competing processes within similar impact parameter intervals are the subsequent pickup of one neutron and the stripping of one proton, both leading to the same final state. By integrating the probability distributions we obtain the SCE total cross sections
$ \sigma = \int_{b_{\min}}^{b_{\max}}2 \pi b P(b){\rm d} b = 2 \pi \sum\limits_{b = b_{\min}}^{b_{\max}}P(b)b \Delta b . $

(13) The numerical values of the calculated cross sections are reported in Fig. 2 where the error bars indicate the statistical error of the cross section calculation. We observe that the magnitudes of the SCE cross sections are of the order of few mb, similar to the magnitudes of nucleon transfer cross sections. This is mainly due to the low incident energy of the collision, which causes a projectile-target interaction time much longer when compared with higher energy collisions and a higher probability of the SCE process occuring. Of course, in this case, the interplay with the nucleon transfer processes is also more relevant. We underline that we are discussing preliminary results which are needed as a test for the CoMD model and for the development of an upgraded version of the model devoted to the study of charge exchange reactions.
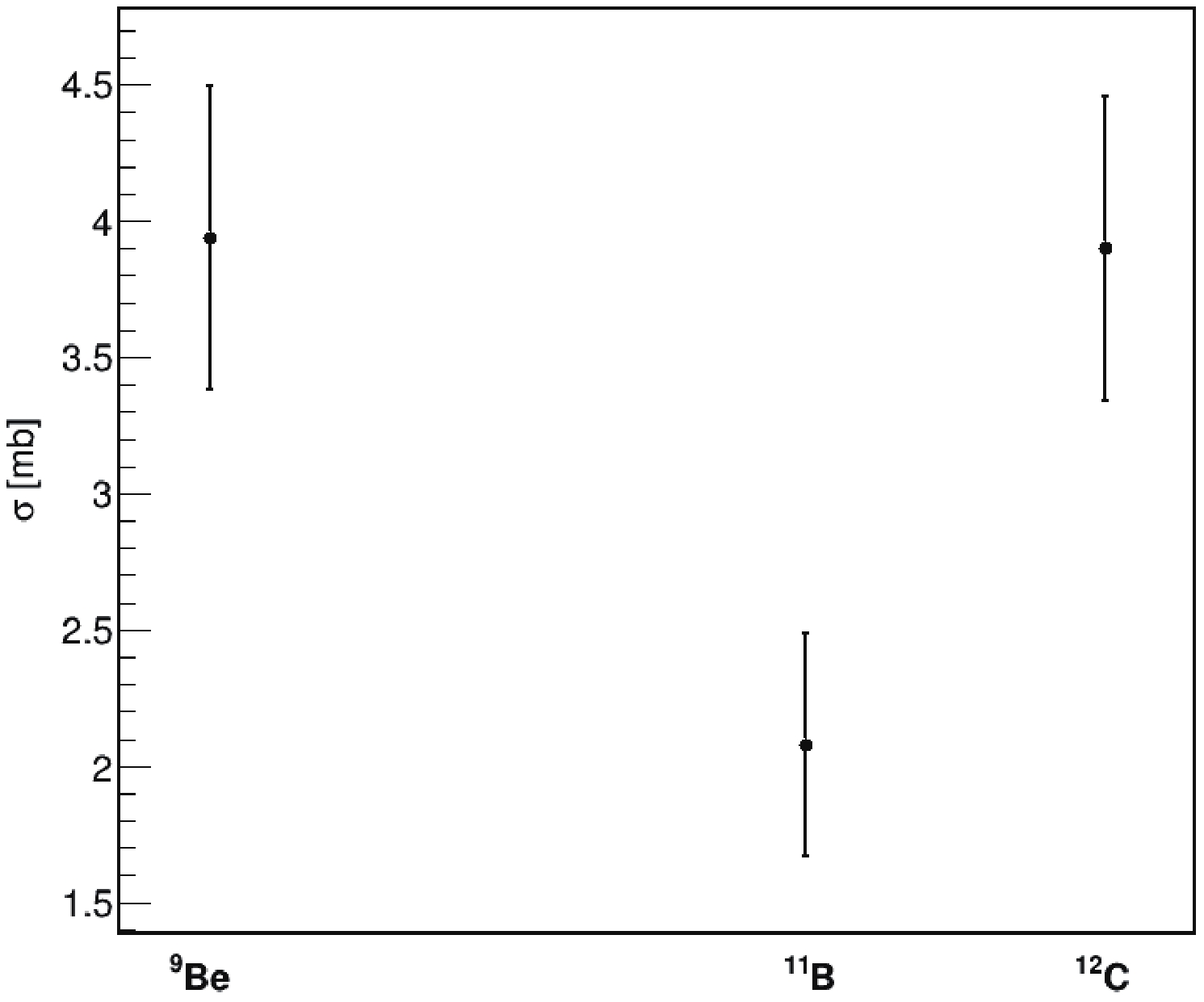
Figure 2. SCE cross sections of the reactions
$\rm ^{18}O+ {}^{9}Be$ ,$\rm {}^{18}O+ {}^{11}B$ ,$\rm ^{18}O+ {}^{12}C$ .The same calculations were performed for DCE reactions, in which we are more interested. In this case, we have second order isospin transitions leading to the exit channels:
$^{18}_{8}{\rm O}+{{}^{A}_{Z}{\rm X}} \rightarrow {{}^{18}_{10}{\rm Ne}}+ {{}^{A}_{Z-2}{\rm Y}}$ ,$^{18}_{8}{\rm O}+ {}^{A}_{Z}{\rm X} \rightarrow {}^{18}_{6}{\rm C}+ {}^{A}_{Z+2}{\rm Y}$ . The predictions of the CoMD model for the targets under examination provide the following DCE exit channels:$^{18}_{8}{\rm O}+ {}^{9}_{4}{\rm Be} \rightarrow {}^{18}_{6}{\rm C}+ {}^{9}_{6}{\rm C}$ ,$^{18}_{8}{\rm O}+ {}^{11}_{5}{\rm B} \rightarrow {}^{18}_{6}{\rm C}+ {}^{11}_{7}{\rm N}$ ,$^{18}_{8}{\rm O}+ {}^{12}_{6}{\rm C} \rightarrow $ $ {}^{18}_{10}{\rm Ne}+ {}^{12}_{4}{\rm Be}$ . These predictions could be significant for the experimental studies on the production of exotic nuclei trough DCE reactions. Figure 3 shows the probability distributions as a function of the reduced impact parameter,${b}/{b_{\max}}$ .
Figure 3. Probability distributions as a function of the reduced impact parameter
$b/b_{\max}$ of the DCE exit channels for reactions$\rm ^{18}O+ {}^{9}Be$ ,$\rm ^{18}O+ {}^{11}B$ ,$\rm ^{18}O+ {}^{12}C$ .The integrated DCE cross sections calculated using Eq. (13) are reported in Fig. 4. We notice that the magnitudes of the DCE cross sections are of the order of some tenths of millibar, and are thus much smaller than the SCE cross sections.

Figure 4. DCE cross sections of reactions
$\rm ^{18}O+ {}^{9}Be$ ,$\rm ^{18}O+ {}^{11}B$ ,$\rm ^{18}O+ {}^{12}C$ .It has already been mentioned that one of the competing processes of DCE reactions is the multi-nucleon transfer. The same final state can be reached through the subsequent transfers of two neutrons and two protons. We have calculated the DCE plus multi-nucleon transfer cross sections, and Fig. 5 shows the comparison between only DCE cross sections and DCE plus multi-nucleon transfer cross sections.

Figure 5. DCE plus multi-nucleon transfer cross sections for reactions
$\rm ^{18}O+ {}^{9}Be$ ,$\rm ^{18}O+ {}^{11}B$ ,$\rm ^{18}O+ {}^{12}C$ .We observe the
$\rm ^{18}O+ {}^{11}B$ entrance channel within the error bars of the values of the cross sections, this highlights the relevance of the competition between the DCE and the multi-nucleon transfer leading to the same final state. In contrast, for the$\rm ^{18}O+ {}^{9}Be$ and$\rm ^{18}O+ {}^{9}Be$ colliding systems, the DCE plus multi-nucleon transfer cross sections are larger than the DCE only cross sections. This result is partly due to some limitations in the model related to details of the nuclear structure. The results herein discussed are only the consequence of the nuclear potential introduced in Section 2 and of the dynamical evolution of the nuclear reactions within the CoMD approach. The dependence of these processes on the features of the symmetry interaction should also be investigated. One of the major steps in the development of this research concerns the dependence of the cross sections on the strength and on the slope of the symmetry energy. Of course, another important step is a calculation campaign regarding the excitation functions of the SCE and DCE cross sections. Note that these are preliminary results for testing the reliability of the CoMD model in treating specific reaction mechanisms, namely DCE reactions. Further developments of the model concern the inclusion of nuclear structure features. In addition, to properly account for the DCE transitions, we aim to include four-body nucleon-nucleon correlations in the isospin space related to the transition of two neutrons to two protons in the target, of two protons to two neutrons in the projectile, and vice versa [1]. Of course, comparison with experimental data could significantly improve model development. -
We calculated SCE and DCE reaction cross sections for the systems:
$\rm ^{18}O+ {}^{9}Be$ ,$\rm ^{18}O+ {}^{11}B$ and$\rm ^{18}O+ {}^{12}C$ at a laboratory incident energy of 84 MeV. These reactions were studied within the framework of the CoMD model. The aim of this preliminary study was to test the perspective for employing a dynamical model to study charge exchange reactions. The obtained results show that the model is able to predict the occurrence of both SCE and DCE reactions and investigate the interplay of the latter with multi-nucleon transfer processes. This work presents the first step in the development of a dynamical model devoted to the study of DCE reactions, which contain, within a unique framework, the dynamics of nucleon-nucleon collisions, the details of the nuclear structure of the collision partners, and the four-body nucleon-nucleon correlations related to the DCE processes. The purpose is to ensure satisfactory model calculations for comparison with experimental data along with the more complete information provided by the nuclear reactions theory.
Heavy ion induced charge exchange reactions: A preliminary study within the Constrained Molecular Dynamics model
- Received Date: 2021-03-24
- Available Online: 2021-08-15
Abstract: We present a preliminary study of charge exchange heavy ion induced reactions based on the constrained molecular dynamics (CoMD) model. The purpose is to test the capability of the model in predicting the occurrence of single charge exchange (SCE) and double charge exchange (DCE) exit channels for three different entrance channels at the same laboratory incident energy. The nuclear reaction dynamics and nuclear interaction within the CoMD approach are the only ingredients that have given, at this stage, promising results for SCE and DCE cross section calculations. The obtained results suggest an upgrade and possible future employment of the model for studies relating to the production of exotic nuclei through charge exchange reactions or DCE reactions and their connection with neutrinoless double beta decay.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: