-
The phase diagram of strongly interacting matter is an important research topic in hadron physics. Under extreme conditions, the hadron state will undergo phase transition from hadron to quark and restoration of spontaneous chiral symmetry [1-4]. At finite a temperature and density, the chiral restoration may be a first-order phase transition; however, the results of different models and even different regularizations are inconsistent. At zero baryon density, although the lattice Monte Carlo simulations provide reliable results, which indicate that the chiral transition is a crossover, when the temperature is zero and density is high, the lattice calculation faces the sign problem [5, 6].
At high density, topological gauge fields with nonzero winding number (instantons and sphalerons) may appear [7-13]. The interaction of quarks with these topological gauge fields will alter the helicities of the quarks, which results in the chiral imbalance between left- and right-hand quarks via the axial anomaly [14-16]. The interaction of quarks with these topological gauge fields would also lead to local P and CP violations. Strong magnetic fields are suggested to be produced at the very first moments of a noncentral heavy ion collision [17, 18]. If the chiral imbalance is significant here, it will result in observable effects in the experiment because the right- and left-hand quarks move in different directions along the magnetic field. This phenomenon is called the chiral magnetic effect (CME) [19] and can be considered as an indirect evidence of P and CP violations [20, 21].
The chiral imbalance indicates an asymmetry in a number of right- and left-handed quarks. To study the effect of this asymmetry, a chiral chemical potential
$ \mu_5 $ , conjugated to the chiral charge density$ n_5 $ , can be introduced [19, 22]. As demonstrated in Refs. [22-24], this chiral chemical potential influences the position of the critical end point (CEP). The verification and determination of the CEP is a critical issue in literature [25-27]. Even if CEP exists, its location remains uncertain. Researchers have attempted to provide relevant information from experiments [28-31] and astronomy [32-35].However, in the effective model, the existence of CEP depends on the choice of the regularisation scheme. Although the CEP exists in the three-momentum cutoff scheme, it disappears in the proper-time regularisation scheme; hence, there is a need to ascertain whether the CEP still exists in a chiral imbalance system. We will examine whether the existence of chiral imbalance could lead to the chiral phase transition from crossover to a first-order transition. If the first-order phase transition is determined in QGP without proper regulation of the chirally imbalance, it remains uncertain whether the first-order transition is triggered by high density or chiral imbalance.
Furthermore, the influence of chiral imbalance on the equation of state (EOS) is interesting. Owing to the quantum anomaly, the chiral density
$ n_5 $ is not a strictly conserved quantity. Therefore, studies on the effect of chiral imbalance are considered as on a time scale significantly larger than the conventional time scale of chirality changing processes [36]. In addition, the possible impact of chiral imbalance on the EOS is neglected in the literature. However, chiral density could induce using electro-magnetic fields. As expressed in the Eq. (1) in Ref. [36], with parallel magnetic fields in the background, the chiral density$ n_5 $ is proportional to the magnetic field strength. With the electric field E and magnetic field B, the flip chirality can take place on a time scale τ and the chiral density is exprssed as$ n_5 = \dfrac{q_f^2}{2\pi^2}\big|eE\big|\big|eB\big|{\rm exp}\left(-\dfrac{\pi M^2}{\big|q_feE\big|}\right)\tau, $

(1) where
$ q_f $ represents the electric charge of the flavor f and M corresponds to the constituent quark mass. It is well known that pulsars are determined with strong magnetic fields. Hence, chiral imbalance has a significant probability of occurring in pulsars, which will make CME more obvious. First, we will study the effect of chiral imbalance on the equation of state (EOS). Its influence on the mass-radius relationship and tidal deformability of quark stars will also be investigated. However, before that, a short discussion on the stability of the two-flavor quark matter is presented here. The most stable particle with the ground state of the strongly interacting matter at zero density is the nucleon. The strange quark matter may be the ground state at a non-zero density [37-40]. This hypothesis has never been validated, and the stability of quark matter may be model dependent. A recent work indicated that quark matter with only u-d quarks can be the ground state of baryonic matter, other than the u-d-s strange quark matter [41]. Accordingly, we study the non-strange quark matter.In this research, the chiral phase transition will be studied under the novel Nambu-Jona-Lasinio (NJL) model [42-44]. The standard two-flavor NJL Lagrangian solely contains scalar and pseudoscalar-isovector channels. However, its Fierz transformation, as a mathematically equivalence, contains more interactive channels [45], especially the vector channel. Except the chiral chemical potential, model calculations indicate that the vector channel will also affect the chiral phase structure and the location of CEP [46, 47]. The critical chemical potential will increase as the vector coupling increases. When the coupling is sufficiently large, the CEP will disappear. The contribution of the vector channel is relatively important at nonzero densities. The vector coupling strength is usually considered a free parameter in the quark model. In the relativistic mean-field model of nuclear matter, the vector couplings are fitted to low-energy data. However, the possibility of being suppressed at high temperatures and densisties is unknown. Subsequently, density-dependent couplings are proposed in exploring hot and dense nuclear matter. Therefore, the detection of CEP in heavy-ion collisions will also provide information on vector channel interactions.
The linear combination of the standard NJL Lagrangian and its Fierz transformation will consistently include the vector channel interaction. The considered channels in the Fierz transformation are the vector
$ -(\bar\psi\gamma^\mu\psi)^2 $ and axial-vector$ -(\bar\psi i\gamma_5\gamma^{\mu}\psi)^2 $ channels. In the mean-field-approximation,$ -(\bar\psi\gamma^\mu\psi)^2 \approx -2n \psi^\dagger \psi +n^2, $

(2) $ -(\bar\psi i\gamma_5\gamma^\mu\psi)^2 \approx 2 n_5\psi^\dagger \gamma_5\psi-n_5^2. $

(3) Here, the n and
$ n_5 $ represent the number and chiral number densities of quarks, respectively.This paper is organized as follows: In Sec. II, we introduce the novel self-consistent mean-field theory of the NJL model. In Sec. III, we present our numerical results and analysis on the phase transition. Sec. IV provides a short summary of our work.
-
In the recently developed self-consistent two-flavor NJL model [42-44], the Lagrangian can be expressed as a linear combination of a standard NJL Lagrangian (
$ {\cal{L}}_{\rm NJL} $ ) and its Fierz transformation ($ {\cal{L}}_{\rm Fierz} $ ) [2, 45, 48], which is expressed as$ {\cal{L}} _C = \left(1-\alpha \right){\cal{L}}_{\rm NJL} + \alpha {\cal{L}} _{\rm Fierz}, $

(4) where α weights the contribution from the Fierz transformation. At a finite density,
$ \mu \psi^\dagger \psi $ can be added to the right-hand side of Eq. (4). Similarly, we can consider the quark chiral imbalance by introducing a term$ \mu_5 \psi^\dagger \gamma_5\psi $ to the right side with$ \mu_5 $ being the chiral chemical potential coupling to the chiral operator. Here, we adopt the conventional NJL Lagrangian with a four-quark interaction for$ {\cal{L}}_{\rm NJL} $ . The$ {\cal{L}}_{\rm NJL} $ and its Fierz transformation$ {\cal{L}}_{\rm Fierz} $ can be written, respectively, as$ {\cal{L}}_{\rm NJL} = \bar{\psi }({\rm i}{\not{\partial }} - m)\psi + G\Big[\left(\bar{\psi }\psi\right)^2+\left(\bar{\psi } {\rm i} \gamma _5 \vec{\tau }\psi \right)^2\Big], $

(5) and
$ \begin{aligned}[b] {\cal{L}} _{\rm Fierz} =& \bar{\psi }({\rm i}{\not{\partial }} - m)\psi + \frac{G} {8 N_c}\Big[2\left(\bar{\psi } \psi \right)^2+2\left(\bar{\psi } {\rm i} \gamma _5 \vec{\tau} \psi \right)^2\\ &- 2\left(\bar{\psi } \vec{\tau} \psi \right)^2 - 2\left(\bar{\psi } {\rm i} \gamma _5 \psi \right)^2 - 4\left(\bar{\psi } \gamma^{\mu } \psi \right)^2\\ & - 4\left(\bar{\psi } {\rm i}\gamma^{\mu } \gamma_5\psi \right)^2 + \left(\bar{\psi } \sigma^{\mu \nu} \psi \right)^2 - \left(\bar{\psi } \sigma^{\mu \nu} \vec{\tau} \psi \right)^2\Big]. \end{aligned} $

(6) Under the mean-field approximation, the effective quark mass is
$ M = m-2G^\prime\sigma. $

(7) Here,
$ \sigma = \left\langle{\bar\psi } \psi\right\rangle $ is the two-quark condensation and$ G^\prime $ represents the four-quark effective coupling for the mixed Lagrangian Eq. (4), which has a relationship with G, expressed as$ G^\prime = \left(1-\alpha+\frac{\alpha}{4N_c}\right)G. $

(8) The new coupling
$ G^\prime $ needs to be recalibrated to fit the low-energy experimental data. The modified chemical and chiral chemical potentials are defined, respectively, as$ \mu_r = \mu- \frac{\alpha G} { N_c }n, $

(9) $ \mu_{5r} = \mu_5+ \frac{\alpha G} { N_c }n_5. $

(10) Here,
$ n = \left\langle{\psi ^\dagger } \psi\right\rangle $ and$ n_5 = \left\langle{\psi ^\dagger } \gamma_5\psi\right\rangle $ represent the quark and chiral number densities, respectively. Note that the modified part of$ \mu_{5r} $ differs from Eq. (34) of Ref. [46] with a negative sign. This is because the four-quark pseudo-vector interaction in Eq. (31) of Ref. [46] has a negative coupling$ -G_V $ .The chiral condensate and (chiral-) quark number densities are given by minimizing the thermodynamic potential density. At a finite density and temperature, the chiral condensate is expressed as
$ \sigma = -\frac{N_cN_f M T}{2\pi ^2} \sum\limits_{s = \pm 1}\sum\limits_{n = -\infty}^\infty\int \frac{ {{p}}^2}{E_s^2+\tilde \omega_n^2} {\rm d}p , $

(11) where
$ \tilde \omega_n $ represents the fermion Matsubara frequency, which is defined as$ \tilde \omega_n = \omega_n+{\rm i} \mu $ and$ \omega_n = (2n+1)\pi T $ with$ n \in {\mathbb{Z}} $ . In addition, the energy for different helicities s is defined as$ E_s $ =$ \sqrt{M^2+(\mu_{5r}-s|{{p}}|)^2} $ with$ s = \pm 1 $ . In the proper-time regularization scheme,$ 1/A(p^2) $ is replaced with$ \int_{\tau_{\rm UV}}^ \infty {\rm d}\tau {\rm e}^{-\tau A(p^2)} $ , with$ \tau_{\rm UV} = 1/\Lambda^2_{\rm UV} $ and$ \Lambda_{\rm UV} $ as the UV cutoff for regularizing the ultraviolet divergence. The chiral condensate at a finite temperature and density can be written as in Ref. [49]:$ \begin{aligned}[b] \sigma =& -\frac{N_cN_f M }{2\pi ^2} \sum\limits_{s = \pm 1}\int_0^\infty \int_{\tau_{ \rm UV}}^\infty \frac{p^2 {\rm e}^{-\tau E_s^2}}{ \sqrt{\pi\tau}}\\&\times \Big[1-f_s^-(p,\mu_r,\mu_{5r},T)-f_s^+(p,\mu_r,\mu_{5r},T)\Big]{\rm d}\tau {\rm d}p, \end{aligned} $

(12) $ \begin{aligned}[b] =& -\frac{N_cN_f M }{2\pi ^2} \sum\limits_{s = \pm 1}\int_0^\infty \frac{p^2}{E_s}{\texttt{Erfc}}(\sqrt{\tau_{\rm UV}}E_s)\\&\times \Big[1-f_s^-(p,\mu_r,\mu_{5r},T)-f_s^+(p,\mu_r,\mu_{5r},T)\Big] {\rm d}p . \end{aligned} $

(13) Here, Erfc
$ (x) $ represents the complementary error function and$ f_s^\pm $ defines the Fermi-Dirac distribution function under the modified (chiral-) chemical potentials and nonzero temperature T, with$ f_s^\pm(p,\mu_r,\mu_{5r},T) = \frac{1}{1+{\rm e}^{(E_s\pm\mu_r)/T}}, $

(14) where
$ E_s $ =$ \sqrt{M^2+(\mu_{5r}-s|{{p}}|)^2} $ with$ s = \pm 1 $ . Similarly, the quark number density n and the chiral number density$ n_5 $ are$ \begin{aligned}[b] n =& \frac{N_cN_f }{2\pi ^2} \sum\limits_{s = \pm 1}\int_0^\infty p^2 \Big[f_s^-(p,\mu_r,\mu_{5r},T) \\ &-f_s^+(p,\mu_r,\mu_{5r},T)\Big] {\rm d}p, \end{aligned} $

(15) $ \begin{aligned}[b] n_5 =& \frac{N_cN_f }{2\pi ^2} \sum\limits_{s = \pm 1}\int_0^\infty p^2\frac{\mu_{5r}-sp}{E_s}{\texttt{Erfc}}(\sqrt{\tau_{\rm UV}}E_s) \\ &\times\Big[1\!-\!f_s^-(p,\mu_r,\mu_{5r},T)\!-\!f_s^+(p,\mu_r,\mu_{5r},T)\Big]{\rm d}p . \end{aligned} $

(16) With
$ f_\pi = 93 $ MeV,$ m_\pi = 135 $ MeV, and$ m = 3.5 $ MeV, three parameters (m,$ G^{\prime} $ , and$ \tau_{\rm UV} $ ) are fixed to fit the Gell-Mann-Oakes-Renner relation:$ - 2 m \left\langle { \bar \psi \psi} \right\rangle $ =$ (f_\pi m_\pi)^2 $ . The quark condensate is$ \left\langle { \bar \psi \psi} \right\rangle)^{1/3} = -282.4 $ MeV. Then we have$ G^\prime = 4.1433 \times 10^{-6} $ MeV-2 and$ \Lambda_{\rm UV} $ = 955 MeV. The coupling G is adjusted with α.To study the response of the chiral condensate to chemical potentials and temperatures, the susceptibilities are defined by
$ \chi_\mu = -\frac{\partial \sigma}{\partial\mu}, \quad \chi_{\mu_5} = \frac{\partial \sigma}{\partial\mu_5}, \quad \chi_T = -\frac{\partial \sigma}{\partial T}. $

(17) -
For different α values, the pseudo-transition point is approximately
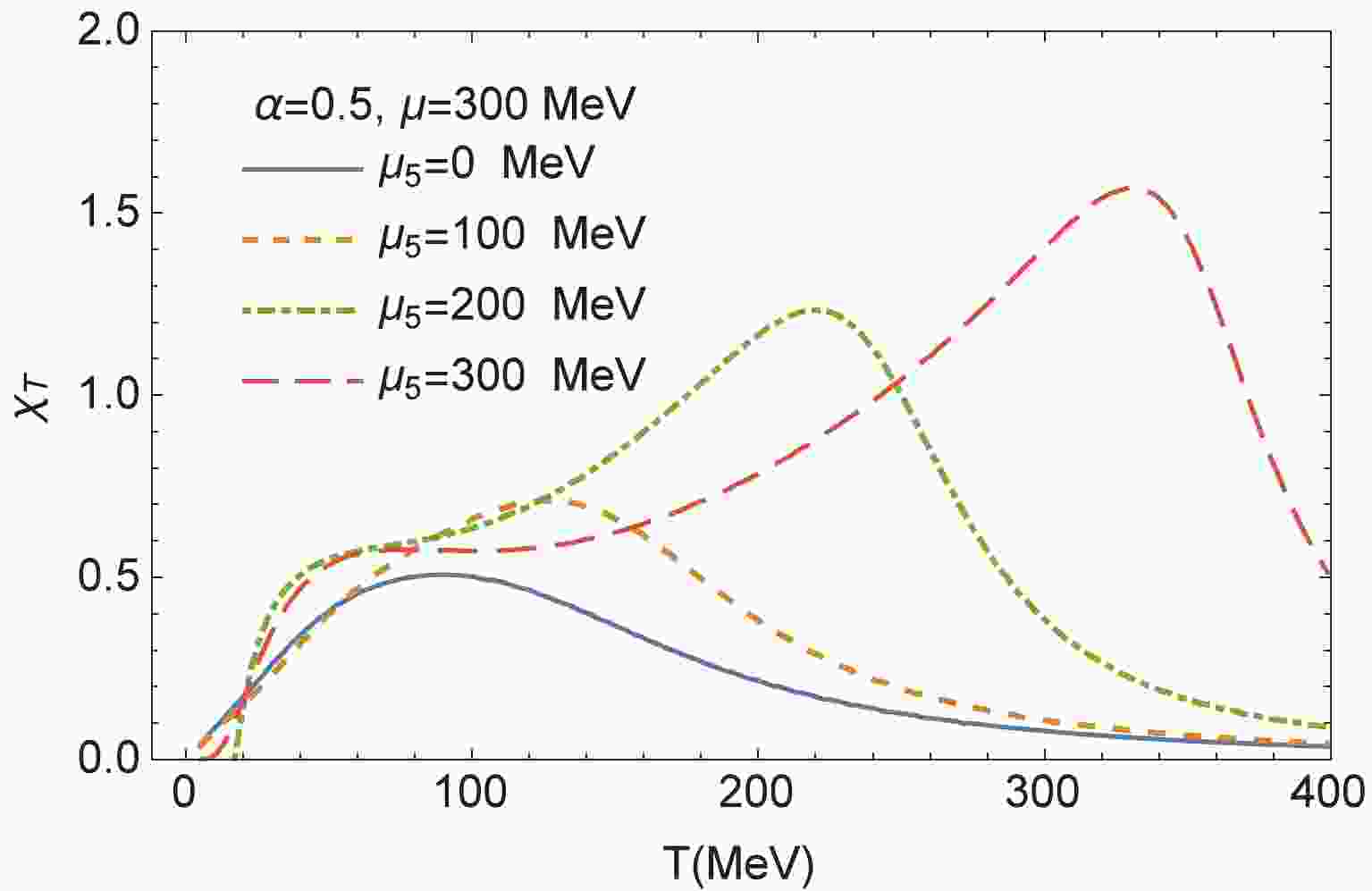
$ \mu = 300 $ MeV at$ T = 0 $ and increases as α increases, which is similar to the results obtained from the three-momentum cutoff scheme. For nonzero temperatures,$ \chi_T $ is presented in Fig. 1. It exhibits a crossover even when$ \mu = 300 $ MeV. However, it differs from the three-momentum cutoff scheme, such that the proper-time regularization scheme exhibits a crossover for the chiral phase transition, even at vary large μ; thus, CEP does not exist in the chirally balanced system ($ \mu_5 = 0 $ ) in this regularization scheme. We present the results with$ \mu_5 \neq 0 $ below. -
As the chiral imbalance appears, a drastic decrease in the
$ M-\mu $ plot emerges, as illustrated in Fig. 2. This alteration occurs at approximately$ \mu = M_{\rm vac} $ , solely for the relatively large$ \mu_5 $ , where$ M_{\rm vac} $ represents the quark mass at$ T = \mu = 0 $ . In addition, this indicates that the quark mass increases at different chiral chemical potentials. The phenomenon in which the chiral condensate increases with some external field is called "catalysis". Similar to the magnetic catalysis [50-53], the catalysis considered here can be called chiral catalysis, as it is triggerd by the chiral imbalance. The inverse magnetic catalysis is observed [54, 55]. In the proper-time scheme of this study, only chiral catalysis exists with constant couplings. In the three-momentum cutoff scheme, inverse chiral catalysis exists because the chiral symmetry is partly restored [24].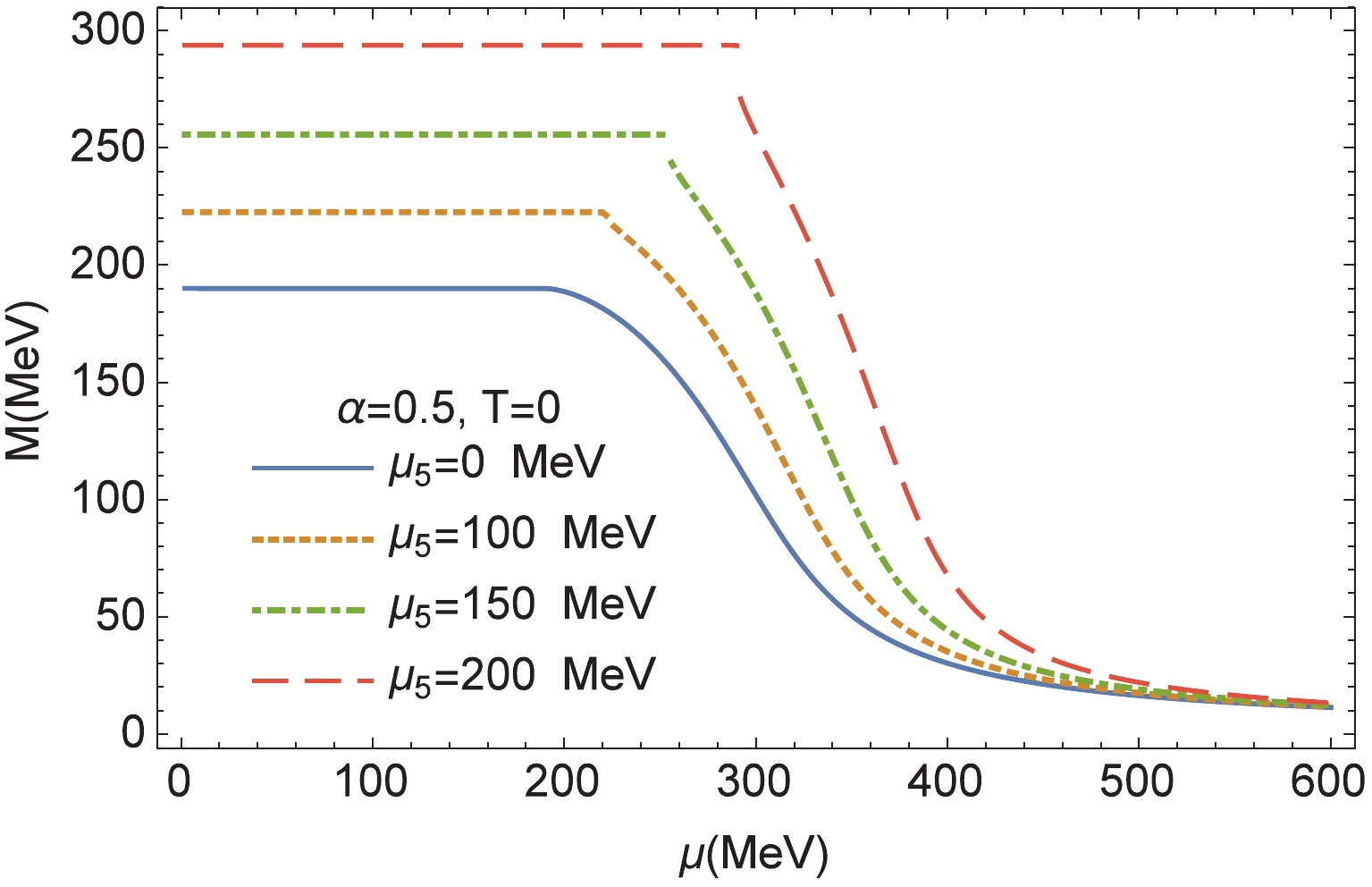
Figure 2. (color online) Quark mass as a function of chemical potential μ for different chiral chemical potentials
$ \mu_5 $ .In Fig. 3, the chemical susceptibilities
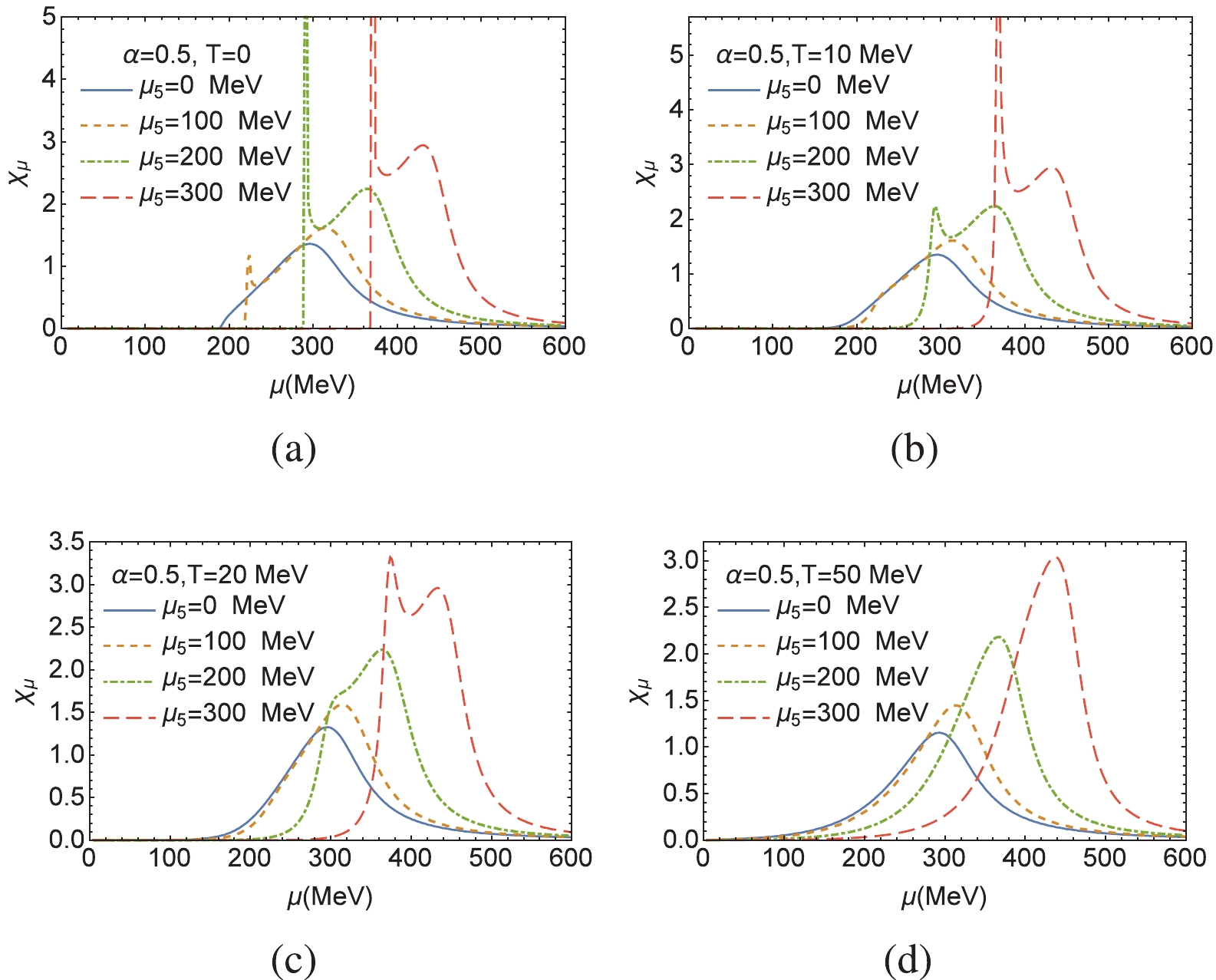
$ \chi_\mu $ for different$ \mu_5 $ at T = 0, 10, 20, 50 MeV are presented. When$ \mu_5 = 0 $ , the chiral transition is always a crossover at any T and μ. Because$ \mu_5 $ is nonzero, peaks and bumps appear in the plots. When$ T = 0 $ and$ \mu_5>0 $ , the increase in μ will trigger significant peaks in the susceptibility lines. This phenomenon differs from that of the results when$ \mu_5 = 0 $ . Therefore, this strongly indicates the existence of a first-order phase transition. It is obvious that the critical chemical potentials increase with$ \mu_5 $ . As temperature increases, the peaks begin to disappear even for nonzero$ \mu_5 $ , and there remains only pump. This change may indicate the existence of CEP in the chiral imbalance system. -
To elucidate the influence of chiral imbalance, we present the quark mass as a function of chiral chemical potential
$ \mu_5 $ in Fig. 4. In addition, the corresponding susceptibilities for fixed baryon chemical potentials are also presented.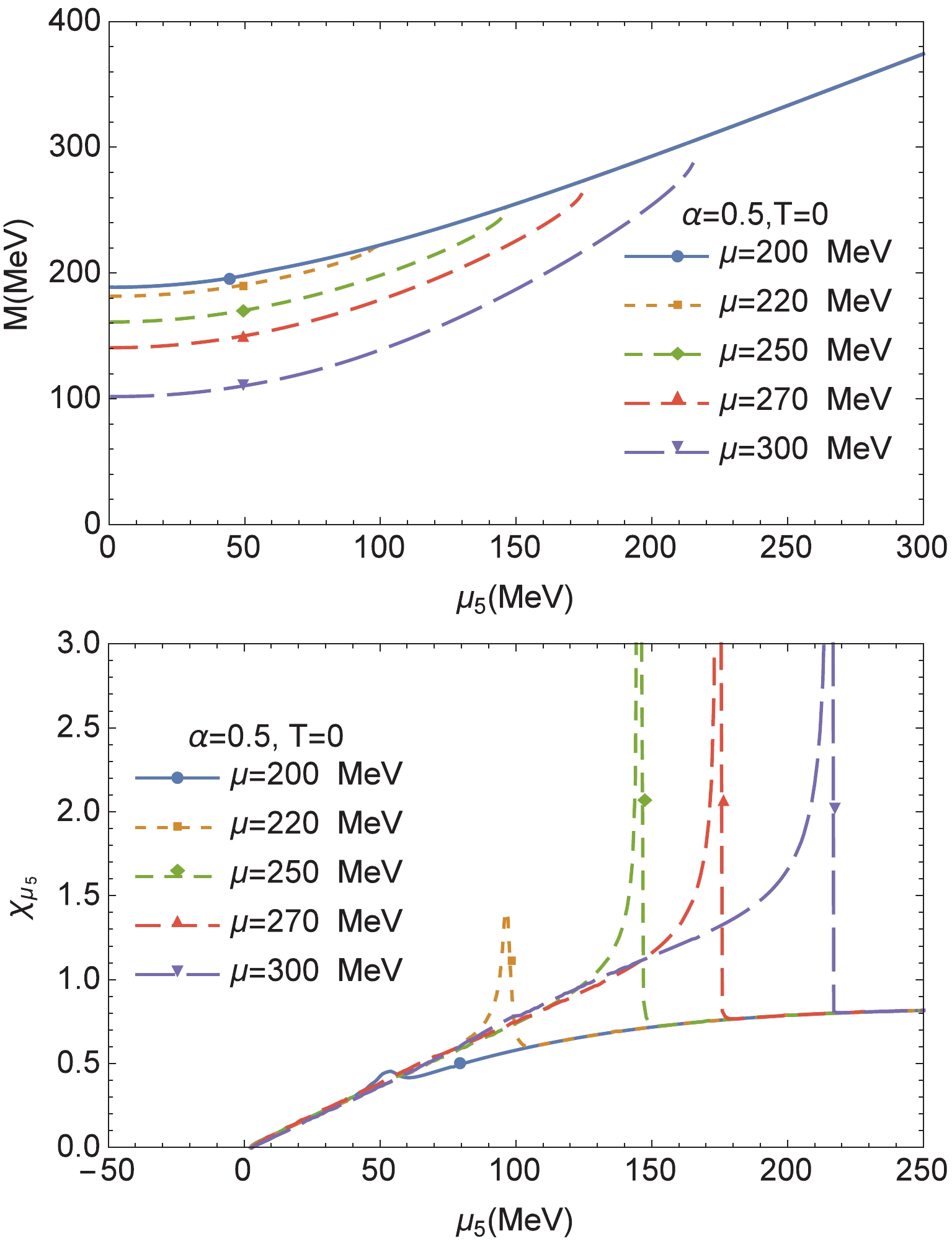
Figure 4. (color online) Chiral catalysis effect and chiral susceptibility at zero temperature. In the up-plane, because
$ \mu_5 $ is larger than some critical values, the lines of$ \mu>200 $ MeV coincide with those of$ \mu = 200 $ MeV.When the chemical potential μ is less than 200 MeV, the quark mass remains almost unchanged with μ; however, it smoothly increases with the chiral chemical potential
$ \mu_5 $ . So, the phase diagram in the$ T-\mu_5 $ plane is a crossover in this μ region. At$ \mu \geq 220 $ MeV, significant peaks emerge in the$ \chi_{\mu_5} $ plot, which indicate the existence of the first order phase transition and CEP5. The plot also demonstrates that even if the CEP5 exists, there is a threshold for chemical potential μ. However, because the quark condensate or mass does not change significantly at the transition point here, it is difficult to precisely determine the origin of the first order phase transition. At T = 0, the origin of the first order transition in the$ \mu_5-\mu $ plane is located in regions of$ \mu\in (200,220) $ MeV and approximate to$ \mu_5 = 100 $ MeV.The critical temperature in the CEP plane increases with temperature. Because it is also difficult to locate the CEP, determining a relationship between CEP and CEP5 seems impossible in the proper-time regularization scheme. Here, we present the pseudo-critical temperature
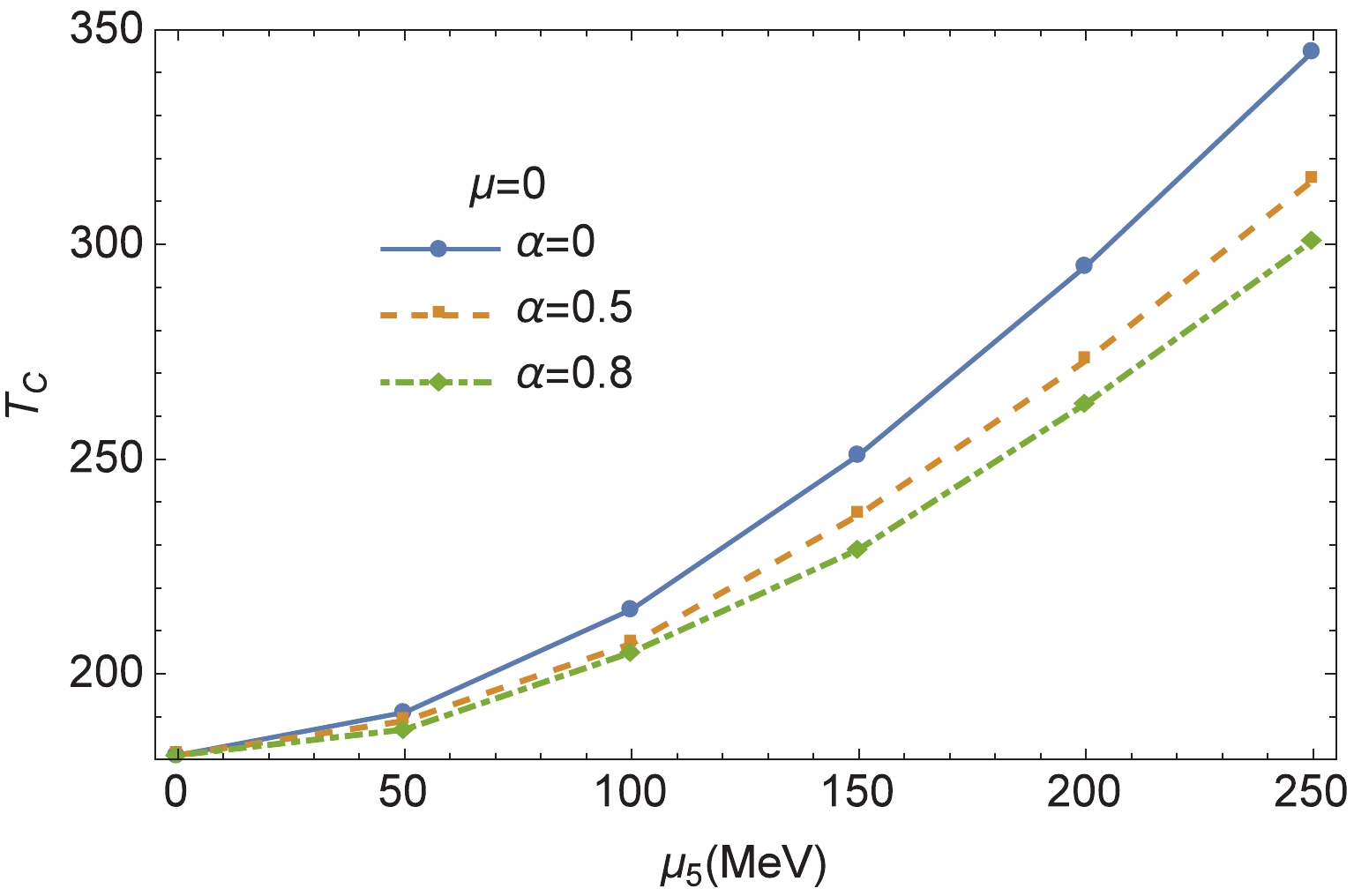
$ T_c $ and critical chemical potential$ \mu_c $ (T = 0) as a function of chiral chemical potential$ \mu_5 $ in Figs. 5 and 6, respectively. At$ \mu = \mu_5 = 0 $ , the pseudo-critical temperature is approximately 181 MeV.$ T_c $ decreases with α, which is similar to the result with the three-momentum cutoff regularization. However,$ T_c $ and$ \mu_c $ increase with$ \mu_5 $ . In Fig. 6, both the pseudo-critical and critical chemical potentials are presented as a function of$ \mu_5 $ at T = 0. The solid lines represent the pseudo-critical chemical potentials, which are larger than the critical chemical potentials (dotted lines). No critical chemical potential exists at small$ \mu_5 $ . The critical chemical potentials increase with α. This trend can also be observed in Fig. 3(a). With the increase in$ \mu_5 $ , the peak and bump converge. -
Here, we study the influence of chiral imbalance on the EOS of quark matter and mass-radius relationship of quark stars. If the first-order phase transition is observed in the astronomical observation, this will verify the existence of CEP [56, 57] and trigger the emergence of a third family of compact stars, in addition to white dwarfs and neutron stars [58-60]. The model-independent equations of state of strongly interacting matter are expressed as [61, 62]
$ P(\mu) = P_0 + \int_ 0^{\mu }{\rm d}\mu n (\mu ), $

(18) $ \varepsilon(\mu) = -P(\mu)+ \mu n(\mu). $

(19) Here,
$ P_0 $ represents the vacuum pressure at$ \mu = 0 $ and is taken as$ P_0 = -(120 $ MeV)4. As noted in the introduction, chiral density is produced via the axial anomaly. Owing to this anomaly, chiral density is not a conserved quantity in QCD. The chiral imbalance influences the quark matter via the chiral interactions; however, it is not significantly present in the EOS.The mass of recently observed pulsars [63-66] is approximately
$ 2M_{\odot} $ . We set$ \alpha = 0.8 $ to ensure the EOS is sufficiently rigid. To study the mass-radius relationship, we adopted the static TOV equations (in units$ G = c = 1 $ )$ \frac {{\rm d}P\left(r \right)} {{\rm d}r} = -\frac {\left(\varepsilon +P \right)\left(M + 4\pi r^3 P \right)} {r \left(r-2M \right)}, $

(20) $ \frac {{\rm d}M\left(r \right)} {{\rm d}r} = 4\pi r^2 \varepsilon. $

(21) Here, P and ε represent the pressure and energy density as defined by Eqs. (18) and (19). In addition,
$ M(r) $ is the quark star mass as a function of radius r. The equations are solved iteratively from a central pressure to zero pressure that defines the edge of the star [67]. Figure 7 demonstrates that the EOS becomes soft as$ \mu_5 $ increases. The maximum masses and radii of the quark star decrease as$ \mu_5 $ increases. When$ \mu_5 $ is greater than$ 150 $ MeV, the maximum mass becomes less than 2$ M_\odot $ . When$ \mu_5 $ is greater than$ 200 $ MeV, the maximum radius becomes less than 10 km. If the observed pulsars of masses larger than 2$ M_\odot $ are identified as quark stars, and the radius is larger than 10 km, then the chiral chemical potential cannot be very large.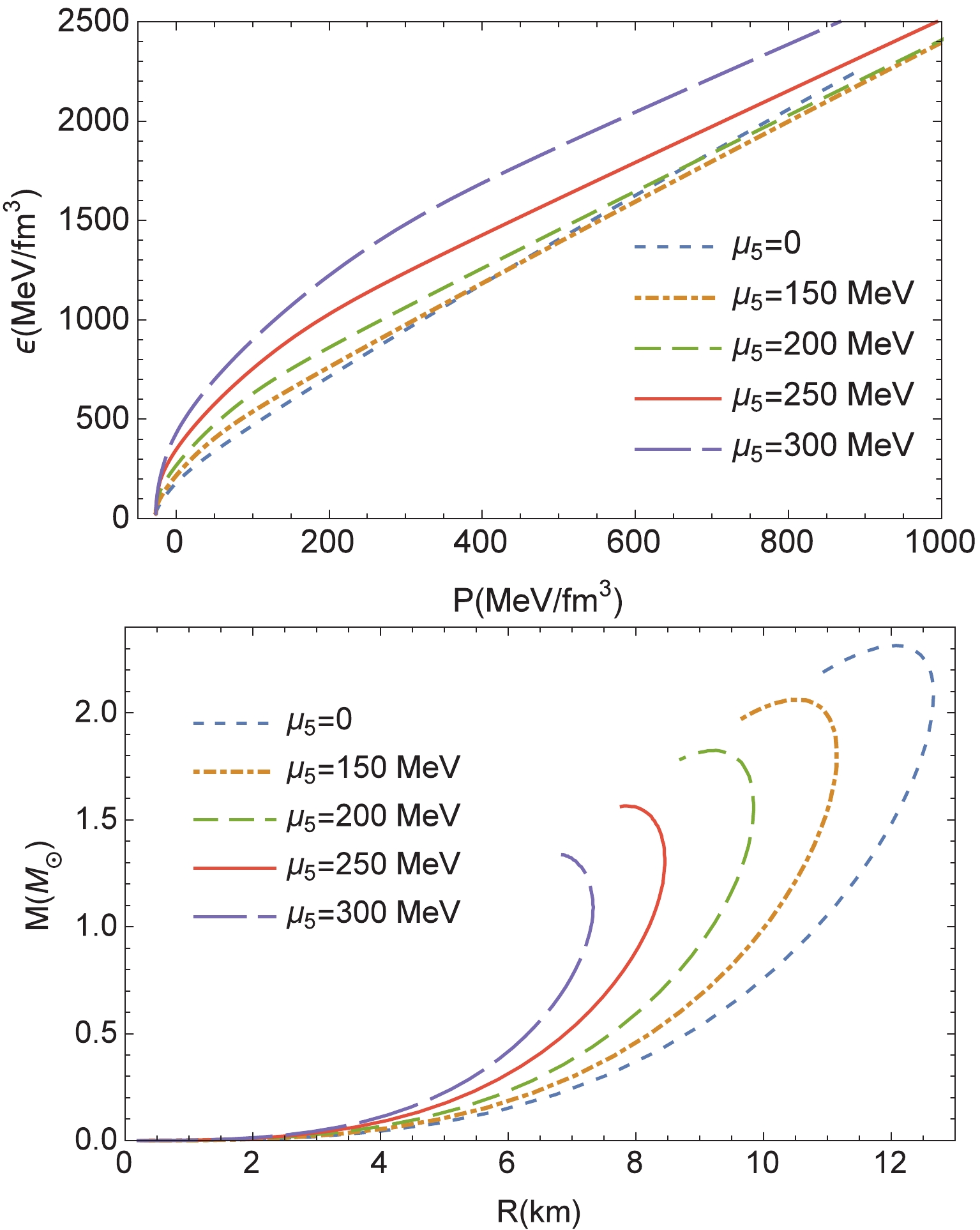
Figure 7. (color online) Influence of chiral imbalance on the EOS of quark matter and the mass-radius relationship of quark stars. The tidal deformabilities are 827.237, 421.616, 194.621, and 56.618, respectively, which decrease as
$ \mu_5 $ increases.During the merger of two compact stars, the tidal formability Λ measures the stars' quadrupole deformation in response to the companion's perturbing tidal field. Tidal deformability can be expressed via compactness
$ C = M/R $ and the Love number$ k_2 $ , where M and R represent the star mass and radius, respectively. The relationship is expressed as$ k_2 = \frac{3}{2}\Lambda\left( \frac{M}{R}\right)^5. $

(22) The method for calculating
$ k_2 $ can be found in Refs. [44, 68, 69]. In Table 1 for the quark star with mass$ 1.4M_\odot $ , the calculated results show that the tidal deformability decreases as the chiral chemical potential increases.α $ \mu_5 $ 

50 100 150 0.5 606.198 450.802 226.158 0.6 648.325 497.448 271.404 0.8 790.556 654.638 421.616 Table 1. Tidal deformability of 1.4
$ M_\odot $ quark star for different α and$ \mu_5 $ (MeV). -
The increases in both the weight factor α and chiral chemical potential
$ \mu_5 $ exhibit opposite effects on the stiffness of EOS. With the increase in α, the EOS becomes stiff, whereas with the increase in$ \mu_5 $ , EOS becomes soft. Therefore, the increase in$ \mu_5 $ will reduce the maximum mass in the mass-radius plot. A comparison of the mass-radius relationship with different α and$ \mu_5 $ values is presented in Fig. 8.
Figure 8. (color online) Mass-radius relationship for different α and
$ \mu_5 $ . When$ \mu_5 $ is fixed, the maximum mass increases with α. Lines with the same$ \mu_5 $ correspond to$ \alpha = $ 0.5, 0.6, 0.8, respectively.In addition, the increase in α will lead to the phase transition from the first-order to crossover, while
$ \mu_5 $ will trigger the transition from crossover to first-order. It seems that the effects of the two parameters may cancel each other out. When we consider them simultaneously, it is impossible determine the factor (vector channel and chiral imbalance) that plays the major role. However, the existence of$ \mu_5 $ may affect the shape of the mass-radius relationship. In other words, without considering other external parameters, but constraining EOS by the maximum mass or tidal deformability from astronomical observations, the shape of mass-radius curves by including vector and axial-vector channels may differ from the one obtained when considering only vector channels.In Fig. 9, when the maximum masses are limited to approximately 2
$ M_\odot $ , the radii corresponding to the maximum mass and the mass-radius curves remain different. For a star with a mass of 1.4$ M_\odot $ , the three curves give different radii that trigger different tidal deformabilities. Therefore, the introduction of the chiral chemical potential can ensure that the tidal deformability exhibits a right value, which indicates the effect of chiral imbalance. If we restrict the tidal deformability of a 1.4$ M_\odot $ star to the range 70$ < \Lambda(1.4 M_\odot)< $ 580 [70-72], the calculated tidal deformabilities with large α and small$ \mu_5 $ lie outside the range, as presented in Table 1. -
The chiral imbalance indicates the unequal densities of left- and right- quarks that may occur in the QGP phase. In this study, we investigated the influence of the chiral chemical potential
$ \mu_5 $ on the chiral phase transition and EOS of quark matter. Here, we adopted the two-flavor NJL model with proper-time regularisation. In addition, we infer that there is no first-order phase transition at$ \mu_5 = 0 $ in this regularization scheme. As$ \mu_5 $ increases, the first-order phase transition appears. However, the phase transition is not very strong; hence, it is difficult to determine the position of CEP. In contrast to fixed μ, the chiral phase transition corresponding to the chiral chemical potential$ \mu_5 $ is determined to be a first-order phase transition, ie., the CEP5 exists.We calculated the pseudo-critical temperature
$ T_c $ and pseudo-critical chemical potentials$ \mu_c $ as a function of$ \mu_5 $ . It was determined that these quantities increase rather than decrease with$ \mu_5 $ . In addition, we calculated the chiral susceptibility$ \chi_{\mu} $ at different temperatures. It was observed that with the increase in temperature, the peaks gradually disappeared, and only the bumps were retained. This further confirmed the existence of CEP when$ \mu_5 $ is not zero. Finally, we calculated the EOS of quark matter and determined the mass-radius relationship at different$ \mu_5 $ . The calculations indicate that the EOS becomes soft with an increase in$ \mu_5 $ .In conclusion, the chiral imbalance significantly influences the chiral phase structure of quark matter. Therefore, its careful consideration is required when determining and locating the position of CEP in future experiments.
Chiral phase transition and equation of state in chiral imbalance
- Received Date: 2021-03-26
- Available Online: 2021-08-15
Abstract: The chiral phase transition and equation of state are studied within a novel self-consistent mean-field approximation of the two-flavor Nambu-Jona-Lasinio model. In this newly developed model, modifications to the chemical μ and chiral chemical





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: