-
The odd-A Ga nuclei, which have three protons above the Z = 28 shell closure, are expected to be highly complex because they include a broken proton pair among their collectivity [1]. The systematics of the ground-state spin and nuclear moments (the magnetic and electrical quadrupole) for
$ ^{71-81} $ Ga, using collinear laser spectroscopy measurement, exhibit an abrupt structural change between N = 40 and N = 50 [2]. The ground states in the odd-A Ga isotopes have been verified to be 3/2$ ^- $ , except in 73Ga42 and 81Ga50, whose ground states were detemined to be 1/2$ ^- $ and 5/2$ ^- $ , respectively [3, 4]. For the negative-parity states in the Ga isotopes, the 3/2$ ^- $ and 5/2$ ^- $ ground states can be interpreted by the unpaired proton occupying a subshell that emerges from the$ p_{3/2} $ and$ f_{5/2} $ orbits, respectively. Other low-lying negative-parity states can be simply interpreted as the coupling of one of these configurations to the positive-parity states of the corresponding even-even cores. In addition, the 9/2+ levels are marked as the band head of the positive-parity cascade in the Ga nuclei, originating from the unpaired proton occupying the$ g_{9/2} $ orbit. The positive-parity decoupled rotational bands in$ ^{63,65,67,69} $ Ga [5-8], odd-A As [9, 10], and Br [11-14] isotopes have also been identified as particles in the$ g_{9/2} $ proton subshell, decoupling from the core under the influence of the Coriolis force. Therefore, when exciting Ga nuclei to higher energies, the breakup of neutron pairs in the$ g_{9/2} $ orbit must be considered.The low-lying levels of 71Ga have been investigated previously via Coulomb excitation [15], neutron-inelastic scattering [16], proton stripping [17], and radioactive decay [18, 19]. Information regarding the nuclear properties of the higher-spin states can be acquired from a deep-inelastic reaction [1]. Several theories have been adopted to identify the low-spin states of 71Ga, such as the Coriolis coupling [1], large scale shell [20], and projected shell models [21]. This work aims to extend the available information on excited states in 71Ga and interpret the obtained experimental data via the shell model (SM) calculations, especially the recently observed negative-parity sideband. In this study, the deduced band structures and single-particle states were analyzed using the large scale SM.
-
The experiment was performed with a 7Li beam at the HI-13 tandem accelerator of the China Institute of Atomic Energy (CIAE) at Beijing, with beam energies of 30 and 35 MeV. The high-spin states of the 71Ga were populated via the 70Zn(7Li,
$ \alpha2n $ )71Ga fusion-evaporation reaction. In the first experiment with 30 MeV beam energy, 2.15$\rm{ mg/cm^{2} }$ thick 70Zn constituted the backing on the 0.93$\rm{ mg/cm^{2}} $ Au. In the second experiment, 3.48$\rm{ mg/cm^{2}} $ thick 70Zn was evaporated on a 15.75$ \rm{mg/cm^{2}}$ Pb backing. Twelve Compton-suppressed high-purity Ge (HPGe) spectrometers and two planar HPGe detectors were used to detect the de-exciting$ \gamma $ rays of residues. The energy and efficiency calibrations of the detectors were achieved using 152Eu and 133Ba standard radioactive sources at the target position. A total of approximately 2.0 × 10$ ^8 $ coincident events were obtained, from which a symmetric$ \gamma-\gamma $ matrix was built. The level-scheme analysis was performed using the RADWARE program. To obtain information on the$ \gamma $ -rays' multipolarity, two asymmetric matrices were created by sorting the data with the detectors at all angles on one axis and the detectors at$ \sim 140^\circ $ or$ \sim 90^\circ $ on the other axis, respectively. From these two asymmetric matrices, the angular distribution orientation (ADO) ratios [22] were extracted to determine the multipolarity of the$ \gamma $ transitions. The common ADO ratio in the obtained geometry was determined to be$ \sim $ 1.1 and$ \sim $ 0.5 for stretched quadrupole and pure dipole transitions, respectively. -
The level scheme of 71Ga has been extended up to excitation energies of 4028.2 and 4165.1 keV for the positive- and negative-parity states, respectively, via the deep-inelastic reaction previously presented in [1]. In this study, approximately 14 and 9 novel
$ \gamma $ rays and levels were respectively built on a previously proposed level scheme. The properties of$ \gamma $ transitions are presented in Table 1. The novel level scheme of 71Ga established from this experiment is presented in Fig. 1. Figures 2, 3, and 4 illustrate the typical coincidence spectra for 71Ga.$E_{\rm x}$ /keV

$E_\gamma$ /keV

$I_\gamma^a$ 

$R_{\rm ADO}$ 

$I_{\rm i}^\pi \rightarrow I_{\rm f}^\pi$ 

390.5 390.5 4.3(5) 0.52(16) $1/2^- \rightarrow 3/2^-$ 

487.5 487.5 100(5) 0.63(4) $1/2^- \rightarrow 3/2^-$ 

511.5 121.0 2.9(16) 0.79(24) $3/2^- \rightarrow 1/2^-$ 

511.5 33.1(48) 0.86(10) $3/2^- \rightarrow 3/2^-$ 

964.1 452.6 3.3(14) 1.15(9) $7/2^{(-)} \rightarrow 3/2^-$ 

964.1 13.2(3) 1.22(15) $7/2^{(-)} \rightarrow 3/2^-$ 

1107.5 143.4 3.8(31) 1.26(31) $7/2^- \rightarrow 7/2^{(-)}$ 

596.0 31.7(65) 1.13(7) $7/2^- \rightarrow 3/2^-$ 

620.0 63.9(80) 0.80(20) $7/2^- \rightarrow 5/2^-$ 

1494.3 386.8 81.2(2) 0.59(6) $9/2^+ \rightarrow 7/2^-$ 

1497.5 1010.0 23.9(3) 1.24(9) $9/2^- \rightarrow 5/2^-$ 

1941.0 976.9 6.0(35) 0.95(13) $11/2^{(-)} \rightarrow 7/2^{(-)}$ 

2069.5 962.0 11.1(38) 1.11(10) $11/2^{(-)} \rightarrow 7/2^-$ 

572.0 3.7(31) 0.57(11) $11/2^{(-)} \rightarrow 9/2^-$ 

2083.1 588.8 39.1(86) 1.21(8) $13/2^+ \rightarrow 9/2^+$ 

2683.1 613.6 1.5(19) 0.67(14) $13/2^- \rightarrow 11/2^{(-)}$ 

1185.6 11.7(9) 1.22(10) $13/2^- \rightarrow 9/2^-$ 

2942.1 859.0 19.0(70) 1.15(9) $17/2^+ \rightarrow 13/2^+$ 

3034.0 1093.0 3.2(24) 1.13(22) $15/2^{(-)} \rightarrow 11/2^{(-)}$ 

3153.5 470.4 1.4(48) 0.70(32) $15/2^{(-)} \rightarrow 13/2^-$ 

1070.4 1.4(14) 0.55(12) $15/2^{(-)} \rightarrow 13/2^+$ 

1084.0 5.6(75) 1.25(21) $15/2^{(-)} \rightarrow 11/2^{(-)}$ 

3694.6 541.1 1.1(11) 0.54(26) $17/2^- \rightarrow 15/2^{(-)}$ 

1011.5 6.9(22) 1.09(18) $17/2^- \rightarrow 13/2^-$ 

3839.1 1156.0 2.2(19) 1.26(32) $17/2^{(-)} \rightarrow 13/2^-$ 

3909.1 875.1 1.2(21) 1.05(33) $ 19/2^{(-)} \rightarrow 15/2^{(-)}$ 

4028.2 1086.1 5.6(22) 1.14(19) $21/2^{(+)} \rightarrow 17/2^+$ 

4165.1 166.0 <1 $21/2^{(-)} \rightarrow 19/2^{(-)}$ 

470.5 3.6(26) 1.12(12) $21/2^{(-)} \rightarrow 17/2^-$ 

4199.5 1046.0 1.4(18) 0.96(24) $19/2^{(-)} \rightarrow 15/2^{(-)}$ 

4873.1 964.0 <1 $(23/2^-) \rightarrow 19/2^{(-)}$ 

5227.9 1199.7 2.5(32) 1.11(27) $25/2^{(+)} \rightarrow 21/2^{(+)}$ 

6573.4 1345.5 1.1(24) 1.03(32) $(29/2^+) \rightarrow 25/2^{(+)}$ 

a: Intensity is normalized to the 487.5 keV transition. Table 1. Excitation energies (
$E_{\rm x}$ ),$\gamma$ -ray energies ($E_\gamma$ ), relative$\gamma$ -ray intensities ($I_\gamma$ ), ADO ratios, and spin-parity assignments of the initial ($I_{\rm i}^\pi$ ) and final ($I_{\rm f}^\pi$ ) states in$^{71}$ Ga.
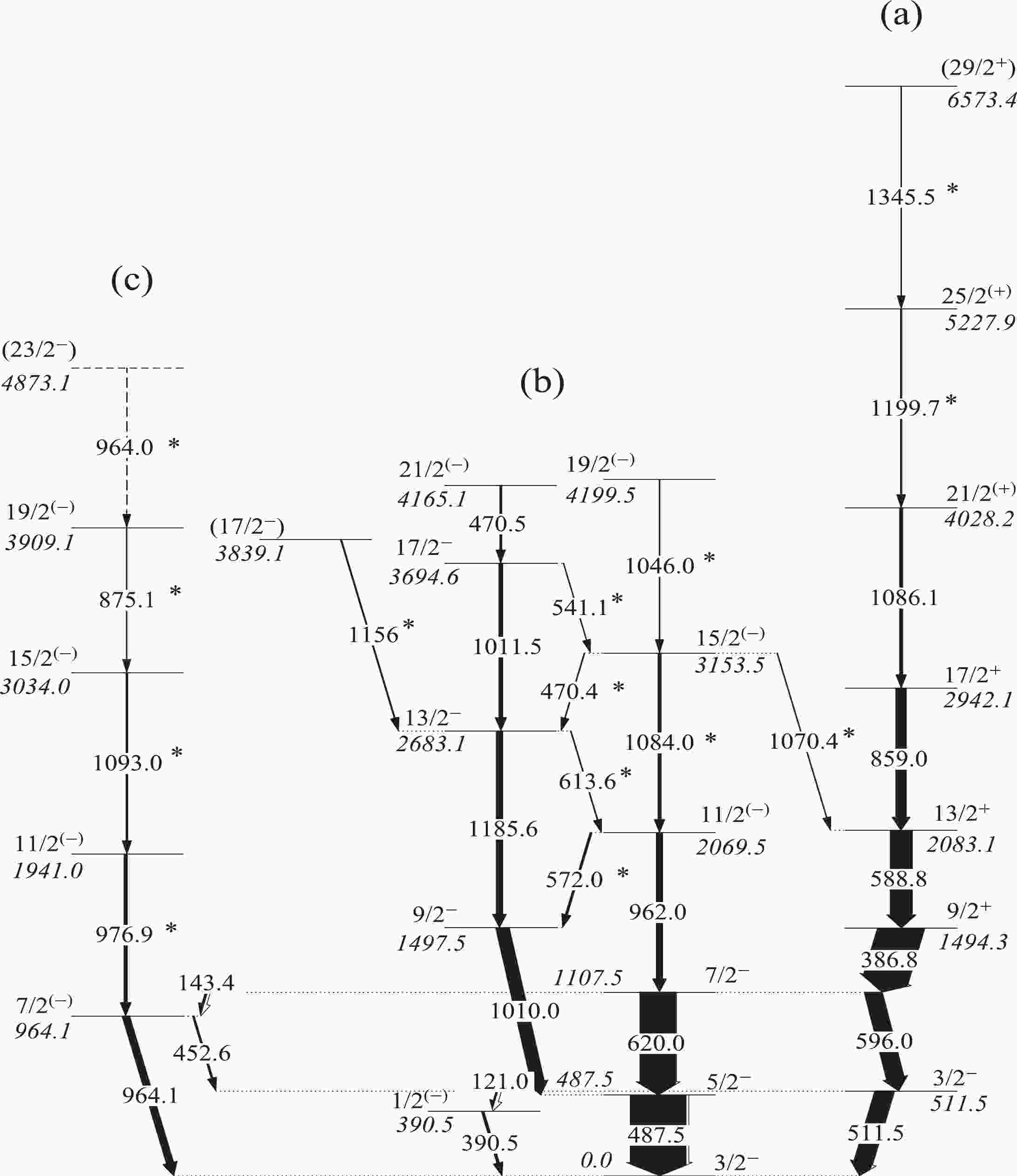
Figure 1. Level scheme of 71Ga established in this study.
$\gamma$ transitions with asterisks are observed in this study.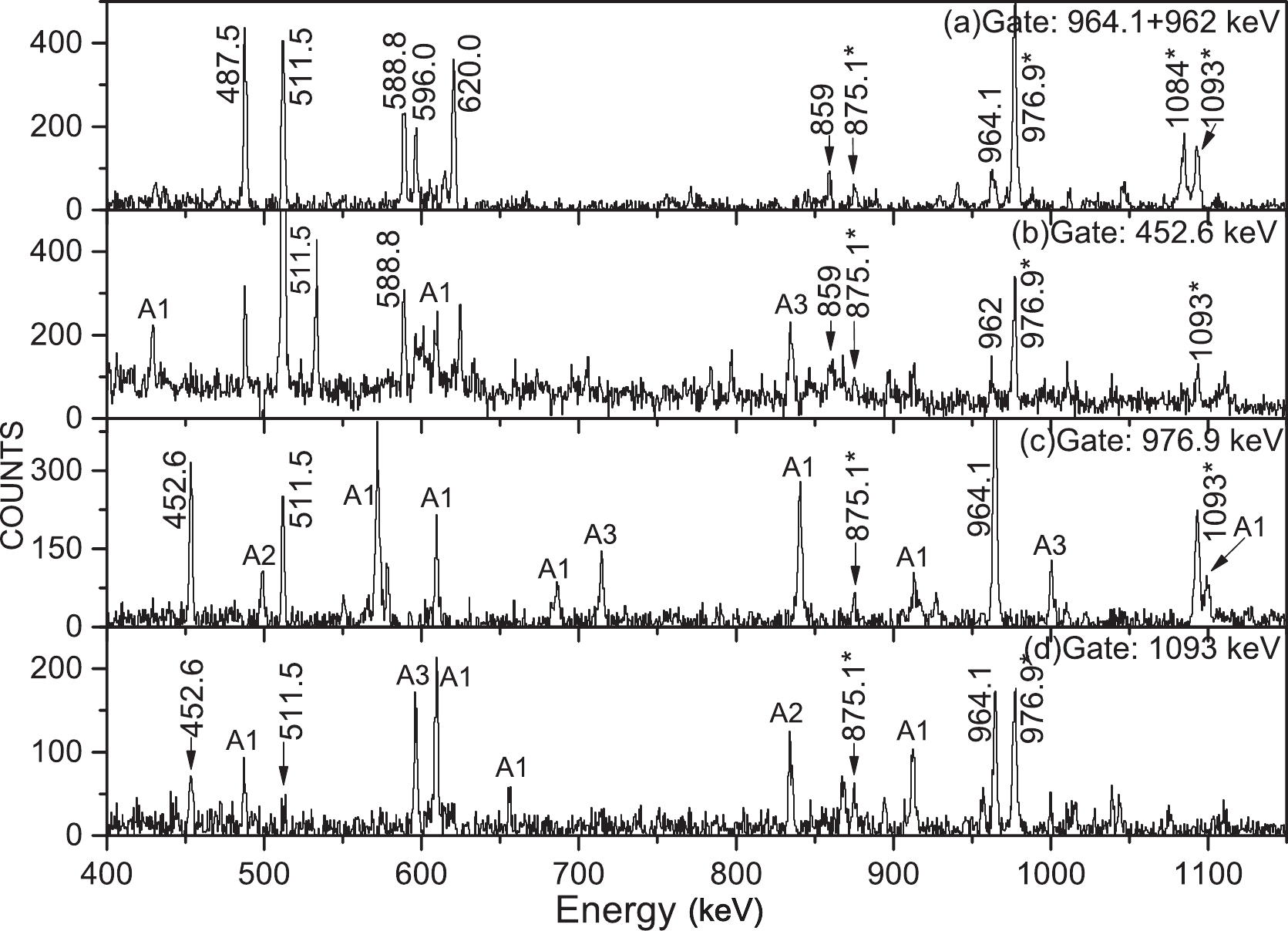
Figure 4. Gating spectra with cuts on (a) 964.1+962.0 keV, (b) 452.6 keV, (c) 976.9 keV, and (d) 1093.0 keV transitions, respectively. New transitions are indicated with asterisks. The peaks labeled as A1, A2, and A3 in the spectra originate from the contaminations of 73As [9], 74As [10], and 74Ge [23], respectively.
-
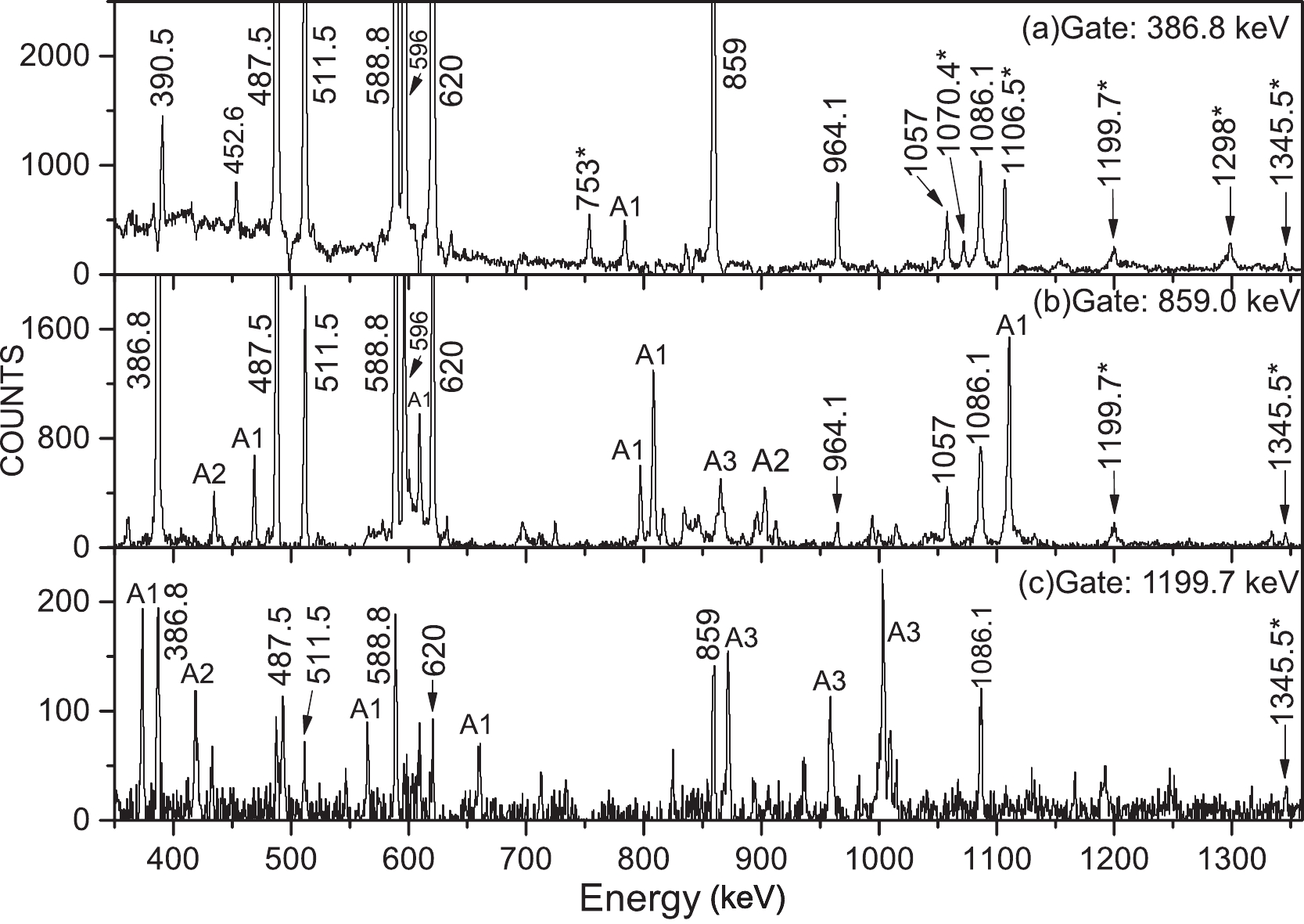
A sequence of the positive-parity cascade is presented in Ref. [1], on top of the 9/2+ level. The highest energy state is extended up to 4028.2 keV with a tentative spin assignment (21/2+). In the analysis of this study, coincidence gates positioned at 386.8- and 859.0 keV exhibited clear peaks at 1199.7 and 1345.5 keV, respectively (see Figs. 2(a) and 2(b)). These two
$ \gamma $ -rays, which were de-excited from the 5227.9 and 6573.4 keV states in the level scheme, were positioned as illustrated in Fig. 1. Furthermore, in the bottom panel of Fig. 2, the gating spectrum of the 1199.7 keV transition presents the various decay paths of the previously reported 17/2+ state. The measured ADO ratios (R$ _{\rm ADO} $ ) for these transitions indicate that they exhibit a$ \bigtriangleup I $ = 2 nature, thus suggesting$ I^{\pi} $ = 25/2+ and 29/2+, respectively. -
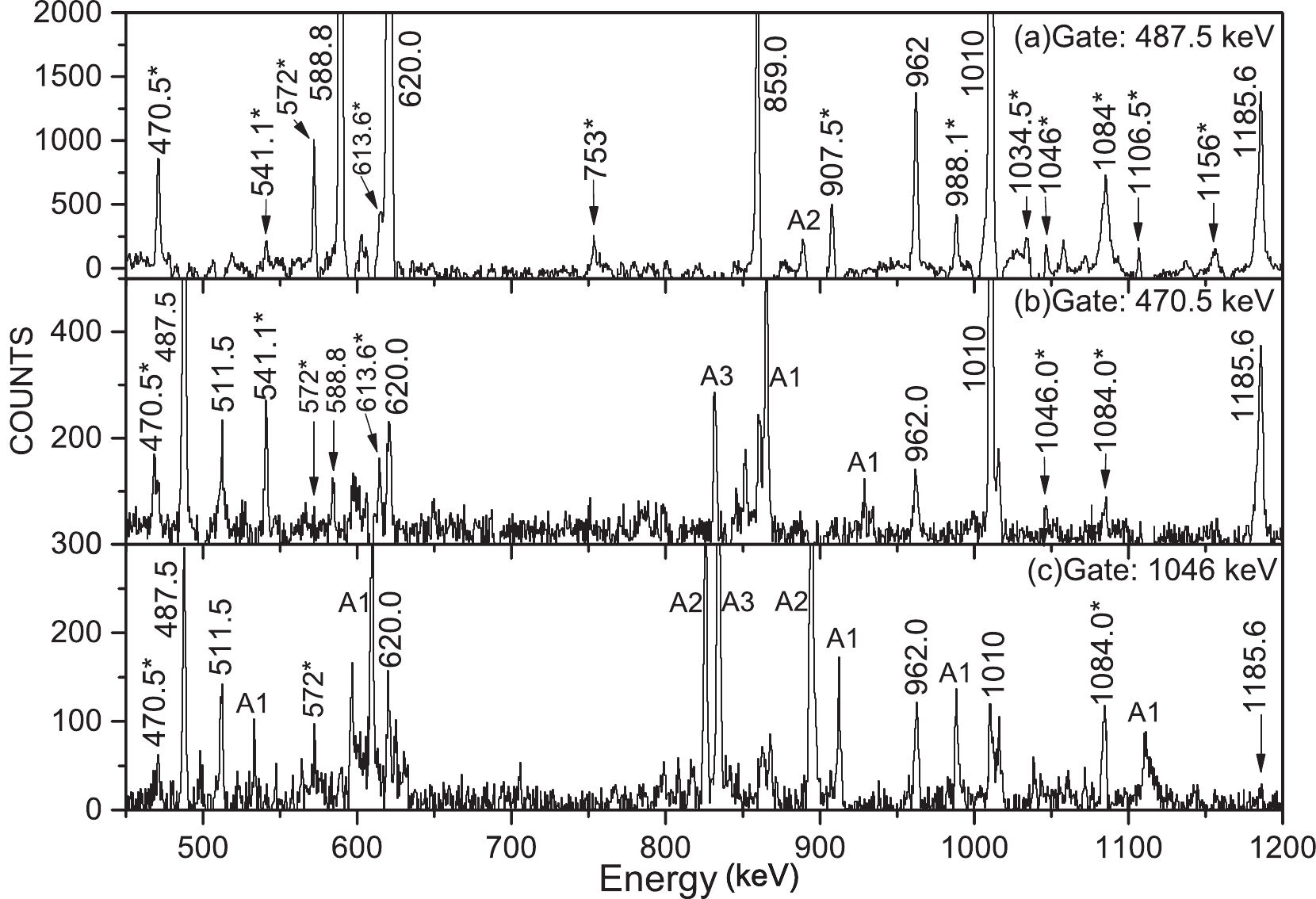
The negative-parity band (b) has been established on top of the 9/2
$ ^{-} $ level. In the top and middle panels of Fig. 3, the gating spectra of 487.5 (Fig. 3(a)), 470.5 (Fig. 3(b)), and 1046.0 keV (Fig. 3(c))$ \gamma $ transitions exhibit newly observed peaks at 572.0, 613.6, 470.4, 541.1, 1084.0, and 1046.0 keV. Based on the intensity and equality of energy, a pair cascade was arranged in the level scheme, as illustrated in Fig. 1. In Ref. [1], the spins and parity for the 7/2$ ^{-} $ state were proposed by comparing them with a similar cascade in the lighter 69Ga isotope. In this study, spins and parities of 9/2$ ^{-} $ , 11/2$ ^{-} $ , 13/2$ ^{-} $ , 15/2$ ^{-} $ , 17/2$ ^{-} $ , 19/2$ ^{-} $ , and 21/2$ ^{-} $ were determined from the ADO analysis of the decaying levels by the 1010.0, 962.0, 1185.6, 1084.0, 1011.5, and 1046.0 keV$ \gamma $ transitions, respectively. The obtaned results of such analyses for these transitions indicate an E2 character. The observed inter-band transitions of 572.0, 613.6, 470.4, and 541.1 keV, together with the ADO ratios obtained from the asymmetric matrix, verified the tentative spin and parity objectives of the band (b). -
Figs. 4(a,b) illustrate the gating spectra of 964.1 and 452.6 keV
$ \gamma $ rays, respectively. where the three peaks at 976.9, 1093.0, and 875.1 keV are clearly presented. Depending on their relative intensities, these three transitions were placed in the level scheme, as illustrated in Fig. 1. Figs. 4(c,d) present the gating spectra of 976.9 and 1093.0 keV$ \gamma $ rays, respectively. A novel negative-parity sequence (c) is established to$ I^{\pi} $ = (23/2$ ^- $ ), with another four newly observed$ \gamma $ -rays of 976.9-, 1093-, 875.1-, and 964 keV energies. The$ R_{\rm ADO} $ values of these transitions indicate that these$ \gamma $ -rays are$ \bigtriangleup I $ = 2 transitions. By comparing this sequence with the neighboring nuclei, in which similar sequence assignments have been distinguished for$ ^{63,65,67} $ Ga [5, 6] and$ ^{73,75} $ Ga [1], the parity of this sequence in this study is tentative as$ I^{\pi} $ = 11/2$ ^{(-)} $ , 15/2$ ^{(-)} $ , 19/2$ ^{(-)} $ , and (23/2$ ^- $ ), respectively. -
In this study, we focus on bands (a) and (b) and the novel sequence (c), as presented Fig. 1. The low excitation energy states of 3/2
$ ^- $ , 5/2$ ^- $ , and 9/2+ originate from the promotion of the unpaired proton into the$ p_{3/2} $ ,$ f_{5/2} $ and$ g_{9/2} $ orbits, respectively. In Ref. [1], the high-spin states, which originate from the coupling of odd protons to the yrast states of$ ^{68}_{28} $ Zn40 (even-even cores), are considered. It is suggested that the 7/2$ ^- $ , 11/2$ ^- $ , 15/2$ ^- $ , 19/2$ ^- $ , and 23/2$ ^- $ states emerge from the$ \pi p_{3/2} \otimes 2^{+} $ ,$ \pi p_{3/2} \otimes 4^{+} $ ,$ \pi p_{3/2} \otimes 6^{+} $ ,$ \pi p_{3/2} \otimes 8^{+} $ , and$ \pi p_{3/2} \otimes 10^{+} $ configurations, respectively. In addition, the 9/2$ ^- $ , 13/2$ ^- $ , 17/2$ ^- $ , and 21/2$ ^- $ states originate from the$ \pi p_{5/2} \otimes 2^{+} $ ,$ \pi p_{5/2} \otimes 4^{+} $ ,$ \pi p_{5/2} \otimes 6^{+} $ , and$ \pi p_{5/2} \otimes 8^{+} $ configurations, respectively. However, it has been suggested that the 1/2$ ^- $ state stems from the collective effects. To study the effect of proton excitations across the Z = 28 gap, as well as the configuration for all the observable states, the large scale SM calculations with the$ f_{5/2}pg_{9/2} $ and$ fpg_{9/2} $ spaces were performed via JUN45, jj44b, and fpg interactions. Recently, SM results of 71Ga via the JUN45 interaction for gallium anomaly were reported in Ref. [24].The ground states in
$ ^{71-81} $ Ga isotopes were studied by Cheal$ et\; al. $ [2] in the framework of nuclear shell models with JUN45 and jj44b interactions, and they reported abrupt structural changes between N = 40 and N = 50. Recently, Srivastava [20] performed large scale SM calculations for the low-spin structures of Ga isotopes. The projected SM results were reported by Verma$ et \; al. $ in Ref. [21]. Their calculations emphasized the substantial significance of the$ \pi f_{7/2} $ proton orbit in the model space for investigating the effect of protons excited across the Z = 28 subshell. However, the high-spin states for 71Ga have not been comprehensively studied in previous studies, owing to insufficient experimental data. As suggested in Ref. [2], we have included the proton$ f_{7/2} $ orbit in our model space, while performing SM calculations in this study.SM calculations with two different valence spaces for 71Ga have been performed to elucidate the results obtained from this study. In the first set,
$ f_{5/2}pg_{9/2} $ valence space obtained via JUN45 and JJ44b interactions were used to perform the SM calculations. As proposed in Refs. [2, 20, 21], proton excitations across Z = 28, including the proton$ f_{7/2} $ orbit, may be important in the model space. The second set of calculations was performed in the$ fpg_{9/2} $ valence space, comprising the$ 1f_{7/2} $ ,$ 2p_{3/2} $ ,$ 1f_{5/2} $ , and$ 2p_{1/2} $ proton orbits and the$ 2p_{3/2} $ ,$ 1f_{5/2} $ ,$ 2p_{1/2} $ , and$ 1g_{9/2} $ neutron orbits (with eight$ 1f_{7/2} $ frozen neutrons). This interaction, called fpg, reported by Sorlin$ et \; al. $ [25], was built using$ fp $ two-body matrix elements (TBME) from Ref. [26], and the remaining TBME from Ref. [27]. Calculations are possible if a truncation is undertaken by allowing a maximum of three particle excitations, as suggested in Ref. [20]. Here, Fig. 5 presents the experimental and calculated results. The moments (magnetic and electric quadrupole moments) for these interactions are also presented in Table 2, and the dominant wave functions (where available for the JUN45 interaction) of each state are provided in Tables 3 and 4 for all states, respectively.
Figure 5. (color online) Experimental and calculated levels in 71Ga using JUN45, jj44b, and fpg interactions.
$3/2^{-}({\rm g.s})$ 

exp JUN45 jj44b fpg $\mu $ /μN

+2.562(2) +2.188 +2.203 +2.198 $Q_{s}/{\rm eb}$ 

+0.106(3) +0.192 −0.244 +0.166 Table 2. Calculated and experimental [2] magnetic (
$\nu$ ) and electric quadrupole moments ($Q_{s}$ ) of 71Ga, theoretical predictions are included for the moments of the lowest state with the experimental nuclear spin.$I_\pi (\hbar)$ 

$E_{\rm exp}$ 

$E_{\rm cal}$ 

Wave function $\pi$ 

Partitions (%) 3/2 $^-$ 

0 0 $\pi(0, 3, 0, 0) \otimes \nu(6, 4, 2, 0)$ 

29.2% $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

13.5% 1/2 $^-$ 

390.5 478 $\pi(0, 2, 1, 0) \otimes \nu(4, 4, 2, 2)$ 

7.9% $\pi(0, 2, 1, 0) \otimes \nu(6, 4, 2, 0)$ 

5.1% 5/2 $^-$ 

487.5 388 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

16.5% $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 0, 4)$ 

9.1% $\pi(1, 2, 0, 0) \otimes \nu(6, 4, 2, 0)$ 

7.8% 3/2 $^-$ 

511.5 881 $\pi(2, 1, 0, 0) \otimes \nu(4, 4, 0, 4)$ 

8.4% $\pi(2, 1, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

5.5% 7/2 $^-$ 

964.1 1168 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

14.2% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

10.2% 7/2 $^-$ 

1107.5 1592 $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

14.4% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

9.8% 9/2 $^-$ 

1497.5 1663 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

16.2% $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 0, 4)$ 

7.9% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

4.4% 11/2 $^-$ 

1941.0 2478 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

11.8% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

9.5% 11/2 $^-$ 

2069.5 2820 $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

13.2% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

9.8% 13/2 $^-$ 

2683.1 3042 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

15.8% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

7.1% 15/2 $^-$ 

3034 3159 $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

15.5% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

5.5% $\pi(0, 3, 0, 0) \otimes \nu(6, 4, 0, 2)$ 

6.1% 15/2 $^-$ 

3153.5 3649 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 0, 4)$ 

6.7% $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

5.4% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

3.3% 17/2 $^-$ 

3694.6 3507 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

17.4% $\pi(1, 2, 0, 0) \otimes \nu(6, 4, 0, 2)$ 

7.3% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

3.8% 15/2 $^-$ 

3839.1 3764 $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

6.5% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

4.1% 19/2 $^-$ 

3909.1 4128 $\pi(0, 3, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

16.4% $\pi(0, 3, 0, 0) \otimes \nu(6, 4, 0, 2)$ 

7.2% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

4.5% 21/2 $^-$ 

4165.1 3947 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

22.1% $\pi(1, 2, 0, 0) \otimes \nu(6, 4, 0, 2)$ 

11.8% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

9.3% 19/2 $^-$ 

4199.5 4346 $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

15.9% $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

6.3% 23/2 $^-$ 

4873.1 4940 $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 1, 2)$ 

21.7% $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 2, 2)$ 

13.8% $\pi(1, 2, 0, 0) \otimes \nu(6, 4, 0, 2)$ 

4.7% Table 3. Main partition of wave functions for the negative-parity states of
$^{71}$ Ga within the JUN45 interaction in the$f_{5/2}pg_{9/2}$ configuration space. The corresponding spins and energies are also presented. Several partitions were included in the wave function of a particular state. Each partition is in the form$P$ =$\pi\big[p(1),p(2),p(3),p(4)] \otimes \nu[n(1),n(2),n(3),n(4)\big]$ , where$p(i)$ and$n(j)$ represent the number of valence protons and valence neutrons occupying the$f_{5/2}$ ,$p_{3/2}$ ,$p_{1/2}$ , and$g_{9/2}$ orbits, respectively.$I^\pi(\hbar)$ 

$E_{\rm exp}$ 

$E_{\rm cal}$ 

Wave fuction $\pi$ 

Partitions (%) 9/2 $^+$ 

1494 2478 $\pi(0, 3, 0, 0) \otimes \nu(6, 4, 1, 1)$ 

12.5% $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 2, 1)$ 

4.4% 13/2 $^+$ 

2083 2894 $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 2, 1)$ 

46.6% $\pi(0, 3, 0, 0) \otimes \nu(5, 2, 2, 3)$ 

4.2% 17/2 $^+$ 

2942 3526 $\pi(0, 3, 0, 0) \otimes \nu(5, 4, 2, 1)$ 

40.4% $\pi(0, 3, 0, 0) \otimes \nu(3, 4, 2, 3)$ 

5.6% $\pi(0, 3, 0, 0) \otimes \nu(5, 2, 2, 3)$ 

5.1% 21/2 $^+$ 

4028 4979 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 1, 3)$ 

14.2% $\pi(1, 2, 0, 0) \otimes \nu(3, 4, 2, 3)$ 

13.5% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 0, 3)$ 

8.8% 25/2 $^+$ 

5228 5869 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 1, 3)$ 

15.1% $\pi(1, 2, 0, 0) \otimes \nu(3, 4, 2, 3)$ 

8.2% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 0, 3)$ 

8.4% 29/2 $^+$ 

6573 7082 $\pi(1, 2, 0, 0) \otimes \nu(4, 4, 1, 3)$ 

16.6% $\pi(1, 2, 0, 0) \otimes \nu(3, 4, 2, 3)$ 

13.9% $\pi(1, 2, 0, 0) \otimes \nu(5, 4, 0, 3)$ 

17.6% Table 4. Main partition of wave functions for positive-parity states of 71Ga within the JUN45 interaction in the
$f_{5/2}pg_{9/2}$ configuration space.Table 2 presents the moments calculated using
$ g_{s}^{\rm eff} = 0.7 g_{s}^{\rm free} $ and electric quadrupole moments with effective charges$ e_{p}^{\rm eff} = 1.5e $ and$ e_{n}^{\rm eff} = 1.1e $ [28]. The theoretical predictions for the magnetic moments with JUN45, jj44b, and fpg interactions (+2.188, +2.203, and +2.198 μN, respectively) are approximately the experimental value (+2.562(2) μN), as well as the effective single-particle moment$g^{\rm eff}(\pi p_{3/2}) = +2.96$ μN; thus, the leading configuration of the wave function is formed by an odd number of protons occupying the$ p_{3/2} $ orbit. The sign of the quadrupole moment for 71Ga predicted by fpg interaction is correct. Corresponding to the$ fpg $ interaction, the average occupancy of$ f_{7/2} $ ,$ p_{3/2} $ ,$ f_{5/2} $ ,$ p_{1/2} $ proton orbits are 7.90, 2.80, 0.152, and 0.147, respectively. This indicates the importance of including the$ \pi f_{7/2} $ orbit in the model space. The theoretical moment value also proves that the ground state of 71Ga has a$ \pi(p^{3}_{3/2} $ ) configuration, which in the case of$ ^{67-81} $ Ga isotopes [2] is a hole configuration$ \pi(p^{-1}_{3/2}) $ , exhibits a positive quadrupole moment; however, in the case of a particle configuration of$ \pi(p^{1}_{3/2} $ ) , it exhibits a negative quadrupole moment. This suggests that the g.s. wave function of 71Ga is dominated by the$ \pi(p^{-1}_{3/2} $ ) one-quasiparticle proton configuration. In Table 3, the JUN45 interaction predicts a leading configuration$ \pi (p_{3/2}^{3}) \otimes $ $ \nu(f_{3/2}^{6} p_{3/2}^{4} p_{1/2}^{2} $ ) for the g.s., with a probability of 29.2%.In Fig. 5, these results indicate that the yrast sequence of levels includes 3/2
$ ^{-} $ , 5/2$ ^{-} $ , and 7/2$ ^- $ , which are connected with strong E2 transitions. The yrast sequences of$ I^\pi $ = 3/2$ ^{-} $ and 7/2$ ^{-} $ states indicate an origin from the$ \pi p_{3/2} \otimes 0^+ $ and$ \pi p_{3/2} \otimes 2^+ $ configurations by the Coriolis coupling model, and they are determined to have a$ \pi p_{3/2}^3 $ proton configuration in Table 3. However, the second excited state for the yrast sequence of 3/2$ ^{-} $ (E$ _{\rm exp} $ = 511.5 keV) exhibits a peculiar proton configuration that has a$ \pi(f_{5/2}^{2} p_{3/2}^{1} $ ) proton configuration. The specific change in the proton orbit configuration for the promotion of two$ \pi p_{3/2} $ valence protons into the$ \pi f_{5/2} $ orbit are significant for the formation of the second excited states. Furthermore, the 5/2$ ^{-} $ state emerges because of the$ \pi p_{5/2} \otimes 0^+ $ structure, while the 1/2$ ^{-} $ state has the$ \pi p_{1/2} \otimes 0^+ $ structure. In addition, they are inferred to be dominated by the$ \pi (f_{5/2}^1 p_{3/2}^2) \otimes \nu(f_{5/2}^4 p_{3/2}^4 p_{1/2}^2 g_{9/2}^2) $ and$ \pi(p_{3/2}^2 p_{1/2}^1) \otimes $ $ \nu(f_{5/2}^4 p_{3/2}^4 p_{1/2}^2 g_{9/2}^2 $ ) configurations, as summarized in Table 3, respectively.Similarly, the band (b) is built on 9/2
$ ^{-} $ , for which the SM calculations predict the energy levels reasonably well. The predicted level energy of this state for the JUN45 interaction is 165 keV, which is higher than the experimental value, 81 keV lower than the jj44b one, and closer to the fpg one, with a difference of only 65 keV. The main configurations of$ I^\pi $ = 9/2$ ^{-} $ , 13/2$ ^{-} $ , 17/2$ ^{-} $ , and 21/2$ ^{-} $ states are dominated by$ \pi(f_{5/2}^1 p_{3/2}^2) \otimes \nu(f_{5/2}^4 p_{3/2}^4 p_{1/2}^2 g_{9/2}^2 $ ) configurations via the calculation of the JUN45 interaction. These sequences appear to emerge from the coupling of the$ f_{5/2} $ proton with the levels expected from a broken pair of$ g_{9/2} $ neutrons. In contrast, the calculated signature splitting of 11/2$ ^{-} $ , 15/2$ ^{-} $ , and 19/2$ ^{-} $ for the band (b) cascade agrees well with the experimental results, and has a mixed configuration dominated by$ \pi(f_{5/2} p_{3/2})^3 $ configurations.A novel sequence (c) is built on the 3/2
$ ^{-} $ state in the experiment, with predicted states 7/2$ ^{-} $ , 11/2$ ^{-} $ , 15/2$ ^{-} $ , 19/2$ ^{-} $ , and 23/2$ ^{-} $ at 1162, 2132, 2955, 3482, and 4387 keV from the fpg interaction, while its corresponding experimental values are 964, 1941, 3034, 3909, and 4873 keV, respectively. In Table 3, the novel sequence (c) is predicted to be dominated by$ \pi(f_{5/2} p_{3/2})^3 \otimes \nu(f_{5/2}^4 p_{3/2}^4 p_{1/2}^2 g_{9/2}^2 $ ) configurations except for 3/2$ ^{-} $ , which is dominated by$ \pi(p_{3/2}^3) \otimes $ $ \nu(f_{5/2}^6 p_{3/2}^4 p_{1/2}^2 $ ) configurations. Possible configurations for the 3/2$ ^{-} $ state involve unpaired protons occupying the negative-parity$ p_{3/2} $ orbit (favored signature$ \alpha $ = -1/2), coupled with positive-parity states for$ ^{68}Zn_{40} $ . A feasible way for these configurations to gain higher spins is by an excited neutron pair entering into the$ g_{9/2} $ orbit from the$ f_{5/2} $ orbit.As illustrated on the right side of Fig. 5, the calculated energies of the positive-parity states, which adopt the 9/2+ level as the reference ground state, agree well with the experimental results. To coincide the levels and configurations for the JUN45 interaction with the observed experimental values, it is assumed that the levels of
$ I^{\pi} $ = 17/2+ (E$ _{\rm exp} $ = 2942.1 keV) and$ I^{\pi} $ = 25/2+ (E$ _{\rm exp} $ = 5227.9 keV) are in the second excited states. As presented in Fig. 5, the level energies of the positive-parity states are reproduced well within the$ f_{5/2}pg_{9/2} $ space of the JUN45 and jj44b interactions; the maximum deviation is just 205.0 keV for the$ I^{\pi} $ = 25/2$ ^{(+)} $ state. However, for the states above$ I^{\pi} $ = 21/2$ ^{(+)} $ (E$ _{\rm exp} $ = 4028.1 keV), the predicted level energies calculated within the$ f_{5/2}pg_{9/2} $ and$ fpg_{9/2} $ configuration spaces diverge significantly, and adopting the$ fpg_{9/2} $ configuration space with the fpg interaction causes an energy difference of approximately 1.0 MeV. Furthermore, the deviation increases as the angular momentum increases. The extent of discrepancy between the experimental results and theoretical prediction depends on the number of neglected configurations that are contributed to the wave function of the states. Neglecting a dominant configuration would make the predicted level energy considerably higher than the observed one [29]. Therefore, the energy disparity between the presented experiment and theory above$ I^{\pi} $ = 21/2$ ^{(+)} $ is probably owing to the impact of the particle pairs that are not considered in the SM calculations.From the results for the JUN45 interaction in Table 4, the band head of the 9/2+ state is dominated by
$ \pi(p_{3/2}^3) \otimes $ $ \nu(f_{5/2}^6 p_{3/2}^4 p_{1/2}^1 g_{9/2}^1 $ ),$ \pi(p_{3/2}^3) \otimes \nu(f_{5/2}^5 p_{3/2}^4 p_{1/2}^2 g_{9/2}^1 $ ) configurations, as well as by the corresponding partitions of 12.5% and 4.4%. The$ I_{\pi} $ = 13/2$ ^{(+)} $ and$ I_{\pi} $ = 17/2$ ^{(+)} $ states are determined to be dominated by the$ \pi(p_{3/2}^3)\! \otimes \! \nu(f_{5/2}^5 p_{3/2}^4 p_{1/2}^2 g_{9/2}^1 $ ) configuration; however, the three main components of the wave function configurations for all the sates from 21/2+ to 29/2+ are$ \pi(f_{5/2}^1 p_{3/2}^2) \otimes $ $ \nu(f_{5/2}^4 p_{3/2}^4 p_{1/2}^1 g_{9/2}^3 $ ),$ \pi(f_{5/2}^1 p_{3/2}^2) \otimes $ $ \nu(f_{5/2}^3 p_{3/2}^4 p_{1/2}^2 g_{9/2}^3 $ ), and$ \pi(f_{5/2}^1 p_{3/2}^2) $ $ \otimes $ $ \nu(f_{5/2}^5 p_{3/2}^4 g_{9/2}^3 $ ), in which the number of particles in the orbits and their partitions are also very close. It is worth noting that the change in dominant configuration is at approximately$ I_{\pi} $ = 25/2+, at which one proton is excited to the$ f_{5/2} $ orbit from the$ p_{3/2} $ orbit, and two neutrons are excited to the$ g_{9/2} $ orbit from the$ f_{5/2} $ and$ p_{1/2} $ orbits. -
In this study, the high-spin states of 71Ga were studied via the 71Zn(7Li,
$ \alpha2n $ )71Ga reaction. The level scheme was established up to a spin and excitation energy of$ I^\pi = (29/2^{+}) $ and 6.6 MeV, respectively. Additional 9 levels and 14 transitions were assigned to 71Ga. Two bands and a novel negative-parity sequence were identified. Accordingly, the observed sequences indicate that the level structures of the 71Ga exhibit a typical particle-core coupling pattern, which can be explained as single-particle excitations coupling to the positive-parity states of$ ^{68}_{28} $ Zn40 (even-even cores).Large-basis SM calculations were performed to interpret the experimental level structures of the 71Ga. The ground state of 3/2
$ ^- $ is dominated by the$ \pi(p_{3/2}^3) \otimes $ $ \nu(f_{5/2}^{6} p_{3/2}^{4} p_{1/2}^{2} $ ) configuration; the main configurations of the$ I^\pi $ = 5/2$ ^- $ , 9/2$ ^- $ , 13/2$ ^- $ , 17/2$ ^- $ , and 21/2$ ^- $ states and the$ I^\pi $ = 7/2$ ^- $ , 11/2$ ^- $ , 15/2$ ^- $ , 19/2$ ^- $ , and 23/2$ ^- $ states are dominated by$ \pi(f_{5/2}p_{3/2}^{2}) \otimes \nu(f_{5/2}^4 p_{3/2}^{4} p_{1/2}^{2} g_{9/2}^{2} $ ) and$ \pi(f_{5/2} p_{3/2})^{3} \otimes $ $ \nu(f_{5/2}^{4} p_{3/2}^{4} p_{1/2}^{2} g_{9/2}^{2} $ ) configurations, respectively. These configurations indicate that gaining higher spins for negative-parity states would require the promotion of the$ p_{3/2} $ unpaired proton into the$ f_{5/2} $ or$ p_{3/2} $ orbits, as well as the coupling of a broken pair of$ g_{9/2} $ neutrons while exciting a neutron pair into the$ g_{9/2} $ orbit from the$ f_{5/2} $ orbit. The alignment of one$ g_{9/2} $ neutron pair leading to the dominant configuration for positive-parity states indicates a significant change, in which one proton is excited to the$ f_{5/2} $ orbit from the$ p_{3/2} $ orbit, and two neutrons are excited to the$ g_{9/2} $ orbit from the$ f_{5/2} $ and$ p_{1/2} $ orbits. -
The authors would like to thank the crew of the HI-13 tandem accelerator at the China Institute of Atomic Energy for the steady operation of the accelerator. SM calculations were performed at the Prayag computational facility at IIT-Roorkee.
High spin states in 71Ga
- Received Date: 2021-02-16
- Available Online: 2021-08-15
Abstract: Excited states in the odd-A nucleus 71Ga have been studied via the 70Zn(7Li,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: