-
Double-
$ \beta $ decay is a type of nuclear radioactive decay process in which two electrons (or positrons) and/or two neutrinos (antineutrinos) are emitted [1]. Owing to the small probability of its occurrence, double-$ \beta $ decay is the rarest known radioactive decay. Depending on the emitted number of neutrinos or antineutrinos, it can be classified into two processes: ordinary two-neutrino double-$ \beta $ decay ($ 2\nu\beta\beta $ ) and neutrinoless double-$ \beta $ decay ($ 0\nu\beta\beta $ ). The occurrence of neutrinoless double-$ \beta $ decay requires that the neutrinos contain a small fraction of massive particles equal to its antiparticles (Majorana neutrino) [2, 3]. As a result, the lepton number is not conserved in$ 0\nu\beta\beta $ decay. Because of its basic importance to particle physics, the research for$ 0\nu\beta\beta $ decay has been a subject of intensive theoretical and experimental activities over the past several decades [4-23]. Neutrinoless double-$ \beta $ decay in$ ^{76} $ Ge was reported in 2011 [24]. However, the result was not consistent with other experimental studies [25, 26] and was not widely accepted by the nuclear physics community.The
$ 2\nu\beta\beta $ decay mode is permitted by conservation laws and can be considered to be a second-order process compared with regular$ \beta $ -decays [11, 12]. To date,$ 2\nu\beta\beta $ decay modes have been observed in only twelve isotopes (including double electron capture in$ ^{130} $ Ba observed in 2001 [27]), and all have a mean lifetime of over$ 10^{18} $ yr. The experimental measurements of$ 2\nu\beta\beta $ decay provide important data that aid theorists in calibrating their models and extracting nuclear structure information that can be used in$ 0\nu\beta\beta $ decay calculations.Theoretically, the calculation of
$ 2\nu\beta\beta $ decay half-life primarily depends on the phase-space factor and nuclear matrix elements. The phase-space factor has been investigated extensively and can now be calculated with very high precision [23, 28]. Sophisticated microscopic models based on the shell model or quasi-particle random-phase approximation (QRPA) or self-consistent renormalized random-phase approximation (RQRPA) have been used to calculate the transition matrix and, consequently, the$ 2\nu\beta\beta $ decay half-lives [22, 23, 28, 29]. These calculations have been very successful in describing experimental$ 2\nu\beta\beta $ decay half-lives in general. However, owing to the inherent complexity of the nuclear multi-body problem, the calculated$ 2\nu\beta\beta $ decay half-lives are model dependent (interaction and model space dependent) and remain a challenge for different models to generate similar predictions in many scenarios. Recently, Ren et al. proposed an empirical formula to calculate the$ 2\nu\beta\beta $ decay half-lives [30]. The new formula indicates that the logarithms of the half-lives are inversely proportional to the$ 2\nu\beta\beta $ decay energies, and it adequately describes available experiment data. However, extracting this empirical formula from traditional double-$ \beta $ decay theory is difficult, and its physical origin remains unclear.Based on a nucleon-lepton interaction without conservation of parity, Primakoff and Rosen primarily focused on the form factor and obtained a simple formula, which includes only the atomic number and decay energy, to calculate the
$ 2\nu\beta\beta $ decay half-lives in the two-step framework of$ 2\nu\beta\beta $ decays. This formula is very useful and was successful in calculating the$ 2\nu\beta\beta $ decay half-lives over past decades. However, with time, more experimental data of$ 2\nu\beta\beta $ decays half-lives was collected [6], and this formula was observed to not accurately reproduce the experimental data. Therefore, we reinvestigate the Primakoff-Rosen formula in this paper based on the systematics of experimental$ 2\nu\beta\beta $ decay half-lives. By considering nuclear shell effects empirically and refining the energy dependence of the phase factor, an improved Primakoff-Rosen (IPR) formula is proposed to calculate the$ 2\nu\beta\beta $ decay half-lives.$ 2\nu\beta\beta $ decay half-lives calculated using this improved formula closely match experimental data, which suggests that this improved formula is useful for analyzing experimental data simply and transparently. Finally, we compare the predictions from this improved formula with other theoretical models or empirical formulae and propose further measurements to distinguish different theoretical scenarios for$ 2\nu\beta\beta $ decays. -
From the general time-dependent perturbation formalism, the double-
$ \beta $ transition probabilities are proportional to the square moduli of the corresponding double-$ \beta $ transition matrix elements [11, 12]:$ \begin{aligned}[b]& <\beta^{\mp}\beta^{\mp};(A,Z\pm2)|(A,Z)> \\=& \sum\limits_{v}\frac{<\chi_{f}^{*}\Psi_{f}^{*}|H_{D}|\Psi_{v}\chi_{v}><\chi_{v}^{*}\Psi_{v}^{*}|H_{D}|\Psi_{i}\chi_{i}>}{E_{v}-E_{i}}. \end{aligned}$

(1) Here,
$ H_{D} $ is nucleon-lepton interaction Hamiltonian density;$ \chi_{i} $ ,$ \chi_{f} $ , and$ \chi_{v} $ are the wave functions (in occupation number space) of the initial, final, and “intermediate” states of the lepton field, respectively;$ \Psi_{i} $ ,$ \Psi_{f} $ , and$ \Psi_{v} $ are the wave functions, in configuration space, of the states of the parent (A, Z), daughter (A,$ Z\pm2 $ ), and “intermediate or virtual” (A,$ Z\pm1 $ ) nuclei, respectively;$ E_{i} $ is the energy of the initial state of the nucleon-lepton system, and$ E_{v} $ is the energy of the vth “intermediate” state [11, 12]. In 1959, Primakoff and Rosen obtained the following analytic expressions to calculate the half-lives of$ 0^{+}\longrightarrow0^{+} $ $ 2\nu\beta^{\mp}\beta^{\mp} $ decays [11, 12]:$ T_{1/2} \simeq 6\times 10^{19\pm2}_{\ }G_{ \rm{int\ }}F_{ \rm{Coul}}\left(\frac{8m_{ \rm{e}}c^{2}}{Q_{2\beta}}\right)^{10} \rm{yr}, $

(2) $ G_{ \rm{int}} = \left(\frac{\Delta E}{10 m_{ \rm{e}}c^{2}}\right)^2 = \left(\frac{m_{ \rm{w}}c^{2} + m_{ \rm{e}}c^{2}-m_{ \rm{i}}c^{2}+0.5Q_{2\beta}}{10 m_{ \rm{e}}c^{2}}\right)^2, $

(3) $ F_{ \rm{Coul}} = \left(\frac{60}{Z}\right)^2\left(1-\exp\left(\mp\frac{2\pi Z}{137}\right)\right)^{2} . $

(4) In Eqs. (2)-(4),
$ \Delta E = m_{ \rm{w}}c^{2}+ m_{ \rm{e}}c^{2}-m_{ \rm{i}}c^{2}+0.5Q_{2\beta} $ is the energy difference between intermediate and initial states [23, 31-36];$ m_{ \rm{i}} $ ,$ m_{ \rm{w}} $ ,$ m_{ \rm{d}} $ , and$ m_{ \rm{e}} $ are the rest masses of the parent (A, Z), intermediate (A,$ Z\pm1 $ ), and daughter (A,$ Z\pm2 $ ) nuclei and electrons, respectively;$ Q_{2\beta} = m_{ \rm{i}}c^{2} - m_{ \rm{d}}c^{2}-2m_{ \rm{e}}c^{2} $ is the double-$ \beta $ decay energy. The double-$ \beta $ decay energies can be calculated from the Ame2012 atomic mass evaluation [37].$ F_{ \rm{Coul}} $ is a factor related to the Coulomb corrections resulting from the effect of the Coulomb field of a daughter nucleus on the emitted electrons or positrons.We calculated the
$ 2\nu\beta^{-}\beta^{-} $ -decay half-lives of the eleven known nuclei using Eqs. (2)-(4) and the results are shown in Table 1. In the calculation, we used a constant coefficient of$ 6\times 10^{19} $ instead of$ 6\times 10^{19\pm2} $ for Eq. (1). Although the discrepancies between experimental and calculated data are within two orders of magnitudes, the agreement with experiment data is insuficient. Note that a constant was used for effective nuclear matrix elements in the Primakoff-Rosen formula [11, 12]. Another approximation is that the formula only maintained the highest term ($ Q_{2\beta}^{10} $ ) for phase-space integration and the lower-order terms were neglected.Nuclei $Q_{2\beta}$ /MeV

$T_{1/2}(\mathrm{exp})$ (Ey)

$T_{1/2}(\mathrm{PR})$ (Ey)

$T_{1/2}(\mathrm{IPR})$ (Ey)

$T_{1/2}(\mathrm{IPR})$ /

$T_{1/2}(\mathrm{exp})$ 

$T_{1/2}(\mathrm{Ren})$ (Ey)

$^{48}$ Ca

4.267 $ 43.9 \pm 5.8 $ 

16.7 46.7 $ 1.06 \pm 0.14 $ 

71.8 $^{76}$ Ge

2.039 $ 1430 \pm 530 $ 

$1.89\times10^{4}$ 

2182 $ 1.53 \pm 0.57 $ 

504 $^{82}$ Se

2.996 $ 91.9 \pm 7.6 $ 

254 46.4 $ 0.51 \pm 0.04 $ 

66.4 $^{96}$ Zr

3.349 $ 21.6 \pm 2.6 $ 

61.3 12.8 $ 0.59 \pm 0.07 $ 

38.6 $^{100}$ Mo

3.034 $ 6.98 \pm 0.44 $ 

192 35.64 $ 5.11 \pm 0.32 $ 

54.7 $^{116}$ Cd

2.813 $ 28.9 \pm 2.5 $ 

416 70.7 $ 2.45 \pm 0.21 $ 

68.2 $^{128}$ Te

0.867 $ (3.49 \pm 1.99)\times10^{6} $ 

$3.92\times10^{7}$ 

$1.63\times10^{6}$ 

$ 0.47 \pm 0.27 $ 

$7.45\times10^{5}$ 

$^{130}$ Te

2.528 $ 714 \pm 104 $ 

873 130 $ 0.18 \pm 0.03 $ 

103 $^{136}$ Xe

2.458 $ 2340 \pm 130 $ 

671 968 $ 0.41 \pm 0.02 $ 

743 $^{150}$ Nd

3.371 $ 8.37 \pm 0.45 $ 

43.3 9.13 $ 1.09 \pm 0.06 $ 

29.72 $^{238}$ U

1.144 $ 2000 \pm 600 $ 

$1.66\times10^{5}$ 

9619 $ 4.81 \pm 1.44 $ 

10351 Table 1. Experimental
$ 2\nu\beta^{-}\beta^{-} $ decay half-lives (column 3) and calculated values using the Primakoff-Rosen formula (Eqs. (2)-(4), column 4), the IPR formula (Eq. (6), column 5), and from Ren et al. [30] (column 7). 1 Ey =$ 10^{18} $ years. -
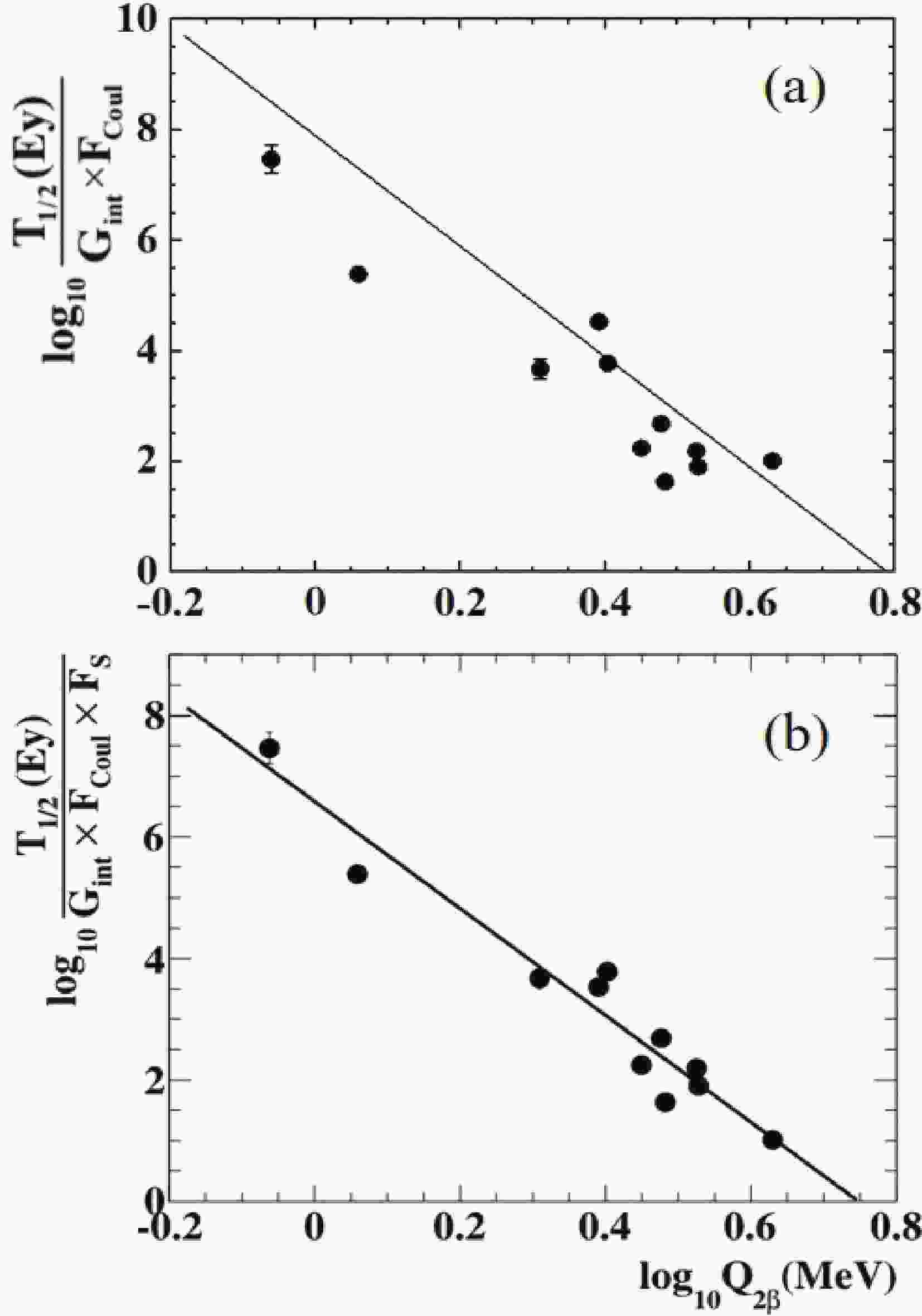
In Fig. 1(a), we plot the scaled
$ 2\nu\beta\beta $ -decay half-lives$ T_{1/2}/(G_{ \rm{int\ }}F_{ \rm{Coul}} $ ) (in$ \log_{10} $ -scale) as a function of decay energy. To demonstrate the ability of Eq. (2) to reproduce experimental data, the line represented by Eq. (2) is also plotted in Fig. 1(a). As shown in Fig. 1(a), there is a systematic deviation between the theoretical line and these data points. In other words, Eq. (2) does not accurately reproduce the experimental data. This systematic deviation means that the parameters in Eq. (2) require further optimization.
Figure 1. (a) Correlation of scaled
$2\nu\beta\beta$ decay half-lives (in$\log_{10}$ -scale) and decay energies in$\log_{10}$ -scale. The line represents Eq. (2). (b) Same as panel (a) with the line representing a linear fit to the data. Only when the neutron number of parent nuclei is a magic number (2, 8, 20, 28, 50, 82, 126),$F_{\rm{S}}$ is equal to 10. When it is not a magic number,$F_{\rm{S}}$ is equal to 1.These experimental data [6] may be used to constrain and optimize the parameters used in the Primakoff-Rosen formula. Eq. (2) indicates a power-law dependence of
$ 2\nu\beta\beta $ -decay half-lives on the$ 2\nu\beta\beta $ decay energies. To indicate exactly the decay energy dependence on the power law, we plot the correlation of the scaled$ 2\nu\beta\beta $ -decay half-lives$ T_{ \rm{corr}} = T_{1/2}/(G_{ \rm{int\ }}F_{ \rm{Coul}}F_{ \rm{S}} $ ) (in$ \log_{10} $ -scale) and decay energies in$ \log_{10} $ -scale in Fig. 1(b).$ F_{ \rm{S}} $ is introduced to account for the shell effects on nuclear transition matrix elements and, consequently, on the half-lives. Empirically, only when the neutron number of parent nuclei is a magic number (2, 8, 20, 28, 50, 82, 126) is$ F_{\rm{S}} $ equal to 10. When it is not the magic number,$ F_{\rm{S}} $ is equal to 1. With the$ F_{ \rm{S}} $ value, a good linear correlation with respect to the decay energies can be determined. The$ F_{ \rm{S}} $ value can be observed to obtain a good description of$ 2\nu\beta\beta $ -decay half-lives in the following calculation. Note when the neutron numbers of parent nuclei are close to major shell or subshell closures, systematical deviations from the exponential law occur [38, 39]. The shell effect generally decreases the transition probabilities and increases the$ \beta $ -decay half-lives. Similarly, we may expect that the shell effect also decreases nuclear transition matrix elements for$ 2\nu\beta\beta $ -decays. Ren et al. [30] used a factor of S in their formula to quantify the effect of nuclear shell structure on$ 2\beta $ -decay half-lives.Fig. 1(b) shows that the data indicate a linear relationship between
$ \log_{10}T_{ \rm{corr}} $ and$ \log_{10}Q_{2\beta} $ , which indicates a power-law between$ T_{ \rm{corr}} $ and decay energies. With a linear function, we obtain the following formula:$ \log_{10}T_{ \rm{corr}} = \log_{10}\frac{T_{1/2}}{G_{ \rm{int\ }}\times F_{ \rm{Coul}} \times F_{ \rm{S}}} = c_{1}\log_{10}Q_{2\beta}+c_{2}. $

(5) Here,
$ c_{1} $ and$ c_{2} $ are two fitting parameters, and$ T_{2\beta} $ and$ Q_{2\beta} $ are in units of Ey and MeV, respectively. With a least-square fit, we obtain the parameters of$c_{1} = $ $ -8.8024\pm0.2266$ and$ c_{2} = 6.5850\pm0.1072 $ . From Fig. 1(b), it can be seen that this linear fit can closely describe experimental data. Instead of the power law of$ T_{ \rm{corr}}\propto $ $ Q^{-10}_{2\beta} $ in Eq. (2), we obtain a power law of$ T_{ \rm{corr}}\propto Q^{-8.8}_{2\beta} $ , which describes the data better. As Primakoff and Rosen stated [11, 12], “The proportionality of the half-lives in equation (80) to$ (\epsilon^{(0)})^{-10} $ arises from a very rough approximation for the integral of$ P^{\prime}\left(\epsilon_{1}\right) $ in equation (71).” Here, equation (80) refers to Eq. (2) in this paper,$ \epsilon^{(0)} $ is the decay energy, and equation (71) refers to the phase-space integration. This integration contains both the 10th power term of the decay energy and the lower power terms of the decay energy. These energy terms in the integration result form a polynomial of decay energy. However, in their formula (Eq. (2)), only one term$ Q^p $ (the power$ p = -10 $ ) is used to approximately replace this energy polynomial.The power p can also be obtained by fitting experimental data. The power p is equivalent to the parameter
$ c_1 $ in Eq. (5). Therefore, we use Eq. (5) to fit the experimental data, and the power p can be determined:$ p = c_1 = -8.8024 $ .In common with
$ T_{ \rm{corr}}\propto Q^{-10}_{2\beta} $ ,$ T_{1/2}\propto Q^{c_{1}}_{2\beta} $ in Eq. (5) is also an approximate expression. However, the power$ c_1 $ is determined by fitting experimental data, which is different from the approximate process by Primakoff and Rosen. Therefore, the change of the power$ c_1 $ from -10 to -8.8 is attributed to the transformation in the selection method. This transformation also makes the relationship ($ T_{1/2}\propto Q^{p}_{2\beta} $ ) more effective in describing the dependence of$ 2\nu\beta^{-}\beta^{-} $ decay half-lives on decay energy.In the phase space integral, the decay energy contains not only one term (
$ Q^{-10} $ ), but also other lower power terms. This can cause an adjustable parameter$ c_2 $ to appear in Eq. (5), which is also used to adjust the dependence of the half-lives on the decay energy. Additionally, a constant matrix element is used in the Primakoff-Rosen formula, and this formula can not closely describe the experimental data. The existence of parameter$ c_2 $ can also adjust the constant matrix element to make the corresponding half-lives more consistent with the experimental data. In summary, parameter$ c_2 $ has two main functions: adjusting the constant matrix element and further coordinating the relationship between the half-lives and the decay energy. This is the meaning of the existence of parameter$ c_2 $ . Our newly obtained parameters can better reflect the decay energies dependence of$ T_{ \rm{corr}} $ . We note that Pritychenko observed$ T_{1/2}\propto Q^{-8}_{2\beta} $ from the$ 2\nu\beta\beta $ -decay half-lives of$ ^{128} $ Te and$ ^{130} $ Te [3].Based on Eq. (5), we can calculate the
$ 2\beta $ -decay half-lives using the following IPR formula:$ T_{1/2} = 10^{c_{2}}\times G_{ \rm{int\ }}\times F_{ \rm{Coul}} \times F_{ \rm{S}}\times Q_{2\beta}^{c_{1}}. $

(6) The numerical results are shown in Table 1, which in columns 5 and 6, shows that the ratios between calculated
$ 2\nu\beta\beta $ -decay half-lives and experimental ones are within a factor of 6 for all nuclei. The standard deviation$ \sigma $ and average deviation$ \Delta $ between the logarithms of the calculated and experimental$ 2\nu\beta\beta $ -decay half-lives are used to denote the reliability of the formula, which can be expressed as [38, 39]$ \sigma= \sqrt{\frac{1}{K} \sum \limits_{i = 1}^K [\log_{10}T_{1/2}^{i}(\mathrm{calc})-\log_{10}T_{1/2}^{i}(\mathrm{exp})]^{2}},$

(7) $ \Delta = \frac{1}{K} \sum \limits_{i = 1}^K |\log_{10}T_{1/2}^{i}( \rm{calc})-\log_{10}T_{1/2}^{i}( \rm{exp})|. $

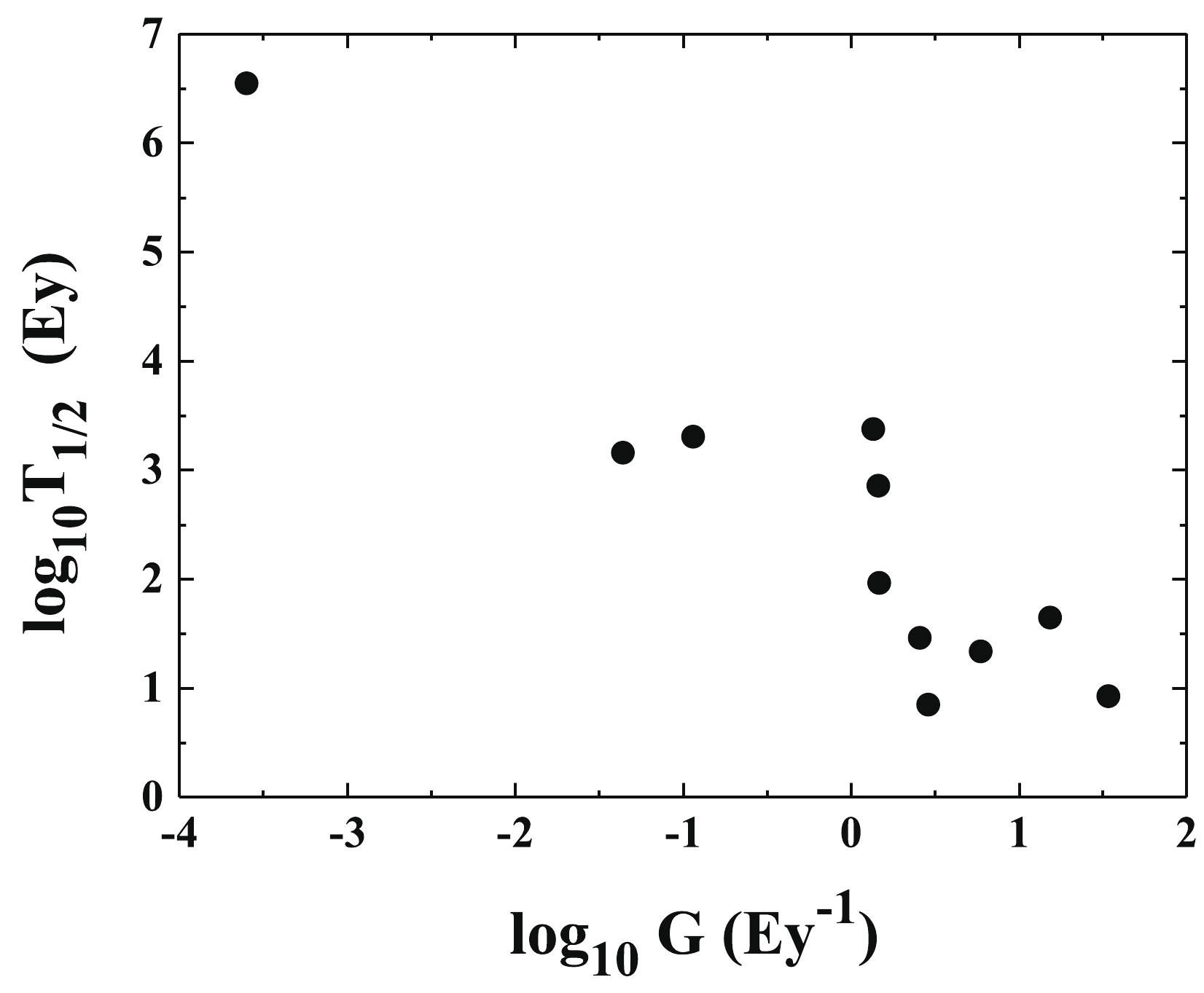
(8) $ \sigma $ for the eleven nuclei is 0.44 (a factor of 2.8) and the average deviation is 0.36 (a factor of 2.3), which suggests that the IPR formula can closely reproduce experimental$ 2\nu\beta\beta $ -decay half-lives. The large changes of proton numbers ($ Z = 20-92 $ ) and large variations of$ 2\nu\beta\beta $ -decay half-lives (8.4 Ey$ - $ $ 3. 5\times10^{6} $ Ey) of the studied nuclei demand that the formula have a firm basis in physics.In Fig. 2, we plot the logarithm of
$ 2\nu\beta\beta $ -decay half-lives versus the phase-space factor (in$ \log_{10} $ -scale). In a good approximation, these quantities can be described with the form$ [{T_{1/2}]}^{-1} = G |M|^2 $ . The logarithm function of this form as the fitted equation including the shell effect can be obtained as follows:$ \log_{10}T_{1/2} = - \log_{10}G - \log_{10}(|M|^{2}/{F_{ \rm{S}}}^{2}), $

(9) where G is a phase-space factor, and
$ |M| $ , here considered a fitting parameter, is the nuclear matrix element. In analogy with Eq. (5),$ F_{ \rm{S}} $ is 10 for the parent nuclei with a neutron magic number and 1 for other nuclei. Through a least-squares fit, the obtained matrix element$ |M| = 0.096 \pm 0.022 $ . The average deviation, calculated using Eq. (8), is 0.52 (a factor of 3.31).We note that Ren et al. [30] proposed an analytic formula to calculate the
$ 2\nu\beta^{-}\beta^{-} $ decay half-lives. Their formula is expressed as$ \log_{10}T_{1/2}( {\rm Ey}) = \left[a-2\log_{10}\left(\frac{2\pi Z} {137}\right)+S\right]/Q_{2\beta}( \rm{MeV}). $

(10) Here, the constant
$ a = 5.843 $ .$ S = 2 $ when the neutron number of parent nuclei is a magic number and$ S = 0 $ otherwise. The calculated results from Ren's formula are listed in column 7 of Table 1 for comparison. Ren's formula also provides a good description of nuclear$ 2\nu\beta\beta $ decay half-lives, with an average deviation$ \Delta = 0.486 $ (a factor of 3.06). In Fig. 3, we plot the ratios of calculated$ 2\nu\beta\beta $ decay half-lives over experimental ones using different formulae. The IPR formula (Eq. 6) reproduces the experimental$ 2\nu\beta\beta $ -decay half-lives better than the original Primakoff-Rosen formula (Eqs. (2)-(4)). Both the IPR and Ren's formulae give a good description on the current experimental data. The two formulae can be used to predict the$ 2\nu\beta\beta $ -decay half-lives of other nuclei in nuclide charts. As Fig. 3 shows, Eq. (9) cannot closely reproduce the experimental values as other models except for the Primakoff-Rosen formula.
Figure 3. (color online) Ratios of calculated
$2\nu\beta\beta$ decay half-lives to experimental ones using different formulae. The gray triangles, red circles, black squares, and blue triangles represent the results from the Primakoff-Rosen formula (Eq. (2)), our IPR formula (Eq. (6)), Ren's formula (Eq. (10)) [30], and Eq. (9), respectively.In Table 2, we predict the
$ 2\nu\beta^{-}\beta^{-} $ -decay half-lives for all candidate nuclei with double-$ \beta $ decay energies above 0.5 MeV. The predicted half-lives correspond to the decays between the ground states of parent and daughter nuclei. The possible$ 2\nu\beta^{-}\beta^{-} $ -decay candidates encompass a wide range of nuclei from$ Z = 20 $ to$ Z = 98 $ . The predicted half-lives range from 3.59$ \times10^{2} $ Ey for$ ^{124} $ Sn to 1.17$ \times10^{8} $ Ey for$ ^{114} $ Cd. Since the listed nuclei here from$ ^{46} $ Ca to$ ^{198} $ Pt are “stable” and naturally occurring isotopes [40], the$ 2\nu\beta\beta $ -decay half-lives of these nuclei can be measured in the laboratory. To check the systematical uncertainties of different predictions, we list the result from Ren's formula [30] as a reference. Columns 3-5 of Table 2 show that the predicted double-$ \beta $ decay half-lives from the two different formulae are close to each other, with the largest deviation of a factor of 6.18 for$ ^{104} $ Ru.Nuclei $Q_{2\beta}$ /MeV

$T_{\mathrm{IPR}}$ (Ey)

$T_{\mathrm{Ren}}$ (Ey)

$T_{\mathrm{IPR}}$ /

$T_{\mathrm{Ren}}$ 

$^{46}$ Ca

0.989 $ 1.85\times10^{6}$ 

$ 9.64\times10^{5}$ 

1.92 $^{70}$ Zn

0.997 $ 4.49\times10^{5}$ 

$^{86}$ Kr

1.258 $ 4.68\times10^{5}$ 

$ 7.74\times10^{5}$ 

0.60 $^{94}$ Zr

1.142 $ 1.58\times10^{5}$ 

$ 4.52\times10^{4}$ 

3.49 $^{104}$ Ru

1.301 $ 6.49\times10^{4}$ 

$ 1.05\times10^{4}$ 

6.18 $^{110}$ Pd

2.017 $ 1.42\times10^{3}$ 

$ 3.77\times10^{2}$ 

3.78 $^{114}$ Cd

0.542 $ 1.17\times10^{8}$ 

$^{124}$ Sn

2.291 $ 3.59\times10^{2}$ 

$ 1.72\times10^{2}$ 

2.09 $^{134}$ Xe

0.826 $ 2.23\times10^{6}$ 

$^{142}$ Ce

1.417 $ 1.34\times10^{4}$ 

$^{148}$ Nd

1.928 $ 9.05\times10^{2}$ 

$ 3.76\times10^{2}$ 

2.41 $^{154}$ Sm

1.251 $ 3.08\times10^{4}$ 

$ 8.81\times10^{3}$ 

3.49 $^{160}$ Gd

1.73 $ 8.76\times10^{2}$ 

$ 6.84\times10^{2}$ 

1.28 $^{170}$ Er

0.656 $ 1.77\times10^{6}$ 

$^{176}$ Yb

1.089 $ 1.99\times10^{4}$ 

$^{198}$ Pt

1.049 $ 3.89\times10^{4}$ 

$ 3.27\times10^{4}$ 

1.19 $^{216}$ Po

1.531 $ 2.60\times10^{3}$ 

$^{232}$ Th

0.838 $ 2.54\times10^{5}$ 

$^{244}$ Pu

1.353 $ 2.30\times10^{3}$ 

$ 2.44\times10^{3}$ 

0.94 $^{256}$ Cf

1.553 $ 9.62\times10^{2}$ 

In Fig. 4, we plot the theoretical values (
$ \log_{10} {T_{1/2}} $ as the function$ Q_{2\beta} $ ) from the IPR and Ren's formulae, with and without shell effects. As the figure shows, the calculated values are smaller for the scenario without the shell effects. For$ ^{136} $ Xe with$ Q_{2\beta} $ $ \sim $ 2.4 MeV, the calculated values increase by approximately ten times after considering the shell effects in these two formulae. For$ ^{48} $ Ca with$ Q_{2\beta} $ $ \sim $ 4.2 MeV, the increased multiple is approximately 3 for Ren's formula and 10 for the IPR formula. Fig. 4 indicates that these two formulae can produce consistent results after including the shell effects, and the shell effects are remarkable in the calculation of the$ 2\nu\beta\beta $ decay half-lives.
Figure 4. (color online) Logarithm of calculated
$2\nu\beta\beta$ decay half-lives overs the decay energy. The red circles and black squares represent the results from the IPR formula (Eq. (6)) and Ren's formula (Eq. (10)) [30], respectively. The solid and open symbols denote the results with and without shell effects, respectively. -
In addition to the double-
$ \beta $ decay between the ground states of parent and daughter nuclei, scholars have discovered recently that the$ 2\nu\beta\beta $ decay can occur from the ground state of a parent nucleus to the first$ 0^{+} $ excited state ($ 0_{1}^{+} $ ) of a daughter nucleus ($ 0^{+}\rightarrow0_{1}^{+} $ transitions) [3, 6]. The$ 2\nu\beta^{-}\beta^{-} $ -transitions of$ ^{100} $ Mo and$ ^{150} $ Nd to the$ 0_{1}^{+} $ states of daughter nuclei have been observed and the decay half-lives have been measured [41, 42]. We calculated the half-lives of such two transitions by Eq. (6) with the same parameters. The results are shown in column 4 of Table 3, which indicates that the measured$ 2\nu\beta\beta $ half-lives of$ ^{100} $ Mo and$ ^{150} $ Nd were closely reproduced by the IPR formula, with the factors of 1.6 and 2.6, respectively. Such a good agreement suggests that the IPR formula can be extended to describe the transitions from ground state of parent nuclei to the$ 0_{1}^{+} $ states of daughter nuclei. We also list the predicted$ 2\nu\beta^{-}\beta^{-} $ -decay half-lives of some unknown$ 0^{+}\rightarrow0_{1}^{+} $ transitions together with other theoretical predictions [39, 43-47] in. It is seen from Table 3 indicates that the predicted half-life for$ ^{76} $ Ge differs significantly for different models. The predicted$ 2\nu\beta\beta $ -decay half-life for$ ^{76} $ Ge is$ 1.25\times10^{6} $ Ey from the IPR formula, while Stoica et al. predicted a half-life of$ 4.5\times10^{3} $ Ey [45]. The deviation is as large as approximately 300 times. Further experimental measurements and theoretical studies on this decay can be very valuable.Nuclei $Q^{*}_{2\beta}$ /MeV

$T_{1/2}^{*}$ (exp)(Ey)

$T_{1/2}^{*}$ (IPR)(Ey)

$T_{1/2}^{*}$ (Ren)(Ey)

$T_{1/2}^{*}$ (other1)(Ey)

$T_{1/2}^{*}$ (other2)(Ey)

$^{48}$ Ca

1.275 $ 7.27\times10^{4} $ 

$ 1.63\times10^{6} $ 

$^{76}$ Ge

0.917 $ 1.25\times10^{6} $ 

$ 1.02\times10^{6} $ 

(7.5 $-$ 310)

$\times10^{3}$ [43, 44]

$ 4.5\times10^{3} $ [45]

$^{82}$ Se

1.506 $ 5.62\times10^{3} $ 

$ 4.21\times10^{3} $ 

(1.5 $-$ 3.3)

$\times10^{3}$ [43, 44]

$^{96}$ Zr

2.203 $ 1.97\times10^{2} $ 

$ 2.59\times10^{2} $ 

(24 $-$ 27)

$\times10^{2}$ [43, 44]

$ 38\times10^{2} $ [45]

$^{100}$ Mo

1.904 $5.9^{+0.8}_{-0.6}\times10^{2}$ 

$ 9.53\times10^{2} $ 

$ 5.89\times10^{2} $ 

16 $\times10^{2}$ [46]

$ 21\times10^{2} $ [45]

$^{116}$ Cd

1.048 $ 1.17\times10^{5} $ 

$ 8.36\times10^{4} $ 

1.1 $\times10^{4}$ [43, 44]

$ 0.11\times10^{4} $ [45]

$^{130}$ Te

0.735 $ 1.50\times10^{6} $ 

$ 8.38\times10^{6} $ 

(5.1 $-$ 14)

$\times10^{4}$ [43, 44, 47]

$^{136}$ Xe

0.879 $ 1.33\times10^{6} $ 

$ 1.06\times10^{8} $ 

$^{150}$ Nd

2.627 $1.33^{+0.45}_{-0.26}\times10^{2}$ 

$ 0.511\times10^{2} $ 

$ 0.776\times10^{2} $ 

Table 3. Double-
$ \beta $ decay half-lives (in Ey) from the ground state of parent nuclei to the first$ 0^{+} $ excited state of daughter nuclei (denoted by$ * $ ). Experimental$ 2\nu\beta\beta $ -decay half-lives are listed in column 2.$ Q^{*}_{2\beta} $ denotes the experimental$ 2\nu\beta\beta $ decay energies of these$ 0^{+}\rightarrow0_{1}^{+} $ transitions.$ T_{1/2}^{*} $ ($ {\rm{IPR}} $ ) (Ey) represents our calculated half-lives with the IPR formula (Eq. (6)). The calculated results from Ren et al. [30] are listed in the fifth column. Other theoretical results are also listed in columns 6$ - $ 7 for comparison [43-47].Our predictions are close to the result of Ren et al. [30] for most of nuclei, but deviate by 22 times and 80 times for
$ ^{48} $ Ca and$ ^{136} $ Xe, respectively. We note that both$ ^{48} $ Ca and$ ^{136} $ Xe have “magic” neutron numbers. This may be related to the different considerations of the shell effects on nuclear transition matrix elements. In the formula of Ren et al., the$ 2\nu\beta\beta $ -decay probability is suppressed by a factor of$ 10^{S/Q_{2\beta}} $ . This suppression is$ Q_{2\beta} $ dependent. As$ Q_{2\beta} $ is smaller in the$ 0^{+}\rightarrow0_{1}^{+} $ transition than that in the corresponding ground-state transition, the suppression becomes stronger in the$ 0^{+}\rightarrow0_{1}^{+} $ transition. In our IPR formula, the suppression factor is set as a constant for the nuclei with “magic” neutron numbers. In addition, the physics behind the two formulae differs. The IPR formula is based on the classical second-order quantum transition theory for weak interactions. It is similar to the Sargent law for$ \beta $ -decay half-lives [48]. Ren's formula has a similar shape to the new Geiger-Nuttall law which describes the$ \alpha $ decay and cluster radioactivity, which are governed by the strong interaction and coulomb interaction [30, 49]. Although it is still very difficult to be derived from basic quantum transition theory, Ren's formula can be experimentally verified. We strongly suggest to measure the$ 0^{+}\rightarrow0_{1}^{+} $ $ 2\nu\beta^{-}\beta^{-} $ -decay half-lives of$ ^{48} $ Ca and$ ^{136} $ Xe to test the validity of these two formulae. This is very important for understanding the basic mechanism of double-$ \beta $ decays and for further studying the shell effects on nuclear transition matrix elements. -
We have studied the systematics of all available
$ 2\nu\beta^{-}\beta^{-} $ -decay half-lives based on the formula proposed by Primakoff and Rosen in 1959. We improve the formula empirically by considering the shell effects on nuclear transition matrix elements and refining the energy dependence of the phase-space factor. This improved formula can closely describe all available experimental half-lives of$ 2\nu\beta^{-}\beta^{-} $ decays, both for ground-state transitions and transitions from ground states of parent nuclei to the first$ 0^{+} $ excited states of daughter nuclei. This newly established systematics illustrate the complex double-$ \beta $ decay process in a simple, transparent, and accurate manner. Further predictions are provided for$ 2\nu\beta^{-}\beta^{-} $ -decay candidates with decay energies above 0.5 MeV. We compare the predictions from this improved formula with other theoretical models or empirical formulae and propose further experimental measurements on the half-lives of double-$ \beta $ transitions between the ground states of$ ^{48} $ Ca,$ ^{76} $ Ge, and$ ^{136} $ Xe and the first$ 0^{+} $ excited states of their corresponding daughter nuclei. The proposed measurements can be very useful for understanding the underlying mechanisms of double-$ \beta $ decays and for further studying the shell effects on nuclear transition matrix elements.
Calculation of double-β decay half-lives using an improved Primakoff-Rosen formula
- Received Date: 2021-01-15
- Available Online: 2021-08-15
Abstract: A systematic analysis on experimental data of the half-lives of nuclear double-





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: