NNLO QCD predictions of electron charge asymmetry for inclusive pp → W + X production in forward region at 13 and 14 TeV

The production of W and Z bosons is an important benchmark measure of past colliders and proton-proton (pp) collisions at the CERN Large Hadron Collider (LHC). Precise measurements of their production cross sections provide important tests for the quantum chromodynamic (QCD) and electroweak (EW) sectors of the Standard Model (SM) and valuable inputs to constrain parton distribution functions (PDFs) in the proton. Their measurements enable improvements of the background modeling for several rare SM and beyond the SM processes, as W and Z boson productions constitute a major background for those processes. In addition, W and Z boson processes are extensively used for calibrating detector responses to improve the reconstruction of leptons, jets, and missing energy signatures with better performances. W and Z bosons are produced in abundance in their leptonic decay channels with larger cross sections and clean experimental signatures in pp collisions.

In experiments, W bosons are reconstructed through their leptonic decay channels $ pp \rightarrow W^{\pm} \rightarrow l^{\pm}\nu $. A typical W boson event is characterized by one isolated charged lepton with high transverse momentum $ p_{T} $ and large missing transverse energy due to the neutrino. W bosons are produced primarily through the annihilation of a valence quark from one of the colliding protons with a sea antiquark from the other: $ u\bar{d}\rightarrow W^{+} $, $ d\bar{u}\rightarrow W^{-} $. $ W^{+} $ bosons are produced more often than $W ^{-} $ bosons due to the presence of two valence u quarks in the proton. This leads to a production asymmetry between $ W^{+} $ and $ W^{-} $ bosons, which is referred to as the W boson charge asymmetry and is usually defined in terms of cross sections $ \sigma(W^{+}) $ and $ \sigma(W^{-}) $ differentials in the W boson rapidity $ y_{W} $ as

The important characteristic of this charge asymmetry variable $ A(y_{W}) $ is the ability to discriminate between PDF models, as $ y_{W} $ is strongly correlated with the initial-state parton momentum fractions x (Bjorken-x values). However, the neutrino from W boson decay leaves the detector unobserved, and its longitudinal momentum cannot be measured directly. Therefore, the full momentum of the W boson and its rapidity $ y_{W} $ cannot be directly reconstructed. Despite this experimental complication, the same information can be accessed by measuring the charge asymmetry from the W boson decay products. A commonly used approach is to measure the charge asymmetry as a function of the decay lepton (electron^①, in this case) pseudorapidity^② $ \eta_{e} $, which is strongly correlated with $ y_{W} $, defined as

The electron charge asymmetry $ A_{e} $ variable poses significant constraints on the ratio of u and d quark distributions in the proton as a function of Bjorken-x values of the partons. It can be used to discriminate among PDF models that predict different shapes of valence and sea quark distributions. Furthermore, this variable can be measured with high accuracy, as numerous sources of systematic uncertainties cancel each other in the ratio, and therefore offer a unique opportunity for precision tests of the SM physics.

The W boson production asymmetry was previously measured in $p{\bar{p}}$ collisions by CDF and D0 collaborations at the Tevatron [1-5]. The W boson lepton charge asymmetry measurements at the LHC were performed in the central lepton pseudorapidity region $ |\eta_{l}|\leqslant $ 2.5 by the ATLAS and CMS collaborations at different center-of-mass energies up to 8 TeV [6-13]. The LHCb collaboration at the LHC has also reported W boson lepton charge asymmetry measurements at 7 TeV [14, 15] and 8 TeV [16, 17] in the forward lepton pseudorapidity region 2.0 $ \leqslant \eta_{l} \leqslant $ 4.5 that go beyond the ATLAS and CMS acceptance. In all these complementary results, measurements are compared with theoretical predictions up to next-to-next-to-leading order (NNLO) accuracy in perturbative QCD convolved with different PDF models. NNLO predictions were obtained either by using the FEWZ [18] or DYNNLO [19] program for theoretical comparisons in these measurements. Among all available experimental results, the measurements of differential cross-sections and thus production charge asymmetries are of particular importance in the forward region of the detector acceptance. The PDFs exhibit large uncertainties at very low and large x values of the interacting leptons, where x values also depend on the acceptance defined by means of the lepton $ \eta_{l} $. Therefore, measurements and theoretical predictions of the W boson production asymmetry in the forward detector acceptance 2.0 $ \leqslant \eta_{l} \leqslant $ 4.5 offer a unique situation to provide valuable inputs on determining accurate PDFs at small and large x values between $ 10^{-4}\leqslant x \leqslant 10^{-1} $.

In this study, we present precise predictions of the electron charge asymmetry between the processes $ pp \rightarrow W^{+}+X \rightarrow e^{+}\nu_{e}+X $ and $ pp \rightarrow W^{-}+X \rightarrow e^{-}\bar{\nu_{e}}+X $ in the forward $ \eta_{e} $ region 2.0 $ \leqslant \eta_{e} \leqslant $ 4.25. The calculations are performed at NNLO accuracy in the perturbative QCD expansion using different PDF models at 8, 13, and 14 TeV LHC pp collision energies. The predicted $ W^{+} $/$ W^{-} $ cross section ratio and charge asymmetry distributions as a function of the $ \eta_{e} $ are compared with the 8 TeV measurement by the LHCb collaboration [17]. The 8 TeV predictions are validated with the data in the fiducial phase space of the LHCb measurement. Further, NNLO calculations are extended to the 13 and 14 TeV LHC pp energies for the precise predictions of the charge asymmetry in bins of the $ \eta_{e} $. The $ W^{+} $ and $W^{-} $ boson differential cross distributions along with their $W^{+} $/$ W^{-} $ ratios and the charge asymmetry distributions are predicted and compared among different PDF sets. The charge asymmetry results are then reported and compared among different PDF sets. These findings represent the first phenomenological study by means of the NNLO predictions for the electron charge asymmetry in the forward $ \eta_{e} $ region 2.0 $ \leqslant \eta_{e} \leqslant $ 4.25 of 13 TeV and 14 TeV pp collisions.

The calculations of differential cross sections and charge asymmetries are performed using the MATRIX (v1.0.3) computational framework [19, 20]. The framework enables calculations of differential cross sections in the form of binned distributions up to NNLO accuracy in perturbative QCD. The so-called transverse momentum $ q_{T} $-subtraction method [21, 22] is employed within the MATRIX computations for cancellations of infrared divergences that arise at the intermediate stages of the calculations. These divergences are regulated by introducing a fixed cut-off value $r_{\rm cut} =$ 0.0015 (0.15%) for the residual dependence parameter, which is defined as $ r = p_{T}/m $ in terms of the $ p_{T} $ distribution and invariant mass m for a system of colorless particles. Moreover, all the spin- and color-correlated tree-level and one-loop scattering amplitudes are acquired with the use of the OpenLoops tool [23-25] along with the computations. To perform theoretical calculations of the differential cross-sections in pp collisions, knowledge of the PDFs is required. The LHAPDF 6.2.0 framework [26] is used for the evaluation of PDFs from data files in the computations. Different PDF sets are used in the calculations, all based on a constant strong coupling $ \alpha_{s} = $ 0.118. The NNPDF3.1 [27], CT14 [28], and MMHT2014 [29] PDF sets are used, each at NNLO accuracy. To this end, all predicted results are obtained by treating leptons and light quarks as massless in the Fermi constant $ G_{F} $ input scheme of the computational setup. The default setup of the MATRIX framework is used for the input scheme, which encompasses the choices for relevant SM parameters that are based on the $ G_{F} $ = 1.16639 × 10$ ^{-5} $ GeV$ ^{-2} $ value.

The 8 TeV LHCb measurement, performed in pp collisions at 8 TeV [17], is chosen as the reference for the justification of the calculations of this study. This reference measurement focuses on the differential cross-sections and charge asymmetries in the electron decay channel of the $W^{\pm}$ bosons in the forward detector acceptance as well. The fiducial phase space requirements in the calculations are employed to be in line with the reference LHCb measurement. The electrons are required to have transverse momentum $ p_{T}> $ 20 GeV and lie in the forward pseudorapidity region of $ 2.0 \leqslant \eta_{e} \leqslant 4.25 $. There is no need to impose any requirements for the final state hadronic jets, as the calculations are considered for the inclusive W boson production. The fiducial acceptance is also relaxed to have no explicit requirement for the missing transverse momentum of the final state (anti)neutrino. Furthermore, no requirement for the W boson transverse mass is imposed, unlike to the ATLAS and CMS W boson charge asymmetry measurements performed in the central $ \eta_{l} $ detector coverage.

Cross section calculations in perturbative QCD acquire dependence on the renormalization $ \mu_{R} $ and factorization $ \mu_{F} $ scales, and the numerical results depend on the choice of these scales. In this study, the central value for the scales is chosen to be the W boson mass $ \mu_{R} $ = $ \mu_{F} $ = $ m(W) $ = 80.385 GeV as in the usual manner. The theoretical uncertainties due to the choice of the scales, which are simply called scale uncertainties, referring to missing higher-order contributions in the calculations, are estimated by independently varying the $ \mu_{R} $ and $ \mu_{F} $ up and down by a factor of two around the central value. All possible combinations are considered in the variations while imposing the constraint $ 0.5 \leqslant \mu_{R}/ \mu_{F} \leqslant 2.0 $. In the cross-section ratio and charge asymmetry calculations, this constraint is generalized to an uncorrelated scale variation, while restricting to $ 0.5 \leqslant \mu/ \mu^{'} \leqslant 2.0 $ between all pairs of scales. Because the scale uncertainties arise from the missing terms in the calculations, a higher calculated perturbative order indicates smaller theoretical uncertainties associated with the renormalization and factorization procedure. Moreover, PDF and $ \alpha_{s} $ uncertainties are also considered. The PDF uncertainties for NNPDF3.1, CT14, and MMHT2014 PDF sets are estimated using the prescription of the PDF4LHC working group [26, 30]. The $ \alpha_{s} $ uncertainty is estimated by varying the $ \alpha_{s} $ value by $ \pm0.001 $ around 0.118. Estimated theoretical uncertainties for the 8 TeV inclusive cross sections of the W$ ^{+} $ and W$ ^{-} $ boson processes at NNLO accuracy are tabulated in Table 1 as an example to compare the relative size of each type of theoretical uncertainty considered in this study. Total theoretical uncertainties are obtained by the summing scale, PDF, and $ \alpha_{s} $ uncertainties in quadrature. Then, total uncertainties are symmetrized by taking the larger values from estimated up and down uncertainties in a conservative approach.

Uncertainty	NNPDF3.1	CT14	MMHT2014
Values for $ W^{+}\rightarrow e^{+}\nu $ process
Scale (%)	0.74	0.76	0.78
PDF (%)	1.96	2.40	1.64
$ \alpha_{s} $ (%)	1.06	1.04	1.10
Total (%)	2.35	2.72	2.12
Values for $ W^{-}\rightarrow e^{-}\nu $ process
Scale (%)	0.72	0.64	0.80
PDF (%)	2.22	2.90	1.50
$ \alpha_{s} $ (%)	1.16	1.00	1.14
Total (%)	2.61	3.13	2.05

Table 1.  Estimated sizes of scale, PDF, and $ \alpha_{s} $ uncertainties for 8 TeV inclusive cross-section predictions of W$ ^{+} $ and W$ ^{-} $ bosons at NNLO accuracy. Estimated uncertainties are given as a percentage (%) of central values of predictions from NNPDF3.1, CT14, and MMHT2014 PDF sets.

NNLO calculations and their comparisons with the reference LHCb results at 8 TeV [17] are reported in this section. The calculations are performed in the fiducial phase space as discussed in Sec. IIB. $ W^{+} $/$ W^{-} $ at the differential cross section ratio $ R_{W^{\pm}} $, where

and electron charge asymmetry $ A_{e} $ (Eq. 2) variables as a function of $ \eta_{e} $ are used in justification of the calculations. The $ R_{W^{\pm}} $ and $ A_{e} $ variables are calculated in the $ \eta_{e} $ bins of (2.0, 2.25), (2.25, 2.5), (2.5, 2.75), (2.75, 3.0), (3.0, 3.25), (3.25, 3.5), (3.5, 3.75), and (3.75, 4.25) in line with the 8 TeV LHCb paper. NNPDF3.1, CT14, and MMHT2014 NNLO PDF sets are used in the calculations. Total theoretical uncertainties that are estimated as discussed in Sec. IIC are propagated to the $ R_{W^{\pm}} $ and $ A_{e} $ calculations. The LHCb data results obtained at the Born level do not incorporate the effect of quantum electrodynamics final-state radiation, and are used to enable direct comparisons to calculations. The data central results in the comparisons are used along with their total experimental uncertainties that are obtained by adding statistical, systematic, and LHC beam energy uncertainties in quadrature.

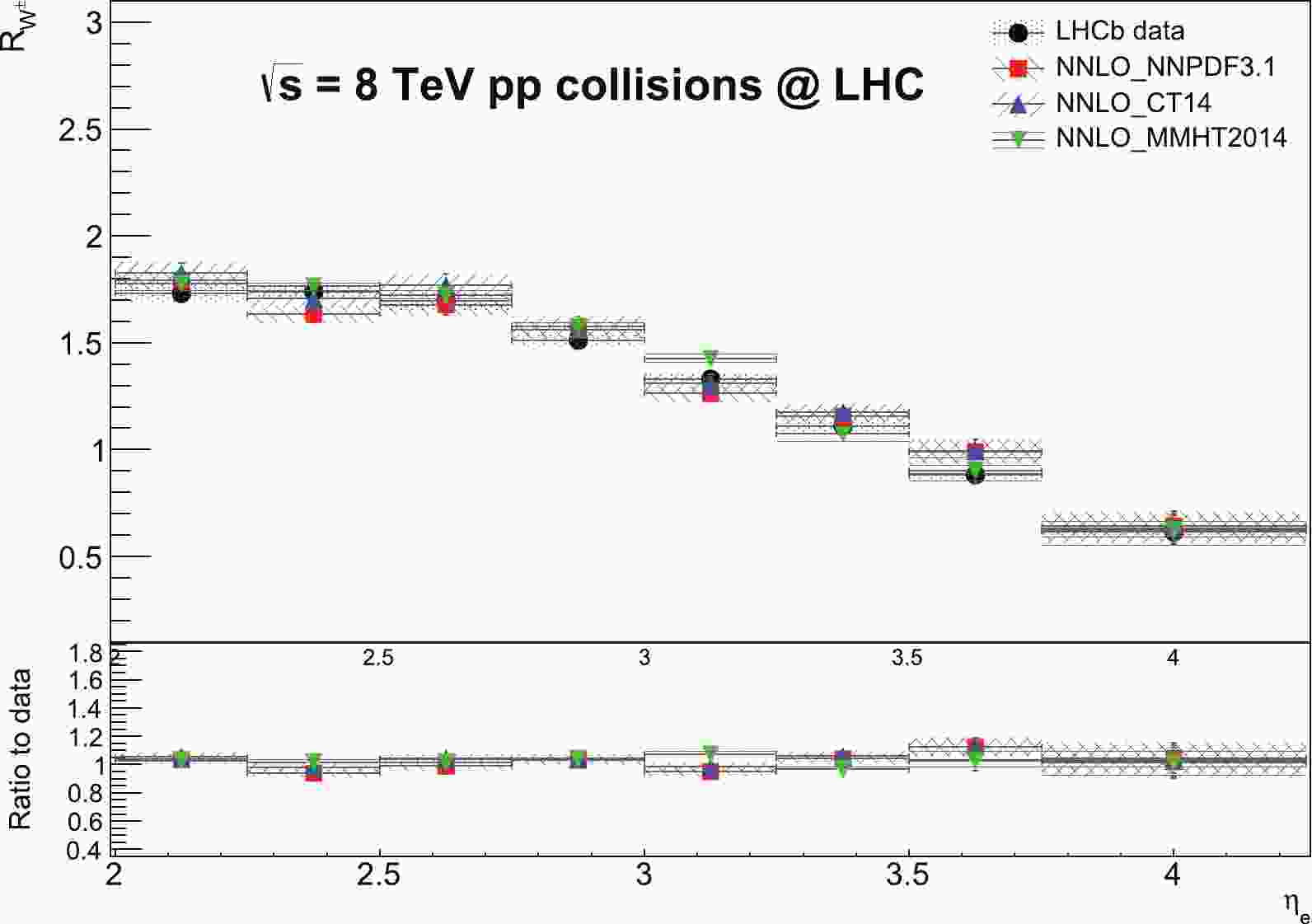
The predicted $ R_{W^{\pm}} $ distributions based on different PDF sets are compared with the data in Fig. 1. The $ R_{W^{\pm}} $ predictions at NNLO accuracy using different PDF sets are generally in good agreement with each other and with the data within uncertainties throughout the entire $ \eta_{e} $ bins. The prediction using the MMHT2014 PDF set provides the best agreement with the data among other predictions, except for the 3.0–3.25 bin, where it overestimates the data by up to 5%. The predictions using NNPDF3.1 and CT14 overestimate the data in the 3.5–3.75 bin by up to 10%, while the prediction using MMHT2014 is in good agreement with the data in this bin. The predictions using different PDF sets are able to describe the data well in the very forward $ \eta_{e} $ bin 3.75–4.25. Notably, the $\rm FEWZ$ predictions provided in the LHCb paper tend to underestimate the $ R_{W^{\pm}} $ data distribution in the far forward bins 3.5–3.75 and 3.75–4.25. The discrepancy between the MATRIX and $\rm FEWZ$ predictions is investigated and attributed mainly to the residual dependence of the $r_{\rm cut}$ = 0.15% value of the $ q_{T} $-subtraction method in the far forward region. The MATRIX framework differs by the $ q_{T} $-subtraction method from the $\rm FEWZ$, which is based on sector decomposition [31]. This residual dependence is due to power-suppressed terms that remain after the subtraction of the infrared singular contribution at a finite $r_{\rm cut}$ value. The impact of the choice of $r_{\rm cut}$ = 0.15% is verified with respect to a lower cut-off value 0.05%, which amounts to $ \sim $2%–7% difference. This difference shows that the power corrections due to a finite $r_{\rm cut}$ = 0.15% value are large in this region, which can only vanish in the limit $r_{\rm cut} \rightarrow$ 0. A systematic uncertainty up to 4% is propagated to the $ R_{W^{\pm}} $ predictions in the last two bins from the extrapolation $r_{\rm cut} \rightarrow$ 0 to account for this dependency on the $r_{\rm cut}$ value by means of large power corrections. Furthermore, the impact of the difference in the input parameter choices of the MATRIX and the $\rm FEWZ$ default setup [18] is found to be 1%–2%. Along with these results, the NNLO calculations in terms of the predicted $ R_{W^{\pm}} $ distributions are therefore justified by using LHCb results.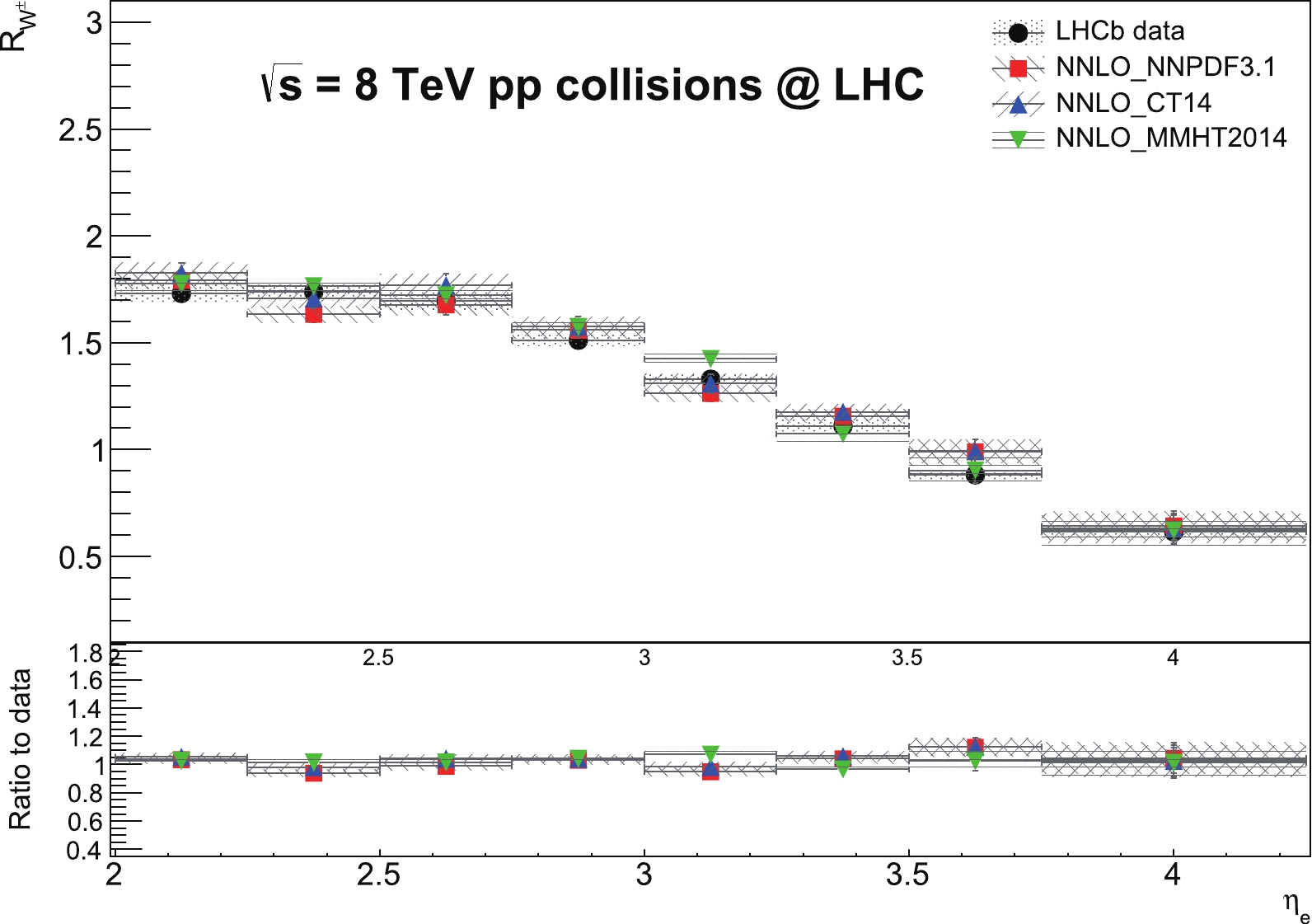

Figure 1.  (color online) Differential cross-section ratio $ R_{W^{\pm}} $ distributions as a function of $ \eta_{e} $, predicted at NNLO accuracy by using NNPDF3.1, CT14, and MMHT2014 PDF sets and their comparisons with the LHCb data at 8 TeV. The predictions include total theoretical uncertainties obtained by adding scale, PDF, and $ \alpha_s $ uncertainties in quadrature. The data includes total experimental uncertainty obtained by adding statistical, systematic, and the LHC beam energy uncertainties in the quadrature. In the lower inset, the ratios of the predictions to the data for the $ R_{W^{\pm}} $ variable are provided.

The predictions from different PDF sets and their comparisons with the data at NNLO accuracy for the $ A_{e} $ variable are shown in Fig. 2 and listed in Table 2. The predictions using different PDF sets generally reproduce the data well within uncertainties throughout the entire $ \eta_{e} $ range. The predictions are also in good agreement with each other and with the data except for bins 3.0–3.25 and 3.5–3.75, where the predictions using NNPDF3.1 and CT14 exhibit lower values compared to the data and the prediction using MMHT2014. The discrepancy between the data and the predictions using NNPDF3.1 and CT14 are up to $ \sim $15% in bins 3.0–3.25 and 3.5–3.75. The best description of the data is achieved with the prediction using MMHT2014 over the other PDF sets for the entire $ \eta_{e} $ ranges. The predictions using different PDF sets are able to describe the data in the far forward bins 3.5–3.75 and 3.75–4.25 in comparison to the $\rm FEWZ$ predictions provided in the LHCb study, where the data was slightly underestimated. More generally, the trend of increasing discrepancy between the data and predictions towards the very forward $ \eta_{e} $ region as presented in the LHCb paper is not observed in Fig. 2 for the central values of the predictions. This discrepancy between the MATRIX and $\rm FEWZ$ predictions for the description of the data in the far forward bins is also mainly due to the large power corrections that appear at the finite cut-off $r_{\rm cut}$ = 0.15% value in the MATRIX calculation. The difference of the choice of $r_{\rm cut}$ = 0.15% relative to a lower cut-off value $r_{\rm cut}$ = 0.05% was found to be $ \sim $14%–19%. Therefore, a systematic uncertainty up to 5% from the extrapolation in the limit $r_{\rm cut} \rightarrow$ 0 is also propagated to the predictions in the last two bins of the $ A_{e} $ variable to account for the effect from the large power corrections at the finite $r_{\rm cut}$ value in the subtraction method. To this end, the NNLO calculations using different PDF sets are successfully justified with the LHCb results also for the $ A_{e} $ variable at 8 TeV.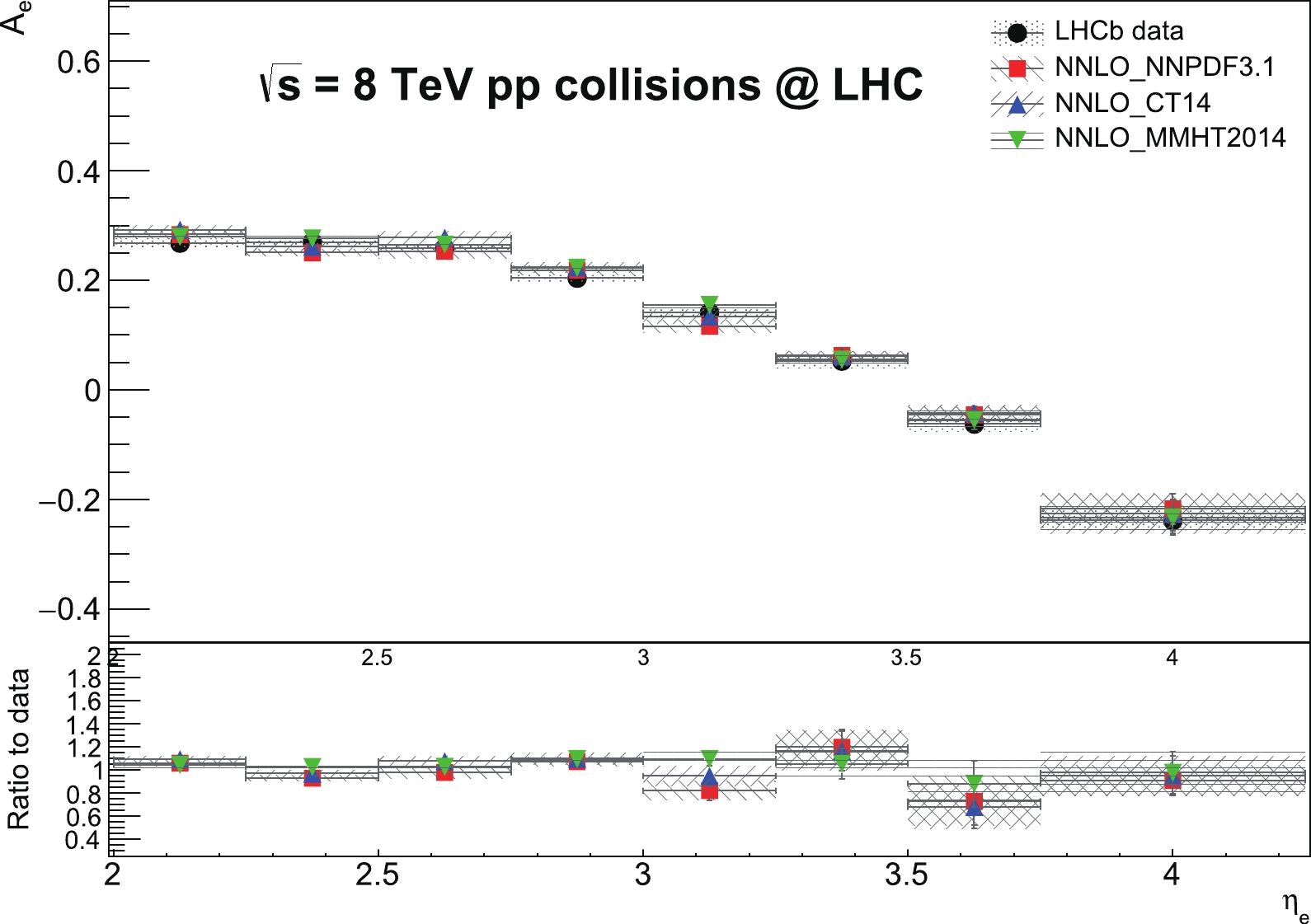

Figure 2.  (color online) Electron charge asymmetry $ A_{e} $ distributions as a function of $ \eta_{e} $ predicted at NNLO accuracy using NNPDF3.1, CT14, and MMHT2014 PDF sets and their comparisons with the LHCb data at 8 TeV. The predictions include total theoretical uncertainties, while the data include total experimental uncertainty. In the lower inset, the ratios of the predictions to the data for the $ A_{e} $ variable are provided.

$ \eta_{e} $	Data	NNPDF	CT	MMHT
2.00–2.25	26.78$ \pm $0.8	28.37$ \pm $0.7	29.24$ \pm $0.8	27.95$ \pm $0.6
2.25–2.50	26.98$ \pm $0.7	25.06$ \pm $0.6	26.14$ \pm $0.7	27.66$ \pm $0.7
2.50–2.75	25.84$ \pm $0.7	25.30$ \pm $1.3	27.78$ \pm $1.2	26.53$ \pm $1.0
2.75–3.00	20.39$ \pm $0.8	21.85$ \pm $0.8	22.37$ \pm $0.9	22.31$ \pm $0.9
3.00–3.25	14.15$ \pm $0.8	11.62$ \pm $1.1	13.40$ \pm $1.2	15.50$ \pm $0.8
3.25–3.50	5.25$ \pm $1.2	6.28$ \pm $0.8	6.12$ \pm $0.9	5.53$ \pm $1.0
3.50–3.75	−6.25$ \pm $1.4	−4.55$ \pm $1.5	−4.26$ \pm $1.5	−5.51$ \pm $1.8
3.75–4.25	−23.85$ \pm $1.9	−21.70$ \pm $2.8	−22.61$ \pm $3.6	−23.30$ \pm $3.2

Table 2.  8 TeV electron charge asymmetry (in percentages) $ A_{e} $(%) predictions using NNPDF3.1, CT14, and MMHT2014 PDF sets at NNLO accuracy and their comparisons with the LHCb data in bins of $ \eta_{e} $. The predictions include total theoretical uncertainties, while the data include total experimental uncertainty.

The predictions from the NNLO calculations are validated using LHCb data at 8 TeV in Sec. III. The 8 TeV predictions using all PDF sets, in particular the MMHT2014 PDF set, described the data efficiently in a consistent manner throughout the entire $ \eta_{e} $ region and motivated extensions of the calculations to 13 and 14 TeV, which are the current and the near-future planned center-of-mass energies of the LHC, respectively. The 13 and 14 TeV NNLO calculations are performed by employing the same fiducial phase space requirements as discussed in Sec. IIB. Total theoretical uncertainties are estimated according to the procedure as detailed in Sec. IIC. Further, a systematic uncertainty is included for the predictions in the last two forward bins to account for the dependency to the finite cut-off $r_{\rm cut}$ = 0.15% value, where the large power corrections can have an impact as already discussed in Sec. III. The PDF sets NNPDF3.1, CT14, and MMHT2014 are used in the calculations.

The 13 and 14 TeV calculations are first performed for the predictions of differential cross sections of the $W^{\pm}$ bosons ${\rm d}\sigma(W^{\pm})$ and their ratios $ R_{W^{\pm}} $ in bins of the $ \eta_{e} $. The differential distributions are predicted and compared among different PDF models in Fig. 3. The 13 TeV differential distributions are predicted consistently within uncertainties for the $ W^{\pm} $ boson processes, only with a few exceptions where the predictions using different PDF sets exhibited slight deviations from each other, such as in bins 2.75–3.0 and 3.0–3.25 for the $ W^{-} $ boson process. The prediction using NNPDF3.1 slightly underestimates the $ W^{-} $ boson cross section for the lower $ \eta_{e} $ bins with respect to the predictions using other PDF sets. However, the predicted $ R_{W^{\pm}} $ distributions are in very good agreement among different PDF models. The $ R_{W^{\pm}} $ distributions tend to decrease towards forward $ \eta_{e} $ bins, as expected. The 14 TeV differential cross sections are also predicted consistently within uncertainties for the $ W^{\pm} $ boson processes, regardless of the PDF model. The predictions only exhibit small discrepancies that are more pronounced in bins 3.25–3.5 and 3.5–3.75. The predicted 14 TeV $ R_{W^{\pm}} $ distributions are also in good agreement among PDF sets; however, they become more sensitive to distinguish among different PDF models as compared to 13 TeV distributions. This is clearly observed in the intermediate to higher bins of $ \eta_{e} $ that the predictions tend to deviate from each other by up to $ \sim $12%. Therefore, the NNLO differential cross section distributions for the $ W^{\pm} $ boson processes can be further used to calculate $ A_{e} $ distributions at 13 and 14 TeV.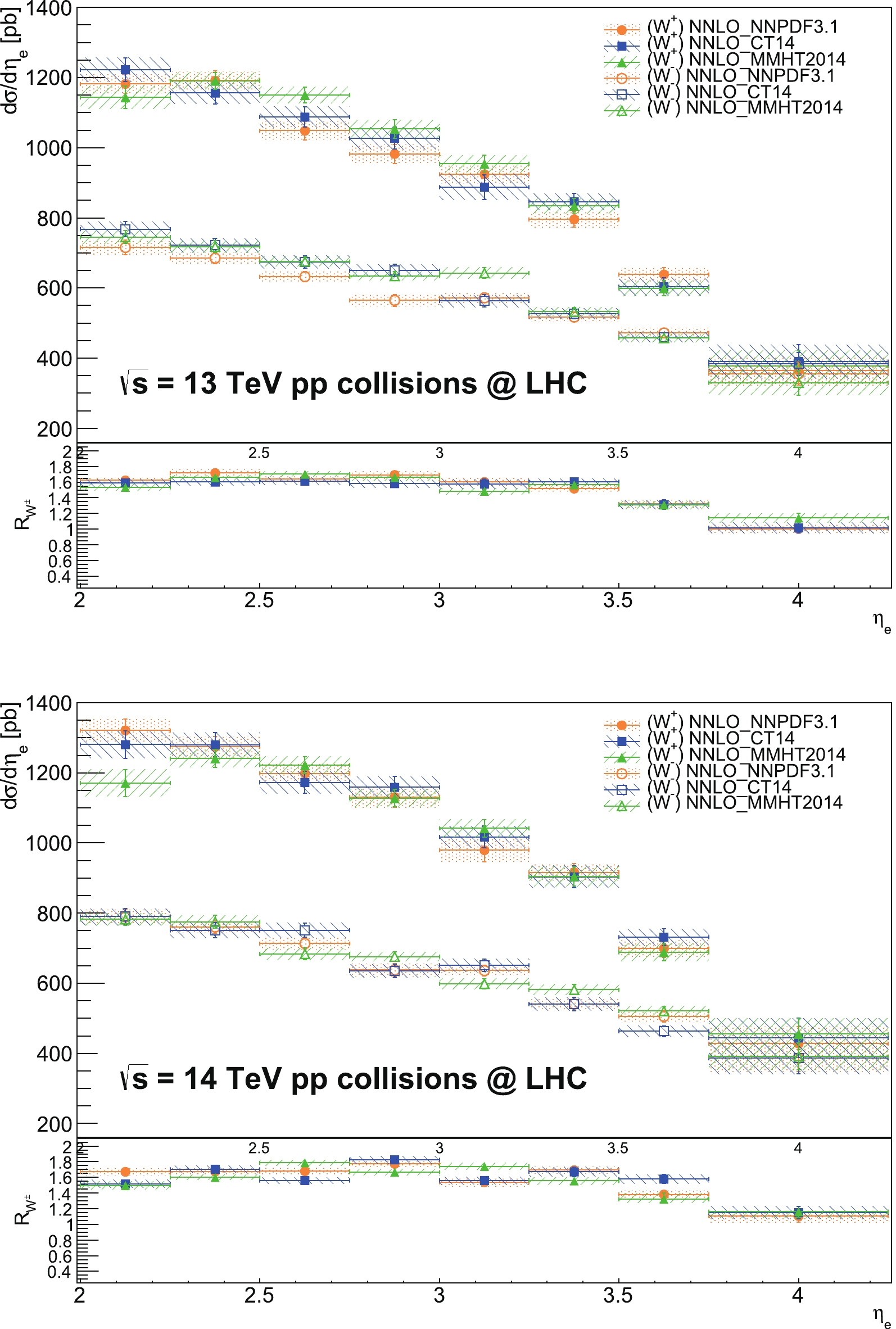

Figure 3.  (color online) 13 TeV (top) and 14 TeV (bottom) differential cross-section ${\rm d}\sigma$ distributions for the W$ ^{+} $ and W$ ^{-} $ boson processes as a function of the $ \eta_{e} $ predicted at NNLO accuracy using NNPDF3.1, CT14, and MMHT2014 PDF sets. Predictions include total theoretical uncertainties. In the lower inset, the predictions for the differential cross-section ratios $ R_{W^{\pm}} $ are provided.

Next, 13 and 14 TeV electron charge asymmetry $ A_{e} $ calculations are performed as a function of the $ \eta_{e} $ based on the differential cross section predictions of the $ W^{\pm} $ boson processes. The differential $ A_{e} $ predictions are compared among the PDF sets, as shown in Fig. 4 and tabulated in Tables 3 and 4. Overall, the 13 TeV predictions for the $ A_{e} $ variable from different PDF sets are in good agreement with each other within uncertainties almost for the entire $ \eta_{e} $ ranges. The $ A_{e} $ predictions in the most forward $ \eta_{e} $ bin 3.75–4.25 distinguish the MMHT2014 PDF set from other PDF sets, where the prediction using MMHT2014 provides a significantly higher $ A_{e} $ result. The 14 TeV predictions for the $ A_{e} $ variable are mostly in good agreement among the PDF sets within uncertainties; however, they are more distinguishable among each other compared to the 13 TeV predictions. The predictions using NNPDF3.1 and CT14 agree with each other more than the prediction using MMHT2014. The prediction using CT14 exhibits some deviations that are more pronounced in the intermediate region. No single PDF set is able to provide consistent agreement with the other throughout the entire $ \eta_{e} $ ranges. The sensitivity to the PDF choice regarding the $ A_{e} $ distributions is clearly increased from 13 TeV results to 14 TeV results.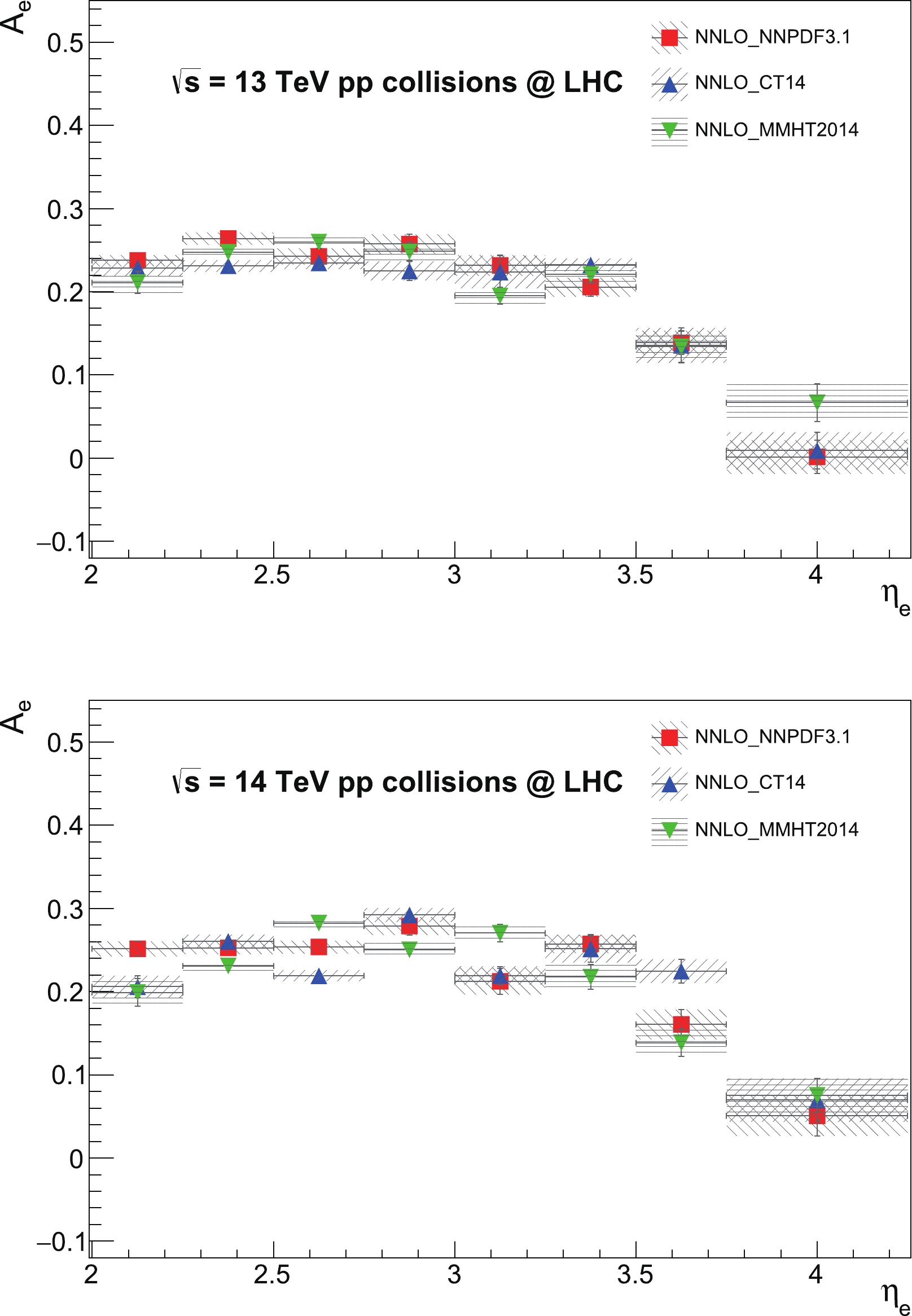

Figure 4.  (color online) 13 TeV (top) and 14 TeV (bottom) electron charge asymmetry $ A_{e} $ distributions as a function of the $ \eta_{e} $, which are predicted at NNLO accuracy using NNPDF3.1, CT14, and MMHT2014 PDF sets. Predictions include total theoretical uncertainties.

$ \eta_{e} $	NNPDF3.1	CT14	MMHT2014
2.00–2.25	23.78$ \pm $0.6	22.84$ \pm $0.9	21.11$ \pm $1.3
2.25–2.50	26.40$ \pm $0.7	23.13$ \pm $0.7	24.77$ \pm $0.6
2.50–2.75	24.27$ \pm $1.0	23.47$ \pm $0.7	26.00$ \pm $1.6
2.75–3.00	25.75$ \pm $1.2	22.51$ \pm $1.1	24.85$ \pm $1.1
3.00–3.25	23.18$ \pm $1.2	22.38$ \pm $1.9	19.50$ \pm $1.0
3.25–3.50	20.57$ \pm $1.1	23.23$ \pm $0.8	22.07$ \pm $1.1
3.50–3.75	13.86$ \pm $1.7	13.57$ \pm $1.9	13.41$ \pm $1.9
3.75–4.25	0.15$ \pm $2.0	0.91$ \pm $2.2	6.67$ \pm $2.3

Table 3.  13 TeV electron charge asymmetry (in percentages) $ A_{e} $(%) predictions using NNPDF3.1, CT14, and MMHT2014 PDF sets at NNLO accuracy in bins of $ \eta_{e} $. Predictions include total theoretical uncertainties.

$ \eta_{e} $	NNPDF3.1	CT14	MMHT2014
2.00–2.25	25.15$ \pm $0.9	20.60$ \pm $1.3	19.90$ \pm $1.6
2.25–2.50	25.26$ \pm $0.7	26.05$ \pm $0.8	23.09$ \pm $0.5
2.50–2.75	25.38$ \pm $0.7	21.91$ \pm $0.7	28.24$ \pm $0.6
2.75–3.00	27.90$ \pm $1.0	29.22$ \pm $0.8	25.04$ \pm $0.8
3.00–3.25	21.24$ \pm $1.5	21.93$ \pm $1.1	27.04$ \pm $1.1
3.25–3.50	25.74$ \pm $1.1	25.13$ \pm $1.6	21.76$ \pm $1.5
3.50–3.75	16.06$ \pm $1.8	22.46$ \pm $1.4	13.87$ \pm $1.7
3.75–4.25	5.08$ \pm $2.4	6.97$ \pm $2.6	7.53$ \pm $2.0

Table 4.  14 TeV electron charge asymmetry (in percent) $ A_{e} $(%) predictions using NNPDF3.1, CT14, and MMHT2014 PDF sets at NNLO accuracy in bins of the $ \eta_{e} $. Predictions include total theoretical uncertainties.

The $ A_{e} $ distributions are also compared at different center-of-mass energies 8, 13, and 14 TeV for the prediction using MMHT2014 as a baseline PDF set in Fig. 5. This has been discussed in Sec. III, where the prediction using MMHT2014 provides the best description of 8 TeV LHCb data and also provides $ A_{e} $ distributions reasonably well at 13 and 14 TeV. The 13 and 14 TeV predictions provided lower distributions in the lower $ \eta_{e} $ bins 2.0–2.5 and higher distributions in the intermediate to higher bins 2.75–4.25 relative to the 8 TeV prediction. The distributions at different energies almost overlap within uncertainties in bins 2.5–3.0. After bin 2.75–3.0, the 13 and 14 TeV predictions separate from the 8 TeV prediction by exhibiting higher distributions towards the very forward $ \eta_{e} $ region. In the most forward bins 3.25–4.25, 13 and 14 TeV predictions overlap within uncertainties; however, the 14 TeV distribution is predicted slightly higher than the 13 TeV distribution. The charge asymmetry increases from 8 TeV to higher energies in the very forward $ \eta_{e} $ bins 3.0–4.25. Another outstanding observation is that the $ \eta_{e} $ bin, where the$ A_{e} $ distribution reaches a peak, shifts towards higher bins in progressing from 8 TeV to higher energies.

Figure 5.  (color online) Comparison of electron charge asymmetry $ A_{e} $ distributions at 8, 13, and 14 TeV as a function of $ \eta_{e} $ predicted using the MMHT2014 PDF set. The prediction includes total theoretical uncertainties.

In this study, a detailed investigation of the theoretical predictions of the electron charge asymmetry for the inclusive $ W^{\pm}+X \rightarrow e^{\pm} \nu +X $ production in the forward region of the pp collisions is presented. The charge asymmetry calculations are performed with the inclusion of QCD NNLO corrections in the perturbation expansion at 8, 13, and 14 TeV LHC energies. The calculations are considered for the fiducial acceptance of the decay electron with transverse momentum $ p_{T}> $ 20 GeV in the forward electron pseudorapidity region $ 2.0 \leqslant \eta_{e} \leqslant 4.25 $. The charge asymmetry in the forward $ \eta_{e} $ region is sensitive to the ratio of u and d quark distributions in the proton as a function of Bjorken-x values of the partons, particularly providing valuable inputs for the accurate determination of PDFs at small and large x values between $ 10^{-4}\leqslant \times \leqslant 10^{-1} $.

NNLO predictions based on PDF sets NNPDF3.1, CT14, and MMHT2014 at 8 TeV are first presented and compared with the reference LHCb measurement [17]. The 8 TeV predictions are obtained for the $ W^{+} $/$ W^{-} $ cross section ratio and the charge asymmetry differential in bins of the $ \eta_{e} $. The predicted results from different PDF sets are found to be in good agreement with each other and with the LHCb data for most $ \eta_{e} $ bins. The results showed that the best description of the 8 TeV data is achieved by the prediction using MMHT2014 for both the cross section ratio and charge asymmetry. Furthermore, the predictions from different PDF sets describe the data quite well in the far forward $ \eta_{e} $ bins 3.5–3.75 and 3.75–4.25 in comparison to the predictions provided with the LHCb measurement, where they tend to underestimate the data within theoretical and experimental uncertainties. NNLO predictions using different PDF sets are therefore successfully justified with LHCb data at 8 TeV.

The 13 and 14 TeV NNLO results presented in this paper represent the first NNLO predictions of the charge asymmetry for the $W^{\pm}$ boson processes in the forward region $ 2.0 \leqslant \eta_{e} \leqslant 4.25 $. The 13 and 14 TeV predictions are reported for the differential cross-sections of the $W^{\pm}$ bosons and the charge asymmetry as a function of the $ \eta_{e} $. The predicted results from NNPDF3.1, CT14, and MMHT2014 are compared to test the sensitivity to discriminate among different PDF models. The $ W^{+} $ and $ W^{-} $ boson differential cross sections are predicted consistently among the PDF sets apart from some $ \eta_{e} $ bins, where the predictions from different PDF models exhibit slight discrepancies with respect to each other. The 14 TeV predictions for differential cross sections and their ratios are found to be more sensitive to distinguish among the PDF models in comparison to the 13 TeV predictions. The NNLO charge asymmetry results are reported to be in good agreement within total theoretical uncertainties among the predictions using different PDF sets for almost the entire $ \eta_{e} $ ranges at 13 and 14 TeV. Further, the sensitivity of the charge asymmetry distributions to the choice of PDF set are shown to be increased with the increasing collision energy from 13 to 14 TeV. Moreover, the predicted charge asymmetry results are compared at 8, 13, and 14 TeV collision energies using MMHT2014 as a baseline PDF set. The 13 and 14 TeV distributions are shown to separate from 8 TeV distribution in the $ \eta_{e} $ bin 3.0–3.25 towards the very forward $ \eta_{e} $ region, where the charge asymmetry is increased from 8 to 13 and 14 TeV distributions. In the forward bins $ \eta_{e} $ 3.25–4.25, the 13 and 14 TeV distributions are observed to overlap within uncertainties; however, the 14 TeV charge asymmetry distribution is predicted to be slightly higher than the 13 TeV distribution. The results clearly show that the very forward $ \eta_{e} $ bins are more of interest to precisely probe u and d quark distributions in the proton by shifting towards 13 and 14 TeV collision energies.

The author declares that he has no conflict of interest.