-
As a many-body problem, and moreover one involving two different kinds of particles, protons and neutrons, the nucleus represents one of the most significant challenges for theoretical physics today. The main difficulties arise from our incomplete knowledge of the nuclear forces acting inside the nucleus, and in the finite number of nucleons [1]. Thus, a numerical treatment has to be applied as the only way towards a reasonable description of the properties of such a system. Despite this situation, full shell model calculations based on first principles are at present affordable for light nuclei (roughly speaking with A
$ \leqslant $ 40) [2]. For heavier nuclei, however, a separation of the constituent nucleons has to be made into closed-shell ones (building a core) and valence nucleons, which are energetically above the core [3]. In some situations, for a better description of the nuclear properties, it may become necessary to break this schematic separation in order to allow excitations involving core nucleons.Naturally, grouping the A nucleons into agglomerations reduces the mathematical complexity of the problem, at the price of more phenomenology. The simplest concept of that type, and an extremely fruitful one, is the formation of pairs of like-nucleons, coupled to a total spin of L = 0
$ \hbar $ (or higher). The closest next step in this direction is the concept of the nucleus as composed of$ \alpha $ -particles, when this is allowed by the specific proton and neutron numbers Z and N, respectively. This approach has found many experimental confirmations in light nuclei [4].$ \alpha $ -cluster states have also been found in heavy nuclei. For example, some states in 212Po have been interpreted as an$ \alpha $ -particle coupled to the doubly-magic 208Pb core [5]. In such mass-asymmetric composite systems, the induced electric dipole moment leads to very strong E1 transitions, depopulating the cluster states to the ground-band levels. Studies of states with similar properties in medium-mass nuclei have provided further evidence of the formation of$ \alpha $ -clusters [6] in that mass region. Larger clusters have been also observed, although predominantly in exotic nuclear decays (e.g. 12C in Ref. [7].) This topic was thoroughly theoretically investigated in Ref. [8] on the basis of data on complex cluster radioactivity with emissions in the range 14C-34Si. Therein, a new formula was proposed describing the half-lives associated with cluster radioactivity, using both semi-empirical and microscopic approaches. These authors point out the importance of the number of$ \alpha $ -particles in the emitted large cluster, and although they state that the formation of large clusters in nuclei is an open theoretical problem, they suggest that several$ \alpha $ -particles and neutron pairs are correlated in such a structure just before the decay. More recently [9, 10], large-scale clustering has been proposed in specific even-even nuclei influencing the low-energy quadrupole excitations, including the observed B(E2) electromagnetic transition strengths. This phenomenon is different from the formation of nuclear molecules [11] in connection with giant resonances at much higher excitation energies. Such ideas are not completely new. In Ref. [12], the 16O$ \times $ 16O system was shown to be responsible for the existence of cluster bands in 32S whose properties were described by means of a unified treatment of bound and scattering states.Other experimental findings also indicate that additional effects may be responsible for the enhanced quadrupole collectivity at low spin in some even-even nuclei, which appeals for clarification. For example, both the shell model [13-15] and mean field (and beyond) (cf. Refs. [16, 17] and references therein) calculations fail to describe the full scale of quadrupole collectivity when applied to the A = 20-30 mass region. Thus, the multiparticle - multihole (mp-mh) configuration mixing approach from Ref. [18], applied to 25 even-even sd-shell nuclei, points to a lack of quadrupole collectivity in the model predictions. In the chain of even-even S isotopes, this effect found a possible explanation in Refs. [9, 19], where the large-scale clustering treatment was applied to 32S, including mixing between cluster states and spherical shell model states. In
$ ^{20,22} {\rm{Ne}}$ , the quadrupole collectivity enhancement effect was explained by the successful interpretation of their structure as strongly involving$ \alpha\;\otimes $ 16O and$ \alpha\;\otimes $ 78O cluster states, respectively, as shown in Refs. [10, 20, 21]. Within a more general context, the nucleus 20Ne represents a case where$ \alpha\;\otimes $ 16O clusterization has been used in a number of studies, sometimes yielding generally new concepts. The work by B. Zhou et al. [22], where the concept of non-localized clustering was proposed, deserves special attention. In that work, in the nuclear volume the two clusters move against each other without a mutual overlap, due to the blocking effect exercised by the Pauli principle. This concept differs from the simple and intuitive geometrical rigid-body picture more often associated with clustering, which we also use in the present work.Our manuscript addresses both new data, obtained by other authors, and older data, part of which were obtained with our participation. In the latter older works [10, 19], a simple toy model was proposed, which is applied here to the new data. The case of 80Zr was already considered within that model in Ref. [19], prior to data on lifetimes and absolute transition probabilities. This nucleus was proposed as an example of very large ground-band deformation much earlier, in Refs. [19, 23, 24], on the basis of level-energy spacings. As discussed below, obtaining deep theoretical insight into the phenomena considered is beyond the scope of our paper. Rather, we consider experimental observations, simultaneously raising a question which should be answered in the future with much more advanced theoretical considerations. Such considerations are beyond the specialization and competence of the authors, who are experimentalists.
-
Very recently, lifetime measurements in the N = Z nuclei 76Sr, 80Zr have been reported for the first time, establishing the maximum ground-state band deformation among other neighboring, non N = Z nuclei [25]. A very large quadrupole deformation (
$ \beta_2 \approx $ 0.4) of the yrast band in 80Zr was estimated by Lister et al. [23] on the basis of the level energy spacings (see also Ref. [24]). The new results of Ref. [25] confirm that earlier suggestion and fit into the general observation that nuclei with N$ \approx $ Z and A$ \approx $ 80 are among the most deformed nuclei observed so far. Superdeformation in 80Zr was discussed by Zheng and Zamick [26] together with the coexistence of a spherical and a superdeformed band (the latter corresponding to an ellipsoid with axis ratio 2/1). Exotic large-cluster decays of that nucleus were considered in Ref. [27].The present work investigates the implications that follow if excitations in 80Zr, and of course of the yrast band, are based on a two-cluster configuration consisting of two doubly-magic 40Ca nuclei. The approach is also implemented with the neighboring nuclei 76Sr and
$ ^{78,80} {\rm{Sr}}$ , 82Zr, whose two-cluster structure eventually also includes non-doubly magic constituents apart from 40Ca. The new findings are then compared to the previous analyses for 32S and 20Ne, with the aim of making conclusions about the existence of such excitations in this special class of nuclei.First, let us consider the systematics of the B(E2;
$ 2^+_1 \rightarrow 0 ^+_1 $ ) values in the above A$ \sim $ 80 Sr and Zr nuclei, shown in Fig. 1. The data are taken from Ref. [25] and the compilation in Ref. [28]. Obviously the N$ \approx $ Z nuclei form a group with B(E2) at least two time larger than the heavier isotopes (the drops in the vicinity of magic N = 50 are out of the scope of the discussion). Of course, it would be very interesting to see what happens in isotopes lighter than those displayed in Fig. 1, but for this purpose new dedicated lifetime measurements are needed.In Fig. 2, a Nilsson scheme [29] presenting the orbitals of importance in the nuclei considered in this work is shown as function of the deformation
$ \beta_2 $ ($ \epsilon_2 \approx $ 0.95$ \beta_2 $ ). The original figure [29] was slightly modified by us (by adding the two neutron numbers shown in red close to$ \beta_2 \approx $ 0). This scheme is valid for neutrons and below Z = 50, and also for protons with sufficient precision. At Z, N$ \approx $ 40, there are interesting subshell-closure effects, just before the filling of the 1g9/2 orbitals starts. The first is the complete filling of the 1f5/2 subshell, which is accomplished at Z, N = 38, as well as that of the 2p1/2 subshell at Z, N = 40. Then, an energy gap opens between 2p1/2 and 1g9/2, whose consequences are seen in many spectroscopic data. These gaps also appear far away from sphericity, at$ \beta_2 \approx $ 0.4, which characterizes the nuclei considered in the present work (see below). However, we do not enter here into any microscopic discussions of the two-cluster system. The Nilsson diagram is shown just to stress the possible importance of the neutron and proton numbers N, Z = 38, 40. The single particle orbitals of the 40Ca+40Ca system would hardly behave exactly as those shown in Fig. 2, of course. This issue will be addressed in somewhat more detail below. Here we only mention that in the case where there are no interactions involving nucleons from both clusters, i.e. when the clusters are considered as intrinsically independent systems, governed only by a nucleus-nucleus potential as at some stage of nuclear fusion reactions, Nilsson schemes of the type shown in Fig. 2 should be approximately valid for both clusters, but have to be displayed for smaller Z, N ($ \approx $ 20). Also, the details of the very process of fusion and its impact on the single particle orbitals occupied depends on the energy of the impinging nucleus. A recent review on this subject can be found in Ref. [30] and references therein. In addition, it should be mentioned that the 40Ca+40Ca system in the case of a very close distance (or, even more so, partial overlap) is subject to the Pauli exclusion principle [31]. The findings of the latter work will enter into the discussion below.
Figure 2. (color online) In the bottom part, a Nilsson scheme relevant for proton and neutron numbers just below Z, N = 50 is shown. The Nilsson scheme in the top part is relevant for neutrons above N = 50 [29]. See also text.
The properties of the Sr (Z = 38) and Zr (Z = 40) nuclei seem to be strongly affected by the above proton and neutron number effects, which combine with the expected enhancement of the quadrupole collectivity for N
$ \approx $ Z nuclei where the valence protons and neutrons occupy the same orbitals, thus ensuring a larger overlap of the wave functions and stronger interaction.Second, let us continue with a consideration of the B(E2;
$ 2^+_1 \rightarrow 0 ^+_1 $ ) transition strengths in the framework of the large-scale cluster approach [9, 10]. Because of the axial and$ {{R}}_\pi $ symmetries (the latter is a symmetry with reflection about a plane perpendicular to the axial symmetry axis and containing the center-of-mass point), it is possible to use the standard rotational formula for the reduced B(E2) transition strength in a K = 0 band,$ B(E2; 2 \rightarrow 0) = \frac{5}{16\pi}<2 0 2 0 |0 0>^2Q^2_0. $

(1) It is possible to show, however, that this formula is valid even in the absence of
${{R}} _\pi $ symmetry for axial rotors [10] (see the private communication by I. Ragnarsson in that work). In the appendix of Ref. [10], expressions for the volume and quadrupole integrals are derived and closed formulae for the intrinsic quadrupole moment presented for a system consisting of two overlapping spheres with different radii (and including the case of equal radii). A number of such systems relevant to the present work are presented schematically in Fig. 3.
Figure 3. (color online) Schematic representation of different systems of two overlapping spheres with radii R1 and R2. For 80Zr R1 = R2 = R. The meanings of some distances from the centers of the spheres to other points or to the intersection planes which are mentioned in the text are illustrated. One symmetric (80Zr) and two asymmetric cases (78Sr and 20Ne) are displayed. See also text.
The general assumption is that the low-lying quadrupole states in such systems can be considered as a superposition of cluster states (cl) and normal (e.g. nearly spherical or less deformed) states (norm),
$ |\Psi > = A_{\rm cl} |\Phi > + A_{\rm norm} |\Theta >. $

(2) Similar mixing with core excitations was employed in Ref. [32] for the interpretation of 44Ti lifetime data, in order to enhance the total transition strength in addition to that predicted by an
$ \alpha $ -cluster model calculation for that nucleus. Here, a more phenomenological approach is followed, concentrating on the B(E2) values while trying to learn more about the possible range of intrinsic quadrupole moments and mixing amplitudes. In principle, and with more data on excited$ 0^+ $ and$ 2^+ $ states, one may perform a two-band mixing calculation, as was done in the case of 32S [9], and find consistent solutions by also fitting the interaction strengths. However, since little data are available for 76Sr and 80Zr (considerations on$ ^{78,80} {\rm{Sr}}$ and 82Zr are also included later), it is preferred simply to assume that the composition of the wave functions of the$ 2^+_1 $ and$ 0^+_1 $ states is similar with respect to the weights of the unperturbed states, and is dominated by the cluster states in these nuclei. By definition,$ B(E2;2^+_1 \rightarrow 0^+_1) = |<0^+_1||E2||2^+_1>|^2/5 $

(3) and then, following the above assumption, the experimental E2 reduced matrix element reduces to
$ \begin{aligned}[b] <0^+_1||E2||2^+_1>_{\rm exp} =& A^2_{\rm cl}\sqrt{\frac{25}{16\pi}}<2 0 2 0 |0 0>Q_0 \\ & +(1-A^2_{\rm cl})<0^+_1||E2||2^+_1>_{\rm norm} \\ \approx& \sqrt{\frac{25}{16\pi}}<2 0 2 0 |0 0>Q_0. \end{aligned} $

(4) This includes another standard assumption, that the contribution of transitions between the cluster and normal wave-function components is negligible.
The procedure for reproducing the data from Refs. [28], [29] and reconsidering earlier investigated cases consists of the following steps.
● First, the root mean square charge radii R of the composite nuclei and of the constituent clusters were taken from the tables in Ref. [33]. When such data were not available due to the rather exotic character of the isotopes (namely, some of them very neutron-deficient) reasonable extrapolations were made. These were the cases of 76Sr (with extrapolation based on the data [33] for
$ ^{77,78,80} {\rm{Sr}}$ ) and$ ^{80,82} {\rm{Zr}}$ (extrapolation based on the data [33] for$ ^{87-91} {\rm{Zr}}$ and$ ^{78} {\rm{Sr}}$ ). The quantity R gives an idea of the actual nuclear dimensions and shape only to a first approximation, because of possible deviations from a spherical shape, diffuseness of the nuclear surface, effects of differences in the space distributions of neutrons and protons etc. However, R can be used to estimate the dimensions (volume) of the specific nucleus, and at least for the constituent clusters which all have shapes close to spherical, employing${{R}} _{1,2} $ seems to be a very good approximation.● Then, the distance
$ \Delta $ between the centers of the cluster spheres was varied until the experimental value of$ Q_0 $ was reproduced (the latter being obtained using Eqs. (3, 4)). The model value of$ Q_0 $ in the fitting procedure was provided by Eq. (A2) in Ref. [10] for a given$ \Delta $ . Attention was paid to the different possibilities displayed in Fig. 4 for symmetric and asymmetric combinations, as well as to the degree of overlap of the two spheres. The case where the center of one of the spheres is positioned inside the other sphere has to be distinguished from the case where both centers are out of the overlapping volume. The following formula for$ \Delta $ holds: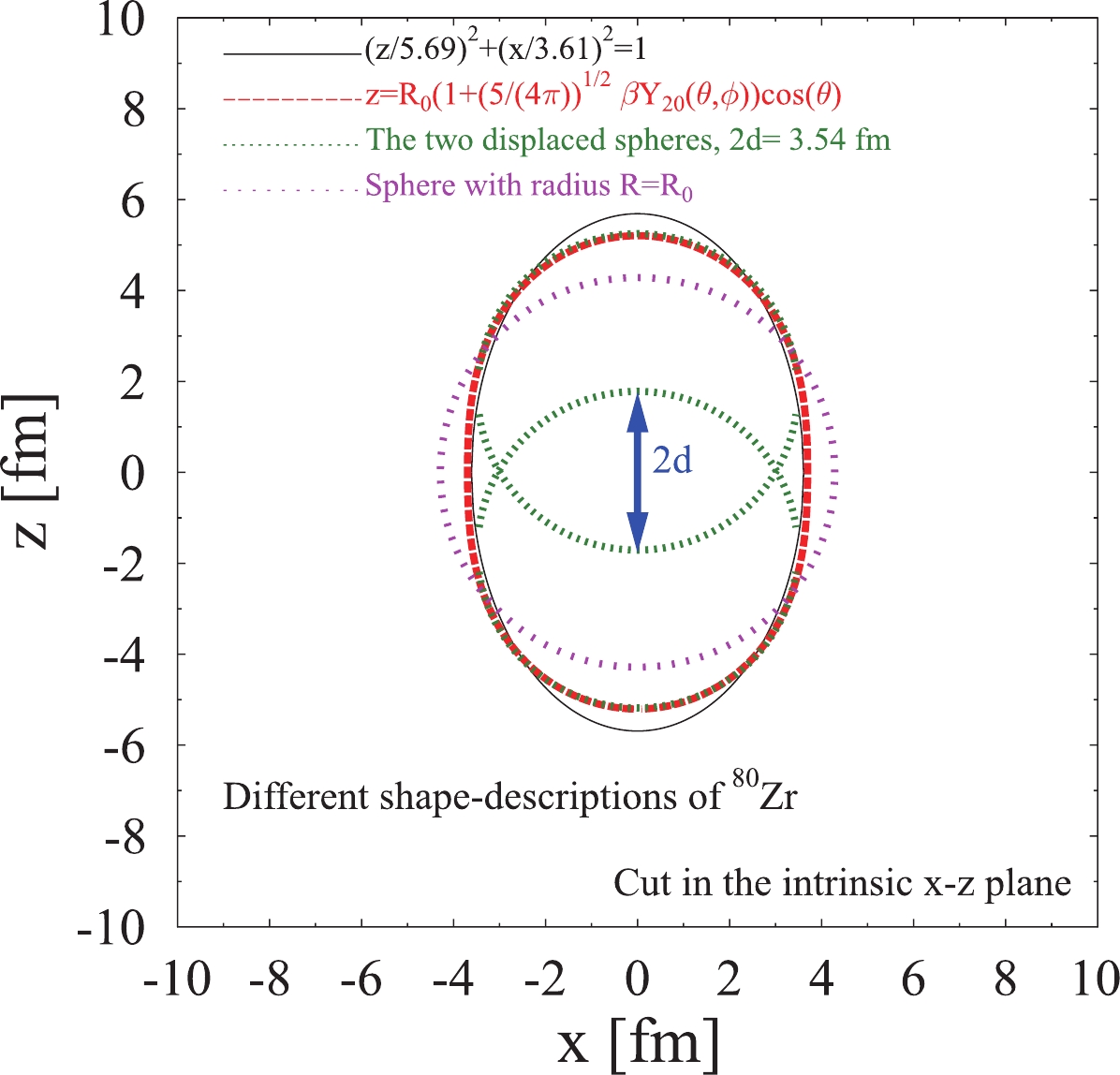
Figure 4. (color online) Geometrical representation of the different parameterizations indicated for the shape of 80Zr. A section of a sphere with a volume equal to the "experimental" volume is also shown, centered in the intersection plane at distance d from the centers of the two cluster spheres. See also text.
$ \Delta = d_2\pm\sqrt{R_1^2-R_2^2+d_2^2} = d_2\pm d_1, $

(5) based on the different geometries. We use the convention that
${{R}} _2 $ is always the radius of the larger sphere and${{R}} _1 $ that of the smaller sphere.The results of the attempts to reproduce the data are summarized in Table 1. In the cases of 32S and 20Ne, the results from the earlier publications [9, 10, 19] are listed, respectively, with some small modifications. For example, in 20Ne it turns out that both solutions for d2 (see Eq. (5)) used to calculate
$ \Delta $ are very similar, i.e. one cannot distinguish between them, but the values of$ \Delta $ are also very similar. Here, the findings from Refs. [20, 21] were used and reconfirmed, namely that the cluster component dominates the wave functions of the$ 0^+_1 $ and$ 2^+_1 $ states in 20Ne. Thus,$ \Delta $ was adjusted to the theoretical B(E2) from these works. In 32S, a two-band mixing calculation was applied and much more data were fitted [10, 23] to finally derive the value for$ \Delta $ shown in Table 1.Nucleus Radius/fm Clusters $ {{R}}^{\rm exp}_1 /{\rm{fm}}$ 

$ {{R}}^{\rm exp}_2 /{\rm{fm}}$ 

B(E2)exp/(e2b2) $ {{Q}}^{\rm exp}_0 /{\rm{(eb)}}$ 

$ \beta^{\rm exp}_2 $ 

$ {{Q}}^{\rm calc}_0 /{\rm{eb}}$ 

d2 or d/fm $ \Delta /{\rm{fm}}$ 

$ {{V}}^{\rm calc} /{\rm{fm}}^3$ 

${ {V} }^{\text{“}{\rm exp}" }$ (R)/fm3

$ ^{76}_{38} {\rm{Sr}} _{38} $ 

4.25 $ ^{36}_{18} {\rm{Ar}} _{18} $ +

$ ^{40C}_{20} {\rm{Ca}} _{20} $ 

3.391(2) 3.478(2) 0.222(27) 3.34(20) 0.45(3) 3.33 d2 = 2.01 3.87 298 322 $ ^{78}_{38} {\rm{Sr}} _{40} $ 

4.256(4) $ ^{38}_{18} {\rm{Ar}} _{20} $ +

$ ^{40}_{20} {\rm{Ca}} _{20} $ 

3.403(2) 3.478(2) 0.184(10) 3.04(8) 0.40(1) 3.04 d2 = 1.89 3.64 293 323 $ ^{80}_{38} {\rm{Sr}} _{40} $ 

4.256(4) $ ^{38}_{18} {\rm{Ar}} _{20} $ +

$ ^{42}_{20} {\rm{Ca}} _{22} $ 

3.403(2) 3.508(2) 0.182(8) 3.02(7) 0.393(9) 3.02 d2 = 1.906 3.61 296 323 $ ^{80}_{40} {\rm{Zr}} _{40} $ 

4.26 $ ^{40}_{20} {\rm{Ca}} _{20} $ +

$ ^{40}_{20} {\rm{Ca}} _{20} $ 

3.478(2) 3.478(2) 0.191(18) 3.10(15) 0.38(2) 3.10 d = 1.77 3.58 299 324 $ ^{82}_{40} {\rm{Zr}} _{42} $ 

4.26 $ ^{40}_{20} {\rm{Ca}} _{20} $ +

$ ^{42}_{20} {\rm{Ca}} _{22} $ 

3.478(2) 3.508(2) 0.182(24) 3.03(20) 0.368(24) 3.03 d2 = 1.77 3.48 301 326 $ ^{32}_{16} {\rm{S}} _{16} $ 

3.261(2) $ ^{16}_{8} {\rm{O}} _{8} $ +

$ ^{16}_{8} {\rm{O}} _{8} $ 

2.699(5) 2.699(5) 0.0050(4) 0.50(2) 0.285(12) 0.72 d = 1.28 2.56 137 145 $ ^{20}_{10} {\rm{Ne}} _{10} $ 

3.006(2) $ ^{4}_{2} {\rm{He}} _{4} $ +

$ ^{16}_{8} {\rm{O}} _{8} $ 

1.676(3) 2.699(5) 0.00645(61) 0.57(3) 0.71(4) 0.54 d2 $ \propto $ 2.55

1.13 102 114 Table 1. Numerical representation of the results of the present work. The investigated nuclei are displayed in the first column, followed by their root mean square radii taken from Ref. [33] (or extrapolated, when given without uncertainties). The two constituent clusters are shown in the 3rd column followed by their root mean square radii. The experimental B(E2;
$ 2^+_1 \rightarrow 0 ^+_1 $ ) values, the extracted$ {{Q}}^{\rm exp}_0 $ and the deformation$ \beta_2^{\rm exp} $ are displayed in the next three columns. Note that$\beta^{\rm exp}$ is calculated from$ {{Q}}^{\rm exp}_0 $ , keeping only the term linear in$ \beta $ in a series relating this quantity to$ {{Q}}_0 $ . The next three columns present the calculated (fitted) values of$ {{Q}}_0 $ , d2 or d, and the inter-sphere distance$ \Delta $ . The last two columns provide the calculated and experimental (see text and related discussion) volumes of the nucleus.The cases of
$ ^{76,78,80} {\rm{Sr}}$ and$ ^{80,82} {\rm{Zr}}$ were treated in a straightforward way as explained above, assuming nearly pure two-cluster configurations. It is remarkable that the obtained values of$ \Delta $ are so close to each other (between 3.48 and 3.87 fm). This is interpreted as pointing to the existence of the two large-scale clusters under discussion. Their formation leads to a strong enhancement of the quadrupole deformation. Of course, some small differences in the volumes${{V}} ^{\rm calc} $ and${{V}} ^{\rm exp} $ , of the order of 6%, have to be mentioned, but they may lie within the uncertainties when the root mean square charge radius R is used to calculate${{V}} ^{\rm exp} $ (see also discussion on R above). It should be mentioned that${{V}} ^{\rm exp} $ is calculated as the volume of a sphere with radius R (second column of Table 1). For${{V}} ^{\rm calc}$ , the expression from Eq. (A4) from the Appendix of Ref. [10] was used. In our simple toy model the nuclear density in the overlap region cannot be consistently discussed within the rigid-body picture. Since the calculated volumes are close to what can be calculated using the root mean square of the charge radius (these are the data we have available), we do not think that this density problem is so important in our schematic case. A much more involved approach may consider possible nucleon flow out of the overlapping region, or a double Fermi-like density distribution for the two clusters as employed normally close to the nuclear surface (where the density decreases from a nearly constant value to zero within a finite radial range). What can be noticed is that the calculated${{V}} ^{\rm calc} $ happens to be systematically smaller than${{V}} ^{\rm exp} $ . This may suggest that the radial dependence of the nuclear density close to the (external) two-cluster surfaces is modified in comparison with the standard case.The symmetric case of overlapping spheres,
$ R_1 $ =$ R_2 $ = R, is considered below in more detail. The distance between the centers of the spheres is 2d. The intrinsic quadrupole moment of this system can be expressed [19] as$ Q_0 = \frac{2Z\pi}{3}\frac{(6d^3R^2-d^5+2d^2R^3-3dR^4)} {\dfrac{4\pi}{3}\left(R^3+\dfrac{3}{2}dR^2-\dfrac{1}{2}d^3\right)}. $

(6) In Fig. 4, the case of 80Zr from the present work is presented, but differently from Fig. 3, here the emphasis is set on a few different ways to represent the nuclear shape geometrically. Apart from the two overlapping spheres with equal radii, a rotational ellipsoid is shown with axes chosen to reproduce the experimental
${{Q}} _0 $ value (${{Q}} ^{\rm ellipsoid}_0 $ = 2Z(c2-a2)/5 where c is the bigger axis and a is the smaller one). In addition, the projection in the (x,z) plane of a body with a radius R($ \theta,\phi $ ) =${{R}} _0 $ $\left(1+ \beta \sqrt{\dfrac{5}{4\pi}}Y_{20}(\theta,\phi)\right )$ in the intrinsic frame is presented, which is the fundamental dependence of that quantity used to describe quadrupole vibrations/rotations of the nuclear surface [34]. The good overall mutual agreement of all these representations hints at the viability of the two-cluster approach. One may ask what can be gained using this approach to describe other observables, e.g. the level energies in the ground-state band of 80Zr and the moment of inertia of that band. Since the shape associated with the two-sphere configuration is very similar to the standard ellipsoid (see Fig. 4), the toy-model output for the moment of inertia and e.g. the energy of the$ 2^+ $ and$ 4^+ $ level is nearly obvious, in line with the findings in Refs. [23, 26]. In principle, we could calculate the moment of inertia for a more precise comparison with what an ellipsoid would give, although without hoping, in either case, to reproduce precisely the experimental energies of the ground-band levels.Finally, and also within the context of the nuclear density in the overlap region, we mention that the toy model presented here may fit some of the results of Ref. [31]. In that work, the authors investigate how the Pauli exclusion principle affects the fusion of nuclei. In particular, Fig. 1 from Ref. [31] (panel a) displays the nucleus-nucleus potential for the system 40Ca+40Ca, calculated using different versions of their newly proposed model, the density-constraint frozen Hartree-Fock method (DCFHF). Within this model, the Pauli principle, inducing repulsion between composite systems formed of identical fermions, is taken into account. The result is a potential pocket at very small distances, with a minimum positioned just below R = 7 fm (R is the inter-nucleus distance). Some stabilization of the 40Ca+40Ca system around that point may take place, accompanied by distance vibrations. However, keeping in mind that the
$ \Delta $ values derived in the present work are about two times smaller (3.5-3.9 fm), one can only suggest some possible rough agreement with the results of Ref. [31]. The Pauli exclusion principle may also lead to some flow out of the overlap region, as suggested in the previous paragraph. -
In principle, both rigid deformation and/or vibrations may be responsible for the establishment of a mean distance
$ \Delta $ between the two spheres. A deep theoretical insight into this picture is beyond the scope of the present paper. We do not see any reason for not considering a two-sphere configuration as an alternative to the standard ellipsoid, and this only for some special N, Z cases as discussed in the text, since the final shapes are very close. The two-center configuration provides an additional degree of freedom, related to possible vibrations of the distance between the two centers. To assess the phenomenon in depth, much more advanced theoretical efforts are needed in order to eventually reach a quantitative quantum mechanical description. Nevertheless, the formation of large-size clusters, and their relative motion as a possible excitation mode, are suggested by this study to be closely related to the origin of deformation in the specific cases of two doubly-magic clusters or two clusters with nearby characterization. In order to check for such effects experimentally, dedicated nuclear reaction studies involving collisions between two possible large clusters for a given residual nucleus may provide very useful information. With the advances of both experimental techniques and radioactive ion beams (RIB), such measurements could soon be realized even in the cases of very exotic composite nuclei.
Strongly enhanced quadrupole deformation in a class of N ≈ Z nuclei driven by large-scale clustering?
- Received Date: 2021-01-26
- Available Online: 2021-06-15
Abstract: The formation of large size clusters, and/or their relative motion as a possible excitation mode, are suggested to be closely related to the origin of deformation in specific cases, namely the case of two doubly-magic clusters or two clusters with nearby characterization. New lifetime data in N = Z 76Sr and 80Zr leading to large B(E2) values are reproduced consistently and well within this approach, along with data for a few neighboring N





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: