-
The singularity theorems proved by Penrose and Hawking state that under the main assumptions of the strong energy condition holding and the existence of global hyperbolicity, in the framework of General Relativity, every black hole inevitably contains a singularity [1]. At a space-time singularity, the curvatures and densities go to infinity [1, 2] and the predictive power of physical laws is completely broken down. It is widely believed that space-time singularities are a reflection of the incompleteness of General Relativity, and can be solved in a quantum theory of gravity. Surprisingly, in 1968 Bardeen [3] obtained a black hole solution without a singularity, which can be interpreted as a gravitationally collapsed magnetic monopole arising in a specific form of nonlinear electrodynamics [4]. After that, more regular (non-singular) black holes such as the Ayón-Beato and García black hole [5], Hayward black hole [6], and Berej-Matyjasek-Trynieki-Wornowicz black hole [7] were proposed. The spherically symmetric Bardeen black hole is described by the metric
$ {\rm{d}}s^{2} = -f\left(r\right){\rm{d}}t^{2}+f\left(r\right)^{-1}{\rm{d}}r^{2}+r^{2}{\rm{d}}\Omega^{2}, $

$ f\left(r\right) = 1-\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}, $

(1) where g and M are the magnetic charge and mass, respectively. It should be noted that the metric behaves like the Schwarzschild metric at large distances (
$ g/r\ll 1 $ ), and near the origin it behaves like de Sitter geometry, which can be realized from$ f\left(r\right)\simeq 1-\frac{2M}{g^{3}}r^{2}, \quad \frac{g}{r}\gg 1. $

(2) Equation (2) suggests that the Bardeen black hole avoids singularities by a de Sitter core, i.e. the pressure is negative and thus would prevent a singular end-state of the gravitationally collapsed matter [8, 9]. All regular black holes (including Bardeen black holes) violate the weak energy condition. However, the region of violation is always shielded by the Cauchy horizon [10-13]. In fact, this violation of classical energy conditions is a natural consequence of the fact that the singularity-free metric might incorporate some quantum gravity effects [12].
Modern cosmological observations reveal that our current universe contains mainly of 4.9% baryon matter, 26.8% dark matter, and 68.3% dark energy, according to the Standard Model of Cosmology [14]. Therefore, it is necessary to consider black hole solutions surrounded by dark matter or dark energy. In recent years, black holes surrounded by quintessence dark energy have attracted much attention. For example, Kiselev [15] considered a Schwarzschild black hole surrounded by quintessence energy and then Toshmatov and Stuchlík [16] extended it to the Kerr-like black hole. The quasinormal modes, thermodynamics and phase transition from a Bardeen black hole surrounded by quintessence was discussed by Saleh and Thomas [17]. Hayward black holes surrounded by quintessence have been studied in Ref. [18], and in Refs. [19-24]. On the other hand, as one candidate for dark matter, perfect fluid dark matter (PFDM) was proposed by Kiselev [15, 25] and further studied in Ref. [26], offering a reasonable explanation for the asymptotically flat rotational velocity in spiral galaxies; see Refs. [27-31] for more recent research. In this work, following Refs. [16, 18], we generalize the Schwarzschild black hole surrounded by PFDM to the spherically symmetric Bardeen black hole. Furthermore, by resorting to the Newman-Janis algorithm, we obtain the rotating Bardeen black hole in PFDM.
The paper is organized as follows. The next section gives the derivation of a spherically symmetric Bardeen black hole surrounded by PFDM. In Sec. III, we discuss its thermodynamic properties. In Sec. IV, by applying the Newman-Janis algorithm, we obtain the rotating Bardeen black hole surrounded by PFDM. The weak energy condition is the subject of Sec. V. In Sec. VI, the horizons and the ergospheres of a Bardeen black hole surrounded by PFDM are studied. In Sec. VII, we investigate the energy extraction by the Penrose process. Discussion and conclusions are presented in Sec. VIII. Planck units,
$ \hbar = G = c = k_{B} = 1 $ , are used throughout the paper. -
Given the coupling between gravitational and non-linear electromagnetic fields, the Einstein-Maxwell equations should be modified as:
$ G_{\mu}^{\,\nu} = 2\left(\frac{\partial{\cal{L}}\left(F\right)}{\partial F}F_{\mu\lambda}F^{\nu\lambda}-\delta_{\mu}^{\,\nu}{\cal{L}}\right)+8\pi T_{\mu}^{\,\nu}, $

(3) $ \nabla_{\mu}\left(\frac{\partial{\cal{L}}\left(F\right)}{\partial F}F^{\nu\mu}\right) = 0, $

(4) $ \nabla_{\mu}\left(*F^{\nu\mu}\right) = 0. $

(5) Here,
$ F_{\mu\nu} = 2\nabla_{[\mu}A_{\nu]} $ and$ {\cal{L}} $ is a function of$ F\equiv\dfrac{1}{4}F_{\mu\nu}F^{\mu\nu} $ given by [4]$ {\cal{L}}\left(F\right) = \frac{3M}{\vert g\vert^{3}}\left(\frac{\sqrt{2g^{2}F}}{1+\sqrt{2g^{2}F}}\right)^{\frac{5}{2}}, $

(6) where g and M are the parameters associated with magnetic charge and mass, respectively.
In this work, we consider black holes surrounded by PFDM, following Kiselev [15, 25] and Li and Yang [26]. The energy-momentum tensor of PFDM in the standard orthogonal basis is given by
$ T_{\nu}^{\,\mu} = {\rm{diag}}(-\epsilon,p_r,p_\theta,p_\phi) $ , with the density, radial and tangential pressures of the PFDM being$ \epsilon = -p_r = -\frac{\alpha}{8\pi r^3}, \qquad p_\theta = p_\phi = -\frac{\alpha}{16\pi r^3}\ . $

(7) To obtain a solution that satisfies Eqs. (3)-(5), we assume a spherically symmetric line element,
$ {\rm{d}}s^{2} = -f\left(r\right){\rm{d}}t^{2}+f\left(r\right)^{-1}{\rm{d}}r^{2}+r^{2}{\rm{d}}\Omega^{2},\quad f\left(r\right) = 1-\frac{2m\left(r\right)}{r}, $

(8) and we use the ansatz for a Maxwell field [4]
$ F_{\mu\nu} = \left(\delta_{\mu}^{\theta}\delta_{\nu}^{\varphi}-\delta_{\nu}^{\theta}\delta_{\mu}^{\varphi}\right)B\left(r,\theta\right). $

(9) Next, using Eqs. (4) and (5), Eq. (9) can be simplified as
$ F_{\mu\nu} = \left(\delta_{\mu}^{\theta}\delta_{\nu}^{\varphi}-\delta_{\nu}^{\theta}\delta_{\mu}^{\varphi}\right)g\sin{\theta}, $

(10) where g is the integration constant. Further, one can get
$ F = g^{2}/2r^{4} $ . In order to give a direct physical interpretation for g, for any 2-sphere S at infinity, we consider the following integral:$ \frac{1}{4\pi}\int_{S}*F = \frac{g}{4\pi}\int_{0}^{\pi}\int_{0}^{2\pi}\sin{\theta}{\rm{d}}\theta{\rm{d}}\varphi = g. $

(11) From Eq. (11), one can confirm that g is the magnetic monopole charge.
Now, with the help of the above equations, the time component of Eq. (3) reduces to
$ -\frac{2}{r^{2}}\frac{{\rm{d}}m\left(r\right)}{{\rm{d}}r} = -\frac{6Mg^{2}}{\left(r^{2}+g^{2}\right)^{\frac{5}{2}}}+\frac{\alpha}{r^{3}}. $

(12) Integrating Eq. (12) from r to
$ \infty $ and using$ M = \lim_{r\to\infty}\left(m\left(r\right)+\dfrac{\alpha}{2}\ln{\dfrac{r}{\vert\alpha\vert}}\right) $ , one finally gets$ f\left(r\right) = 1-\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}. $

(13) Note that, in the absence of PFDM, i.e.
$ \alpha = 0 $ , the above space-time recovers that of the Bardeen black hole; in the case of$ g = 0 $ [3, 4], it reduces to the Schwarzschild black hole surrounded by PFDM [25, 26]; and if$ \alpha = 0 $ and$ g = 0 $ , we obtain the Schwarzschild black hole.As mentioned in the introduction, a Bardeen black hole (
$ \alpha = 0 $ ) is regular everywhere. To check whether this characteristic is changed by the presence of PFDM, we calculate the following curvature scalars:$ R = \frac{6M g^{2}\left(4g^{2}-r^{2}\right)}{\left(g^{2}+r^{2}\right)^{\frac{7}{2}}}-\frac{\alpha}{r^{3}}, $

(14) $\begin{aligned}[b] R_{\mu\nu} R^{\mu\nu} =& \frac{18M^{2}g^{4}\left(8g^{4}-4g^{2}r^{2}+13r^{4}\right)}{\left(g^{2}+r^{2}\right)^{7}}\\&-\frac{6Mg^{2}\left(2g^{2}+7r^{2}\right)\alpha}{r^{3}\left(g^{2}+r^{2}\right)^{\frac{7}{2}}}+\frac{5\alpha^{2}}{2r^{6}}, \end{aligned}$

(15) $ \begin{aligned}[b] {\cal{K}} =& R_{\mu\nu\sigma\tau}R^{\mu\nu\sigma\tau} = \frac{12 \alpha^2 \ln^2\dfrac{r}{\left| \alpha\right| }}{r^6}\\&+\frac{13 \alpha^2}{r^6}+\frac{4 \alpha \ln\dfrac{r}{\left|\alpha\right| } \left[\dfrac{6 M r^5 \left(3 g^2-2 r^2\right)}{\left(g^2+r^2\right)^{7/2}}-5 \alpha\right]}{r^6} \\ &+ \frac{4 \alpha M \left(-2g^4-37 g^2 r^2+10 r^4\right)}{r^3 \left(g^2+r^2\right)^{7/2}}\\&+\frac{12 M^2 \left(8 g^8-4 g^6 r^2+47 g^4 r^4-12 g^2 r^6+4 r^8\right)}{\left(g^2+r^2\right)^7}. \end{aligned} $

(16) It turns out that a Bardeen black hole surrounded by PFDM is singular at
$ r = 0 $ . In fact, the future singularity comes from the dark matter background. -
Let us now turn to the thermodynamic properties of a Bardeen black hole in PFDM. For convenience, we write here the line element of a spherically symmetric black hole, obtained in the previous section, as
$ \begin{aligned}[b] {\rm{d}}s^{2} =& -f\left(r\right){\rm{d}}t^{2}+f\left(r\right)^{-1}{\rm{d}}r^{2}+r^{2}{\rm{d}}\Omega^{2},\\ f\left(r\right) =& 1-\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}. \end{aligned} $

(17) The black hole mass M can be expressed in terms of event horizon
$ r_+ $ as$ M = \frac{\left(r_+^{2}+g^{2}\right)^{\frac{3}{2}}}{2r_+^{2}}\left(1+\frac{\alpha}{r_+}\ln\frac{r_+}{\vert\alpha\vert}\right), $

(18) which comes from
$ f\left(r_{+}\right) = 0 $ . According to the Bekenstein area law, the entropy S of the black hole can be calculated as$ S = \frac{{\cal{A}}}{4} = \int_{0}^{2\pi}\int_{0}^{\pi}\sqrt{g_{\theta\theta}g_{\varphi\varphi}}{\rm{d}}\theta{\rm{d}}\varphi = \pi r_+^{2}. $

(19) Making use of this, one can rewrite Eq. (18) as
$ M = \frac{\left(S+\pi g^{2}\right)^{\frac{3}{2}}}{2\sqrt{\pi}S}\left(1+\frac{\sqrt{\pi}\alpha}{\sqrt{S}}\ln\frac{\sqrt{S}}{\sqrt{\pi}\vert\alpha\vert}\right). $

(20) Other thermodynamic quantities can be obtained through thermodynamic identities. For examples, the temperature T, the magnetic potential
$ \Psi $ , and the conjugate quantity to the dark matter parameter$ \alpha $ are given by$\begin{aligned}[b] T =& \left(\frac{\partial M}{\partial S}\right)_{g,\alpha} \\=& \frac{\sqrt{r_+^2+g^2}\left(r_+\left(r_+^{2}-2g^{2}\right)+\alpha\left(r_+^{2}+g^{2}\right)-3g^{2}\alpha\ln{\dfrac{r_+}{\vert\alpha\vert}}\right)}{4\pi r_+^{5}}, \end{aligned}$

(21) $ \Psi = \left(\frac{\partial M}{\partial g}\right)_{T,\alpha} = \frac{3g\sqrt{r_+^{2}+g^2}\left(r_++\alpha\ln\dfrac{r_+}{\vert\alpha\vert}\right)}{2r_+^3}, $

(22) $ \Pi = \left(\frac{\partial M}{\partial \alpha}\right)_{T,\,g} = \frac{(r_+^{2}+g^2)^{\frac{3}{2}}\left(-1+\ln\dfrac{r_+}{\vert\alpha\vert}\right)}{2r_+^3}. $

(23) Note that here we have treated the dark matter parameter
$ \alpha $ as a new thermodynamic variable and$ \Pi $ is its conjugate quantity, as shown in Refs. [32-35]. It is easy to check that those thermodynamic quantities satisfy the first law of black hole thermodynamics,$ {\rm{d}}M = T{\rm{d}}S+\Psi{\rm{d}}g+\Pi{\rm{d}}\alpha, $

(24) and the Smarr formula,
$ M = 2TS+\Psi g+\Pi \alpha, $

(25) which is exactly consistent with the scaling dimensional argument.
In what follows, we will investigate the thermodynamic stability of a Bardeen black hole in PFDM. The heat capacity at constant volume is defined as
$ C_{V} = T\frac{\partial{S}}{\partial{T}} = T\frac{\partial{S}}{\partial{r_+}}\left(\frac{\partial{T}}{\partial{r_+}}\right)^{-1}. $

(26) Plugging Eqs. (19) and (21) into Eq. (26), one finally arrives at
$ \begin{aligned}[b]C_{V} = -\frac{2\pi r_+^{2}\left(r_+^{2}+g^{2}\right)\left(r_+^{3}+\alpha r_+^{2}-2g^{2}r_++g^{2}\alpha-3g^{2}\alpha\ln\dfrac{r_+}{\vert\alpha\vert}\right)}{r_+^{4}\left(r_++2\alpha\right)-8g^{4}\left(r_+-\alpha\right)+2g^{2}r_+^{2}\left(5\alpha-2r_+\right)-3g^{2}\left(5g^{2}+4r_+^{2}\right)\alpha\ln\dfrac{r_+}{\vert\alpha\vert}}.\end{aligned} $ 
(27) The behavior of
$ C_{V} $ as a function of$ r_{+} $ is plotted in Fig. 1 for different values of magnetic charge g and dark matter parameter$ \alpha $ . For given values of parameters a and g, there is a critical radius$ r_{+}^{C} $ where heat capacity$ C_{V} $ diverges and the second order phase transition occurs. Figure 1 indicates that the heat capacity is positive and the black hole is thermodynamically stable in the range$ 0<r_{+}<r_{+}^{C} $ . Clearly, the critical radius$ r_{+}^{C} $ increases with magnetic charge g and decreases with dark matter parameter$ \alpha $ . -
In this section, with the Newman-Janis algorithm (NJA), we will generalize the spherically symmetric Bardeen black hole solution in PFDM to the Kerr-like rotational black hole solution. The NJA was first proposed by Newman and Janis in 1965 [36] and has been widely used in many studies [16, 18, 37-45]. In this work, we adopt the NJA modified by Azreg-Aïnou [46, 47], which can generate rotating regular black hole solutions without complexification.
Consider the general static and spherically symmetric metric:
$\begin{aligned}[b]& {\rm{d}}s^{2} = -f\left(r\right){\rm{d}}t^{2}+g\left(r\right)^{-1}{\rm{d}}r^{2}+h\left(r\right){\rm{d}}\Omega^{2},\\& {\rm{d}}\Omega^{2} = {\rm{d}}\theta^{2}+\sin^{2}{\theta}{\rm{d}}\varphi^{2}.\end{aligned} $

(28) At the first step of this algorithm, we transform the spherically symmetric space-time metric (28) from the Boyer-Lindquist (BL) coordinates (
$ t, r, \theta, \varphi $ ) to the Eddington-Finkelstein (EF) coordinates ($ u, r, \theta, \varphi $ ) by carrying out the coordinate transformation$ {\rm{d}}u = {\rm{d}}t-\frac{{\rm{d}}r}{\sqrt{f(r)g(r)}}. $

(29) As the result of this transformation, the line element (28) takes the form
$\begin{aligned}[b] {\rm{d}}s^{2} =& -f\left(r\right){\rm{d}}u^{2}-2\sqrt{\frac{f\left(r\right)}{g\left(r\right)}}{\rm{d}}u{\rm{d}}r\\&+h\left(r\right)\left({\rm{d}}\theta^{2}+\sin^{2}{\theta}{\rm{d}}\varphi^{2}\right). \end{aligned}$

(30) In terms of the null tetrads satisfying the relations
$ l_{\mu}l^{\mu} = $ $ n_{\mu}n^{\mu} = m_{\mu}m^{\mu} = l_{\mu}m^{\mu} = n_{\mu}m^{\mu} = 0,\, l_{\mu}n^{\mu} = -m_{\mu}\bar{m}^{\mu} = 1$ , thecontravariant metric tensor associated with the line element (30) can be expressed as$ g^{\mu\nu} = -l^{\mu}n^{\nu}-l^{\nu}n^{\mu}+m^{\mu}\bar{m}^{\nu}+m^{\nu}\bar{m}^{\mu}, $

(31) where
$ \begin{aligned}[b] & l^{\mu} = \delta^{\mu}_{r},\qquad n^{\mu} = \sqrt{\frac{g\left(r\right)}{f\left(r\right)}}\delta^{\mu}_{0}-\frac{f\left(r\right)}{2}\delta^{\mu}_{r},\\ &m^{\mu} = \frac{1}{\sqrt{2h\left(r\right)}}\delta^{\mu}_{\theta}+\frac{\rm i}{\sqrt{2h\left(r\right)}\sin{\theta}}\delta^{\mu}_{\varphi},\\&\bar{m}^{\mu} = \frac{1}{\sqrt{2h\left(r\right)}}\delta^{\mu}_{\theta}-\frac{\rm i}{\sqrt{2h\left(r\right)}\sin{\theta}}\delta^{\mu}_{\varphi}. \end{aligned} $

(32) Next, we take the critical step of the NJA, which is to perform complex coordinate transformations in the
$ u-r $ plane,$ \begin{array}{l} u\rightarrow u-{\rm i}a\cos{\theta},\quad r\rightarrow r+{\rm i}a\cos{\theta}. \end{array} $

(33) At the same time, we assume that as a result of these transformations, the metric functions also turn into a new form:
$ f\left(r\right)\rightarrow F\left(r, a, \theta\right) $ ,$ g\left(r\right)\rightarrow G\left(r, a, \theta\right) $ , and$ h\left(r\right)\rightarrow\Sigma = $ $ r^{2}+a^{2}\cos^{2}{\theta} $ [46, 47]. Furthermore, the null tetrads also take new forms,$ \begin{aligned}[b] l^{\mu} =& \delta^{\mu}_{r},\quad n^{\mu} = \sqrt{\frac{G}{F}}\delta^{\mu}_{0}-\frac{1}{2}F\delta^{\mu}_{r},\\ m^{\mu} =& \frac{1}{\sqrt{2\Sigma}}\left(\delta^{\mu}_{\theta}+{\rm i}a\sin{\theta}\left(\delta^{\mu}_{0}-\delta^{\mu}_{r}\right)+\frac{\rm i}{\sin{\theta}}\delta^{\mu}_{\varphi}\right),\\ \bar{m}^{\mu} = &\frac{1}{\sqrt{2\Sigma}}\left(\delta^{\mu}_{\theta}-{\rm i}a\sin{\theta}\left(\delta^{\mu}_{0}-\delta^{\mu}_{r}\right)-\frac{\rm i}{\sin{\theta}}\delta^{\mu}_{\varphi}\right). \end{aligned} $

(34) Then by means of Eq. (31), the contravariant components of the metric
$ g^{\mu\nu} $ can be obtained as:$ \begin{aligned}[b] g^{uu} =& \frac{a^{2}\sin^{2}{\theta}}{\Sigma},\quad g^{rr} = G+\frac{a^{2}\sin^{2}{\theta}}{\Sigma},\\ g^{\theta\theta} =& \frac{1}{\Sigma},\quad g^{\varphi\varphi} = \frac{1}{\Sigma\sin^{2}{\theta}},\\ g^{ur} =& g^{ru} = -\sqrt{\frac{G}{F}}-\frac{a^{2}\sin^{2}{\theta}}{\Sigma},\\ g^{u\varphi} = &g^{\varphi u} = \frac{a}{\Sigma},\quad g^{r\varphi} = g^{\varphi r} = -\frac{a}{\Sigma}. \end{aligned} $

(35) Accordingly, the rotating metric in the EF coordinates of (
$ u, r, \theta, \varphi $ ) reads$ \begin{aligned}[b] {\rm{d}}s^{2} =& -F{\rm{d}}u^{2}-2\sqrt{\frac{F}{G}}{\rm{d}}u{\rm{d}}r+2a\left(F-\sqrt{\frac{F}{G}}\right)\sin^{2}{\theta}{\rm{d}}u{\rm{d}}\varphi\\&+\Sigma{\rm{d}}\theta^{2} +2a\sin^{2}{\theta}\sqrt{\frac{F}{G}}{\rm{d}}r{\rm{d}}\varphi\\&+\sin^{2}{\theta}\left[\Sigma+a^{2}\left(2\sqrt{\frac{F}{G}}-F\right)\sin^{2}{\theta}\right]{\rm{d}}\varphi^{2}. \end{aligned} $

(36) The last step of the NJA is to bring Eq. (36) to BL coordinates by using the following coordinate transformations:
$ {\rm{d}}u = {\rm{d}}t+\lambda\left(r\right){\rm{d}}r,\quad {\rm{d}}\varphi = {\rm{d}}\phi+\chi\left(r\right){\rm{d}}r, $

(37) where the functions
$ \lambda\left(r\right) $ and$ \chi\left(r\right) $ can be found using the requirement that all the nondiagonal components of the metric tensor, except the coefficient$ g_{t\phi} $ $ (g_{\phi t}) $ , are equal to zero [46, 47]. Thus,$ \lambda\left(r\right) = -\frac{k(r)+a^{2}}{g\left(r\right)h\left(r\right)+a^{2}},\quad \chi\left(r\right) = -\frac{a}{g\left(r\right)h\left(r\right)+a^{2}}, $

(38) with
$ k\left(r\right) = \sqrt{\frac{g\left(r\right)}{f\left(r\right)}}h\left(r\right), $

(39) and
$ F\left(r,\theta\right) = \frac{\left(gh+a^{2}\cos^{2}{\theta}\right)\Sigma}{\left(k^{2}+a^{2}\cos^{2}{\theta}\right)^{2}}, \quad G\left(r,\theta\right) = \frac{gh+a^{2}\cos^{2}{\theta}}{\Sigma}. $

(40) Here, for convenience, we omit the variables of
$ f(r) $ ,$ g(r) $ ,$ h(r) $ and$ k(r) $ .Finally, the rotating solution corresponding to the spherically symmetric metric (28) can therefore be obtained as
$ \begin{aligned}[b] {\rm{d}}s^{2} =& -\frac{\left(gh+a^{2}\cos^{2}{\theta}\right)\Sigma}{\left(k+a^{2}\cos^{2}{\theta}\right)^{2}}{\rm{d}}t^{2}+\frac{\Sigma}{gh+a^{2}}{\rm{d}}r^{2}\\&-2a\sin^{2}\theta\left[\frac{k-gh}{\left(k+a^{2}\cos^{2}{\theta}\right)^{2}}\right]\Sigma{\rm{d}}\phi{\rm{d}}t +\Sigma{\rm{d}}\theta^{2}\\ &+\Sigma\sin^{2}\theta\left[1+a^{2}\sin^{2}\theta\frac{2k-gh+a^{2}\cos^{2}\theta}{\left(k+a^{2}\cos^{2}{\theta}\right)^{2}}\right]{\rm{d}}\phi^{2}. \end{aligned} $

(41) In the case of Bardeen black holes in PFDM, comparing the line elements (17) with (28), one can find
$ f\left(r\right) = g\left(r\right) = 1-\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}, \quad h\left(r\right) = k\left(r\right) = r^{2}. $

(42) Substituting the above expressions into Eq. (41), we obtain the metric of rotating Bardeen black holes in PFDM in the form
$ \begin{aligned}[b] {\rm{d}}s^{2} =& -\left(1-\frac{2\rho r}{\Sigma}\right){\rm{d}}t^{2}+\frac{\Sigma}{\Delta_{r}}{\rm{d}}r^{2}+\Sigma{\rm{d}}\theta^{2}-\frac{4a\rho r\sin^{2}{\theta}}{\Sigma}{\rm{d}}t{\rm{d}}\phi\\ &+\sin^{2}{\theta}\left(r^{2}+a^{2}+\frac{2a^{2}\rho r\sin^{2}{\theta}}{\Sigma}\right){\rm{d}}\phi^{2}, \end{aligned} $

(43) with
$ \begin{aligned} 2\rho =& \frac{2Mr^{3}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}-\alpha\ln{\frac{r}{\vert\alpha\vert}},\\ \Sigma =& r^{2}+a^{2}\cos^{2}{\theta},\\ \Delta_{r} =& r^{2}+a^{2}-\frac{2Mr^{4}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\alpha r\ln{\frac{r}{\vert\alpha\vert}}. \end{aligned} $

(44) Now, we come to consider the energy-momentum tensor. With the help of the
$ Mathematica $ package, from the metric (43), the nonvanishing components of the Einstein tensor$ G_{\mu\nu} $ are given by:$ \begin{aligned}[b] G_{tt} =& \frac{2\left(r^{4}+a^{2}r^{2}-2r^{3}\rho-a^{4}\sin^{2}{\theta}\cos^{2}{\theta}\right)\rho'}{\Sigma^{3}}-\frac{a^{2}r\sin^{2}{\theta}\rho''}{\Sigma^{2}},\\ G_{t\phi} =& \frac{2a\sin^{2}{\theta}\left[\left(r^{2}+a^{2}\right)\left(a^{2}\cos^{2}{\theta}-r^{2}\right)+2r^{3}\rho\right]\rho'}{\Sigma^{3}}\\ &+\frac{ar\sin^{2}{\theta}\left(r^{2}+a^{2}\right)\rho''}{\Sigma^{2}}, \end{aligned} $

$ \begin{aligned}[b] G_{rr} =& -\frac{2r^{2}\rho'}{\Sigma\Delta_{r}},\quad G_{\theta\theta} = -\frac{2a^{2}\cos^{2}{\theta}\rho'}{\Sigma}-r\rho'',\\ G_{\phi\phi} =& -\frac{a^{2}\sin^{2}{\theta}\left(r^{2}+a^{2}\right)\left[a^{2}+\left(2r^{2}+a^{2}\right)\cos{2\theta}\right]}{\Sigma^{3}}\\&-\frac{4a^{2}r^{3}\sin^{4}{\theta}\rho\rho'}{\Sigma^{3}}-\frac{r\sin^{2}{\theta}\left(a^{2}+r^{2}\right)^{2}\rho''}{\Sigma^{2}}, \end{aligned} $

(45) in which the prime
$ ' $ denotes the derivative with respect to r.In order to obtain the components of the energy-momentum tensor, as shown in Refs. [16, 18], we introduce the standard orthonormal basis of the rotating Bardeen black hole in PFDM:
$ \begin{aligned}[b] e^{\mu}_{\left(t\right)} =& \frac{1}{\sqrt{\Delta_{r}\Sigma}}\left(r^{2}+a^{2},0,0,a\right),\\ e^{\mu}_{\left(r\right)} =& \sqrt{\frac{\Delta_{r}}{\Sigma}}\left(0,1,0,0\right),\\ e^{\mu}_{\left(\theta\right)} =& \frac{1}{\sqrt{\Sigma}}\left(0,0,1,0\right),\\ e^{\mu}_{\left(\phi\right)} =& -\frac{1}{\sqrt{\Sigma\sin^{2}{\theta}}}\left(a\sin^{2}{\theta},0,0,1\right). \end{aligned} $

(46) Combining Eqs. (45), (46), and the Einstein field equation
$ G_{\mu\nu} = 8\pi T_{\mu\nu} $ , the components of the energy-momentum tensor can be obtained as:$ \begin{aligned}[b] \epsilon =& -p_{r} = T_{\left(t\right)\left(t\right)} = \frac{1}{8\pi}e^{\mu}_{\left(t\right)}e^{\nu}_{\left(t\right)}G_{\mu\nu} = \frac{1}{4\pi}\frac{r^{2}\rho'}{\Sigma^{2}},\\ p_{\theta} =& p_{\phi} = T_{\left(\theta\right)\left(\theta\right)} = \frac{1}{8\pi}e^{\mu}_{\left(\theta\right)}e^{\nu}_{\left(\theta\right)}G_{\mu\nu} = \epsilon-\frac{2\rho'+r\rho''}{8\pi\Sigma}. \end{aligned} $

(47) From Eq. (47), it is easy to find that
$ \epsilon $ ,$ p_{r} $ ,$ p_{\theta} $ , and$ p_{\phi} $ all contain two contributions: a nonlinear magnetic-charged part and the PFDM. -
The weak energy condition states that all physically reasonable classical matter, as measured by any observer in space-time, must be nonnegative [48], i.e.,
$ T_{\mu\nu}\xi^{\mu}\xi^{\nu}\geqslant0, $

for all timelike
$ \xi^{\mu} $ . With the decomposition of the energy-momentum tensor$ T_{\mu\nu} $ , the weak energy condition is equivalent to$ \epsilon\geqslant0,\quad\epsilon+p_{i}\geqslant0. $

(48) Substituting Eqs. (44) and (47) into Eq. (48) leads to:
$ \epsilon = \frac{1}{4\pi}\frac{r^{2}}{\Sigma^{2}}\left[\frac{3g^{2}Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{5}{2}}}-\frac{\alpha}{2r}\right]\geqslant0, $

(49) $ \epsilon+p_{r} = 0, $

(50) $ \epsilon+p_{\theta} = \epsilon+p_{\phi} = \frac{2\left(r^{2}-a^{2}\cos^{2}{\theta}\right)\rho'-r\Sigma\rho''}{8\pi\Sigma^{2}}\geqslant0. $

(51) According to Eq. (47), as examples, we depict the variations of
$ \epsilon $ and$ \epsilon+p_{\theta}/\epsilon+p_{\phi} $ with r and$ \cos{\theta} $ under two sets of parameters in Figs. 2 and 3. It turns out that the weak energy condition is violated near the origin of the rotating Bardeen in PFDM, which happens for all rotating regular black holes [10-13]. In fact, one can realize this by considering the asymptotic behavior of the matter density$ \epsilon $ and$ \epsilon+p_{\theta} $ near the origin:
Figure 2. (color online) Dependence of matter density
$ \epsilon $ and$ \epsilon+p_{\theta} $ on radius and angle for a rotating Bardeen black hole in PFDM with$ M = 1, a = 0.2, g = 0.5, \alpha = -1 $ .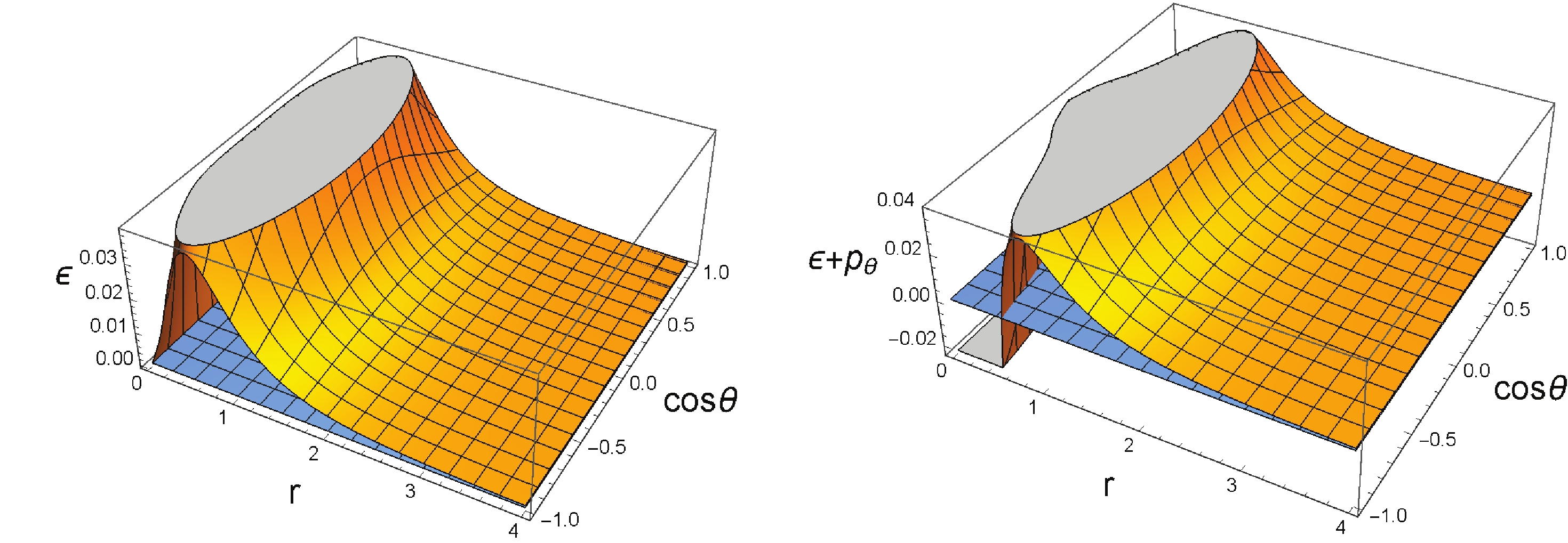
Figure 3. (color online) Dependence of matter density
$ \epsilon $ and$ \epsilon+p_{\theta} $ on radius and angle for a rotating Bardeen black hole in PFDM with$ M = 1, a = 0.9, g = 0.5, \alpha = -1 $ .$ \epsilon\simeq\frac{6Mr^{4}-\alpha g^{3}r}{8\pi g^{3}\left(r^{2}+a^{2}\right)^{2}}\simeq-\frac{\alpha r}{8\pi \left(r^{2}+a^{2}\right)^{2}},\quad r\rightarrow 0, $

(52) $\begin{aligned}[b] \epsilon+p_{\theta}\simeq&-\frac{3a^{2}Mr^{2}}{2\pi g^{3}\left(r^{2}+a^{2}\right)^{2}}+\frac{\alpha a^{2}}{16\pi r\left(r^{2}+a^{2}\right)^{2}}\\\simeq&\frac{\alpha}{16\pi a^{2}r},\quad r \rightarrow 0, \end{aligned}$

(53) where we set
$ \cos{\theta} = \pm 1 $ . Equation (53) implies that, for a rotating Bardeen black hole ($ \alpha = 0 $ ), the violation of weak energy cannot be prevented if$ a\neq 0 $ . As a verification of Eqs. (52) and (53), the dependence of$ \epsilon $ and$ \epsilon+p_{\theta} $ on a and$ \alpha $ is plotted in Fig. 4. Furthermore, at large r, the matter density$ \epsilon $ and$ \epsilon+p_{\theta} $ behave as
Figure 4. (color online) Plot showing
$ \epsilon $ and$ \epsilon+p_{\theta} $ as a function of r for various black hole parameters.$ \epsilon\simeq\frac{3g^{2}M}{4\pi r\left(r^{2}+a^{2}\right)^{2}}-\frac{\alpha r}{8\pi\left(r^{2}+a^{2}\right)^{2}}\simeq-\frac{\alpha}{8\pi r^{3}},\quad r\rightarrow \infty, $

(54) $ \epsilon+p_{\theta}\simeq\frac{15Mg^{2}}{8\pi r^{5}}-\frac{3\alpha}{16\pi r^{3}}\simeq-\frac{3\alpha}{16\pi r^{3}},\quad r\rightarrow\infty $

(55) for
$ \cos{\theta} = \pm 1 $ . From Eqs. (54) and (55), one can find that for a Bardeen black hole in PFDM, if$ \alpha>0 $ , then both$ \epsilon $ and$ \epsilon+p_{\theta} $ are negative at large distances, which is quite unreasonable from the perspective of observation. Therefore, we always assume$ \alpha<0 $ in the following discussions. -
Similar to the Kerr black hole, the space-time metric (43) is singular at
$ \Delta_{r} = 0 $ , which corresponds to the horizons of a rotating black hole. In other words, the horizons of a rotating Bardeen black hole in PFDM are solutions of$ \Delta_{r} = r^{2}+a^{2}-\frac{2Mr^{4}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\alpha r\ln{\frac{r}{\vert\alpha\vert}} = 0. $

(56) Obviously, the radii of the horizons depend on the rotation parameter a, magnetic charge g and dark matter parameter
$ \alpha $ . Numerical analysis of Eq. (56) suggests the possibility of two roots for a set of values of parameters, which correspond to the Cauchy horizon$ r_{-} $ (smaller root) and the event horizon$ r_{+} $ (larger root), respectively. The variation of$ \Delta_{r} $ with respect to r for the different values of parameters a, g, and$ \alpha $ is shown in Figs. 5 and 6. As can be seen from Fig. 5, for any fixed parameters g and$ \alpha $ , when$ a<a_{E} $ , the radii of the Cauchy horizons increase with increasing a while the radii of event horizons decrease with a. For$ a = a_{E} $ , these two horizons meet at$ r_{E} $ , that is, we have an extremal black hole with degenerate horizons. Here, the critical rotation parameter$ a_{E} $ and the corresponding critical radius$ r_{E} $ can be obtained by combining$ \Delta_{r} = 0 $ with$ \partial_r\Delta_{r} = 0 $ . If$ a>a_{E} $ , Eq. (56) has no root, i.e., no horizon exists, which means there is no black hole. A similar analysis can be applied to Fig. 6. The result shows that, for any given values of parameters a and$ \alpha $ , the two horizons first get closer with increasing g, then coincide when$ g = g_{E} $ , and eventually disappear.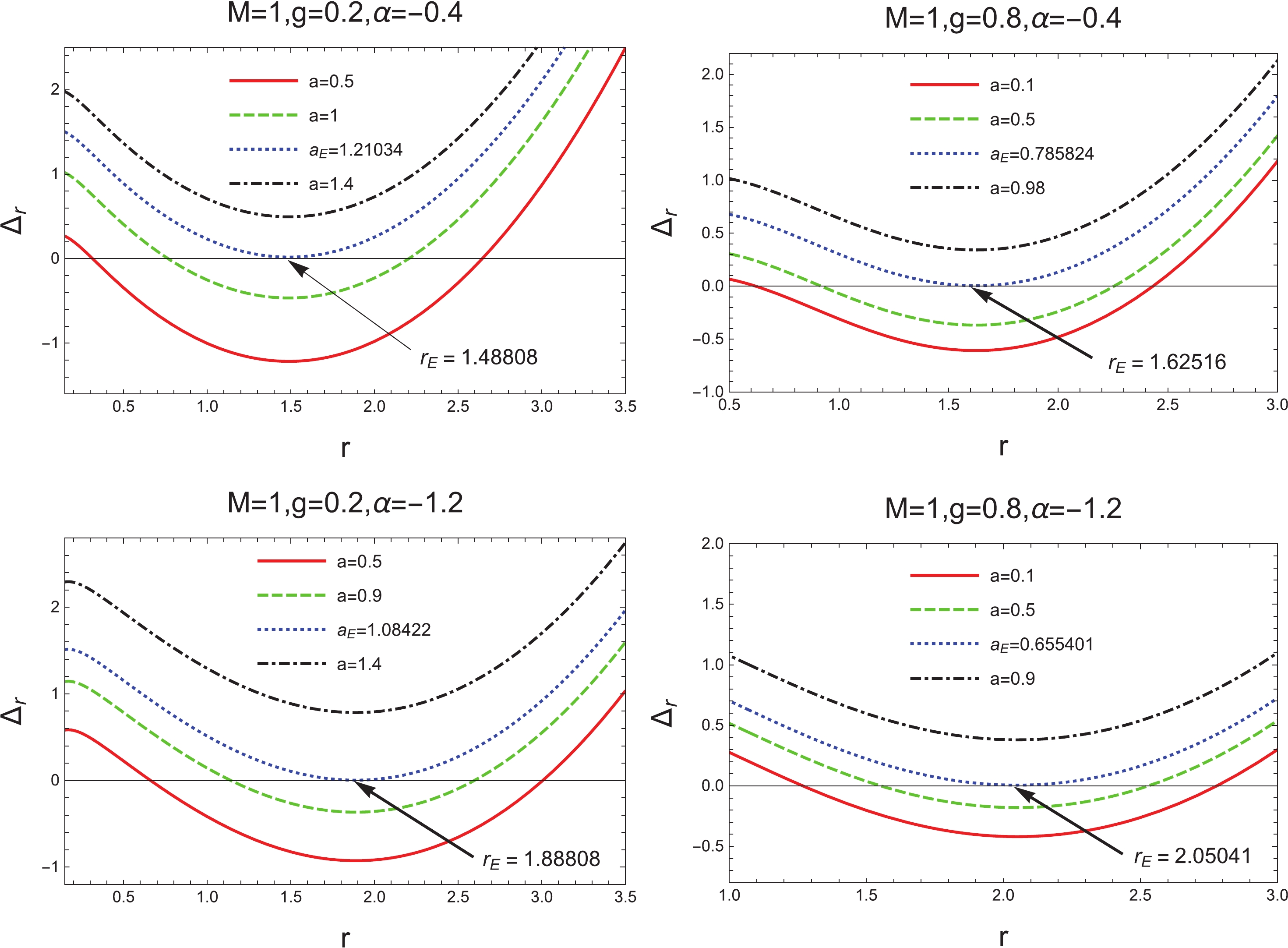
Figure 5. (coronline) Behavior of horizons as a function of r, with varying a, for a set of fixed values of
$ M=1, g$ , and$ \alpha$ .
Figure 6. (color online) Behavior of horizons as a function of r, with varyingg, for a set of fixed values of
$ M=1, a$ , and$ \alpha$ .Next, we further analyze the behavior of the horizons of rotating Bardeen black holes in PFDM. As shown in Fig. 5, when the dark matter parameter
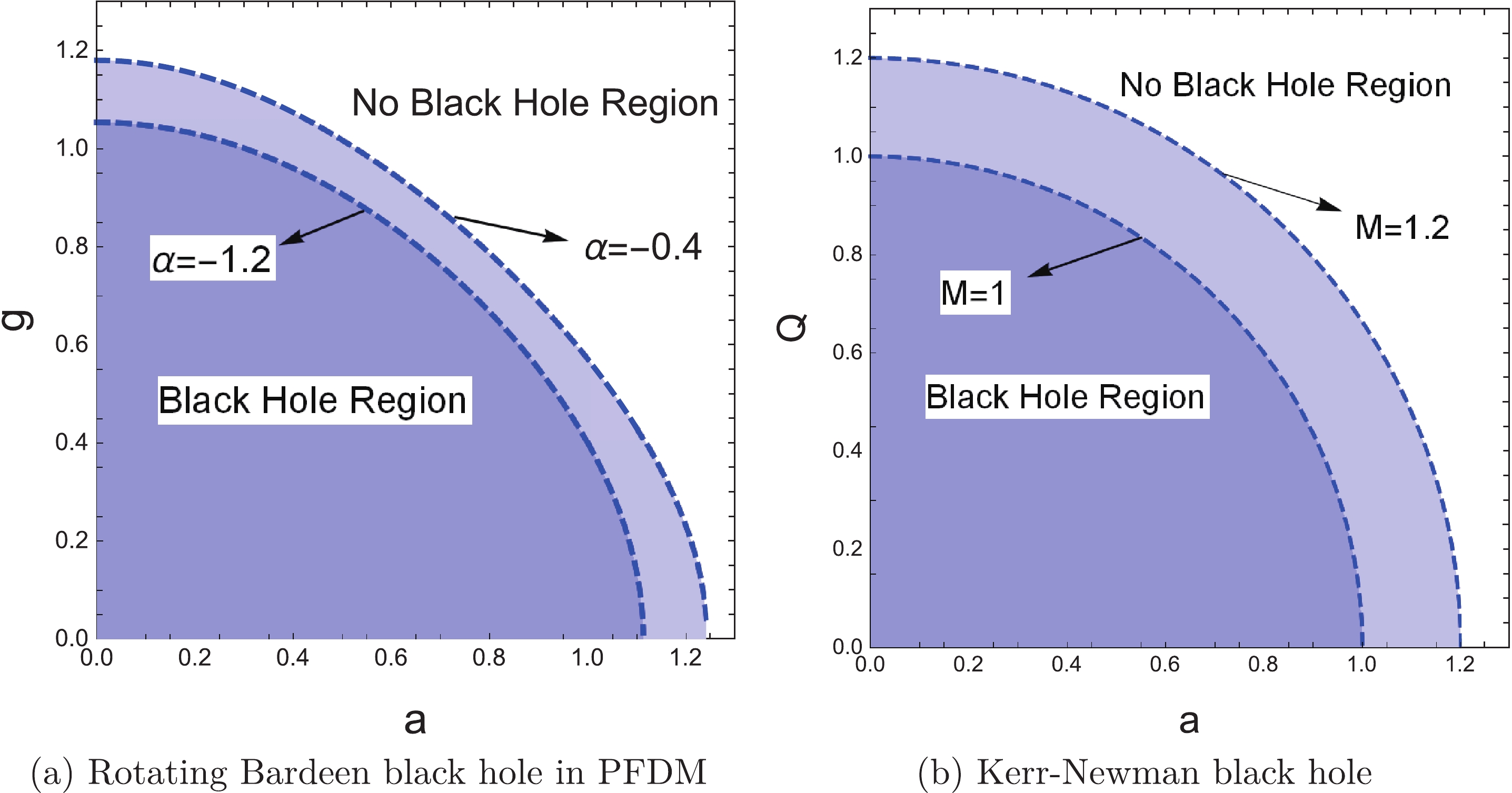
$ \alpha $ is fixed, for any given magnetic charge g, there always exists a critical value of$ a_{E} $ at which the two horizons coincide. Varying g, we thus obtain a critical curve with$ M = 1 $ in the parameter space ($ a, g $ ) (see Fig. 7(a)), and every point on the curve corresponds to an extremal black hole with degenerate horizons. The critical curve separates the black hole region from the no black hole region. Figure 7(a) implies that the extremal value of the rotation parameter$ a_{E} $ decreases with increasing magnetic charge g. As a comparison, the critical curve of Kerr-Newman black holes is also depicted in Fig. 7(b). One can give the analytic expression of the curve,$ a^{2}+Q^{2} = M^{2} $ , with Q denoting the total charge of the black holes. From this expression as well as Fig. 7(b), it is easily found that the critical curve is part of a circle. -
The ergosphere is a region bounded by the event horizon
$ r_{+} $ and the outer stationary limit surface (denoted by$ r_{+}^{S} $ ); in fact, it lies outside the black hole. Interestingly, the ergosphere can be used to extract energy from a rotating black hole, which is known as the Penrose process [48]. We will discuss it in detail in the next section. The stationary limit surface, that is, infinite redshift surface, is a surface where the time-translation Killing vector$ K^\mu = \partial_t $ satisfies$ K^{\mu}K_{\mu} = 0 $ , or equivalently,$ r^{2}+a^{2}\cos^{2}{\theta}-\frac{2Mr^{4}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+\alpha r\ln{\frac{r}{\vert\alpha\vert}} = 0. $

(57) Solving Eq. (57) for various values of the parameters numerically, one can generally get two roots, i.e. an inner stationary limit surface
$ r_{-}^{S} $ and outer stationary limit surface$ r_{+}^{S} $ . Figure 8 shows the shapes of the ergospheres and horizons for a rotating Bardeen black hole surrounded by PFDM. It can be seen that the size of the ergosphere increases with the rotation parameter a (see Fig. 8 horizontally) and increases slightly with increasing g (see Fig. 8 from the top down). Moreover, there exists a critical value$ a_{E} $ at which the inner horizon and outer horizon degenerate into one, and when$ a>a_{E} $ , the ergosphere disappears. -
Since the Killing vector
$ K^\mu = \partial_t $ becomes space-like inside the ergosphere, there exist negative energy orbits. Base on this, Penrose first proposed that one can extract rotational energy from a black hole. Consider, for example, a particle A moving in the ergosphere which breaks into two particles B and C. We arrange the breakup so that the energy of particle B falling into the black hole is negative and particle C escapes to infinity. Due to the local conservation of energy along the geodesics for this process, the energy of particle C will be greater than that of particle A. In order to study the Penrose process quantitatively, we have followed Refs. [49-51]. For simplicity, we will restrict the motion to particles in the equatorial plane$ \left(\theta = \dfrac{\pi}{2}\right) $ .The geodesic motion for test particles in the space-time (43) are determined by the following Lagrangian:
$\begin{aligned}[b] 2{\cal{L}} =& -\left(1-\frac{2\rho}{r}\right)\dot{t}^2-\frac{4a\rho}{r}\dot{t}\dot{\phi}+\frac{r^2}{\Delta_r}\dot{r}^2\\&+\left(r^2+a^2+\frac{2a^2\rho}{r}\right)\dot{\phi}^2, \end{aligned}$

(58) where
$ 2\rho=\dfrac{2Mr^{3}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}-\alpha\ln{\dfrac{r}{\vert\alpha\vert}} $ and$ \Delta_{r}=r^{2}+a^{2}-\dfrac{2Mr^{4}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}+ $ $ \alpha r\ln{\dfrac{r}{\vert\alpha\vert}}. $ In terms of the Euler-Lagrange equation, one gets two conserved quantities, i.e. the energy E and the angular momentum L of the test particle:$ E\equiv-\frac{\partial{\cal{L}}}{\partial\dot{t}} = -g_{tt}\dot{t}-g_{t\phi}\dot{\phi},\; \; \; \; \; \; L\equiv\frac{\partial{\cal{L}}}{\partial\dot{\phi}} = g_{t\phi}\dot{t}+g_{\phi\phi}\dot{\phi}, $

(59) where the dot (
$ \cdot $ ) denotes derivatives with respect to the affine parameter$ \lambda $ .The radial equation for the geodesic motion of a test particle can be obtained by means of Eqs. (58) and (59) as
$\begin{aligned}[b] r^4\dot{r}^2 =& E^2\left(r^4+a^4+a^2(2r^2-\Delta_r)\right)\\&+L^2(a^2-\Delta_r)-4aLE\rho r+\delta r^2\Delta_r,\end{aligned} $

(60) where
$ \delta = -1,0,1 $ correspond to time-like, null and space-like geodesics respectively. Suppose that the breakup happens at the turning point of the geodesic, where$ \dot{r} = 0 $ , then from the radial equation for an equatorial geodesic it follows that$ E = \frac{2a\rho rL\pm r\sqrt{\Delta_r}\sqrt{L^2r^2-\delta(r^4+a^4+a^2(2r^2-\Delta_r))}}{r^4+a^4+a^2(2r^2-\Delta_r)}, $

(61) and
$ L = \frac{-2a\rho rE\pm r\sqrt{\Delta_r}\sqrt{E^2r^2+\delta(r^2-2\rho r)}}{\Delta_r-a^2}. $

(62) Using Eq. (61), one can derive the condition where the value of the energy is negative: in order to have positive energy in the limit
$ a\rightarrow0 $ , we must retain only the positive sign; on the other hand, when$ a\ne0 $ , a necessary criterion for having negative energy is$ L<0 $ . Thus in order to have negative energy, we must also have$ 4a^2\rho^2 r^2L^2>r^2\Delta_r\left[L^2r^2-\delta(r^4+a^4+a^2(2r^2-\Delta_r))\right], $

or alternatively
$ 1-\frac{2\rho}{r}<\delta\frac{\Delta_r}{L^2}. $

(63) Since
$ g_{tt}(\theta = \dfrac{\pi}{2}) = -\left(1-\dfrac{2\rho}{r}\right) $ , the above inequality clearly suggests that this can happen in the ergosphere.Let us now consider a massive particle (
$ \delta = -1 $ ) with$ E_A = 1>0 $ (without loss of generality) and angular momentum$ L_A $ entering the ergosphere. This particle then decays into two photons ($ \delta = 0 $ ) with energies and angular momenta ($ E_B,L_B $ ) and ($ E_C,L_C $ ) respectively. We could arrange this process such that the photon which falls into the event horizon has negative energy and the photon which escapes to infinity has positive energy. From Eq. (62), we have$ \begin{aligned}[b] L_A =& \frac{-2a\rho r+r\sqrt{\Delta_r}\sqrt{2\rho r}}{\Delta_r-a^2} = \alpha_A,\\ L_B =& \frac{-2a\rho r-r^2\sqrt{\Delta_r}}{\Delta_r-a^2}E_B = \alpha_B(r) E_B,\\ L_C =& \frac{-2a\rho r+r^2\sqrt{\Delta_r}}{\Delta_r-a^2}E_C = \alpha_C(r) E_C. \end{aligned} $

(64) The conservation of energy and angular momentum gives
$ E_B+E_C = E_A = 1 $

(65) and
$ L_B+L_C = \alpha_B(r)E_B+\alpha_C(r)E_C = L_A = \alpha_A(r). $

(66) Solving Eqs. (65) and (66) and using Eq. (64), one finally gets:
$\begin{aligned}[b] E_B =& \frac{1}{2}\left(1-\sqrt{1+\frac{a^2-\Delta_r}{r^2}}\right)\\ =& \frac{1}{2}\left(1-\sqrt{\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}-\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}}\right), \end{aligned}$

(67) $\begin{aligned}[b] E_C =& \frac{1}{2}\left(1+\sqrt{1+\frac{a^2-\Delta_r}{r^2}}\right)\\ =& \frac{1}{2}\left(1+\sqrt{\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}-\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}}\right).\end{aligned} $

(68) Clearly, the photon C that escapes from the black hole to infinity has more energy than the initial particle A, and the energy gain
$ \Delta E $ in this process is$ \Delta E = \frac{1}{2}\left(\sqrt{\frac{2Mr^{2}}{\left(r^{2}+g^{2}\right)^{\frac{3}{2}}}-\frac{\alpha}{r}\ln{\frac{r}{\vert\alpha\vert}}}-1\right) = -E_B. $

(69) It follows from Eq. (67) that the maximum gain in energy occurs at the event horizon,
$ \Delta_r = 0 $ , and the maximal efficiency of the Penrose process is then given by$ E_{\rm ffmax} = \frac{E_A+\Delta E}{E_A} = \frac{1}{2}\left(1+\sqrt{\frac{2Mr_+^{2}}{\left(r_+^{2}+g^{2}\right)^{\frac{3}{2}}}-\frac{\alpha}{r_+}\ln{\frac{r_+}{\vert\alpha\vert}}}\right), $

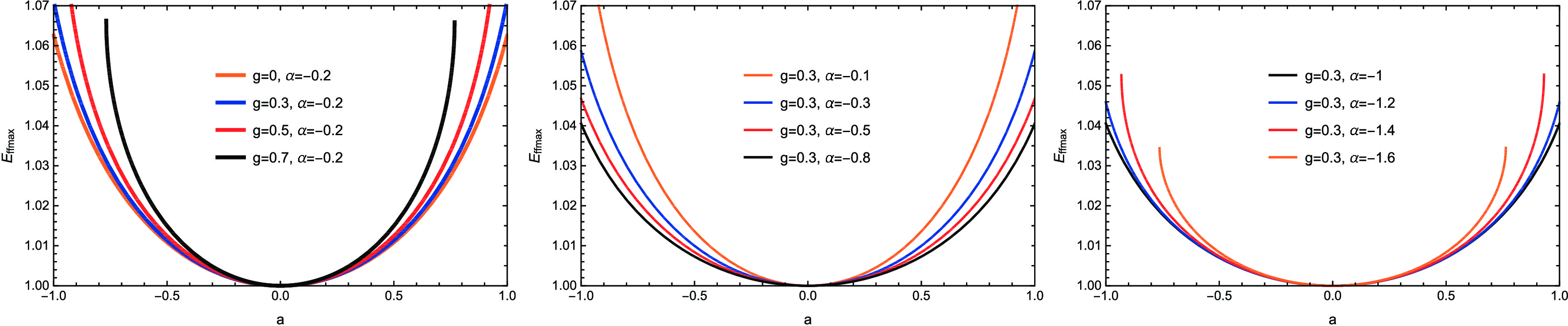
(70) which is shown visually in Fig. 9. It is easy to see that the maximal efficiency
$ E_{\rm ffmax} $ increases with the increase of spin parameter a and magnetic parameter g. Interestingly, the effect of the dark matter parameter$ \alpha $ on$ E_{\rm ffmax} $ is nonmonotonic. When$ \alpha>\alpha^C\left({\rm{critical}}\;{\rm{value}}\right) $ , the maximal efficiency$ E_{\rm ffmax} $ decreases with its decrease; however, when$ \alpha<\alpha^C $ ,$ E_{\rm ffmax} $ increases with its decrease. In fact, this is caused by the influence of$ \alpha $ on the event horizon. -
In this paper, we have obtained the exact solution for a static spherically symmetric Bardeen black hole surrounded by perfect fluid dark matter and then studied its thermodynamic properties. We first derived the first law of thermodynamics and the corresponding Smarr formula by treating the magnetic charge g and dark matter parameter
$ \alpha $ as thermodynamic variables. Furthermore, we discussed the thermodynamic stability of the black hole by means of heat capacity. The result showed that there exists a critical radius$ r_{+}^{C} $ , where the heat capacity diverges and the second order phase transition occurs. The critical radius$ r_{+}^{C} $ increases with the magnetic charge g and decreases with the dark matter parameter$ \alpha $ .With the Newman-Janis algorithm, we generalized the static spherically symmetric Bardeen black hole surrounded by PFDM to the corresponding rotating solution. According to the components of the energy-momentum tensor, we found that the weak energy condition is violated near the origin of rotating Bardeen black holes surrounded by PFDM, which happens for all rotating regular black holes. Meanwhile, we constrained the dark matter parameter to
$ \alpha<0 $ in terms of the weak energy condition.The structure of the black hole horizons was studied in detail. By solving the relevant equation numerically, we found that for any fixed parameters g and
$ \alpha $ , when$ a<a_{E} $ , the radii of Cauchy horizons increase with increasing a, while the radii of event horizons decrease with a. For$ a = a_{E} $ , we have an extremal black hole with degenerate horizons. If$ a>a_{E} $ , no black hole will form. Similarly, for any given values of parameters a and$ \alpha $ , the two horizons first get closer with the increase of g, then coincide when$ g = g_{E} $ , and eventually disappear. Furthermore, for a fixed dark matter parameter$ \alpha $ , we can obtain a critical curve in the parameter space ($ a, g $ ), which separates the black hole region from the no black hole region. We found that the extremal value of the rotation parameter$ a_{E} $ decreases with the magnetic charge parameter g. By the analysis of ergospheres, we have seen that the size of the ergosphere increases with the rotation parameter a and increases slightly with the increase of g. Moreover, when$ a>a_{E} $ , we have no ergosphere.Finally, energy extraction was discussed by considering the Penrose process in a rotating Bardeen black hole surrounded by PFDM. We have demonstrated that the maximal efficiency
$ E_{\rm ffmax} $ increases with the increase of spin parameter a and magnetic parameter g. However, the effect of the dark matter parameter$ \alpha $ on$ E_{\rm ffmax} $ is nonmonotonic, which is caused by the influence of$ \alpha $ on the event horizon.Very recently, the first image of the M87* black hole was obtained using the sub-millimeter Event Horizon Telescope, based on very-long baseline interferometry [52]. The observation of black hole shadows will be a useful tool for better understanding astrophysical black holes and also for testing modified gravity models. Hence, as done in Refs. [53-55], we intend to further constrain the relevant black hole parameters by studying the optical properties of Bardeen black holes surrounded by perfect fluid dark matter.
-
The authors declare that there are no conflicts of interest regarding the publication of this paper.
-
This work makes use of the Black Hole Perturbation Toolkit.
Bardeen black hole surrounded by perfect fluid dark matter
- Received Date: 2020-10-31
- Available Online: 2021-05-15
Abstract: We derive an exact solution for a spherically symmetric Bardeen black hole surrounded by perfect fluid dark matter (PFDM). By treating the magnetic charge g and dark matter parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: