-
Quantum chromodynamics (QCD) is a fundamental theory for describing the strong interaction, and its phase structure has become an important subject of considerable interest in recent decades. The first-principle results from lattice QCD simulation [1, 2] have indicated that with increasing temperature
$ T $ , the transition from ordinary nuclear matter to chiral symmetric quark-gluon plasma (QGP) is a smooth crossover at low or zero chemical potential$ \mu $ . At a high chemical potential, lattice QCD simulation, as a reliable tool for obtaining the chiral properties of QCD matter, confronts a great challenge due to the fermion sign problem [3]. However, strategies (for reviews see, e.g., Refs. [4-6]) such as Taylor series expansion [7-9], imaginary chemical potential, reweighting techniques [10, 11], and the complex Langevin method [12, 13] have been developed to attempt to tackle this problem. In this context, some alternative theoretical tools, such as QCD low-energy effective models (e.g., the Nambu-Jona-Lasinio model [14-16], the Polyakov-loop extended NJL (PNJL) model [17-19], the quark-meson model or linear sigma model [20-24], the Polyakov quark-meson (PQM) model [25-28]), the Dyson-Schwinger equation approach [29, 30], and the functional renormalization group approach [31-34], which are not restricted by the chemical potential, have been proposed to explore the QCD phase structure at high chemical potentials better. Further, the results obtained from the effective model calculations [35, 36] demonstrate that the chiral phase transition of the strongly interacting matter is a first-order transition at high density, and a second-order critical endpoint (CEP) can exist between the crossover line and the first-order phase transtion line in the ($ \mu $ ,$ T $ )-plane. Apart from the phase transition, other important information, such as the thermodynamic properties, in-medium properties of mesons [36, 37], and transport properties [38-40], for the strongly interacting matter has also been extensively studied in these QCD effective models.To take into account the intricacy of the realistic quark matter produced in relativistic heavy-ion collisions (HICs) at the RHIC and the LHC, different improved versions of the QCD effective models have been proposed by including the effects of the finite volume of the system [41-56], the non-extensive effects in terms of long-distance correlation [57, 58], the presence of magnetic fields [59-68], and the effect of electric fields [69-73] to better explore the chiral/confinement properties of the strongly interacting matter at finite temperatures or quark chemical potentials. Conventionally, in the literature, all the effective models or improved effective models have been based on an ideal assumption that the constituents of quark matter are completely isotropic in the momentum-space in the absence of magnetic fields. However, due to the asymmetric geometry of the fireball created in HICs, the system evolves with different pressure gradients along different directions. As a result, the expansion and cooling rate along the beam direction (denoted as the longitudinal direction) is greater than that in the radial direction [74], and this momentum anisotropy can survive at all stages of the HICs; consequently, the parton-level momentum distribution functions may become anisotropic. Thus, it is essential to consider the momentum-space anisotropy induced by the rapid longitudinal asymptotic expansion in the phenomenological investigation of different observables. Thus far, extensive investigations have been performed to explore the effects of momentum anisotropy on the parton self-energy [74-77], photon and dilepton production [78-81], dissociation of quarkonium [82-84], heavy-quark potential [85, 86], various transport coefficients [87-90], and jet quenching parameter [91], which are sensitive to the evolution of the QGP. The associated results have indicated that the momentum-space anisotropy has a significant effect on the observables of the QGP. However, to the best of our knowledge, thus far, there has not been a study of momentum anisotropy in the framework of effective QCD models or research regarding the effect of momentum-space anisotropy on the chiral phase transition. Inspired by this fact, one major goal of the present study is to reveal how the momentum anisotropy qualitatively affects the chiral phase structure as well as transport properties in strongly interacting matter.
The present paper is a first attempt to study the effect of the momentum-space anisotropy induced by the rapid longitudinal expansion of the fireball created in HICs on the QCD chiral phase transition. We adopt the 2+1 flavor quark-meson model, which has been successful in describing the mechanism of spontaneous chiral symmetry breaking, to approximate quark matter. The effect of momentum anisotropy enters in the quark-meson model by substituting the isotropic (local equilibrium) distribution function in the total thermodynamic potential with the anisotropic one. This introduces an additional degree of freedom, viz., the direction of anisotropy. The anisotropic parameter,
$ \xi $ , representing the degree of momentum anisotropy or the tendency of the system to stay away from the isotropic state, is also considered to be an argument in the isotropic distribution function. Based on this momentum anisotropy-dependent quark-meson model, we first explore how the momentum anisotropy affects the chiral phase diagram and the location of the CEP. Next, we investigate the thermodynamic properties and thermal properties of various scalar (pseudoscalar) meson masses for the vanishing chemical potential in both isotropic and anisotropic quark matter. Finally, transport coefficients, such as the shear viscosity, electrical conductivity, and bulk viscosity, which are crucial for understanding the dynamical evolution of QCD matter, are also estimated in (an-)isotropic quark matter. Note that we restrict ourselves, here, to the anisotropic system close to the isotropic local equilibrium state; consequently, the calculations of thermodynamic quantities, meson masses, and transport coefficients in the anisotropic system are methodologically similar to those in the isotropic system. In particular, for a small$ \xi $ limit, the anisotropic distribution can just linearly expand to the linear order of$ \xi $ . Using this linear approximation of the anisotropic distribution, the mathematical expression of the transport coefficients, which are obtained by solving the relativistic Boltzmann equation under the relaxation time approximation, can be explicitly separated into an equilibrium part and an anisotropic correction part [87-90]. For$ \xi\rightarrow 0 $ , the analytic expressions can be reduced to the standard expressions in the local equilibrium medium, which will be discussed in Sec. IV.The remainder of this paper is organized as follows. In Sec. II, we give a brief overview of the three-flavor quark-meson model. In Sec. III, the modification of the thermodynamic potential within momentum-space anisotropy is presented. In Sec. IV, we discuss the chiral phase transition, thermodynamic properties, meson masses, and transport coefficients in both isotropic and anisotropic quark matter. In Sec. V, we summarize the main results and present an outlook.
-
The quark-meson model, as a successful QCD-like effective model, can capture an important feature of QCD, namely, chiral symmetry breaking and restoration at a high temperature/density. The Lagrangian of the three-flavor quark-meson model presently used in this study is taken from Ref. [23]:
$ \begin{array}{l} {\cal{L}}_{ \rm{QM}} = \bar{\Psi}({\rm i}\gamma_{\mu}D^{\mu}-g\phi_5)\Psi+{\cal{L}}_{\mathrm{M}}, \end{array} $

(1) where
$ \Psi = u,d,s $ is the quark field with three flavors ($ N_{f} = 3 $ ) and three color degrees of freedom ($ N_{c} = 3 $ ). The first term on the right hand side of Eq. (1) represents the interaction between the quark field and the scalar ($ \sigma $ ) and pseudoscalar ($ \pi $ ) fields with a flavor-blind Yukawa coupling,$ g $ , of the quarks to the mesons. The meson matrix is given as$ \begin{array}{l} \phi_5 = T_a(\sigma_{a}+{\rm i}\gamma_5\pi_a), \end{array} $

(2) where
$ T_{a} = \lambda_a/2 $ , with$a = 0,\cdots,8$ , are the nine generators of the U(3) symmetry;$ \lambda_{a} $ is the Gell-Mann matrix with$\lambda_{0} = \sqrt{\dfrac{2}{3}}1$ ; and$ \sigma_{a} $ and$ \pi_a $ denote the scalar meson nonet and the pseudoscalar meson nonet, respectively.The second term in Eq. (1) is the purely mesonic contribution,
$ {\cal{L}}_{\mathrm{M}} $ , which describes the chiral symmetry breaking pattern in strong interaction. It is given by [23]$ \begin{aligned}[b] {\cal{L}}_{\mathrm{M}} =& \mathrm{Tr}(\partial_\mu\phi^{\dagger}\partial^{\mu}\phi-m^2\phi^{\dagger}\phi)-\lambda_1[\mathrm{Tr}(\phi^{\dagger}\phi)]^2\\ &-\lambda_2\mathrm{Tr}(\phi^{\dagger}\phi)^2+c[\mathrm{Det}(\phi)+\mathrm{Det}(\phi^{\dagger})]\\ &+\mathrm{Tr}[H(\phi+\phi^{\dagger})], \end{aligned} $

(3) with
$\phi = T_{a}\phi_{a} = T_{a}(\sigma_{a}+{\rm i}\pi_a)$ representing a complex ($ 3\times3 $ )-matrix. Explicit chiral symmetry breaking is expressed by the last term of Eq. (3), where$ H = T_{a}h_{a} $ is a ($ 3\times3 $ )-matrix with nine external fields,$ h_{a} $ . Explicit$ U(1)_{A} $ symmetry is given by the 't Hooft determinant term with anomaly term$ c $ ;$ m^2 $ is the tree-level mass of the fields in the absence of symmetry breaking;$ \lambda_1 $ and$ \lambda_2 $ are the two possible quartic coupling constants.Under the mean-field approximation [36], the total thermodynamic potential density of the quark-meson model at finite temperature
$ T $ and quark chemical potential$ \mu_f $ is given by$ \begin{array}{l} \Omega(T,\mu_f) = \Omega_{q\bar{q}}(T,\mu_f)+U(\sigma_{x},\sigma_{y})_{}. \end{array} $

(4) The first term on the right hand side of Eq. (4),
$ \Omega_{q\bar{q}} $ , denotes the fermionic part of the thermodynamic potential [36]:$ \begin{aligned}[b] \Omega_{q\bar{q}}(T,\mu_f) =& 2N_{c}\sum_{f = u,d,s}^{}T\int_{}^{}\dfrac{{\rm d}^3{{p}}}{(2\pi)^3}\Bigg[\ln\Big(1-f_{q,f}^0(T,\mu_{f},{{p}})\Big)\\ &+\ln\Big(1-f_{\bar{q},f}^0(T,\mu_{f},{{p}})\Big)\Bigg], \end{aligned} $

(5) with the isotropic equilibrium distribution function of the (antiquark) quark for the
$ f $ -th flavor$ \begin{array}{l} f^0_{q(\bar{q}),f}(T,\mu_{f},{{p}}) = \dfrac{1}{\exp[E_{f}\mp\mu_{f}/T]+1}. \end{array}$

(6) Here,
$ E_{f} = \sqrt{p^{2}+m_f^{2}} $ is the single-particle energy with flavor-dependent constituent quark mass$ m_{f} $ . The$ \mp $ sign corresponds to quarks and antiquarks, respectively. In the present work, a uniform quark chemical potential,$ \mu\equiv\mu_{u}\equiv\mu_{d}\equiv\mu_{s} $ , is assumed. Further, the breaking of the$ SU(2) $ isospin symmetry is not considered; consequently, the up and down quarks have approximately the same masses, i.e.,$ m_{u}\approx m_{d} $ . In the quark-meson model, the constituent quark masses are given as$ \begin{array}{l} m_{l} = g\sigma_x/2,\;\;\;\; \;\;\;\; m_{s} = g\sigma_y/\sqrt{2}, \end{array}$

(7) where
$ l $ denotes light quarks ($ l\equiv u,d $ ); and$ \sigma_x $ and$ \sigma_y $ denote the non-strange and strange chiral condensates, respectively. The Yukawa coupling,$ g $ , is fixed to reproduce a light constituent quark mass of$ m_l\approx300 $ MeV. The second term,$ U(\sigma_{x},\sigma_{y})_{} $ ,$ viz $ , the purely mesonic potential, is given as [20, 23, 28]$ \begin{aligned}[b] U =& -h_x \sigma_x-h_y \sigma_y+ \dfrac{m^2\left(\sigma^2_x+\sigma^2_y\right)}{2} -\dfrac{c\sigma^2_x \sigma_y }{2\sqrt{2}} \\& + \dfrac{\lambda_1 \sigma^2_x \sigma^2_y}{2} +\dfrac{(2 \lambda_1 +\lambda_2)\sigma^4_x}{8} + \dfrac{ (\lambda_1+\lambda_2)\sigma^4_y}{4}, \end{aligned} $

(8) where model parameters
$ m^2 $ ,$ h_x $ ,$ h_y $ ,$ \lambda_1 $ ,$ \lambda_2 $ , and$ c $ , as reported in Ref. [36], are listed in Table 1. Finally, the behavior of$ \sigma_{x} $ and$ \sigma_{y} $ as functions of temperature and quark chemical potential can be obtained by minimizing the total thermodynamic potential density, i.e.,$m^2/\mathrm{MeV^2}$ 

$h_x/\mathrm{MeV^3}$ 

$h_y/\mathrm{MeV^3}$ 

$\lambda_1$ 

$\lambda_2$ 

$c/\mathrm{MeV}$ 

$(342.252)^2$ 

$(120.73)^3$ 

$(336.41)^3$ 

1.4 46.68 4807.84 Table 1. Parameters used in our work, taken from Ref. [36].
$ \begin{array}{l} \dfrac{\partial\Omega}{\partial \sigma_{x}} = \dfrac{\partial\Omega}{\partial \sigma_{y}}\bigg|_{\sigma_{x} = \bar{\sigma}_x,\sigma_{y} = \bar{\sigma}_y} = 0, \end{array} $

(9) with
$ \sigma_{x} = \bar{\sigma}_x, \sigma_{y} = \bar{\sigma}_y $ being the global minimum. -
Due to the rapid longitudinal expansion of the partonic matter created in the HICs, an anisotropic deformation of the argument of the isotropic (equilibrium) parton distribution functions is generally used to simulate the momentum anisotropy of QGP [74-90]. A special and widely used spherical momentum deformation introduced by Romatschke and Strickland [74], which is characterized by the removal and addition of particles along a single momentum anisotropy direction, is applied in this study. Accordingly, the local distribution function of
$ f $ -th flavor quarks (antiquarks) in an anisotropic system can be obtained from the isotropic (local equilibrium) distribution function by rescaling one preferred direction in the momentum space, which is given as$ \begin{array}{l} f_{\rm aniso}^{0}(T,\mu_{f},{{p}}) = \dfrac{1}{{\rm e}^{\left(\sqrt{{{p}}^2+\xi({{p}}\cdot{{n}})^2+m_f^2}\mp\mu_{f}\right)/T}+1}. \end{array} $

(10) Here, the anisotropy parameter,
$ \xi $ , presenting the degree of momentum-space anisotropy, can generally be defined as$ \begin{array}{l} \xi = \dfrac{\left\langle{{p}}_{T}^2\right\rangle}{2\langle p_{L}^2\rangle}-1, \end{array} $

(11) where
$ p_{L} $ and$ {{p}}_{T} $ are the components of momentum, parallel and perpendicular to the direction of anisotropy,$ {{n}} $ , respectively;$ {{p}} = (p\sin\theta\cos\phi,\;p\sin \theta\sin\phi,\;p\cos\theta) $ , where we use the notation$ |{{p}}|\equiv p $ for convenience;$ {{n}} = (\sin\alpha,0,\cos\alpha) $ ; and$ \alpha $ is the angle between$ {{p}} $ and$ {{n}} $ . Accordingly,$({{p}}\cdot{{n}})^2 = p^2(\sin\theta\cos\phi\sin\alpha+\cos\theta\cos\alpha)^2 = p^2c (\theta,\phi,\alpha)$ . Note that$ \xi>0 $ corresponds to a contraction of the particle distribution in the direction of anisotropy, whereas$ -1<\xi<0 $ represents a stretching of the particle distribution in the direction of anisotropy.If the system is close to the ideal massless parton gas and
$ \xi $ is small,$ \xi $ is also related to the ratio of shear viscosity to entropy density$ \eta/s $ , as well as proper time$ \tau $ of the medium. The relation for one-dimensional Bjorken expansion in the Navier-Stokes limit is given as [92]$ \begin{array}{l} \xi = \dfrac{10}{T\tau}\dfrac{\eta}{s}. \end{array} $

(12) This implies that the non-vanishing shear viscosity, combined with a finite momentum relaxation rate in an expanding system, can also contribute to the momentum-space anisotropy. At the RHIC energy with a critical temperature of
$ T_{c}\approx160 $ MeV,$ \tau\approx6 $ fm/c, and$ \eta/s = 1/4\pi $ , we can obtain$ \xi\approx 0.3 $ .In this work, we assume that the system has a small deviation from the momentum-space isotropy; therefore, the value of
$ \xi $ is small ($ |\xi|\ll1 $ ), and Eq. (10) can be expanded up to linear order in$ \xi $ :$ \begin{aligned}[b] f_{\rm aniso}^0({{p}})&\approx f^0_{q,f}-\dfrac{\xi({p\cdot{{n}}})^2}{2E_{f}T}{\rm e}^{(E_{f}-\mu_{f})/T}f_{q,f}^{02}\\ &= f_{q,f}^0-\dfrac{\xi({p\cdot{{n}}})^2}{2E_{f}T}f_{q,f}^{0}(1-f_{q,f}^0). \end{aligned} $

(13) By replacing the isotropic distribution functions in Eq. (5) with Eq. (13), we finally obtain the
$ \xi $ -dependent thermodynamic potential density of the fermionic part:$ \begin{aligned}[b] \Omega_{q\bar{q}} =& 2N_{c}\sum_{f}^{}\int_{}^{}\dfrac{T{\rm d}^3{{p}}}{(2\pi)^3}\\& \times \left\{\ln \left(1-f_{q,f}^0+\dfrac{\xi p^2c(\theta,\phi,\alpha)}{2E_{f}T}f_{q,f}^{0}(1-f_{q,f}^0) \right)\right.\\&\left.+\ln\left(1-f_{\bar{q},f}^0+\dfrac{\xi p^2c(\theta,\phi,\alpha)}{2E_{f}T}f_{\bar{q},f}^{0}(1-f_{\bar{q},f}^0)\right)\right\}. \end{aligned} $

(14) Similar to the studies on the finite-size effect [41] and the non-extensive effect [57], we also treat anisotropy parameter
$ \xi $ as a thermodynamic argument in the same footing as$ T $ and$ \mu $ and do not have any modifications to the usual quark-meson model parameters due to the presence of momentum anisotropy. Replacing the fermionic thermodynamic potential in Eq. (9) with Eq. (14), we can finally obtain the$ \xi $ -dependent chiral condensates at a finite temperature and quark chemical potential. -
In the 2+1 flavor quark-meson model, the chiral condensates of both light quarks and strange quarks can be regarded as order parameters to analyze the feature of the chiral phase transition. The anisotropy parameters we use here are artificially taken as
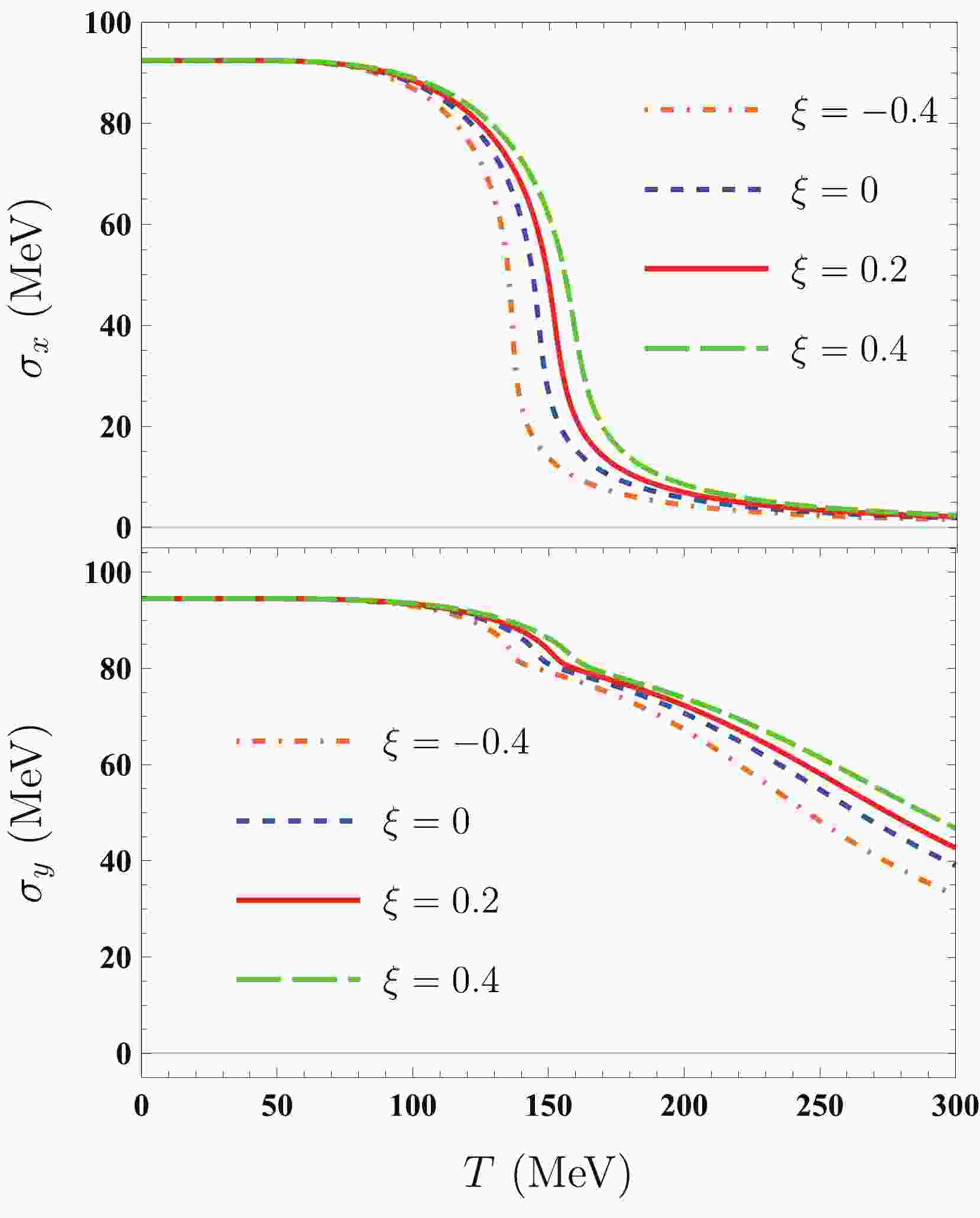
$ \xi = -0.4,\; 0,\; 0.2,\; 0.4 $ , even though the value of$ \xi $ in realistic HICs always remains positive in sign. In Fig. 1, temperature$ T $ dependences of non-strange chiral condensate$ \sigma_{x} $ and strange chiral condensate$ \sigma_{y} $ for both isotropic and anisotropic quark matter for a vanishing quark chemical potential are plotted. For$T = 0\; {\rm MeV},\; \sigma_{x}^0\approx92.4 \;{\rm MeV},\; \sigma_{y}^0\approx94.5$ MeV. As can be seen,$ \sigma_{x} $ and$ \sigma_{y} $ in both isotropic and anisotropic quark matter decrease continuously with increasing temperature. This means that at the vanishing quark chemical potential, the restoration of the chiral symmetry for (an-)isotropic quark matter is always a crossover phase transition. Further, the restoration of the chiral symmetry in the strange sector is always slower than that in the non-strange sector. As$ \xi $ increases, the values of$ \sigma_{x} $ and$ \sigma_{y} $ increase, and their melting behaviors become smoother. This demonstrates that an increase in the anisotropy parameter tends to delay the chiral symmetry restoration.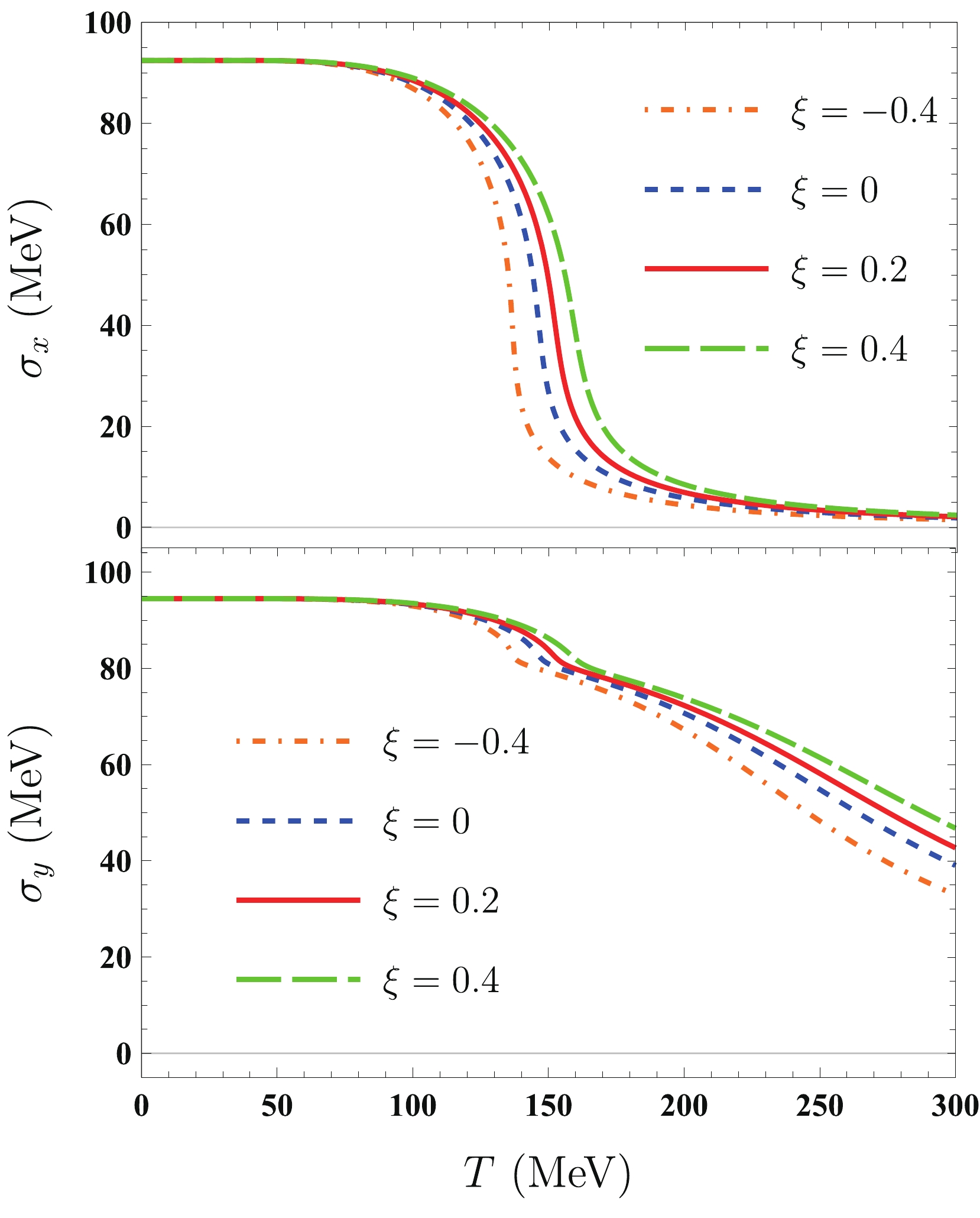
Figure 1. (color online) Temperature dependences of non-strange chiral condensate
$\sigma_{x}$ (upper panel) and strange chiral condensate$\sigma_{y}$ (lower panel) at the vanishing quark chemical potential for both isotropic ($\xi=0$ (blue dashed lines)) and anisotropic ($\xi=$ $-0.4$ (orange dotted-dashed lines), 0.2 (red solid lines), and 0.4 (green wide dashed lines)) quark matter in the quark-meson model. The values of$\sigma_{x}$ and$\sigma_{y}$ in the vacuum are approximately 92.4 MeV and 94.5 MeV, respectively.To obtain the chiral critical temperature, we introduce the susceptibilities of light quarks
$ \chi_{l} $ and strange quarks$ \chi_{s} $ , which are defined as$ \begin{array}{l} \chi_{l} = -\dfrac{\partial\sigma_{x}}{\partial T}, \;\;\;\;\;\;\;\chi_{s} = -\dfrac{\partial\sigma_{y}}{\partial T}. \end{array} $

(15) The thermal behaviors of both
$ \chi_{l} $ and$ \chi_{s} $ are presented in Fig. 2. We can see that$ \chi_{l} $ and$ \chi_{s} $ have peaks at particular temperatures. The peak position of$ \chi_{l} $ determines the critical temperature,$ T^{\chi}_{c} $ , for the chiral transition in the non-strange sector. Unlike$ \chi_{l} $ ,$ \chi_{s} $ has two peaks in the entire temperature domain of interest. The temperature coordinate of the first peak of$ \chi_{s} $ is almost the same as that of$ \chi_{l} $ , and the location of the second broad peak of$ \chi_{s} $ determines the critical temperature,$ T^{\chi}_{s} $ , for the chiral transition of the strange sector. The chiral critical temperature,$ T_{c}^{\chi} $ , at the vanishing quark chemical potential is the origin of the crossover phase transition in the QCD chiral phase diagram. Furthermore, these chiral critical temperatures are sensitive to the variation of$ \xi $ . As$ \xi $ increases,$ T^{\chi}_{c,s} $ shifts toward higher temperatures, and the height of$ {\chi}_{l,s} $ decreases. The exact values of both$ T^{\chi}_{c} $ and$ T^{\chi}_{s} $ for different anisotropy parameters are listed in Table 2. Compared with the case of$ \xi = 0 $ , chiral critical temperatures$ T^{\chi}_c $ and$ T^{\chi}_s $ decrease by approximately 6% for$ \xi = -0.4 $ . For the cases of$ \xi = 0.2 $ and 0.4, both$ T^{\chi}_c $ and$ T^{\chi}_s $ increase by approximately 4% and 9%, respectively.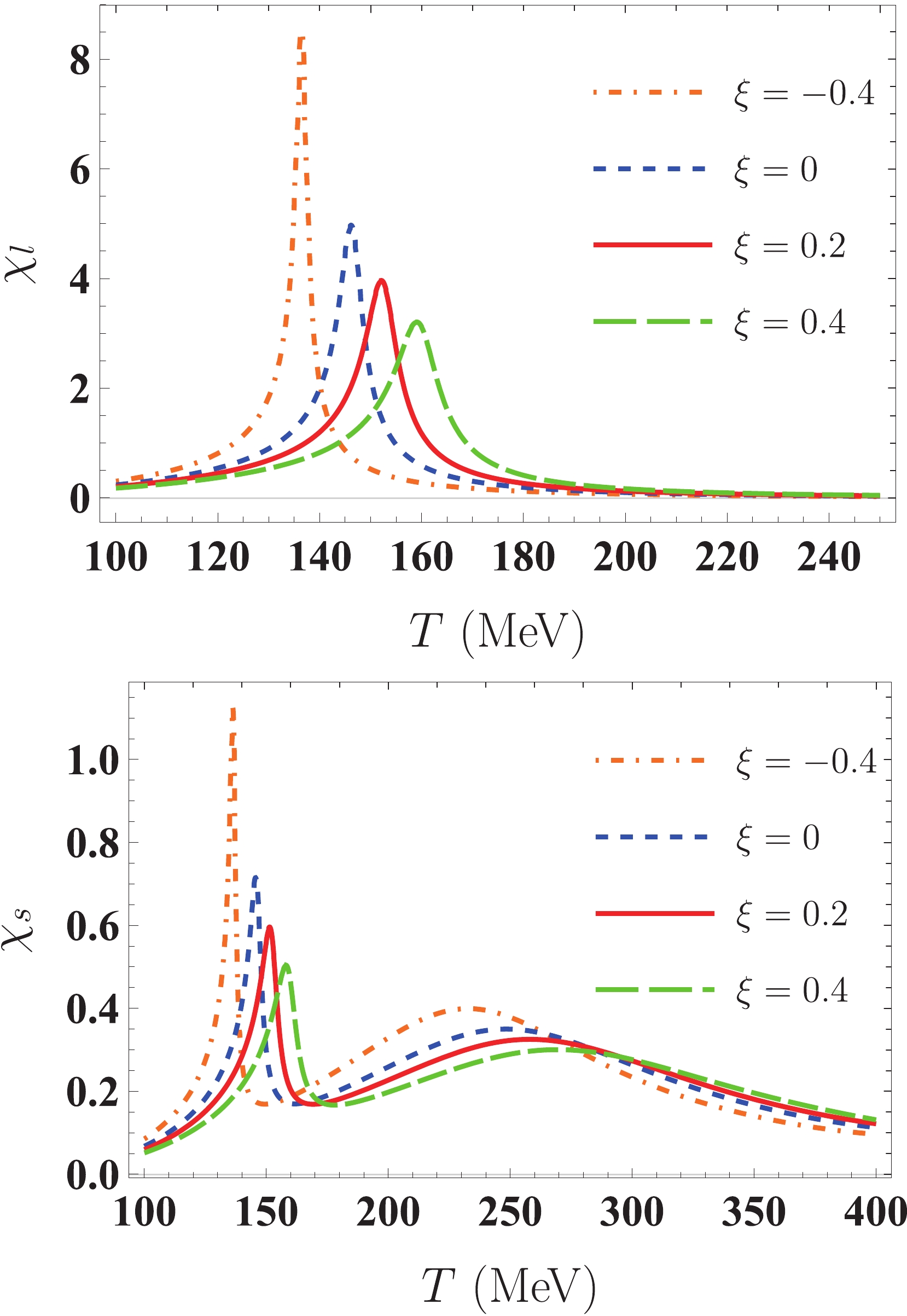
Figure 2. (color online) Temperature dependence of the susceptibilities in non-strange sector
$\chi_{l}$ (upper panel) and strange sector$\chi_{s}$ (lower panel) at$\mu=0$ GeV for both isotropic ($\xi=0$ (blue dashed line)) and anisotropic ($\xi=$ $-0.4$ (orange dotted-dashed line), 0.2 (red solid line), and 0.4 (green wide dashed line)) quark matter in the quark-meson model.$ \xi $ 

$-0.4$ 

$0$ 

$0.2$ 

$0.4$ 

$T^{\chi}_c/\mathrm{MeV}$ 

137 146 152 159 $T^{\chi}_s/\mathrm{MeV}$ 

233 248 258 270 Table 2. Chiral critical temperatures,
$T^{\chi}_c$ and$T^{\chi}_s$ , for the non-strange condensate and strange condensate, respectively, at the vanishing quark chemical potential for different anisotropy parameters.Next, we extend our exploration to the finite quark chemical potential to analyze the effect of momentum anisotropy on the structure of the QCD phase diagram. In Fig. 3, the temperature dependence of non-strange chiral condensate
$ \sigma_{x} $ for both isotropic and anisotropic quark matter at different quark chemical potentials ($ viz $ .,$ \mu = $ 150, 200, and 250 MeV) is plotted. At$\mu = 150\; {\rm{MeV}}$ , the chiral symmetry restoration with different values of$ \xi $ still occurs as the crossover phase transition. For$\mu = 200\; {\rm{MeV}}$ , the value of$ \sigma_{x} $ in the anisotropic quark matter with$ \xi = -0.4 $ decreases from 60 to 23 MeV, and the associated susceptibility presents a divergent behavior at$T = 90\;{\rm{MeV}}$ , which signals the appearance of a first-order phase transition. For$\mu = 250\;{\rm{MeV}}$ , the discontinuity of$ \sigma_{x} $ (i.e., the first-order phase transition) also occurs at$ \xi = -0.4,\; 0 $ , and 0.2, whereas at$ \xi = 0.4 $ , the phase transition is still a smooth crossover. Thus, for the anisotropic matter with$ \xi = 0.4 $ , a first-order phase transition occurs at the higher quark chemical potential. Accordingly, the chiral phase transition diagram can be studied by outlining the location of$ T^{\chi}_{c} $ for a wide range of quark chemical potentials. The first-order phase transition has to end, and then it changes into a crossover at the QCD critical endpoint (CEP), at which the phase transition is of the second order. In Fig. 4, the 2+1 flavor chiral phase diagram in the ($ \mu $ ,$ T $ )-plane for the quark-meson model within the effect of momentum-space anisotropy is presented. Along the first-order phase transition line (crossover phase transition line), the chiral critical temperature increases from zero up to the CEP temperature (from the$ T_{\rm CEP} $ up to$ T_{c}^{\chi}(\mu = 0) $ ), whereas the critical quark chemical potential decreases from$ \mu_{c}(T = 0) $ to$ \mu_{\rm CEP} $ (from$ \mu_{\rm CEP} $ to zero). We observe that the phase boundary in the ($ \mu $ ,$ T $ )-plane of the quark-meson model phase diagram is shifted to higher values of$ \mu $ and$ T $ , with the increasing anisotropy parameter. We can also clearly see that the position of the CEP significantly depends on the variation of the momentum anisotropy parameter. As$ \xi $ increases, the location of the CEP shifts to a higher$ \mu $ and a smaller$ T $ domain, which is similar to that in the study of the non-extensive effect in the linear sigma model [58]. A similar phenomenon is also observed in the literature for the analysis of the finite size effects on chiral phase transitions [50-53, 56]. In Ref. [50], when the system size is reduced to 4 fm, the CEP in the quark-meson model vanishes, and the whole chiral phase boundary becomes a crossover curve. Based on this result, we deduce that as$ \xi $ increases further, the CEP may disappear. In this work, for$ \xi = -0.4,\; 0,\; 0.2,\; 0.4 $ , the location of the CEP is at$ (T_{\rm CEP},\; \mu_{\rm CEP}) = (100,\; 174) $ MeV, (91,222) MeV, (84,247) MeV and (79,270) MeV, respectively. The value of$ \mu_{\rm CEP} $ from$ \xi = -0.4 $ to$ \xi = 0.4 $ increases by approximately 50%, whereas the value of$ T_{\rm CEP} $ increases by approximately 20%. This means that the influence of momentum-space anisotropy on the quark chemical potential coordinate of the CEP is more prominent than that on the temperature of the CEP. An opposite trend can be observed in the study of the finite volume effect [50], where the temperature coordinate of the CEP in the quark-meson model appears to be affected more strongly by the finite volume than the quark chemical potential coordinate of the CEP.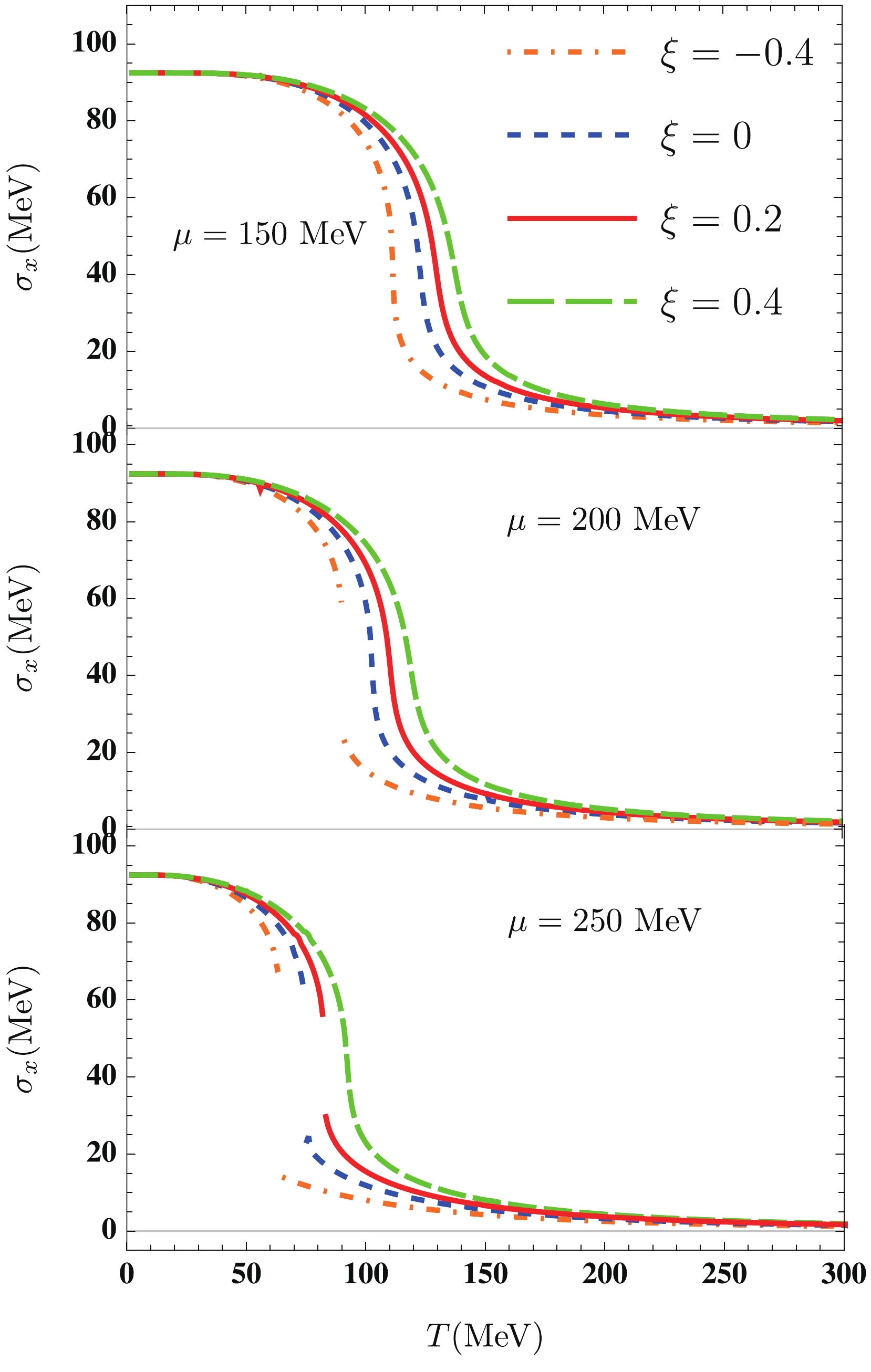
Figure 3. (color online) Temperature dependences of the non-strange chiral condensate at
$\mu=150\;\mathrm{MeV}$ (upper panel),$\mu=200\;\mathrm{MeV}$ (middle panel), and$\mu=250\;\mathrm{MeV}$ (lower panel) in quark matter with different anisotropy parameters, i.e.,$\xi=\;-0.4$ (orange dotted-dashed lines), 0.0 (blue dash lines), 0.2 (red solid lines), and 0.4 (green wide dashed lines).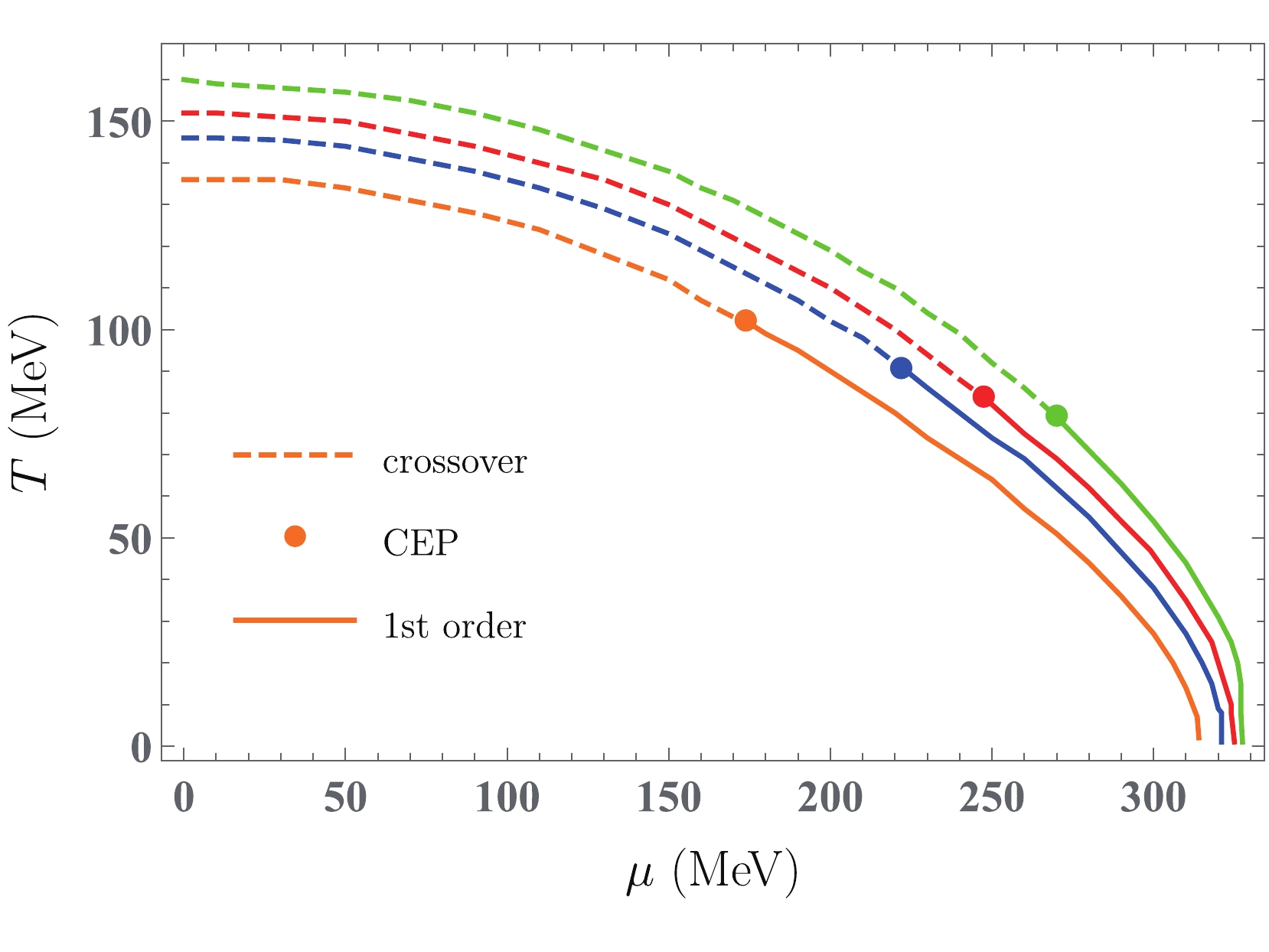
Figure 4. (color online) Chiral phase diagram for different anisotropy parameters in the quark-meson model. The solid lines represent the first-order phase transition curves, the dashed lines denote the crossover transition curves, and the solid dots represent the position CEP (
$\mu_{\rm CEP}, T_{\rm CEP}$ ). -
Let us now study the influence of anisotropy parameter
$ \xi $ on the thermodynamics at the vanishing quark chemical potential. The$ T $ - and$ \xi $ -dependent pressure,$ P(T,\xi) $ , which is derived from the thermodynamic potential, is given as$ \begin{array}{l} P(T,\xi) = -\Omega(T,\xi), \end{array} $

(16) with vacuum normalization
$ P(0,\xi) = 0 $ . Entropy density$ s $ and energy density$ \epsilon $ are defined as$ \begin{array}{l} s(T,\xi) = -\dfrac{\partial\Omega(T,\xi)}{\partial T} \end{array} $

(17) and
$ \begin{array}{l} \epsilon(T,\xi) = -P(T,\xi)+Ts(T,\xi), \end{array} $

(18) respectively.
In Fig. 5, the variations in scaled pressure
$ P/T^{4} $ , scaled entropy density$ s/T^{3} $ , and scaled energy density$ \epsilon/T^{4} $ with respect to temperature in the quark-meson model for both isotropic and anisotropic quark matter are presented. It can be seen that the thermal behaviors of$ P/T^{4} $ ,$ s/T^{3} $ , and$ \epsilon/T^{4} $ for the anisotropic quark matter are in agreement with those for the isotropic system. Specifically, with increasing temperature,$ P/T^{4} $ ,$ s/T^{3} $ , and$ \epsilon/T^{4} $ first rise rapidly and then tend toward a saturation value. At a high enough temperature, the limit values of$ P/T^4 $ ,$ s/T^3 $ , and$ \epsilon/T^{4} $ for the case of$ \xi = -0.4 $ stabilize at approximately 4.0, 16.5, and 12.5, respectively, even th-ough all these values are lower than their respective QCD Stefan-Boltzmann (SB) limit values:$\dfrac{P_{\rm SB}}{T^4} = \left(N_{c}^2-1\right)\dfrac{\pi^2}{45} + N_{c}N_{f}\dfrac{2\pi^2}{180} \simeq 5.2$ ,$\dfrac{s_{\rm SB}}{T^3} = \dfrac{4P_{\rm SB}}{T^4}\simeq20.8, \; \dfrac{\epsilon_{\rm SB}}{T^4} = \dfrac{3P_{\rm SB}}{T^4}\simeq15.6$ . From Fig. 5, we can also see that the limit values of these thermodynamics at a high enough temperature are still decreasing functions of$ \xi $ , which is opposite to their qualitative behaviors with non-extensive parameter$ q $ . In Ref. [57], at a high temperature, the limit values of these scaled thermodynamics increase as$ q $ increases. Moreover, their features with$ \xi $ are significantly different from those with the finite volume effect. For example, Refs. [42, 53] indicate that with increasing temperature,$ P/T^4 $ first decreases with increasing volume and then quickly saturates to the infinite volume value; in other words, these thermodynamics are insensitive to volume changes in the high temperature domain.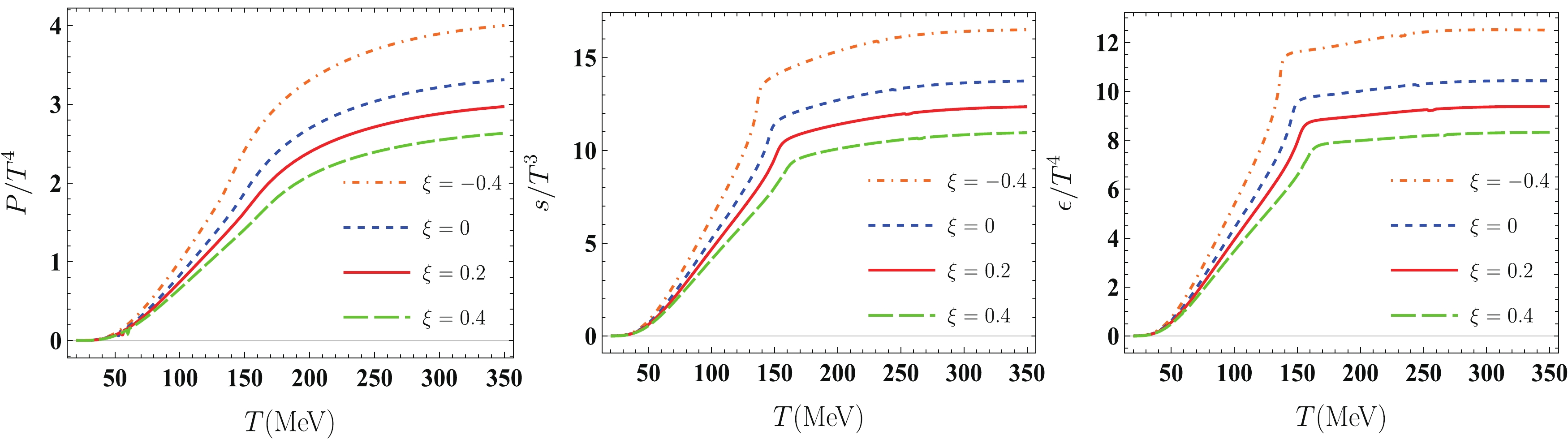
Figure 5. (color online) Temperature dependences of scaled pressure
$P/T^4$ (left panel), scaled entropy density$s/T^3$ (middle panel), and scaled energy density$\epsilon/T^4$ (right panel) for$\mu=0\;\mathrm{MeV}$ in quark matter with different anisotropy parameters, i.e.,$\xi=$ $-0.4$ (orange dotted-dashed lines), 0.0 (blue dash lines), 0.2 (red solid lines), and 0.4 (green wide dashed lines).The speed of sound squared,
$ c_{s}^2 $ , as an important quantity in the HICs, is also studied in the present work. It is defined by$ \begin{array}{l} c_{s}^2(T,\xi) = \dfrac{\partial P}{\partial \epsilon}\bigg|_{V} = \dfrac{\partial P}{\partial T}\bigg|_{V}\bigg/\dfrac{\partial\epsilon}{\partial T}\bigg|_{V} = \dfrac{s}{C_{V}}, \end{array} $

(19) with the specific heat at constant volume
$ V $ $ \begin{array}{l} C_{V}(T,\xi) = \dfrac{\partial \epsilon}{\partial T}\bigg|_{V} = -T\dfrac{\partial^2\Omega}{\partial T^2}\bigg|_{V}. \end{array} $

(20) As shown in the upper panel of Fig. 6, the scaled specific heat,
$ C_{V}/T^{3} $ , first rises rapidly with increasing temperature, reaches the maximum near chiral critical temperature$ T^{\chi}_c $ , and then decreases and eventually remains constant. Similar to$ P/T^{4} $ ,$ s/T^{3} $ , and$ \epsilon/T^{4} $ , the limit value of$ C_{V}/T^{3} $ at high temperatures also decreases as$ \xi $ increases. The peak of$ C_{V}/T^{3} $ decreases as$ \xi $ increases; in other words, as$ \xi $ increases, the critical behavior of$ C_{V}/T^{3} $ is smoothed out. From the lower panel of Fig. 6, we can observe that the thermal behavior of the speed of sound squared,$ c_{s}^{2} $ , for$ \xi = -0.4 $ exhibits a sharp drop near the corresponding chiral critical temperature$ T_{c}^{\chi} $ ; then, it increases rapidly up to the ideal gas value of$ 1/3 $ . Moreover, as$ \xi $ increases, the dip structure of$ c_{s}^{2} $ is gradually weakened, and the location of its minimum shifts to higher temperatures, which is qualitatively similar to$ C_V/T^3 $ . At high temperatures, we can see that$ c_{s}^2 $ is nearly unaffected by$ \xi $ because the reduction in entropy density and the increment in the inverse specific heat almost cancel each other out. The literature on studies of the finite-size effect [41, 42] and the non-extensive effect [57] in the PNJL model has also indicated that as system size$ L $ (non-extensive parameter$ q $ ) decreases (increases), the critical behavior of$ c_{s}^2 $ gradually dilutes and even vanishes. Therefore, these results for thermodynamics again emphasize that an increase in$ \xi $ can hinder the restoration of chiral symmetry.
Figure 6. (color online) Temperature dependences of scaled specific heat
$C_{V}/T^3$ (upper panel) and squared speed of sound$c_{s}^2$ (lower panel) at$\mu=0$ MeV for isotropic ($\xi=0$ (blue dashed lines)) and anisotropic ($\xi=$ $-0.4$ (orange dotted-dashed lines), 0.2 (red solid lines), and 0.4 (green wide dashed lines)) quark matter in the quark-meson model. -
In this part, we study the chiral structures of scalar (
$ J^P = 0^+ $ ) and pseudoscalar ($ J^P = 0^- $ ) meson masses at the vanishing quark chemical potential. A detailed procedure for calculating the meson mass at a finite temperature and quark chemical potential in the quark-meson model can be found in Ref. [36]. Here, we just sketch the outline of the related computation. In quantum field theory, scalar and pseudoscalar meson masses can generally be obtained from the second derivative of the temperature- and quark chemical potential-dependent thermodynamic potential density,$ \Omega(T,\mu_{f}) $ , with respect to the corresponding scalar fields$ \alpha_{S,a} = \sigma_{a} $ and pseudoscalar fields$ \alpha_{P,a} = \pi_{a} (a = 0,...,8) $ , which can be expressed as [36]$ \begin{array}{l} m_{i,ab}^2 = \dfrac{\partial^2\Omega\left(T,\mu_{f}\right)}{\partial\alpha_{i,a}\partial\alpha_{i,b}}\bigg|_{\rm{min}} = \left(m_{i,ab}^{\rm{M}}\right)^2+\left(m_{i,ab}^{\rm{T}}\right)^2, \end{array}$

(21) where the
$ i = S(P) $ subscript denotes the scalar (pseudoscalar) mesons. The first term on the right-hand side of Eq. (21) denotes the vacuum mass squared matrices calculated from the second derivative of purely mesonic potential. The second term represents the modification of the mass squared matrices due to fermionic thermal correction at a finite temperature and quark chemical potential, which in an anisotropic system can be written as$ \begin{aligned}[b] (\delta m_{i,ab}^{T})^2 =& \dfrac{\partial\Omega_{q\bar{q}}(T,\mu_{f},\xi)}{\partial\alpha_{i,a}\partial\alpha_{i,b}} = 2N_{c}\sum_{f = l,s}\int\dfrac{{\rm d}p}{4\pi^2}\dfrac{p^2}{E_{f}}\left\{\left[f_{q,f}^0\left(m^2_{f,ab}-\dfrac{m^2_{f,a}m_{f,b}^2}{2E_{f}^2}\right)-\dfrac{f_{q,f}^0\left(1-f_{q,f}^0\right)}{2E_{f}T}m_{f,a}^2m_{f,b}^2\right]\right.\\& \left.\times\left[1-\dfrac{\xi p^2}{6E_{f}T}\left(1-f_{q,f}^0+\dfrac{T}{E_{f}}\right)\right]+\dfrac{\xi p^2f_{q,f}^0}{12E_{f}^2T^2}m_{f,a}^2m_{f,b}^2\left[\dfrac{2T^2}{E_{f}^2}+\dfrac{T}{E_{f}}-\dfrac{Tf^0_{q,f}}{E_{f}}-f_{q,f}^0\left(1-f_{q,f}^0\right)\right]+q\rightarrow\bar{q}\right\} . \end{aligned}$

(22) The squared constituent quark mass derivative with respect to meson field
$ \partial m_{f}^2/\partial\alpha_{i,a}\equiv m_{f,a}^2 $ , and that with respect to meson fields$ \partial^2 m_{f}^2/(\partial\alpha_{i,a}\partial\alpha_{i,b})\equiv m_{f,ab}^2 $ for different flavors are listed in Table 3 of Ref. [36]. When$ \xi = 0 $ , Eq. (22) can be reduced to the result for an isotropic system. Thereafter, the squared masses of four scalar meson states are given as [23, 36, 37]$ \begin{array}{l} m_{a_{0}}^2 = (m_{a_{0}}^\mathrm{M})^2+(\delta m_{S,11}^T)^2, \end{array} $

(23) $ \begin{array}{l} m_{\kappa}^2 = (m_{\kappa}^\mathrm{M})^2+(\delta m_{S,44}^T)^2, \end{array} $

(24) $ \begin{aligned}[b] \; m_{\sigma}^2 =& m_{S,00}^2\cos^2\theta_{S}+m_{S,88}^2\sin^2\theta_{S}\\ &+2m_{S,08}^2\sin\theta_{S}\cos\theta_{S}, \end{aligned} $

(25) $ \begin{aligned}[b] m_{f_{0}}^2 =& m_{S,00}^2\sin^2\theta_{S}+m_{S,88}^2\cos^2\theta_{S}\\ &-2m_{S,08}^2\sin\theta_{S}\cos\theta_{S}. \end{aligned} $

(26) The four pseudoscalar meson masses are
$ \begin{array}{l} m_{\pi}^2 = (m_{\pi}^{\mathrm{M}})^2+(\delta m_{P,11}^T)^2, \end{array} $

(27) $ \begin{array}{l} m_{K}^2 = (m_{K}^{\mathrm{M}})^2+(\delta m_{P,44}^T)^2, \end{array} $

(28) $ \begin{aligned}[b] \;\;m_{\eta^{'}}^2 = & m_{P,00}^2\cos^2\theta_{P}+m_{P,88}^2\sin^2\theta_{P}\\ &+2 m_{P,08}^2\sin\theta_{P}\cos\theta_{P}, \end{aligned} $

(29) $ \begin{aligned}[b] \;\;m_{\eta}^2 =& m_{P,00}^2\sin^2\theta_{P}+m_{P,88}^2\cos^2\theta_{P}\\& -2 m_{P,08}^2\sin\theta_{P}\cos\theta_{P}, \end{aligned} $

(30) where the mixing angles,
$ \theta_{S(P)} $ , read as$ \begin{array}{l} \tan 2{\theta _i} = \left( {\dfrac{{2m_{i,08}^2}}{{m_{i,00}^2 - m_{i,88}^2}}} \right),\;\;\;\;\;i - S,P. \end{array} $

(31) and
$ m_{i,00/88/08}^2 = (m_{i,00/88/08}^\mathrm{M})^2+\delta(m_{i,00/88/08}^{T})^2 $ . The detailed descriptions of the vacuum contributions$\Big[ (m_{a_{0}}^\mathrm{M})^2$ ,$ (m_{\kappa}^\mathrm{M})^2 $ ,$ (m_{\pi}^{\mathrm{M}})^2 $ ,$ (m_{K}^{\mathrm{M}})^2 $ and$(m_{i,00/88/08}^\mathrm{M})^2 \Big]$ from the purely mesonic potential in Eqs. (23)-(30) can be found in Refs. [36, 37].The left panels and right panels of Fig. 7 display the
$ T $ -dependent masses of the pseudoscalar ($ \pi $ ,$ K $ ,$ \eta' $ ,$ \eta $ ) and scalar ($ f_{0} $ ,$ \sigma $ ,$ a_{0} $ ,$ \kappa $ ) mesons for both isotropic and anisotropic quark matter in the quark-meson model, respectively. We can see that for a fixed anisotropy parameter, the masses of pseudoscalar meson sectors$ \pi $ ,$ K $ , and$ \eta $ remain constant up to near the chiral critical temperature of non-strange condensate,$ T_{c}^{\chi} $ , whereas the masses of$ \eta' $ and scalar meson sectors$ \sigma $ ,$ a_{0} $ ,$ \kappa $ remain constant at a low temperature and then decrease before reaching$ T_{c}^{\chi} $ . For pseudoscalar meson sector$ f_{0} $ , its mass also remains constant at a low temperature but decreases before reaching the chiral critical temperature of strange condensate,$ T_{s}^{\chi} $ . For pseudoscalar meson sectors$ \pi $ ,$ K $ , and$ \eta $ , their masses always decrease with increasing$ \xi $ at$ T>140 $ MeV. However, for$ \eta' $ and pseudoscalar meson sectors ($ \pi $ ,$ K $ ,$ \eta' $ ,$ \eta $ ), the dependence of their masses on anisotropy parameter$ \xi $ is nonmonotonic in the entire temperature domain of interest. More precisely, with an increase in$ \xi $ , the masses of$ \eta' $ $ \sigma $ ,$ a_{0} $ ,$ \kappa $ first increase in the low temperature domain ($ 100\; \mathrm{MeV}<T<160\;{\rm{MeV}} $ ) and then decrease in the higher temperature domain ($ T>160 \;{\rm{MeV}}$ ). For$ f_{0} $ , its mass increases with increasing$ \xi $ at$ T<270 \;{\rm{MeV}}$ ($ viz $ .,$ T_{s}^{\chi}(\xi = 0.4) $ ) and decreases thereafter. As a whole, near above$ T_{c}^{\chi} $ or$ T_{s}^{\chi} $ , all mesons have unphysical degrees of freedom, and their masses become degenerate, which signals the restoration of chiral symmetry. In Fig. 7, we can also see that with an increase in$ \xi $ , the temperature coordinate at which meson masses begin to degenerate can be shifted to higher temperatures. This again demonstrates that an increase in the momentum-space anisotropy parameter can hinder the restoration of chiral symmetry. The qualitative behaviors of these meson masses with$ \xi $ are different from the results for analyzing the finite size dependence of meson masses within the PNJL model [42, 46], where$ K $ ,$ \eta $ , and$ \eta' $ have a significant volume dependence in the lower temperature domain ($ T<100\; $ MeV).
Figure 7. (color online) Temperature dependences of pseudoscalar mesons
$ \pi $ ,$ K $ ,$ \eta' $ ,$ \eta $ (left panels) and scalar mesons$ f_{0} $ ,$ \sigma $ ,$ a_{0} $ ,$ \kappa $ (right panels) at$ \mu = 0\; \mathrm{MeV} $ for both isotropic ($ \xi = 0 $ (blue dashed lines)) and anisotropic ($ \xi = $ $ -0.4 $ (orange dotted-dashed lines), 0.2 (red solid lines), and 0.4 (green wide dashed lines)) quark matter in the quark-meson model. -
Studying transport properties is essential for a deep understanding of the dynamical evolution of strongly interacting matter. In this part, we discuss the influence of momentum-space anisotropy on transport coefficients, such as shear viscosity
$ \eta $ , electrical conductivity$ \sigma_{\rm el} $ , and bulk viscosity$ \zeta $ in quark matter. Due to the effect of momentum-space anisotropy encoded in the parton distribution functions, the general expressions of these transport coefficients, which are obtained by solving the relativistic Boltzmann equation in relaxation time approximation, require some modifications [87-90]. Therefore, using the results in Refs. [88, 89], the formulas of$ \xi $ -dependent transport coefficients at zero quark chemical potential are given as$ \begin{aligned}[b] \eta_{} = \sum\limits_{f}\dfrac{d_f}{15T}\int \dfrac{{\rm d}p}{\pi^2}\dfrac{p^6}{E_{f}^2}\left[\tau_{q,f}f_{q,f}^0(1-f_{q,f}^0)\right]-\sum\limits_{f}\dfrac{\xi d_{f}}{90T^2}\int \dfrac{{\rm d}p}{\pi^2}\dfrac{p^8}{E_{f}^3}\left[\tau_{q,f}f_{q,f}^0(1-f_{q,f}^0) \times \left(1-2f_{q,f}^0+\dfrac{T}{E_{f}}\right)\right], \end{aligned} $

(32) $ \begin{aligned} \sigma_{\rm el} = \displaystyle\sum\limits_{f}\dfrac{d_{f}q_{f}^2}{3T}\int \dfrac{{\rm d}p}{\pi^2}\dfrac{p^4}{E_{f}^2}\left[\tau_{q,f}f_{q,f}^0(1-f_{q,f}^0)\right](1+\dfrac{\xi}{3})-\sum\limits_{f}\dfrac{q_{f}^2\xi d_f}{18T^2}\int\dfrac{{\rm d}p}{(2\pi)^3}\dfrac{p^6}{E_{f}^3}\left[f_{q,f}^0(1+f_{q,f}^0)\left(1-2f_{q,f}^0+\dfrac{T}{E_{f}}\right)\right], \end{aligned} $

(33) $ \begin{aligned}[b] \zeta_{} =& \displaystyle\sum\limits_{f}\dfrac{d_{f}}{T}\displaystyle\int \dfrac{{\rm d}p}{\pi^2}\dfrac{p^2}{E_{f}^2}\left[\left(\dfrac{1}{3}-c_{s}^2\right)p^2-c_{s}^2m_{f}^2+c_{s}^2m_{f}T\dfrac{{\rm d}m_{f}}{{\rm d}T}\right]^2\left[\tau_{q,f}f_{q,f}^0\left(1-f_{q,f}^0\right)\right] \\ &-\displaystyle\sum\limits_{f}\dfrac{\xi d_{f}}{6T^2}\displaystyle\int \dfrac{{\rm d}p}{\pi^2} \dfrac{p^4}{E_{f}^3}\left[\left(\dfrac{1}{3}-c_{s}^2\right)p^2-c_{s}^2m_{f}^2+c_{s}^2m_{f}T\dfrac{{\rm d}m_{f}}{{\rm d}T}\right]^2\left[\tau_{q,f}f_{q,f}^0\left(1-f_{q,f}^0\right)\left(1-2f_{q,f}^0\right)\right]\\ &-\displaystyle\sum\limits_{f}\dfrac{\xi d_{f}}{6T}\displaystyle\int \dfrac{{\rm d}p}{\pi^2} \dfrac{p^4}{E_{f}^4}\left[\dfrac{1}{9}p^4 -\left(c_{s}^2(m_{f}^2+p^2)-c_{s}^2m_{f}T\dfrac{{\rm d}m_{f}}{{\rm d}T}\right)^2\right]\tau_{q,f}f_{q,f}^0\left(1-f_{q,f}^0\right). \end{aligned} $

(34) Here,
$ d_{f} $ is the degeneracy factor for$ f $ -flavor quarks. The quark electric charge,$ q_f $ , is given explicitly by$ q_u = -q_{\bar{u}} = 2e/3 $ and$ q_{d,s} = -q_{\bar{d},\bar{s}} = -e/3 $ . The electron charge reads$ e = (4\pi\alpha_s)^{1/2 } $ with fine structure constant$ \alpha_s\simeq1/137 $ . Different from the formula for bulk viscosity in Ref. [89], we replace the original term$\left[\left(\dfrac{1}{3}-c_{s}^2\right)p^2\right]^2$ in the integrand with$\left[\left(\dfrac{1}{3}-c_{s}^2\right)p^2-c_{s}^2m_{f}^2+c_{s}^2m_{f}T\dfrac{{\rm d}m_{f}}{{\rm d}T}\right]^2$ to incorporate the in-medium effect. In the treatment of relaxation time$ \tau_{q,f} $ , we roughly take a constant value of$ \tau_{q,f} = 1\ \mathrm{fm} $ for the computation. In the weakly anisotropic system, the former terms in Eqs. (32)-(34) are significantly larger than the latter terms in magnitude due to the difference in momentum power of the respective integrands. Therefore, the transport coefficients are still mainly dominated by the first term of the related quantitative expressions.The variation of shear viscosity
$ \eta $ with temperature at the vanishing quark chemical potential for both isotropic and anisotropic quark matter is shown in Fig. 8. We see that$ \eta $ in the (an-)isotropic quark matter rises monotonically with increasing temperature because the$ T $ dependence of$ \eta $ mainly comes from quark distribution function$ f_{q,f}^0 $ in the associated integrand. The qualitative behavior of$ \eta $ with$ \xi $ can also be understand well from the associated expression. In the vicinity of chiral critical temperature$ T_{c}^{\chi} $ ,$ \eta $ slightly decreases as$ \xi $ increases due to the decreasing behavior of Boltzmann factor$ {\rm e}^{-m_{f}(T)/T} $ with$ \xi $ . In the higher temperature domain ($ T>{ }160 $ MeV), the decreasing feature of$ \eta $ is negligible due to the unsensitivity of the constituent quark masses to$ \xi $ . However, the absolute value of the second term in Eq. (32) significantly increases with an increase in$ \xi $ . As a result,$ \eta $ decreases as$ \xi $ increases. This is similar to the result in Ref. [89], where$ \eta $ for the QGP is calculated in the quasiparticle model. For electrical conductivity$ \sigma_{\rm el} $ , its thermal behavior is similar to that of$ \eta $ , and the quantitative difference between$ \eta $ and$ \sigma_{el} $ mainly comes from the different momentum power of the respective integrands. Similar to the shear viscosity, the$ \xi $ dependence of$ \sigma_{\rm el} $ is also determined by the second term in the associated expression. In Fig. 9, we observe that$ \sigma_{\rm el} $ decreases as$ \xi $ increases, which is also qualitatively consistent with the results of$ \sigma_{\rm el} $ for the QGP in the quasiparticle model [87, 90]. The dependence of$ \eta $ and$ \sigma_{\rm el} $ on momentum-space anisotropy is different from that on finite system size$ L $ in the framework of the (P)NJL model. In Ref. [41], both$ \eta $ and$ \sigma_{\rm el} $ first increase as$ L $ decreases in the low temperature domain, whereas the size effect nearly vanishes in the high temperature domain. Furthermore, the results in Ref. [57] also indicate that both$ \eta $ and$ \sigma_{\rm el} $ in the PNJL model increase as non-extensive parameter$ q $ increases for$ T>150\;{\rm{MeV}} $ .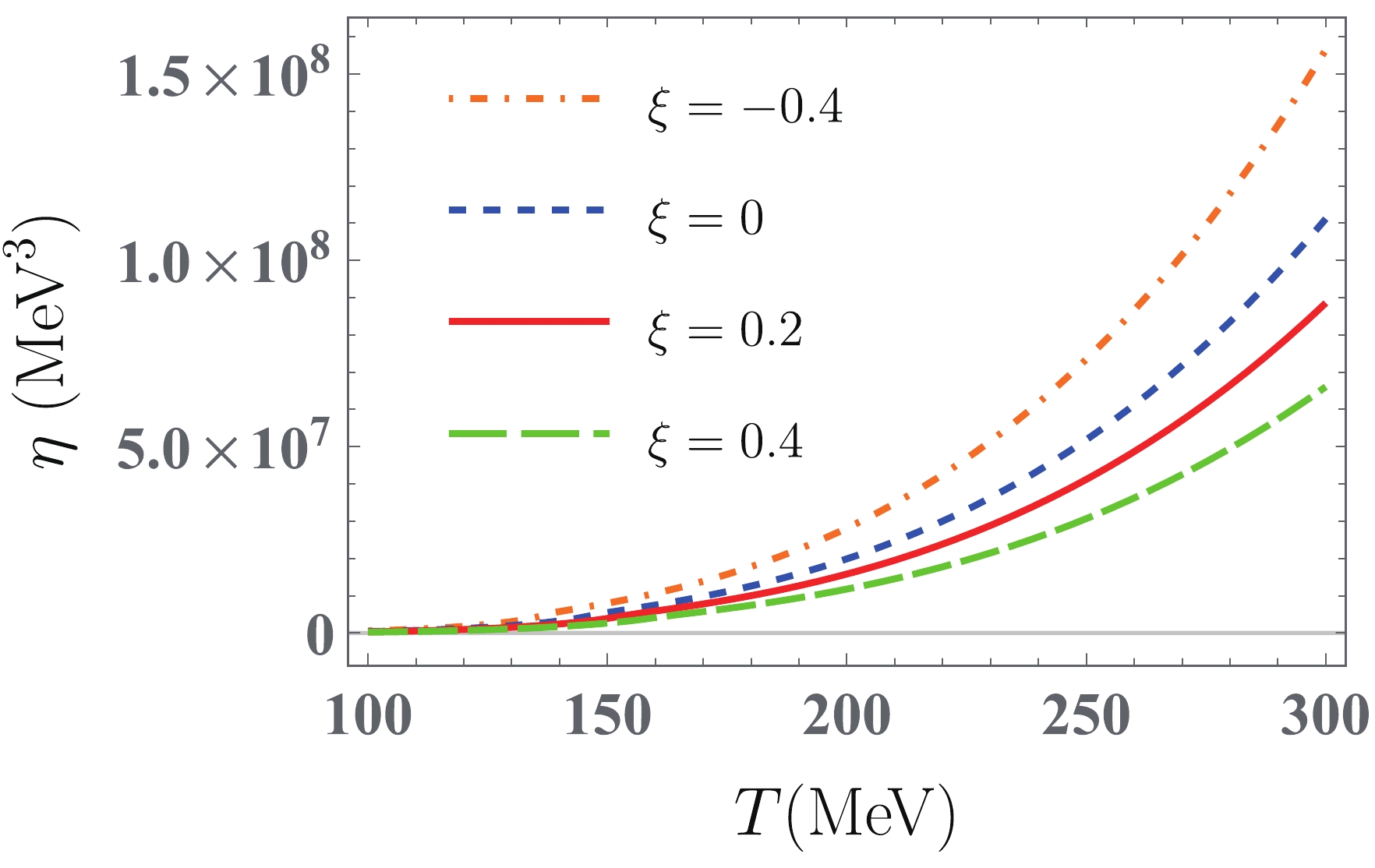
Figure 8. (color online) Temperature dependence of shear viscosity
$\eta$ at$\mu=0$ MeV in quark matter with$\xi= -0.4$ (orange dotted-dashed line), 0.0 (blue dashed line), 0.2 (red solid line), and 0.4 (green wide dashed line).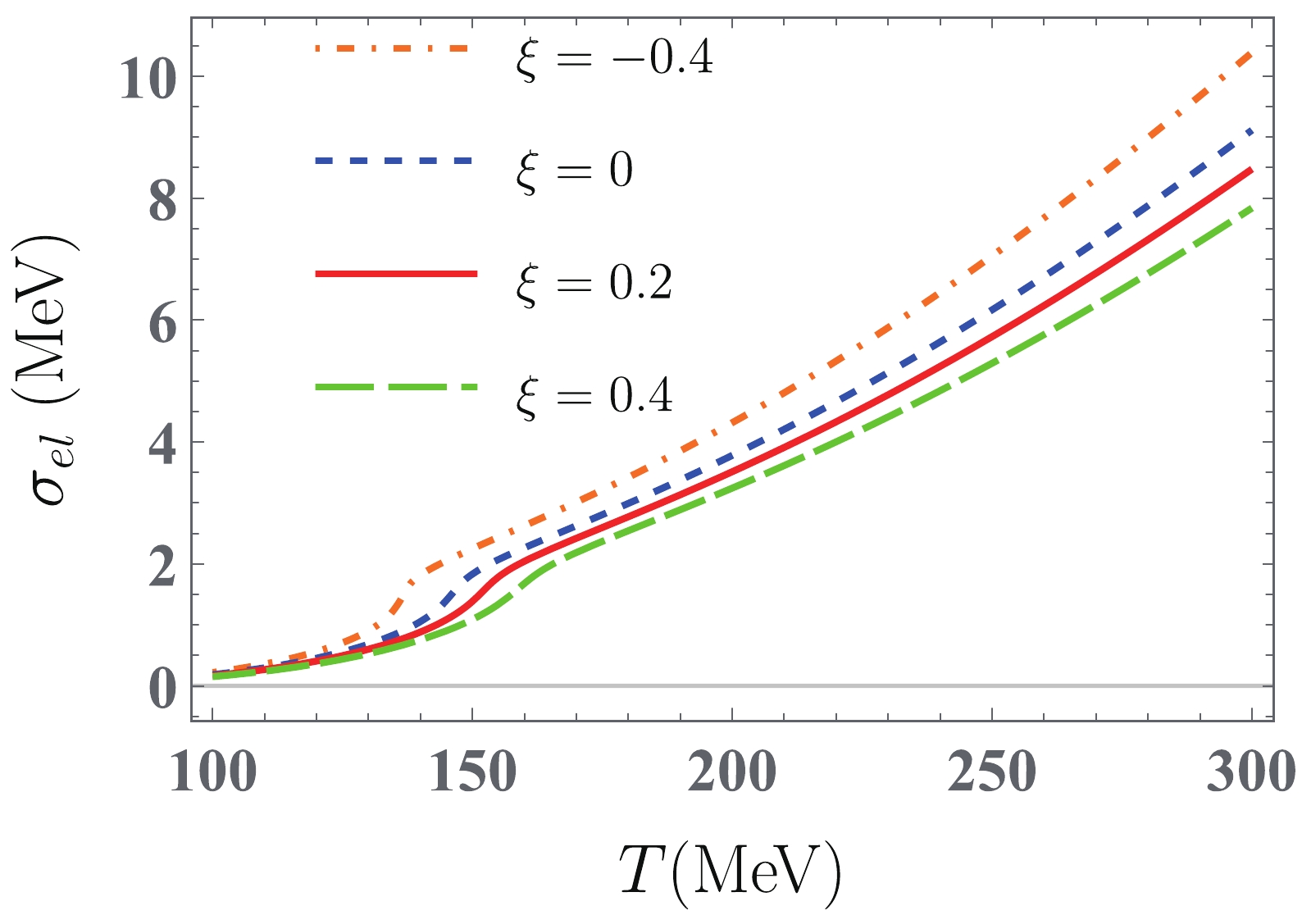
Figure 9. (color online) Temperature dependence of electrical conductivity
$\sigma_{\rm el}$ at$\mu=0$ MeV in quark matter with$\xi= -0.4$ (orange dotted-dashed line), 0.0 (blue dashed line), 0.2 (red solid line), and 0.4 (green wide dashed line).Next, we discuss the temperature dependence of bulk viscosity
$ \zeta $ at zero quark chemical potential for both isotropic and anisotropic quark matter. As shown in Fig. 10, for a fixed anisotropy parameter,$ \zeta $ has peaks in the vicinity of both$ T^{\chi}_{c} $ and$ T^{\chi}_{s} $ , which is significantly different from the thermal behavior of$ \eta $ and$ \sigma_{\rm el} $ . We also note that the thermal profile of$ \zeta $ is similar to$ {\rm d}m_{s}/{\rm d}T $ or$ \chi_{s} $ , which may be attributed to the fact that the qualitative behavior of$ \zeta $ is mainly governed by$ {\rm d}m_{s}/{\rm d}T $ rather than the quark distribution function in the associated integrand of Eq. (34). Due to the decreasing feature of the peak of$ {\rm d}m_{s}/{\rm d}T $ with increasing$ \xi $ , the double-peak structure of$ \zeta $ is weakened as$ \xi $ increases, and the positions of the peaks shift to higher temperatures, as shown in Fig. 10. The diluting effect of$ \xi $ on the critical behavior of$ \zeta $ is similar to that in studies of the finite volume effect and the non-extensive effect. In Ref. [41], the double-peak structure of$ \zeta $ even converts to one broadened peak structure when the system size is reduced to$ 2\ \mathrm{fm} $ . In Ref. [57], as non-extensive parameter$ q $ increases to 1.1, the two peaks of$ \zeta $ begin to merge into a broad peak. -
In this work, an anisotropy parameter,
$ \xi $ , which reflects the degree of momentum-space anisotropy arising from different expansion rates of the fireball generated in HICs along the longitudinal and radial direction was introduced, for the first time, in the 2+1 flavor quark-meson model by replacing the isotropic distribution function in the thermodynamic potential of the quark-meson model with the anisotropic one. The effect of$ \xi $ on the chiral properties, thermodynamics, meson masses, and transport properties in quark matter were investigated. We found that the chiral phase transition of quark matter with different anisotropy parameters is always a crossover at the vanishing quark chemical potential. At the finite quark chemical potential, the temperature of the CEP is affected more significantly by the anisotropy parameter than its quark chemical potential, which is opposite to that in the study of the finite volume effect. We also demonstrate that at a high temperature, the limit values of various scaled thermodynamic parameters ($ P/T^4 $ ,$ s/T^3 $ ,$ \epsilon/T^4 $ ,$ C_{V}/T^3 $ ) are quite sensitive to$ \xi $ . As$ \xi $ increases, their limit values decrease, which is different from the finite size effect, but rather similar to the non-extensive effect. Further, the critical behavior of$ C_{V}/T^3 $ and$ c_{s}^2 $ can be smoothed out with increasing$ \xi $ . For scalar and pseudoscalar mesons, the temperature at which their masses begin to degenerate is enhanced as$ \xi $ increases, which implies that an increase in$ \xi $ can hinder the restoration of chiral symmetry. Finally, the transport coefficients, such as shear viscosity$ \eta $ , electrical conductivity$ \sigma_{\rm el} $ , and bulk viscosity$ \zeta $ for both isotropic and anisotropic quark matter, were also calculated. Our results show that$ \eta $ and$ \sigma_{\rm el} $ rise with increasing temperature, whereas the thermal behavior of$ \zeta $ exhibits a noticeable double-peak structure. It was found that$ \eta $ and$ \sigma_{\rm el} $ decrease monotonically as$ \xi $ increases, whereas the qualitative behavior of$ \zeta $ with$ \xi $ was similar to$ \chi_{s}(\xi) $ . With increasing$ \xi $ , the double-peak structure of$ \zeta $ can be weakened, and the positions of the peaks shift to higher temperatures.In the present study, we only focused on the chiral aspect of the QCD phase diagram. The exploration of the confinement phase transition in anisotropic quark matter can also be addressed via the Polyakov-loop potential. In the Polyakov-loop improved quark-meson model, the chiral phase transition and the location of the CEP are affected further. For the calculation of the transport coefficients in this study, the quark relaxation time was assumed to be a constant. However, in a realistic interaction scenario, the relaxation time may also vary with the momentum anisotropy. These issues comprise our future research directions. Moreover, note that a spheroidal momentum-space anisotropy specified by one anisotropy parameter in one preferred propagation direction was considered in this work; however, the introduction of additional anisotropy parameters is necessary to provide a better characterization of the QGP properties. The chiral and confinement phase transitions in quark matter with ellipsoidal momentum-anisotropy [76, 77], characterized by two independent anisotropy parameters, can also be modeled using the PNJL model or PQM model. Research on these directions is in progress, and we expect to report our results soon.
Effect of momentum anisotropy on quark matter in the quark-meson model
- Received Date: 2021-10-19
- Available Online: 2021-04-15
Abstract: We investigate the chiral phase structure of quark matter with spheroidal momentum-space anisotropy specified by one anisotropy parameter






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: