-
Axions are light pseudo-Goldstone bosons proposed to solve the strong CP problem in QCD [1-3]. Many new physics models beyond the standard model also suggest the existence of axion-like particles (ALPs) [4, 5]. These particles may play an important role in the evolution of the universe and have rich phenomenology in high-energy and astrophysics experiments. Considering the effective coupling between ALPs and photons, many investigations for the ALP-photon conversion effect have been performed [6-11]. For instance, the CAST experiment investigated the photon signal induced by ALPs from the Sun and has set a stringent constraint on the ALP-photon coupling as
$ g_{a\gamma}\leqslant 6.6\times 10^{-11}\; {{{\rm{GeV}}}^{-1}} $ [12].A promising avenue of investigation is to explore ALPs through the ALP-photon oscillation effect in high-energy astrophysical processes [13]. The initial high-energy photons emitted from an astrophysical source may be converted into ALPs by the external magnetic field around the source [14-16]. The ALPs would then propagate in extragalactic space without energy loss, whereas high-energy photons could interact with the extragalactic background light (EBL). Finally, the ALPs could be converted into detectable high-energy photons by the Galactic magnetic field. Therefore, it is expected that the ALP-photon oscillation would reduce the attenuation effect of high-energy photons from distant sources and affect the final photon spectrum.
Using data from observations of high-energy photons, many studies on ALP-photon conversion have been performed [10, 11, 15-39]. For instance, the
$ \gamma $ -ray spectra from the sources NGC 1275 and PKS 2155$ - $ 304 at high redshifts measured by Fermi-LAT have been used to set constraints on$ g_{a\gamma} $ in Ref. [22] and Ref. [25], respectively. Compared with the detectable energy range of Fermi-LAT$ \sim 0.1 $ -300 GeV, imaging atmospheric Cherenkov telescopes detect high-energy$ \gamma $ -rays above$ {\cal{O}}(10^2) $ GeV, which opens a different window for ALP research. For instance, the data for PKS 2155$ - $ 304 from H.E.S.S. I observations have been used to search for ALPs in Ref. [18].Compared with H.E.S.S. I, H.E.S.S. II with the fifth telescope added in 2012 is sensitive to the
$\gamma$ -ray spectra at lower energies. The H.E.S.S. II measurements of the very high energy (VHE, E$ \gtrsim 100\;{{{\rm{GeV}}}} $ ) gamma-ray spectra of two extragalactic sources, PKS 2155$ - $ 304 and PG 1553$ + $ 113, have been reported in Ref. [40]. These two sources are high-frequency peaked BL Lac objects with high statistics in the VHE$ \gamma $ -ray sky. Since they are located at high red-shifts (z = 0.116 and 0.49 for PKS 2155$ - $ 304 and PG 1553$ + $ 113, respectively), the EBL attenuation effects for their spectra are expected to be significant. Consequently, the measurements of VHE spectra are suitable to detect the ALP-photon oscillation, which can compensate the EBL attenuation effect.This paper is organized as follows. In Sec. II, we describe the EBL attenuation effect and introduce the two EBL models adopted in this work. In Sec. III, we introduce the ALP-photon oscillation effects in the extragalactic source and the Milky Way. In Sec. IV, we describe our fitting method to the observed γ-ray spectra. In Sec. V, we investigate the implications of ALPs in the data for the two EBL models. The conclusions are given in Sec. VI.
-
Before entering the Galaxy, high-energy
$ \gamma $ -rays would interact with the EBL and lose energy through the pair production process$ \gamma + \gamma_{\rm{EBL}} \to e^+ + e^- $ . This attenuation effect can be described by the factor$ e^{-\tau\left(E_\gamma, z_0\right)} $ , where$ \tau\left(E_\gamma, z_0\right) $ is the optical length of a photon with a detectable energy of$ E_\gamma $ , which is emitted from the source at redshift of$ z_0 $ :$ \begin{aligned}[b] \tau\left(E_\gamma,z_0\right) =& c\int_0^{z_0}\frac{{\rm{d}}z}{\left(1+z\right)H_0} \\& \times \left[\left(1+z\right)^2(1+\Omega_{m}z)-z(z+2)\Omega_{\Lambda}\right]^{-1/2}\\& \times \int^{}_{E'_{\gamma}\geqslant E_{\rm{th}}}{\rm{d}}\omega\frac{{\rm{d}}n(z)}{{\rm{d}}\omega}\bar{\sigma}(E'_\gamma,\omega), \end{aligned}$

where
$ H_{0} $ is the Hubble constant,$ \Omega_{m} $ is the matter density,$ \Omega_{\Lambda} $ is the dark energy density,$ E_{\rm{th}} $ is the threshold energy of pair production,$ {\rm{d}}n(z)/{\rm{d}}\omega $ is the proper number density per unit energy of the EBL at redshift z,$ E'_\gamma $ is the photon energy at z, and$ \bar{\sigma}\left(E'_\gamma,\omega\right) $ is the integral cross section of pair production:$ \bar{\sigma}(E'_\gamma, \omega) = \int^2_{0} {\rm d}x\frac{x}{2}\sigma_{\gamma\gamma}, $

(1) where x equals
$ 1-{\rm{cos}}\theta $ , with$ \theta $ the angle between the two scattering photons, and$ \begin{aligned}[b] \sigma_{\gamma\gamma} =& \frac{3}{16}\sigma_{\rm{T}}\left(1-\beta^2\right) \\&\times\left[(3-\beta^4)\ln\frac{1+\beta}{1-\beta} -2\beta (2-\beta^2)\right], \end{aligned} $

(2) where
$ \sigma_{\rm{T}} $ is the Thomson cross section, which equals$ 6.25\!\times \!10^{-29}\; {{\rm{m}}}^2 $ and$ \beta $ equals$ \left(1\!-\!4m^2_{e}c^4/s\right)^{1/2} $ with$ s\! =\! 2E'_{\gamma}\omega x $ .The main contributions to the EBL at wavelengths from UV to IR are expected to be from starlight and dust re-radiation, accumulated over the history of the universe. In order to predict the EBL, detailed modeling of the evolution of galaxy populations is needed. Many EBL models based on empirical or semi-analytical approaches have been developed [41-45]. Depending on the method of dealing with the evolution of galaxy populations and the EBL, these models can be classified into four types [43]. Using the cosmological survey data from a variety of ground-based experiments and space telescopes, Franceschini et al. built a backward evolutionary model to extrapolate the evolution of the EBL [41] (hereafter the FRV08 model). The observed galaxy luminosity functions are used to derive the contributions from different galaxy populations based on morphology. In our work, we adopt this EBL model to compute the gamma-ray attenuation effect.
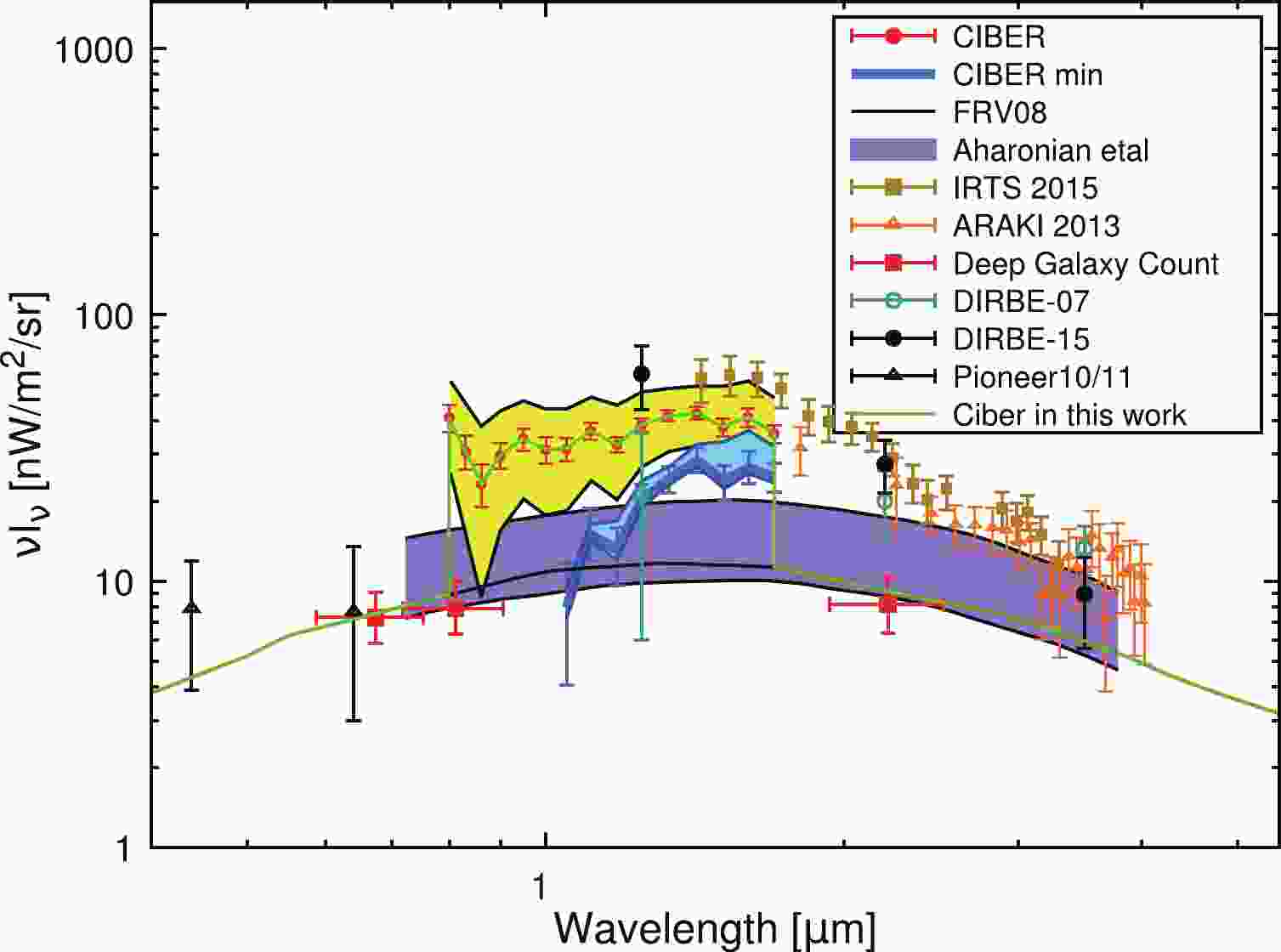
It is difficult to directly measure the EBL spectrum due to the bright foregrounds, such as the zodiacal light, which is sunlight scattered by interplanetary dust. Some efforts have been made to directly derive the EBL at near-IR wavelengths by subtracting the foregrounds from the data [46-51]. It is interesting to note that many analyses suggest an isotropic excess in the range
$\sim 1-4\; \mu {\rm{m}}$ compared with the integrated light from galaxies predicted from deep galaxy counts and theoretical models. Recently, Ref. [51] reported the derived EBL in the wavelength range 0.8$ - $ 1.7$\mu$ m from the CIBER observation, as shown in Fig. 1. The absolute brightness of the derived EBL is highly dependent on the subtraction of zodiacal light. Assuming the Kelsall zodiacal light model [52], the residual brightness is$42.7 ^{+11.9}_{-10.6} {\rm{nW}}\cdot {\rm{m}}^{-2}{{\rm{sr}}}^{-1} $ at$1.4 \; \mu{\rm{m}}$ . Using a model-independent method for the subtraction, the derived minimum EBL brightness is 28.7$ ^{+5.1}_{-3.3}\; {\rm{nW}}\cdot {\rm{m}}^{-2}{\rm{sr}}^{-1} $ at$1.4 \; \mu{\rm{m}}$ , which still exceeds the theoretical results.This excess may be explained by a new foreground component or a new EBL component. For instance, the radiation from Population III stars at redshifts
$ \sim 10-20 $ may contribute to this component [53]. Some studies also investigate the possibility that this component is produced by the decay of ALPs [54-56].It is expected that the high-energy
$ \gamma $ -ray spectrum of the astrophysical source at high redshifts would suffer from a significant attenuation effect after considering the excess. Therefore, the VHE gamma-ray observations set constraints on the EBL. There is a conflict between the results from these analyses and the directly derived EBL at${\cal{O}}(1) \; \mu{\rm{m}}$ (see e.g. Refs. [57, 58]). Reference [38] found that this conflict can be reconciled by oscillation between the photons and ALPs, and finds an ALP parameter region favored by observations. In this work, we consider the EBL model with an excess at$ {\cal{O}}(1) $ µm based on the CIBER result [51] (hereafter the Ciber model) and investigate the ALP implication using a different method to calculate ALP-photon conversion compared with Ref. [38]. We incorporate the CIBER result into the FRV08 spectrum at present and only consider the redshift evolution for this excess at$ z\sim 0-0.5 $ . -
In this section we describe the ALP-photon oscillation effect in propagation. The ALP-photon conversion arises from the effective coupling between ALPs and photons through the triangle graph with internal fermion lines. The effective Lagrangian is written as
$ {\cal{L}}_{a\gamma} = -\frac{1}{4}g_{a\gamma}a F_{\mu\nu}\tilde{F}^{\mu\nu} = g_{a\gamma}a {{E}}\cdot{{B}}, $

(3) where a is the ALP field,
$ F_{\mu\nu} $ is the electromagnetic field tensor,$ \tilde{F}^{\mu\nu} $ is the dual tensor, and E and B represent the electric and magnetic field, respectively. The ALP-photon beam can be described by$ \Psi = (A_1, A_2, a)^T $ , where$ A_1 $ and$ A_2 $ represent the photon transverse polarization states along two orthogonal directions$\hat{{{x}}}_1$ and$\hat{{{x}}}_2$ , respectively. The ALP-photon beam obeys the Von-Neumann-like equation [15, 16]$ \frac{{\rm{d}}\rho}{{\rm{d}}s} = \left[\rho,{\cal{M}}_0\right], $

(4) where s represents the traveling distance of the ALP-photon beam along the propagation direction
$\hat{{{x}}}_3 \equiv \hat{{{x}}}_1 \times \hat{{{x}}}_2$ ,$ {\cal{M}}_0 $ is the mixing matrix, and$ \rho $ is the density matrix of the beam$ \rho = \Psi \otimes \Psi^\dagger $ .$ {\cal{M}}_0 $ is only related to the transverse magnetic field${{B}}_\perp$ .Assuming that
${{B}}_\perp$ is aligned along$\hat{{{x}}}_2$ , the mixing matrix is [14, 35]$ {{\cal{M}}_0} = \left[ {\begin{array}{*{20}{c}} {{\Delta _{{\rm{pl}}}}}&0&0\\ 0&{{\Delta _{{\rm{pl}}}}}&{{\Delta _{a\gamma }}}\\ 0&{{\Delta _{a\gamma }}}&{{\Delta _{aa}}} \end{array}} \right],$

(5) where
$ \Delta_{\rm{pl}} = -\omega^2_{\rm {pl}}/(2E) $ represents the plasma effect with the plasma frequency$ \omega_{\rm{pl}} $ and photon energy E,$ \Delta_{aa} = - m^2_a / (2E) $ represents the kinetic term for an ALP with mass$ m_a $ , and$ \Delta_{a\gamma} $ is the ALP-photon coupling term$ g_{a\gamma}B_\perp/2 $ . The Faraday rotation, QED vacuum polarization effect, and dispersion and absorption effects in the Milky Way are neglected here due to their small contributions.If
$ B_\perp $ is not aligned along$\hat{{{x}}}_2$ , the mixing matrix becomes$ {\cal{M}} = V\left(\psi\right){\cal{M}}_0V^\dagger\left(\psi\right), $

(6) with
$ V\left( \psi \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\psi }&{{\rm{sin}}\psi }&0\\ { - {\rm{sin}}\psi }&{{\rm{cos}}\psi }&0\\ 0&0&1 \end{array}} \right], $

(7) where
$ \psi $ is the angle between$ B_\perp $ and$\hat{{{x}}}_2$ . In the general case, the magnetic field of the astrophysical system changes its direction along the propagation direction$\hat{{{x}}}_3$ . In order to describe this effect, the propagation path is divided into n small regions. In each region, the magnetic field can be treated as approximately constant. The transfer matrix$ T\left(s\right) $ is given by$ T\left(s\right) = \prod\limits_{i=1}^{n}T(i), $

(8) where
$ {T}(i) $ represents the transfer matrix in the i-th region.In this work, we consider the high-energy
$ \gamma $ -ray spectra from the two extragalactic sources PKS 2155$ - $ 304 and PG 1553$ + $ 113, which are high-frequency peaked BL Lac objects. It is known that BL Lac objects are hosted in elliptical galaxies. However, it is not easy to determine the exact cluster environments around these objects. There is evidence that some BL Lac objects are harboured in small galaxy groups or clusters [61, 62]. Some studies [63, 64] also show that PKS 2155$ - $ 304 is located at the center of a galaxy cluster. Thus it can be expected that the high-energy photons emitted from the BL Lac objects oscillate with ALPs in the inter-cluster magnetic field (ICMF). The strength of the regular magnetic field in the galaxy cluster ranges from$ \sim $ 1$\mu$ G to 10$\mu$ G [65]. We assume that the ICMF is a Gaussian turbulent field as described in Ref. [66], with a mean value of zero and variance of$ \sigma_B $ . Since no concrete ICMF model is available, we randomly generate the configuration of ICMF following Ref. [22]. Four hundred realizations of the ICMF for each source are taken in the analysis. The fiducial parameters of the ICMF shown in Table 1 are adopted, following Ref. [25].ICMF parameters Fiducial values $\sigma_{B}$ /(

$\mu {\rm{G} }$ )

3 $\eta$ 

0.5 $r_c$ /kpc

200 $k_H/{\rm{kpc} }^{-1}$ 

4 $\pi$ 

$k_L/{\rm{kpc} }^{-1}$ 

0.1 $\pi$ 

q −11/3 $r_{\rm{max}}$ /kpc

350 Table 1. Fiducial parameters of the ICMF model in this work.
In this analysis, we do not consider the impact of the magnetic field in the extragalactic space. Some studies show that the upper limit of its strength is
$ {\cal{O}}(1) $ nG [67], but the exact value remains unclear. Thus only the EBL attenuation effect is taken into account for$ \gamma $ -ray propagation in extragalactic space.The ALP-photon oscillation would also occur in the Milky Way. The galactic magnetic field consists of two components: a random component at small scale and a regular component at large scale. The impact of the random component is neglected here due to the short coherence length. For the regular component, we take the model in Ref. [68].
The final transfer matrix consists of the contributions from three regions
$ T\left(s\right) = T_{{\rm{MW}}}T_{{\rm{EBL}}}T_{{\rm{ICMF}}}, $

(9) where
$ T_{\rm{MW}} $ ,$ T_{\rm{EBL}} $ and$ T_{\rm{ICMF}} $ are the transfer functions in the Milky Way, extragalactic space, and the inter-cluster environment, respectively. The density matrix can be solved by$ \rho\left(s\right) = T\left(s\right)\rho\left(0\right)T^\dagger\left(s\right), $

(10) where
$ \rho\left(0\right) $ represents the density matrix for the initial beam, which is assumed to be a pure photon beam without polarization,$ \rho(0) = \frac{1}{2}\; {\rm{diag}}(1, 1, 0) $ . The survival probability of photons in the final beam is given by$ P_{\gamma} = \rho_{1}\left(s\right)+\rho_{2}\left(s\right) $ , where$ \rho_{1}\left(s\right) $ and$ \rho_{2}\left(s\right) $ are the first and second diagonal elements in the density matrix$ \rho\left(s\right) $ , respectively.In Fig. 2, we show the photon survival probability with
$ m_a = 1.26 \times 10^{-8} $ eV and$ g_{a\gamma} = 6.31\times 10^{-11} $ GeV$ ^{-1} $ as a function of the photon energy for one ICMF realization of PG 1553$ + $ 113. The FRV08 model is used for the EBL [41]. In order to describe the impact of the randomness of the ICMF, we also plot the 68% and 95% bands of the photon survival probability using 400 generated realizations of the ICMF. The photon survival probability with only the EBL attenuation effect is also shown for comparison. We can see that the oscillation effect becomes significant above$ {\cal{O}}(10) $ GeV. For VHE$ \gamma $ -rays above$ {\cal{O}}(300) $ GeV, the oscillation effect induces a larger survival probability in comparison with the pure EBL absorption effect.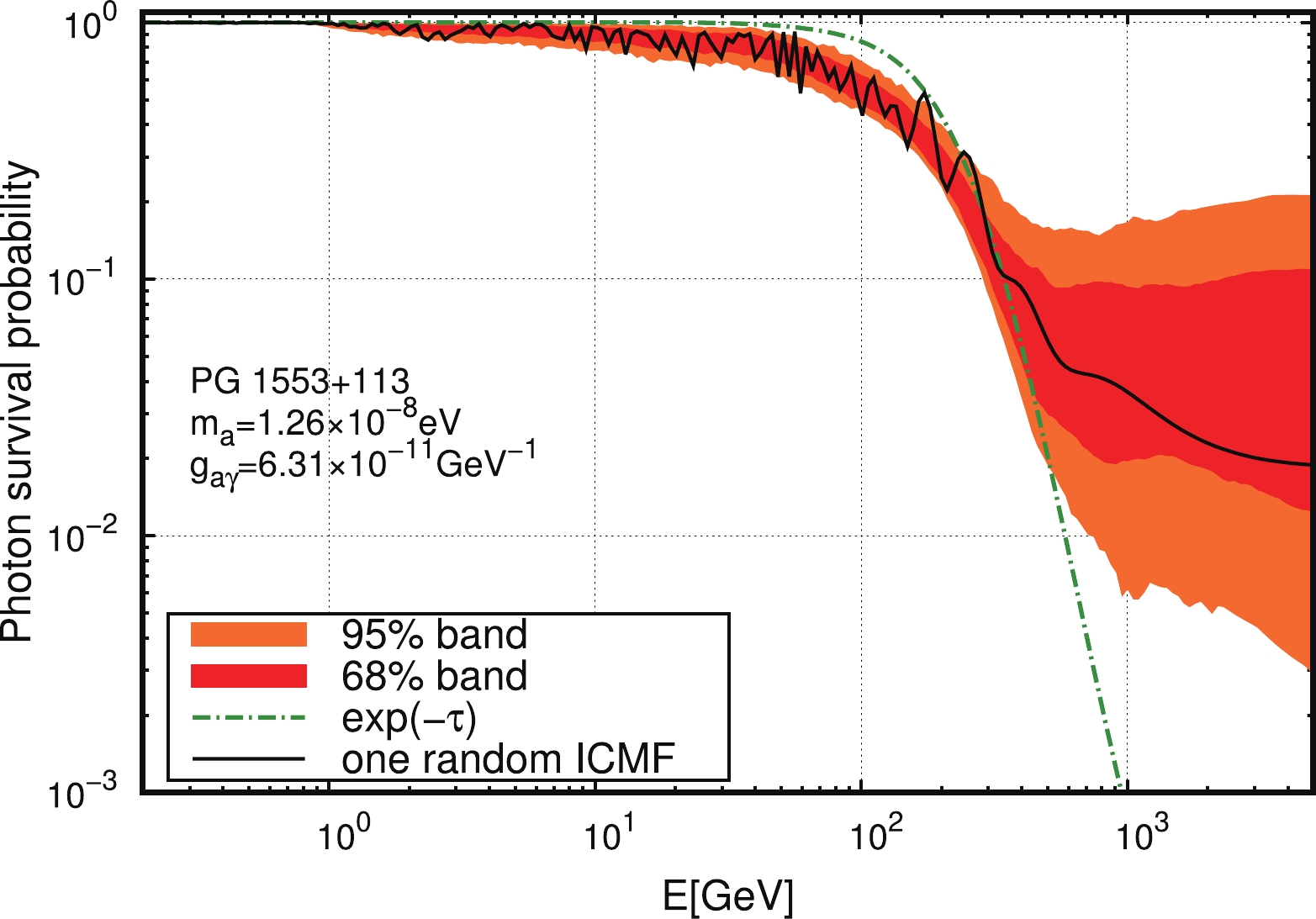
Figure 2. (color online) Survival probability of
$\gamma$ -rays emitted from PG 1553+113 with$ m_a=1.26 \times 10^{-8}$ eV and$g_{a\gamma}=6.31\times $ $ 10^{-11}$ GeV$^{-1}$ for the FRV08 model. The solid line represents the result for one randomly selected realization of the ICMF. The red (yellow) band represents the 68% (95%) band for 400 realizations of the ICMF, respectively. The dotted dashed line represents the survival probability of$\gamma$ -ray without the ALP-photon oscillation. -
In this work, we assume that the initial
$ \gamma $ -ray spectrum of PKS 2155$ - $ 304 is described by a broken power law with a transition region [69],$ F(E) = N(E/E_c)^{-\Gamma _1}(1+(E/E_{\rm{break}})^{f})^{(\Gamma _1-\Gamma _2)/f}. $

(11) The spectrum of PG 1553
$ + $ 113 is fitted with a logarithmic parabola function,$ F(E) = N(E/E_0)^{-\alpha - \beta \cdot \ln (E/E_0)}, $

(12) where N,
$ \Gamma _1 $ ,$ E_{\rm{break}} $ ,$ \Gamma _2 $ ,$ \alpha $ and$ \beta $ are taken to be free parameters,$ E_c $ is a normalization parameter, f is taken to be 100, and$ E_0 $ is taken to be 10 GeV. Compared with some other spectral forms, these two spectra can provide a better fit to the data under the null hypothesis. Then we derive the expected$ \gamma $ -ray spectra by using the photon survival probability and fit the experimental data. The observed spectra given by the H.E.S.S. II (CT5 mono) and Fermi-LAT contemporaneous observations [40] are used in this analysis.It is known that PG 1553
$ + $ 113 and PKS 2155$ - $ 304 are time-varying sources [70, 71]. However, these two sources were in low states during the H.E.S.S. II observation times (PG 1553$ + $ 113 in 2013 and PKS 2155$ - $ 304 in 2013 and 2014) [40]. For PG 1553$ + $ 113, no nightly or weekly variability of the H.E.S.S. II data is found and the data are consistent with many previous observations [71-75] and the Fermi-LAT data. For PKS 2155$ - $ 304, the data which were collected in 2013 and 2014 by H.E.S.S. II are in accordance with the level of the quiescent state in the previous H.E.S.S observation [76]. However, variability has been found in the H.E.S.S. II lightcurve [40]. The H.E.S.S. II analysis including variability shows that the spectral parameters are not significantly changed and the 2013 data are more suitable to determine the spectral form of PKS 2155$ - $ 304. Thus we only utilize the PKS 2155$ - $ 304 data in 2013 to investigate the ALP implications in this work.In order to include the energy resolution of the experiment, the expected
$ \gamma $ -ray flux in an energy bin between$ E_1 $ and$ E_2 $ is smeared as$ \frac{{\rm{d}}\Phi}{{\rm{d}}E} = \frac{\displaystyle\int^{E_2}_{E_1} {\rm{d}}E \displaystyle\int^{\infty}_{0} S(E^\prime, E)F(E^\prime){\rm{d}}E^\prime}{E_2-E_1} , $

(13) where E and
$ E^\prime $ are the measured and original photon energies, respectively, and$ S(E^\prime, E) $ is a Gaussian function with a standard deviation of$ \sigma $ . Here the energy resolutions of H.E.S.S. II and Fermi-LAT are set as 25% [40] and 15%①, respectively.After integrating the observed energy, the expected photon flux is
$ \frac{{\rm{d}}\Phi}{{\rm{d}}E} = \frac{\displaystyle\int^{\infty}_{0} A(E^\prime, E_1, E_2)F(E^\prime){\rm d}E^\prime}{E_2-E_1}, $

(14) where A(
$ E^\prime $ ,$ E_1 $ ,$ E_2 $ ) is given by$ A(E^\prime, E_1, E_2) = \frac{1}{2}\left[{\rm{erf}}\left(\frac{E_2-E^\prime}{\sqrt{2}\sigma}\right)-{\rm{erf}}\left(\frac{E_1-E^\prime}{\sqrt{2}\sigma}\right)\right], $

(15) where
${\rm erf}(x)$ is the error function.Considering the difference between the energy reconstruction of two different kinds of experiments, we also introduce an extra parameter to incorporate a possible systematic uncertainty in the analysis. In the fit we rescale all the energies of the H.E.S.S. II data by a factor f and add a corresponding contribution
$ (f-1)^2/\sigma_f $ to the log-likelihood$ -2 \ln {\cal{L}} $ . We assume$ \sigma_f $ to be 19%, which equals the systematic uncertainty of the energy scale of H.E.S.S. II [40].Following Ref. [22], the ALP hypothesis is evaluated by a likelihood ratio test. The maximal likelihoods under the null and ALP hypothesis are denoted by
$ {\cal{L}}(\mu_0|D) $ and$ {\cal{L}}(\mu_{95}|D) $ , respectively, where$ \mu $ is the expected photon spectrum with the best fit nuisance parameters,$ \mu_0 $ ($ \mu_{95} $ ) is the best fit scenario without ALPs (with ALPs in the 0.95 quantile), respectively, and D is the observed data. For each set in the$ (m_a, g_{a\gamma}) $ plane, the adopted ICMF realization is the one among 400 realizations that corresponds to the 0.95 quantile of the likelihood distribution (the quantile of the best fit scenario corresponds to 1).In order to test the ALP hypothesis, the probability distribution of the test statistic
$ TS \equiv -2 \ln ({\cal{L}}(\mu_0|D) / {\cal{L}}(\mu_{95}|D)) $ is required. Note that the relation between the spectral irregularities and ALP parameters is non-linear. Moreover only the ALP hypothesis depends on the ICMF realizations, while the null hypothesis does not. Therefore the commonly used Wilks' theorem [77] is not valid in this case. Instead, a Monte-Carlo method is needed to derive the TS distribution.Four hundred sets of mock data for each source were generated in pseudo-experiments that were realized by Gaussian samplings [24]. For the sampling, the mean values were taken to be the best-fit fluxes under the null hypothesis; the standard deviations were taken to be the errors of the experimental data. We then calculated the TS value in the fit for each mock data set and derived the TS distribution. As an example, the TS distribution of PG 1553
$ + $ 113 for the FRV08 model is shown in Fig. 3. We use a non-central$ \chi^2 $ distribution to fit this TS distribution and obtain the degree of freedom$ {\rm{d.o.f.}} = 2.94 $ and non-centrality$ \lambda = 0.01 $ . Thus this TS distribution can be taken as a standard$ \chi^2 $ distribution. The threshold of TS distribution at 95% C.L. is found to be 7.74 and is used to set the constraint on the ALP parameter space. -
In this section, we investigate the implication of ALPs for the FRV08 EBL model. The best fit spectra under the null and ALP hypothesis for the two selected sources are shown in Fig. 4. It can be seen that the null hypothesis fits the data well. The values of the best fit reduced
$ \chi^2 $ are shown in Table 2.Source PKS 2155−304 PG 1553+113 EBL model FRV08 Ciber FRV08 Ciber Best fit reduced $\chi^2$ w/o ALP

22.27/16 42.45/16 12.95/12 28.46/12 Best fit rescale factor w/o ALP 0.96 0.81 1.12 0.81 Best fit $\chi^2$ w ALP

16.48 18.06 10.02 10.81 Best fit rescale factor w ALP 1.02 1.03 1.17 0.92 Best fit ALP parameter sets 251.19, 0.59 2.51, 10.00 398.11, 5.01 25.12, 6.31 Effective d.o.f of TS distribution 3.99 3.65 2.94 1.89 Table 2. The best fit
$\chi^2$ and rescale factors under the null and ALP hypotheses for two sources in the two EBL models. Under the ALP hypothesis, the best fit ALP parameters$(m_a, g_{a\gamma})$ in units of$({\rm{neV}}, 10^{-10}~{\rm{GeV}}^{-1})$ and the effective degrees of freedom of the TS distribution are also listed.
Figure 4. (color online) Best-fit
$\gamma$ -ray spectra of PKS 2155−304 (left panels) and PG 1553+113 (right panels). The green and black lines represent the results under the null and ALP hypothesis, respectively. The top and bottom panels represent the results for the FRV08 and Ciber EBL models, respectively. The experimental data include the results from Fermi-LAT and H.E.S.S. II [40].Compared with the null hypothesis, the ALP-photon oscillation may reduce the EBL attenuation effect at energies above
$ \sim {\cal{O}}(10^2) $ GeV. Therefore, the corresponding$ \gamma $ -ray spectra in this energy region may significantly deviate from the experimental data. The maps of$ \Delta \chi^2\equiv \chi^2_{\rm{ALP}}-\chi^2_{\rm{null}} $ in the ($ m_a, g_{a\gamma} $ ) plane for the two sources are shown in Fig. 5. The boundaries of the excluded parameter regions can be derived by requiring$ \chi^2 = \chi^2_{\rm{best}}+ \chi^2_{\rm{th}} $ , where$ \chi^2_{\rm{best}} $ is the best-fit$ \chi^2 $ under the ALP hypothesis.$ \chi^2_{\rm{th}} $ depending on the confidence level is taken to be the corresponding threshold of the TS distribution. Note that the probability distributions of TS with the ALP and null hypothesis are assumed to be same here [22]. For instance,$ \chi^2_{\rm{th}} $ at 95% C.L. for PG 1553$ + $ 113 is taken to be 7.74.
Figure 5. (color online)
$\Delta \chi^2\equiv \chi^2_{\rm{ALP}}-\chi^2_{\rm{null}}$ maps of PKS 2155−304 (left panel) and PG 1553+113 (right panel). The triangle symbols represent the best fit parameters.We show the 95% C.L. excluded contour for PG 1553
$ + $ 113 in Fig. 6. Considering the constraint from CAST, we find that the 95% limit from PG 1553$ + $ 113 on the ALP-photon coupling is$ g_{a\gamma} \lesssim 5 \times 10^{-11}\; {{\rm{GeV}}}^{-1} $ in the ALP mass range of$ \sim 8 \; {\rm{neV}} < m_{a} < 23 \; {\rm{neV}} $ . For PKS 2155$ - $ 304, the 95% C.L. contour is found to be above the CAST limit and is not shown here.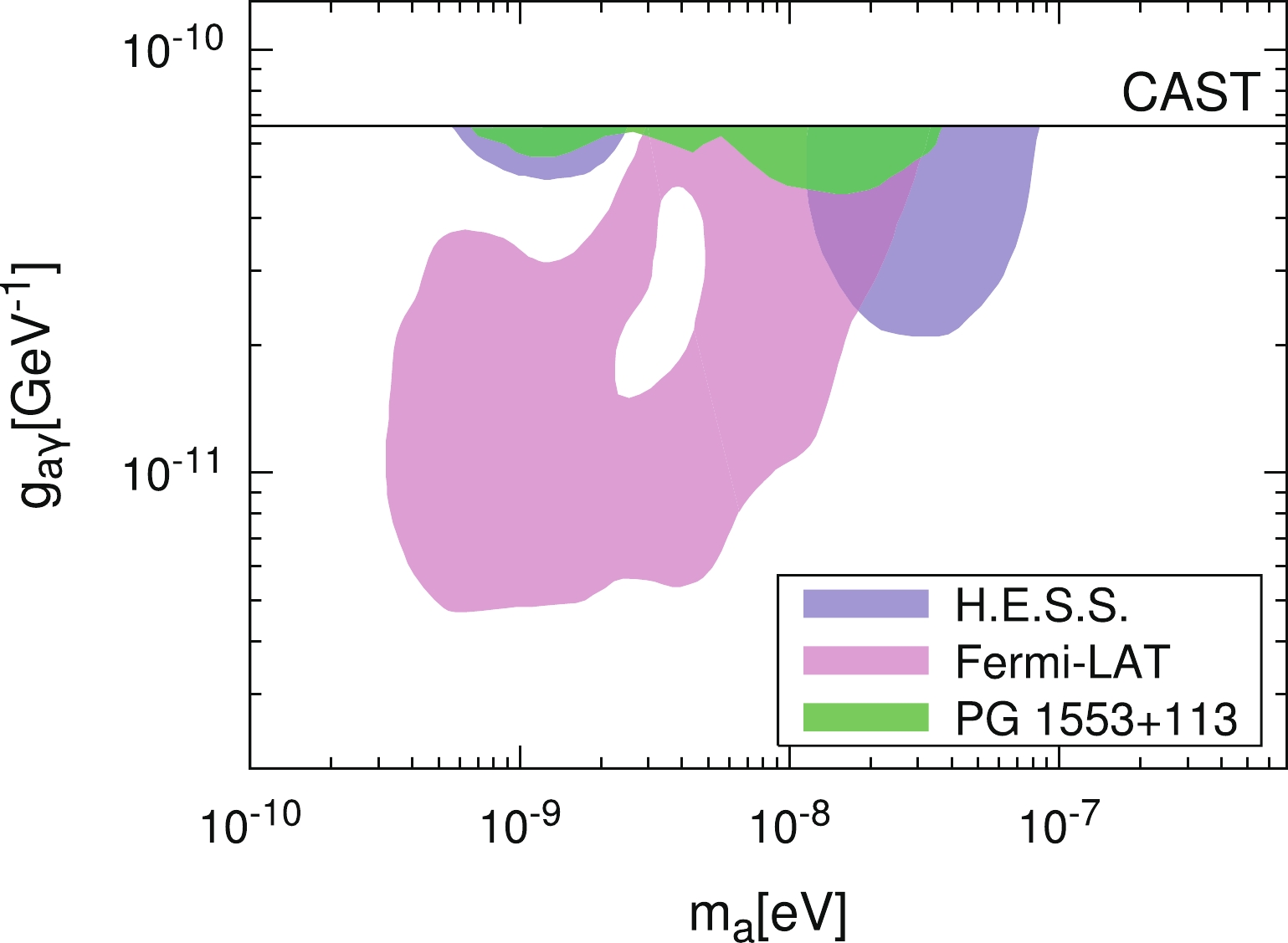
Figure 6. (color online) The 95% C.L. excluded region in the (
$m_a, g_{a\gamma}$ ) plane. The green region represents our result for PG 1553+113 with$ \sigma_B=3~\mu{\rm{G}}$ and the FRV08 model. For comparison, the constraints from the CAST [12], Fermi-LAT observation of NGC 1275 [22] and H.E.S.S. observation of PKS 2155−304 [18] are also shown.For comparison, the limits from Fermi-LAT observation of NGC 1275 [22] and H.E.S.S. [18] observation of PKS 2155
$ - $ 304 are also shown. The limit set by the Fermi-LAT collaboration is derived from the fit to its measured spectrum of NGC 1275. Compared with the experimental data used in this analysis, the NGC 1275 data contain more data points with narrow energy bins below$ \sim 300 $ GeV. It is expected that the deviations from the data caused by the ALP-photon oscillation would be more significant at low energies. Therefore, the Fermi-LAT analysis has excluded a large parameter region at low ALP masses$ \sim {\cal{O}}(1) $ neV, which corresponds to low critical energies for the ALP-photon oscillation. The PKS 2155$ - $ 304 analysis of the H.E.S.S. collaboration focuses on the spectral irregularities induced by the ALP-photon oscillation in the variations of neighboring energy bins and provides a stricter limit in comparison with our result for PKS 2155$ - $ 304.The dominant uncertainty in this analysis arises from the ICMF model. We should consider the impact of the ICMF parameters on the constraints. For PG 1553
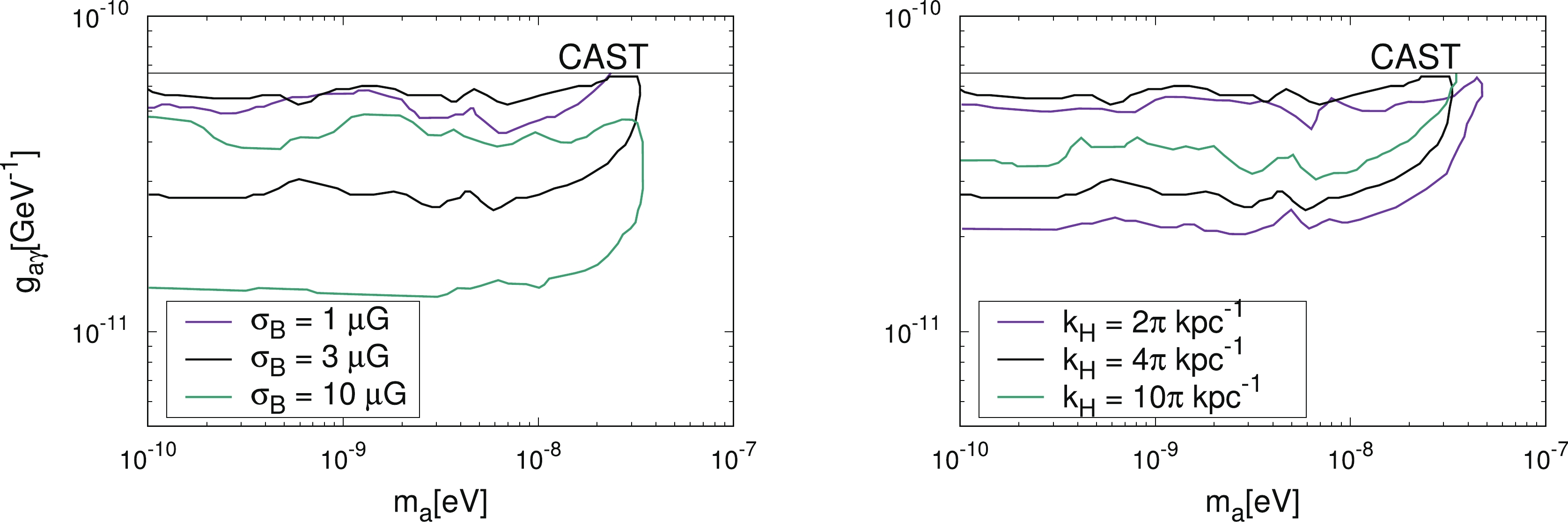
$ + $ 113 and the FRV08 EBL model, we show the constraints on the ALP parameter space with different values of six ICMF parameters, including$ \sigma_B $ ,$ r_{\rm{max}} $ ,$ k_L $ ,$ \eta $ , q, and$ k_H $ , in Fig. 7. We can see that the change of$ \sigma_B $ or$ k_{H} $ has a significant impact on the final results by a factor of$ {\cal{O}}(1) $ . For$\sigma_{B} = 10\; \mu{\rm{G}}$ , the constraint on$ g_{a\gamma} $ can be improved as$ g_{a\gamma}\lesssim 4.5\times 10^{-11} \; {\rm{GeV}}^{-1} $ for an ALP mass smaller than 33 neV. The influences of the other four parameters are less important.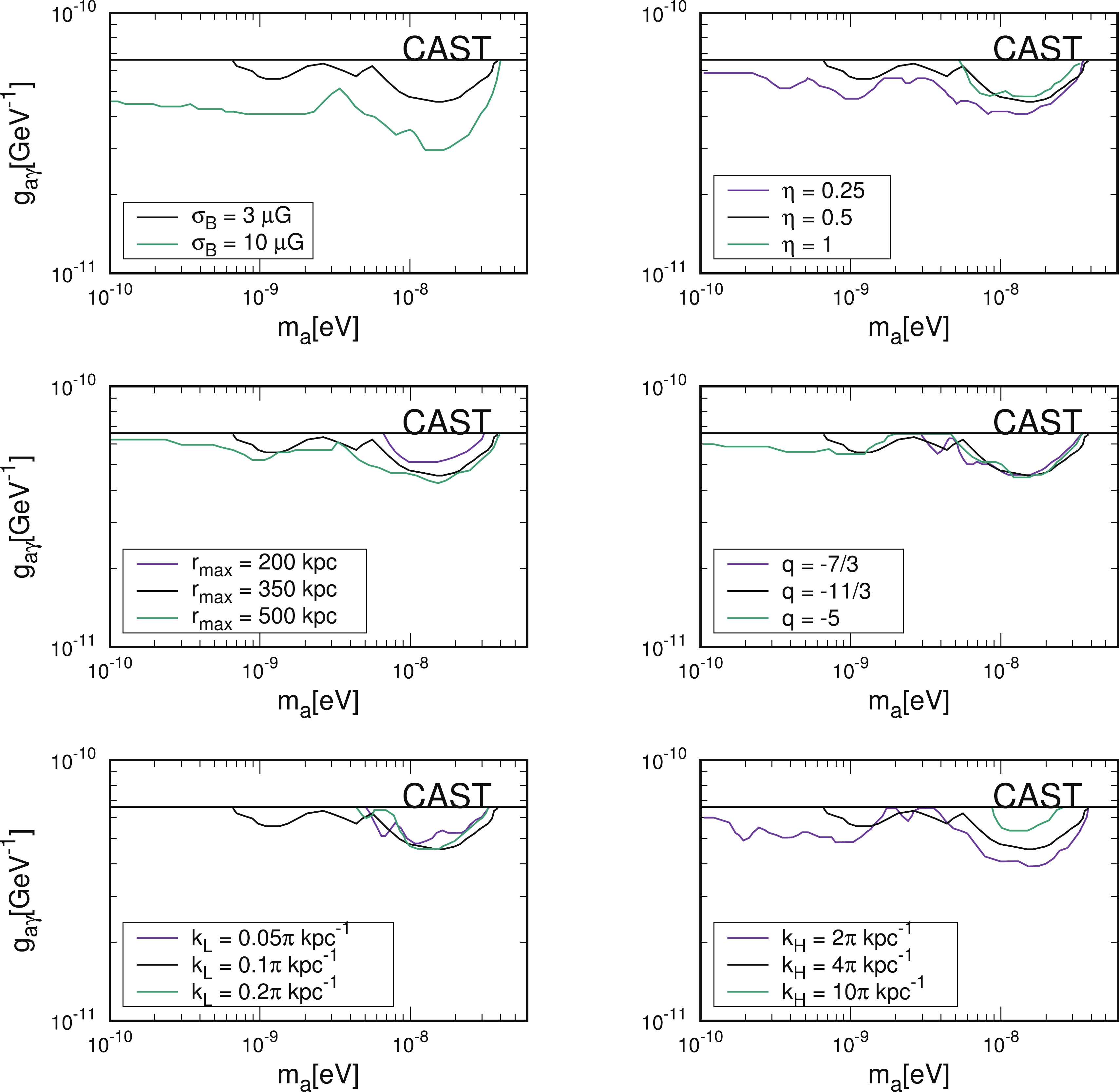
Figure 7. (color online) Constraints for PG 1553+113 and the FRV08 model with different values of six ICMF parameters, including
$\sigma_B$ ,$r_{\rm{max}}$ ,$k_L$ ,$\eta$ , q, and$k_H$ . The black lines represent the constraints with the fiducial parameters. The constraint with$\sigma_B=1~\mu{\rm{G}}$ is above the CAST limit and is not shown. -
The implications of ALPs are different for the Ciber EBL model. The best fit spectra of the null and ALP hypotheses for the two sources are shown in the bottom panels of Fig. 4. Compared with the FRV08 model, the excess at
$\sim \mu$ m in the Ciber model induces an additional attenuation effect above$ \sim 300$ GeV and leads to more significant deviations from the data, which can be seen from Table 2. The ALP-photon oscillation may compensate this additional attenuation effect and improve the fit to the data. This improvement method has been discussed for the Fermi-LAT and H.E.S.S. observations of two sources H2356-309 (z = 0.165) and 1ES1101-232 (z = 0.186) through the$ \chi^2 $ fit in Ref. [38].We show the improvement regions at 95% C.L. with the fiducial parameters of the ICMF model for PKS 2155
$ - $ 304 and PG 1553$ + $ 113 in Fig. 8. The favored ALP parameter region for PG 1553$ + $ 113 is an almost rectangular region with$ g_{a\gamma}\gtrsim 2.7\times 10^{-11}\; {\rm{GeV}}^{-1} $ and$ m_a \lesssim 11\; {\rm{neV}} $ . The favored region for PKS 2155$ - $ 304 is about$ g_{a\gamma}\gtrsim 5.5\times 10^{-11}\; {\rm{GeV}}^{-1} $ and$ m_a \lesssim 21\; {\rm{neV}} $ . Compared with the favored region derived in Ref. [38] ($g_{a\gamma}\gtrsim 2\times 10^{-11}\; {\rm{GeV}}^{-1}$ for$1\; {\rm neV}\lesssim m_a \lesssim 40\; {\rm neV}$ ), there is no lower boundary on$ m_a $ in our results. This is because the ALP-photon oscillation effect in extragalactic space is neglected in this analysis.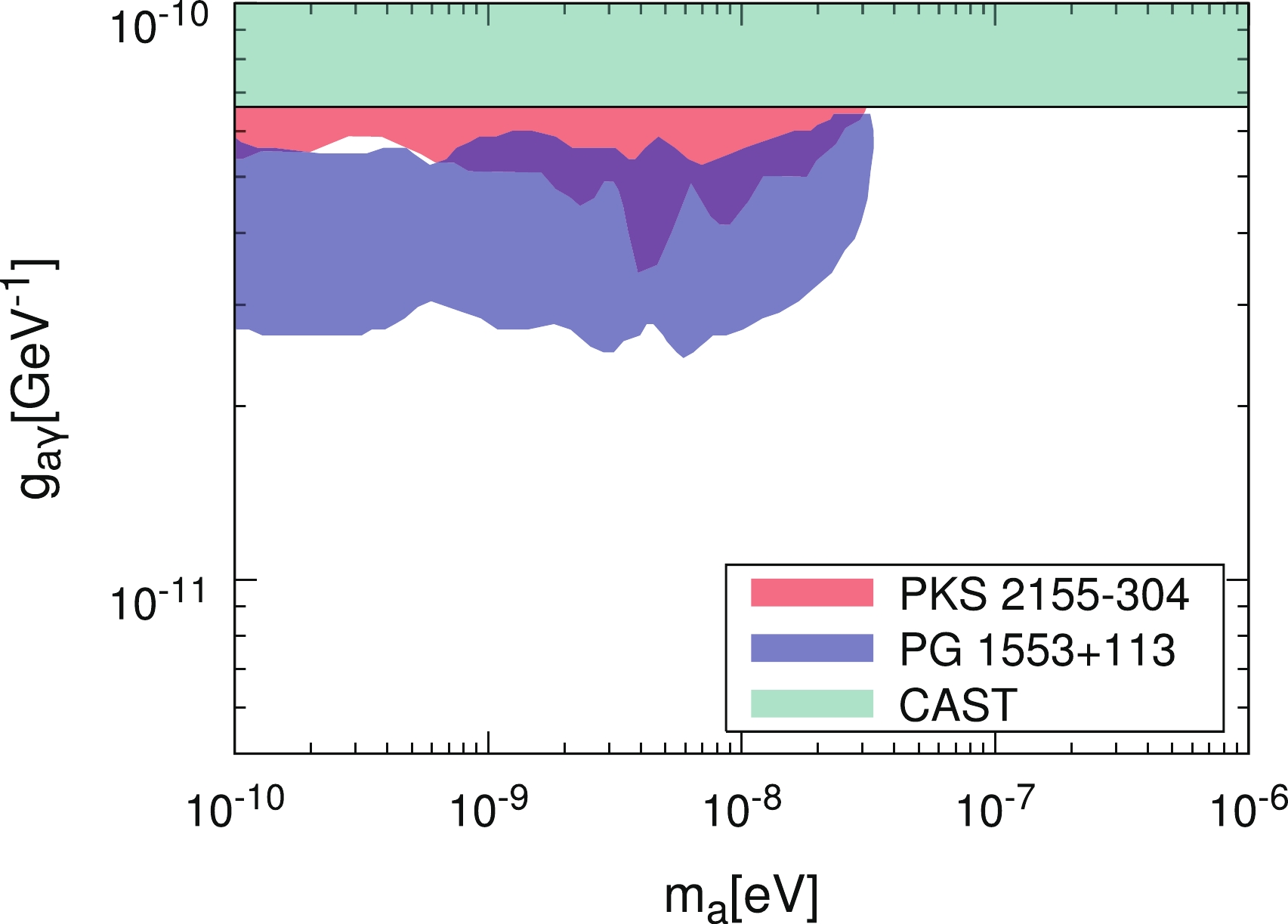
Figure 8. (color online) Favored ALP parameter regions where the fit to the PKS 2155−304 and PG 1553+113 observations can be improved at 95%C.L..
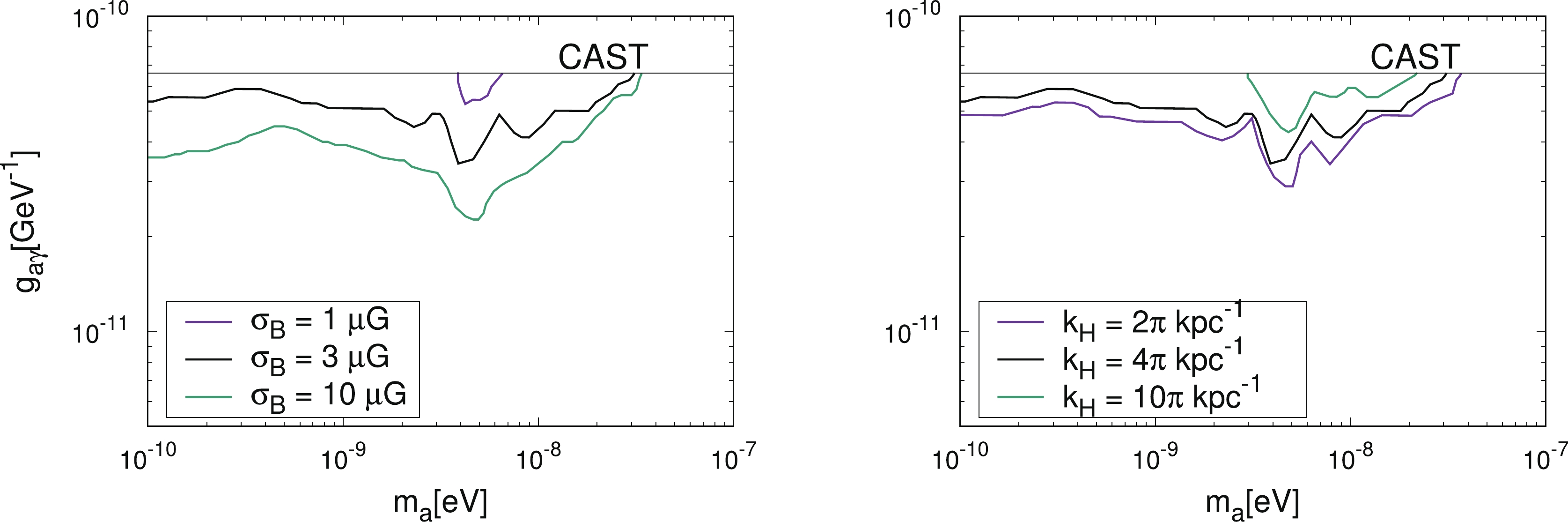
Considering the uncertainty of the ICMF model for the Ciber model, we only show the favored ALP parameter regions with different values of
$ \sigma_B $ and$ k_{H} $ in Fig. 9 and Fig. 10, since these two parameters induce more significant changes in the final results than the other parameters. For$\sigma_{B} = 10\; \mu{\rm{G}}$ , the favored ALP parameter region for PG 1553$ + $ 113 is enlarged as an almost rectangular region with$ 1.4\times 10^{-11} \; {\rm{GeV}}^{-1} \lesssim g_{a\gamma} \lesssim 4\times 10^{-11} \; {\rm{GeV}}^{-1} $ and$ m_a \lesssim 10\; {\rm{neV}} $ . From Fig. 9 and Fig. 10, we can also see that$ k_H $ has a less significant influence on the final result compared with$ \sigma_B $ . -
In this work, we have investigated the implications of ALPs in the Fermi-LAT and H.E.S.S. II gamma-ray observations of the two sources PG 1553
$ + $ 113 and PKS 2155$ - $ 304. Two EBL models were considered in the analysis. We find that the best fit spectra under the null hypothesis can fit the experimental data well for the FRV08 EBL model, and set constraints on the ALP parameter region in the ($ m_a,g_{a\gamma} $ ) plane. For$\sigma_B = 3\; \mu$ G, the constraint on$ g_{a\gamma} $ at 95% C.L. is$ g_{a\gamma}\lesssim 5\times 10^{-11} \; {\rm{GeV}}^{-1} $ for an ALP mass between$ 8 $ and$ 23 $ neV. On the other hand, we found that the ALP-photon oscillation would improve the fit to the PKS 2155$ - $ 304 and PG 1553$ + $ 113 observations for the Ciber model with an excess at$\sim 1 \; \mu$ m. The favored parameter regions are given.In future, Cherenkov high energy gamma-ray telescopes will provide more accurate results. Large ground-based telescopes, such as the CTA [78] and LHAASO [79], will measure the spectra of extragalatic gamma-ray sources at very high energies. Combined with these results, it will be possible to search for the spectral regularities induced by the ALP-photon oscillation and accurately investigate the implications of ALPs in high-energy astrophysical processes.
Implications of axion-like particles from the Fermi-LAT and H.E.S.S. observations of PG 1553+113 and PKS 2155−304
- Received Date: 2020-07-02
- Accepted Date: 2020-09-30
- Available Online: 2021-02-15
Abstract: We investigate the axion-like particle (ALP)-photon oscillation effect in the high-energy





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: