-
Generally, the perception of
$ \alpha $ -decay is that an$ \alpha $ particle exists as an entity inside the parent nucleus before emission from it. Explained by Gamow as a quantum-tunneling effect,$ \alpha $ preformation factors$ P_\alpha $ , which are used to describe the formed amplitude, may be determined by the ratios between experimental and calculated$ \alpha $ -decay half-lives, depending on various theoretical models. The behaviors of$ P_\alpha $ incorporate nuclear structure information such as the shell closure effect of nucleons, blocking effect of unpaired nucleons in the open shells of the parent nucleus, proton-neutron interaction, and deformation of the daughter nucleus [1]. The$ \alpha $ preformation factor is expected to be a superposition of the different nuclear structure effects.Recent evidence shows that the
$ \alpha $ preformation factor clearly depends on the product of valence protons (holes) and valence neutrons (holes)$ N_pN_n $ as well as isospin asymmetry [2-4]. In the work of Sun et al. [5], the result considering the isospin asymmetry effect on nuclear potential has an obvious improvement to reproduce$ \alpha $ -decay half-lives of 164 even-even nuclei in the two-potential model (TPM). Furthermore, it shows that the$ \alpha $ -decay width in the neutron skin-type (NST) case considering the effect of isospin asymmetry on proton and neutron density is about 30% greater than that in the Hartree-Fock formalism (HF) case [6]. Therefore, the effect of isospin asymmetry may play a key role in the determination of$ \alpha $ preformation factors. Accumulating evidence shows that the interaction of valence nucleons and the effect of isospin asymmetries are incredibly important for determining$ \alpha $ preformation factors.There are many firsthand approaches to obtain
$ \alpha $ preformation factors. The cluster formation model (CFM) [7-11] is based on the quantum-mechanical dynamic states of the$ \alpha $ cluster and daughter nucleus to calculate$ P_\alpha $ and to study the shell effect and clusterization mechanisms around the nucleus surface. The preformed cluster model (PCM) [12-14] uses the solution of the stationary Schrödinger equation to determine$ P_\alpha $ in$ \eta $ coordinates. The$ \alpha $ preformation factors are also studied in the double-folding model of the density dependence (DMDD) [15], the cluster model (CM), the Bardeen-Cooper-Schrieffer (BCS) approach, and potential models such as the density-dependent Michigan 3-range Yukawa (DDM3Y) [16, 17] from different perspectives. It is also suggested that the tendency of$ \alpha $ preformation factors is not dependent on the model [18].It is challenging to calculate
$ \alpha $ preformation factors using the microscopic method, which is necessarily a complex quantum multibody problem. At present, the determination of$ \alpha $ preformation factors is mostly empirical. For instance, Ref. [19] proposes that$ P_\alpha $ shows an exponential relationship with a polynomial of$ \alpha $ -decay energy,$ P_\alpha $ has a linear correlation with the product of valence nucleons, put forward in Ref. [20], and the original formula of Zhang et al. is related to the shell closure effect [21]. These formulas incorporate some nuclear structural information, but there are some limitations, such as too many parameters or limited nuclear range of application, which make it difficult to promote them further. In our present work, we aim to obtain a new formula with fewer parameters, a broader range of application, and higher precision. We extract$ \alpha $ preformation factors for 606 nuclei in the framework of a generalized liquid drop model (GLDM). Based on the shell closure effect and features of$ \alpha $ preformation factors, we propose a new improved formula for the calculation of$ P_\alpha $ . In the next section, the theoretical framework of extracting$ P_\alpha $ is presented. The results of our numerical calculation, discussion, and prediction are presented in Sec. III. A brief summary is given in Sec. IV. -
Classically, assuming that an
$ \alpha $ particle is moving back and forth inside the parent nucleus with a velocity$ v = \sqrt{\dfrac{2E_\alpha}{M}} $ , it penetrates the barrier with a classical frequency$ \nu_0 = \frac{1}{2R}\sqrt{\frac{2E_\alpha}{M}}, $

(1) where R is the radius of the nucleus, given by
$ R = \left( 1.28A^\frac{1}{3}-0.76+0.8A^{-\frac{1}{3}}\right){\rm fm} , $

(2) The barrier penetration probability is calculated by the Wentzel-Kramers-Brillouin(WKB) approximation as
$ P = {\rm exp}\left[ -\frac{2}{\hbar}\int_{R_{\rm in}}^{R_{\rm out}}\sqrt{2B(r)(E(r)-E(\rm parent)) }\,{\rm d}r\right], $

(3) where
$ R_{\rm in} $ and$ R_{\rm out} $ are the two turning points of the WKB action integral, and the mass inertia$ B(r) $ is approximated to the reduced mass$ \mu $ . The barriers are constructed by the GLDM including the volume, surface, Coulomb, proximity, and centrifugal energy [22]:$ E(r) = E_{\rm V}+E_{\rm S}+E_{\rm C}+E_{\rm prox}+E_{\rm cen}, $

(4) where
$ E(r) $ is a function of the distance between the centroids of two fragments during evolution. The terms$ E_{\rm V} $ ,$ E_{\rm S} $ ,$ E_{\rm C} $ ,$ E_{\rm prox} $ , and$ E_{\rm cen} $ are the volume, surface, Coulomb, proximity, and centrifugal energies, respectively. For one-body shapes [22-24], the volume, surface, and Coulomb energies are given by$ E_{\rm V} = -15.494(1-1.8I^2)A{\rm MeV}, $

(5) $ E_{\rm S} = 17.9439(1-2.6I^2)A^{2/3}(S/4\pi R_0^2){\rm MeV}, $

(6) $ E_{\rm C} = 0.6e^2(Z^2/R_0)\times 0.5\int(V(\theta)/V_0)(R(\theta)/R_0)^3{\rm sin}{\theta} {\rm d}\theta. $

(7) where
$ I = (N-Z)/A $ is the relative neutron excess, S is the surface of the deformed nucleus,$ V_0 $ is the surface potential of the sphere, and$ V(\theta) $ is the electrostatic potential at the surface.When the nuclei are separated,
$ E_{\rm V} = -15.494[(1-1.8I_I^2)A_1+(1-1.8I_2^2)A_2]{\rm MeV}, $

(8) $ E_{\rm S} = 17.9439[(1-2.6I_1^2)A_1^{2/3}+(1-2.6I_2^2)A_2^{2/3}]{\rm MeV}, $

(9) $ E_{\rm C}= 0.6e^2(Z_1^2/R_1)+0.6e^2(Z_2^2/R_2)+e^2Z_1Z_2/r, $

(10) $ A_i, Z_i, R_i \; {\rm and} \; I_i $ are the mass numbers, charge numbers, radii, and relative neutron excesses. The radius$ R_i $ is given by Eq. (2). The proximity energy$ E_{\rm prox} $ is given by:$ E_{\rm prox}(r) = 2\gamma\int_{h_{\rm min}}^{h_{\rm max}}\Phi \left[D(r,h)/b \right] 2\pi h{\rm d}h, $

(11) where
$ h = R(\theta){\rm sin}\theta $ is the distance varying from the neck radius or zero to the height of the neck border, D is the distance between the opposite infinitesimal surfaces,$ b = 0.99 $ fm is the surface width, and$ \Phi $ is the proximity function. The surface parameter$ \gamma $ is the geometric mean between the surface parameters of the two fragments. The centrifugal energy$ E_{\rm cen} $ is given by$ {E_{\rm cen}(r)} = \frac{\hbar^2l(l+1)}{2\mu {\rm{r}}^2}. $

(12) where l is the minimum angular momentum taken away by the
$ \alpha $ particle determined by the angular momentum and parity conservation laws:$ l = \left\{ {\begin{array}{*{20}{llll}} {\triangle_j} & {\rm{for}}\;{\rm{even}}\;{\triangle_j} &\hspace{-3mm} {\rm{and}} &\hspace{-2mm} {\pi _p} = {\pi _d},\\ {\triangle_j} + 1 & {\rm{for}}\;{\rm{even}}\;{\triangle_j}&\hspace{-3mm} {\rm{and}} &\hspace{-2mm} {\pi _p}\not = {\pi _d},\\ {\triangle_j} & {\rm{for}}\;{\rm{odd}}\;{\triangle_j}&\hspace{-3mm} {\rm{and}} &\hspace{-2mm} {\pi _p}\not = {\pi _d},\\ {\triangle_j} + 1 & {\rm{for}}\;{\rm{odd}}\;{\triangle_j} &\hspace{-3mm} {\rm{and}} &\hspace{-2mm} {\pi _p} = {\pi _d}, \end{array}} \right. $

(13) The decay constant is
$ \lambda = P_{\alpha}\nu_0P = \frac{\rm ln2}{T_{1/2}^{\rm \,exp}}, $

(14) ${{T}}_{1/2}^{\rm\,{exp}}$ is the experimental half-life of$ \alpha $ decay. The term$ P_{\alpha} $ can be extracted as$ P_\alpha^{\rm \,ext} = \frac{\lambda}{\nu_0P}. $

(15) -
The closed shell structure is one of the fundamental pillars of the nucleus that affects the behavior of the
$ \alpha $ preformation factors significantly. As one consequence, the closer the proton or neutron number is to the magic number, the smaller the$ \alpha $ preformation factor is, and the$ \alpha $ preformation factor decreases dramatically near the magic number [25, 26]. Fig. 1 shows the$ \alpha $ preformation factors of five isotopic chains of even-even Po to Th nuclei versus neutron number N. The shell closure effect of$ N = 126 $ from Po ($ Z = 84 $ ) to Th ($ Z = 90 $ ) isotopes is prominent. The$ \alpha $ preformation factors decrease rapidly when N is below 126 and increase dramatically above 126 with increasing neutron number.$ N = 126 $ is a traditional magic number, where the$ \alpha $ preformation factor should be minimal as in the even-even Po-Th isotopic chains shown in Fig. 1, but the$ \alpha $ preformation factor of$ ^{216} $ U ($ N = 124 $ ) is apparently smaller than that of$ ^{216} $ U ($ N = 126 $ ). In addition, the$ \alpha $ preformation factors of U isotopes increase more gently than Po-Th isotopes from N = 126 to 130. In Fig. 2, from Po ($ Z = 84 $ ) to Th ($ Z = 90 $ ) for$ N = 126 $ isotones, the$ \alpha $ preformation factors rise smoothly with increasing Z, but a sudden increase occurs at$ ^{218} $ U ($ N = 126 $ ). The above phenomena indicate an obvious weakening of the$ N = 126 $ shell effect for U. This is consistent with the results of a recent experimental work by Khuyagbaatar [27], pointing out that there is a significant weakening of the influence of the$ N = 126 $ shell closure in U, which is determined by analyzing the reduced widths and neutron-shell gaps of Po-U isotopes.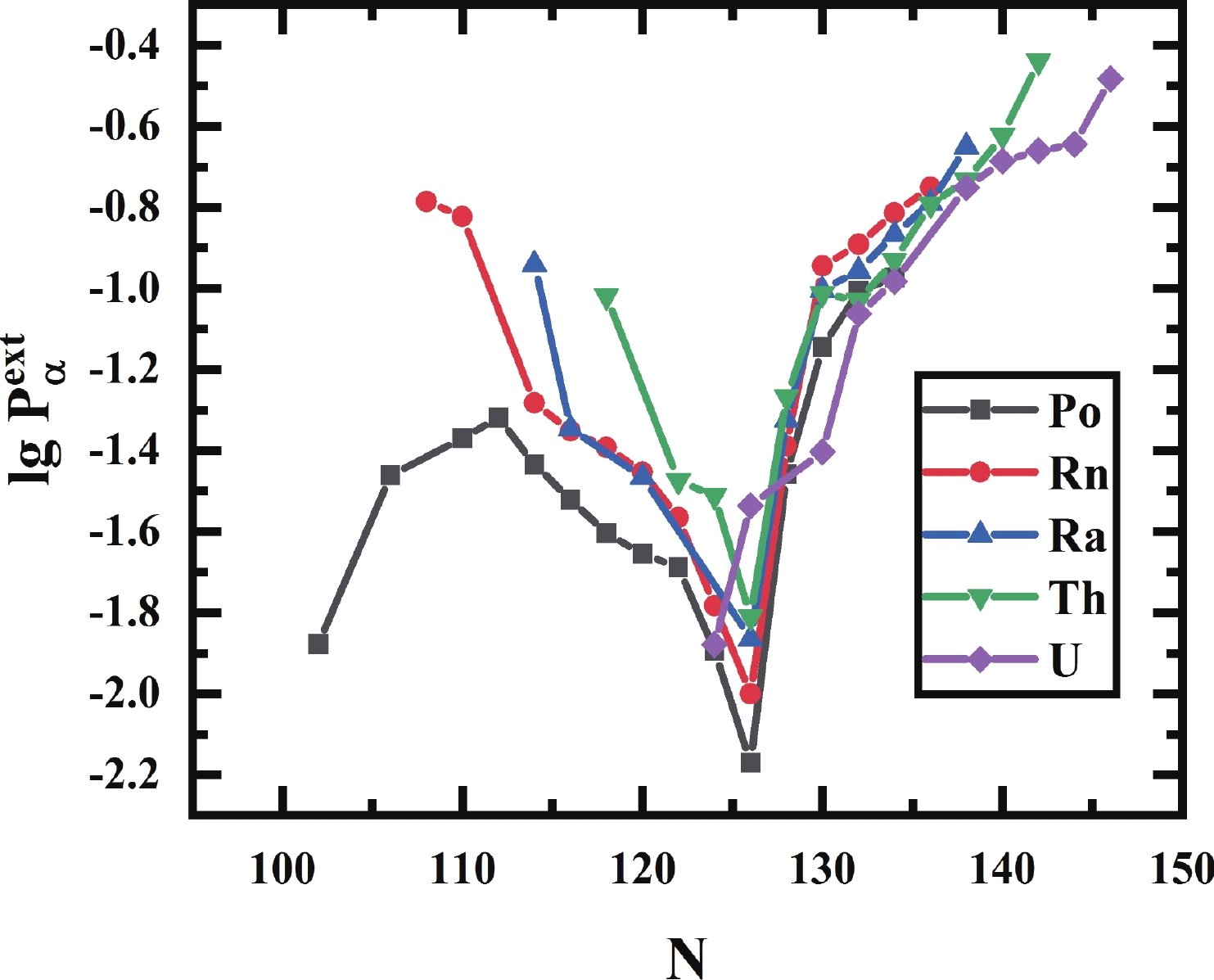
Figure 1. (color online) The
$ \alpha$ preformation factors of Po, Rn, Ra, Th, and U isotopes extracted by GLDM.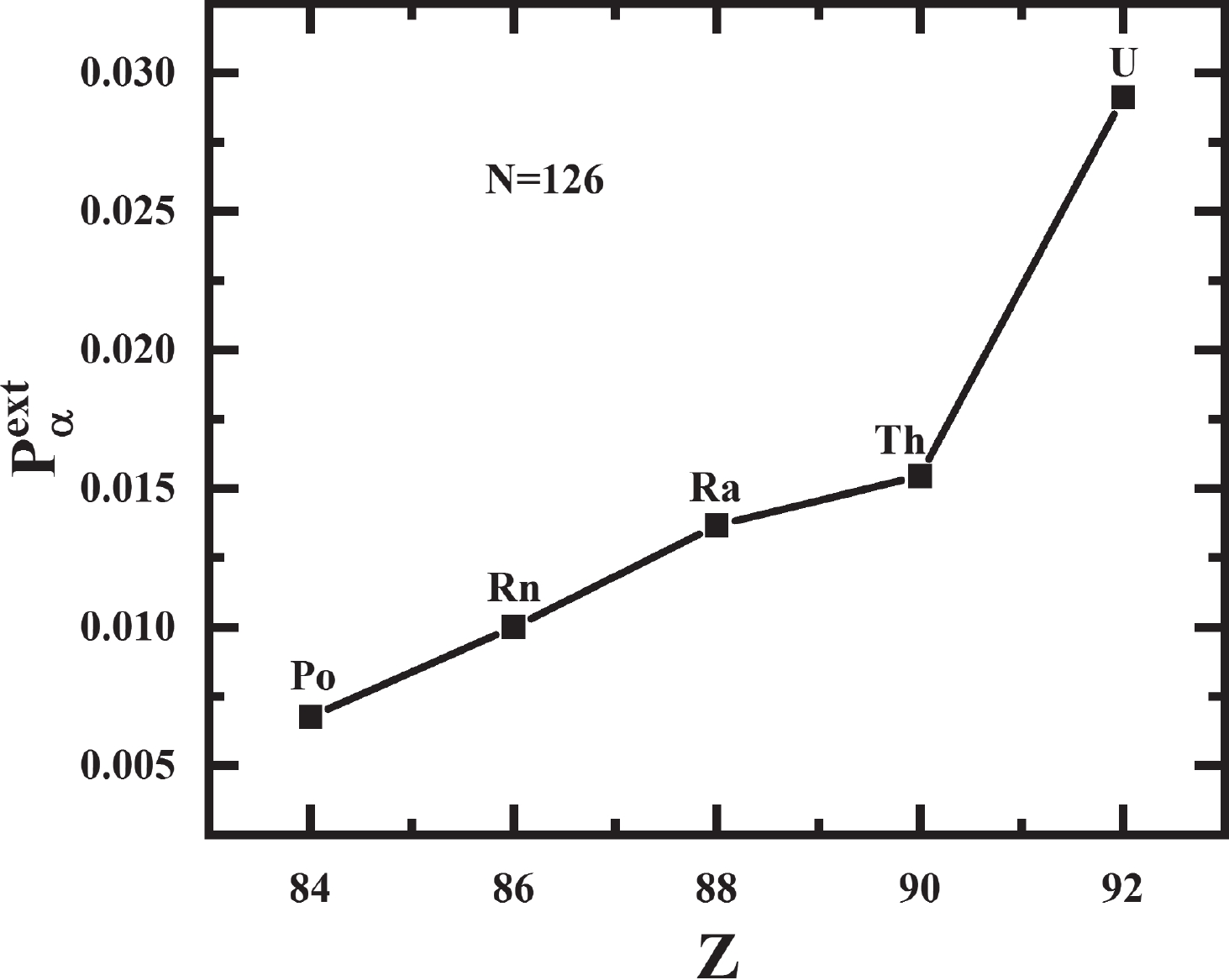
Figure 2. The extracted
$ \alpha$ preformation factors of$ N = 126$ isotones for Po, Rn, Ra, Th, and U.In addition to the shell closure effect, sufficient evidence suggests that the correlation of valence nucleons plays an important role in the
$ \alpha $ preformation factors [20, 28-30]. It has been previously shown that there is a linear relationship between$ P_\alpha $ and the product of valence protons (holes) and valence neutrons (holes)$ N_pN_n $ [2-4]. At the same time, a recent calculation using the scheme of microscopic$ N_pN_n $ can accurately reproduce the extracted$ \alpha $ preformation factors [31]. It is also indicated that the interaction of valence nucleons reflects the effect of deformation [32, 33]. In addition, it is reported that the$ \alpha $ cluster formation energy and surface energy depending on differences in binding energies are critical for determining the values of$ \alpha $ preformation probabilities [7, 11].The consensus is that the increase in valence nucleons is considered to be beneficial to the formation of
$ \alpha $ particles in the parent nucleus. The interaction of valence protons with valence neutrons cannot be neglected in$ \alpha $ preformation; it reflects the role of proton-neutron correlation in$ \alpha $ -decay. The shell closure effect for the preformation factors is intuitive and obvious, and it is indispensable to the construction of an$ \alpha $ preformation factor formula, which is reflected well in the concise formula of Zhang et al. It has been reported that the proton-neutron pair number, neutron-neutron pair number, and gap energy have significant correlations with isospin [34, 35]. The more direct evidence is that$ P_\alpha $ is positively correlated with isospin asymmetry of parent nuclei having the same$ N_pN_n $ values [2]. Isospin asymmetry is an important factor affecting the density distribution of protons and neutrons, which is expected to play a more important role in the preformation of the$ \alpha $ nucleus [17, 36-40]. This leads us to consider that isospin asymmetry may be a key for determination of$ \alpha $ preformation factors. At the same time, protons and neutrons are in different charge states of the same nucleon, and the nuclear force is charge independent; the new formula should be able to reflect this feature. According to the discussion above, we propose a new improved formula based on the original formula of Zhang et al [21].$ \begin{aligned}[b] {\rm lg}P_{\alpha} = &\{ a+b\left[(Z-Z_1)(Z_2-Z)^3+(N-N_1)(N_2-N)^3\right] \\ &+c/\left[(Z-Z_1)(N-N_1)+1\right]+a_p+a_ll\} I+dA, \end{aligned} $

(16) where Z, N, and A are the charge, neutron, and mass number of the parent nucleus, respectively;
$ Z_1 $ and$ Z_2 $ are the proton magic numbers around$ Z\;(Z_1<Z\leqslant Z_2) $ ;$ N_1 $ and$ N_2 $ are the neutron magic numbers around$ N\;(N_1<N\leqslant N_2) $ . Proton magic numbers can be 50, 82, and 120, and neutron magic numbers can be 82, 126, 162, and 184. The term I is the isospin asymmetry,$ I = (N-Z)/(N+Z) $ . The second term represents the shell closure effect of protons and neutrons, and the third term represents the interaction of valence protons with valence neutrons. The parameter$ a_p $ is a constant representing the blocking effect of unpaired nucleons for odd-A and odd-odd nuclei; l is the minimum angular momentum transferred to an$ \alpha $ particle in$ \alpha $ -decay.We found that the values of
$ a_p $ for even-odd and odd-even nuclei are approximately equal because the proton and neutron are in different charge states of the same nucleon, the pairing force is the same for proton-neutron and neutron-neutron interaction, and an unpaired proton or neutron has the same effect on the calculation of$ \alpha $ preformation factors. Therefore, the parameter$ a_p $ for even-odd and odd-even nuclei is fixed to the same value. In the second term of Eq. (16), the representations of the proton and neutron shell closure effect are of the same form with one parameter b, also reflecting that the nuclear force is charge independent. Although the effect of centrifugal potential is involved in the GLDM method, we consider the influence of angular momentum in our formula. On the one hand, it is difficult to produce an$ \alpha $ particle with high angular momentum on the surface of the nucleus according to the principle of least action. On the other hand, the centrifugal potential is calculated in the condition of the sphere daughter nucleus. Therefore, it is necessary to consider the role of angular momentum in the formula.The coefficients of Eq. (16) for fitting the extracted preformation factors of 606 nuclei are listed in Table 1, and the parameter
$ a_p $ for odd-odd nuclei is smaller than that for odd-A and even-even nuclei, revealing that the blocking effect is stronger for odd-odd nuclei, and it is difficult for the formation of$ \alpha $ particles in odd-odd nuclei, including two unpaired nucleons. Fig. 3 shows the variation in$ \alpha $ preformation factors for different types of nuclei versus Z and N. The$ \alpha $ preformation factors calculated by Eq. (16) can reproduce the trend of the extracted ones.Parameter Value Parameter value a 2.65991 $a_l$ 

−0.69111 b 1.07 $\times 10^{-5}$ 

$a_p$ (e-e)

0 c −2.66753 $a_p$ (odd A)

−1.82248 d −0.00964 $a_p$ (o-o)

−4.68543 Table 1. Coefficient sets of Eq. (16) determined by fitting to 606 nuclei's extracted preformation factors.
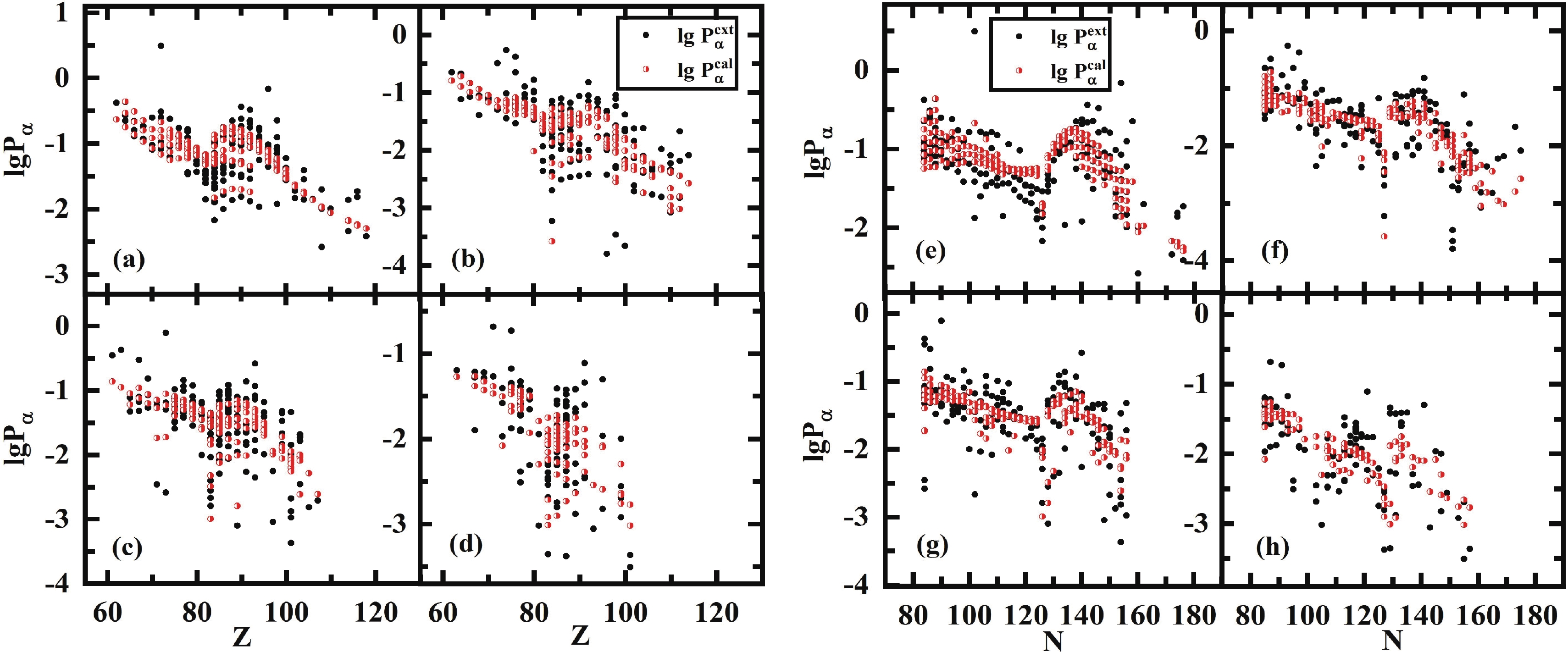
Figure 3. (color online) (a)(e), (b)(f), (c)(g), and (d)(h) are extracted and calculated [from Eq. (16)]
$\alpha$ preformation factors of 172 even Z-even N, 167 even Z-odd N, 163 even Z-odd N,and 105 odd Z-odd N nuclei, respectively. To measure the agreement of the theoretical values with the experimental values, the standard deviation between the extracted and calculated
$ \alpha $ preformation factors is defined as$ \sigma = \sqrt{\sum ({\rm lg}P_{\alpha}^{\rm \,ext}-{\rm lg}P_{\alpha}^{\rm \,cal})^2/n}. $

(17) The standard deviations for even-even, even-odd, odd-even, and odd-odd nuclei are 0.280, 0.417, 0.359, and 0.397, respectively. As for all 606 nuclei, the value of
$ \sigma $ is 0.365 with a factor of$ 10^{0.365} = 2.32 $ , which is better than the result of Seif et al. [41] of$ \sigma $ = 0.529 for 445 nuclei utilizing 16 parameters. Compared to the previous formula of Zhang et al. [21] with 48 parameters, the importance of angular momentum is firstly considered in our present work, and the effect for unfavored$ \alpha $ -decay is prominent, especially for odd-A and odd-odd nuclei, while the neutron number$ N>126 $ . The detailed comparison of our improved formula [Eq. (16)] with the formulas of Zhang et al. and Seif et al. is listed in Table 2. To show the precision of Eq. (16) explicitly, Fig. 4 displays the extracted and calculated$ \alpha $ preformation factors of Po, Rn, and Pa isotopes. The preformation factors calculated from Eq. (16) are very close to the extracted data and can reflect the nuclear microscopic properties such as the neutron magic number$ N = 126 $ and the odd-even effect.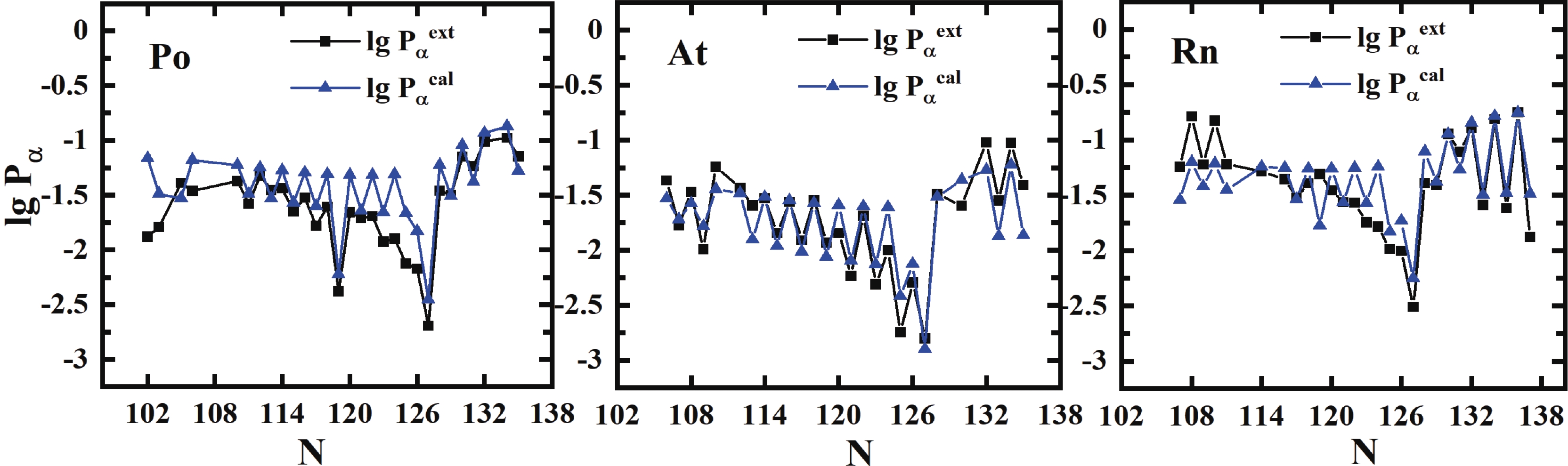
Figure 4. (color online) Extracted and calculated
$\alpha$ preformation factors [from Eq. (16)${\rm{lg }}P_\alpha^{\rm{\,cal}}$ ] for Po (Z = 84), for (Z = 85) and Rn (Z = 86) isotopes.We also compare our calculations with the results of Ren et al. [28-30, 42], as shown in Fig. 5. The theoretical
$ P_{\alpha} $ of N = 125, 126, and 127 isotones are consistent with the trend of extracted values, and the values calculated by our improved formula show significant agreement with the extracted ones. Notably, with the increase in the proton number when$ Z>92 $ , the$ \alpha $ preformation factors calculated by Ren et al. still increase, but the values calculated by our formula gradually decrease. This is because the formula of Ren et al. mainly considers the role of valence nucleons rather than the shell closure effect. Our formula is closely related to the shell closure effect and can give the trend more accurately; the preformation factors increase when Z is further away from the magic number and then decrease when it is closer to the next one. Overall, our formula can accurately describe the features of$ \alpha $ preformation factors and reproduce the extracted values with only 7 parameters.
Figure 5. (color online) Extracted and calculated
$\alpha$ preformation factors [from Ren et al. [42]${\rm{lg }}P_\alpha^{\rm\,{Ren}}$ and Eq. (16)${\rm{lg }}P_\alpha^{\rm\,{cal}}$ ] for$N = 125,126$ and$127$ isotones.Considering the
$ \alpha $ preformation factor, the calculated and experimental$ \alpha $ -decay half-lives of actinide elements are listed in Table 3. In this table, the first four columns denote$ \alpha $ -decay channel, experimental decay energy, spin and parity transition, and the minimum angular momentum taken away by$ \alpha $ particles, respectively. The fifth column presents the half-lives from GLDM with$ P_\alpha = 1 $ , and the sixth column presents the calculated$ \alpha $ preformation factors by Eq. (16); the parameters are listed in Table 1. By taking$ P_\alpha^{\rm cal} $ into account, it can be seen that the calculated$ \alpha $ -decay half-lives$ T_{1/2}^{\rm cal} $ can accurately reproduce most of the$ \alpha $ -decay experimental half-lives. However, for some nuclei, such as$ ^{212} $ Pa,$ ^{250} $ Cm,$ ^{249} $ Md,$ ^{236} $ Am,$ ^{256} $ Cf,$ ^{237} $ Cf,$ ^{233} $ Np,$ ^{243} $ Es,$ ^{253} $ Cf,$ ^{247} $ Fm,$ ^{225} $ Pa,$ ^{255} $ Es,$ ^{220} $ Pa,$ ^{254} $ Cf,$ ^{238} $ U,$ ^{231} $ Np,$ ^{227} $ Np,$ ^{218} $ Ac, the differences significantly increase. Firstly, this may be because we did not consider the effects of different decay channels while extracting$ \alpha $ preformation factors; the branching ratio transmitting to the first excited state can be as large as 30% [46]. Secondly, the experimental data, such as half-lives, spin, and parity, used for these special nuclei are not accurate enough and should be re-examined.parent $\rightarrow$ daughter

$Q\alpha$ 

$j_p^\pi\rightarrow j_d^\pi$ 

l $T^{\rm cal}_{1/2,P_\alpha=1}$ 

$P_\alpha^{\rm cal}$ 

$T_{1/2}^{\rm exp}$ 

$T_{1/2}^{\rm cal}$ 

$^{216}$ Ac

$\rightarrow^{212}$ Fr

9.24 (1 $^-$ )

$\rightarrow$ 5

$^+$ 

$^*$ 

5 1.3 $\times10^{-6}$ 

2.3 $\times10^{-3}$ 

4.4 $\times10^{-4}$ 

5.8 $\times10^{-4}$ 

$^{215}$ Ac

$\rightarrow^{211}$ Fr

7.75 9/2 $^-$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

0 1.9 $\times10^{-3}$ 

9.9 $\times10^{-3}$ 

1.7 $\times10^{-1}$ 

1.9 $\times10^{-1}$ 

$^{207}$ Ac

$\rightarrow^{203}$ Fr

7.85 9/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

0 1.2 $\times10^{-3}$ 

2.9 $\times10^{-2}$ 

3.1 $\times10^{-2}$ 

4.3 $\times10^{-2}$ 

$^{216}$ Ac

$^m$ 

$\rightarrow^{212}$ Fr

9.28 (9 $^-$ )

$\rightarrow$ 5

$^+$ 

$^*$ 

5 1.0 $\times10^{-6}$ 

2.3 $\times10^{-3}$ 

4.4 $\times10^{-4}$ 

4.5 $\times10^{-4}$ 

$^{211}$ Ac

$\rightarrow^{207}$ Fr

7.62 9/2 $^-$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

0 5.7 $\times10^{-3}$ 

2.8 $\times10^{-2}$ 

2.1 $\times10^{-1}$ 

2.0 $\times10^{-1}$ 

$^{227}$ Ac

$\rightarrow^{223}$ Fr

5.04 3/2 $^-$ 

$\rightarrow$ 3/2

$^-$ 

$^*$ 

0 2.5 $\times10^{9}$ 

7.1 $\times10^{-2}$ 

5.0 $\times10^{10}$ 

3.5 $\times10^{10}$ 

$^{206}$ Ac

$^m$ 

$\rightarrow^{202}$ Fr

$^m$ 

7.91 (10 $^-$ )

$\rightarrow$ 10

$^-$ 

$^*$ 

0 8.4 $\times10^{-4}$ 

1.2 $\times10^{-2}$ 

4.1 $\times10^{-2}$ 

7.1 $\times10^{-2}$ 

$^{217}$ Ac

$\rightarrow^{213}$ Fr

9.83 9/2 $^-$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

0 3.6 $\times10^{-9}$ 

3.8 $\times10^{-2}$ 

6.9 $\times10^{-8}$ 

9.6 $\times10^{-8}$ 

$^{206}$ Ac

$\rightarrow^{202}$ Fr

7.96 (3 $^+$ )

$\rightarrow$ 3

$^+$ 

$^*$ 

0 5.7 $\times10^{-4}$ 

1.2 $\times10^{-2}$ 

2.5 $\times10^{-2}$ 

4.8 $\times10^{-2}$ 

$^{225}$ Ac

$\rightarrow^{221}$ Fr

5.94 3/2 $^-$ 

$\#$ 

$\rightarrow$ 5/2

$^-$ 

$^*$ 

2 4.8 $\times10^{4}$ 

3.7 $\times10^{-2}$ 

8.6 $\times10^{5}$ 

1.3 $\times10^{6}$ 

$^{217}$ Ac

$^m$ 

$\rightarrow^{213}$ Fr

11.84 (29/2) $^+$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

11 1.4 $\times10^{-8}$ 

1.6 $\times10^{-3}$ 

1.7 $\times10^{-5}$ 

8.4 $\times10^{-6}$ 

$^{205}$ Ac

$\rightarrow^{201}$ Fr

$^n$ 

7.90 9/2 $^-$ 

$\#$ 

$\rightarrow$ (13/2

$^+$ )

3 2.8 $\times10^{-3}$ 

1.6 $\times10^{-2}$ 

8.0 $\times10^{-2}$ 

1.8 $\times10^{-1}$ 

$^{219}$ Ac

$\rightarrow^{215}$ Fr

8.83 9/2 $^-$ 

$\rightarrow$ 9/2

$^-$ 

0 9.4 $\times10^{-7}$ 

5.1 $\times10^{-2}$ 

1.2 $\times10^{-5}$ 

1.8 $\times10^{-5}$ 

$^{222}$ Ac

$\rightarrow^{218}$ Fr

7.14 1 $^-$ 

$\rightarrow$ 1

$^-$ 

0 2.0 $\times10^{-1}$ 

1.8 $\times10^{-2}$ 

5.0 $\times10^{0}$ 

1.1 $\times10^{1}$ 

$^{223}$ Ac

$\rightarrow^{219}$ Fr

6.78 (5/2 $^-$ )

$\rightarrow$ 9/2

$^-$ 

2 7.8 $\times10^{0}$ 

3.6 $\times10^{-2}$ 

1.3 $\times10^{2}$ 

2.2 $\times10^{2}$ 

$^{221}$ Ac

$\rightarrow^{217}$ Fr

7.78 9/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

0 1.1 $\times10^{-3}$ 

6.2 $\times10^{-2}$ 

5.2 $\times10^{-2}$ 

1.9 $\times10^{-2}$ 

$^{218}$ Ac

$\rightarrow^{214}$ Fr

9.37 1 $^-$ 

$\#$ 

$\rightarrow$ (1

$^-$ )

0 3.8 $\times10^{-8}$ 

1.3 $\times10^{-2}$ 

1.0 $\times10^{-6}$ 

2.9 $\times10^{-6}$ 

$^{226}$ Ac

$\rightarrow^{222}$ Fr

5.51 (1)( $^-$ 

$\#$ )

$\rightarrow$ 2

$^-$ 

$^*$ 

2 8.8 $\times10^{6}$ 

9.0 $\times10^{-3}$ 

1.7 $\times10^{9}$ 

9.8 $\times10^{8}$ 

$^{220}$ Ac

$\rightarrow^{216}$ Fr

8.35 (3 $^-$ )

$\rightarrow$ (1

$^-$ )

2 3.5 $\times10^{-5}$ 

8.8 $\times10^{-3}$ 

2.6 $\times10^{-2}$ 

4.0 $\times10^{-3}$ 

$^{214}$ Th

$\rightarrow^{210}$ Ra

7.83 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.7 $\times10^{-3}$ 

5.3 $\times10^{-2}$ 

8.7 $\times10^{-2}$ 

5.0 $\times10^{-2}$ 

$^{219}$ Th

$\rightarrow^{215}$ Ra

9.51 9/2 $^+$ 

$\#$ 

$\rightarrow$ 9/2

$^+$ 

$\#$ 

0 3.7 $\times10^{-8}$ 

4.3 $\times10^{-2}$ 

1.0 $\times10^{-6}$ 

8.6 $\times10^{-7}$ 

$^{222}$ Th

$\rightarrow^{218}$ Ra

8.13 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.1 $\times10^{-4}$ 

1.3 $\times10^{-1}$ 

2.2 $\times10^{-3}$ 

1.6 $\times10^{-3}$ 

$^{218}$ Th

$\rightarrow^{214}$ Ra

9.85 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 6.3 $\times10^{-9}$ 

7.6 $\times10^{-2}$ 

1.2 $\times10^{-7}$ 

8.3 $\times10^{-8}$ 

$^{212}$ Th

$\rightarrow^{208}$ Ra

7.96 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.1 $\times10^{-3}$ 

5.1 $\times10^{-2}$ 

3.2 $\times10^{-2}$ 

2.1 $\times10^{-2}$ 

$^{224}$ Th

$\rightarrow^{220}$ Ra

7.30 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.2 $\times10^{-1}$ 

1.5 $\times10^{-1}$ 

1.0 $\times10^{0}$ 

8.1 $\times10^{-1}$ 

Continued on next page Table 3. Calculations of
$\alpha$ -decay half-lives of actinide nuclei. The experimental$\alpha$ -decay half-lives, spin and parity are taken from the latest evaluated nuclear properties table NUBASE2016 [43]. The$\alpha$ -decay energies are taken from the latest evaluated atomic mass table AME2016 [44]. Elements with superscripts 'm', 'n', 'p', or 'x' indicate assignments to excited isomeric states; '$()$ ' means uncertain spin or parity; '$\#$ ' means spin and parity values estimated from trends in neighboring nuclides with the same Z and N parities. The$\alpha$ -decay energy and half-lives are in units of MeV and s, respectively. The experimental data is consistent with Ref. [45], and$T_{1/2}^{\rm \,cal}$ is the calculations in the framework of GLDM with$P_\alpha^{\rm \,cal}$ .Table 3-continued from previous page parent $\rightarrow$ daughter

$Q\alpha$ 

$j_p^\pi\rightarrow j_d^\pi$ 

l $T^{cal}_{1/2,P_\alpha=1}$ 

$P_\alpha^{cal}$ 

$T_{1/2}^{exp}$ 

$T_{1/2}^{cal}$ 

$^{209}$ Th

$^m$ 

$\rightarrow^{205}$ Ra

$^m$ 

8.28 (13/2 $^+$ )

$\rightarrow$ (13/2

$^+$ )

0 1.3 $\times10^{-4}$ 

2.7 $\times10^{-2}$ 

3.1 $\times10^{-3}$ 

4.6 $\times10^{-3}$ 

$^{220}$ Th

$\rightarrow^{216}$ Ra

8.95 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 9.4 $\times10^{-7}$ 

1.1 $\times10^{-1}$ 

9.7 $\times10^{-6}$ 

9.0 $\times10^{-6}$ 

$^{223}$ Th

$\rightarrow^{219}$ Ra

7.57 (5/2) $^+$ 

$\rightarrow$ (7/2)

$^+$ 

2 2.4 $\times10^{-2}$ 

3.4 $\times10^{-2}$ 

6.0 $\times10^{-1}$ 

7.0 $\times10^{-1}$ 

$^{226}$ Th

$\rightarrow^{222}$ Ra

6.45 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 3.0 $\times10^{2}$ 

1.6 $\times10^{-1}$ 

1.8 $\times10^{3}$ 

1.8 $\times10^{3}$ 

$^{208}$ Th

$\rightarrow^{204}$ Ra

8.20 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.3 $\times10^{-4}$ 

4.9 $\times10^{-2}$ 

2.4 $\times10^{-3}$ 

4.7 $\times10^{-3}$ 

$^{216}$ Th

$\rightarrow^{212}$ Ra

8.07 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 4.0 $\times10^{-4}$ 

2.0 $\times10^{-2}$ 

2.6 $\times10^{-2}$ 

2.0 $\times10^{-2}$ 

$^{228}$ Th

$\rightarrow^{224}$ Ra

5.52 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.1 $\times10^{7}$ 

1.6 $\times10^{-1}$ 

6.0 $\times10^{7}$ 

6.8 $\times10^{7}$ 

$^{215}$ Th

$\rightarrow^{211}$ Ra

7.67 (1/2 $^-$ )

$\rightarrow$ 5/2(

$^-$ )

2 1.5 $\times10^{-2}$ 

1.6 $\times10^{-2}$ 

1.2 $\times10^{0}$ 

9.4 $\times10^{-1}$ 

$^{230}$ Th

$\rightarrow^{226}$ Ra

4.77 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 5.7 $\times10^{11}$ 

1.6 $\times10^{-1}$ 

2.4 $\times10^{12}$ 

3.5 $\times10^{12}$ 

$^{217}$ Th

$\rightarrow^{213}$ Ra

9.44 9/2 $^+$ 

$\#$ 

$\rightarrow$ 1/2

$^-$ 

5 9.0 $\times10^{-7}$ 

7.6 $\times10^{-3}$ 

2.5 $\times10^{-4}$ 

1.2 $\times10^{-4}$ 

$^{231}$ Th

$\rightarrow^{227}$ Ra

4.21 5/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

2 2.0 $\times10^{16}$ 

3.1 $\times10^{-2}$ 

2.3 $\times10^{17}$ 

6.6 $\times10^{17}$ 

$^{232}$ Th

$\rightarrow^{228}$ Ra

4.08 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.6 $\times10^{17}$ 

1.5 $\times10^{-1}$ 

4.4 $\times10^{17}$ 

1.1 $\times10^{18}$ 

$^{225}$ Th

$\rightarrow^{221}$ Ra

6.92 (3/2 $^+$ )

$\rightarrow$ 5/2

$^+$ 

2 5.6 $\times10^{0}$ 

3.6 $\times10^{-2}$ 

5.8 $\times10^{2}$ 

1.6 $\times10^{2}$ 

$^{221}$ Th

$\rightarrow^{217}$ Ra

8.63 7/2 $^+$ 

$\#$ 

$\rightarrow$ (9/2

$^+$ )

2 1.3 $\times10^{-5}$ 

3.0 $\times10^{-2}$ 

1.8 $\times10^{-3}$ 

4.2 $\times10^{-4}$ 

$^{229}$ Th

$\rightarrow^{225}$ Ra

5.17 5/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

2 2.3 $\times10^{9}$ 

3.4 $\times10^{-2}$ 

2.5 $\times10^{11}$ 

6.8 $\times10^{10}$ 

$^{227}$ Th

$\rightarrow^{223}$ Ra

6.15 (1/2 $^+$ )

$\rightarrow$ 3/2

$^+$ 

2 1.1 $\times10^{4}$ 

3.5 $\times10^{-2}$ 

1.6 $\times10^{6}$ 

3.1 $\times10^{5}$ 

$^{217}$ Pa

$\rightarrow^{213}$ Ac

8.49 9/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

$\#$ 

0 5.0 $\times10^{-5}$ 

9.8 $\times10^{-3}$ 

3.5 $\times10^{-3}$ 

5.1 $\times10^{-3}$ 

$^{227}$ Pa

$\rightarrow^{223}$ Ac

6.58 (5/2 $^-$ )

$\rightarrow$ (5/2

$^-$ )

0 2.0 $\times10^{2}$ 

6.4 $\times10^{-2}$ 

2.7 $\times10^{3}$ 

3.1 $\times10^{3}$ 

$^{215}$ Pa

$\rightarrow^{211}$ Ac

8.24 9/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

0 3.1 $\times10^{-4}$ 

2.6 $\times10^{-2}$ 

1.4 $\times10^{-2}$ 

1.2 $\times10^{-2}$ 

$^{213}$ Pa

$\rightarrow^{209}$ Ac

8.40 9/2 $^-$ 

$\#$ 

$\rightarrow$ (9/2

$^-$ )

0 1.1 $\times10^{-4}$ 

2.6 $\times10^{-2}$ 

7.0 $\times10^{-3}$ 

4.3 $\times10^{-3}$ 

$^{229}$ Pa

$\rightarrow^{225}$ Ac

5.84 (5/2 $^+$ )

$\rightarrow$ 3/2

$^-$ 

$\#$ 

1 8.0 $\times10^{5}$ 

4.6 $\times10^{-2}$ 

2.7 $\times10^{7}$ 

1.7 $\times10^{7}$ 

$^{221}$ Pa

$\rightarrow^{217}$ Ac

9.25 9/2 $^-$ 

$\rightarrow$ 9/2

$^-$ 

0 3.4 $\times10^{-7}$ 

4.6 $\times10^{-2}$ 

5.9 $\times10^{-6}$ 

7.4 $\times10^{-6}$ 

$^{223}$ Pa

$\rightarrow^{219}$ Ac

8.33 9/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

0 1.2 $\times10^{-4}$ 

5.5 $\times10^{-2}$ 

5.1 $\times10^{-3}$ 

2.2 $\times10^{-3}$ 

$^{224}$ Pa

$\rightarrow^{220}$ Ac

7.69 5 $^-$ 

$\#$ 

$\rightarrow$ (3

$^-$ )

2 2.1 $\times10^{-2}$ 

9.4 $\times10^{-3}$ 

8.5 $\times10^{-1}$ 

2.3 $\times10^{0}$ 

$^{228}$ Pa

$\rightarrow^{224}$ Ac

6.27 3 $^+$ 

$\rightarrow$ (0

$^-$ )

3 1.5 $\times10^{4}$ 

6.5 $\times10^{-3}$ 

4.3 $\times10^{6}$ 

2.3 $\times10^{6}$ 

$^{220}$ Pa

$\rightarrow^{216}$ Ac

9.65 1 $^-$ 

$\#$ 

$\rightarrow$ (1

$^-$ )

0 3.6 $\times10^{-8}$ 

1.3 $\times10^{-2}$ 

7.8 $\times10^{-7}$ 

2.7 $\times10^{-6}$ 

$^{230}$ Pa

$\rightarrow^{226}$ Ac

5.44 2 $^-$ 

$\rightarrow$ (1)(

$^-$ 

$\#$ )

2 1.7 $\times10^{8}$ 

8.1 $\times10^{-3}$ 

4.7 $\times10^{10}$ 

2.1 $\times10^{10}$ 

$^{225}$ Pa

$\rightarrow^{221}$ Ac

7.40 5/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

$\#$ 

2 2.3 $\times10^{-1}$ 

3.4 $\times10^{-2}$ 

1.7 $\times10^{0}$ 

7.0 $\times10^{0}$ 

$^{231}$ Pa

$\rightarrow^{227}$ Ac

5.15 3/2 $^-$ 

$\rightarrow$ 3/2

$^-$ 

0 5.7 $\times10^{9}$ 

6.0 $\times10^{-2}$ 

1.0 $\times10^{12}$ 

9.4 $\times10^{10}$ 

$^{212}$ Pa

$\rightarrow^{208}$ Ac

8.42 7 $^+$ 

$\#$ 

$\rightarrow$ (3

$^+$ )

4 5.8 $\times10^{-4}$ 

4.1 $\times10^{-3}$ 

7.5 $\times10^{-3}$ 

1.4 $\times10^{-1}$ 

$^{221}$ U

$\rightarrow^{217}$ Th

9.89 (9/2 $^+$ )

$\rightarrow$ 9/2

$^+$ 

$\#$ 

0 2.1 $\times10^{-8}$ 

3.8 $\times10^{-2}$ 

6.6 $\times10^{-7}$ 

5.6 $\times10^{-7}$ 

$^{227}$ U

$\rightarrow^{223}$ Th

7.23 (3/2 $^+$ )

$\rightarrow$ (5/2)

$^+$ 

2 2.0 $\times10^{0}$ 

3.2 $\times10^{-2}$ 

6.6 $\times10^{1}$ 

6.3 $\times10^{1}$ 

$^{224}$ U

$\rightarrow^{220}$ Th

8.63 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 3.4 $\times10^{-5}$ 

1.1 $\times10^{-1}$ 

4.0 $\times10^{-4}$ 

3.2 $\times10^{-4}$ 

$^{226}$ U

$\rightarrow^{222}$ Th

7.70 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.8 $\times10^{-2}$ 

1.2 $\times10^{-1}$ 

2.7 $\times10^{-1}$ 

2.3 $\times10^{-1}$ 

$^{218}$ U

$\rightarrow^{214}$ Th

8.78 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.6 $\times10^{-5}$ 

1.8 $\times10^{-2}$ 

5.5 $\times10^{-4}$ 

8.7 $\times10^{-4}$ 

$^{222}$ U

$\rightarrow^{218}$ Th

9.48 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.9 $\times10^{-7}$ 

8.8 $\times10^{-2}$ 

4.7 $\times10^{-6}$ 

2.1 $\times10^{-6}$ 

$^{229}$ U

$\rightarrow^{225}$ Th

6.48 (3/2 $^+$ )

$\rightarrow$ (3/2

$^+$ )

0 1.5 $\times10^{3}$ 

5.9 $\times10^{-2}$ 

1.7 $\times10^{4}$ 

2.6 $\times10^{4}$ 

$^{219}$ U

$\rightarrow^{215}$ Th

9.94 9/2 $^+$ 

$\#$ 

$\rightarrow$ (1/2

$^-$ )

5 2.1 $\times10^{-7}$ 

7.6 $\times10^{-3}$ 

5.5 $\times10^{-5}$ 

2.8 $\times10^{-5}$ 

$^{230}$ U

$\rightarrow^{226}$ Th

5.99 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 3.1 $\times10^{5}$ 

1.4 $\times10^{-1}$ 

1.7 $\times10^{6}$ 

2.3 $\times10^{6}$ 

$^{232}$ U

$\rightarrow^{228}$ Th

5.41 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 4.5 $\times10^{8}$ 

1.3 $\times10^{-1}$ 

2.2 $\times10^{9}$ 

3.4 $\times10^{9}$ 

$^{234}$ U

$\rightarrow^{230}$ Th

4.86 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.7 $\times10^{12}$ 

1.3 $\times10^{-1}$ 

7.7 $\times10^{12}$ 

1.3 $\times10^{13}$ 

Continued on next page Table 3-continued from previous page parent $\rightarrow$ daughter

$Q\alpha$ 

$j_p^\pi\rightarrow j_d^\pi$ 

l $T^{\rm cal}_{1/2,P_\alpha=1}$ 

$P_\alpha^{\rm cal}$ 

$T_{1/2}^{\rm exp}$ 

$T_{1/2}^{\rm cal}$ 

$^{236}$ U

$\rightarrow^{232}$ Th

4.57 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.7 $\times10^{14}$ 

1.2 $\times10^{-1}$ 

7.4 $\times10^{14}$ 

1.4 $\times10^{15}$ 

$^{216}$ U

$\rightarrow^{212}$ Th

8.53 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 9.1 $\times10^{-5}$ 

4.6 $\times10^{-2}$ 

6.9 $\times10^{-3}$ 

2.0 $\times10^{-3}$ 

$^{233}$ U

$\rightarrow^{229}$ Th

4.91 5/2 $^+$ 

$\rightarrow$ 5/2

$^+$ 

0 7.6 $\times10^{11}$ 

5.4 $\times10^{-2}$ 

5.0 $\times10^{12}$ 

1.4 $\times10^{13}$ 

$^{238}$ U

$\rightarrow^{234}$ Th

4.27 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 4.6 $\times10^{16}$ 

1.1 $\times10^{-1}$ 

1.4 $\times10^{17}$ 

4.3 $\times10^{17}$ 

$^{225}$ U

$\rightarrow^{221}$ Th

8.02 5/2 $^+$ 

$\#$ 

$\rightarrow$ 7/2

$^+$ 

$\#$ 

2 4.3 $\times10^{-3}$ 

3.0 $\times10^{-2}$ 

6.1 $\times10^{-2}$ 

1.4 $\times10^{-1}$ 

$^{231}$ U

$\rightarrow^{227}$ Th

5.58 (5/2)( $^+$ 

$\#$ )

$\rightarrow$ (1/2

$^+$ )

2 8.9 $\times10^{7}$ 

3.0 $\times10^{-2}$ 

8.9 $\times10^{9}$ 

2.9 $\times10^{9}$ 

$^{233}$ Am

$\rightarrow^{229}$ Np

7.06 5/2 $^-$ 

$\#$ 

$\rightarrow$ 5/2

$^+$ 

$\#$ 

1 1.2 $\times10^{2}$ 

3.2 $\times10^{-2}$ 

4.2 $\times10^{3}$ 

3.6 $\times10^{3}$ 

$^{243}$ Am

$\rightarrow^{239}$ Np

5.44 5/2 $^-$ 

$^*$ 

$\rightarrow$ 5/2

$^+$ 

1 9.1 $\times10^{9}$ 

2.0 $\times10^{-2}$ 

2.3 $\times10^{11}$ 

4.6 $\times10^{11}$ 

$^{239}$ Am

$\rightarrow^{235}$ Np

5.92 (5/2) $^-$ 

$\rightarrow$ 5/2

$^+$ 

1 1.7 $\times10^{7}$ 

2.5 $\times10^{-2}$ 

4.2 $\times10^{8}$ 

6.8 $\times10^{8}$ 

$^{237}$ Am

$\rightarrow^{233}$ Np

6.20 5/2( $^-$ )

$\rightarrow$ 5/2

$^+$ 

$\#$ 

1 6.9 $\times10^{5}$ 

2.8 $\times10^{-2}$ 

1.7 $\times10^{7}$ 

2.5 $\times10^{7}$ 

$^{241}$ Am

$\rightarrow^{237}$ Np

5.64 5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

1 6.3 $\times10^{8}$ 

2.2 $\times10^{-2}$ 

1.4 $\times10^{10}$ 

2.8 $\times10^{10}$ 

$^{240}$ Am

$\rightarrow^{236}$ Np

5.47 (3 $^-$ )

$\rightarrow$ (3

$^-$ )

0 5.2 $\times10^{9}$ 

8.3 $\times10^{-3}$ 

4.8 $\times10^{11}$ 

6.2 $\times10^{11}$ 

$^{229}$ Am

$\rightarrow^{225}$ Np

8.14 5/2 $^-$ 

$\#$ 

$\rightarrow$ 9/2

$^-$ 

$\#$ 

2 2.0 $\times10^{-2}$ 

2.4 $\times10^{-2}$ 

2.0 $\times10^{0}$ 

8.4 $\times10^{-1}$ 

$^{235}$ Am

$\rightarrow^{231}$ Np

6.59 5/2 $^-$ 

$\#$ 

$\rightarrow$ (5/2)(

$^+$ 

$\#$ )

1 1.0 $\times10^{4}$ 

3.0 $\times10^{-2}$ 

1.5 $\times10^{5}$ 

3.4 $\times10^{5}$ 

$^{236}$ Am

$\rightarrow^{232}$ Np

6.26 ( $^-$ 5)

$\rightarrow$ (4

$^+$ )

1 3.4 $\times10^{5}$ 

8.0 $\times10^{-3}$ 

6.8 $\times10^{6}$ 

4.2 $\times10^{7}$ 

$^{242}$ Am

$^m$ 

$\rightarrow^{238}$ Np

5.64 5 $^-$ 

$\rightarrow$ 2

$^+$ 

3 1.5 $\times10^{9}$ 

2.6 $\times10^{-3}$ 

9.8 $\times10^{11}$ 

5.8 $\times10^{11}$ 

$^{240}$ Cm

$\rightarrow^{236}$ Pu

6.40 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.6 $\times10^{5}$ 

7.1 $\times10^{-2}$ 

2.3 $\times10^{6}$ 

2.3 $\times10^{6}$ 

$^{241}$ Cm

$\rightarrow^{237}$ Pu

6.19 1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

3 5.0 $\times10^{6}$ 

1.1 $\times10^{-2}$ 

2.8 $\times10^{8}$ 

4.5 $\times10^{8}$ 

$^{234}$ Cm

$\rightarrow^{230}$ Pu

7.37 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.5 $\times10^{1}$ 

8.1 $\times10^{-2}$ 

1.9 $\times10^{2}$ 

1.8 $\times10^{2}$ 

$^{246}$ Cm

$\rightarrow^{242}$ Pu

5.48 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.2 $\times10^{10}$ 

5.8 $\times10^{-2}$ 

1.5 $\times10^{11}$ 

2.1 $\times10^{11}$ 

$^{236}$ Cm

$\rightarrow^{232}$ Pu

7.07 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.9 $\times10^{2}$ 

7.9 $\times10^{-2}$ 

2.2 $\times10^{3}$ 

2.4 $\times10^{3}$ 

$^{242}$ Cm

$\rightarrow^{238}$ Pu

6.22 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.2 $\times10^{6}$ 

6.6 $\times10^{-2}$ 

1.4 $\times10^{7}$ 

1.9 $\times10^{7}$ 

$^{237}$ Cm

$\rightarrow^{233}$ Pu

6.78 5/2 $^+$ 

$\#$ 

$\rightarrow$ 5/2

$^+$ 

$\#$ 

0 3.2 $\times10^{3}$ 

3.5 $\times10^{-2}$ 

6.7 $\times10^{4}$ 

9.1 $\times10^{4}$ 

$^{244}$ Cm

$\rightarrow^{240}$ Pu

5.90 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 5.1 $\times10^{7}$ 

6.2 $\times10^{-2}$ 

5.7 $\times10^{8}$ 

8.3 $\times10^{8}$ 

$^{233}$ Cm

$\rightarrow^{229}$ Pu

7.47 3/2 $^+$ 

$\#$ 

$\rightarrow$ 3/2

$^+$ 

$\#$ 

0 6.2 $\times10^{0}$ 

3.8 $\times10^{-2}$ 

1.3 $\times10^{2}$ 

1.6 $\times10^{2}$ 

$^{238}$ Cm

$\rightarrow^{234}$ Pu

6.67 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 9.2 $\times10^{3}$ 

7.6 $\times10^{-2}$ 

2.1 $\times10^{5}$ 

1.2 $\times10^{5}$ 

$^{248}$ Cm

$\rightarrow^{244}$ Pu

5.16 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.2 $\times10^{12}$ 

5.5 $\times10^{-2}$ 

1.2 $\times10^{13}$ 

2.1 $\times10^{13}$ 

$^{245}$ Cm

$\rightarrow^{241}$ Pu

5.62 7/2 $^+$ 

$^*$ 

$\rightarrow$ 5/2

$^+$ 

2 2.6 $\times10^{9}$ 

1.2 $\times10^{-2}$ 

2.6 $\times10^{11}$ 

2.2 $\times10^{11}$ 

$^{243}$ Cm

$\rightarrow^{239}$ Pu

6.17 5/2 $^+$ 

$^*$ 

$\rightarrow$ 1/2

$^+$ 

2 3.5 $\times10^{6}$ 

1.4 $\times10^{-2}$ 

9.2 $\times10^{8}$ 

2.5 $\times10^{8}$ 

$^{250}$ Cm

$\rightarrow^{246}$ Pu

5.17 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 9.9 $\times10^{11}$ 

5.2 $\times10^{-2}$ 

1.4 $\times10^{12}$ 

1.9 $\times10^{13}$ 

$^{247}$ Cm

$\rightarrow^{243}$ Pu

5.35 9/2 $^-$ 

$^*$ 

$\rightarrow$ 7/2

$^+$ 

1 8.0 $\times10^{10}$ 

1.5 $\times10^{-2}$ 

4.9 $\times10^{14}$ 

5.2 $\times10^{12}$ 

$^{247}$ Bk

$\rightarrow^{243}$ Am

5.89 3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

$^*$ 

2 2.4 $\times10^{8}$ 

1.0 $\times10^{-2}$ 

4.4 $\times10^{10}$ 

2.4 $\times10^{10}$ 

$^{245}$ Bk

$\rightarrow^{241}$ Am

6.45 3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

2 3.2 $\times10^{5}$ 

1.2 $\times10^{-2}$ 

3.5 $\times10^{8}$ 

2.8 $\times10^{7}$ 

$^{248}$ Cf

$\rightarrow^{244}$ Cm

6.36 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.5 $\times10^{6}$ 

4.4 $\times10^{-2}$ 

2.9 $\times10^{7}$ 

3.4 $\times10^{7}$ 

$^{246}$ Cf

$\rightarrow^{242}$ Cm

6.86 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 7.1 $\times10^{3}$ 

4.7 $\times10^{-2}$ 

1.3 $\times10^{5}$ 

1.5 $\times10^{5}$ 

$^{245}$ Cf

$\rightarrow^{241}$ Cm

7.26 1/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

0 1.6 $\times10^{2}$ 

2.1 $\times10^{-2}$ 

7.4 $\times10^{3}$ 

7.4 $\times10^{3}$ 

$^{247}$ Cf

$\rightarrow^{243}$ Cm

6.50 7/2 $^+$ 

$\#$ 

$\rightarrow$ 5/2

$^+$ 

$^*$ 

2 5.5 $\times10^{5}$ 

9.8 $\times10^{-3}$ 

3.2 $\times10^{7}$ 

5.6 $\times10^{7}$ 

$^{251}$ Cf

$\rightarrow^{247}$ Cm

6.18 1/2 $^+$ 

$\rightarrow$ 9/2

$^-$ 

$^*$ 

5 1.5 $\times10^{8}$ 

2.8 $\times10^{-3}$ 

2.8 $\times10^{10}$ 

5.3 $\times10^{10}$ 

$^{250}$ Cf

$\rightarrow^{246}$ Cm

6.13 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.2 $\times10^{7}$ 

4.1 $\times10^{-2}$ 

4.1 $\times10^{8}$ 

5.3 $\times10^{8}$ 

$^{242}$ Cf

$\rightarrow^{238}$ Cm

7.52 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.9 $\times10^{1}$ 

5.4 $\times10^{-2}$ 

2.6 $\times10^{2}$ 

3.5 $\times10^{2}$ 

$^{244}$ Cf

$\rightarrow^{240}$ Cm

7.33 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 9.4 $\times10^{1}$ 

5.0 $\times10^{-2}$ 

1.2 $\times10^{3}$ 

1.9 $\times10^{3}$ 

Continued on next page Table 3-continued from previous page parent $\rightarrow$ daughter

$Q\alpha$ 

$j_p^\pi\rightarrow j_d^\pi$ 

l $T^{\rm cal}_{1/2,P_\alpha=1}$ 

$P_\alpha^{\rm cal}$ 

$T_{1/2}^{\rm exp}$ 

$T_{1/2}^{\rm cal}$ 

$^{240}$ Cf

$\rightarrow^{236}$ Cm

7.71 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 3.6 $\times10^{0}$ 

5.7 $\times10^{-2}$ 

4.1 $\times10^{1}$ 

6.4 $\times10^{1}$ 

$^{255}$ Cf

$\rightarrow^{251}$ Cm

5.74 (7/2 $^+$ )

$\rightarrow$ (1/2

$^+$ )

4 1.3 $\times10^{10}$ 

3.3 $\times10^{-3}$ 

2.6 $\times10^{12}$ 

3.8 $\times10^{12}$ 

$^{241}$ Cf

$\rightarrow^{237}$ Cm

$^p$ 

7.46 7/2 $^-$ 

$\#$ 

$\rightarrow$ 7/2

$^-$ 

0 3.3 $\times10^{1}$ 

2.5 $\times10^{-2}$ 

5.6 $\times10^{2}$ 

1.3 $\times10^{3}$ 

$^{252}$ Cf

$\rightarrow^{248}$ Cm

6.22 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 7.3 $\times10^{6}$ 

4.0 $\times10^{-2}$ 

8.6 $\times10^{7}$ 

1.8 $\times10^{8}$ 

$^{243}$ Cf

$\rightarrow^{239}$ Cm

7.42 (1/2 $^+$ )

$\rightarrow$ (7/2

$^-$ )

3 1.2 $\times10^{2}$ 

9.1 $\times10^{-3}$ 

4.6 $\times10^{3}$ 

1.3 $\times10^{4}$ 

$^{254}$ Cf

$\rightarrow^{250}$ Cm

5.93 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.1 $\times10^{8}$ 

3.9 $\times10^{-2}$ 

1.7 $\times10^{9}$ 

5.4 $\times10^{9}$ 

$^{253}$ Cf

$\rightarrow^{249}$ Cm

$^m$ 

6.08 (7/2 $^+$ )

$\rightarrow$ (7/2

$^+$ )

0 3.8 $\times10^{7}$ 

1.5 $\times10^{-2}$ 

4.9 $\times10^{8}$ 

2.5 $\times10^{9}$ 

$^{256}$ Cf

$\rightarrow^{252}$ Cm

5.56 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.7 $\times10^{10}$ 

3.8 $\times10^{-2}$ 

1.2 $\times10^{11}$ 

7.0 $\times10^{11}$ 

$^{238}$ Cf

$\rightarrow^{234}$ Cm

8.13 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.3 $\times10^{-1}$ 

5.9 $\times10^{-2}$ 

1.1 $\times10^{1}$ 

2.1 $\times10^{0}$ 

$^{237}$ Cf

$\rightarrow^{233}$ Cm

8.23 5/2 $^+$ 

$\#$ 

$\rightarrow$ 3/2

$^+$ 

$\#$ 

2 1.0 $\times10^{-1}$ 

1.7 $\times10^{-2}$ 

1.1 $\times10^{0}$ 

6.1 $\times10^{0}$ 

$^{249}$ Cf

$\rightarrow^{245}$ Cm

6.29 9/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

$^*$ 

1 3.8 $\times10^{6}$ 

1.2 $\times10^{-2}$ 

1.1 $\times10^{10}$ 

3.1 $\times10^{8}$ 

$^{249}$ Es

$\rightarrow^{245}$ Bk

$^p$ 

6.90 7/2 $^+$ 

$\rightarrow$ (7/2

$^-$ )

1 1.6 $\times10^{4}$ 

1.2 $\times10^{-2}$ 

1.1 $\times10^{6}$ 

1.4 $\times10^{6}$ 

$^{246}$ Es

$\rightarrow^{242}$ Bk

$^p$ 

7.50 4 $^-$ 

$\#$ 

$\rightarrow$ 4

$^-$ 

0 4.6 $\times10^{1}$ 

5.1 $\times10^{-3}$ 

4.5 $\times10^{3}$ 

9.0 $\times10^{3}$ 

$^{247}$ Es

$\rightarrow^{243}$ Bk

$^p$ 

7.44 (7/2 $^+$ )

$\rightarrow$ (7/2

$^-$ )

1 8.5 $\times10^{1}$ 

1.3 $\times10^{-2}$ 

3.9 $\times10^{3}$ 

6.6 $\times10^{3}$ 

$^{248}$ Es

$\rightarrow^{244}$ Bk

7.16 2 $^-$ 

$\#$ 

$\rightarrow$ (4

$^-$ )

2 1.6 $\times10^{3}$ 

2.3 $\times10^{-3}$ 

5.8 $\times10^{5}$ 

6.9 $\times10^{5}$ 

$^{245}$ Es

$\rightarrow^{241}$ Bk

$^p$ 

7.87 (3/2 $^-$ )

$\rightarrow$ (3/2

$^-$ )

0 1.9 $\times10^{0}$ 

1.9 $\times10^{-2}$ 

1.6 $\times10^{2}$ 

1.0 $\times10^{2}$ 

$^{253}$ Es

$\rightarrow^{249}$ Bk

6.74 7/2 $^+$ 

$\rightarrow$ 7/2

$^+$ 

0 6.0 $\times10^{4}$ 

1.4 $\times10^{-2}$ 

1.8 $\times10^{6}$ 

4.4 $\times10^{6}$ 

$^{255}$ Es

$\rightarrow^{251}$ Bk

$^m$ 

6.40 (7/2 $^+$ )

$\rightarrow$ 7/2

$^+$ 

$\#$ 

0 2.0 $\times10^{6}$ 

1.3 $\times10^{-2}$ 

4.3 $\times10^{7}$ 

1.6 $\times10^{8}$ 

$^{252}$ Es

$\rightarrow^{248}$ Bk

6.79 (4 $^+$ )

$\rightarrow$ 6

$^+$ 

$\#$ 

2 6.3 $\times10^{4}$ 

1.8 $\times10^{-3}$ 

5.2 $\times10^{7}$ 

3.6 $\times10^{7}$ 

$^{254}$ Es

$^m$ 

$\rightarrow^{250}$ Bk

6.70 2 $^+$ 

$\rightarrow$ 

$^-$ 2

1 9.0 $\times10^{4}$ 

2.2 $\times10^{-3}$ 

4.4 $\times10^{7}$ 

4.1 $\times10^{7}$ 

$^{243}$ Es

$\rightarrow^{239}$ Bk

$^p$ 

8.04 (7/2 $^+$ )

$\rightarrow$ (3/2

$^-$ )

3 1.6 $\times10^{0}$ 

8.8 $\times10^{-3}$ 

3.5 $\times10^{1}$ 

1.8 $\times10^{2}$ 

$^{252}$ Fm

$\rightarrow^{248}$ Cf

7.15 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.5 $\times10^{3}$ 

3.1 $\times10^{-2}$ 

9.1 $\times10^{4}$ 

8.1 $\times10^{4}$ 

$^{244}$ Fm

$\rightarrow^{240}$ Cf

8.55 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 2.4 $\times10^{-2}$ 

4.0 $\times10^{-2}$ 

7.8 $\times10^{-1}$ 

6.0 $\times10^{-1}$ 

$^{247}$ Fm

$^m$ 

$\rightarrow^{243}$ Cf

8.31 (1/2 $^+$ )

$\rightarrow$ (1/2

$^+$ )

0 1.3 $\times10^{-1}$ 

1.6 $\times10^{-2}$ 

5.8 $\times10^{0}$ 

8.2 $\times10^{0}$ 

$^{253}$ Fm

$\rightarrow^{249}$ Cf

$^m$ 

7.05 (1/2) $^+$ 

$\rightarrow$ 5/2

$^+$ 

2 1.1 $\times10^{4}$ 

6.5 $\times10^{-3}$ 

2.1 $\times10^{6}$ 

1.7 $\times10^{6}$ 

$^{248}$ Fm

$\rightarrow^{244}$ Cf

8.00 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.5 $\times10^{0}$ 

3.5 $\times10^{-2}$ 

3.6 $\times10^{1}$ 

4.4 $\times10^{1}$ 

$^{254}$ Fm

$\rightarrow^{250}$ Cf

7.31 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 4.8 $\times10^{2}$ 

3.0 $\times10^{-2}$ 

1.2 $\times10^{4}$ 

1.6 $\times10^{4}$ 

$^{257}$ Fm

$\rightarrow^{253}$ Cf

6.86 (9/2 $^+$ )

$\rightarrow$ (7/2

$^+$ )

2 5.9 $\times10^{4}$ 

5.6 $\times10^{-3}$ 

8.7 $\times10^{6}$ 

1.1 $\times10^{7}$ 

$^{256}$ Fm

$\rightarrow^{252}$ Cf

7.03 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 7.0 $\times10^{3}$ 

2.9 $\times10^{-2}$ 

1.2 $\times10^{5}$ 

2.4 $\times10^{5}$ 

$^{243}$ Fm

$\rightarrow^{239}$ Cf

8.70 7/2 $^-$ 

$\#$ 

$\rightarrow$ 5/2

$^+$ 

$\#$ 

1 1.1 $\times10^{-2}$ 

1.5 $\times10^{-2}$ 

2.5 $\times10^{-1}$ 

7.1 $\times10^{-1}$ 

$^{247}$ Fm

$\rightarrow^{243}$ Cf

8.26 (7/2 $^+$ )

$\rightarrow$ (1/2

$^+$ )

4 1.0 $\times10^{0}$ 

4.9 $\times10^{-3}$ 

4.8 $\times10^{1}$ 

2.1 $\times10^{2}$ 

$^{251}$ Fm

$\rightarrow^{247}$ Cf

7.43 (9/2 $^-$ )

$\rightarrow$ 7/2

$^+$ 

$\#$ 

1 2.3 $\times10^{2}$ 

9.8 $\times10^{-3}$ 

1.1 $\times10^{6}$ 

2.4 $\times10^{4}$ 

$^{247}$ Md

$\rightarrow^{243}$ Es

8.77 (7/2 $^-$ )

$\rightarrow$ (7/2

$^+$ )

1 1.2 $\times10^{-2}$ 

1.1 $\times10^{-2}$ 

1.2 $\times10^{0}$ 

1.1 $\times10^{0}$ 

$^{247}$ Md

$^m$ 

$\rightarrow^{243}$ Es

9.03 (1/2 $^-$ )

$\rightarrow$ (7/2

$^+$ )

3 4.5 $\times10^{-3}$ 

6.4 $\times10^{-3}$ 

3.1 $\times10^{-1}$ 

7.1 $\times10^{-1}$ 

$^{251}$ Md

$\rightarrow^{247}$ Es

7.96 (7/2 $^-$ )

$\rightarrow$ (7/2

$^+$ )

1 5.3 $\times10^{0}$ 

9.2 $\times10^{-3}$ 

2.5 $\times10^{3}$ 

5.8 $\times10^{2}$ 

$^{249}$ Md

$^m$ 

$\rightarrow^{245}$ Es

8.54 (1/2 $^-$ )

$\rightarrow$ (3/2

$^-$ )

2 8.8 $\times10^{-2}$ 

7.6 $\times10^{-3}$ 

1.9 $\times10^{0}$ 

1.2 $\times10^{1}$ 

$^{253}$ Md

$\rightarrow^{249}$ Es

7.57 (7/2 $^-$ )

$\rightarrow$ 7/2

$^+$ 

1 1.6 $\times10^{2}$ 

8.4 $\times10^{-3}$ 

1.2 $\times10^{5}$ 

1.9 $\times10^{4}$ 

$^{256}$ Md

$^m$ 

$\rightarrow^{252}$ Es

7.91 (1 $^-$ )

$\rightarrow$ (4

$^+$ )

3 1.6 $\times10^{1}$ 

9.6 $\times10^{-4}$ 

5.0 $\times10^{4}$ 

1.6 $\times10^{4}$ 

$^{257}$ Md

$\rightarrow^{253}$ Es

7.56 (7/2 $^-$ )

$\rightarrow$ 7/2

$^+$ 

1 1.4 $\times10^{2}$ 

7.3 $\times10^{-3}$ 

1.3 $\times10^{5}$ 

1.9 $\times10^{4}$ 

$^{258}$ Md

$\rightarrow^{254}$ Es

7.27 8 $^-$ 

$\#$ 

$\rightarrow$ (7

$^+$ )

1 1.9 $\times10^{3}$ 

1.7 $\times10^{-3}$ 

4.4 $\times10^{6}$ 

1.1 $\times10^{6}$ 

$^{255}$ Md

$\rightarrow^{251}$ Es

7.91 (7/2 $^-$ )

$\rightarrow$ 3/2

$^-$ 

2 9.7 $\times10^{0}$ 

5.6 $\times10^{-3}$ 

2.3 $\times10^{4}$ 

1.7 $\times10^{3}$ 

Continued on next page Table 3-continued from previous page parent $\rightarrow$ daughter

$Q\alpha$ 

$j_p^\pi\rightarrow j_d^\pi$ 

l $T^{\rm cal}_{1/2,P_\alpha=1}$ 

$P_\alpha^{\rm cal}$ 

$T_{1/2}^{\rm exp}$ 

$T_{1/2}^{\rm cal}$ 

$^{254}$ No

$\rightarrow^{250}$ Fm

8.23 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.1 $\times10^{0}$ 

2.4 $\times10^{-2}$ 

5.7 $\times10^{1}$ 

4.6 $\times10^{1}$ 

$^{259}$ No

$\rightarrow^{255}$ Fm

7.85 (9/2 $^+$ )

$\rightarrow$ 7/2

$^+$ 

2 3.4 $\times10^{1}$ 

4.6 $\times10^{-3}$ 

4.6 $\times10^{3}$ 

7.4 $\times10^{3}$ 

$^{256}$ No

$\rightarrow^{252}$ Fm

8.58 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 6.7 $\times10^{-2}$ 

2.3 $\times10^{-2}$ 

2.9 $\times10^{0}$ 

3.0 $\times10^{0}$ 

$^{251}$ No

$^m$ 

$\rightarrow^{247}$ Fm

$^m$ 

8.82 (1/2 $^+$ )

$\rightarrow$ (1/2

$^+$ )

0 1.5 $\times10^{-2}$ 

1.2 $\times10^{-2}$ 

1.0 $\times10^{0}$ 

1.3 $\times10^{0}$ 

$^{258}$ No

$\rightarrow^{254}$ Fm

8.15 0 $^+$ 

$\rightarrow$ 0

$^+$ 

0 1.8 $\times10^{0}$ 

2.2 $\times10^{-2}$ 

1.2 $\times10^{2}$ 

8.0 $\times10^{1}$ 

$^{255}$ No

$\rightarrow^{251}$ Fm

$^m$ 

8.23 (1/2 $^+$ )

$\rightarrow$ 5/2

$^+$ 

2 1.7 $\times10^{0}$ 

5.3 $\times10^{-3}$ 

6.9 $\times10^{2}$ 

3.2 $\times10^{2}$ 

$^{251}$ No

$\rightarrow^{247}$ Fm

8.76 (7/2 $^+$ )

$\rightarrow$ (7/2

$^+$ )

0 2.3 $\times10^{-2}$ 

1.2 $\times10^{-2}$ 

9.6 $\times10^{-1}$ 

1.9 $\times10^{0}$ 

$^{253}$ No

$\rightarrow^{249}$ Fm

8.42 (9/2 $^-$ )

$\rightarrow$ (7/2

$^+$ )

1 3.3 $\times10^{-1}$ 

7.9 $\times10^{-3}$ 

1.7 $\times10^{2}$ 

4.2 $\times10^{1}$ 

$^{255}$ Lr

$\rightarrow^{251}$ Md

$^p$ 

8.50 (1/2 $^-$ )

$\rightarrow$ (1/2

$^-$ )

0 2.9 $\times10^{-1}$ 

9.2 $\times10^{-3}$ 

3.1 $\times10^{1}$ 

3.2 $\times10^{1}$ 

$^{257}$ Lr

$\rightarrow^{253}$ Md

9.08 (1/2 $^-$ )

$\rightarrow$ (7/2

$^-$ )

4 2.1 $\times10^{-2}$ 

2.4 $\times10^{-3}$ 

6.0 $\times10^{0}$ 

8.6 $\times10^{0}$ 

$^{259}$ Lr

$\rightarrow^{255}$ Md

$^p$ 

8.58 1/2 $^-$ 

$\#$ 

$\rightarrow$ 1/2

$^-$ 

$\#$ 

0 1.5 $\times10^{-1}$ 

8.2 $\times10^{-3}$ 

7.9 $\times10^{0}$ 

1.8 $\times10^{1}$ 

$^{253}$ Lr

$^m$ 

$\rightarrow^{249}$ Md

$^m$ 

8.86 (1/2 $^-$ )

$\rightarrow$ (1/2

$^-$ )

0 2.4 $\times10^{-2}$ 

1.0 $\times10^{-2}$ 

1.5 $\times10^{0}$ 

2.4 $\times10^{0}$ 

$^{253}$ Lr

$\rightarrow^{249}$ Md

8.93 (7/2 $^-$ )

$\rightarrow$ (7/2

$^-$ )

0 1.5 $\times10^{-2}$ 

1.0 $\times10^{-2}$ 

7.0 $\times10^{-1}$ 

1.5 $\times10^{0}$ 

The predictions of
$ \alpha $ -decay half-lives of actinide elements within GLDM adding the$ \alpha $ preformation factor calculated by our improved formula are shown in Table 4, which may be useful in future experiments. Specifically, the experimental$ \alpha $ -decay half-lives of two new isotopes,$ ^{219} $ Np and$ ^{220} $ Np, are 1.50$ \times10^{-4} $ [49] and 2.50$ \times10^{-5} $ s [50]; the calculated$ \alpha $ -decay half-lives are 2.52$ \times10^{-4} $ and 3.4$ \times10^{-5} $ s, respectively. This shows excellent accuracy, indicating that the predictions with our formula are more reliable.parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

$^{195}$ Ac

$\rightarrow$ 

$^{191}$ Fr

5/2 $^+$ 

$\rightarrow$ 5/2

$^+$ 

9.32 0 2.7 $\times10^{-6}$ 

$^{251}$ Cm

$\rightarrow$ 

$^{247}$ Pu

1/2 $^+$ 

$\rightarrow$ 7/2

$^+$ 

5.21 4 6.9 $\times10^{14}$ 

$^{197}$ Ac

$\rightarrow$ 

$^{193}$ Fr

11/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

9.23 3 2.9 $\times10^{-5}$ 

$^{252}$ Cm

$\rightarrow$ 

$^{248}$ Pu

0 $^+$ 

$\rightarrow$ 0

$^+$ 

5.09 0 6.4 $\times10^{13}$ 

$^{199}$ Ac

$\rightarrow$ 

$^{195}$ Fr

5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

9.03 1 2.7 $\times10^{-5}$ 

$^{253}$ Cm

$\rightarrow$ 

$^{249}$ Pu

11/2 $^-$ 

$\rightarrow$ 1/2

$^+$ 

4.77 5 3.2 $\times10^{18}$ 

$^{201}$ Ac

$\rightarrow$ 

$^{197}$ Fr

5/2 $^-$ 

$\rightarrow$ 11/2

$^+$ 

8.9 3 2.0 $\times10^{-4}$ 

$^{254}$ Cm

$\rightarrow$ 

$^{250}$ Pu

0 $^+$ 

$\rightarrow$ 0

$^+$ 

4.49 0 1.7 $\times10^{18}$ 

$^{203}$ Ac

$\rightarrow$ 

$^{199}$ Fr

7/2 $^-$ 

$\rightarrow$ 11/2

$^+$ 

8.58 3 1.5 $\times10^{-3}$ 

$^{255}$ Cm

$\rightarrow$ 

$^{251}$ Pu

1/2 $^+$ 

$\rightarrow$ 11/2

$^-$ 

4.18 5 2.3 $\times10^{23}$ 

$^{209}$ Ac

$\rightarrow$ 

$^{205}$ Fr

7/2 $^-$ 

$\rightarrow$ 13/2

$^+$ 

7.51 3 3.4 $\times10^{0}$ 

$^{231}$ Bk

$\rightarrow$ 

$^{227}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

8.81 2 4.2 $\times10^{-2}$ 

$^{213}$ Ac

$\rightarrow$ 

$^{209}$ Fr

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

7.44 2 2.3 $\times10^{0}$ 

$^{233}$ Bk

$\rightarrow$ 

$^{229}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

8.17 2 4.1 $\times10^{0}$ 

$^{229}$ Ac

$\rightarrow$ 

$^{225}$ Fr

3/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

4.44 0 6.4 $\times10^{14}$ 

$^{235}$ Bk

$\rightarrow$ 

$^{231}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

7.87 2 3.8 $\times10^{1}$ 

$^{231}$ Ac

$\rightarrow$ 

$^{227}$ Fr

1/2 $^-$ 

$\rightarrow$ 3/2

$^+$ 

3.53 1 3.1 $\times10^{23}$ 

$^{237}$ Bk

$\rightarrow$ 

$^{233}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

7.52 2 7.3 $\times10^{2}$ 

$^{233}$ Ac

$\rightarrow$ 

$^{229}$ Fr

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

3.18 2 1.1 $\times10^{28}$ 

$^{239}$ Bk

$\rightarrow$ 

$^{235}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

7.14 2 2.4 $\times10^{4}$ 

$^{203}$ Th

$\rightarrow$ 

$^{199}$ Ra

1/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

8.83 2 3.4 $\times10^{-4}$ 

$^{241}$ Bk

$\rightarrow$ 

$^{237}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

6.8 2 7.2 $\times10^{5}$ 

$^{204}$ Th

$\rightarrow$ 

$^{200}$ Ra

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.77 0 1.2 $\times10^{-4}$ 

$^{243}$ Bk

$\rightarrow$ 

$^{239}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

6.51 2 1.6 $\times10^{7}$ 

$^{205}$ Th

$\rightarrow$ 

$^{201}$ Ra

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

8.58 2 1.7 $\times10^{-3}$ 

$^{249}$ Bk

$\rightarrow$ 

$^{245}$ Am

7/2 $^+$ 

$\rightarrow$ 5/2

$^-$ 

5.43 1 6.4 $\times10^{12}$ 

$^{206}$ Th

$\rightarrow$ 

$^{202}$ Ra

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.52 0 5.6 $\times10^{-4}$ 

$^{251}$ Bk

$\rightarrow$ 

$^{247}$ Am

7/2 $^+$ 

$\rightarrow$ 5/2

$^-$ 

5.74 1 9.2 $\times10^{10}$ 

$^{207}$ Th

$\rightarrow$ 

$^{203}$ Ra

1/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

8.21 2 2.1 $\times10^{-2}$ 

$^{253}$ Bk

$\rightarrow$ 

$^{249}$ Am

3/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

5.45 2 1.0 $\times10^{13}$ 

$^{210}$ Th

$\rightarrow$ 

$^{206}$ Ra

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.81 0 6.9 $\times10^{-2}$ 

$^{233}$ Cf

$\rightarrow$ 

$^{229}$ Cm

1/2 $^-$ 

$\rightarrow$ 3/2

$^-$ 

8.59 2 4.8 $\times10^{-1}$ 

$^{211}$ Th

$\rightarrow$ 

$^{207}$ Ra

1/2 $^-$ 

$\rightarrow$ 1/2

$^-$ 

7.66 0 3.9 $\times10^{-1}$ 

$^{234}$ Cf

$\rightarrow$ 

$^{230}$ Cm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.67 0 4.8 $\times10^{-2}$ 

$^{213}$ Th

$\rightarrow$ 

$^{209}$ Ra

3/2 $^-$ 

$\rightarrow$ 1/2

$^-$ 

7.64 2 1.2 $\times10^{0}$ 

$^{235}$ Cf

$\rightarrow$ 

$^{231}$ Cm

3/2 $^+$ 

$\rightarrow$ 1/2

$^-$ 

8.54 1 3.3 $\times10^{-1}$ 

Continued on next page Table 4. The
$\alpha$ -decay energy is calculated by the finite-range droplet model (FRDM); the spin and parity of nuclei are taken from the calculations of odd-nucleon spin and parity at the nuclear ground state by Möller [47, 48]. The$\alpha$ -decay energy and half-lives are in units of MeV and s, respectively.Table 4-continued from previous page parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

$^{233}$ Th

$\rightarrow$ 

$^{229}$ Ra

7/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

3.72 1 1.5 $\times10^{22}$ 

$^{236}$ Cf

$\rightarrow$ 

$^{232}$ Cm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.34 0 4.4 $\times10^{-1}$ 

$^{234}$ Th

$\rightarrow$ 

$^{230}$ Ra

0 $^+$ 

$\rightarrow$ 0

$^+$ 

3.58 0 1.0 $\times10^{23}$ 

$^{239}$ Cf

$\rightarrow$ 

$^{235}$ Cm

5/2 $^+$ 

$\rightarrow$ 5/2

$^-$ 

7.63 1 4.3 $\times10^{2}$ 

$^{235}$ Th

$\rightarrow$ 

$^{231}$ Ra

1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

3.34 3 1.2 $\times10^{27}$ 

$^{257}$ Cf

$\rightarrow$ 

$^{253}$ Cm

1/2 $^+$ 

$\rightarrow$ 11/2

$^-$ 

5.1 5 1.5 $\times10^{17}$ 

$^{205}$ Pa

$\rightarrow$ 

$^{201}$ Ac

3/2 $^+$ 

$\rightarrow$ 5/2

$^-$ 

8.97 1 1.9 $\times10^{-4}$ 

$^{258}$ Cf

$\rightarrow$ 

$^{254}$ Cm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

4.73 0 3.6 $\times10^{17}$ 

$^{207}$ Pa

$\rightarrow$ 

$^{203}$ Ac

5/2 $^-$ 

$\rightarrow$ 7/2

$^-$ 

8.77 2 1.1 $\times10^{-3}$ 

$^{259}$ Cf

$\rightarrow$ 

$^{255}$ Cm

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

4.49 2 3.1 $\times10^{20}$ 

$^{209}$ Pa

$\rightarrow$ 

$^{205}$ Ac

5/2 $^-$ 

$\rightarrow$ 7/2

$^-$ 

8.31 2 2.4 $\times10^{-2}$ 

$^{260}$ Cf

$\rightarrow$ 

$^{256}$ Cm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

4.39 0 2.2 $\times10^{20}$ 

$^{211}$ Pa

$\rightarrow$ 

$^{207}$ Ac

7/2 $^-$ 

$\rightarrow$ 7/2

$^-$ 

8.13 0 2.9 $\times10^{-2}$ 

$^{235}$ Es

$\rightarrow$ 

$^{231}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

9.02 3 1.1 $\times10^{-1}$ 

$^{219}$ Pa

$\rightarrow$ 

$^{215}$ Ac

5/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

10.48 0 1.6 $\times10^{-8}$ 

$^{237}$ Es

$\rightarrow$ 

$^{233}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

8.65 3 1.4 $\times10^{0}$ 

$^{233}$ Pa

$\rightarrow$ 

$^{229}$ Ac

3/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

4.33 0 8.5 $\times10^{16}$ 

$^{239}$ Es

$\rightarrow$ 

$^{235}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

8.16 3 5.9 $\times10^{1}$ 

$^{235}$ Pa

$\rightarrow$ 

$^{231}$ Ac

1/2 $^+$ 

$\rightarrow$ 1/2

$^-$ 

3.94 1 3.8 $\times10^{20}$ 

$^{241}$ Es

$\rightarrow$ 

$^{237}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

7.83 3 9.1 $\times10^{2}$ 

$^{237}$ Pa

$\rightarrow$ 

$^{233}$ Ac

1/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

3.57 2 5.6 $\times10^{24}$ 

$^{251}$ Es

$\rightarrow$ 

$^{247}$ Bk

3/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

6.47 3 6.0 $\times10^{8}$ 

$^{212}$ U

$\rightarrow$ 

$^{208}$ Th

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.37 0 7.6 $\times10^{-3}$ 

$^{257}$ Es

$\rightarrow$ 

$^{253}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

5.95 3 2.9 $\times10^{11}$ 

$^{213}$ U

$\rightarrow$ 

$^{209}$ Th

1/2 $^-$ 

$\rightarrow$ 1/2

$^-$ 

8.39 0 1.1 $\times10^{-2}$ 

$^{259}$ Es

$\rightarrow$ 

$^{255}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

5.27 3 4.1 $\times10^{15}$ 

$^{214}$ U

$\rightarrow$ 

$^{210}$ Th

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.45 0 4.0 $\times10^{-3}$ 

$^{261}$ Es

$\rightarrow$ 

$^{257}$ Bk

7/2 $^+$ 

$\rightarrow$ 3/2

$^-$ 

4.86 3 3.5 $\times10^{18}$ 

$^{215}$ U

$\rightarrow$ 

$^{211}$ Th

3/2 $^-$ 

$\rightarrow$ 1/2

$^-$ 

8.33 2 4.3 $\times10^{-2}$ 

$^{239}$ Fm

$\rightarrow$ 

$^{235}$ Cf

5/2 $^-$ 

$\rightarrow$ 3/2

$^+$ 

8.85 1 2.3 $\times10^{-1}$ 

$^{217}$ U

$\rightarrow$ 

$^{213}$ Th

1/2 $^-$ 

$\rightarrow$ 3/2

$^-$ 

8.51 2 1.2 $\times10^{-2}$ 

$^{240}$ Fm

$\rightarrow$ 

$^{236}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.61 0 4.1 $\times10^{-1}$ 

$^{220}$ U

$\rightarrow$ 

$^{216}$ Th

0 $^+$ 

$\rightarrow$ 0

$^+$ 

10.63 0 8.7 $\times10^{-9}$ 

$^{241}$ Fm

$\rightarrow$ 

$^{237}$ Cf

1/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

8.41 2 1.1 $\times10^{1}$ 

$^{223}$ U

$\rightarrow$ 

$^{219}$ Th

1/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

8.52 2 4.6 $\times10^{-3}$ 

$^{242}$ Fm

$\rightarrow$ 

$^{238}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.29 0 4.6 $\times10^{0}$ 

$^{228}$ U

$\rightarrow$ 

$^{224}$ Th

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.13 0 2.2 $\times10^{1}$ 

$^{245}$ Fm

$\rightarrow$ 

$^{241}$ Cf

1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

8.09 3 2.7 $\times10^{2}$ 

$^{235}$ U

$\rightarrow$ 

$^{231}$ Th

7/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

4.52 1 1.5 $\times10^{16}$ 

$^{246}$ Fm

$\rightarrow$ 

$^{242}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.9 0 9.4 $\times10^{1}$ 

$^{237}$ U

$\rightarrow$ 

$^{233}$ Th

1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

4.3 3 5.1 $\times10^{18}$ 

$^{249}$ Fm

$\rightarrow$ 

$^{245}$ Cf

7/2 $^+$ 

$\rightarrow$ 5/2

$^+$ 

7.39 2 6.1 $\times10^{4}$ 

$^{239}$ U

$\rightarrow$ 

$^{235}$ Th

5/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

3.9 2 1.0 $\times10^{22}$ 

$^{250}$ Fm

$\rightarrow$ 

$^{246}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.15 0 8.3 $\times10^{4}$ 

$^{240}$ U

$\rightarrow$ 

$^{236}$ Th

0 $^+$ 

$\rightarrow$ 0

$^+$ 

3.74 0 4.6 $\times10^{22}$ 

$^{255}$ Fm

$\rightarrow$ 

$^{251}$ Cf

11/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

7.22 3 6.9 $\times10^{5}$ 

$^{213}$ Np

$\rightarrow$ 

$^{209}$ Pa

5/2 $^-$ 

$\rightarrow$ 5/2

$^-$ 

8.9 0 9.1 $\times10^{-4}$ 

$^{258}$ Fm

$\rightarrow$ 

$^{254}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

6.4 0 1.9 $\times10^{8}$ 

$^{215}$ Np

$\rightarrow$ 

$^{211}$ Pa

11/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

8.82 3 7.9 $\times10^{-3}$ 

$^{259}$ Fm

$\rightarrow$ 

$^{255}$ Cf

1/2 $^+$ 

$\rightarrow$ 9/2

$^+$ 

6.05 4 7.6 $\times10^{11}$ 

$^{217}$ Np

$\rightarrow$ 

$^{213}$ Pa

11/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

8.73 3 1.4 $\times10^{-2}$ 

$^{260}$ Fm

$\rightarrow$ 

$^{256}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

5.68 0 1.7 $\times10^{12}$ 

$^{220}$ Np

$\rightarrow$ 

$^{216}$ Pa

$^a$ 

1 $^-$ 

$\#$ 

$\rightarrow$ 5

$^+$ 

$\#$ 

10.23 5 3.4 $\times10^{-5}$ 

$^{261}$ Fm

$\rightarrow$ 

$^{257}$ Cf

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

5.47 2 3.1 $\times10^{14}$ 

$^{221}$ Np

$\rightarrow$ 

$^{217}$ Pa

1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

10.65 3 1.8 $\times10^{-7}$ 

$^{262}$ Fm

$\rightarrow$ 

$^{258}$ Cf

0 $^+$ 

$\rightarrow$ 0

$^+$ 

5.31 0 3.6 $\times10^{14}$ 

$^{223}$ Np

$\rightarrow$ 

$^{219}$ Pa

7/2 $^+$ 

$\rightarrow$ 5/2

$^-$ 

9.18 1 9.2 $\times10^{-5}$ 

$^{241}$ Md

$\rightarrow$ 

$^{237}$ Es

7/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

9.27 1 3.3 $\times10^{-2}$ 

$^{241}$ Np

$\rightarrow$ 

$^{237}$ Pa

5/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

4.24 2 3.4 $\times10^{19}$ 

$^{243}$ Md

$\rightarrow$ 

$^{239}$ Es

7/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

9.01 1 1.9 $\times10^{-1}$ 

$^{219}$ Np

$\rightarrow$ 

$^{215}$ Pa

$^a$ 

9/2 $^-$ #

$\rightarrow$ 9/2

$^-$ 

$\#$ 

9.21 0 2.52 $\times10^{-4}$ 

$^{245}$ Md

$\rightarrow$ 

$^{241}$ Es

7/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

8.93 1 3.2 $\times10^{-1}$ 

$^{222}$ Pu

$\rightarrow$ 

$^{218}$ U

0 $^+$ 

$\rightarrow$ 0

$^+$ 

10.87 0 1.3 $\times10^{-8}$ 

$^{259}$ Md

$\rightarrow$ 

$^{255}$ Es

7/2 $^-$ 

$\rightarrow$ 3/2

$^-$ 

6.84 2 4.0 $\times10^{7}$ 

$^{223}$ Pu

$\rightarrow$ 

$^{219}$ U

3/2 $^+$ 

$\rightarrow$ 9/2

$^+$ 

10.06 4 1.6 $\times10^{-5}$ 

$^{261}$ Md

$\rightarrow$ 

$^{257}$ Es

7/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

6.12 1 7.8 $\times10^{10}$ 

$^{224}$ Pu

$\rightarrow$ 

$^{220}$ U

0 $^+$ 

$\rightarrow$ 0

$^+$ 

9.57 0 7.0 $\times10^{-6}$ 

$^{263}$ Md

$\rightarrow$ 

$^{259}$ Es

7/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

5.67 1 2.5 $\times10^{13}$ 

$^{225}$ Pu

$\rightarrow$ 

$^{221}$ U

1/2 $^+$ 

$\rightarrow$ 3/2

$^+$ 

9.29 2 1.8 $\times10^{-4}$ 

$^{246}$ No

$\rightarrow$ 

$^{242}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

9.47 0 6.6 $\times10^{-3}$ 

$^{226}$ Pu

$\rightarrow$ 

$^{222}$ U

0 $^+$ 

$\rightarrow$ 0

$^+$ 

9.04 0 1.3 $\times10^{-4}$ 

$^{247}$ No

$\rightarrow$ 

$^{243}$ Fm

1/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

9.34 3 2.0 $\times10^{-1}$ 

$^{227}$ Pu

$\rightarrow$ 

$^{223}$ U

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

8.7 2 6.4 $\times10^{-3}$ 

$^{248}$ No

$\rightarrow$ 

$^{244}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

9.21 0 3.7 $\times10^{-2}$ 

$^{229}$ Pu

$\rightarrow$ 

$^{225}$ U

1/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

8.15 3 6.1 $\times10^{-1}$ 

$^{249}$ No

$\rightarrow$ 

$^{245}$ Fm

5/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

9.04 2 7.4 $\times10^{-1}$ 

$^{237}$ Pu

$\rightarrow$ 

$^{233}$ U

7/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

5.56 1 2.0 $\times10^{10}$ 

$^{250}$ No

$\rightarrow$ 

$^{246}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.89 0 3.3 $\times10^{-1}$ 

$^{243}$ Pu

$\rightarrow$ 

$^{239}$ U

7/2 $^+$ 

$\rightarrow$ 5/2

$^+$ 

4.64 2 7.7 $\times10^{16}$ 

$^{252}$ No

$\rightarrow$ 

$^{248}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.37 0 1.6 $\times10^{1}$ 

$^{245}$ Pu

$\rightarrow$ 

$^{241}$ U

9/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

4.26 1 4.4 $\times10^{19}$ 

$^{257}$ No

$\rightarrow$ 

$^{253}$ Fm

11/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

8.34 3 3.1 $\times10^{2}$ 

Continued on next page Table 4-continued from previous page parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

parent $\rightarrow$ daughter

$j_p\rightarrow j_d$ 

Q $_\alpha$ 

l $T_{1/2}^{\rm cal}$ 

$^{246}$ Pu

$\rightarrow$ 

$^{242}$ U

0 $^+$ 

$\rightarrow$ 0

$^+$ 

4.18 0 4.9 $\times10^{19}$ 

$^{260}$ No

$\rightarrow$ 

$^{256}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.38 0 6.7 $\times10^{4}$ 

$^{223}$ Am

$\rightarrow$ 

$^{219}$ Np

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

10.88 2 1.3 $\times10^{-7}$ 

$^{261}$ No

$\rightarrow$ 

$^{257}$ Fm

1/2 $^+$ 

$\rightarrow$ 9/2

$^+$ 

7.03 4 1.1 $\times10^{8}$ 

$^{225}$ Am

$\rightarrow$ 

$^{221}$ Np

5/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

9.9 2 1.3 $\times10^{-5}$ 

$^{262}$ No

$\rightarrow$ 

$^{258}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

6.61 0 1.8 $\times10^{8}$ 

$^{227}$ Am

$\rightarrow$ 

$^{223}$ Np

5/2 $^-$ 

$\rightarrow$ 7/2

$^+$ 

9.35 1 1.4 $\times10^{-4}$ 

$^{263}$ No

$\rightarrow$ 

$^{259}$ Fm

3/2 $^+$ 

$\rightarrow$ 1/2

$^+$ 

6.35 2 2.6 $\times10^{10}$ 

$^{231}$ Am

$\rightarrow$ 

$^{227}$ Np

5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

7.74 1 9.2 $\times10^{0}$ 

$^{264}$ No

$\rightarrow$ 

$^{260}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

6.16 0 3.0 $\times10^{10}$ 

$^{245}$ Am

$\rightarrow$ 

$^{241}$ Np

5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

4.9 1 1.5 $\times10^{15}$ 

$^{265}$ No

$\rightarrow$ 

$^{261}$ Fm

13/2 $^-$ 

$\rightarrow$ 3/2

$^+$ 

6.12 5 9.2 $\times10^{12}$ 

$^{247}$ Am

$\rightarrow$ 

$^{243}$ Np

5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

4.6 1 2.8 $\times10^{17}$ 

$^{266}$ No

$\rightarrow$ 

$^{262}$ Fm

0 $^+$ 

$\rightarrow$ 0

$^+$ 

6.38 0 1.8 $\times10^{9}$ 

$^{249}$ Am

$\rightarrow$ 

$^{245}$ Np

5/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

4.85 1 3.8 $\times10^{15}$ 

$^{247}$ Lr

$\rightarrow$ 

$^{243}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

9.88 1 3.7 $\times10^{-3}$ 

$^{251}$ Am

$\rightarrow$ 

$^{247}$ Np

5/2 $^+$ 

$\rightarrow$ 5/2

$^+$ 

4.68 0 4.1 $\times10^{16}$ 

$^{249}$ Lr

$\rightarrow$ 

$^{245}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

9.54 1 3.3 $\times10^{-2}$ 

$^{229}$ Cm

$\rightarrow$ 

$^{225}$ Pu

3/2 $^-$ 

$\rightarrow$ 1/2

$^+$ 

9.4 1 2.2 $\times10^{-4}$ 

$^{251}$ Lr

$\rightarrow$ 

$^{247}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

9.16 1 4.3 $\times10^{-1}$ 

$^{230}$ Cm

$\rightarrow$ 

$^{226}$ Pu

0 $^+$ 

$\rightarrow$ 0

$^+$ 

8.73 0 5.2 $\times10^{-3}$ 

$^{261}$ Lr

$\rightarrow$ 

$^{257}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

7.72 1 3.4 $\times10^{4}$ 

$^{231}$ Cm

$\rightarrow$ 

$^{227}$ Pu

1/2 $^-$ 

$\rightarrow$ 3/2

$^+$ 

8.39 1 1.7 $\times10^{-1}$ 

$^{263}$ Lr

$\rightarrow$ 

$^{259}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

6.94 1 5.5 $\times10^{7}$ 

$^{232}$ Cm

$\rightarrow$ 

$^{228}$ Pu

0 $^+$ 

$\rightarrow$ 0

$^+$ 

7.89 0 2.3 $\times10^{0}$ 

$^{265}$ Lr

$\rightarrow$ 

$^{261}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

6.47 1 9.9 $\times10^{9}$ 

$^{235}$ Cm

$\rightarrow$ 

$^{231}$ Pu

5/2 $^-$ 

$\rightarrow$ 3/2

$^+$ 

7.28 1 1.1 $\times10^{3}$ 

$^{267}$ Lr

$\rightarrow$ 

$^{263}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

6.78 1 2.8 $\times10^{8}$ 

$^{239}$ Cm

$\rightarrow$ 

$^{235}$ Pu

7/2 $^-$ 

$\rightarrow$ 5/2

$^+$ 

6.54 1 1.8 $\times10^{6}$ 

$^{269}$ Lr

$\rightarrow$ 

$^{265}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

6.8 1 2.1 $\times10^{8}$ 

$^{249}$ Cm

$\rightarrow$ 

$^{245}$ Pu

7/2 $^+$ 

$\rightarrow$ 9/2

$^-$ 

5.36 1 5.0 $\times10^{12}$ 

$^{271}$ Lr

$\rightarrow$ 

$^{267}$ Md

9/2 $^+$ 

$\rightarrow$ 7/2

$^-$ 

6.15 1 4.2 $\times10^{11}$ 

a: the $\alpha$ -decay energy, spin and parity of

$^{220}$ Np and

$^{219}$ Np are from [49] and [50], respectively.

-
In summary, we extracted
$ \alpha $ preformation factors for 606 nuclei in the framework of the GLDM and analyzed the characteristics of$ \alpha $ preformation factors for even-even nuclei from Po to U isotopes. The case of$ N = 126 $ is a well-known magic number, which shows a significant shell closure effect for Po to Th isotopes. However, for U isotopes, the signal of the$ N = 126 $ shell closure effect is weak, implying that$ N = 126 $ may not be the magic number for U isotopes. Based on the previous formula of Zhang et al., we proposed a unified formula with 7 parameters to calculate the$ \alpha $ preformation factor, which is adapted to different types of$ \alpha $ -decay. The coefficients were obtained by fitting the extracted$ \alpha $ preformation factors of 606$ \alpha $ -decay nuclei. The standard deviation of the total 606 nuclei is 0.37 with a factor of 2.3, showing significant precision. Compared with the work of Zhang et al. and Seif et al., our improved formula, Eq. (16), has the fewest parameters, high precision, and a wide application scope. Finally,$ \alpha $ -decay half-lives of actinides were calculated in the framework of GLDM. Taking$ \alpha $ preformation factors into account with our improved formula, the theoretical half-lives are in good agreement with the experimental data, indicating that our improved formula is reliable. The$ \alpha $ -decay half-lives of even-even and odd-A nuclei of actinide were predicted. The predicted$ \alpha $ -decay half-lives of the new isotopes$ ^{219,220}{\rm Np} $ are also in good agreement with the experimental values. The predictions of$ \alpha $ -decay half-lives can provide references for synthesis of new elements and microscopic studies of the nuclear structure. -
We would like to thank J. -G. Deng and K. Wei for valuable discussion.
Improved empirical formula for α particle preformation factor
- Received Date: 2020-07-23
- Available Online: 2021-01-15
Abstract: In this contribution, the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




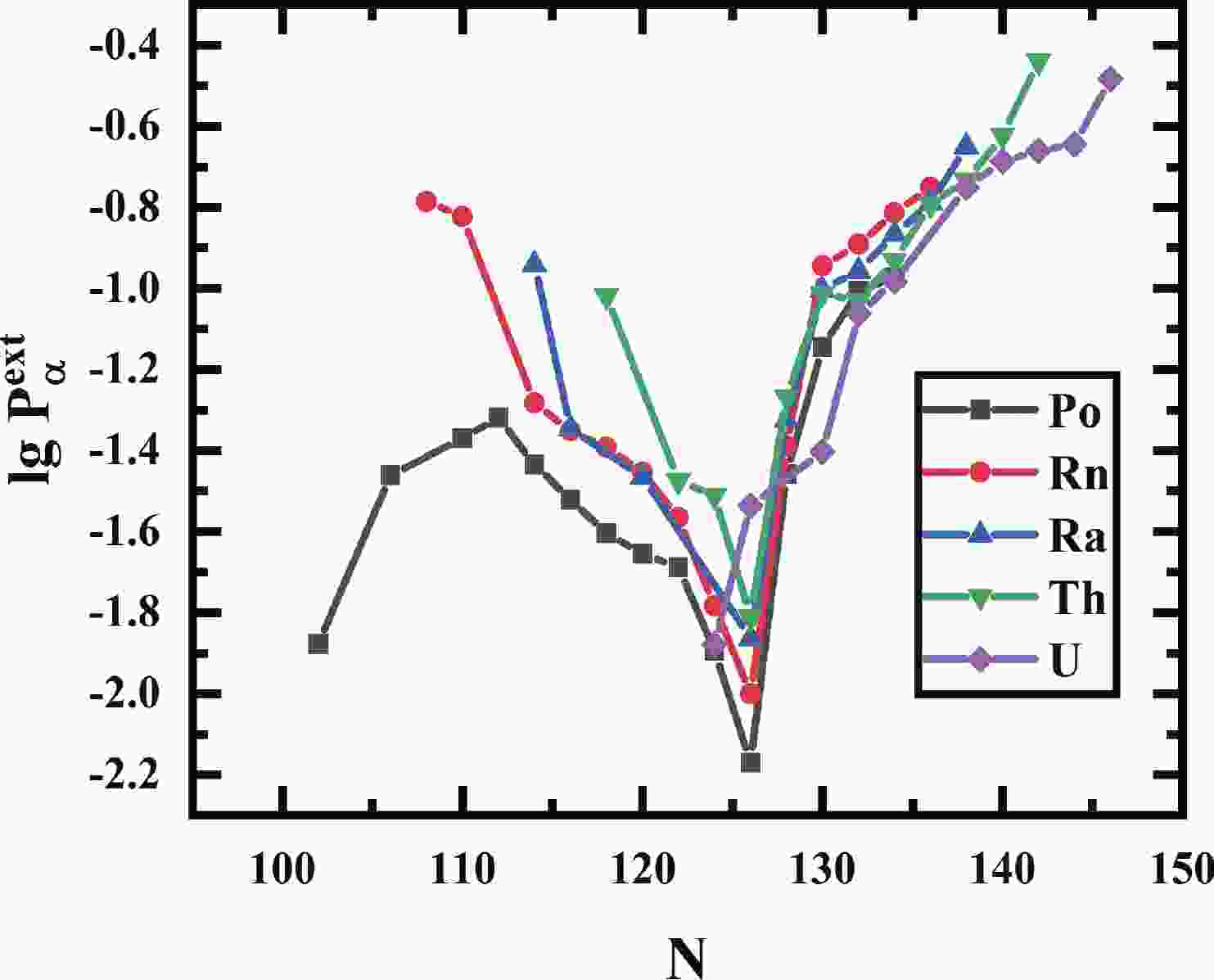





















 DownLoad:
DownLoad: