Orientation dichroism effect of proton scattering on deformed nuclei

The scattering of light or particles by an object of arbitrary shape is of significant importance in many fields in physics. In optics, the anisotropic structure of microscopic particles causes birefringence, which alters the polarization state of the passing light, leading to improvements in polarization microscopy for extensive applications [1–4]. In astrophysics, the discrete dipole approximation (DDA) method has been developed to compute the extinction and scattering of star light by interstellar grains, which are not necessarily spherical in shape [5, 6]. In nanoscience, large local-field enhancement and light-scattering efficiencies have been demonstrated for nanorods and compared to those for metal nanosphere particles, making the former interesting for optical applications [7].

In nuclear physics, experiments involving the scattering of protons and alpha particles on even-even nuclei were conducted in 1970s, leading to the discovery of the large multipole deformation of various even-even nuclei on the $ 0^+ $ ground state [8–10]. For reactions induced by very exotic nuclei, it has been found that the deformation causes the extension of matter distribution and enhances the total reaction cross section in the Glauber model analysis [11]. Very recently, the deformability of ²³⁸U has received increasing attention. In the synthesis of super heavy elements (SHEs) via multi-nucleon transfer mechanisms in $ ^{238} {\rm{U}}$+$ ^{238} {\rm{U}}$, the number of transferred nucleons and the survival probability of the giant system that is formed depend sensitively on the geometric configurations of the projectile and the target, according to the predictions by time-dependent Hartree-Fock (TDHF) theory [12] and the improved quantum molecular dynamics (ImQMD) model [13]. Very recently, the significant orientation effect of the octupole deformed nuclei in fusion reactions has been demonstrated by calculations based on transport models [14]. In relativistic heavy ion collisions (HICs) at RHIC energies, the deformation and orientation effect of the colliding nuclei has also been noticed. It has been shown that the tip-tip configuration of ²³⁸U+²³⁸U collisions is favorable for achieving the largest stopping, while the body-body collisions make it possible to study the initial geometry effect of the flow formation [15–19]. Moreover, the STAR collaboration has succeeded in selecting different overlap geometry configurations of ²³⁸U+²³⁸U in extremely central collisions [20].

On the other hand, the idea of utilizing the deformed nuclei for producing highly compressed nuclear matter or enhancing the probability of synthesizing SHEs will likely be compromised unless the orientation of ²³⁸U can be determined before the collision occurs. For such even-even nuclei at ground state, however, the spin is zero and the conventional way to polarize the nuclei using a magnetic field cannot work effectively. Thus, before one can take advantage of the deformed nuclei, further research on the deformation and orientation effect of the reactions involving deformed nuclei is required.

In this letter, we revisit the scattering process involving the deformed nucleus. Instead of the reactions involving the deformation of the projectile and the target, our motivation is to study the peripheral scattering of a light particle by a deformed nucleus to discern the deformation and orientation effect of the latter owing to the scattering. It is expected that, because of the small mass, the projectile will be deflected easily with the deflection behavior depending sensitively on the deformation and orientation of the target nuclei. If this scenario is true, the deflected light projectile will carry clear information concerning the orientation of the deformed nucleus and potentially lead to novel implications in the usage of deformed nuclei. In contrast to extremely central collisions, peripheral scattering has an additional benefit: neither partners of the colliding system is disintegrated.

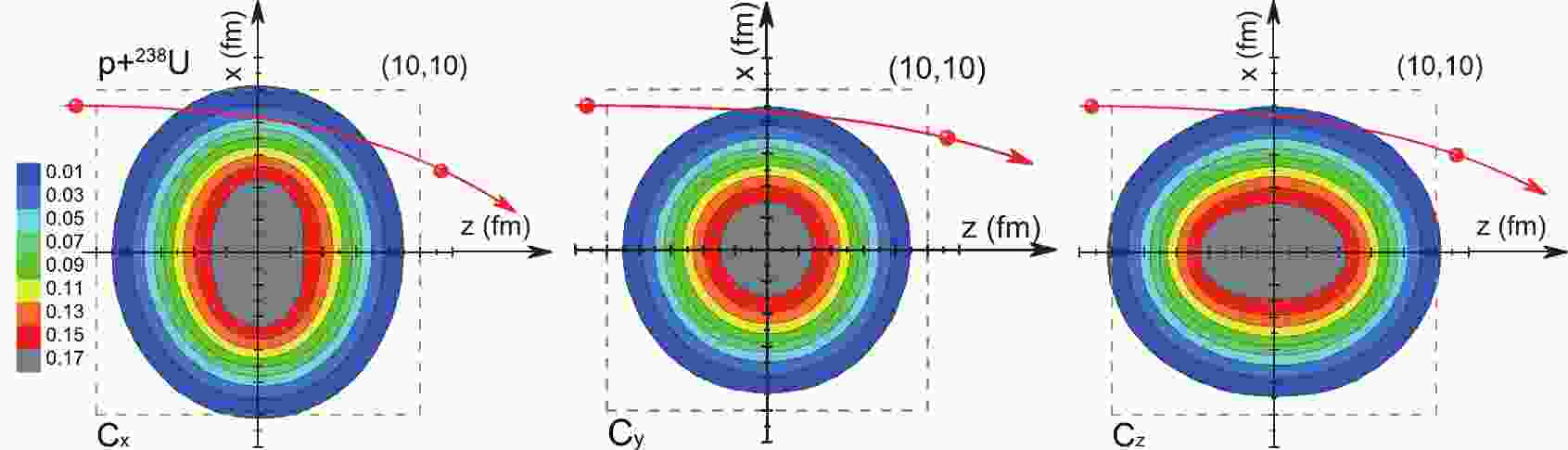
In order to circumvent the complication brought by the structure of the beam nucleus, the proton induced scattering of ²³⁸U is investigated. We use the conventional definition of the coordinator system. The incident direction of the projectile is defined as the z axis and the reaction plane is in the x-z plane in the laboratory. Figure 1 depicts schematically three typical configurations for the scattering of protons by $ ^{238} {\rm{U}}$. The symmetrical long axis of ²³⁸U is parallel to the x, y, and z axes, marked by ${{C}} _{{{x}}} $, C_y, and ${{C}} _{{{z}}} $, respectively. The shape of the ²³⁸U nucleus is represented by its density distribution projected onto the x-z plane with quadrupole deformation $ \beta_2 = 0.236 $ (see text later). It can be viewed that, at a given impact parameter of peripheral scattering, the flight path length $ L_{\rm f} $ of the proton experiencing the field of ²³⁸U is different in the configurations of ${{C}} _{{{x}}} $, C_y, and ${{C}} _{{{z}}} $. For the specific impact parameter $ b = 9 $ fm, as shown in Fig. 1, the $ L_{\rm f} $ in C_x is moderate and the proton penetrates farthest into the target, while the $ L_{\rm f} $ in C_y is the shortest and the proton just grazes the target. Different paths lead to different deflections of the projectile in these special cases, as shown later.

Figure 1.  (color online) Schematic view of three typical configurations, C_x, C_y, and C_z in the x-z plane for the scattering of p+²³⁸U. The contour depicts the density distribution of ²³⁸U projected onto the x-z plane.

The ImQMD model is an extended version of the quantum molecular dynamics model with improvements that make it suitable for describing the transport process for light-particle-induced reactions as well as for HICs in a wide energy range. The model has been applied in nucleon-induced [21, 22] and deuteron-induced reactions [23, 24], leading to the prediction of the isovector orientation effect of polarized deuteron scattering. For the details of the ImQMD model, we refer to the literature [25–27]. As in the above studies, the calculations performed in this study only consider beam energies above 100 MeV, at which the de Broglie wavelength of the beam is much smaller than the radius of the target nucleus, and hence, the effects of target granularity (including its size, shape, surface, etc.) are exhibited. In addition, the validity of the transport model as a semi-classic approach is retained. The maximum energy considered here is 300 MeV, above which the inelastic channels of $ NN $ scattering are open and contribute increasingly.

The initialization of the projectile and target is important to stabilize the properties of the two nuclei in simulating the reaction process. In particular, the aim of this work is to study the orientation effect of deformed heavy nuclei in proton-induced scattering; therefore, special attention should be paid to the shape and orientation of the initial nuclei. For this purpose, the nuclei are sampled according to the density distribution with deformed Fermi form, which reads

where $ a = 0.54 $ fm and

where $ Y(\theta) $ are the spherical harmonics. $ R_0 = 1.142A^{1/3}- 0.60 $ fm for the proton distribution, and $ R_0 $ is multiplied by a factor $ 0.93(N/Z)^{1/3} $ for the neutron distribution to obtain a reasonable neutron skin. Only the quadrupole deformation is considered in this work. The quadrupole deformation parameter is taken as $ \beta_2 = 0.236 $ for $ ^{238} {\rm{U}}$. In this scheme, the symmetrical long axis of the sampled nuclei is parallel to the z axis initially. To initiate a scattering event, the nucleus can be rotated around its center of mass to set the symmetrical long axis parallel to the x axis, y axis, or a random direction. In Fig. 1, the initial density distributions of the nucleons projected onto the x-z plane of ²³⁸U simulated by the ImQMD model for the ${{C}} _{{{x}}} $, C_y, and C_z configurations are presented. The shape and the density distribution are examined up to 200 fm/c, and it is found that they remain sufficiently stable to satisfy the investigation request because the incident proton departs the nuclear field of the target sufficiently far after 200 fm/c in the peripheral scattering at a 100 MeV incident energy.

To visualize the geometry effect of the ²³⁸U target nuclei, we first fix the impact parameter in the simulations. The incident proton is in the x-z plane with the target fixed at the origin point and the impact parameter $ b = x $ when the proton crosses the x-axis, while the orientation of the long axis of ²³⁸U can be varied to investigate the geometrical effect of the scattering. First, the orientation of $ ^{238} {\rm{U}}$ target is fixed in the laboratory frame by hand. Figure 2 presents the angular distribution of the scattered proton at the impact parameter $ b = 9 $ fm for the three geometrical configurations ${{C}} _{{{x}}} $, C_y, and C_z in p+$ ^{238} {\rm{U}}$at 200 MeV beam energy. Nuclear attraction dominates at this impact parameter since the scattering angles are negative, as shown in Fig. 1. To ensure that only elastic or quasi-elastic scattering occurs, the total multiplicity $ M_{\rm t} = 2 $ is required, and one of the outgoing particles must be proton with an energy close to the beam energy. For comparison, the case where the deformed target nucleus is randomly orientated is also calculated, as indicated by $ rand $ in Fig. 2 and elsewhere in the paper. Generally, it is shown that the scattering angle decreases with the beam energy. More interestingly, it is commonly shown that, at all beam energies, the angular deflection distributions exhibit obvious differences between the ${{C}} _{{{x}}} $, C_y, and C_z configurations. The smallest deflection is seen in ${{C}} _{{{y}}} $, i.e., the proton passes near to the waist of the target, with the symmetrical long axis perpendicular to the beam direction, while the largest deflection occurs for the C_x configuration, where the proton traverses the tip of the target and experiences the strongest nuclear attraction. The angular deflection distribution for the C_z configuration is situated between those for C_x and ${{C}} _{{{y}}} $ and is similar to the $ rand $ case, in which the direction of the symmetrical long axis of the target is randomly aligned in the laboratory. The difference between the peak of the angular distributions for the C_x and C_y cases is larger than $ 10^\circ $, which is a large measurable quantity.

Figure 2.  (color online) Angular distribution of the deflected proton in p+²³⁸U with b = 9 fm at 100 (left), 200 (middle), and 300 (right) MeV beam energies for the three configurations C_x, C_y, and C_z, respectively.

It is observed that the discrimination among the three configurations depends on the impact parameter. When the impact parameter decreases, the collision becomes violent, and the competition between nuclear attraction and Coulomb repulsion takes effect and changes the deflective behavior of the proton. Figure 3 presents the angular deflection distribution at various impact parameters for p+$ ^{238} {\rm{U}}$ at a 200 MeV beam energy. It is shown that the cross section of the elastic or quasi-elastic scattering events increases with the impact parameter b. At $ b = 7 $ fm, there are far fewer total events because nucleons or clusters may be dislodged from the target, leading to the opening of inelastic scattering channels. Compared to $ b = 9 $ fm, as shown in Fig. 2, the peaks of the angular distribution at $ b = 8 $ fm for the C_y and C_z configurations move to the right side and are situated close to the C_x and $ rand $ cases. This implies that the length of the interaction path converges in these configurations, with the geometric effect disappearing as the impact parameter is reduced. This trend is even more pronounced for the smaller impact parameter $ b = 7 $ fm. On the contrary, when the impact parameter increases to $ b = 10 $ fm, where the nuclear interaction becomes weaker, the configuration of C_x clearly stands out as showing the largest deflection, while the other configurations typically show much smaller deflections, peaking at very forward angles. This indicates that at larger impact parameter values, the deflection depends mainly on the length of the flight path in the field of the target.

Figure 3.  (color online) Angular distribution of the deflected proton in p+²³⁸U with b = 7 (a), 8 (b), and 10 (c) fm at 200 MeV beam energy for the three configurations C_x, C_y, and C_z, respectively.

It must be pointed out that in real experiments, the azimuth cannot be identified if only the inclusive proton is recorded. We further investigated the effect of the orientation of $ ^{238} {\rm{U}}$ in the transverse plane. Figure 4(a) presents the angular distribution of the deflected proton as a function of the azimuthal angle of the long axis of $ ^{238} {\rm{U}}$ in the x-y plane. Here, $ \phi_{\rm U} $ indicates the angle of the long axis of $ ^{238} {\rm{U}}$ relative to the x axis in the x-y plane. It is seen that when $ \phi_{\rm U} $ increases from 0° to $ 90^\circ $, the peak of the $ \theta_{\rm{lab}} $ distribution moves to the left. When $ \phi_{\rm U} $ continues to increase from $ 90^\circ $ to $ 180^\circ $, it returns to the right side. More careful surveillance reveals that the width of the distribution also changes. At $ \phi_{\rm U} = 90^\circ $, the width of the $ \theta_{\rm{lab}} $ distribution is smaller than that at $ \phi_{\rm U} = 0^\circ $. Figure 4 (b) further presents the distribution of $ \theta_{\rm{lab}} $ by varying the orientation of ²³⁸U with respect to the beam direction in the x-z plane, characterized by $ \theta_{\rm U} $ as the angle of the long axis of ²³⁸U relative to the z axis. As $ \theta_{\rm U} $ increases, the peak of the $ \theta_{\rm{lab}} $ distribution first moves to the right when $ \theta_{\rm U}<90^\circ $ and then moves back toward the left when $ \theta_{\rm U}>90^\circ $. The largest deflection occurs at $ \theta_{\rm U} = 90^\circ $.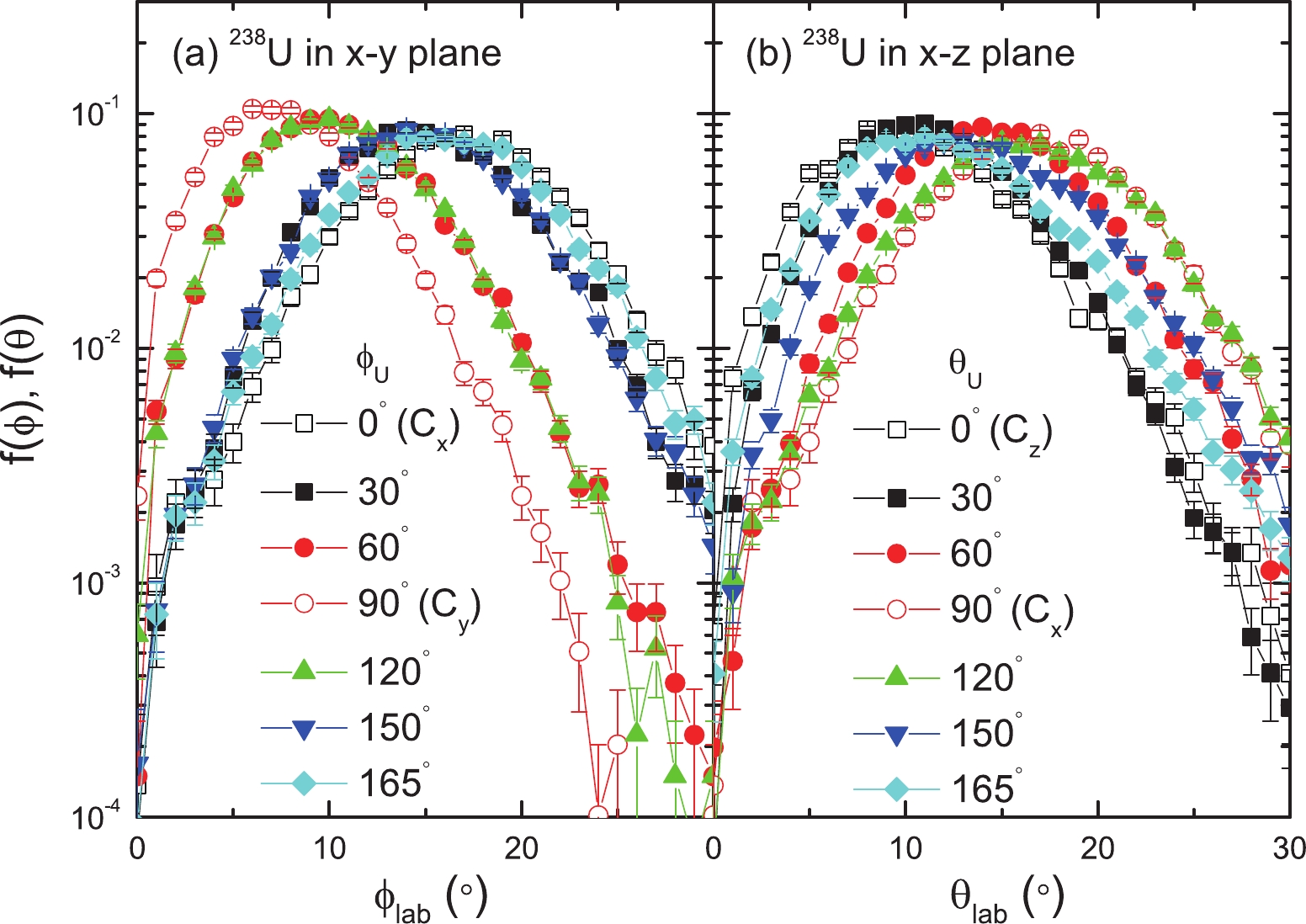

Figure 4.  (color online) $\theta_{\rm{lab}}$ distribution of the deflected proton in p+²³⁸U with $b = 9$ fm at $E_{ p} = 200$ MeV by rotating the long axis of ²³⁸U in the x-y plane (a) and the x-z plane (b). The meaning of $\phi_U$ and $\theta_U$ are clarified in the text.

The different behaviors of the $ \theta_{\rm{lab}} $ distribution reveal that the deformation and orientation of p+²³⁸U scattering affect the deflection of the incident nucleon depending on the orientation of the symmetrical long axis of the deformed target nuclei. Combining all the effects of varying the orientation of ²³⁸U and the impact parameter, it is interesting to explore whether one can identify a certain orientation of the target nuclei in the scattering when measuring the scattered proton at certain angles coincidentally. Typical experimental convention is to select the polar orientation, i.e., the polar angle of the symmetric axis of ²³⁸U with respect to the beam. Thus, without counting the azimuth, one shall integrate over the azimuthal angle. Figure 5 presents the percentage of two different configurations that are selected as a function of the deflection angle of the proton in p+²³⁸U summing over $ 7\leqslant b\leqslant 10 $ fm. At the initial state, the long symmetrical axis of ²³⁸U is randomly and isotropically oriented. Then, after the scattering, the events corresponding to different configurations are counted and plotted as the ordinate in Fig. 5. Here, C_⊥ denotes the events with the symmetrical axis of ²³⁸U being approximately perpendicular to the beam direction with a cut $ \eta\leqslant 10^\circ $ (a) and $ \eta\leqslant 30^\circ $ (b), where $ \eta $ is the angle of the long axis of ²³⁸U with respect to the x-y plane, while C_z denotes the events for which the long axis of ²³⁸U corresponds to an angle of $ \eta\leqslant 10^\circ $ (a) and $ \eta\leqslant 30^\circ $ (b) with the beam axis. Thus, C_⊥ and ${{C}} _{{{z}}} $ can be viewed as the parallel and perpendicular orientations of $ ^{238} {\rm{U}}$, respectively. It is evident from Fig. 5 that the percentage of C_⊥ exhibits an increasing trend as a function of $ \theta_{\rm{lab}} $, which is opposite to the decreasing trend for C_z but with much larger scattering cross section. This suggests that if the scattered proton is measured in coincidence, the scattering angle can be used to select statistically, as opposed to event-by-event, the scattering events with different weights of the two polar orientations of C_⊥ and ${{C}} _{{{z}}} $.

Figure 5.  (color online) Percentage of various geometric configurations selected as a function of the deflection angle of the proton for 200 MeV p+²³⁸U with b = 7-10 fm.

The deformation and orientation effect of the heavy target leads to an orientation dichroism effect in reverse kinetic scattering using ²³⁸U as the incident beam. After the primary ²³⁸U beam with intensity $ I_0(\Theta_s) $ passes through a proton target with thickness t, the remaining intensity $ I(\Theta_s,t) $ of the ²³⁸U in the original beam direction can be written independently of the model as

where $ \Theta_s $ is the polar angle of the long symmetric axis of ²³⁸U with respect to the beam direction. $ \Theta_s\approx0^\circ $($ 90^{\circ} $) denotes the parallel (perpendicular) orientation corresponding to C_z (${{C}} _{\perp} $) in Fig. 5, respectively. $ \sigma(\Theta_s) $ is the scattering cross section of p+²³⁸U, and $ \rho_{n}(t) $ is the areal number density of the target nuclei. Since the scattering cross section of the parallel orientation is much less than that of the perpendicular orientation, as summarized in Table 1 , the parallel-oriented ²³⁸U nuclei are absorbed relatively less than for the perpendicular orientation, leading to an orientation dichroism effect. It is expected that the ansatz (3) is model-independent, and the orientation dichroism effect is universal for the medium energy scattering induced by deformed nuclei.

$\eta$	$\sigma$[Cz] /mb	$\sigma$[C⊥] /mb	$\sigma$[all] /mb
$\le 10^{\circ}$	24.6 (8.4)	259 (112)	1527 (609)
$\le 30^{\circ}$	212 (73.6)	748 (317)

Table 1.  Elastic and quasi-elastic (inelastic) scattering cross sections for $ 7\leqslant b\leqslant 10 $ fm for different configurations.

We note some points of caution here. The nucleons are treated as Gaussian packages in the ImQMD model. The spin of the incident proton is not taken into account in the calculation, and the results do not contain the effect arising from the spin projection of the proton. In addition, the resonance scattering channels coupled to the excited states of ²³⁸U are not included. Therefore, it is necessary to perform further theoretical calculation of the elastic or quasi-elastic scattering of the proton on the deformed target within the framework based on quantum mechanics in order to reproduce the novel effect predicted in our study, for instance, by the approach developed in [28]. From an experimental perspective, it is feasible in principle to observe the deformation and orientation effect in p+²³⁸U scattering, whereby the target nuclei of ²³⁸U are excited to the low-lying states of the yrast rotational band for which the angular momentum is nonzero. Thus, the angular correlation of the cascade $ \gamma $-rays from the rotational band contains the information of the orientation of $ ^{238} {\rm{U}}$. If, as expected, the angular correlation of the $ \gamma $-rays shows dependence on the laboratory angle of the deflected proton, it will signify the orientation effect in p+²³⁸U scattering.

In summary, the proton-induced scattering of deformed even-even ²³⁸U nuclei with spheroidal shape has been simulated with the ImQMD model. By surveying three special geometrical configurations ${{C}} _{{{x}}} $, C_y, and ${{C}} _{{{z}}} $, it has been found that the angular distribution of the deflected proton exhibits clear dependence on the orientation of the deformed nucleus with various impact parameters. Summing over all impact parameters in peripheral scattering for the whole azimuth, the intensities of the deflected proton are split between the parallel and perpendicular orientations of ²³⁸U as a function of scattering angle in the laboratory. It is suggested that the polar orientation of the deformed nucleus in the scattering can be characterized by imposing an angular condition on the deflected proton. In reverse kinetics, the different scattering cross section between the parallel and perpendicular configurations causes an orientation dichroism effect, implying a novel method to produce a polarized secondary beam of deformed nuclei with nonzero spin, to which our method of calculation can be extended without changing the conclusion.

We thank Prof. Hui Ma, Prof. Chunguang Du and Prof. Pengfei Zhuang from Tsinghua University, Prof. Zhuxia Li and Prof. Zhaochun Gao from CIAE for their valuable discussions.