-
With the advent of the first image of a black hole and the observation of an increasing number of gravitational wave events, black hole physics is playing an increasingly prominent role in our understanding of gravity. It is now generally believed that the black hole hides clues about how to unify general relativity and quantum mechanics. The emergence of the thermodynamics of black holes provides a powerful approach to explore their secrets [1-4]. In particular, the introduction of the extended phase space [5,6] enriches the research of black hole thermodynamics, enabling use of the analogy between the charged AdS black hole and van der Waals fluid [7], application of the Maxwell equal area law [7,8], microscopic analysis of black hole phase transition [9-12], etc. A large number of research results have revealed the microstructures of black holes. Nevertheless, describing the microscopic behavior of black holes remains a significant challenge in the current gravitational problem.
Recently, a new concept, i.e., the black hole molecule, has been proposed, which provides a new perspective for a phenomenological study of the micro-mechanism of black holes [9,11-13]. This new scheme is mainly based on the Ruppeiner thermodynamic geometry, which introduced a Riemannian metric structure to represent the thermodynamic fluctuation theory [14]. To provide a mathematical description method of the thermodynamic theory in the geometric sense, Weinhold [15] introduced a thermodynamic metric
$ g^{W}_{\mu\nu} = \partial^2 U/(\partial X^{\mu}\partial X^{\nu}) $ in terms of the internal energy. However, the Weinhold geometry has no physical meaning in the context of pure equilibrium thermodynamics. Subsequently, Ruppeiner further developed the geometric theory of thermodynamics, and put forward a theory later referred to as the Ruppeiner thermodynamic geometry, which is based on the second-order partial derivative structure of the entropy with respect to other thermodynamic quantities and has a physical meaning in the fluctuation theory of equilibrium thermodynamics. The components of the inverse Ruppeiner metric yield second moments of fluctuations. The above two geometries prove to be conformally equivalent to the conformal factor$ 1/T $ . Subsequently, the Ruppeiner geometry was widely used to explore micro-information of the black hole thermodynamic system and the ordinary fluid thermodynamic system. Meanwhile, the Weinhold geometry is incapable of such application.Thermodynamic curvature is the most important parameter in the Ruppeiner thermodynamic geometry. For the better understood statistical mechanical models in ordinary thermodynamics, the sign of thermodynamic curvature qualitatively reflects information on the character of the molecular interaction for a thermodynamic system. Empirical observations indicate that a positive (or negative) thermodynamic scalar curvature implies a repulsive (or attractive) interaction, and a vanishing thermodynamic scalar curvature corresponds to no interaction [16,17]. Meanwhile, the absolute value of the thermodynamic scalar curvature reflects the strength of molecular interaction. A large absolute value of the thermodynamic curvature implies strong interaction, whereas a small one corresponds to weak interaction [18]. For black hole systems, because there is no complete theory of quantum gravity, the exploration of the microscopic structure of black holes is bound to contain some speculative assumptions. Owing to the well-established black hole thermodynamics, as an analogy analysis and a primary description of the micro-behavior of black holes, the empirical observation mentioned above provides information about interactions of black holes, phenomenologically or qualitatively [19-28].
For the Reissner-Nordström (RN) black hole, we already know that its thermodynamic behaviors and the temperature of the black hole exhibits a maximum. However, a series of studies [29-31] using the Ruppeiner thermodynamic geometry have suggested that the RN black hole is a non-interacting system. In contrast, the study presented in Ref. [32] pointed out that the results of the RN black hole must be reduced from those of the Kerr-Newmann-AdS black holes, and the coordinate space of the thermodynamic geometry of the RN black hole adopted in Refs. [29-31] may be incomplete. Their results indicated that the RN black hole is an interacting system. Thus, there is a divergence in claims on whether molecules of the RN black hole interact. Intuitively, as an independent thermodynamic system, the coordinate space of the thermodynamic geometry of the RN black hole must be complete, and its metric of the thermodynamic geometry is well described (as presented in the following analysis). The reasoning behind the claim of non-interaction between RN black hole molecules in Refs. [29-31] deserves further investigation. Moreover, as a charged black hole, interaction between its molecules must occur, in the form of electromagnetic interaction. Hence, we believe that the RN black hole is a complete and interacting system. These are the main motivations of this study.
In the present study, by choosing the appropriate extensive variables, we show that the black hole has repulsive interactions. More importantly, with the help of a new quantity, namely the thermal-charge density, we describe the fine micro-thermal structures of this black hole in detail. It has three different phases, the free phase, balanced phase, and interactive phase. More meaningfully, we provide the thermodynamic micro-mechanism for the formation of the naked singularity of the RN black hole. Throughout this paper, we adopt the units
$ \hbar = c = k_{_{B}} = G = 1 $ . -
For the RN black hole, its mass
$ M $ , charge$ q $ and the horizon radius$ r_{\pm} $ satisfy the following relationship$ r_{\pm} = M \pm \sqrt{M^2-q^2}. $

(1) The black hole has two horizons, and
$ r_{+}>r_{-} $ . Hence, the event horizon is marked as$ r_h = r_{+} $ . When$ M = q $ , two horizons merge into one. This is the extreme black hole, and the condition$ M\geqslant q $ is also known as the Bogomol'nyi boundary.The basic thermodynamic properties of the RN black hole assume the following forms in terms of the event horizon radius
$ r_h $ [29-31],$ {\rm{Internal}}\;{\rm{energy}}\;:\;U = M = \frac{{{r_h}}}{2} + \frac{{{q^2}}}{{2{r_h}}}, $

(2) $ {\rm{Temperature}}\;:\;T = \frac{1}{{4\pi {r_h}}} - \frac{{{q^2}}}{{4\pi r_h^3}}, $

(3) $ {\rm{Entropy}}\;:\;S = \pi r_h^2. $

(4) In previous discussions, the internal energy
$ U $ of the black hole was defined as a function of entropy$ S $ and charge$ q $ , i.e.,$ U = U(S, q) $ . Correspondingly, the first law of thermodynamics is written as${\rm d} U = T {\rm d} S+\varphi {\rm d}q$ , where the$ \varphi = q/r_h $ is the electrostatic potential. In the coordinate space$ \{S, q\} $ , the RN black hole is a non-interacting system [29-31]. Furthermore, Ref. [32] suggested that the RN black hole is an interacting system according to the degeneration of results of the Kerr-Newmann-AdS black holes and indicated that the coordinate space$ \{S, q\} $ is not complete. Our current view is that the RN black hole is a complete and interacting system. It is likely that the divergence of previous studies regarding the interaction between molecules of the RN black hole could be attributed to the selection of the coordinate space for the Ruppeiner thermodynamic geometry.Inspired by the result of Ref. [33], where the authors used
$ q^2 $ as an independent thermodynamic quantity to analyze the critical behavior and microscopic structure of the charged AdS black hole for the first time, and where the black hole exhibits the van der Waals-type phase transition behavior in the new phase space, without extended phase space. Similar phenomena also appear in the Gauss-Bonnet gravity, as well as in higher dimensional spacetime [34]. In this study, we find that the coordinate space$ \{S, Q\} $ is appropriate to eliminate the above divergence, where the new thermodynamic quantity thermal-charge$ Q $ is taken as$ q^2 $ . Then, we have$ Q = q^2, \qquad \Psi = \left(\frac{\partial U}{\partial Q}\right)_S = \frac{1}{2r_h}, $

(5) and the first law of thermodynamics and Smarr relation can be written in terms of the thermodynamic quantities mentioned above as follows:
$ {\rm d} U = T {\rm d} S+\Psi {\rm d} Q, \qquad U = 2(TS+\Psi Q). $

(6) The following comments concern the above description:
● For the phrase "the coordinate space" mentioned above, let us make a simple explanation. In classical mechanics, a system with
$ n $ degrees of freedom has a$ 2n $ dimensional phase space. In analogy, in a thermodynamic system, the phase space must contain both the conjugated extensive and intensive quantities (or generalized coordinates and their conjugate generalized forces). Here, the phase space of the RN black hole in our scheme must be$ \{T, \Psi, S, Q\} $ . For the theory of thermodynamics geometry, we employ a space of generalized coordinates, such as$ \{T, \Psi\} $ ,$ \{S, Q\} $ ,$ \{T, Q\} $ and$ \{S, \Psi\} $ for the RN black hole.● The RN black hole has a zero thermodynamic curvature in the coordinate space
$ \{S,q\} $ , indicating that it is a non-interacting system. This seems to be inconsistent with our intuitive understanding of the RN black hole. To address this problem, we introduce a new scheme. By observing the form of solution of the RN black hole and the expressions of its related basic thermodynamics quantities, we find that the parameter of charge appears in the form of$ q^2 $ . Therefore, for simplicity, we regard$ Q = q^2 $ as an independent thermodynamic quantity. Its conjugate quantity is$ \Psi = 1/(2r_h) $ with the simplest form (it is only a function of the horizon radius$ r_h $ , while the electric potential$ \varphi = q/r_h $ is a function of$ q $ and$ r_h $ .). With the help of such a pair of new quantities, as shown in the following, we obtain that the RN black hole is indeed an interacting system in the new coordinate space$ \{S,Q\} $ .● The new physical quantity
$ \Psi $ conjugated with$ Q $ does not depend on the charge$ q $ , which is different from the electric potential$ \varphi $ . However, their contributions to the internal energy of the system are the same, i.e.,$ 2Q\Psi = q\varphi $ . In contrast, according to the idea of the black hole micromolecule introduced by Wei and Liu in Ref. [9], we see clearly that$ \Psi $ is equal to the number density of black hole micromolecules in natural units, which is the inverse of the specific volume defined in Ref. [7].In the new coordinate space
$ \{S, Q\} $ , we show that the RN black hole is indeed an interaction system and also provide some fine microstructures of the RN black hole completely from the thermodynamic point of view, with the help of the Ruppeiner thermodynamic geometry. The metric can be written in the internal energy form$ g_{\mu\nu} = \frac{1}{T}\frac{\partial^2 U}{\partial X^{\mu}\partial X^{\nu}}, $

(7) where
$ X^{\mu} $ represents independent thermodynamic quantities. For the RN black hole,$ X^{\mu} $ are$ S $ and$ Q $ . The line element takes the form$ {\rm d} l^2 = \frac{1}{C_{_Q}}{\rm d} S^2+\frac{2}{T}\left(\frac{\partial T}{\partial Q}\right)_S {\rm d} S {\rm d} Q+\frac{1}{T}\left(\frac{\partial \Psi}{\partial Q}\right)_S {\rm d} Q^2, $

(8) where
$ C_{_Q} : = T(\partial S/\partial T)_{_Q} = 2S(S-\pi Q)/(3\pi Q-S) $ and we have used the Maxwell relation$ (\partial T/\partial Q)_{_S} = (\partial \Psi/\partial S)_{_Q} $ based on the first law of thermodynamics of the RN black hole (see Eq. (6)). The line element${\rm d} l^2$ measures the distance between two neighbouring fluctuation states in the state space.Naturally, we obtain the thermodynamic scalar curvature
$ R = \frac{1}{S-\pi Q}. $

(9) According to the above formula, we note that the curvature is not zero, which indicates that the RN black hole is indeed an interacting system. This is also consistent with our understanding of the electromagnetic interaction between charged black hole molecules. Meanwhile, this also verifies the rationality of the coordinate space
$ \{S,Q\} $ we choose. In light of Eqs. (3) and (4), because of the non-negative requirement of temperature for the black hole, we have$ R>0 $ , which may be related to the information of repulsion interactions between black hole molecules for the RN black hole, i.e., electromagnetic repulsion interactions.We provide some further explanations of the above obtained results.
A series of studies [29-31] suggested that the RN black hole has zero thermodynamic curvature. Meanwhile, in Refs. [32,35,36], the authors reported that the RN black hole has a non-zero thermodynamic curvature. With regard to the condundrum on whether the thermodynamic curvature of the RN black hole is non-zero, our present results are qualitatively consistent with those in Refs. [32,35,36]. The results show that the RN black hole has a non-zero and positive thermodynamic curvature.
In Ref. [32], authors calculate the thermodynamic curvature of the Kerr-Newmann-AdS black hole in the coordinate space
$ \{S,q,J\} $ and subsequently take the zero-limit of cosmological constant$ \Lambda $ and angular momentum$ J $ to obtain the non-zero thermodynamic curvature of the RN black hole. This is a possible approach to solve the problem of the RN black hole as a non-interacting system. Meanwhile, the authors have pointed out that the coordinate space of the thermodynamic geometry of the RN black hole itself is incomplete. However, the evidence provided to the above conclusion, stating that the coordinate space of the thermodynamic geometry of the RN black hole is incomplete according to the degenerated result of the Kerr-Newmann-AdS black hole, seems insufficient and is questionable. In this study, we treat the RN black hole as an independent thermodynamic system instead. We propose another approach, in which a novel thermodynamic coordinate$ Q = q^2 $ is adopted to achieve a non-zero thermodynamic curvature for the RN black hole, without the help of the degenerated case of the Kerr-Newmann-AdS black hole.In Ref. [35], the geometrothermodynamic scheme was proposed to obtain non-zero thermodynamic curvature of the RN black hole. In Ref. [36], authors employed the redefinition of the internal energy of the system to realize non-zero thermodynamic curvature for the RN black hole (there is a sign difference in the Christoffel symbol between this study and our work in the calculation of the thermodynamic curvature).
Next, we introduce a new quantity, the thermal-charge density
$ \sigma = \frac{3\pi Q}{S}. $

(10) The main reasons behind the introduction of the thermal-charge density are as follows:
● Because the entropy of a black hole is proportional to its horizon area, we call this quantity a kind of density (specifically, surface density).
● Using the thermal-charge density
$ \sigma $ , we clearly describe the microstructure of the RN black hole. Meanwhile, the new physical quantity plays a role similar to the order parameter.Evidently,
$ 0<\sigma\leq 3 $ , and at$ \sigma = 3 $ the temperature equals zero (extreme black hole). The term$ 3\pi Q $ in the numerator implies the existence of electromagnetic repulsion interaction. Meanwhile, the denominator$ S $ denotes the disorder of molecules in a black hole system. The larger the entropy$ S $ , the stronger the disorder of the system, which leads to more violent irregular thermal motion of molecules. In the following analysis, we consider the case of fixed thermal-charge$ Q $ . Then, the temperature Eq. (3) and the thermodynamic scalar curvature Eq. (9) for the RN black hole can also be expressed as rescaled temperature$ T_r $ and rescaled thermodynamic scalar curvature Rr$ \begin{split} {T_r} =& 4\pi \sqrt Q T = \sqrt {\frac{\sigma }{3}} \left( {1 - \frac{\sigma }{3}} \right),\\ {R_r} =& \pi QR = \frac{\sigma }{{3 - \sigma }}. \end{split} $

(11) Hence, we obtain three different situations:
● When
$ \sigma = 1 $ , the temperature$ T_r $ reaches its maximum$T_r = T_{\max} = 2/(3\sqrt{3})$ , and the thermodynamic scalar curvature$ R_{\sigma = 1} = 1/2 $ .● When
$ 0<\sigma<1 $ , we have$T_r: 0\rightarrow T_{\max}$ and$ R_r: 0 \rightarrow 1/2 $ .● When
$ 1<\sigma\leqslant 3 $ , we have$T_r: T_{\max}\rightarrow 0$ and$ R_r: 1/2 \rightarrow +\infty $ . In particular at$ \sigma = 3 $ , we have$ T_r = 0 $ and$ R_r = +\infty $ . This situation corresponds to the extreme black hole.Here, along the direction of increasing thermal-charge density
$ \sigma $ , we show the curve of the temperature$ T_r $ and curvature$ R_r $ in Fig. 1. We clearly observe that there is an inflection point in the$ T_r-R_r $ plot, i.e., the maximum point. Simultaneously, we can observe the existence of three different phases.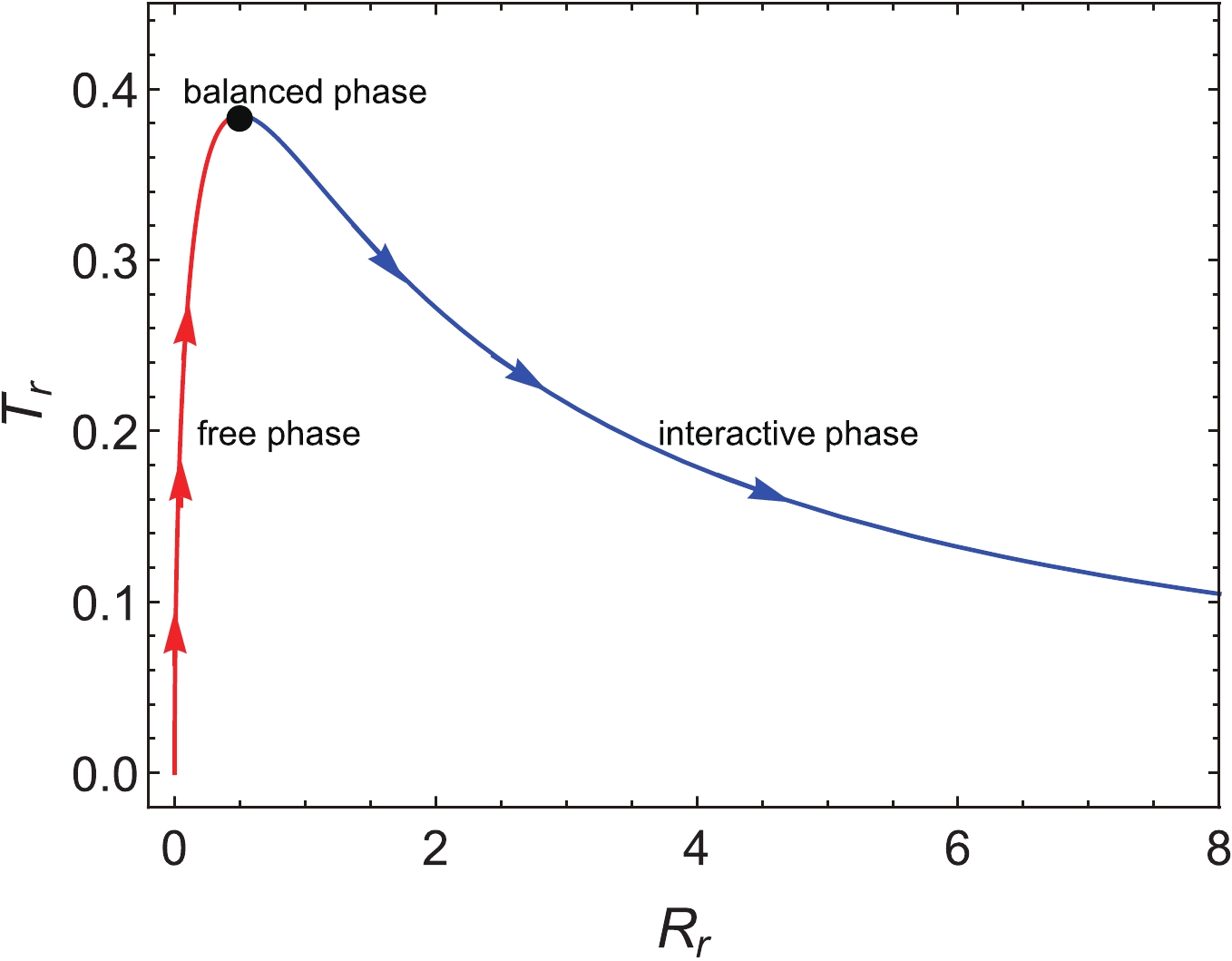
Figure 1. (color online) Diagram of rescaled temperature
$ T_r $ with respect to rescaled thermodynamic scalar curvature$ R_r $ . Arrows indicate the direction of the thermal-charge density increase.Case 1: free phase– With the increasing of thermal-charge density
$ \sigma $ from 0 to 1, according to Eq. (10), we deduce that the irregular thermal motion of molecules plays a major role. We call this situation the free phase. In contrast, the thermodynamic curvature increases with the increasing thermal-charge density, which may indicate that the repulsive interaction between black hole molecules is enhanced. The repulsive interaction between a large number of molecules leads to the existence of interactive phase, which suppresses the free phase. Thus, there will be a competitive relationship between the two phases. However, at the interval$ \sigma \in (0,1) $ , the free phase dominates the whole black hole system, and thus the temperature of the black hole increases.Case 2: balanced phase– At
$ \sigma = 1 $ , the competition between the free phase and the interactive phase is balanced, such that the temperature of a black hole can reach a maximum. This also reflects the microscopic mechanism behind the existence of a maximum temperature of the RN black hole.Case 3: interactive phase– With the increase in the thermal-charge density
$ \sigma $ from 1 to 3, the thermodynamic curvature rapidly increases, which may imply that the repulsive interaction between black hole molecules is increasing rapidly. At this time, the interactive phase dominates the entire black hole system, which leads to a decrease in the temperature of the black hole.When
$ \sigma = 3 $ , we have$ T_r = 0 $ and$ R_r = +\infty $ . This is the extreme RN black hole, i.e.,$ M = q $ . At this moment, a strong repulsive interaction dominates between the black hole molecules. The entire black hole system is completely in the interactive phase, and the temperature equals to zero. Next, we consider the near-extreme circumstances, i.e.,$ \sigma\rightarrow 3 $ , where we have the following relation with the help of Eq. (11),$ R_r = \frac{1}{T_r}-\frac32-\frac{3T_r}{8}-\frac{T_r^2}{2}+{\cal{O}}(T_r^3). $

(12) Hence, we obtain
$ \lim\limits_{T_r\rightarrow 0} T_r R_r = 1,\quad {\rm{or}} \quad \lim\limits_{M\rightarrow q} T R = \frac{1}{4\pi^2 q^3}. $

(13) That is to say, when the Bogomol'nyi boundary is saturated, although the temperature
$ T $ tends to zero and the thermodynamic scalar curvature$ R $ tends to infinite, the combination$ T R $ of the two is a finite value.When the thermal-charge density exceeds 3, this situation corresponds to the case
$ M<q $ for the RN black hole. In light of Eq. (1), it is clear that the event horizon of a black hole does not exist, and the RN black hole becomes a naked singularity. From our current point of view, at that moment of$ \sigma>3 $ , according to Eq. (9) or Eq. (11), we see that the thermodynamic scalar curvature tends to be negative infinite, which implies that a strong attraction interaction dominates between black hole molecules. This causes the entire system to collapse into one point, i.e., the naked singularity. In this manner, we provide the thermodynamic micro-mechanism for the formation of the naked singularity.At the end of this section, we investigate whether the black hole has a phase transition. We know that the micro-mechanism of the phase transition results from the competition between the interaction among the molecules that make up the system and the irregular thermal motion of the molecules themselves. Employing the Ruppeiner thermodynamics geometry, we can reflect the micro-mechanism of the black hole phase transition to a certain extent. According to the theory of the molecular thermal motion and the significance of the thermodynamic curvature [11,18], the temperature can be regarded as a measure of irregular thermal motion, while the thermodynamic curvature can be regarded as a measure of the molecular interaction.
According to Fig. 2 shows a gap between the free phase and the interactive phase, where "gap-1" indicates that the black hole system is dominated by thermal motion, while "gap-2" indicates that the system is dominated by the interaction. Hence, the RN back hole undergoes a new phase transition between the free phase and interactive phase, and the phase transition point is exactly at the balanced phase, i.e., the thermal-charge density
$ \sigma = 1 $ . -
By choosing the appropriate extensive variables, we show that the RN black hole may contain repulsive interactions. More importantly, with the help of a new quantity, the thermal-charge density, we describe the fine micro-thermal structures of the black hole in detail. The RN black hole has three different phases, the free phase, balanced phase, and interactive phase. The thermal-charge density plays a role similar to the order parameter, and the back hole undergoes a new phase transition between the free phase and interactive phase. We also observe that the competition between the free phase and the interactive phase exists for the RN black hole. In the balanced phase, the temperature reaches its maximum value. For the extreme RN black hole, the entire system is completely in the interactive phase, and the temperature equals to zero. Furthermore, when the Bogomol'nyi boundary is saturated, i.e.,
$ M = q $ , we obtain an interesting constant, see Eq. (13). Meanwhile, we provide the thermodynamic micro-mechanism for the formation of the naked singularity for the RN black hole. This is because of the strong attraction interaction when$ M<q $ , which leads the entire system to become a naked singularity.When
$ \sigma = 0 $ , i.e.,$ Q = 0 $ , the scenario degenerates to that of the Schwarzschild black hole. For this black hole, its first law of thermodynamics is${\rm d} U_{{\rm{Schwarzschild}}} = T_{{\rm{Schwarzschild}}} {\rm d} S_{{\rm{Schwarzschild}}}$ , and the coordinate space of the thermodynamic geometry has only one quantity$ S_{{\rm{Schwarzschild}}} $ . This renders the metric of the thermodynamic geometry singular, and consequently the micro information of the associated black hole is not revealed from the thermodynamic geometry. From this point of view, it is quite possible that the coordinate space of the thermodynamic geometry of the Schwarzschild black hole is incomplete, and we have to analyze some of its micro-behavior with the help of the results of other black holes, such as the RN black hole. According to Eqs. (3) and (9), at$ Q = 0 $ , we obtain the expression of the thermodynamic scalar curvature with respect to the temperature for the Schwarzschild black hole$ R_{{\rm{Schwarzschild}}} = 16\pi T_{{\rm{Schwarzschild}}}^2. $

(14) From above formula, we see that the thermodynamic scalar curvature is positive, i.e.,
$ R_{{\rm{Schwarzschild}}}>0 $ , which may be related to the information of repulsive interaction between black hole molecules for the Schwarzschild black hole. Because the black hole is not charged, there will be no electromagnetic interaction, hence the repulsion interaction of the black hole is likely to reflect short-range repulsion between molecules. Details require further analysis and discussion.Finally, we must emphasize several points on the calculation contents of the current paper. First, there is a general lore that if the microscopic dynamics of a system are known, its thermodynamical properties can be derived from statistic physics of the system, while the inverse process does not hold in general, i.e., the micro-dynamics of the system cannot be known from its thermodynamics. However, for black hole systems, because a complete theory of quantum gravity does not exist (although the most likely candidate theories, string theory and loop quantum gravity theory, have achieved good results to some extent), the exploration of the microscopic structure of black holes is bound to speculative assumptions. Meanwhile, the constituents of black holes are unclear. Hence, in comparison to the methods of studying the usual statistical models, we believe that the inverse process mentioned above may be feasible for the black hole system as a primary description. Second, owing to the well-established black hole thermodynamics, as an analogy analysis and a primary description of the micro-behavior of black holes, the empirical observation, i.e., a positive (or negative) thermodynamic scalar curvature, implies a repulsive (or attractive) interaction. Moreover, a vanishing thermodynamic scalar curvature corresponds to no interaction, and it can provide information about interactions of black holes phenomenologically or qualitatively. Third, the Ruppeiner thermodynamic geometry is based on the Hessian matrix describing the black hole entropy, in which the thermodynamic potential plays an important role in the second-order partial differential of other independent thermodynamic quantities. This leads to a completely different result when
$ q $ or$ q^2 $ is used as an independent thermodynamic quantity. Possibly, when we treat the charge$ q $ as a thermodynamic quantity, some information may be cancel each other, while when we treat the charge square$ q^2 $ as a thermodynamic quantity, this information can be displayed. The Appendix provides the comparison of thermodynamic metric of the RN black hole under the two schemes.Furthermore, we hope that our current analysis can be extended to other types of black holes, especially those with AdS background, where we can predict that the AdS background will place the black hole in a new phase. As reported in the literature [9,11-13,18,37], the Schwarzschild AdS black hole contains attractive interactions, while the charged AdS black hole has both repulsion and attraction. These issues likewise need to be further explored in the future.
This research was supported by the Double First-class University Construction Project of Northwest University. The authors would like to thank the anonymous reviewers for the helpful comments that significantly improved this work.
-
In Refs. [29-31], the thermodynamic metric of the RN black hole in coordinate space
$ \{S,q\} $ is$\tag{A1}\begin{array}{l} {\rm d}l_q^2 = \dfrac{{2S(S - \pi {q^2})}}{{3\pi {q^2} - S}}{\rm d}{S^2} + \dfrac{{4\pi q}}{{\pi {q^2} - S}}{\rm d}S{\rm d}q + \dfrac{{4\pi S}}{{S - \pi {q^2}}}{\rm d}{q^2}. \end{array} $

With the new coordinate
$\tag{A2} u = \frac{\sqrt{\pi}q}{S}, \qquad -1\leqslant u \leqslant 1, $

the above thermodynamic metric reads as in diagonal form
$ \tag{A3} {\rm d} l^2_q = -\frac{1}{2S}{\rm d} S^2+\frac{4S}{1-u^2}{\rm d} u^2. $

Then, under the proper coordinate transformations
$ \tag{A4} \tau = \sqrt{2S}, \quad \sin\frac{\sigma}{\sqrt{2}} = u, $

and
$\tag{A5} t = \tau\cosh\sigma, \quad x = \tau\sinh\sigma, $

the thermodynamic metric is finally turned into a Minkowski one
$ \tag{A6} {\rm d} l^2_q = -{\rm d} \tau^2+\tau^2 {\rm d} \sigma^2 = -{\rm d} t^2+{\rm d} x^2, $

which impiles vanishing scalar curvature in terms of the coordinate space
$ \{S,q\} $ .In our study, the thermodynamic metric of the RN black hole in the coordinate space
$ \{S,Q\} $ is$\tag{A7} {\rm d} l^2 = \frac{2S(S-\pi Q)}{3\pi Q-S}{\rm d} S^2+\frac{\pi}{\pi Q-S}{\rm d}S {\rm d}Q. $

Using the above introduced coordinate
$ u $ , we can write the thermodynamic metric as$ \tag{A8} {\rm d} l^2 = -\frac{1}{2S}{\rm d} S^2-\frac{2u}{1-u^2}{\rm d} S {\rm d} u. $

In comparison with Eq. (A3), we can clearly see that because of the introduction of
$ Q = q^2 $ and its conjugated quantity$ \Psi = 1/(2r_h) $ (it is only a function of the horizon radius$ r_h $ ), the thermodynamic metric that we obtain is always off-diagonal. Hence, the Ruppeiner geometry in our present scheme is non-trivial. In this manner, we obtain a non-zero thermodynamic curvature and deduce that the RN black hole is an interaction system.
Fine micro-thermal structures for Reissner-Nordström black hole
- Received Date: 2020-02-25
- Accepted Date: 2020-04-21
- Available Online: 2020-09-01
Abstract: We solve the condundrum on whether the molecules of the Reissner-Nordström black hole interact through the Ruppeiner thermodynamic geometry, basing our study on the concept of the black hole molecule proposed in [Phys. Rev. Lett. 115 (2015) 111302] and choosing the appropriate extensive variables. Our results show that the Reissner-Nordström black hole is indeed an interaction system that may be dominated by repulsive interaction. More importantly, with the help of a novel quantity, namely the thermal-charge density, we describe the fine micro-thermal structures of the Reissner-Nordström black hole in detail. Three different phases are presented, namely the free, interactive, and balanced phases. The thermal-charge density plays a role similar to the order parameter, and the back hole undergoes a new phase transition between the free phase and interactive phase. The competition between the free phase and interactive phase exists, which leads to extreme behavior of the temperature of the Reissner-Nordström black hole. For the extreme Reissner-Nordström black hole, the entire system is completely in the interactive phase. More importantly, we provide the thermodynamic micro-mechanism for the formation of the naked singularity of the Reissner-Nordström black hole.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: