-
Top-quark pair production
$ pp \to t(p_t) + \bar{t}(p_{\bar{t}}) + X $ is among the most important scattering processes at the Large Hadron Collider (LHC). The experimental measurements of its differential cross-sections have achieved remarkably high resolutions [1-4] in the Run 2 of the LHC with a center-of-mass energy$\sqrt s = 13\;{\rm{TeV}}$ . In the meantime, the theoretical modeling of the kinematic distributions in quantum chromodynamics (QCD) was significantly improved with the emergence of the next-to-next-to-leading order (NNLO) predictions [5-7] supplemented with the resummation of large logarithms to the next-to-next-to-leading logarithmic accuracy (NNLL') [8-10]. The complete next-to-leading order (NLO) corrections incorporating electroweak (EW) effects [11, 12] have also been combined with the higher order QCD corrections, resulting in the state-of-the-art standard model (SM) predictions for this process [13, 14].Despite these developments, small discrepancies between the high precision theoretical and experimental results are persistent. A notable discrepancy is the
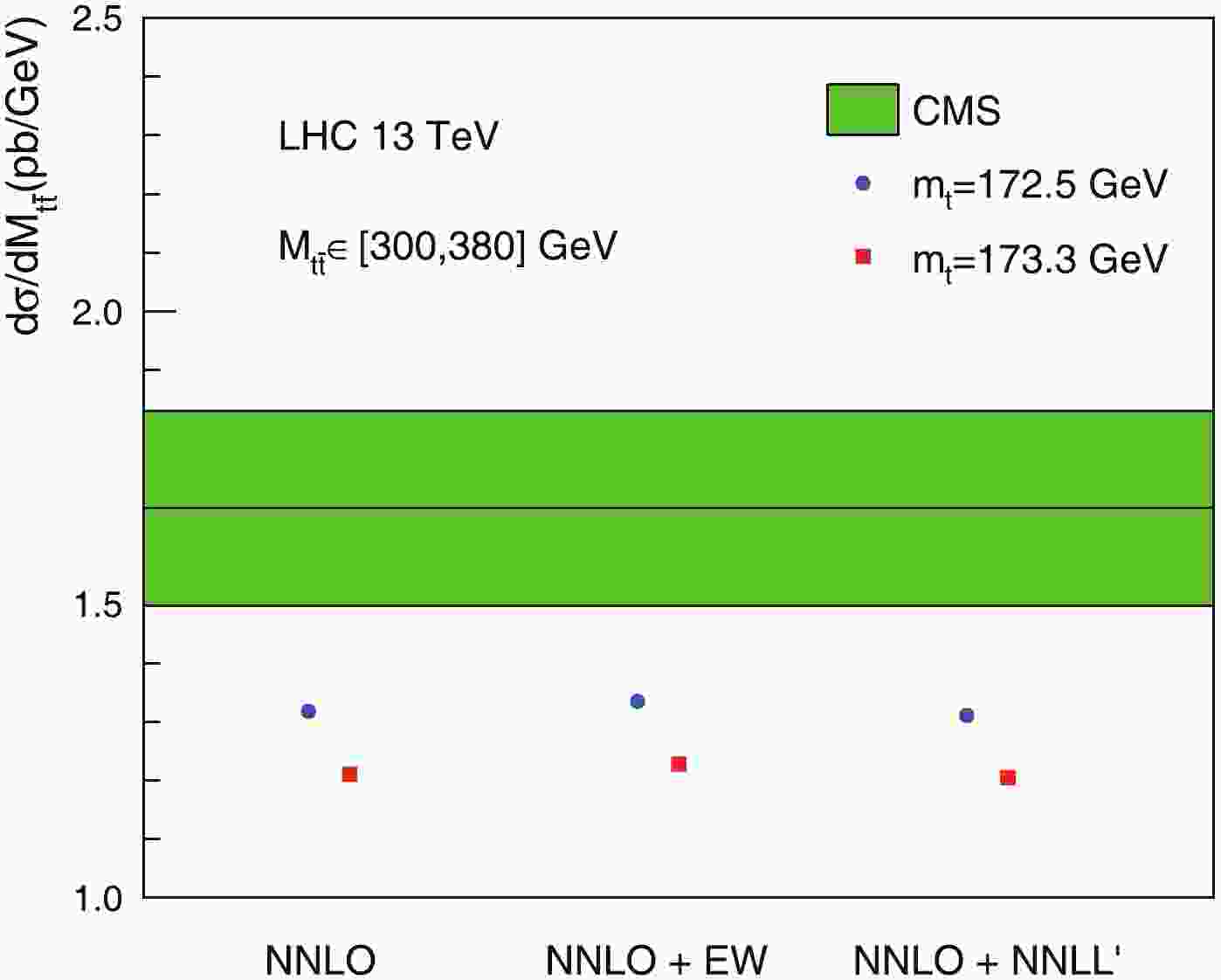
$ t\bar{t} $ invariant-mass distribution near the$ 2m_t $ threshold, measured by the CMS collaboration at the 13 TeV LHC [2, 3], where$ m_t $ is the top-quark mass, and the invariant mass$ M_{t\bar{t}} $ is defined as$ M_{t\bar{t}}^2 \equiv (p_t + p_{\bar{t}})^2 $ . In Fig. 1, we depict the averaged$ M_{t\bar{t}} $ distribution in the [300, 380] GeV range. The CMS result [2] is shown as the green band, which reflects the combined statistical and systematic uncertainty. The central values of various theoretical predictions (NNLO from [6], NNLO+EW from [13], and NNLO+NNLL' from [9]) are shown for comparison. There is a clear gap between the experimental and theoretical results. The theoretical predictions in this region are strongly dependent on$ m_t $ . Consequently, this discrepancy has a strong impact on the extraction of$ m_t $ from kinematic distributions [15], which favors a value of$ m_t $ that is significantly lower than the current world average. Therefore, it is of interest to investigate whether the top quark is indeed lighter than expected, or whether there are missing contributions in this region that are not incorporated in the most up-to-date theoretical predictions.
Figure 1. (color online) Averaged
$t\bar{t}$ invariant mass distribution in [300, 380] GeV range. The CMS result [2] is shown as the green band, while the central-values of various theoretical predictions are shown in comparison.In this study, we investigate a class of higher order QCD corrections in the threshold region
$ M_{t\bar{t}} \sim 2m_t $ . These originate from exchanges of Coulomb-type gluons as well as soft gluons between the top and anti-top quarks. The leading contributions take the form$ (\alpha_s/\beta)^n $ , where$ \beta \equiv \sqrt{1-4m_t^2/M_{t\bar{t}}^2} $ is the velocity of the top and anti-top quarks in the$ t\bar{t} $ rest frame. The region$ M_{t\bar{t}} \sim 2m_t $ corresponds to$ \beta \sim 0 $ , where the top and anti-top quarks are slowly moving with respect to each other. In the small$ \beta $ region, the$ 1/\beta^n $ contributions (as well as those of$ \ln^n\beta $ ) are enhanced and lead to large corrections beyond the NNLO(+NNLL') results. These corrections are divergent as$ \beta \to 0 $ , signaling a breakdown of the perturbative expansion in this limit. At NNLO (order$ \alpha_s^2 $ ), this does not pose a severe problem, as the integration over$ M_{t\bar{t}} $ is still convergent, which yields a finite prediction for the averaged differential cross-section, as shown in Fig. 1. However, at order$ \alpha_s^4 $ and beyond, even the integration across$ M_{t\bar{t}} $ becomes divergent, and one has to perform an all-order resummation to restore the validity of theoretical predictions. Furthermore, at fixed orders in perturbation theory,$ M_{t\bar{t}} \geqslant 2m_t $ due to the phase-space constraint. This is not physical, because bound-state effects can make the mass of the$ Q\bar{Q} $ system smaller than$ 2m_Q $ , where Q is a heavy quark. For charm quarks and bottom quarks, such bound-state effects are genuinely non-perturbative. For top-quark pairs, the bound-state effects can be (to a good approximation) studied in perturbation theory, as long as we integrate in a large enough range around the threshold$ M_{t\bar{t}} = 2m_t $ .In the following part of this study, we present a factorization formula for the partonic differential cross-sections that is valid in the region
$ M_{t\bar{t}} \sim 2m_t $ , which schematically takes the form$ d\hat{\sigma} \sim H \times J $ . The hard function H describes exchanges and emissions of hard gluons with typical momenta of$ \mathcal{O}(M_{t\bar{t}}) $ , while the potential function J resums exchanges of Coulomb and soft gluons between the top and anti-top quarks. Notably, we do not take the limit$ \sqrt{\hat{s}} \to M_{t\bar{t}} $ here, where$ \sqrt{\hat{s}} $ is the partonic center-of-mass energy. Consequently, extra hard radiations are allowed and incorporated in our framework into the hard function H. Therefore, our factorization formula is intrinsically different from those in [16-18], where the$ \sqrt{\hat{s}} \to M_{t\bar{t}} $ approximation was employed. Our formalism is similar to that of [19, 20]; however, it takes into account the kinematic dependence of the renormalization and factorization scales, and differs in the treatment of subleading corrections in$ \beta $ . Subsequently, we present numeric results that are relevant to LHC phenomenology based on our factorization formula. We show that the resummation effects indeed enhance the$ M_{t\bar{t}} $ distribution significantly in the threshold region, and make the theoretical prediction more compatible with the experimental data. -
We begin with the
$ t\bar{t} $ invariant mass distribution written as a convolution of the partonic luminosity functions and partonic differential cross-sections$\frac{{{\rm d}\sigma }}{{{\rm d}{M_{t\bar t}}}} = \sum\limits_{i,j} {\int_\tau ^1 {\frac{{{\rm d}z}}{z}} } \frac{\tau }{z}\int {\rm d} \Theta {\mkern 1mu} \frac{{{\rm d}{{\hat \sigma }_{ij}}(z,{\mu _f})}}{{{\rm d}{M_{t\bar t}}{\mkern 1mu} {\rm d}\Theta }}{\mkern 1mu} f\!\!{f_{ij}}\left(\frac{\tau }{z},{\mu _f}\right){\mkern 1mu} ,$

(1) where
$ i,j \in \{q,\bar{q},g\} $ denote partons within the colliding protons;$ z \equiv M_{t\bar{t}}^2/\hat{s} $ ,$ \tau \equiv M_{t\bar{t}}^2/s $ , and$ \mu_f $ is the factorization scale. The parton luminosity functions$ f\!\!f_{ij}(y,\mu_f) $ are defined by$f\!\!{f_{ij}}(y,{\mu _f}) \equiv \int_y^1 {\frac{{{\rm d}\xi }}{\xi }} {\mkern 1mu} {f_{i/p}}(\xi ,{\mu _f}){\mkern 1mu} {f_{j/p}}(y/\xi ,{\mu _f}){\mkern 1mu} ,$

(2) where
$ f_{i/p} $ is the parton distribution function (PDF) of the parton i in the proton p. Notably, in writing down Eq. (1), we have taken into account that the factorization scale$ \mu_f $ may depend on kinematic variables (which we collectively denote as$ \Theta $ ) other than$ m_t $ and$ M_{t\bar{t}} $ . This is necessary, as we combine our result with the NNLO result of [6], where the scales are correlated with the variable$ H_T \equiv \sqrt{p_{T,t}^2+m_t^2} + \sqrt{p_{T,\bar{t}}^2+m_t^2} $ , where$ p_{T,t} $ and$ p_{T,\bar{t}} $ are the transverse momenta of the top and anti-top quarks, respectively.We are concerned with QCD corrections to the partonic differential cross-sections. At the leading order (LO) in
$ \alpha_s $ , only the$ q\bar{q} $ and gg channels yield non-vanishing contributions$\begin{split} \frac{{{{\rm d}^2}\hat \sigma _{q\bar q}^{(0)}}}{{{\rm d}{M_{t\bar t}}{\mkern 1mu} {\rm d}\cos {\theta _t}}} =& \frac{{2\pi \beta \alpha _s^2({\mu _r})}}{{M_{t\bar t}^3}}\frac{{{C_F}{C_A}}}{9}{\mkern 1mu} {c_{q\bar q,8}}(\cos {\theta _t}){\mkern 1mu} \delta (1 - z){\mkern 1mu} ,\\ \frac{{{{\rm d}^2}\hat \sigma _{gg}^{(0)}}}{{{\rm d}{M_{t\bar t}}{\mkern 1mu} {\rm d}\cos {\theta _t}}} =& \frac{{2\pi \beta \alpha _s^2({\mu _r})}}{{M_{t\bar t}^3}}\bigg[\frac{{{C_F}}}{{32}}{\mkern 1mu} {c_{gg,1}}(\cos {\theta _t})\\ & + \frac{{(C_A^2 - 4){C_F}}}{{64}}{\mkern 1mu} {c_{gg,8}}(\cos {\theta _t})\bigg]{\mkern 1mu} \delta (1 - z){\mkern 1mu} , \end{split}$

(3) where
$ \mu_r $ is the renormalization scale, and$ \theta_t $ is the scattering angle of the top quark in the$ t\bar{t} $ rest frame. The coefficients$ c_{ij,\alpha} $ , with$ \alpha = 1,8 $ labelling the color configuration of the$ t\bar{t} $ system, are given by$\begin{split} {c_{q\bar q,8}}(\cos {\theta _t}) =& \frac{1}{4}[2 - {\beta ^2}(1 - {\cos ^2}{\theta _t})]{\mkern 1mu} ,\\ {c_{gg,1}}(\cos {\theta _t}) =& \frac{1}{{2{{(1 - {\beta ^2}{{\cos }^2}{\theta _t})}^2}}}[4 - 2{(1 - {\beta ^2})^2}\\ & - 2{\beta ^2}(1 - {\beta ^2}{\cos ^2}{\theta _t}) - {(1 + {\beta ^2}{\cos ^2}{\theta _t})^2}]{\mkern 1mu} ,\\ {c_{gg,8}}(\cos {\theta _t}) =& 2{c_{gg,1}}(\cos {\theta _t}){\mkern 1mu} \left[\frac{{16}}{5} - \frac{9}{{10}}(3 - {\beta ^2}{\cos ^2}{\theta _t})\right]{\mkern 1mu} . \end{split}$

(4) Eq. (3) is proportional to
$ \beta $ due to the two-body phase space. This indicates that the LO differential cross-section approaches zero at the threshold$ M_{t\bar{t}} = 2m_t $ . This is no longer true at higher orders in$ \alpha_s $ , essentially because of the$ 1/\beta^n $ terms mentioned in the Introduction. More precisely, the NLO differential cross-section approaches a positive constant in the$ \beta \to 0 $ limit, at which the NNLO and higher order ones diverge. This behavior makes the perturbative expansion badly convergent in the threshold region. In the following, we analyze the factorization properties of the differential cross sections and resum the large$ 1/\beta^n $ and$ \ln^n\beta $ corrections to all orders of$ \alpha_s $ . This is the only way to restore the predictive power of perturbative QCD near threshold.In the threshold limit
$ M_{t\bar{t}} \to 2m_t $ or$ \beta \to 0 $ , there are large hierarchies among the energy scales$ M_{t\bar{t}} $ ,$ M_{t\bar{t}}\beta $ , and$ M_{t\bar{t}}\beta^2 $ . Using the method of regions, we identify the following momentum modes in the$ t\bar{t} $ rest frame [21]$\begin{array}{*{20}{l}} {{\rm{hard: }}\;}&{{k^\mu } \sim {M_{t\bar t}}{\mkern 1mu} ,}&{{\rm{potential: }}\;}&{{k^0} \sim {M_{t\bar t}}{\beta ^2}{\mkern 1mu} ,\;\vec k \sim {M_{t\bar t}}\beta {\mkern 1mu} ,}\\ {{\rm{soft: }}\;}&{{k^\mu } \sim {M_{t\bar t}}\beta {\mkern 1mu} ,}&{{\rm{ultrasoft: }}\;}&{{k^\mu } \sim {M_{t\bar t}}{\beta ^2}{\mkern 1mu} .} \end{array}$

(5) The top and anti-top quarks move very slowly and are non-relativistic objects, whose residue momenta correspond to the potential mode. They can interact with each other through soft, ultrasoft, and potential gluons, which are described by the effective Lagrangian of potential non-relativistic QCD (pNRQCD) [22, 23]. The hard mode describes fluctuations with typical momenta of
$ \mathcal{O}(M_{t\bar{t}}) $ , resulting in Wilson coefficients of effective operators in pNRQCD. We note that there are no collinear modes in our setup. This is related to the fact that we are not taking the limit$ \sqrt{\hat{s}} \to M_{t\bar{t}} $ , such that the extra emissions are not constrained. Consequently, we do not need to employ the soft-collinear effective theory, as opposed to [17, 18]. Using the method of effective field theory (EFT), we derive a factorization formula for the partonic cross-sections in the threshold region. The power expansion of pNRQCD is according to the counting$ \alpha_s \sim \beta \sim 1/\ln\beta $ . Up to the next-to-leading power (NLP), the factorization formula reads$\begin{split} \frac{{{\rm d}\hat \sigma _{ij}^{{\rm{NLP}}}}}{{{\rm d}{M_{t\bar t}}{\mkern 1mu} {\rm d}\Theta }} =& \frac{{16{\pi ^2}\alpha _s^2({\mu _r})}}{{M_{t\bar t}^5}}\sqrt {\frac{{{M_{t\bar t}} + 2{m_t}}}{{2{M_{t\bar t}}}}} \sum\limits_\alpha {{c_{ij,\alpha }}} (\cos {\theta _t})\\ &\times {H_{ij,\alpha }}(z,{M_{t\bar t}},{Q_T},Y,{\mu _r},{\mu _f}){\mkern 1mu} {J^\alpha }(E) + {\cal O}({\beta ^3}){\mkern 1mu} , \end{split}$

(6) where
$ H_{ij,\alpha} $ are hard functions describing hard gluon exchanges and emissions, which depend on the transverse momentum$ Q_T $ and the rapidity Y of the$ t\bar{t} $ pair;$ J^\alpha $ (E) with$ E = M_{t\bar{t}}-2m_t $ are potential functions describing exchanges of potential, soft and ultrasoft gluons between the top and anti-top quarks. At NLP, ultrasoft gluon exchanges among initial-state partons and the$ t\bar{t} $ pair do not contribute. Consequently, there is no soft function in our factorization formula. This contribution could be present at higher powers in$ \alpha_s $ and$ \beta $ , which is an interesting subject of study for the future. The prefactors in Eq. (6) are chosen such that the LO cross-sections in the EFT reproduce the exact ones in Eq. (3). These prefactors take into account subleading corrections in$ \beta $ at LO and have significant impacts at higher orders in$ \alpha_s $ . This, along with the explicit kinematic dependence of the hard function, makes our factorization formula substantially different from that in [19, 20].The hard functions are calculated order-by-order in
$ \alpha_s $ in terms of differential cross-sections in the limit$ p_{t} = p_{\bar{t}} = P_{t\bar{t}}/2 $ . For resummation at NLP, we must find the hard functions up to the NLO. The LO hard functions are given by$\begin{split} H_{q\bar q,1}^{(0)} =& 0{\mkern 1mu} ,\quad H_{q\bar q,8}^{(0)} = \frac{{{C_A}{C_F}}}{9}{\mkern 1mu} \delta (1 - z){\mkern 1mu} \delta ({Q_T}){\mkern 1mu} \delta (Y){\mkern 1mu} ,\\ H_{gg,1}^{(0)} =& \frac{{{C_F}}}{{32}}{\mkern 1mu} \delta (1 - z){\mkern 1mu} \delta ({Q_T}){\mkern 1mu} \delta (Y){\mkern 1mu} ,\\ H_{gg,8}^{(0)} =& \frac{{(C_A^2 - 4){C_F}}}{{64}}{\mkern 1mu} \delta (1 - z){\mkern 1mu} \delta ({Q_T}){\mkern 1mu} \delta (Y){\mkern 1mu} . \end{split}$

(7) We analytically calculated the NLO corrections to the hard functions, which were hereto unknown in the literature. They receive contributions from both virtual exchanges and real emissions of gluons. The virtual and real contributions are separately infrared divergent. The divergences cancel when combined with the PDF counterterms. After the cancellation, we obtain finite NLO hard functions involving singular distributions of
$ 1-z $ ,$ Q_T $ , and Y. The results are more complicated than those in the literature [19, 20], as we must maintain the dependencies on kinematic variables in order to use the$ H_T $ -based renormalization and factorization scales. The potential function$ J^\alpha(E) $ is related to the imaginary part of the pNRQCD Green function$ G^\alpha(\vec{r}_1,\vec{r}_2;E) $ of the$ t\bar{t} $ pair at the origin. It receives contributions from potential, soft, and ultrasoft modes. The explicit expressions for the Green function up to NLP can be found in, e.g., [18, 24]. The finite width of the top quark is considered by the replacement of$ E \to E+i\Gamma_t $ in the potential function. This treatment is valid at NLP; however, additional considerations are required at higher powers (we count$ \Gamma_t/m_t \sim \beta^2 $ ) [25-29].Combining the hard and potential functions, we can now produce NLP resummed predictions for the
$ M_{t\bar{t}} $ distribution near threshold. These can be further combined with fixed-order ones via the matching formula$\frac{{{\rm d}{\sigma ^{{\rm{(N)NLO + NLP}}}}}}{{{\rm d}{M_{t\bar t}}}} = \frac{{{\rm d}{\sigma ^{{\rm{NLP}}}}}}{{{\rm d}{M_{t\bar t}}}} + \frac{{{\rm d}{\sigma ^{{\rm{(N)NLO}}}}}}{{{\rm d}{M_{t\bar t}}}} - \frac{{{\rm d}{\sigma ^{{\rm{(n)nLO}}}}}}{{{\rm d}{M_{t\bar t}}}}{\mkern 1mu} ,$

(8) where we used “nLO” and “nnLO” to denote fixed-order expansions of the NLP resummed result (6) up to the second and third order in
$ \alpha_s(\mu_r) $ . Their differences with respect to the full NLO and NNLO results are higher-power terms in$ \beta $ , which we wish to consider through the matching procedure. -
We present the numerical results based on our factorization formula (6) and the matching formula (8). Throughout our calculation, we take
${m_t} = 172.5\;{\rm{GeV}}$ ,${\Gamma _t} = 1.4\;{\rm{GeV}}$ , and use the NNPDF3.1 NNLO PDFs with$ \alpha_s(m_Z) = 0.118 $ . Because the small-$ \beta $ resummation is valid only at low$ M_{t\bar{t}} $ , we restrict ourselves to${M_{t\bar t}} \in \left[ {300,380} \right]$ GeV in this work, which is the region most sensitive to$ m_t $ . Following [9, 13], we choose the default values of the renormalization scale$ \mu_r $ and the factorization scale$ \mu_f $ to be$ H_T/4 $ , the corresponding results are regarded as central values. We then vary the scales simultaneously up and down by a factor of two to estimate the remaining theoretical uncertainties. With such a procedure, the error bands are not necessarily symmetric around the central values.First, in Fig. 2 we show the exact NLO correction computed using
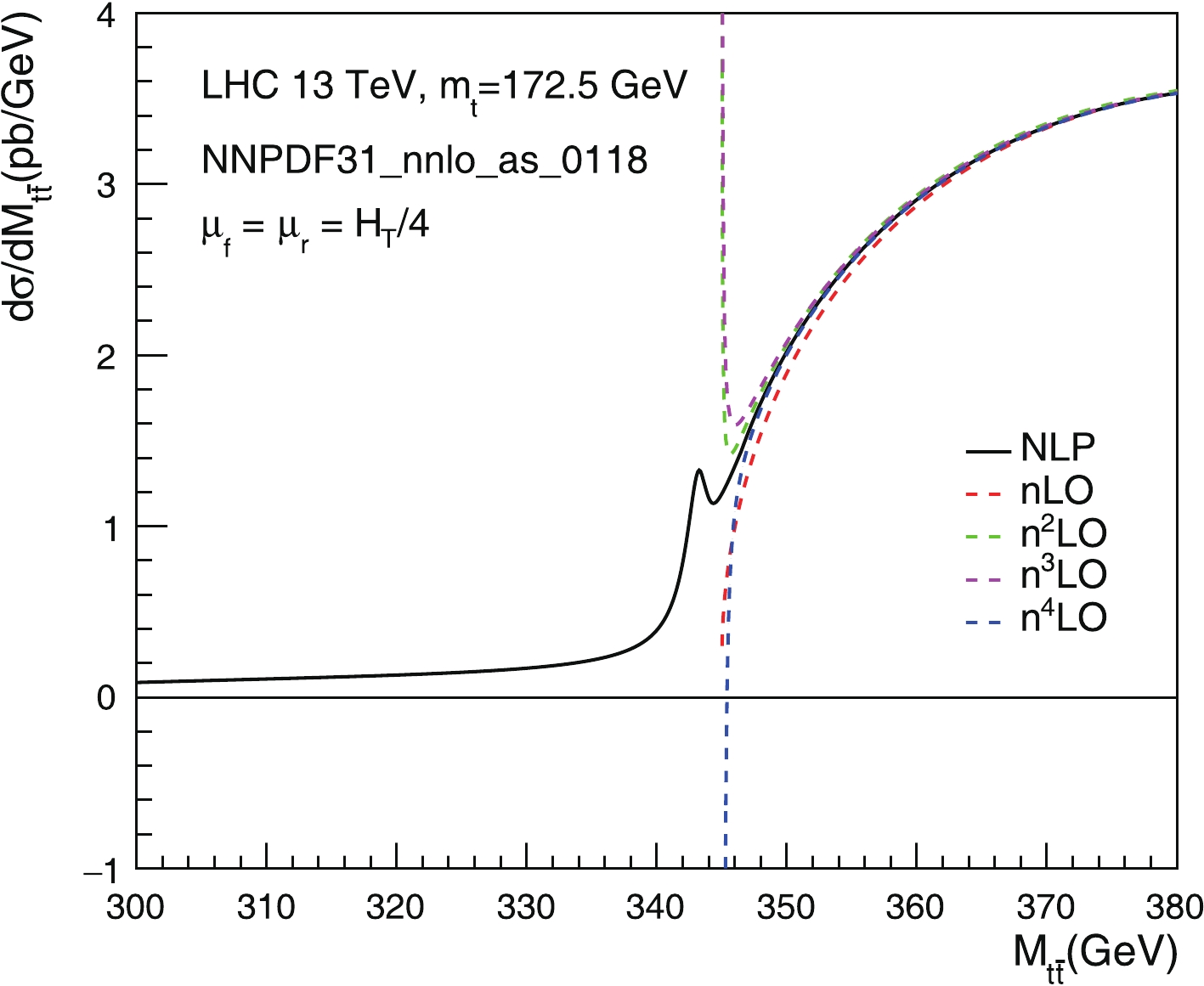
$\texttt{MCFM}$ [30], in comparison with its approximations in various kinematic limits. Such a comparison is important to assess the validity of the approximations within the phase-space region of interest. Fig. 2 has a few significant implications, which we like to elaborate on. 1) The$ \beta \to 0 $ result corresponds to the second term in the fixed-order expansion of our NLP formula (6). It provides an excellent description of the full NLO correction in the range [340, 380] GeV. This demonstrates that our small-$ \beta $ approximation is indeed valid and supports the resummation performed in this work. 2) The$ z \to 1 $ result corresponds to the “soft” or “threshold” limit$ \sqrt{\hat{s}} \to M_{t\bar{t}} $ considered in e.g., [8, 31]. It should be stressed that the concept of “soft” or “threshold” has a completely different meaning than those used in this work. We observe that, while not perfect, the$ z \to 1 $ limit provides a reasonable approximation to the full result in the low$ M_{t\bar{t}} $ region. It is known that this limit works better in the high$ M_{t\bar{t}} $ region [8, 31]. 3) Finally, the double limit$ \beta \to 0 $ and$ z \to 1 $ corresponds to the “soft” limit considered in [16, 20]. This approximation does not capture the dominant contribution at NLO. This is essentially the reason why we do not consider such a “soft” resummation in this work.We now turn to compare the NLP resummed result Eq. (6) and its fixed-order expansion. As in Eq. (8), we label the expansion up to the i-th term (
$ i = 0,1,2,\ldots $ ) as niLO. Here, the lower-case ‘n’ implies that these are approximations to the full NiLO results in the$ \beta \to 0 $ limit. The n0LO result equals exactly the full LO result because of the prefactors in Eq. (6). We show such a comparison in Fig. 3, from which we can draw several important conclusions. 1) The fixed-order expansion converges rather quickly when$ M_{t\bar{t}} $ is significantly larger than$ 2m_t $ . However, when$ M_{t\bar{t}} $ approaches the threshold, the behavior becomes out-of-control. In particular, the n3LO result tends to$ +\infty $ , while the n4LO tends to$ -\infty $ in the$ \beta \to 0 $ limit (${M_{t\bar t}} \to 345\;{\rm{GeV}}$ ). 2) The singularity at$ \beta = 0 $ is regularized by the resummation effects, and we obtain a finite prediction near$ M_{t\bar{t}} = 2m_t $ with the NLP resummation formula. In the resummed result, the region$ M_{t\bar{t}} < 2m_t $ is allowed due to bound-state effects. The shape of the NLP curve for$ M_{t\bar{t}} < 2m_t $ depends crucially on the top quark width. However, we have verified that the integrated cross-section in the [300, 380] GeV range is insensitive to the value of$ \Gamma_t $ . 3) As a final implication of Fig. 3, we note that the NLP curve almost overlaps with the nLO and n2LO curves for${M_{t\bar t}} > 360\;{\rm{GeV}}$ . This indicates that in this region, the matched (N)NLO+NLP results of Eq. (8) are governed by the fixed-order (N)NLO calculations. Effectively, this shows that we do not apply the small-$ \beta $ resummation to regions where the break down of the EFT description is a possibility. Indeed, we have checked that the dominant beyond-NNLO correction comes from the region${M_{t\bar t}} < 350\;{\rm{GeV}}$ , where$ \beta < 0.17 $ and pNRQCD is perfectly applicable.Finally, we match our resummed calculation to the NLO and NNLO results according to Eq. (8). The NLO results are computed using
$\texttt{MCFM}$ and the NNLO results are obtained from [6, 7, 32, 33]. The NLO+NLP and NNLO+NLP results are shown in Fig. 4 and Table 1 along with the NLO and NNLO results, compared against the CMS measurement. We find that the resummation effects enhance the NNLO differential cross-section by about 9%, and make the theoretical prediction more compatible with experimental data. As discussed in the Introduction, this enhancement will have a significant influence on the extraction of the top-quark mass from kinematic distributions. Although we cannot repeat the analysis of [15], we can estimate the impact by studying the$ m_t $ -dependence of the NLO (used in the fit of [15]) and NNLO+NLP predictions for the [300, 380] GeV range. For example, the central value of the NNLO+NLP differential cross-section for${m_t} = 172.5\;{\rm{GeV}}$ is given by 1.434 pb/GeV. To achieve the same differential cross-section using the NLO calculation, one must lower the value of$ m_t $ to approximately 171 GeV. This roughly explains the outcome of [15] and shows that using our prediction in the fit will lead to a shift of about 1.5 GeV resulting in a value closer to the world average.CMS $1.664^{+0.166}_{-0.166}$ 

NLO $1.208^{+0.150}_{-0.139}$ 

NNLO $1.319^{+0.035}_{-0.070}$ 

NLO+NLP $1.367^{+0.107}_{-0.124}$ 

NNLO+NLP $1.434^{+0.014}_{-0.060}$ 

Table 1. Differential cross-sections (in units of pb/GeV) entering Fig. 4.

Figure 4. (color online) Averaged
$t\bar{t}$ invariant mass distribution in [300, 380] GeV range. CMS result [2] is depicted by the green band. Various theoretical predictions are shown in comparison, with NNLO+NLP being our best prediction. -
We studied the
$ t\bar{t} $ invariant-mass distribution near the$ 2m_t $ threshold. In this region, a small gap exists between the most up-to-date theoretical predictions and the experimental measurements by the CMS collaboration at the LHC. This leads to a discrepancy between the values of$ m_t $ determined from direct measurements and from fitting kinematic distributions in$ t\bar{t} $ production. We show that higher-order non-relativistic effects lead to large corrections to the differential cross-section in the threshold region, which were not included in the state-of-the-art theoretical predictions. We derive a factorization formula to resum such corrections to all orders in strong coupling, and calculate necessary ingredients to perform the resummation at next-to-leading power. We combine the resummation with NLO and NNLO results, and present numeric results relevant for LHC phenomenology. We find that the resummation effect increases the differential cross-section in the range${M_{t\bar t}} \in \left[ {300, 380} \right]\;{\rm{GeV}}$ by about 9%. This makes the theoretical prediction more compatible with experimental data, and leads to a shift of about 1.5 GeV on the extracted top-quark mass from kinematic distributions, resulting in a value that is more consistent with the world average.Our results can be easily combined with the soft gluon resummation of [8-10, 31] and with electroweak corrections of [11-14]. This allows a precision prediction for the
$ t\bar{t} $ invariant-mass spectrum across the entire phase space. Our framework can be extended to study the$ t\bar{t}+{\rm{jets}} $ production process, which is also used to extract the top quark mass [34, 35].L. L. Yang would like to thank A. Mitov for useful discussions.
Invariant-mass distribution of top-quark pairs and top-quark mass determination
- Received Date: 2020-04-09
- Available Online: 2020-09-01
Abstract: In this study, we investigate the invariant-mass distribution of top-quark pairs near the 2mt threshold, which strongly influences the determination of the top-quark mass mt. Higher-order non-relativistic corrections lead to large contributions, which are not included in the state-of-the-art theoretical predictions. A factorization formula is derived to resum such corrections to all orders in the strong-coupling, and necessary ingredients are calculated to perform the resummation at next-to-leading power. We combine the resummation with fixed-order results and present phenomenologically relevant numerical results. The resummation effect significantly increases the differential cross-section in the threshold region and makes the theoretical prediction more compatible with experimental data. We estimate that using our prediction in the determination of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: