-
Nuclear fragmentation, in which several intermediate-mass fragments (IMFs) are produced, has been the subject of numerous experimental and theoretical studies [1-4], and has been observed in nearly all types of high-energy nuclear reactions induced by hadrons, photons, and heavy ions [5, 6]. From a basic science perspective, understanding the fragmentation is important not only for studying the reaction mechanism of nuclear collisions [7, 8], but also to extract the nuclear equation of state (EOS) [9].
A fragmentation is predicted to be related to the coexistence of liquid and gas phases in expanding nuclear matter [4]. Owing to the monotonically increasing trend of the density-dependent symmetry energy at subnormal densities, a low-density phase (gas) should have a larger isospin asymmetry than a high density phase (liquid) in an equilibrated two-phase system, which is an isospin fractionation (IsoF) phenomenon. Indications of an IsoF have been reported since the early 1980s, although the concept of a liquid–gas phase transition has not been used [10]. Other models predict the IsoF as a general phenomenon during the liquid–gas phase transition of neutron-rich nuclear matter [11-15]. Comparisons among the data on the N/Z ratios of fragments and the light clusters in HICs at the Fermi energy levels have been conducted for probing of IsoF [16, 17]. In particular, the experiments and analyses conducted by Xu et al. at NSCL/MSU unambiguously confirmed the IsoF phenomenon occurring in nuclear multifragmentation [18].
IsoF is the manifestation of isospin drift, which is driven by the density gradient. However, isospin diffusion (IsoD) refers to the isospin transport between regions separated by the isospin gradient. IsoD is known to be a rapid process [19, 20]. There have been no consistent conclusions regarding its relaxation time, although studies have suggested an order of 100 fm/c [21-23]. Isospin drift has a longer timescale [24]. Using the rotation angle as a clock, it has been shown that the isospin transport takes effect at beyond 1200 fm/c [25, 26]. Both the IsoD and drift are related to the symmetry energy, which is an important but uncertain part of the EOS of asymmetrical nuclear matter [27, 28]. The progress on constraining the symmetry energy at densities below and around the saturation value by the IsoD data has been widely reported [29-33]. Isospin observables related to the long isospin drift process have also been proposed [15, 24]. Another opportunity to investigate the symmetry energy is the IsoF in projectile fragmentations at GeV/u energy levels [34, 35].
In our previous study, to investigate the secondary decay effects of projectile fragmentations in 124Sn and 107Sn + 120Sn collisions at 600 MeV/u, the isospin-dependent quantum molecular dynamics (IQMD) model was coupled with the statistical code GEMINI [36]. In this study, we continue this investigation and extend it to the isospin dependence of the projectile fragmentation at hundreds of MeV/u. We focused on searching for isospin observables related to the isospin fractionation to extract the symmetry energy. The remainder of this paper is organized as follows. In Sec. 2, we briefly describe the proposed method. In Sec. 3, we present both the results and a discussion. Finally, some concluding remarks are given in Sec. 4.
-
In this study, both the formation of a projectile spectator and the fragmentation processes are described using the IQMD model. The version of the IQMD code applied is IQMD-BNU from Beijing Normal University. The GEMINI model is used to simulate the light-particle evaporation of the prefragments. Readers can refer to the theoretical description in [36]. Here, we emphasize the improvements over the standard version, which are significant to describe the emission of IMFs. First, the phase-space density constraint method is applied to compensate for the fermionic feature. This improvement clearly increases the production of IMFs. Second, we stop the IQMD evolution of each event when the excitation energy of the largest fragment becomes less than a special value Estop, which corresponds to the threshold energy of the multiple fragmentation. Here, Estop = 3 MeV/u is used. Third, except for the light-particle evaporation, other decay modes in the GEMINI code, such as symmetric and asymmetric fission, are switched off. In this case, the emission of the IMFs is described dynamically. Finally, fragments can be recognized using a minimum spanning tree (MST) algorithm at any time during the reaction process. In the IQMD model, the positions and momenta of the nucleons as a function of time can be obtained. The nucleons with a relative distance of the coordinates and a momentum of
$ |r_{i} - r_{j}| \leqslant R_{0} $ and$ |p_{i} - p_{j}| \leqslant P_{0} $ belong to a fragment. Here,$ R_{0} $ = 3.5 fm and$ P_{0} $ = 250 MeV/c are phenomenological parameters that have been found to best reproduce the experimental fragment multiplicities and production cross sections.The nuclear potential energy density of the asymmetric nuclear matter with density
$ \rho $ and asymmetry$ \delta $ is given by$ V(\rho, \delta) = \frac{\alpha}{2} \frac{\rho^2}{\rho_0} + \frac{\beta}{\gamma+1} \frac{\rho^{\gamma+1}}{\rho_0^{\gamma}} + \frac{C_{sp}}{2}\left(\frac{\rho}{\rho_{0}}\right)^{\gamma_{i}} \rho \delta ^{2}, $

(1) where
$ \rho_0 $ is the normal density. The chosen parameters are$ \alpha $ = 356.00 MeV,$ \beta $ = 303.00 MeV, and$ \gamma $ = 7/6, which provide a compressibility of 200 MeV at the saturation density for isospin symmetric nuclear matter. The density dependence of the symmetry energy depends on the parameters$ C_{sp} $ and$ \gamma_{i} $ . In addition,$ C_{sp} $ = 38.06 MeV provides asymmetry energy of 31.60 MeV at the saturation density. The parameter$ \gamma_{i} $ is varied to study the possible consequences of the slope of the symmetry energy. The parameters$ \gamma_{i} $ = 0.35, 0.75, and 2 will be applied, providing the slopes of the symmetry energy at a normal density of 45.12, 67.96, and 139.32 MeV, respectively. -
The mean neutron-to-proton ratio
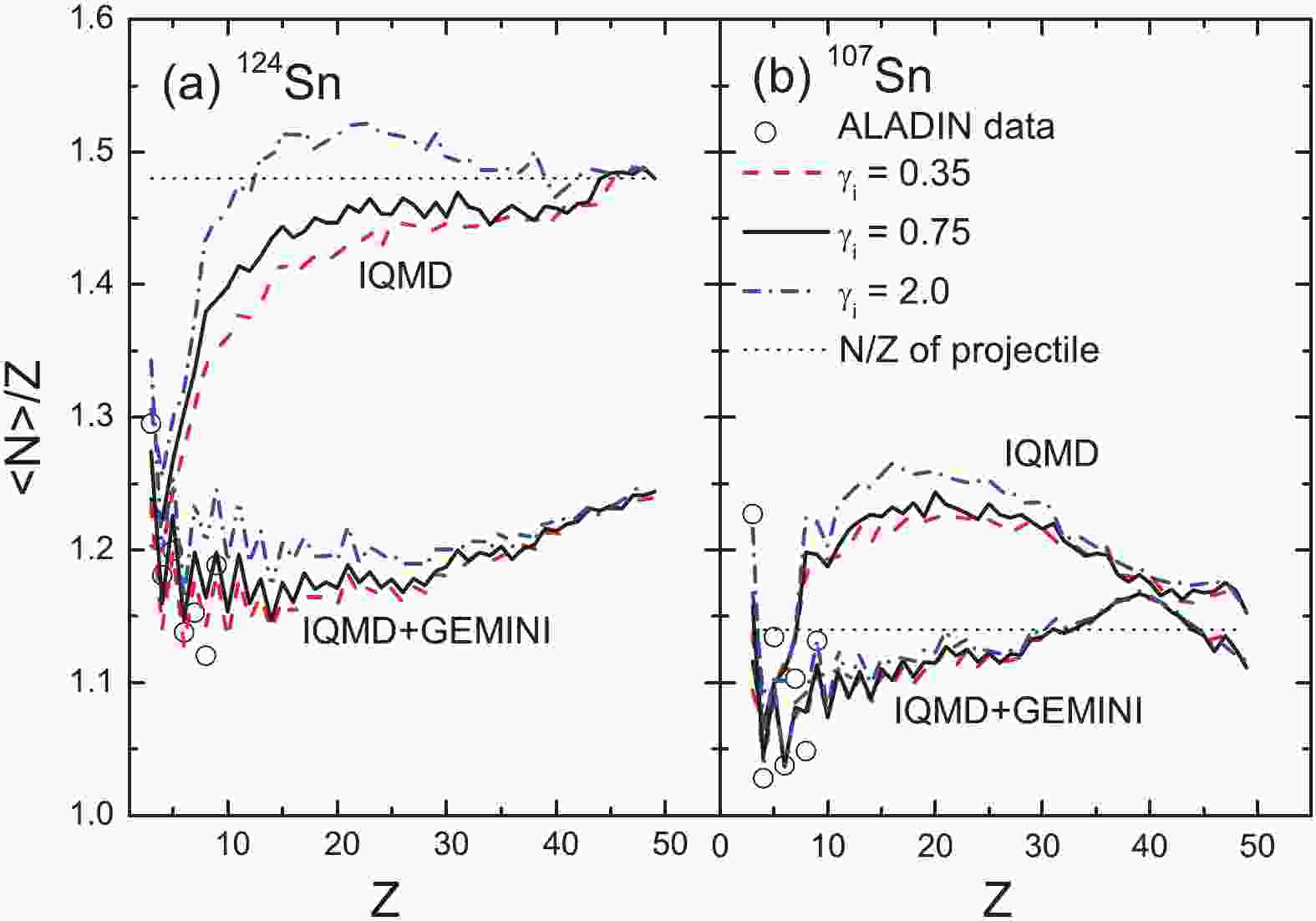
$ \langle {{N}} \rangle /{{Z}}$ of the light fragments was investigated to display the secondary decay effects shown in our previous study [36]. We begin the discussion by showing the$ \langle {{N}} \rangle/{{Z}} $ of the elements produced in the projectile fragmentation of 124Sn and 107Sn + 120Sn at 600 MeV/u, as shown in Fig. 1. In [3], the experimental$ \langle {{N}} \rangle/{{Z}} $ data of the elements for Z > 4 produced in the projectile fragmentations of 136Xe and 124Xe + 208Pb at 1000 MeV/u were demonstrated, as also indicated in Fig. 2. The data show the obvious odd-even staggering for elements with Z < 15. However, the odd-even staggering for the heavy fragments (Z > 15) is weak. In our previous study, we demonstrated that the evaporation of nucleons during the secondary decay stage is responsible for the odd-even staggering of the light elements. It has also been proposed that the$ \gamma $ emission becomes a competitive decay channel during the last decay steps for heavy fragments and is responsible for the vanishing of the even-odd staggering with increasing mass [37]. The data also show the isospin dependence, i.e., a larger N/Z of the projectile results in a larger$ \langle {{N}} \rangle/{{Z}} $ of the productions.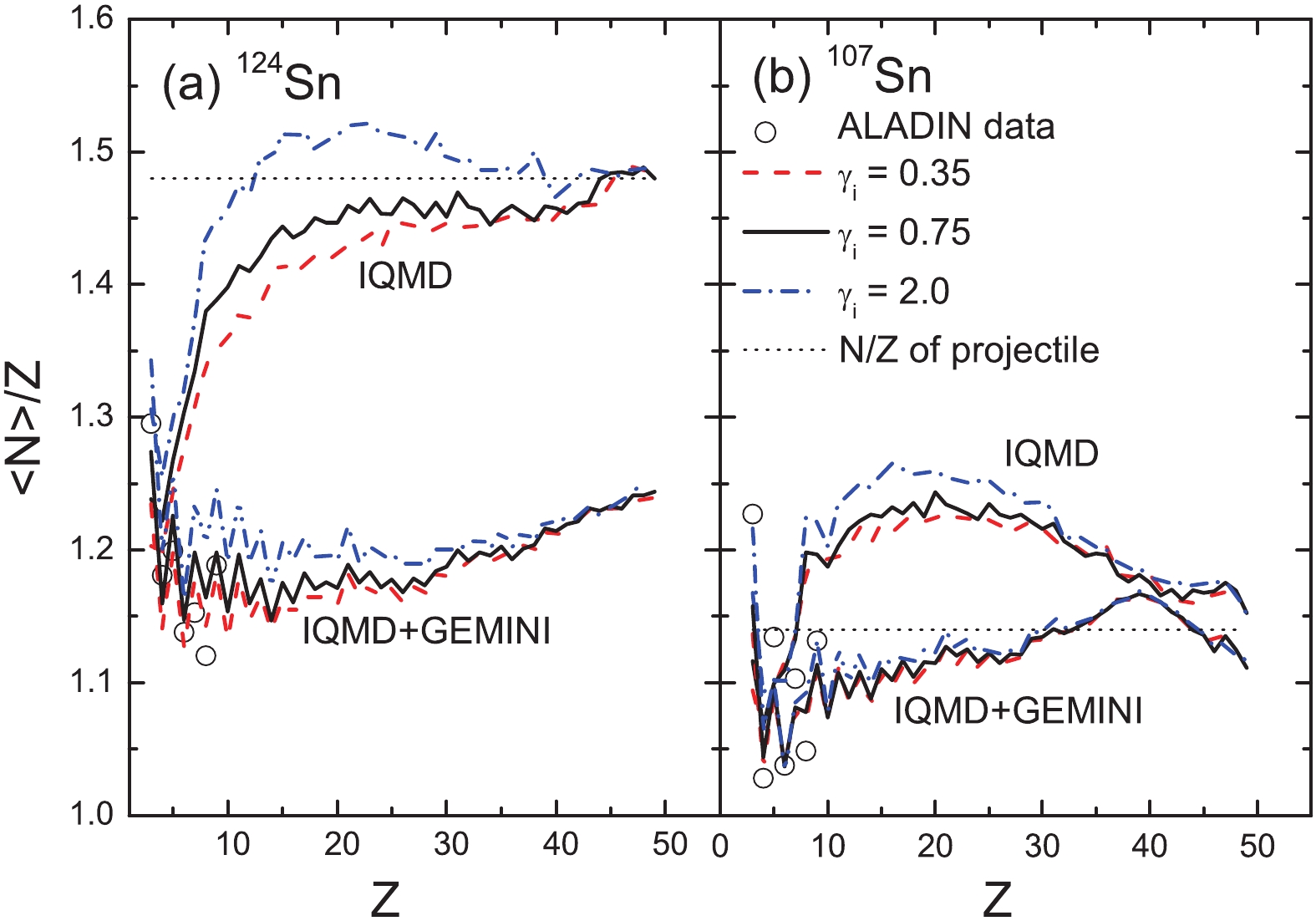
Figure 1. (color online) Mean neutron-to-proton ratios
$ \langle {{N}} \rangle/{{Z}} $ of the elements produced in the projectile fragmentations of 124Sn and 107Sn + 120Sn at 600 MeV/u. The data are taken from [2].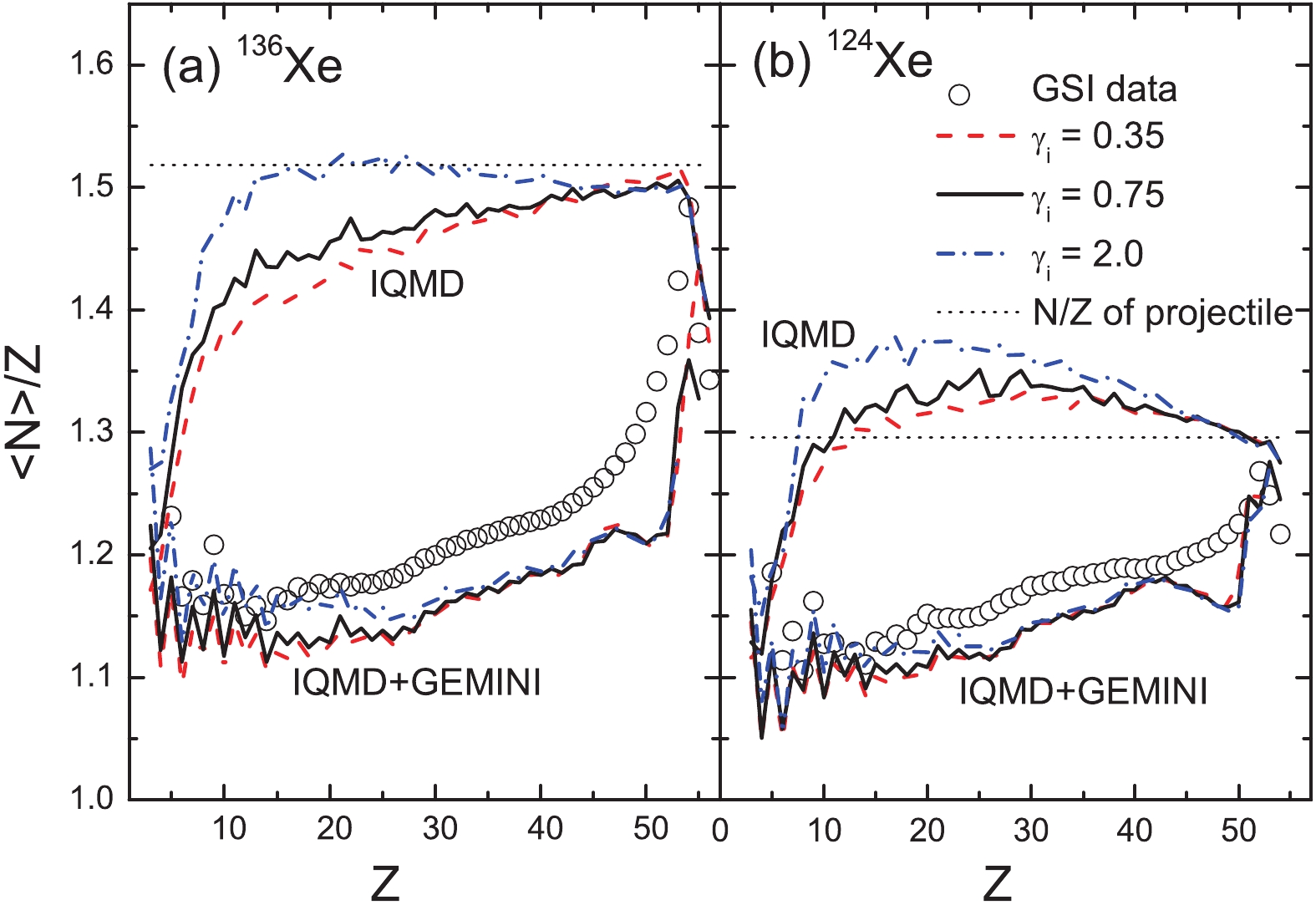
Figure 2. (color online) Mean neutron-to-proton ratios
$ \langle {{N}} \rangle/{{Z}} $ of the elements produced in the projectile fragmentations of 136Xe and 124Xe + 208Pb at 1000 MeV/u. The data are taken from [3].The calculations conducted using the IQMD+GEMINI model reproduce the general features of the data, i.e., the odd-even staggering and isospin dependence. However, the experimental values are not well described, especially for the heavy elements. The
$ \langle {{N}} \rangle/{{Z}} $ values are related to the isotope distributions, which are also not well described with the chosen parameter Estop = 3 MeV/u [36]. Here, Estop = 3 MeV/u is used because it is close to the threshold energy of the multiple fragmentation. With a larger Estop, the model can manifest stronger structural effects in the secondary evaporation stage and better describe the$ \langle {{N}} \rangle/{{Z}} $ and isotope distributions. However, a larger Estop value than the threshold energy of the multiple fragmentation is dynamically in contrast to the purpose of the IMF emissions.The
$ \langle {{N}} \rangle/{{Z}} $ values of the pre-fragments calculated by IQMD show a uniform increase over Z in the IMF region, but depend strongly on the projectile in the residue region. The residues produced in the 124Sn and 136Xe projectile fragmentation maintain the memory of the initial N/Z. For the 107Sn and 124Xe projectiles, the$ \langle {{N}} \rangle/{{Z}} $ value of the residues are larger than the initial N/Z of the projectile. Two types of isospin dynamics may enlarge the N/Z of the projectile-like source and are responsible for exceeding the$ \langle {{N}} \rangle/{{Z}} $ values. Being attracted by the valley of stability ($ \langle {{N}} \rangle/{{Z}} $ = 1.37 in the Sn region and 1.42 in the Xe region), the projectile loses several protons during the early stage of a collision. With the role of the IsoD, the projectile-like source obtains several neutrons from the neutron-richer target.In the calculations, two soft (
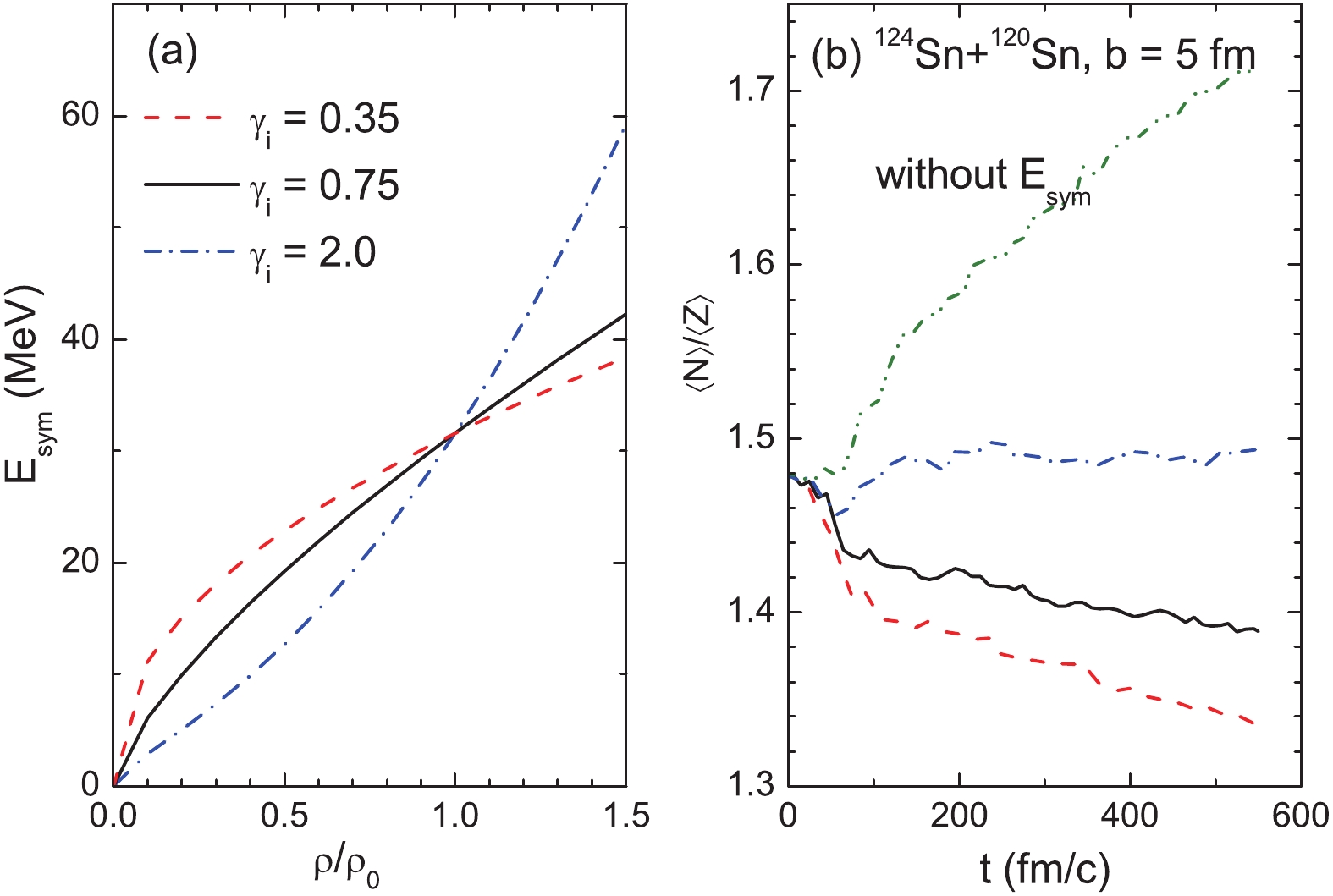
$ \gamma_{i} $ = 0.35 and 0.75) and stiff ($ \gamma_{i} $ = 2) symmetry energies are used. The stiff symmetry energy causes a larger$ \langle {{N}} \rangle/{{Z}} $ than the two soft cases. The strong dependence of the calculations when using IQMD on the symmetry energies indicates the significance of the isospin degree of freedom in the projectile fragmentation. However, the secondary decay reduces the$ \langle {{N}} \rangle/{{Z}} $ values and weakens the symmetry energy dependence.Figure 3(a) shows the density dependence of the symmetry energy with
$ \gamma_{i} $ = 0.35, 0.75, and 2, the slopes of which at normal density are 45.12, 67.96, and 139.32 MeV, respectively. At a subnormal density, the larger$ \gamma_{i} $ provides a smaller symmetry energy. During the projectile fragmentation, the fragmenting source does not undergo a compression stage. Thus, the symmetry energy at subnormal and approximately normal densities will take effect. Figure 3(b) shows the neutron-to-proton ratio$ \langle N\rangle / \langle Z\rangle $ of the heaviest fragment as a function of time in the collisions of 124Sn + 120Sn at 600 MeV/u with an impact parameter of b = 5 fm. The calculation using the IQMD model with$ \gamma_{i} $ = 0.35, 0.75, and 2, as well as without the symmetry energy are compared to show the role of the symmetry energy. When the symmetry energy is not considered, the protons continue emitting with the role of the Coulomb repulsive force, resulting in an increase in$ \langle N\rangle / \langle Z\rangle $ over time. The symmetry energy provides an attractive force for the proton in the neutron-rich system, resulting in smaller$ \langle N\rangle / \langle Z\rangle $ values. The$ \langle N\rangle / \langle Z\rangle $ as a function of time depends on the slope of the symmetry energy. With the increase in the value of parameter$ \gamma_{i} $ , the decrease of$ \langle N\rangle / \langle Z\rangle $ is more rapid. The calculations with$ \gamma_{i} $ = 2 even slightly increase. Most of the fragmentations for b = 5 fm take place before 600 fm/c [36]. However, the values of$ \langle N\rangle / \langle Z\rangle $ do not reach saturation. This indicates that not only the fragmentation but also the evaporation of light particles affect the isospin of the heaviest fragment. -
The productions are divided into light particles (Z < 3), IMFs (3 ≤ Z ≤ 20), and fragmenting residues (Z > 20). The time evolutions of the multiplicity and neutron-to-proton ratio
$ \langle N\rangle / \langle Z\rangle $ of the three types of productions with rapidity y > 0 during the reactions of 124Sn, 107Sn + 120Sn at 600 MeV/u are shown in Fig. 4. The condition y > 0 is applied to select roughly the productions from the projectile fragmentation. In the calculations,$ \gamma_{i} $ = 0.75 is considered. The time evolutions of the multiplicity for projectile fragmentations of 124Sn and 107Sn are similar. Because of the emissions from the participator, the multiplicity of light particles is approximately 30 at 50 fm/c. This increases rapidly from 50 to 100 fm/c, accompanied with an increase in the IMFs and a decrease of the fragmenting residues. After 100 fm/c, the multiplicity of the IMFs reaches saturation. However, this is a dynamic balance in which some of the IMFs will be produced by a splintering of fragmenting residues or large IMFs, and other IMFs break into light particles.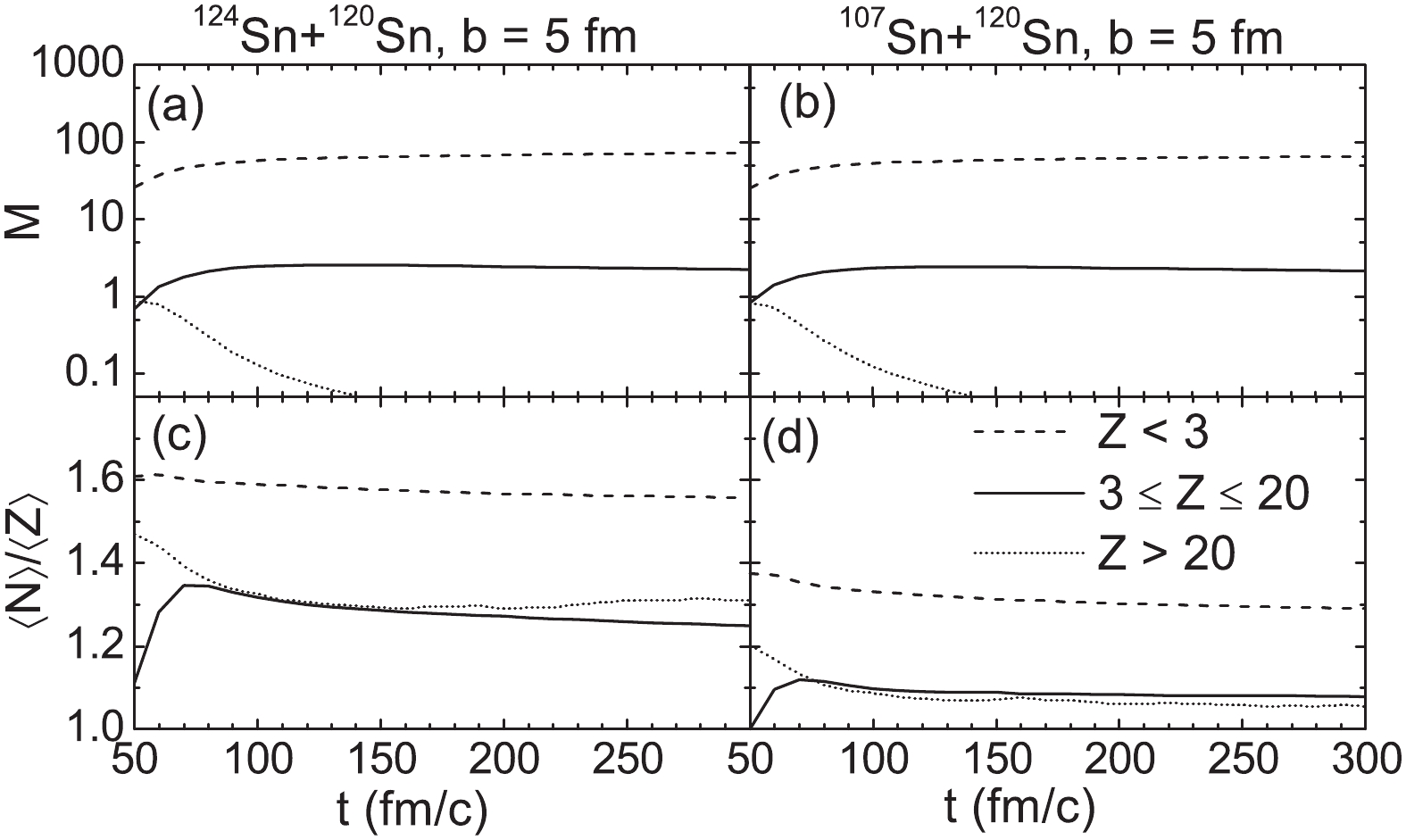
Figure 4. Time evolutions of the multiplicity and neutron-to-proton ratio of the light particles (Z < 3), intermediate-mass fragments (
$3 \leqslant Z \leqslant 20 $ ), and residues (Z > 20) with positive rapidity in the reactions of 124Sn and 107Sn + 120Sn at 600 MeV/u with an impact parameter b = 5 fm.Despite the different values, the trends of the
$ \langle N\rangle / \langle Z\rangle $ evolutions for the 124Sn and 107Sn cases are similar. At the violent collision stage (before 50 fm/c), more neutrons are emitted than protons. Thus, the values of$ \langle N\rangle / \langle Z\rangle $ of light particles at 50 fm/c are larger than the N/Z of the projectiles. After 50 fm/c, a fragmenting stage occurs because the multiplicity of fragmenting residues decreases whereas that of the IMFs increases. IsoF can be seen from the decreasing$ \langle N\rangle / \langle Z\rangle $ of the fragmenting residues.The interaction time between the projectile and target is approximately 50 fm/c for the central collisions, whereas the timescale of the IsoD is on the order of 100 fm/c. This mean that IsoD in the 107Sn + 120Sn and 124Xe + 208Pb collisions will take place, particularly for the central collisions. Figure 5 shows the density and N/Z distributions in the pre-equilibrium stage of a 107Sn + 120Sn collision at 600 MeV/u with b = 5 fm. The N/Z distributions at t = 0 fm/c show that the isospin gradient between the projectile and target is significant. The N/Z distributions at 50 fm/c, when the PLS and target-like source (TLS) separate, indicate that a portion of the projectile-like source has N/Z values of larger than 1.3. The IsoD between the projectile and target is more obvious for a smaller impact parameter because of the longer interaction time between the projectile and target. This results in a richer neutron-to-proton ratio of the PLS than that of the projectile, and hence larger extracted
$ \rho_{n}/\rho_{p} $ values for the central collisions.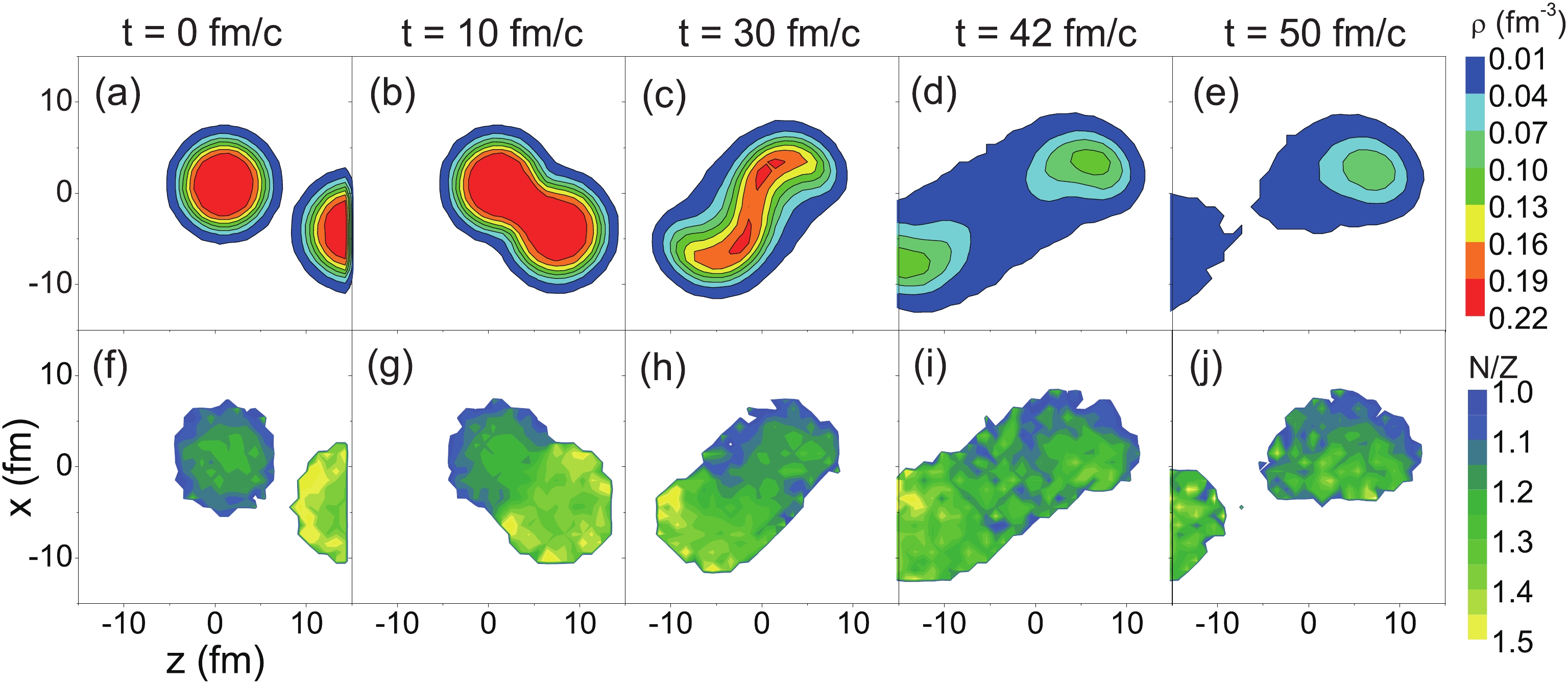
Figure 5. (color online) Density
$ \rho $ and N/Z distributions in the pre-equilibrium stage of 107Sn + 120Sn collision at 600 MeV/u with b = 5 fm.The correlation between the rapidity y and transverse momentum pt is generally applied to sort the emission sources. In Fig. 6, the multiplicity of the light particlessemitting at different stages of 107Sn + 120Sn collision at 600 MeV/u with impact parameter b < 10 fm are shown as functions of the rapidity y and transverse momentum pt in the center-of-mass frame. The transverse momentum pt is normalized to the mass of the nucleon, i.e., 938 MeV, whereas the rapidity y is normalized to the incident momentum. The sources of the light particles in different panels can be distinguished in an approximate manner. In general, there are several sources for the emission of the light particles. For the first, i.e., a pre-equilibrium emission, the projectile and target are in touch with each other and some nucleons in the participant-region will emit after a few nucleon-nucleon collisions. Such nucleons have rapidity at near the initial collision (y = ±1) and a small transverse momentum. The pt-y map of such nucleons is shown in Fig. 6(a). For the second, i.e., the participant source, during collisions with a small impact parameter, one of the participants is completely stopped and has zero rapidity after a violent nucleon-nucleon collision. The violent stage of the central collisions is longer than that of the peripheral collision, for which the projectile and target have separated at t = 50–100 fm/c. The light particles not only from the stopped participant but also from the PLS and TLS contribute to the image in Fig. 6(b). However, the former has dominance owing to the maximum multiplicity at y = 0 in Fig. 6(b). In addition, the PLS and TLS form after the projectile and target have separated. Multiple fragmentation then takes place before the excitation energy becomes lower than the threshold energy. The light particles from the PLS have an average rapidity at near y = 1, whereas those for the TLS are at y = -1. Thus, two peaks are shown in Figs. 6(c) and (d). As the temperatures of the PLS and TLS decrease, the emission of the light particles reduces. The multiplicities in Fig. 6(d) are smaller than those in Fig. 6(c). For the final source, after the multiple fragmentation, the light particles also evaporate from the residual nucleus, which occurs at nearly zero temperature. The rapidity and transverse momentum of the residual nucleus are similar to the initial values. The multiplicity of the evaporated light particles is shown in Fig. 6(e).
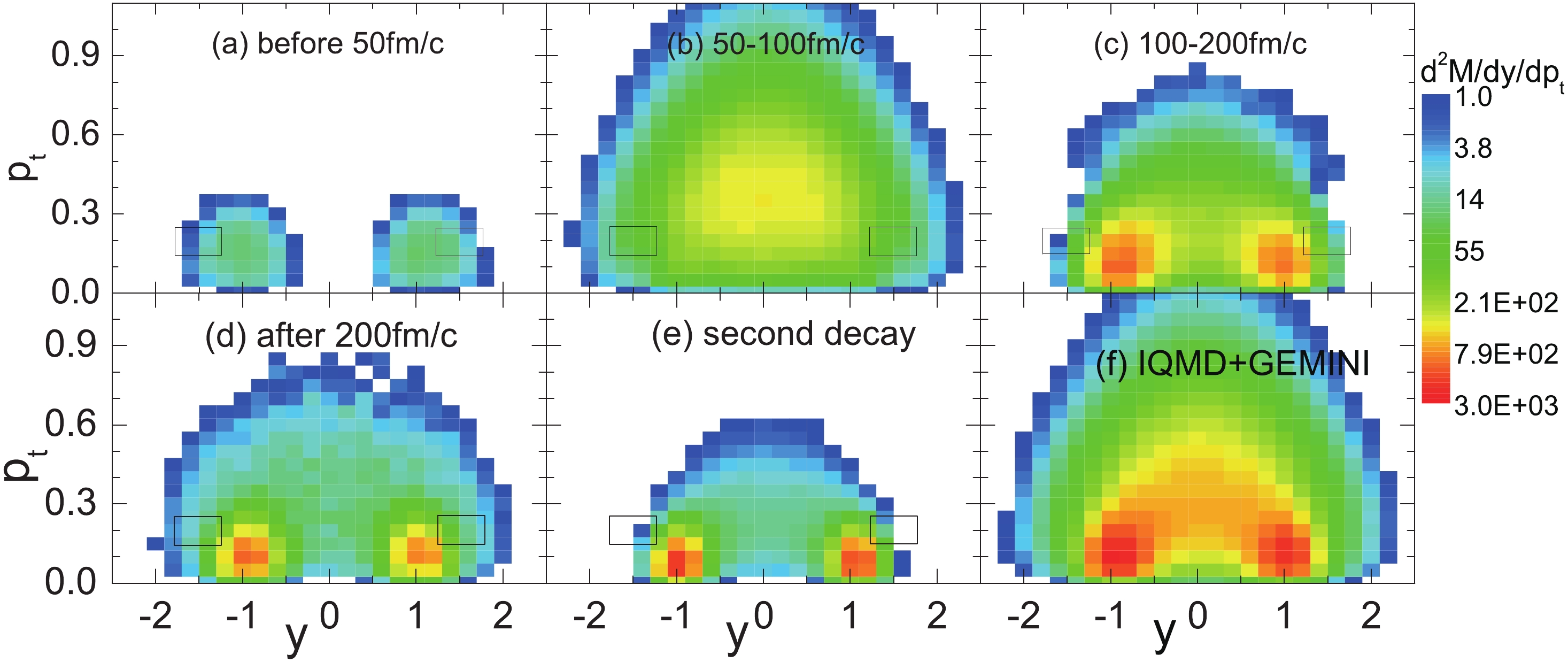
Figure 6. (color online) Multiplicity of the light particles emitted at different stages as functions of the transverse momentum pt and rapidity y in the center-of-mass frame for a 107Sn + 120Sn collision at 600 MeV/u with impact parameter b < 10 fm. The transverse momentum pt is normalized to the mass of the nucleon, i.e., 938 MeV, whereas the rapidity y is normalized to the incident case. The squares indicate a filter with 1.25 < y < 1.75 and 0.15 < pt < 0.25.
Note that the above sorting of the sources is approximated. The momentum yields of the particles emitted from an equilibrium source fit the Maxwell–Boltzmann distribution. This results in a higher relative energy than the source, and a lower yield of the light particles. Specifically, to distinguish the PLS from other sources, we sort the light particles from the PLS using a filter with 1.25 < y < 1.75 and 0.15 < pt < 0.25. The squares in Fig. 6 indicate the filter. The light particles mainly come from the PLS. The double differential multiplicities in these regions are approximately 100. Similarly, the light particles from the TLS are sorted by −1.75 < y < −1.25 and 0.15 < pt < 0.25.
-
The neutron-to-proton ratios of the sorted light particles are used to study the symmetry energy dependence of the projectile fragmentation. Two soft (
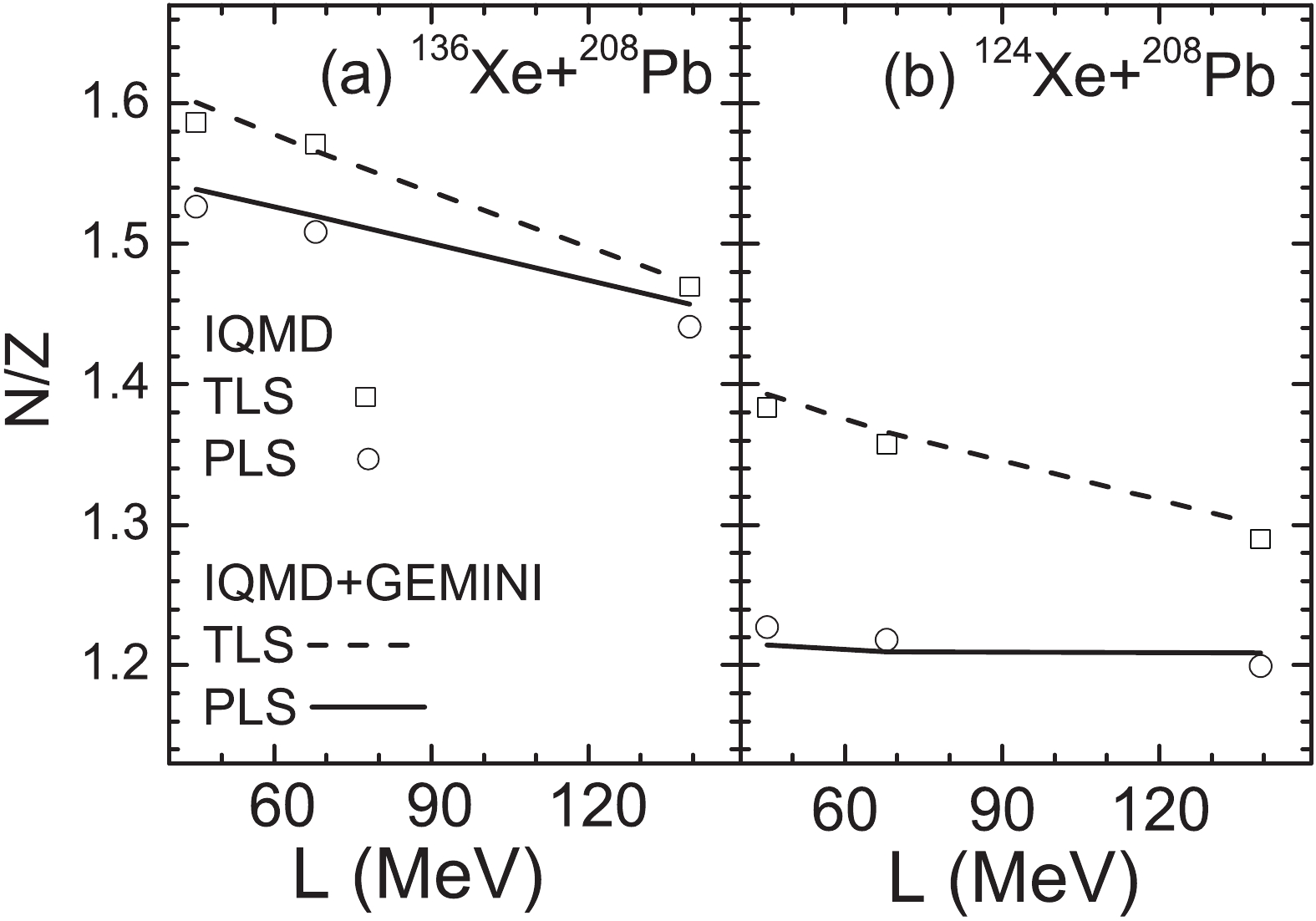
$ \gamma_{i} $ = 0.35 and 0.75) and a stiff ($ \gamma_{i} $ = 2) symmetry energies are used in the calculations and provide the slopes of the symmetry energy at normal densities of 45.12, 67.96, and 139.32 MeV. The results for 124Sn and 107Sn + 120Sn collisions at 600 MeV/u and for 136Xe and 124Xe + 208Pb collisions at 1000 MeV/u are shown in Fig. 7 and Fig. 8, respectively.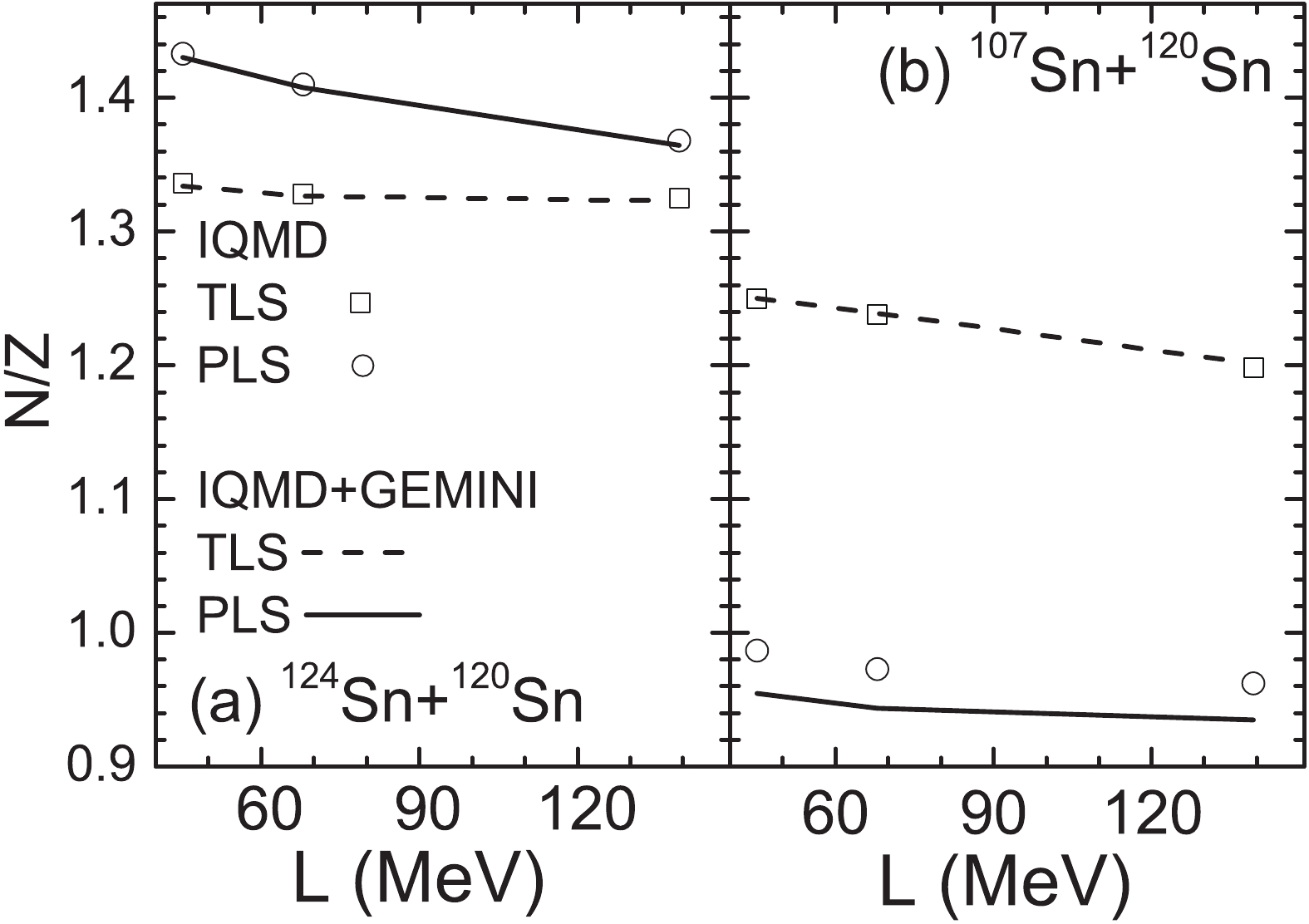
Figure 7. Neutron-to-proton ratios of the light particles emitted from the fragmenting sources in the 124Sn and 107Sn + 120Sn collisions at 600 MeV/u. The filter with rapidity 1.25 < y < 1.75 and transverse momentum 0.15 < pt < 0.25 is applied to sort the light particles from the PLS, whereas that at -1.75 < y < -1.25 and 0.15 < pt < 0.25 is applied to TLS. The neutron-to-proton ratios are shown as a function of the slopes of symmetry energy applied in the model. The curves show the calculations by the IQMD+GEMINI model, and the squares and circles show those by the IQMD model.
After using the sorting method, the symmetry energy dependence of the IsoF is clearly displayed by the neutron-to-proton ratios of the light particles, as shown in Figs. 7 and 8. Furthermore, comparing the calculations with and without GEMINI, it can be seen that the secondary decay effect of the isopin observable is weak for the PLS 107Sn. From Fig. 6, it can be seen that the double differential multiplicities of the sorted light particles from the TLS are larger than 100, but smaller than 5 for the secondary decay. The contribution of the secondary decay to the sortied light particles from the PLS is greater. The double differential multiplicity is approximately 15 at (y, pt) = (1.4, 0.2). However, the secondary decay effect can be further weakened by increasing the rapidity of the filter.
It is worth briefly discussing the isospin observable. First, by comparing the values of N/Z for the 120Sn-like fragmenting sources between the 124Sn + 120Sn and 107Sn + 120Sn collisions, it can be seen that both IsoD and IsoF take place. However, the effect of the IsoD can be eliminated by using a symmetric collision such as 208Pb + 208Pb. This is an advantage for the experiment because a radioactive beam is not a requisite. Second, for the PLS, the measuring angle in the laboratory frame is approximately 15°, and the kinetic energy of the particles is close to the incident energy. A measurement is possible. Moreover, the yields of the sorting particles are sufficiently large to reduce the statistical error. Finally, because many transport models have difficulty reproducing the relative abundances of the light isotopes, all light particles other than an isotope are included. The uncertainty of the transport models can be further minimized using the double ratio of the neutron-to-proton ratio between the two systems with different isospin asymmetries of the projectiles.
-
It was demonstrated in our previous study that, by conducting a fragmentation using an isospin-dependent quantum molecular dynamics (IQMD) model and permitting only evaporation in the statistical model GEMINI, the IQMD+GEMINI model is able to reproduce the main features of the projectile fragmentation. In this study, we continue and extend this approach to the isospin dependence of the projectile fragmentation at hundreds of MeV/u. The calculations of the mean neutron-to-proton ratio
$ \langle {{N}} \rangle/{{Z}} $ of the elements produced in the projectile fragmentations of 124Sn and 107Sn + 120Sn at 600 MeV/u and 136Xe and 124Xe + 208Pb at 1000 MeV/u are compared with the previous data. It was shown that the IQMD+GEMINI model reproduces the general trend of the data but underestimates the$ \langle {{N}} \rangle/{{Z}} $ values for elements with Z > 15. The calculations of$ \langle {{N}} \rangle/{{Z}} $ without GEMINI indicate the significant role of the symmetry energy at a subnormal density on the projectile fragmentation. However, the secondary decay weakens the symmetry energy dependence of the isospin observable$ \langle {{N}} \rangle/{{Z}} $ .The isospin transport in HICs at hundreds of MeV/nucleon was investigated. The interaction time between the projectile and the target is approximately 50 fm/c for central collisions at 600 MeV/u, whereas the timescale of the isospin diffusion is on the order of 100 fm/c. Thus, isospin diffusion will take place at the pre-equilibrium stage of the collisions. At the fragmenting stage, the isospin fractionation plays a part. It is believed that the gas phase (light particles) is steamed out from the periphery of the fragmenting source, which is at a subnormal density. Compared to the soft symmetry energy, the stiff symmetry energy provides a smaller repulsive force for neutrons and an attractive force for the protons in a neutron-rich system at a subnormal density, and hence causes a smaller isospin asymmetry of the light particles, leaving a more neutron-rich liquid phase.
A robust isospin observable was proposed for extracting the slope of the symmetry energy at normal density through the isospin dependence of the projectile fragmentation at hundreds of MeV/u, which is the neutron-to-proton ratio of the light particles emitted from the projectile-like source. Several suggests for additional study are as follows. First, a filter with a rapidity of 1.25 < y < 1.75 and a transverse momentum of 0.15 < pt < 0.25 in the center-of-mass frame will be applied to sort the light particles emitted from the projectile-like source. This means that the light particles will be measured at near an angle of 15° in the laboratory frame. Second, a symmetric collision and a stable beam will be applied to eliminate the effects of the isospin diffusion. Finally, because many transport models have a difficulty reproducing the relative abundances of the light isotopes, all light particles other than an isotope will be included. The uncertainty of the transport models can be further minimized by using the double ratio of the neutron-to-proton ratio between two systems with different isospin asymmetries of the projectiles.
The authors are grateful to W. Trautmann for the helpful and detailed discussions.
Isospin dependence of projectile fragmentation at hundreds of MeV/u
- Received Date: 2020-01-08
- Accepted Date: 2020-03-19
- Available Online: 2020-08-01
Abstract: By modeling the fragmentation process using a dynamic model and permitting only evaporation in the statistical code, the main features of a projectile fragmentation at 600 MeV/u were considered in our previous study [Phys. Rev. C, 98: 014610 (2018)]. In this study, we extend this to the isospin dependence of a projectile fragmentation at several hundreds of MeV/u. We searched for isospin observables related to the isospin fractionation to extract the symmetry energy, and found that at the pre-equilibrium stage of the collisions an isospin diffusion will take place and affect the isospin of the final fragments. The isospin fractionation plays a part during the fragmenting stage. Compared to the soft symmetry energy, the stiff symmetry energy provides a smaller repulsive force for neutrons and an attractive force for the protons in a neutron-rich system at a subnormal density, and hence causes a smaller isospin asymmetry of the gas phase, leaving a more neutron-rich liquid phase. An observable robust isospin is proposed to extract the slope of the symmetry energy at normal density based on the isospin dependence of the projectile fragmentation at hundreds of MeV/u.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: