-
Over the last two decades, the nuclear symmetry energy has been one of the most studied topics in nuclear physics [1]. Indeed, the behavior of the isovector part of the nuclear effective interaction, and the corresponding region of the nuclear Equation of State (EoS), is quite controversial once we move away from normal density. Nevertheless, this information is essential in the astrophysical context for understanding the properties of compact objects such as neutron stars, whose crust behaves as low density asymmetric nuclear matter (ANM), and whose core may touch extreme values of density and asymmetry [2, 3]. The low density behavior of the symmetry energy also affects the structure of exotic nuclei and the appearance of new features of the neutron skin, which are currently under intense investigation [4, 5]. Moreover, the symmetry energy also plays a crucial role in the dynamics of heavy-ion collisions involving neutron-rich nuclei, on which several studies are concentrating nowadays [1, 6–9]. The theoretical study of the nuclear matter symmetry energy has been conducted starting from realistic interactions, including meson exchange [10, 11] and chiral forces [12], and from phenomenological interactions, such as the Skyrme forces [13] and relativistic approaches [14, 15].
The symmetry energy is the response of symmetric nuclear matter (SNM) to a small neutron-to-proton imbalance β (we assume
$ \beta > 0 $ ). Consistent with the empirical nuclear mass table, where the symmetry energy is introduced to reproduce the binding energies in isobaric chains, the symmetry energy is obtained from the second-order truncation of the energy per particle in calculations of isospin ANM in terms of the asymmetry parameter β. The symmetry energy has been frequently calculated as the energy shift between pure neutron matter (PNM) and SNM assuming a$ \beta ^2 $ linearity in the full asymmetry range, i.e.$ 0<\beta<1 $ . This assumption, henceforth referred to as the$ \beta^2 $ law, has been validated by one of the first$ \it ab\,initio $ ANM calculations in the Brueckner-Hartree-Fock (BHF) approximation with realistic two-body forces (2BF) [10], and was confirmed by extending the calculations to three-body forces (3BF) [16]. More recently, the$ \beta^2 $ law was used to extrapolate all asymmetry range$ \it ab\,initio $ calculations performed for neutron matter with small proton fractions [12]. However, there is not enough awareness that this behavior could be invalidated when the mean field approximation is applied far from the saturation density. Here, we intend to revisit this feature in connection with the basic properties of the interaction, which requires the spin-isospin decomposition of the potential energy in ANM. Although such a decomposition has been previously introduced in several studies [10, 11, 17–20], the origin of the$ \beta^2 $ law, in terms of the individual components, deserves further investigation, in view of future extensions of the mean field approximation requested by the investigations of neutron stars and exotic nuclei in density and asymmetry ranges beyond the presently accessible. -
The symmetry energy is the linear response of the nuclear system to a small neutron-to-proton imbalance
$ \beta\ll 1 $ , that induces an isospin shift of the single-particle potential$ \Delta u_\tau \equiv u_\tau(\beta)-u_\tau(0) $ between protons and neutrons$ (\tau = n,p) $ . It is easily proved that at the total density ρ, this is [21]$ \Delta u_n - \Delta u_p = \frac{1}{4}\rho\beta N_0^{-1} \big[ {\cal{F}}_{nn} + {\cal{F}}_{pp} - 2{\cal{F}}_{np} \big], $

(1) where
$ N_0^{-1}{\cal{F}} $ is the effective interaction, and$ N_0 $ is the single-particle level density at the Fermi energy$ \epsilon_F $ of SNM. The difference$ F'_\tau = {\cal{F}}_{\tau\tau} - {\cal{F}}_{\tau\tau'} $ ($ \tau\neq\tau' $ ) is related to the isovector Landau-Migdal parameter. Introducing the parameter$ F' = (F'_n + F'_p)/4 $ [21], the symmetry energy can be written as$ E_{\rm{sym}} = T_{\rm{sym}} + U_{\rm{sym}} = T_{\rm{sym}} + \frac{2}{3} \epsilon_F F', $

(2) where
$ T_{\rm{sym}} $ and$ U_{\rm{sym}} $ are the kinetic and potential components of the symmetry energy. Eq. (1) is only valid for$ \beta^2\ll 1 $ . Let us consider first the low density limit, where 2BF gives the dominant contribution to the nuclear force. To make a closer contact with the bare interaction, let us consider the Brueckner theory, where the G matrix plays the role of the effective interaction. Assuming the angle average approximation in the Brueckner-Bethe-Goldstone equation [22], the G matrix$ {\cal{G}}^{JST}_{LL'} $ in SNM keeps the symmetries of the bare interaction$ {\cal{V}}^{JST}_{LL'} $ , where J, S and T are the total two-body angular momentum, spin and isospin, respectively. In the case of low density,$ L = 0 $ is by far the most important partial wave (the contributions with$ L>0 $ can be neglected), Eq. (1) can be recast in the form$ \Delta u_n -\Delta u_p = \frac{1}{2}\rho\beta \big[ {\cal{G}}^{01}_{nn} + {\cal{G}}^{01}_{pp} - {\cal{G}}^{01}_{np} - {\cal{G}}^{10}_{np} \big] \:, $

(3) where J is omitted for simplicity.
$ {\cal{G}}^{01} $ ($ {\cal{G}}^{10} $ ) is the isospin triplet (isospin singlet) part of the effective interaction that is coupled to the spin singlet (spin triplet) due to the Pauli principle. In the low density region, we can assume a weak density dependence of the G matrix. Since$ {\cal{G}}^{01}_{nn} + {\cal{G}}^{01}_{pp}\approx 2{\cal{V}}^{01} $ and$ {\cal{G}}^{ST}_{np}\approx {\cal{V}}^{ST} $ , one can conclude that the energy asymmetry is driven by the difference between the spin singlet and spin triplet components, as expected from the basic property of the spin dependent interaction. Since the latter is independent of isospin, the isospin shift of the single-particle potential, Eq. (3), is linear in β and, consequently, the isospin shift of the potential energy is quadratic in β. When$ L>0 $ and L is odd, there are contributions from the$ S = T = 0 $ singlet and the$ S = T = 1 $ triplet. Both are expected to be isospin independent for the same reason as in the preceding cases.This property means that the potential energy is linear in
$ \beta^2 $ . Therefore, one can extend the calculations of the symmetry energy potential as a difference of the energy potential$ U(\rho) $ between$ \beta = 1 $ (PNM) and$ \beta = 0 $ (SNM):$ U_{\rm sym}(\rho) = U_{\rm PNM}(\rho) - U_{\rm SNM}(\rho). $

(4) This is a simple form of the
$ \beta^2 $ law, used to calculate the symmetry energy of nuclear matter.Let us consider the high density regime, in which 3BF is dominant. It is well known that 3BF is necessary to reproduce not only the saturation density of nuclear matter but also the observed masses of neutron stars [23, 24]. The simplest way to extend the BHF approximation while keeping its mean field character, is to replace 3BF by a density-dependent 2BF, weighted by the third particle through its correlation with the other two particles [25]. In the coordinate space, it can be formally written as
$ W(r_{12}) = \rho \int {\rm d}^3 r_3\; g^2(r_{13}) g^2(r_{23}) V(r_1,r_2,r_3) \:, $

(5) where
$ g(r) = 1-\eta(r) $ , and$ \eta(r) $ is the defect function at a distance$ r = r_i-r_j $ between particles i and j. In the momentum representation, the 3BF contribution to the isospin shift of the single-particle potential$ \Delta u_\tau $ is given by$ \Delta u_n - \Delta u_p = \frac{1}{2}\rho\beta \big[ \tilde{\cal{W}}^{01}_{nn} + \tilde{\cal{W}}^{01}_{pp} - \tilde{\cal{W}}^{01}_{np} - \tilde{\cal{W}}^{10}_{np}\big] \:, $

(6) where, in the uncoupled isospin representation,
$ \tilde{\cal{W}}_{\tau\tau'} = \sum\limits_{\tau''} n_{\tau''} V_{\tau\tau'\tau''} g_{\tau\tau''} g_{\tau'\tau''} \:, $

(7) and
$ n_{\tau''} $ is the occupation number of the third nucleon (we omit the momentum and spin labels for simplicity). Extending the discussion of Eq. (3) to Eq. (6), we can conclude that the symmetry energy is driven by the difference between the spin singlet and spin triplet components of 3BF.The reduction of 3BF to a density dependent 2BF entails a non linear dependence on
$ \rho_n $ and$ \rho_p $ in ANM. In particular, the contribution of 3BF stemming from the relativistic corrections [25] takes the form$ \tilde{\cal{W}}_{\tau\tau'} \sim V \cdot\sum\limits_{\tau''}\rho_{\tau''}^{5/3}g_{\tau\tau''} g_{\tau'\tau''}, $

(8) which is the isospin independent defect function.
Therefore, 3BF is strongly isospin dependent and we expect the energy potential shift to violate the
$ \beta^2 $ law, and Eq. (4) to be unsuitable for the calculation of the symmetry energy at high nuclear density. Of course, these theoretical considerations are restricted, at least in part, to the mean field approximations, such as BHF and the adopted model for 3BF. -
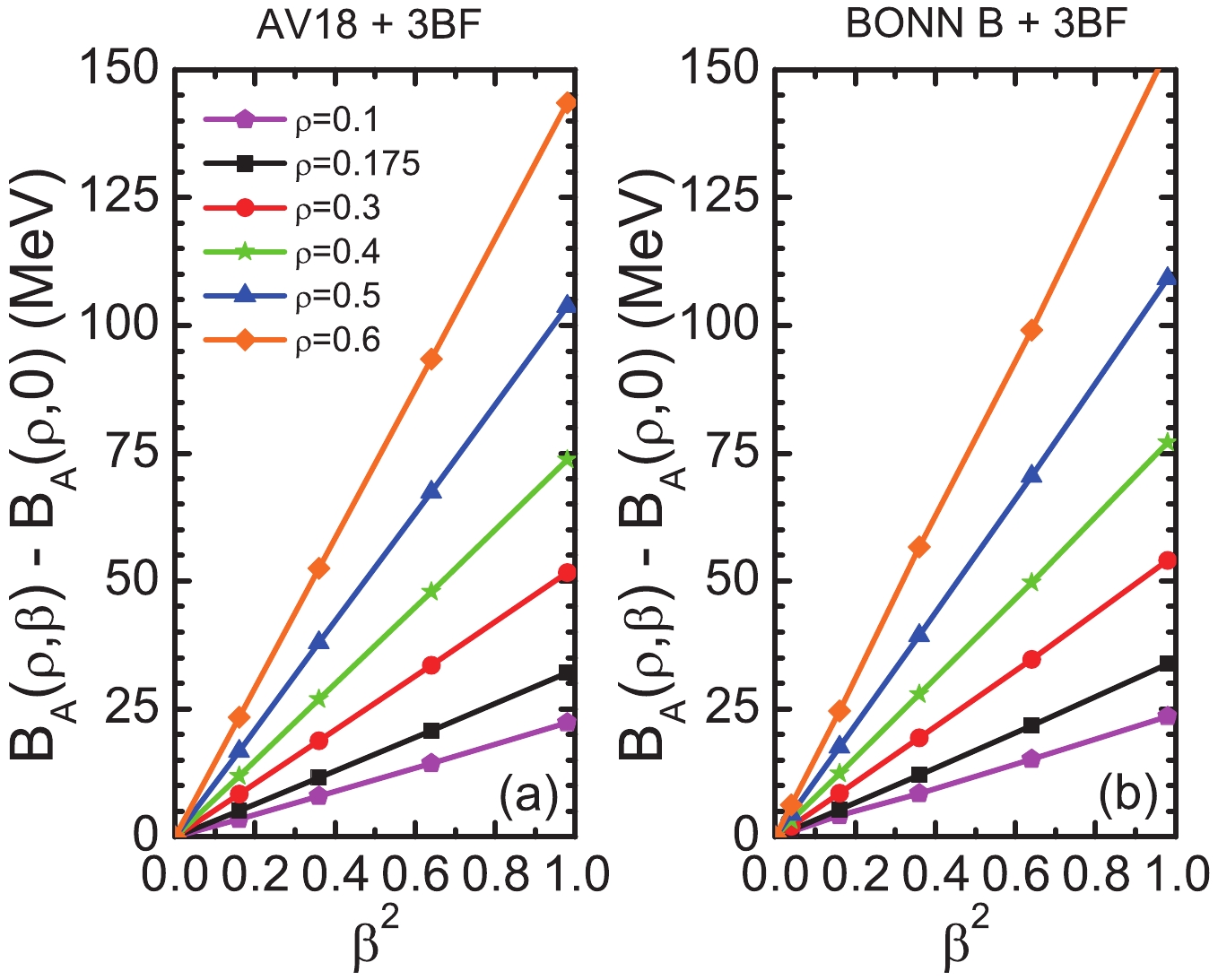
The energy per particle of ANM has been calculated in the framework of the BHF approximation. Two versions of 2BF and 3BF have been used: Argonne V18 plus consistent 3BF [26], and Bonn B plus consistent meson exchange 3BF [24, 27]. From the calculations with 2BF only, plotted in Fig. 1, it turns out that the symmetry energy is 30 MeV at the saturation density and 50 MeV at 0.4 fm-3 with both forces. In the calculations with 2BF plus 3BF, plotted in Fig. 2, the agreement is not very good. We obtained 32.1 MeV with Argonne V18 and 33.8 MeV with Bonn B at low density, and 73.7 MeV with Argonne V18 and 77.1 MeV with Bonn B at high density. This discrepancy comes from the meson parameters of the two 3BFs which are slightly different.
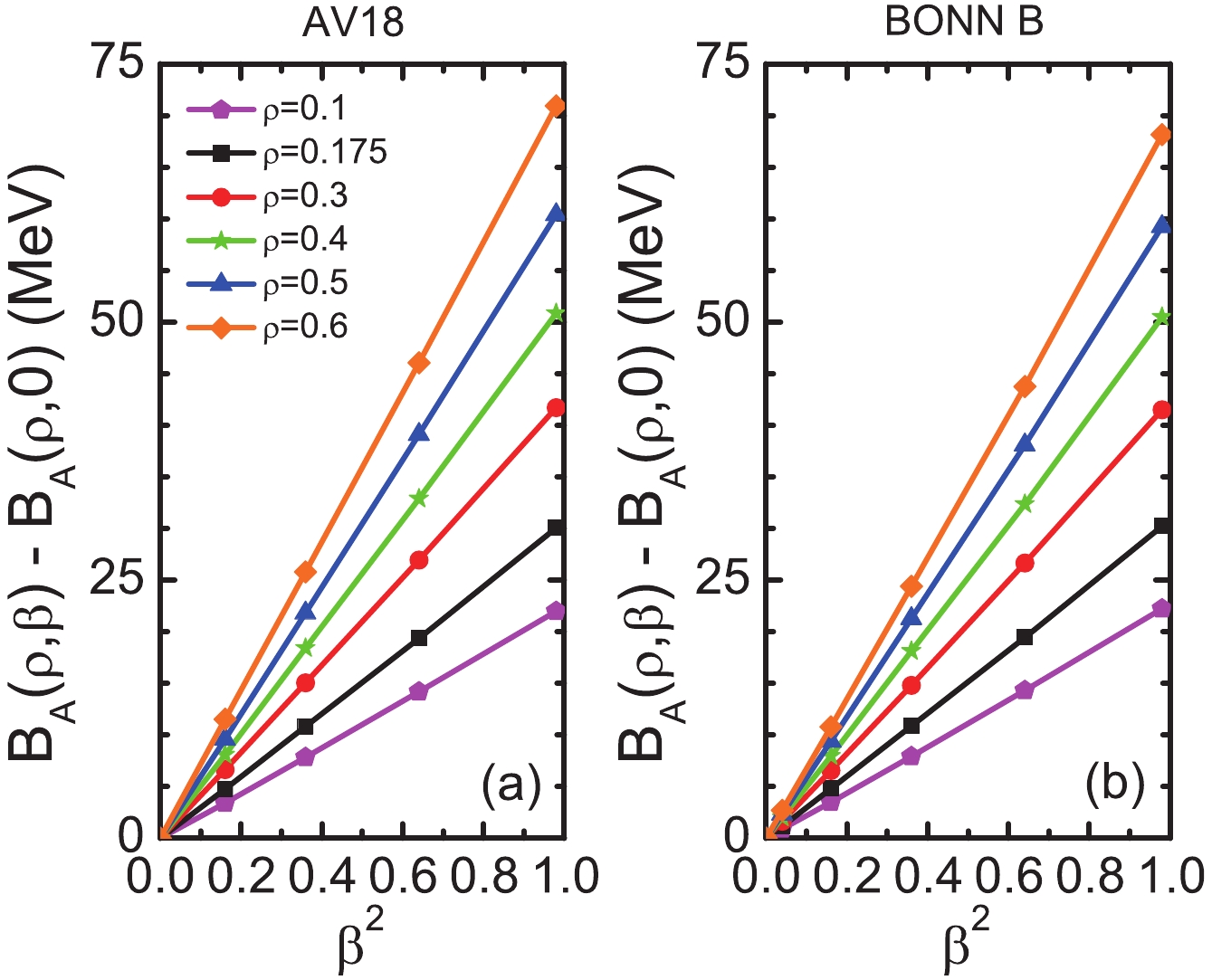
Figure 1. (color online) Energy shift vs. asymmetry parameter for various densities with the two-body Argonne (left) and Bonn B (right) potentials.
As clearly seen in Fig. 1 and Fig. 2, the results exhibit a linear dependence on
$ \beta^2 $ , which supports the application of the$ \beta^2 $ law, expressed by Eq. (4), in calculations of the symmetry energy. This study is intended to discuss the microscopic origin of the$ \beta^2 $ law in view of the possible extensions to very high densities and calculations beyond the mean field approximation. We are not concerned with the contribution of the kinetic part to the symmetry energy because its departure from the$ \beta^2 $ law is negligible at any density.In Table 1, we report the spin-isospin partial wave decomposition of the potential energy per particle for two densities, where L is the two-body orbital angular momentum. In the last two columns, the odd vs. even angular momentum contributions to the symmetry potential
$ U_{\rm sym} $ , defined in Eq. (4), is reported. At the saturation density, the total$ U_{\rm sym} $ , including the kinetic component (12.96 MeV), gives a symmetry energy on the order of 30 MeV for both two-body potentials, which is in good agreement with the empirical value. At high densities, the role of the odd angular momentum becomes increasingly important when 3BF is included. It is noteworthy that the aforementioned agreement of the symmetry energy between the two interactions adopted in the BHF calculations, occurs despite the different values of the partial wave components, especially in the isospin singlet channel. At the saturation density, the isospin triplet components change slightly when going from SNM to PNM, so that the isospin singlet$ T = 0 $ term plays a major role in determining the symmetry energy, as previously discussed. In contrast, at the higher densities, the isospin triplet$ T = 1 $ significantly contributes to the enhancement of the symmetry energy.POT $\rho/{\rm{fm}}^{-3}$ 

$U_{\rm{PNM}}^{T=1}$ 

$U_{\rm{SNM}}^{T=1}$ 

$U_{\rm{SNM}}^{T=0}$ 

$U_{\rm{sym}}$ 

odd L even L odd L even L odd L even L odd L even L AV18 0.175 −0.25 −23.44 −0.34 −19.98 5.05 −24.86 −4.96 21.4 0.400 11.74 −39.21 3.22 −36.34 13.62 −35.88 −5.1 33.01 BONN B 0.175 0.29 −23.41 −0.14 −20.44 5.77 −25.46 −5.34 22.49 0.400 10.10 −39.63 2.95 −37.17 16.22 −39.07 −9.07 36.61 AV18 0.175 −1.75 −17.52 −2.71 −15.79 3.57 −23.33 −2.61 21.60 +3BF 0.400 17.47 −6.63 −4.15 −15.16 7.39 −27.88 14.23 36.41 BONN B 0.175 −2.67 −15.51 −3.19 −16.57 2.40 −21.51 −1.88 22.57 +3BF 0.400 14.26 6.49 −6.04 −8.77 2.19 −20.58 18.11 35.84 Table 1. Angular momentum decomposition of the potential energy per particle (MeV) calculated with Argonne V18 and Bonn B without 3BF (upper values), and with their respective consistent 3BF (lower values) in the BHF approximation. Due to anti- symmetrization of the effective interaction, the sum L+S+T must be odd, and in PNM, T = 1. In the last two columns, the angular momentum decomposition of the symmetry potential, Eq. (4), is reported.
Since the 3BF strength is still small at the saturation density, the isospin triplet is much smaller than the isospin singlet. However, at the density of 0.4 fm-3, owing to the dominance of the odd L components, 3BF reinforces the spin triplet component of the symmetry energy, and the symmetry energy becomes enhanced.
In the further discussion of the spin-isospin decomposition of the potential energy per particle, we concentrate only on the results with the Bonn B potential, because the main conclusions do not change when moving from Bonn B to Argonne V18 potential. Thus, in Fig. 3, we report the spin-isospin decomposition of the symmetry potential shift
$ \Delta U(\rho,\beta)_{ST} = U(\rho,\beta)_{ST}-U(\rho,0)_{ST} $ with the Bonn B potential. With 2BF only (left side of Fig. 3), all components exhibit a linear behavior in$ \beta^2 $ up to high density. Such a result was expected from the discussion following Eq. (3). A small deviation in$ U_{01} $ is irrelevant for the behavior of the total potential energy.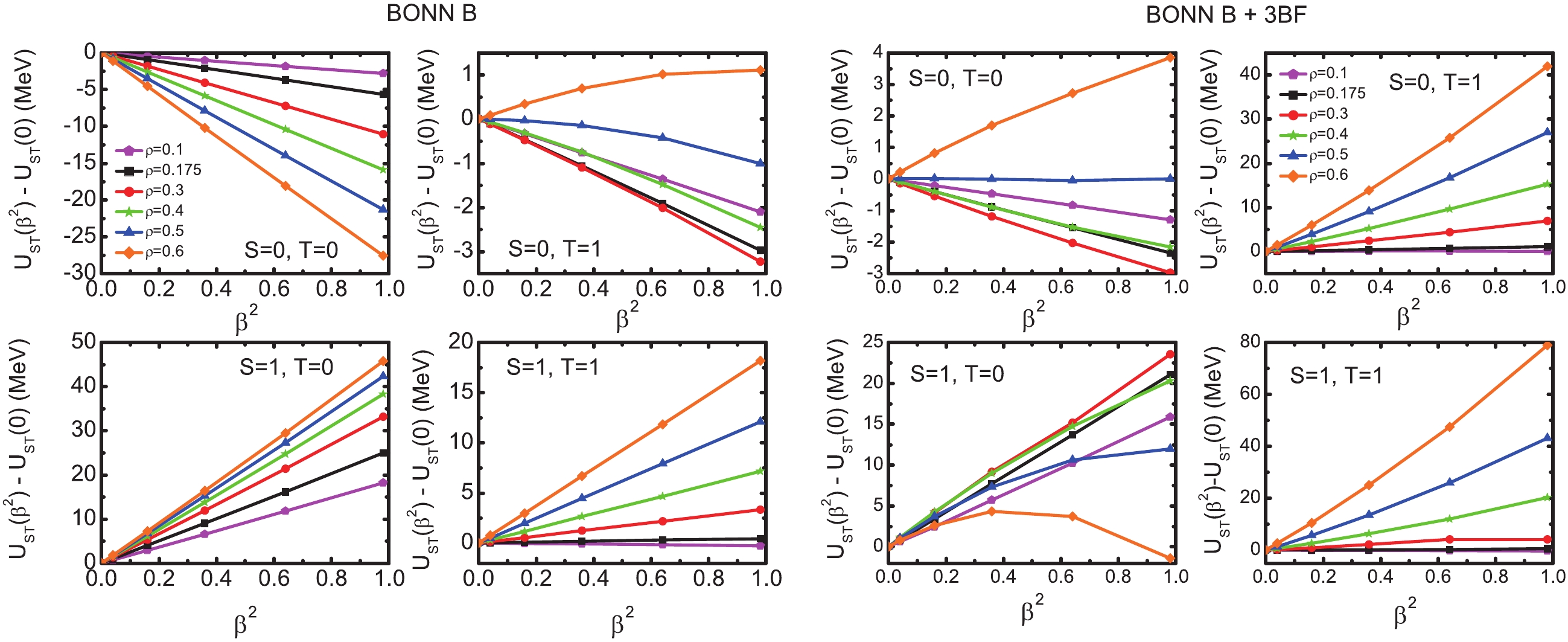
Figure 3. (color online) Spin-isospin decomposition of the isospin shift of the symmetry potential vs. β2 for Bonn B (left), and Bonn B plus consistent 3BF (right).
Up to the saturation density, the isospin singlet
$ U_{S0}\ (S = 0, 1) $ gives by far the largest contribution to the isospin shift, whereas the isospin triplet part, dominated by$ U_{11} $ , is approximately constant, which is consistent with the discussion in Sec. II. In particular, the$ L = 0 $ tensor component of the$ ^3SD_1 $ channel is the largest, a well-known result of the first$ \it ab\ initio $ calculations [10, 28], more recently confirmed in Ref. [29]. At higher densities, the repulsive effect of the$ S = 1 $ and$ T = 1 $ channel becomes important. Thus, the isospin triplet term becomes increasingly competitive, resulting in a monotonic increase of the symmetry energy.Above the saturation density, the effects of 3BF on the potential energy cannot be neglected, as shown in Fig. 3 (right). As firmly established long ago, 3BF is necessary to reproduce not only the saturation density of nuclear matter but also the empirical masses of neutron stars [10]. In the high density range, 3BF is increasingly repulsive for all channels and is strongly isospin dependent, as shown by Eq. (8). At
$ \rho = 0.6 $ fm-3, the individual spin-isospin channels exhibit a considerable deviation from the$ \beta^2 $ law. In particular, the$ S = 1 $ and$ T = 0 $ energy potential shift driven by 3BF exhibits an isospin transition from positive to negative slope. This is a most impressive result because$ \Delta U_{10} $ at$ \beta = 0 $ and$ \beta = 1 $ is large in both cases, but because of the opposite sign, the$ \beta^2 $ law yields a small and unphysical result. The other components are also important, but the$ \beta^2 $ law does not have such a dramatic effect. All deviations are expected to become more pronounced at higher densities. At such densities, the convergence of the present BHF numerical code is not yet satisfactory. However, the present calculations show that the total energy potential does not violate the$ \beta^2 $ law in the considered density range. This can only be justified by accidental compensation of various corrections of the order higher than$ \beta^2 $ . -
The primary objective of this work is to study the nuclear symmetry energy and the
$ \beta^2 $ law, which is used in calculations of the symmetry energy in ANM in the microscopic BHF framework. The$ \beta^2 $ law is supported by numerical calculations in the mean field approximation in a density range up to four times the saturation density. To relate this study to the nuclear interaction symmetries, a calculation regarding the spin-isospin decomposition of the potential energy was performed in the BHF approximation with 2BF and 3BF. This latter force is necessary to extend the calculation beyond the saturation density. At lower densities, it turns out that the symmetry energy is essentially driven by the isospin singlet components of the nuclear two-body interaction, which is weakly dependent on the isospin (Sec. 2), so that the mean field approximation alone can justify the validity of the$ \beta^2 $ law. At higher densities, the isospin triplet components play a major role, but they all slightly depart from the$ \beta^2 $ law due to the strong isospin dependence of 3BF. In particular, the contribution of the$ S = 1 $ and$ T = 0 $ channel changes sign when going from low to high asymmetry. Despite the fact that the total potential energy still agrees with the$ \beta^2 $ law, a noticable violation of the$ \beta^2 $ law is expected from 3BF at densities higher than 0.6 fm-3, in addition to the mean field approximation which is not discussed here.Therefore, it is worthwhile to extend this investigation in two directions. First, the density range should be enlarged beyond 0.6 fm-3 for an application to neutron star cores. For this purpose, an effort is being made to improve the convergence of the BHF numerical code at higher densities. Second, the generalization of the Brueckner theory beyond the mean field approximation to include the medium polarization is also expected to violate the
$ \beta^2 $ law, especially at low densities. Such calculations are now possible after the recent extension of the induced interaction theory of collective excitations to ANM [30].
The spin-isospin decomposition of the nuclear symmetry energy from low to high density
- Received Date: 2019-10-14
- Accepted Date: 2020-01-30
- Available Online: 2020-05-01
Abstract: The energy per particle BA in nuclear matter is calculated up to high baryon density in the whole isospin asymmetry range from symmetric matter to pure neutron matter. The results, obtained in the framework of the Brueckner-Hartree-Fock approximation with two- and three-body forces, confirm the well-known parabolic dependence on the asymmetry parameter β = (N − Z)/A (β2 law) that is valid in a wide density range. To investigate the extent to which this behavior can be traced back to the properties of the underlying interaction, aside from the mean field approximation, the spin-isospin decomposition of BA is performed. Theoretical indications suggest that the β2 law could be violated at higher densities as a consequence of the three-body forces. This raises the problem that the symmetry energy, calculated according to the β2 law as a difference between BA in pure neutron matter and symmetric nuclear matter, cannot be applied to neutron stars. One should return to the proper definition of the nuclear symmetry energy as a response of the nuclear system to small isospin imbalance from the Z = N nuclei and pure neutron matter.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: