-
The
$ \Xi $ and$ \Omega $ hypernuclei are relatively simple and of fundamental interest regarding the interaction between nucleons and strange particles. Hyperon interactions are not known sufficiently well due to the limited scattering data. However, more precise data on light hypernuclei (from high-resolution gamma-ray experiments [1]), advanced few-body theoretical methods [2–9], quark delocalization, color screening [10], constituent quark models [11], lattice QCD calculations [12–14], and femtoscopic analyses of pp, pA, and AA collisions in the ALICE and STAR experiments [15] have recently provided us with valuable information. The KEK-E373 experiment reported the first evidence of a bound$ \Xi $ -hypernucleus$ ^{14}N+\Xi $ , i.e., the so-called KISO event [16]. Recently, the first experimental observation of an attractive strong interaction between a proton and a hyperon$ \Xi $ has been reported by ALICE collaboration [15].The theoretical efforts in the lattice HAL QCD collaboration have led to the derivation of baryon-baryon interactions near the physical pion mass [17]. The most recent results of these efforts hint to the existence of shallow bound states in
$ \Omega N $ systems [18]. We study the$ \Omega+\alpha $ system, making use of this$ \Omega N $ potential. The depth of the potential in$ \Omega \alpha $ and$ \Xi \alpha $ systems is uncertain, as there are not sufficient experimental data for their nuclear bound states. However, for the latter, some diverse phenomenological potentials are considered [19–21].Motivated by the above-mentioned description, vast applications of
$ \Omega \alpha $ and$ \Xi \alpha $ interactions in 3-,4-, and 5-body cluster structures of$ \Omega $ hypernuclei (describing the response of$ 3\alpha $ system to the addition of the$ \Omega $ particle) [2], the$ \alpha $ cluster model approach [4], and variational four-body calculation [22], we present$ \Omega \alpha $ and$ \Xi \alpha $ interactions in a simple Woods-Saxon-type form.To test and validate our method, we apply it to
$ \Xi \alpha $ systems and compare the results with the phenomenological Dover-Gal (DG) potential type [19]. Furthermore, we employ the ESC08c Nijmegen model$ \Xi N $ potential in the$ ^{3}S_{1} $ channel [23].Here, we consider a
$ Y +\alpha $ system because of the low compressibility of the$ \alpha $ -cluster and high reaction thresholds that enable us to employ a one-channel approximation over a wide energy range. The$ Y+\alpha $ system is studied using a single-folding potential (SFP) method. In this model, the$ Y+\alpha $ system consists of an alpha and a Y particle moving in the effective$ Y \alpha $ potential. The effective nuclear potential is approximated by the single-folding of nucleon density$ \rho\left(\vec{r}^{\prime}\right) $ in the$ \alpha $ -particle and hyperon-nucleon potential$ V_{YN}\left(\left|\vec{r}-\vec{r}^{\prime}\right|\right) $ between the Y particle at$ \vec{r}^{\prime} $ and the nucleon at$ \vec{r} $ [24, 25]. The resulting$ Y\alpha $ potential is then fitted to a separable form. Finally, we solve the Schrödinger equation using the fitted$ Y \alpha $ potential in the infinite volume and extract its scattering observables from the asymptotic behavior of the wave function. The model is expected to be accurate only for the low-energy properties of the$ Y+\alpha $ system, as it is based on a$ Y N $ potential, which is fitted to low energy$ Y N $ scattering parameters.We emphasize that the coupling of
$ \Omega N $ to higher-mass ($ \Lambda\Xi^{*} $ ) and lower-mass ($ \Lambda\Xi $ and$ \Sigma\Xi $ ) channels is not taken into account, as we assume that these contributions are of second order to the binding energy of few-body systems [18]. To draw a definite conclusion regarding the binding energy of the$ \Omega +\alpha $ system, it is necessary to perform a coupled-channel analysis of the HAL QCD method [26]. Moreover, in the calculations, the Coulomb force is not taken into account.This paper is organized as follows. In Sec. 2, after a brief discussion on the single-folding potential method, we introduce and parametrize all dominating sets of input parameters, i.e., those of the two-body potentials. In Sec. 3, we present and discuss the results. Finally, a summary and conclusions are presented in Sec. 4.
-
We obtain the effective potential of
$ Y+\alpha $ systems using the single-folding potential model [24, 25]. This method is briefly outlined in the following. The$ Y \alpha $ potential is defined as$ V_{Y\alpha}\left(\vec{r}\right) = \int\rho\left(\vec{r}^{\prime}\right)V_{Y N}\left(\left|\vec{r}-\vec{r}^{\prime}\right|\right){\rm d}\tau^{\prime}, $

(1) where
$ \rho\left(\vec{r}^{\prime}\right) $ is the nucleon density in the$ \alpha $ -particle at a distance$ \vec{r}^{\prime} $ from its center-of-mass, which is given by [27],$ \rho\left(\vec{r}^{\prime}\right) = 4\left(\frac{4\beta}{3\pi}\right)^{3/2}\exp\left(-\frac{4}{3}\beta r^{\prime2}\right). $

(2) The integration in Eq. (1) spans all space, as permitted by
$ \rho\left(\vec{r}^{\prime}\right) $ . The required normalization condition is satisfied by$ \int\rho\left(\vec{r}^{\prime}\right){\rm d}\tau^{\prime} = 4\left(\frac{4\beta}{3\pi}\right)^{3/2}\intop_{0}^{\infty}\mathop{\exp\left(-\frac{4}{3}\beta r^{\prime2}\right)4\pi r^{\prime2}{\rm d}r^{\prime}} = 4. $

(3) The constant
$ \beta $ is determined from the root-mean-square radius of$ \rm{{^{4}}He} $ [27],$ \rm{{r_{r.m.s}}} = \frac{3}{\sqrt{8\beta}} = 1.47\; \rm{fm}. $

(4) In Eq. (1),
$ V_{YN}\left(\left|\vec{r}-\vec{r}^{\prime}\right|\right) $ is the potential in configuration space between the Y particle at$ \vec{r} $ and the nucleon at$ \vec{r}^{\prime} $ .We take the
$ \Xi N $ potential in$ ^{3}S_{1} $ channel and simulate the ESC08c Nijmegen model, which consists of local central Yukawa-type potentials with attractive and repulsive terms [21, 23],$ V_{\Xi N}\left(\vec{r}\right) = -568\frac{\exp\left(-4.56r\right)}{r}+425\frac{\exp\left(-6.73r\right)}{r}. $

(5) The low-energy data of this potential are listed in Table 1. In the case of
$ \Omega N $ , we use the S-wave and spin$ 2 $ $ \Omega N $ potential, which is given by the HAL QCD collaboration with nearly physical quark masses [18]. The lattice discrete potential is fitted by an analytic function composed of an attractive Gaussian core, plus a long range$ \rm(Yukawa{)^{2}} $ attraction with a form factor from Ref. [28],System Channel $a_{0}$ (fm)

$r_{0}$ (fm)

$B_{Y N}$ (MeV)

$\Omega N$ 

$ ^5S_{2}$ 

5.30 1.26 1.54 $\Xi N$ 

$^3S_{1}$ 

4.91 0.527 1.67 $ V_{\Omega N}\left(r\right) = b_{1}e^{\left(-b_{2}r^{2}\right)}+b_{3}\left(1-e^{-b_{4}r^{2}}\right)\left(\frac{e^{-m_{\pi}r}}{r}\right)^{2}.$

(6) The pion mass in Eq. (6), which is taken from the simulation, is
$ {{m_{\pi}} = 146} $ MeV. The lattice results are fitted reasonably well,$ \chi^{2}/d.o.f\simeq1 $ , with four different sets of parameters given in Table 2. The low-energy data of this potential is also given in Table 1.$P_{1}$ 

$P_{2}$ 

$P_{3}$ 

$P_{4}$ 

$b_{1}\left({\rm{MeV}} \right)$ 

−306.5 −313.0 −316.7 −296 $b_{2}\left({\rm{fm}}^{-2}\right)$ 

73.9 81.7 81.9 64 $b_{3}\left({\rm{MeV} }.{\rm fm}^{-2}\right)$ 

−266 −252 −237 −272 $b_{4}\left({\rm{fm}}^{-2}\right)$ 

0.78 0.85 0.91 0.76 Table 2. Fitting parameters in Eq. (6) for different models
$P_{i}$ for$^{5}S_{2}$ $\Omega N$ interaction [18]. -
To test the
$ \Xi \alpha $ potential obtained from the SFP model, we employed the phenomenological potential of the Woods-Saxon type for the$ \Xi \alpha $ interaction using the Dover-Gal (DG) model given in Refs. [19, 20]$ V_{\Xi\alpha}^{\rm DG}\left(r\right) = -V_{0}\left[1+\exp\left(\frac{r-R}{c}\right)\right]^{-1} , $

(7) where
$ V_{0} $ is the depth parameter,$ R = 1.1A^{\left(1/3\right)} $ with A depicting the mass number of the nuclear core (here,$ A = 4 $ for the alpha particle) and c is the surface diffuseness. The values of these three parameters in DG model are given in Table 3. The$ \Xi+\alpha $ system is bound by this potential with an energy of$ E_{B} = -2.1 $ MeV. Notably, the DG potential has no repulsive core.Model $ V_{0} $ (MeV)

R(fm) c(fm) $a_{0}$ (fm)

$r_{0}$ (fm)

$B_{\Xi \alpha}$ (MeV)

DG 24 1.74 0.65 −4.9 1.9 −2.1 SFP 24.4 1.72 0.31 −6.6 1.9 −1.54 Table 3. DG potential model parameters of Eq. (7) from Refs. [19, 20]. The fitting parameters of
$\Xi \alpha$ are obtained by fitting the SFP model to a function of the same form as Eq. (7). The corresponding low-energy parameters, scattering length, effective range, and binding energy of both models are given. The obtained results, using experimental masses of$\alpha$ and$\Xi$ , are$3727.38\; \rm{MeV}/c^{2}$ and$1318.07\; \rm{MeV}/c^{2}$ , respectively.To obtain observables such as scattering phase shifts and binding energy, we fit
$ V_{Y\alpha}\left(\vec{r}\right) $ to the Wood-Saxon form using the function presented in Eq. (7) with three parameters$ V_{0}, R $ , and c. The results of fitting these parameters are presented in Table 3.The obtained single-folding potential,
$ V_{\Xi\alpha}\left(\vec{r}\right) $ , its corresponding fit function,$ V_{\rm fit}(r) $ , and$ V_{\Xi\alpha}^{\rm DG}\left(r\right) $ (for comparison) are shown in Fig. 1. We solve the Schrödinger equation with the fitted potential in the infinite volume and extract its scattering observables from the asymptotic behavior of the wave function. For comparison, in Fig. 2, the phase shifts from DG and SFP model potentials are shown.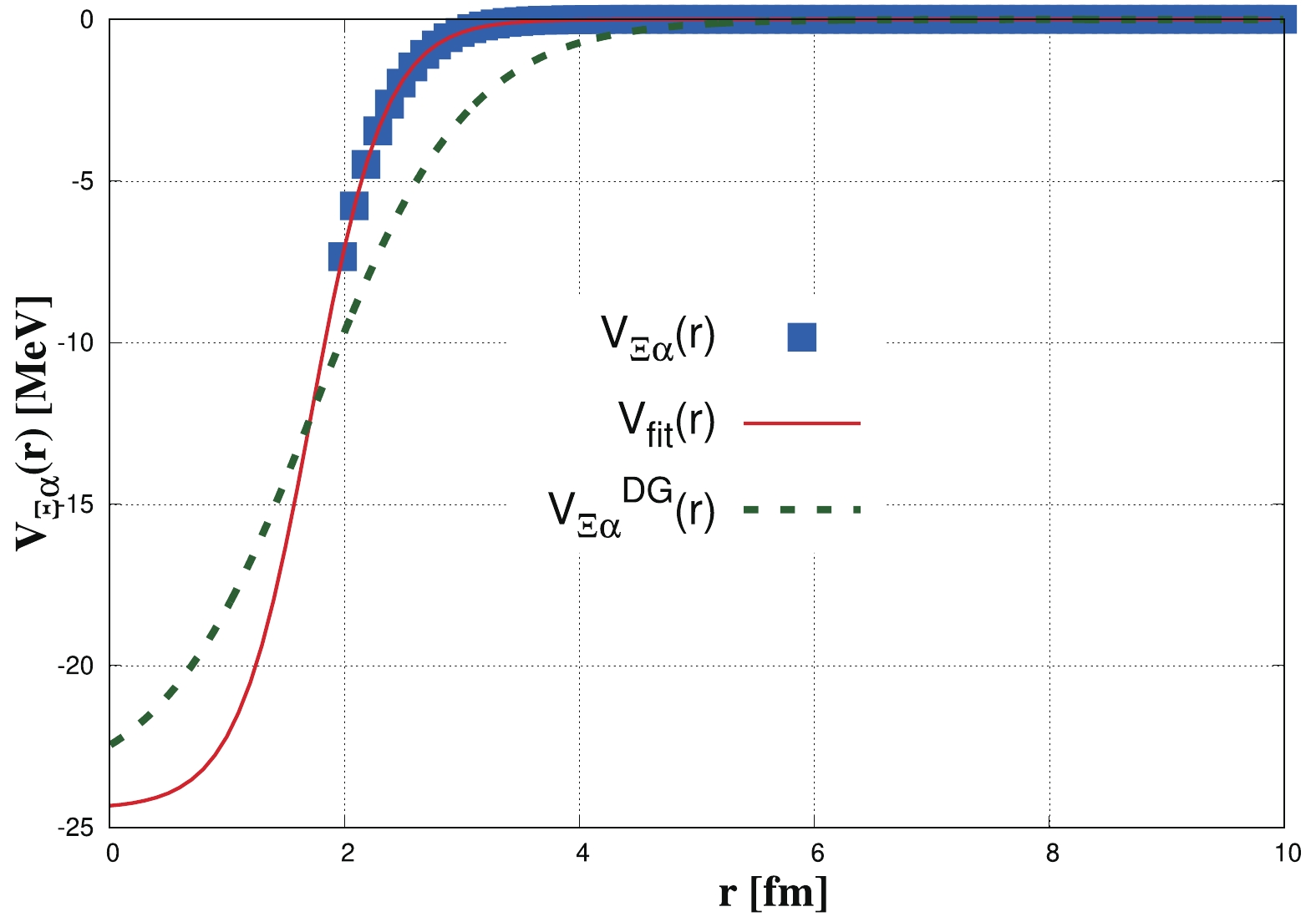
Figure 1. (color online) Single-folding potential,
$V_{\Xi\alpha}\left(\vec{r}\right)$ , for$\Xi N$ interaction in$^{3}S_{1}$ channel given in Refs. [21, 23].$V_{\rm fit}(r)$ (red line) shows results of the fitting by using the same form as Eq. (7). For comparison, we also present the Dover-Gal$\Xi\alpha$ potential (green dashed line) [19, 20], i.e.,$V_{\Xi\alpha}^{\rm DG}\left(r\right)$ in Eq. (7).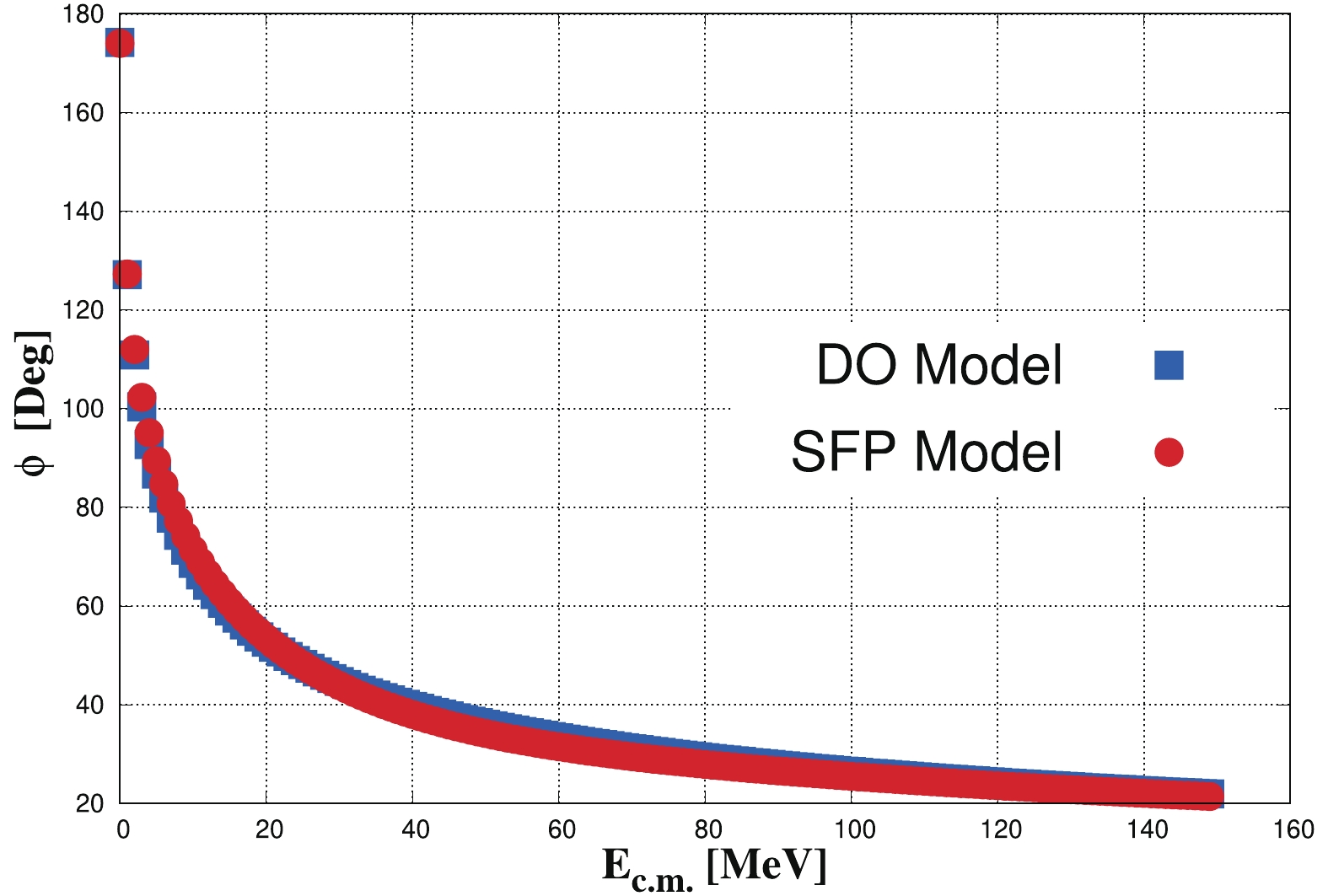
Figure 2. (color online) Extracted
$\Xi\alpha$ phase shifts for two potential models, DG and SFP, are given in Fig. 1 for comparison. According to this figure, a fairly good agreement is observed between these two models.The effective range expansion (ERE) of the phase shifts up to the next-leading-order (NLO) reads
$ k\cot\delta_{0} = -\frac{1}{a_{0}}+\frac{1}{2}r_{0}k^{2}+{\cal O}\left(k^{4}\right), $

(8) where
$ \left(a_{0}\right) $ and$ \left( r_{0}\right) $ depict the scattering length and effective range, respectively. The results of the calculations for the binding energy and the ERE parameters$ \left(a_{0}, r_{0}\right) $ are given in Table 3. According to the results in Table 3, a good agreement can be observed between the single-folding potential method and the phenomenological potential of the Dover-Gal model.The single-folding potential
$ V_{\Omega\alpha}\left(\vec{r}\right) $ for different models of the$ \Omega N $ interaction ($ P_{i} $ , Table 2) are shown in Fig. 3(a). We summarize the results of fitting and the corresponding parameters in Fig. 3(b) and Table 4, respectively. We adjust the depth$ V_{0} $ in such a way to produce the best fit for R and c parameters, i.e.,$ \chi^{2}/d.o.f\simeq1 $ .
Figure 3. (color online) (a) Single-folding potential,
$V_{\Omega\alpha}\left(\vec{r}\right)$ , for different models of$\Omega N$ interaction ($ P_{i} $ ) given in Table 2. (b) Single-folding potential,$V_{\Omega\alpha}\left(\vec{r}\right)$ , and$V_{\rm fit}(r)$ fit function (red line) with same form as Eq. (7) for set$P_{1}$ .$P_{1}$ 

$P_{2}$ 

$P_{3}$ 

$P_{4}$ 

$V_{0}\left( \rm{MeV}\right)$ 

−61 −61 −61 −61 $R\left( \rm{fm}\right)$ 

1.7 1.7 1.7 1.7 $c\left( \rm{ \rm{fm}}\right)$ 

0.47 0.47 0.47 0.47 Table 4. Parameter values are obtained by fitting
$\Omega \alpha$ SFP potential to a function of same form as Eq. (7), for different models$P_{i}$ of$\Omega N$ interaction [18].Garcilazo and Valcarce [8] showed that
$ \Omega N $ $ ^{5}S_{2} $ and$ NN $ $ ^{3}S_{1} $ channels give rise to a$ \Omega d $ bound state in the state with maximal spin$ \left(I,J^{P}\right) = \left(0,5/2^{+}\right) $ with a binding energy of$ \sim17 $ MeV, measured with respect to the$ NN\Omega $ threshold by solving the three-body bound-state Faddeev equations. Here, we obtain an$ \Omega\alpha $ binding energy of$ \sim23 $ MeV, as shown in Table 5. Since the potential must be more attractive than the approximated single-folding potential, the resulting energy is only an upper bound for the$ \Omega \alpha $ system, and the binding energy of$ \Omega\alpha $ is greater than that of$ \Omega d $ , which is reasonable.$P_{1}$ 

$P_{2}$ 

$P_{3}$ 

$P_{4}$ 

$a_{0}$ (fm)

−0.99(−0.93) −1.01(−0.96) −1.05(−1.00) −0.98(−0.92) $r_{0}$ (fm)

0.67(0.67) 0.67(0.67) 0.67(0.67) 0.67(0.68) $B_{\Omega\alpha}$ (MeV)

−22.9 (−23.3) −22.8(−23.2) −22.4(−22.8) −23.0(−23.4) Table 5. Scattering length,
$a_{0}$ , effective range$r_{0}$ , and binding energy$B_{\Omega\alpha}$ , of$\Omega\alpha$ for different models of$\Omega N$ interaction given in Table 2 [18]. Results obtained using the experimental masses of$\alpha$ and$\Omega$ are$3727.38\; \rm{MeV}/c^{2}$ and$1672.45\; \rm{MeV}/c^{2}$ , respectively. The values in parentheses correspond to the masses of$\alpha$ and$\Omega$ derived by the HAL QCD collaboration, i.e.,$3818.8\; \rm{MeV}/c^{2}$ and$1711.5\; \rm{MeV}/c^{2}$ , respectively [18].Shown in Fig. 4 is the S-wave scattering phase shift
$ \delta_{0} $ as a function of the kinetic energy. In Table 5, we present the binding energies and ERE parameters$ \left(a_{0},r_{0}\right) $ obtained from$ \Omega \alpha $ phase shifts, for different models of$ \Omega N $ interaction reported in Ref. [18] and summarized in Table 2. -
We derived a simple Woods-Saxon-type form for the potentials of
$ \Xi+\alpha $ and$ \Omega+\alpha $ systems by making use of the ESC08c Nijmegen$ \Xi N $ potential in$ ^{3}S_{1} $ channel and the HAL QCD Collaboration$ \Omega N $ potential in the$ ^{5}S_{2} $ channel, with the density function of the alpha particle in the single-folding potential method.We show that the effective central folding potential of
$ \Omega \alpha $ may assume a simple Wood-Saxon form and estimated the upper bound for the binding energy of the$ \Omega $ particle on a$ \alpha $ .Our method was tested against the phenomenological potential of the Woods-Saxon type for the
$ \Xi\alpha $ interaction by the Dover-Gal model, and a fairly good agreement was found between the two methods.The scattering length and the effective range were obtained by solving the Schrödinger equation using the resultant potential. The binding energies of
$ \Xi+\alpha $ and$ \Omega+\alpha $ systems were about$ -1.5 $ and$ -23 $ MeV, respectively. These results indicate that$ \Omega\alpha $ hypernuclei are deeply bound states or resonances, which may be experimentally observed in the real world.We emphasize that the cases of coupling of
$ Y N $ to higher- and lower-mass channels were not taken into account. The calculations also do not take into account the Coulomb force. To draw a definite conclusion regarding the binding energy of$ Y \alpha $ , it is necessary to perform a coupled-channel analysis.We hope that our results can be applicable as tests of various theoretical models for exotic nuclei structures, especially in few
$ \alpha $ cluster structures of$ \Omega $ hypernuclei (describing the response of the few$ \alpha $ systems to the addition of the$ \Omega $ particle) [2],$ \alpha $ cluster model approach [4], and other possible future experiments, where these lattice-QCD-based predictions may be tested.
Simple Woods-Saxon-type form for Ωα and Ξα interactions using folding model
- Received Date: 2019-12-26
- Available Online: 2020-05-01
Abstract: We derive a simple Woods-Saxon-type form for potentials between





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





























 DownLoad:
DownLoad: