-
With the discovery of fission and its application to the production of nuclear energy in the late 1940s, most attempts of nuclear scientists had been focused logically on the study of binary fission. Ternary fission was diagnosed as an interesting source of high energy alpha particles. This rare type of nuclear reaction was discovered by the Chinese and French scientists [1–5].
Disintegration of an unstable heavy/superheavy nucleus into three fission fragments, by ignoring neutrons and other types of radiation, is termed a cold ternary fission [6–12]. Ternary fission is an appropriate tool to study the behavior of a nuclear system at the scission point of a fissioning nucleus.
True ternary fission, in which the parent nucleus breaks up into three fragments with comparable (large) masses, occurs very rarely in some heavy/superheavy nuclei with high fissility parameters [13,14]. This type of ternary fission has been studied extensively in refs. [15–25], but all of its theoretical characteristics are still not well understood.
By using the double-folding nuclear potential, a coplanar three-cluster approach was introduced into the study of the cold ternary fission of 252Cf accompanied by an
$ \alpha $ particle [26]. Poenaru et al. [27–36] have developed a macroscopic-microscopic model to study ternary fission.According to Sǎndulescu et al. [37, 38], cold ternary fission can be considered like a process of cluster radioactivity; i.e., a large number of nucleons are re-arranged in a cold process from the ground state of the parent to the ground state of the three final products.
Without considering the cluster preformation factors, Sǎndulescu et al. [39–42] have calculated the isotopic yields in the cold ternary fission of 248Cm, using the double-folding potential plus M3Y nucleon-nucleon forces. Later, Florescu et al. [43] developed this model by including the preformation probability of 4He and 10Be that accompany the ternary fission of 252Cf.
In the framework of the cluster picture, and as an extension of the preformed cluster model (PCM) [44], the 'Three-Cluster Model' (TCM) was introduced for studying the ternary fission process [45]. This model has been used extensively to investigate the different theoretical aspects of ternary fission for various isotopes of Cf, U, Pu and Cm [46–51].
Despite the macroscopic approach of the three-cluster model, its predictions and the obtained results are in good agreement with the available experimental data and other models [52–60].
In our first publication [61], we studied the cold ternary fission of 250Cm by using the three-cluster model in the equatorial geometry and considering the light charged particle as the fixed third fragment. In our second paper [62], a relatively heavy nucleus (34Mg) is considered as the third fixed fragment, and is compared to the results with the light fragments in ternary fission of 242Pu. The obtained results revealed that ternary fission of 242Pu accompanied by 34Mg occurs with very low probability in the equatorial configuration. In our recent investigation [63], the equatorial and collinear configurations in the ternary fission of 242Pu accompanied by a relatively heavy (A= 14) fragment were compared. We also compared there the results which were obtained using the proximity and Yukawa plus exponential potentials as the nuclear part of the total potential.
In the present study, we focus on the true ternary fission of 242Pu in a defined region of mass and charge of the three fragments. The new aspect of this study is the variation of both the charge and mass numbers for all three fragments, which means that the area of investigation is expanded considering all possible combinations in the considered region of true ternary fission. Both equatorial and collinear geometries are considered, and the kinetic energies of the fragments for the most favorable fragmentations are calculated.
In Section 2, the theoretical framework of TCM is presented. The obtained results are presented and discussed in Section 3. Finally, a summary of the present study along with the concluding remarks is provided in Section 4.
-
In the cold ternary fission based on the three-cluster model [45], the interaction potential of the fragments is defined by
$ V = \sum\limits_{i = 1}^{3}\sum\limits_{j>i}^{3}{(m^i_x+V_{Cij}+V_{Nij})}. $

(1) Here,
$ m^i_x $ are the mass excesses of three fragments in units of energy, taken from the standard mass tables [64].$ V_{Cij} $ and$ V_{Nij} $ are the Coulomb and nuclear potentials between each pair of the three interacting fragments, respectively. The repulsive Coulomb potential between fragments i and j, is as follows$ V_{Cij} = \frac{Z_i Z_j e^2}{C_{ij}}, $

(2) where
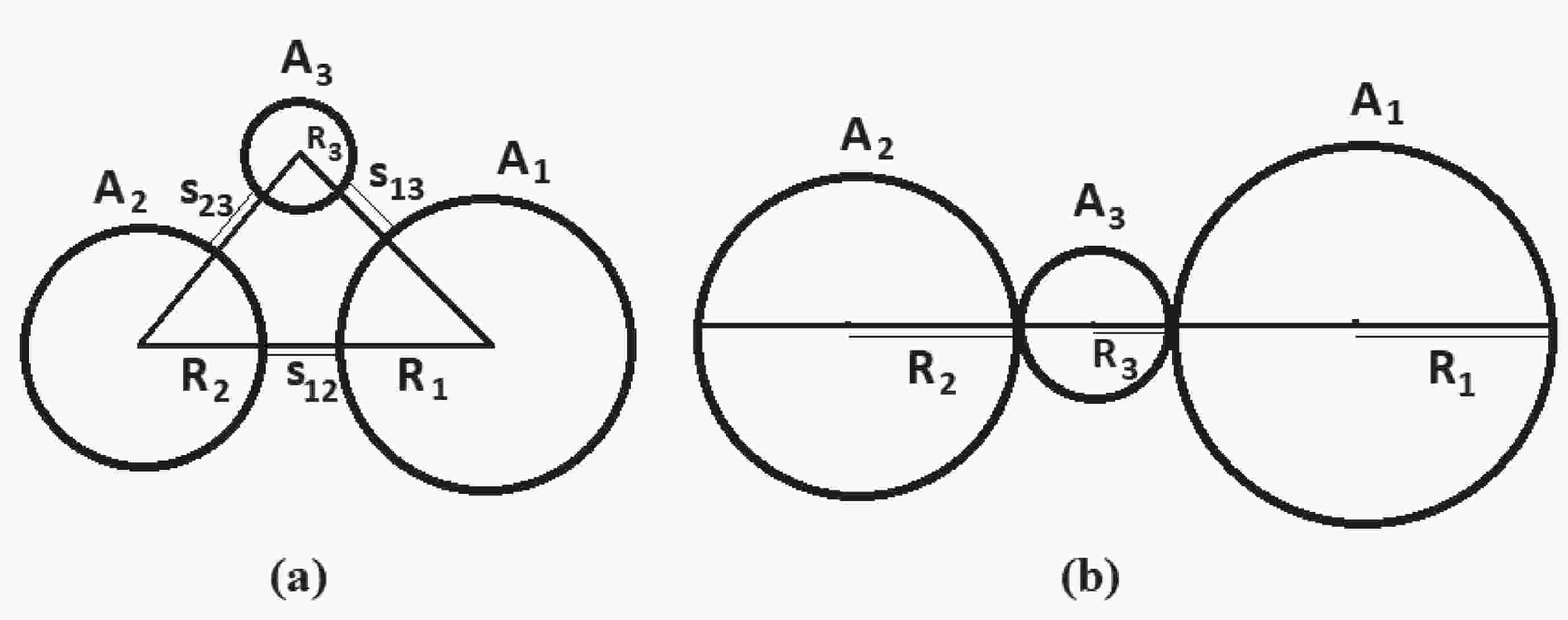
$ Z_i $ and$ Z_j $ are the charge numbers, and$ C_{ij} $ is the distance between the centers of the two fragments i and j:$ {C_{ij} = C_i+C_j+s_{ij}}. $

(3) Here,
$ C_i $ and$ C_j $ are the Süssmann central radii of the nuclei, and$ s_{ij} $ is the distance between near surfaces of the nascent fragments i and j. Note that s = 0,$ s>0 $ , and$ s<0 $ are related to the 'touching configuration', 'separated geometry', and 'overlap region' of a pair of interacting nuclei, respectively. The Süssmann radii are taken from Ref. [65]:$ {C_x} = {R_x}\left[1-\left(\frac{b}{R_x}\right)^2\right], $

(4) where the subscript x indicates the fragment number (i and j = 1, 2 or 3), and
$ R_x = 1.28A_x^{1/3}-0.76+0.8 A_x^{-1/3} $

(5) is the sharp radius of the fragment 'x' with the mass number
$ A_x $ . b is the diffusivity parameter of the nuclear surface (i.e.,$ b = \displaystyle\frac{\pi}{\sqrt{3}} a $ with$ a = 0.55 \;{\rm fm} $ ) which has been evaluated to be close to unity [66]. Note that in TCM spherical shapes are considered for the decaying nucleus and all fragments [45].In the present study, the latest version of the proximity nuclear potential (Prox2010) [66] is used. According to this version of the proximity potential,
$ V_{Nij} $ is defined as$ V_{Nij}(s) = V_{Pij}(s) = 4 \pi b \gamma \overline{C} \Phi\left(\frac{s}{b}\right). $

(6) Here,
$ \gamma $ is the coefficient of nuclear surface tension, which is given by$ \gamma = 1.25284[1-2.345(N-Z)^2/A^2] \quad {\rm MeV/fm}^2, $

(7) where Z, N, and A are the proton, neutron and mass numbers of the compound system, respectively. The compound system means a nuclear system composed of a pair of fission products.
$ \overline{C} $ , the mean radius of curvature, is evaluated as$ \overline{C} = \frac{C_i C_j}{C_i+C_j}. $

(8) The universal function of the proximity potential depends on the distance between each pair of fragments. This function is defined as follows
$ \Phi(\xi) = \Bigg\{ \begin{array}{lc} -1.7817+0.9270 \xi+0.0169 \xi^2-0.05148 \xi^3 & {\rm{for}} \quad 0\leqslant\xi\leqslant 1.9475 \\ -4.41 \exp(-\xi/0.7176) & {\rm{for}} \quad \xi>1.9475. \end{array} $

(9) Here,
$ \xi = s/b $ is a function of the distance between interacting nuclei. It is assumed that in the equatorial configuration, the three fission products are separated symmetrically and have the same speed. Therefore, one can assume that the separation distances between each pair of fragments are equal; i.e.,$ s = s_{12} = s_{13} = s_{23} $ . In fact, the lightest fragment moves faster than the two heavier ones, due to the repulsive Coulomb force. If$ A_3 $ is the lightest fragment, the relation between the separation distances is$ k\times s_{12} = s_{13} = s_{23} $ , with$ 0 < k \leqslant 1 $ . However, it was shown in the Ref. [45] that the trends of relative yields and fragmentation potential barriers are not affected by the k-value, so consideration of k=1 seems a reliable assumption.On the other hand, in the collinear configuration with
$ A_3 $ in the middle, the surface distance between fragments 1 and 3 or 2 and 3 is$ s = s_{13} = s_{23} $ . For fragments 1 and 2, this parameter is written as$ s_{12} = 2(C_3+s), $

(10) where in both geometries s = 0 corresponds to the touching configuration. The Q-value of the cold ternary fission is given by
$ Q = M-\sum\limits_{i = 1}^{3}{m_i}, $

(11) which should be positive to make a spontaneous reaction possible. M is the mass excess of the fissioning nucleus, and
$ m_i $ is the mass excess of the fission products in units of energy. Also, since the parent and all fragments are considered in their ground state, the Q-value appears as the kinetic energy of the three fragments and can be defined as$ Q = E_1 + E_2 + E_3 $ with$ E_i (i = 1,2,3) $ .The relative yield of a fragmentation channel is calculated using
$ Y(A_i,Z_i) = \frac{P(A_i,Z_i)}{\sum{P(A_i,Z_i)}}, $

(12) where
$ P(A_i, Z_i) $ is the penetrability of the i-th fragment through the three-body potential barrier. The one-dimensional WKB approximation is used to calculate the probability of penetration through the potential barrier [45],$ P = \exp\left\{-\frac{2}{\hbar}\int^{s_2}_{s_1}{\sqrt{2\mu(V-Q)}{\rm d}s}\right\}. $

(13) The touching configuration has been chosen as the first turning point
$ s_1 = 0 $ , and the second turning point$ s_2 $ should satisfy the equation$ V(s_2) = Q $ in the above integral.The reduced mass of the three fission products is defined as
$ \mu = m \left(\frac{A_1 A_2 A_3}{A_1 A_2+A_1 A_3+A_2 A_3}\right), $

(14) where m is the average mass of the nucleon, and
$ A_1 $ ,$ A_2 $ , and$ A_3 $ are the mass numbers of the three fragments.A scheme of the ternary fragments in equatorial and collinear geometries is shown in Fig. 1. The touching configuration in this figure (s = 0), is related to the first turning point in the integral of Eq. (13).
-
In the first step of the study of true ternary fission of 242Pu, all possible fragmentations with
$ 28\leqslant Z \leqslant 38 $ are extracted. The imposed condition in this research is$ Z_3\leqslant Z_2 \leqslant Z_1 $ , to avoid the repetition of fragment arrangements in the calculation of potential energies. Considering this condition, 14 groups of fragments with various atomic numbers are selected.In the second step, for each group, all possible combinations with different mass numbers are listed. In each of the 14 groups, about 300 subgroups were identified. Subsequently, the interaction potentials, Q-values, penetration probabilities and relative yields were calculated for each individual fragmentation in the collinear (with the lightest fragment in the middle of the arrangement) and equatorial geometries. Note that interaction potentials are calculated in the touching-fragment configuration.
Due to the huge amount of data, presentation of all calculated results is virtually impossible. Therefore, to be able to compare the results, the minimum of potential was chosen in each category.
The Q-values and minimum interaction potentials in the collinear and equatorial geometries are presented in Table 1. As is evident from this table, in this region of mass and charge numbers, the potential barriers of collinear configurations are lower than the equatorial ones. This result has been verified with the results presented in Refs. [13, 47, 48]. Also, in most combination groups, there is at least one fragment with a neutron and/or proton closed shell (bold numbers in Table 1).
Z1 Z2 Z3 Z1 Z2 Z3 Z1 Z2 Z3 Q/MeV Vtot - collinear/MeV Vtot - equatorial/MeV 32 31 31 82 79 81 50 48 50 240.3094 78.1659 100.605 32 32 30 82 82 78 50 50 48 243.032 74.4898 97.7208 33 31 30 83 81 78 50 50 48 239.4991 77.9527 101.1142 33 32 29 83 82 77 50 50 48 238.313 77.4297 101.9928 33 33 28 83 83 76 50 50 48 235.6672 78.0857 103.7011 34 30 30 84 78 80 50 48 50 239.7981 76.8431 99.9926 34 31 29 84 81 77 50 50 48 236.8043 78.8 102.739 34 32 28 86 82 74 52 50 46 239.0969 75.2326 100.4867 35 30 29 87 78 77 52 48 48 234.6038 80.6331 104.5678 35 31 28 87 81 74 52 50 46 234.6986 79.3986 104.4263 36 29 29 90 75 77 54 46 48 232.6591 82.0497 105.9731 36 30 28 90 78 74 54 48 46 235.621 78.0305 102.8422 37 29 28 93 75 74 56 46 46 230.2699 82.7749 107.2704 38 28 28 94 74 74 56 46 46 230.4843 81.81 105.7355 Table 1. Q-values and minimum interaction potentials for 14 groups of
$ Z_1 $ ,$ Z_2 $ and$ Z_3 $ between 28 and 38, with the condition$ Z_3\leqslant Z_2\leqslant Z_1 $ . Seven highlighted groups are shown in Fig. 9 for visual comparison.In the group
$ Z_1 = 32 $ ,$ Z_2 = 32 $ , and$ Z_3 = 30 $ , which has the lowest minimum interaction potential among all 14 groups, the most favorable combinations with the same$ A_1 $ are chosen and the variations of the interacting potentials, Q-values and relative yields are plotted as a function of the fragment mass number$ A_1 $ . The results are presented in Fig. 2. Note that the three vertical axes in this figure have a different scale.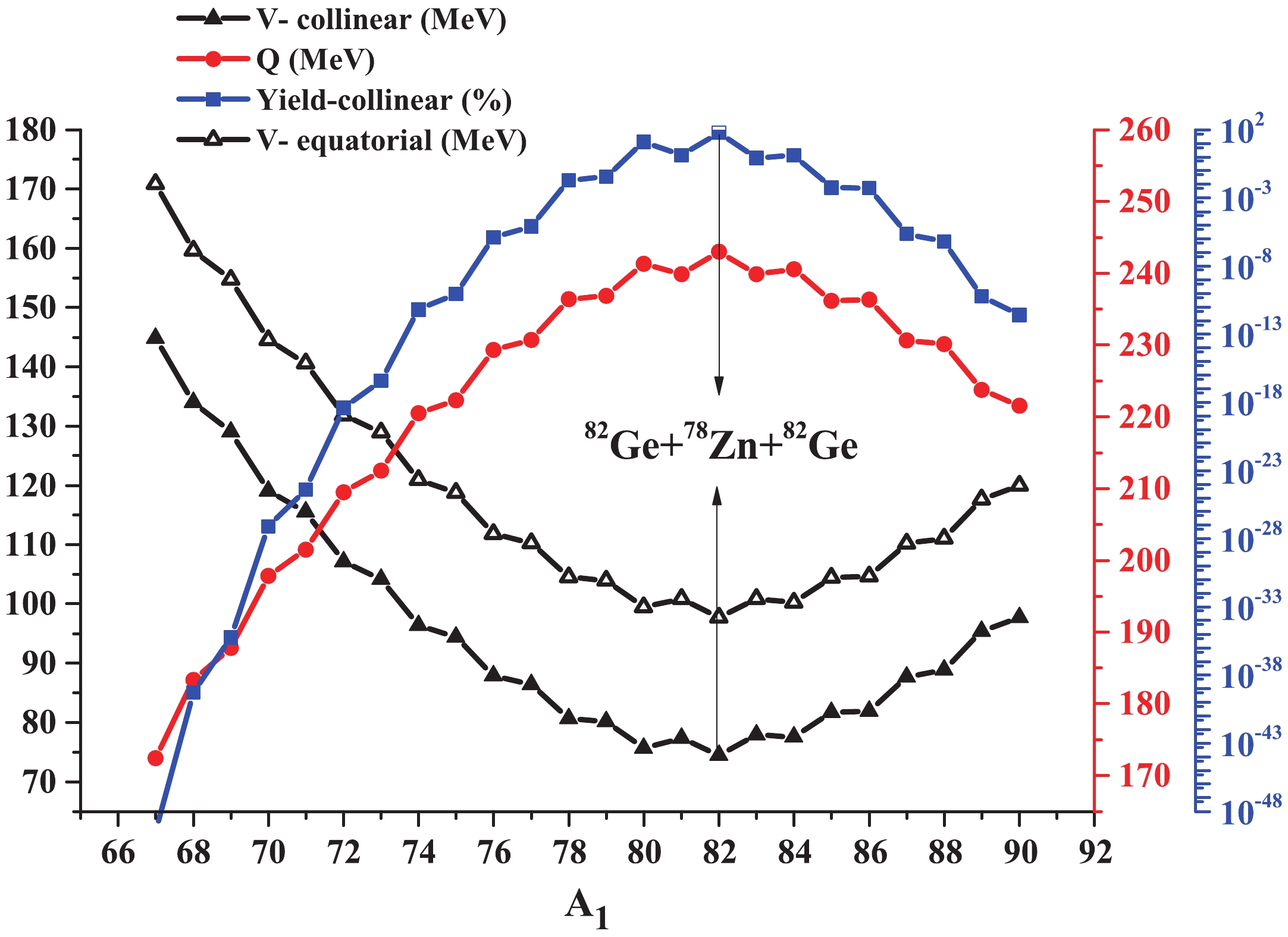
Figure 2. (color online) Interaction potentials in the collinear and equatorial configurations (left vertical axis), Q-values (right vertical axis), and relative yields in the collinear geometry (logarithmic axis) for the combinations with
$ Z_1 = 32 $ ,$ Z_2 = 32 $ ,$ Z_3 = 30 $ and different mass numbers, plotted as a function of$ A_1 $ .From Fig. 2, it is obvious that an increase of the Q-value and relative yield is equivalent to a decrease of the interaction potential, and vice versa. However, this equivalence is not always valid. In Fig. 2, the Z values are constant in all considered combinations. If both Z and A vary among different combinations, one may see that there is no specific relation between the Q-values and relative yields or interaction potentials (see subsection 3.1).
In Fig. 2, the minimum of the interaction potential and the maximum of the yields and Q-values occurs for the combination
$ ^{82}{\rm{Ge}}+^{78}{\rm{Zn}}+^{82}{\rm{Ge}} $ with the magic neutron number for the two Ge isotopes (N = 50). For this group ($ Z_1 = 32 $ ,$ Z_2 = 32 $ , and$ Z_3 = 30 $ ), the contour map is generated considering all 300 possible combinations with various mass numbers. It can be seen that the maxima of the Q-values (Fig. 3) , which correspond to the minima of the interaction potentials (Fig. 4), belong to a region where the mass numbers$ A_1 $ and$ A_2 $ (and consequently$ A_3 $ ) are close together. This region can be considered as the region of true ternary fission.
Figure 3. (color online) Contour map of the Q-values for all possible combinations of the breakup
$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ $ $ ^{A_3}{\rm Zn}+^{A_2}{\rm Ge} $ , plotted as a function of fragment mass numbers$ A_1 $ and$ A_2 $ .
Figure 4. (color online) Contour map of the interaction potentials (collinear geometry) for all possible combinations of the breakup
$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ , plotted as a function of fragment mass numbers$ A_1 $ and$ A_2 $ .From an analysis of Table 1 one can conclude that: (1) even-mass fragments have lower potential barriers than the odd-mass ones (in agreement with [46, 47, 67, 68]); (2) neutron closed shell structures are more important than the proton closed shells for lowering the potential barrier (compatible with [45, 69]); (3) the closed shell structure of the heaviest fragment plays a key role for the more favorable channels (in agreement with [69]); (4) fragments with smaller difference of mass numbers have lower potential barriers and higher Q-values compared to other fragmentations (upper and lower rows of Table 1).
-
In this part of the study, we consider a double magic nucleus (
$ ^{132}{\rm Sn} $ ) as the fixed fragment and compare it with the previous results for true ternary fission of$ ^{242}{\rm Pu} $ . Like in the previous section, all possible ternary channels are considered. The Q-values and charge minimized potentials in the equatorial and collinear configurations were calculated and are plotted as a function of$ A_3 $ (the lightest fragment) in Figs. 5 and 6, respectively. As is clear from these figures, there is no specific relation between the Q-values and the interaction potentials, due to the variation of both A and Z. In fact, the actual possibility of ternary fission is related to the potential barrier properties and not to the released energy.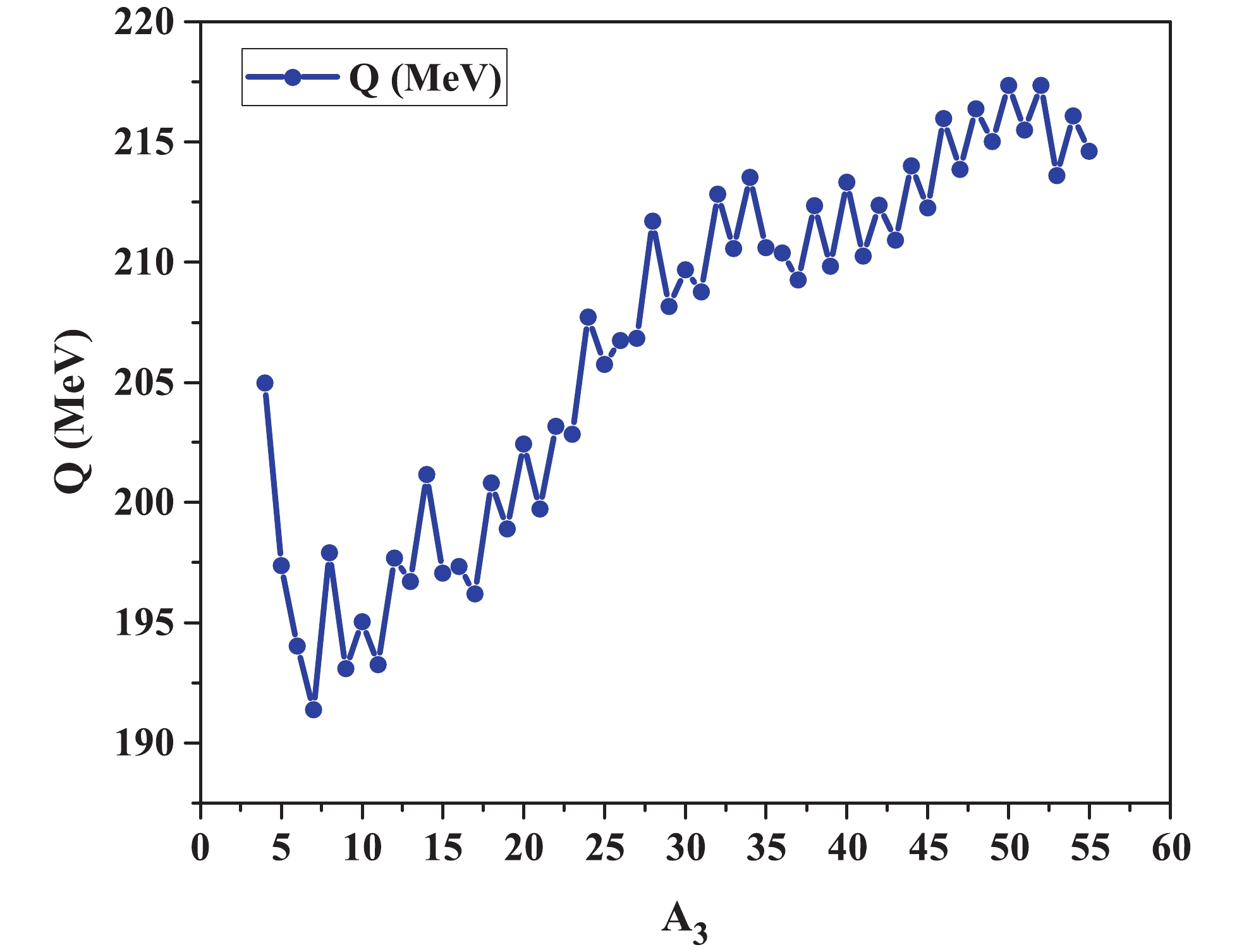
Figure 5. (color online) Q-values for the breakup
$ ^{242}{\rm Pu}\rightarrow ^{132}{\rm Sn}+ $ $ A_3+ A_2$ .
Figure 6. (color online) Charge minimized interaction potentials for the breakup
$ ^{242}{\rm Pu}\rightarrow ^{132}{\rm Sn}+ A_3+ A_2 $ in the collinear and equatorial geometries.It can be seen in Fig. 6 that collinear geometry has a lower potential barrier than the equatorial geometry, except for very light third fragment. The lowest barrier in collinear geometry is obtained for the combination
$^{132}{\rm Sn}+ ^{22}{\rm O}+$ $ ^{88}{\rm Kr} $ . A similar results for ternary fission of$ ^{252}{\rm Cf} $ were reported in Ref. [53].Variation of the potential barrier (
$ V_{\rm C}+V_{\rm P} $ ) as a function of separation parameter (s) is presented in Fig. 7 for the combination$ ^{132}{\rm Sn}+ ^{22}{\rm O}+ ^{88}{\rm Kr} $ . The potential is calculated by varying s uniformly, starting from the touching point. It should be mentioned here that the potentials in the overlap region are not favored in this model. Indeed, shifting the first turning point from the touching configuration$ (s_1 = 0) $ to the point$ s_0 $ $ (V(s_0) = Q) $ leads to the model of Shi and Swiatecki (Ref. [70]) for penetrability calculations. More information about the calculation of penetrability by using the two turning points is given in Refs. [44, 45, 61, 62].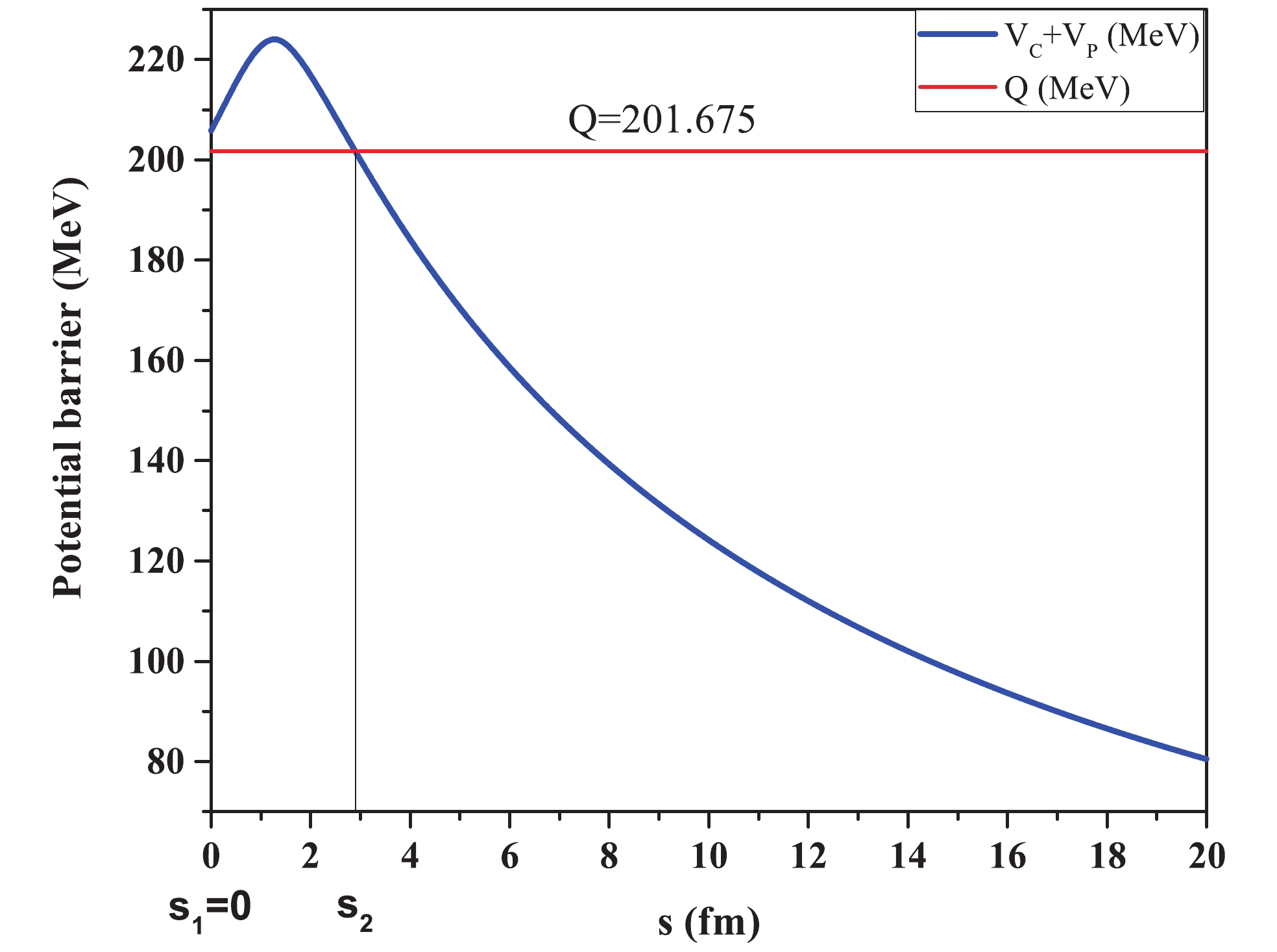
Figure 7. (color online) Potential barrier
$ (V_{\rm C}+V_{\rm P}) $ as a function of separation parameter s for the breakup$ ^{242}{\rm Pu}\rightarrow ^{132}{\rm Sn}+ $ $ ^{22}{\rm O}+ ^{88}{\rm Kr} $ . The turning points and the Q-value are also shown.In Fig. 8, the interaction potentials in the region of true ternary fission (
$ Z_1 = 32 $ ,$ Z_2 = 32 $ ,$ Z_3 = 30 $ ) and Tin-accompanied ternary fission of$ ^{242}{\rm Pu} $ are compared. It is obvious from this figure that in collinear configuration the ternary potential barriers with$ ^{132}{\rm Sn} $ as the fixed fragment are much lower than for the other groups. Since$ ^{132}{\rm Sn} $ is a double magic isotope (Z = 50 and N = 82), this result emphasizes the importance of the closed shell structures for the favorable ternary channels.
Figure 8. (color online) Comparison of the potential barriers for true ternary fission and Tin-accompanied ternary fission of
$ ^{242}{\rm Pu} $ in the collinear configuration.In order to get a better visual comparison, seven groups with different
$ Z_1 $ (highlighted in Table 1) are shown in Fig. 9 as a bar graph. The combination$ ^{132}{\rm Sn}+^{22}{\rm O}+^{88}{\rm Kr} $ is also shown in this figure. It is evident that in these seven groups there is no significant difference between the magnitudes of interaction potentials for fragments with various Z (less than 10 MeV). But the ternary fragmentation potential barrier with$ ^{132}{\rm Sn} $ as the fixed fragment is almost 30 MeV lower than the others. -
In order to calculate the kinetic energies of the fragments, we concentrate on the fragmentation
$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ $ $ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ , which has the lowest potential barrier among the 14 groups. Also, the collinear tripartition is considered as a sequential decay, which means that the ternary fragmentation happens in two steps. In the first step, the unstable parent nucleus with mass number A breaks into fragments$ A_i $ and$ A_{jk} $ . Then in the next step, the composite fragment$ A_{jk} $ fissions into fragments$ A_j $ and$ A_k $ . In this study, i, j and k are referred to fragment numbers 1, 3, and 2, respectively. We assume that in both steps the energy and momentum of the system are conserved. In order to calculate the kinetic energy, we employ the method presented in Ref. [49]. The mathematical method for calculating the kinetic energy is presented here briefly. For more details, the interested reader can consult Ref. [49]$ Q_I = M_x(A)-[m_x(A_1)+m_x(A_{23})]. $

(15) $ Q_{II} = m_x(A_{23})-[m_x(A_2)+m_x(A_3)]. $

(16) Equations (15) and (16) are related to the steps one and two, respectively.
$ M_x $ is the mass excess of the parent, and$ m_x $ is the mass excess of the fragments in each step.In the first step, the velocity of the composite nucleus is obtained using
$ v_{23} = +\sqrt{\left(\frac{2m_1}{m_1+m_{23}}\right)\left(\frac{Q_I}{m_{23}}\right)}, $

(17) and similarly, the velocity of fragment 1 is as follows
$ v_1 = -\sqrt{\left(\frac{2m_{23}}{m_1+m_{23}}\right)\left(\frac{Q_I}{m_1}\right)}. $

(18) Here, m is the mass of the fragments expressed in units of energy.
For the velocities of fragments 2 and 3 in the second step, we have
$ v_2 = \frac{m_2 m_{23} v_{23}\pm\sqrt{\zeta^2}}{m_2^2+m_2 m_3}, $

(19) where
$ \begin{split} \zeta^2 =& m_2^2 m_{23}^2 v_{23}^2-[(m_2^2+m_2 m_3)\\&\times(m_{23}^2 v_{23}^2- 2 m_3 Q_{II}- m_3 m_{23} v_{23}^2)]. \end{split}$

(20) $ v_3 = -\left[\frac{m_2 v_2- m_{23} v_{23}}{m_3}\right]. $

(21) Finally, using the well known formula
$ E = \displaystyle\frac{1}{2} m v^2 $ , the kinetic energies of all three fragments are obtained.The kinetic energies of the fragments
$ ^{A_1}{\rm Ge} $ and$ ^{A_3}{\rm Zn} $ are shown in Figs. 10 and 11 as a function of$ A_1 $ and$ A_2 $ for all 300 combinations.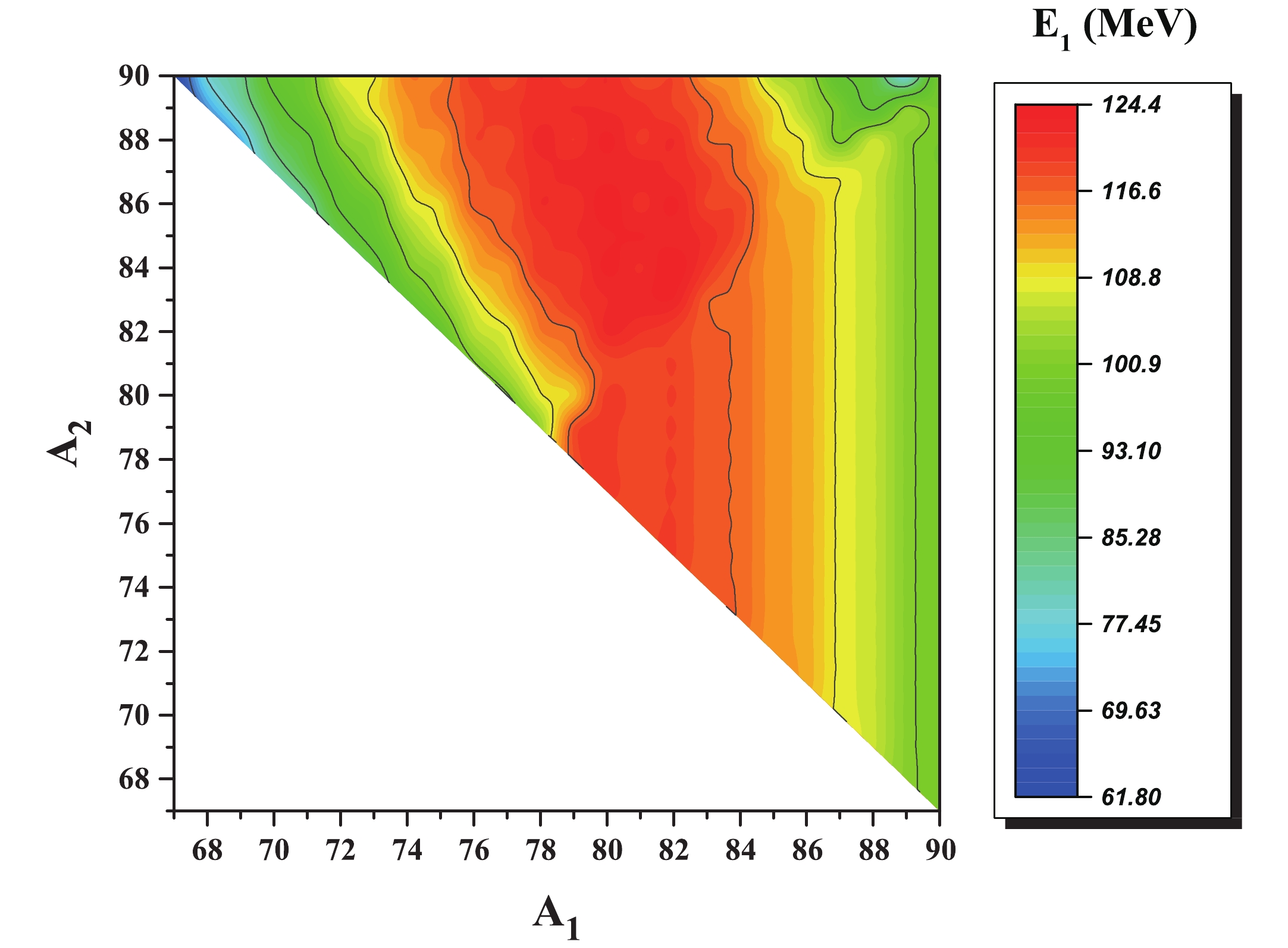
Figure 10. (color online) Kinetic energy of the fragment
$ ^{A_1}{\rm Ge} $ as a function of$ A_1 $ and$ A_2 $ for the collinear breakup$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ .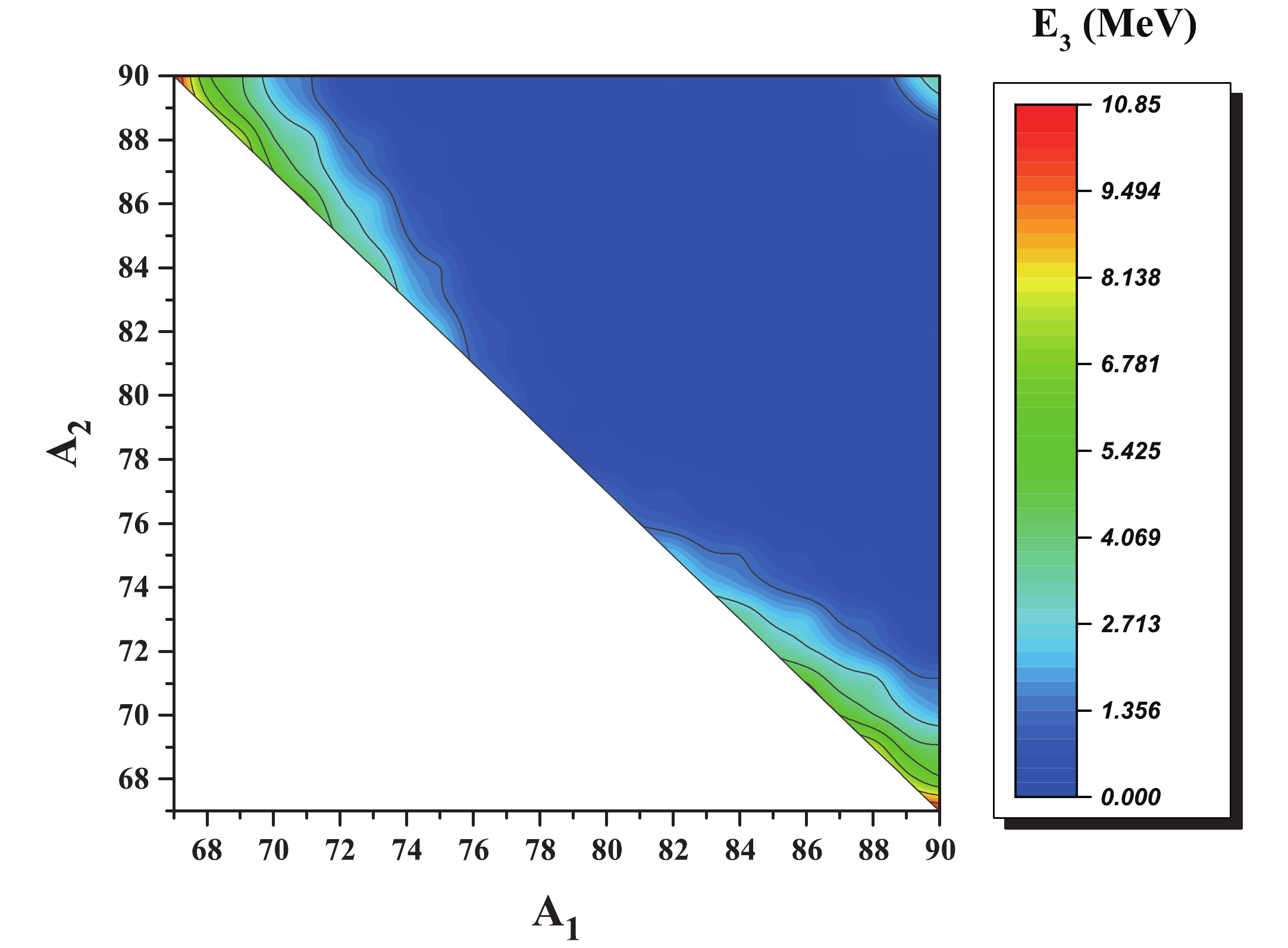
Figure 11. (color online) Kinetic energy of the fragment
$ ^{A_3}{\rm Zn} $ as a function of$ A_1 $ and$ A_2 $ for the collinear breakup$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ .As is clear from Fig. 11, the light fragment that is located in the middle of the collinear arrangement takes a very small part of the total kinetic energy, and the major part of the total kinetic energy is removed by the other two fragments. This observation could be the reason why the light fragment has escaped experimental detection. This result is in agreement with Ref. [49].
The kinetic energies of the fragments for the combinations mentioned in Fig. 2 are presented as a two dimensional graph in Fig. 12. The relative yields, Q-values and total kinetic energies of this group are also listed in Table 2. One may observe that the Q-values and total kinetic energies for each fragmentation in Table 2 are almost equal. This result is due to the assumption that ternary fission is a cold process.
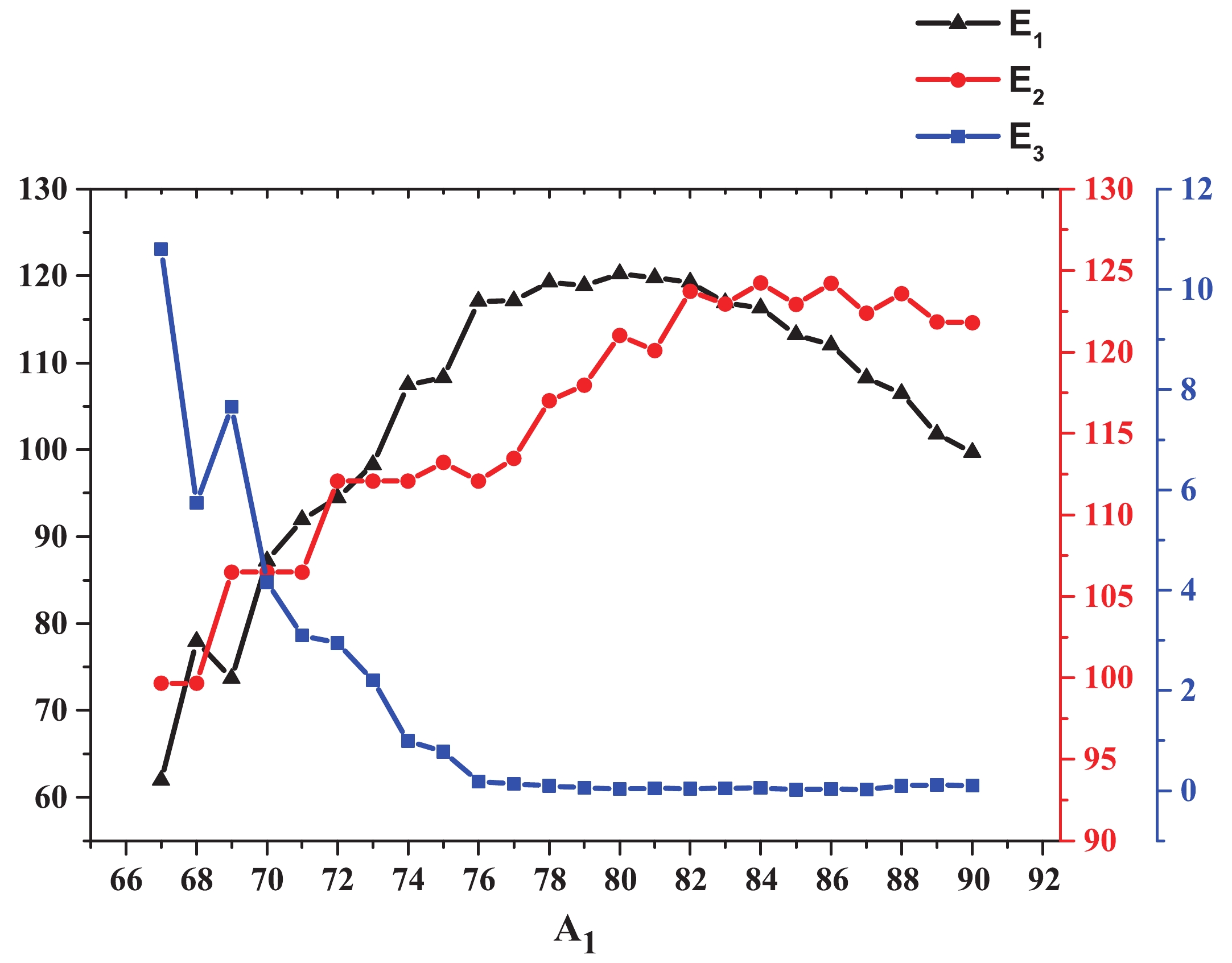
Figure 12. (color online) Kinetic energies of the fragments
$ A_1 $ ,$ A_2 $ and$ A_3 $ for the sequential collinear decay$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ . Vertical axes are (from left to right) for$ E_1 $ ,$ E_2 $ , and$ E_3 $ . It is clear that the fragment number 3 is almost at rest.A1 A2 A3 relative yield – collinear (%) relative yield – equatorial (%) Q /MeV total kinetic energy /MeV 67 90 85 0.000 0.000 172.437 172.438 68 90 84 0.000 0.000 183.327 183.329 69 88 85 0.000 0.000 187.799 187.801 70 88 84 0.000 0.000 197.830 197.832 71 88 83 0.000 0.000 201.505 201.506 72 86 84 0.000 0.000 209.474 209.476 73 86 83 0.000 0.000 212.516 212.517 74 86 82 0.000 0.000 220.511 220.512 75 85 82 0.000 0.000 222.309 222.310 76 86 80 1.26×10−6 0.000 229.340 229.341 77 85 80 8.34×10−6 0.000 230.703 230.704 78 84 80 1.98×10−2 1.25×10−3 236.377 236.379 79 83 80 3.66×10−2 2.78×10−3 236.874 236.875 80 82 80 13.00 5.23 241.318 241.319 81 82 79 1.39 0.457 239.858 239.859 82 82 78 61.7 92.1 243.032 243.033 83 82 77 0.817 0.512 239.899 239.901 84 82 76 1.38 1.68 240.585 240.586 85 80 77 5.79×10−3 8.85×10−4 236.166 236.167 86 80 76 5.17×10−3 1.25×10−3 236.317 236.318 87 79 76 2.28×10−6 0.000 230.632 230.633 88 80 74 6.11×10−7 0.000 230.151 230.152 89 79 74 0.000 0.000 223.735 223.737 90 78 74 0.000 0.000 221.557 221.559 Table 2. Calculated data for the breakup
$ ^{242}{\rm Pu}\rightarrow ^{A_1}{\rm Ge}+ ^{A_3}{\rm Zn}+ ^{A_2}{\rm Ge} $ . For each value of$ A_1 $ , the interaction potential is minimized. Therefore, 24 combinations among 300 are chosen (yields less than$ 10^{-7} $ are denoted as "0"). -
True ternary fission of
$ ^{242}{\rm Pu} $ was studied and compared with the Tin-accompanied ternary fission of the parent. The most probable ternary fission path is predicted to be the one with the minimum interaction potential with respect to the mass and charge asymmetries. The obtained results revealed that in the considered region of mass and charge numbers ($ 28\leqslant Z_1,Z_2,Z_3\leqslant 38 $ ), the collinear geometry is preferred to the equatorial geometry. Also, closed shell structures play an inevitable role in the potential barrier height. Indeed, closed neutron shells are more effective in lowering the potential barrier than the closed proton shells. The most favorable combinations are in a region where the fragments have comparable mass and charge numbers.However, it is found that the Tin-accompanied ternary fission of
$ ^{242}{\rm Pu} $ is more favorable than the true ternary fission. This can be interpreted in two ways: (1)$ ^{132}{\rm Sn} $ is a magic nucleus, both in proton and neutron numbers; (2) three fragments with comparable sizes (true ternary fission) are less likely to appear in the exit channel.The kinetic energies of the fragments in the group
$ Z_1 = 32 $ ,$ Z_2 = 32 $ , and$ Z_3 = 30 $ were also calculated in the collinear geometry as a sequential decay. The obtained results showed that a large fraction of the total kinetic energy is carried by the two$ {\rm Ge} $ nuclei, and$ {\rm Zn} $ , as the middle part of the arrangement, does not have significant kinetic energy. This fact can be the reason why it has escaped experimental detection.
Tin-accompanied and true ternary fission of 242Pu
- Received Date: 2019-04-19
- Available Online: 2019-09-01
Abstract: True ternary fission and Tin-accompanied ternary fission of 242Pu are studied by using the 'Three Cluster Model'. True ternary fission is considered as a formation of heavy fragments in the region





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: