-
In high-energy heavy-ion collisions, people study the entire collision process and the properties of matter produced in the early stage of collisions by analyzing the observables of particles in final state. The interactions within the dense medium before the kinetic freeze-out may affect the experimental observables and dilute the early signals, so the study of interactions between the particle and the dense medium has always been a topic of concern [1–7]. In the late 1990s, M. Asakawa et al. proposed that particle mass might be modified by the interactions between the particle and the medium formed in high-energy heavy-ion collisions. This may therefore lead to a squeezed back-to-back correlation (BBC) of boson-antiboson [8,9]. The BBC is the result of a quantum-mechanical transformation relating in-medium quasi-particles to two-mode squeezed states of their free, observable counterparts [8–10]. This is achieved by means of a Bogolioubov transformation linking the creation (annihilation) operators of the observed bosons to the creation (annihilation) operators of the quasi-particles in the medium [8-10]. Since the BBC is related to the dense source, investigations on the BBC may provide new insight for people to understand the interactions between the particle and the dense medium formed in high-energy heavy-ion collisions.
The BBC function is defined as [8,9]
$ C({ k},-{ k}) = 1 + \frac{|G_s({ k},-{ k})|^2}{G_c({ k},{ k}) G_c(-{ k},-{ k})}, $

(1) where
$ G_c({ k}_1,{ k}_2) $ and$ G_s({ k}_1,{ k}_2) $ are the chaotic and squeezed amplitudes, respectively. For hydrodynamic sources, with the formula derived by Makhlin and Sinyukov [11,12], the chaotic and squeezed amplitudes can be expressed as [9,10,13-15]$ \begin{split} G_c({{ k}_1},{{ k}_2}) =&\int \frac{{\rm d}^4\sigma_{\mu}(r)}{(2\pi)^3} K^\mu_{1,2}\, {\rm e}^{{\rm i}\,q_{1,2}\cdot r}\,\! \Bigl\{|c'_{{ k}'_1,{ k}'_2}|^2\, n'_{{ k}'_1,{ k}'_2} \\ &+\,|s'_{-{ k}'_1,-{ k}'_2}|^2\,[\,n'_{-{ k}'_1,-{ k}'_2}+1]\Bigr\}, \end{split} $

(2) $ \begin{split} G_s({{ k}_1},{{ k}_2})\! = &\int \frac{{\rm d}^4\sigma_{\mu}(r)}{(2\pi)^3} K^\mu_{1,2}\, {\rm e}^{2{\rm i}\,K_{1,2}\cdot r}\!\Bigl\{s'^*_{-{ k}'_1,{ k}'_2} c'_{{ k}'_2,-{ k}'_1} \\ & \times n'_{-{ k}'_1,{ k}'_2}+c'_{{ k}'_1,-{ k}'_2} s'^*_{-{ k}'_2,{ k}'_1} [n'_{{ k}'_1,-{ k}'_2} + 1] \Bigr\}, \end{split} $

(3) where
$ {\rm d}^4\sigma_{\mu}(r) $ is the four-dimensional element of the freeze-out hypersurface, which can be determined by a hydrodynamic source for a fixed freeze-out temperature.$ q^{\mu}_{1,2} = k^{\mu}_1-k^{\mu}_2 $ ,$ K^{\mu}_{1,2} = (k^{\mu}_1+k^{\mu}_2)/2 $ , and$ { k}_i' $ is the local-frame momentum corresponding to$ { k}_i\; (i = 1,2) $ . The quantities$ c'_{{ k}'_1,{ k}'_2} $ and$ s'_{{ k}'_1, { k}'_2} $ are the coefficients of the Bogoliubov transformation between creation (annihilation) operators of quasiparticles and free particles, and$ n'_{{ k}'_1,{ k}'_2} $ is the boson distribution associated with the particle pair [8–10,13–15].$ s'_{{ k}'_1,{ k}'_2} $ is zero in the case where there is no mass modification, and the BBC function will be 1. In Eq. (3), the factor${\rm e}^{2{\rm i}K_{1,2}\cdot r} $ is equal to$ {\rm e}^{2{\rm i}\omega_{{ k}}t} $ for$ { k}_1 = { k} $ ,$ { k}_2 = -{ k}_1 = -{ k} $ . Thus, the BBC function$ C({ k},-{ k}) $ is sensitive to the temporal distribution of the freeze-out points [9,10,13-16], which will be larger for a narrow temporal distribution of the particles' freeze-out points [9,10,13,15].In experiment, the first search of BBC signals was performed by the PHENIX collaborations [17], and the
$ K^+ $ $ K^- $ BBC function is only 1% larger than one in the central Au + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV, hence not present on a significant level. The simulation results indicate that the$ K^+ $ $ K^- $ BBC function is suppressed by the wide temporal distribution of the particles' freeze-out points, and cannot be detected in Au + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV for central collisions [15].Recently, the long-range angular correlations have been first detected by the CMS collaboration in
$ pp $ collisions at 7 TeV at the LHC [18], and later they were also observed in$ pp $ collisions [19,20] and p + Pb collisions [21-24] in other collaborations at the LHC. This phenomenon and the elliptic anisotropy of inclusive and identified hadrons were likewise successfully detected by the PHENIX collaboration in 5% of the most central d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV at the RHIC [25,26]. This indicates that the hydrodynamically expanding quark-gluon plasma (QGP) medium may be created in small systems, and hydrodynamic calculations are in good agreement with measured$ v_2 $ in small systems [27–31]. The BBC function is sensitive to the temporal distribution of the particles' freeze-out points, and the narrow temporal distribution corresponding to a small hydrodynamic source may lead to a large BBC. Motivated by this, we study the BBC function of$ K^+ $ $ K^- $ in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV by using the VISH2+1 code [32,33] to simulate the evolution of the particle-emitting sources. Moreover, we calculate the BBC functions in Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV. The event-by-event initial conditions of MC-Glb [34] are employed at$ \tau_0 = 0.6 $ fm/c in the simulations, and the ratio of the shear viscosity to entropy density of the QGP is taken to be 0.08 [35,36].In Ref. [37], the squeezed correlation of the boson-antiboson for
$ { k}_1\neq-{ k}_2 $ was studied. The squeezed correlation increases with the increasing angle between the transverse momenta of the boson and antiboson, and the squeezed correlation functions reach their maxima when$ { k}_1 = -{ k}_2 $ . In this work, we focus on studying the observability of the BBC of$ K^+ $ $ K^- $ in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV, and calculate the squeezed correlation for$ { k}_1 = -{ k}_2 $ .The rest of this paper is organized as follows. In Sec. 2, we present the transverse momentum spectra of kaons, and the spatio-temporal properties of the kaon emission source. In Sec. 3, we calculate the BBC functions of
$ K^+ $ $ K^- $ for central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. Considering that some particles may not be affected by the medium, we further introduce a Gaussian factor to describe the probability that a particle is affected by the medium and study the BBC functions of$ K^+ $ $ K^- $ when parts of all kaons are affected by the medium. Finally, a summary and conclusions are presented in Sec. 4. -
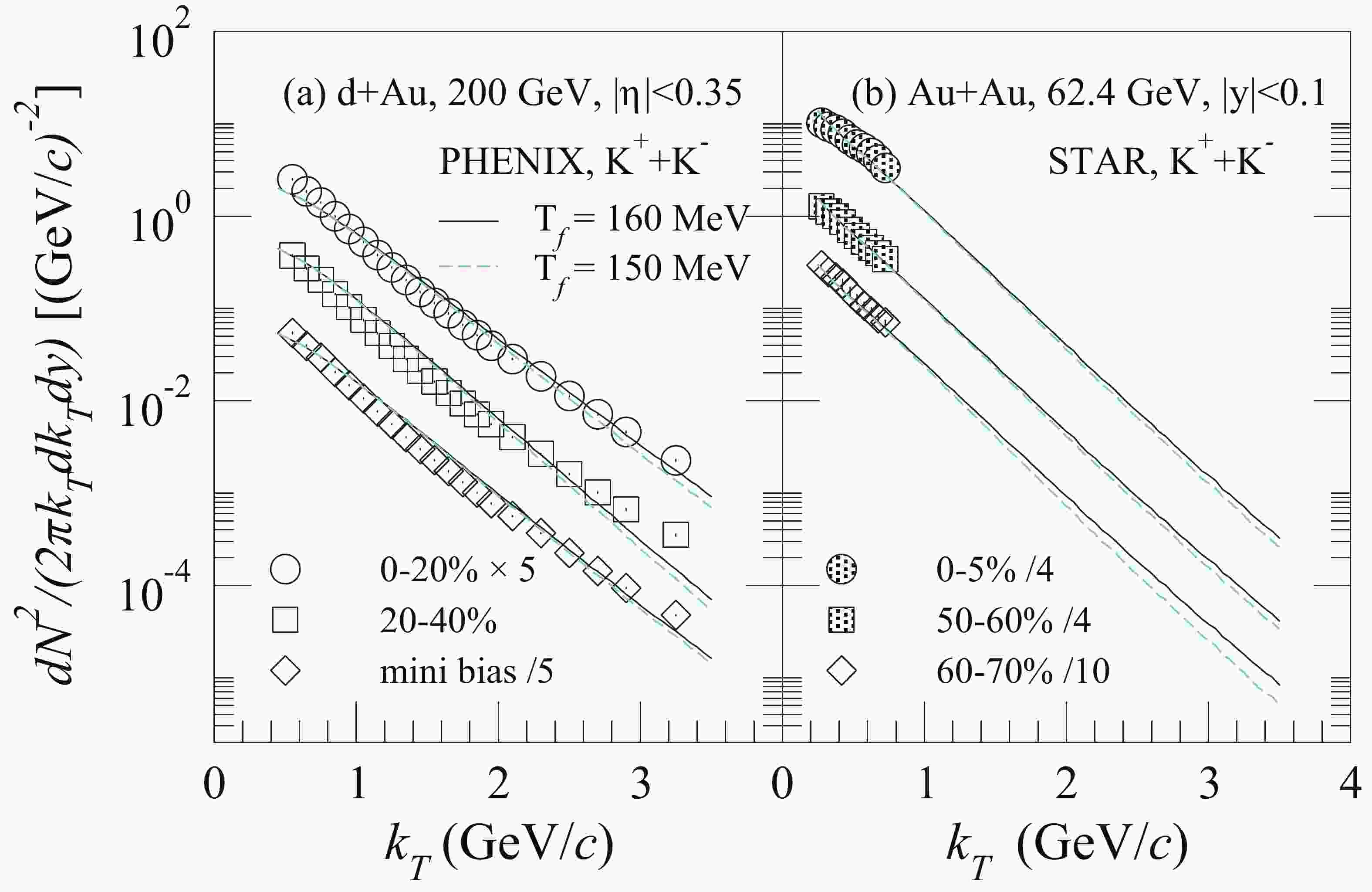
In Fig. 1, we show the transverse momentum spectra of kaons simulated by the viscous hydrodynamic code for the collisions of different centrality ranges. The experimental data [38,39] are likewise plotted. One can see that the simulated spectra for the freeze-out temperature
$ T_f = 160 $ MeV fit the experimental data slightly better (especially at high$ k_T $ ) than for$ T_f = 150 $ MeV. Hence, the freeze-out temperature$ T_f $ of kaons will be selected as 160 MeV in this study.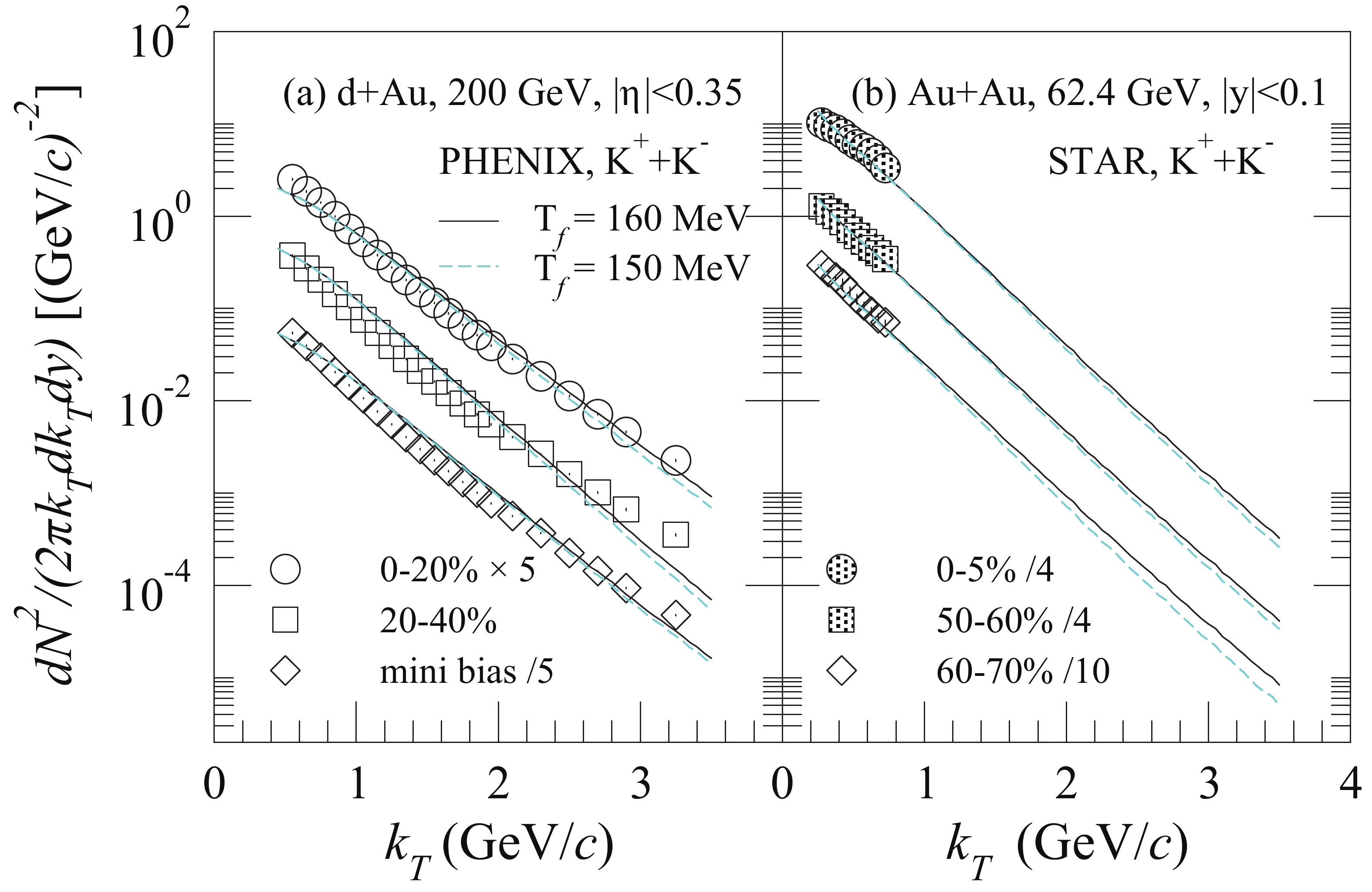
Figure 1. (color online) Transverse momentum spectra of kaons calculated with VISH2+1 for d + Au collisions at
$ \sqrt{s_{NN}} = 200 $ GeV (left panel) and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV (right panel). The experimental data of d + Au collisions are measured by the PHENIX Collaboration [38], and the experimental data of Au + Au collisions are from the STAR Collaboration measurements [39]. Solid lines depict the simulated spectra for the freeze-out temperature$ T_f = 160 $ MeV, and the dashed lines depict the simulated spectra for$ T_f = 150 $ MeV.For hydrodynamic sources with a Bjorken cylinder, the four-dimensional element of the freeze-out hypersurface can be written as
$ {\rm d}^4\sigma_{\mu}(r) = f_{\mu}(\tau, { r}_{\perp}, \eta)\, {\rm d}\tau {\rm d}^2 { r}_{\perp} {\rm d}\eta, $

(4) where
$ \tau $ ,$ { r}_{\perp} $ , and$ \eta $ are the proper time, transverse coordinate, and space-time rapidity of the element. The function$ f_{\mu} (\tau,{ r}_{\perp},\eta) $ is related to the freeze-out mechanism that is considered, and$ K^{\mu}_{1,2}f_{\mu}(\tau,{ r}_{\perp},\eta) $ corresponds to the source distributions of proper time and space in the calculations [see Eqs. (2) and (3)].In Fig. 2 (a) and (b), we show the space-time distributions of the freeze-out points,
$ k^{\mu}f_{\mu}(\tau,{ r}_{\perp},\eta) $ , of kaons in the$ z = 0 $ plane in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV for two centrality ranges. The spatial distribution is wide, and the temporal distribution is narrow for d + Au collisions. The freeze-out points of kaons in central and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV are plotted in Fig. 2 (c) and (d), showing that the width of the distributions increases towards central collisions. In Fig. 3, we show the normalized distributions of time and transverse coordinates of kaon freeze-out points in the$ z = $ 0 plane of the collisions, as in Fig. 2.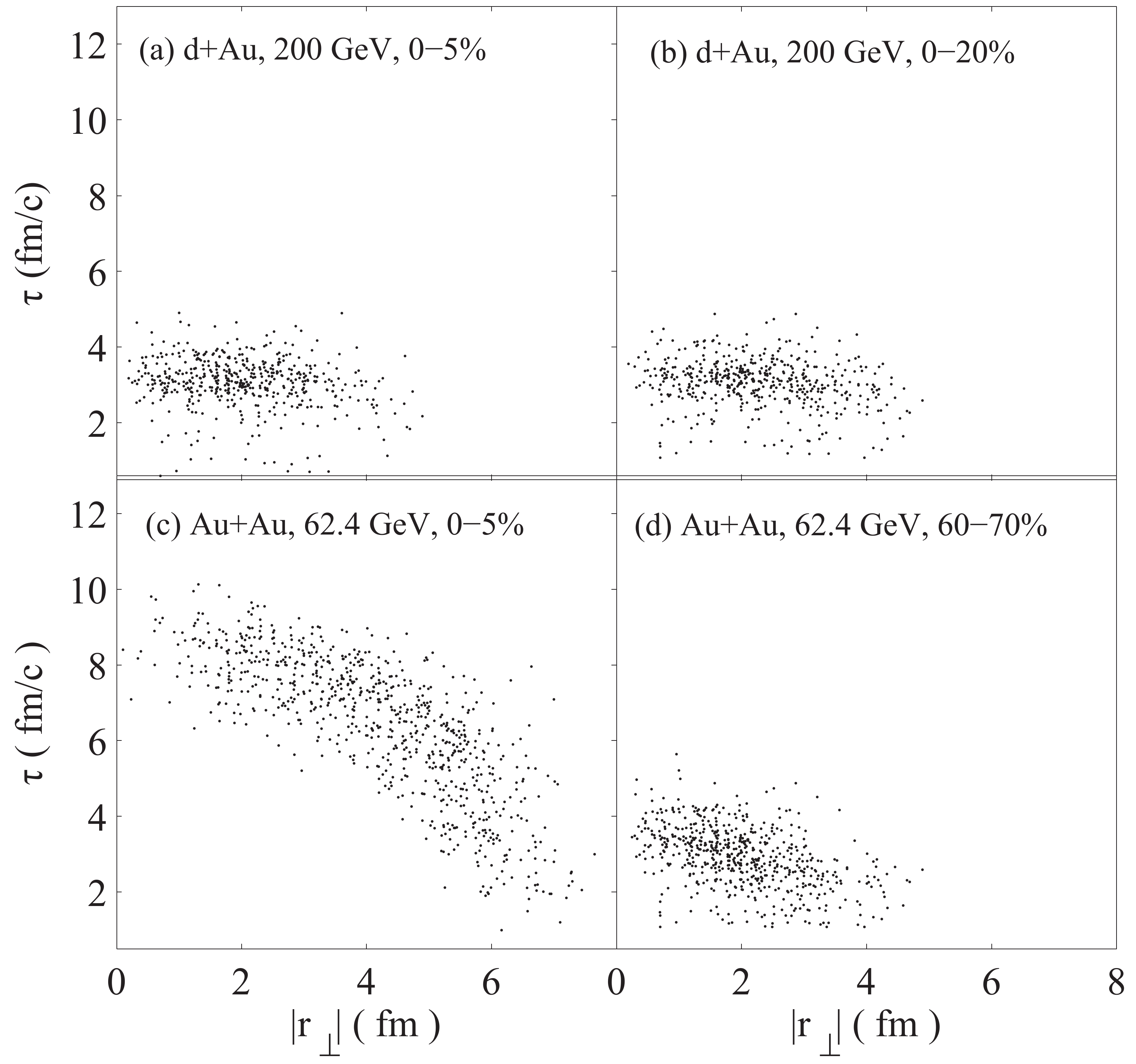
Figure 2. Distributions of kaon freeze-out points in the
$ z = 0 $ plane for d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV (top panel) and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV (bottom panel).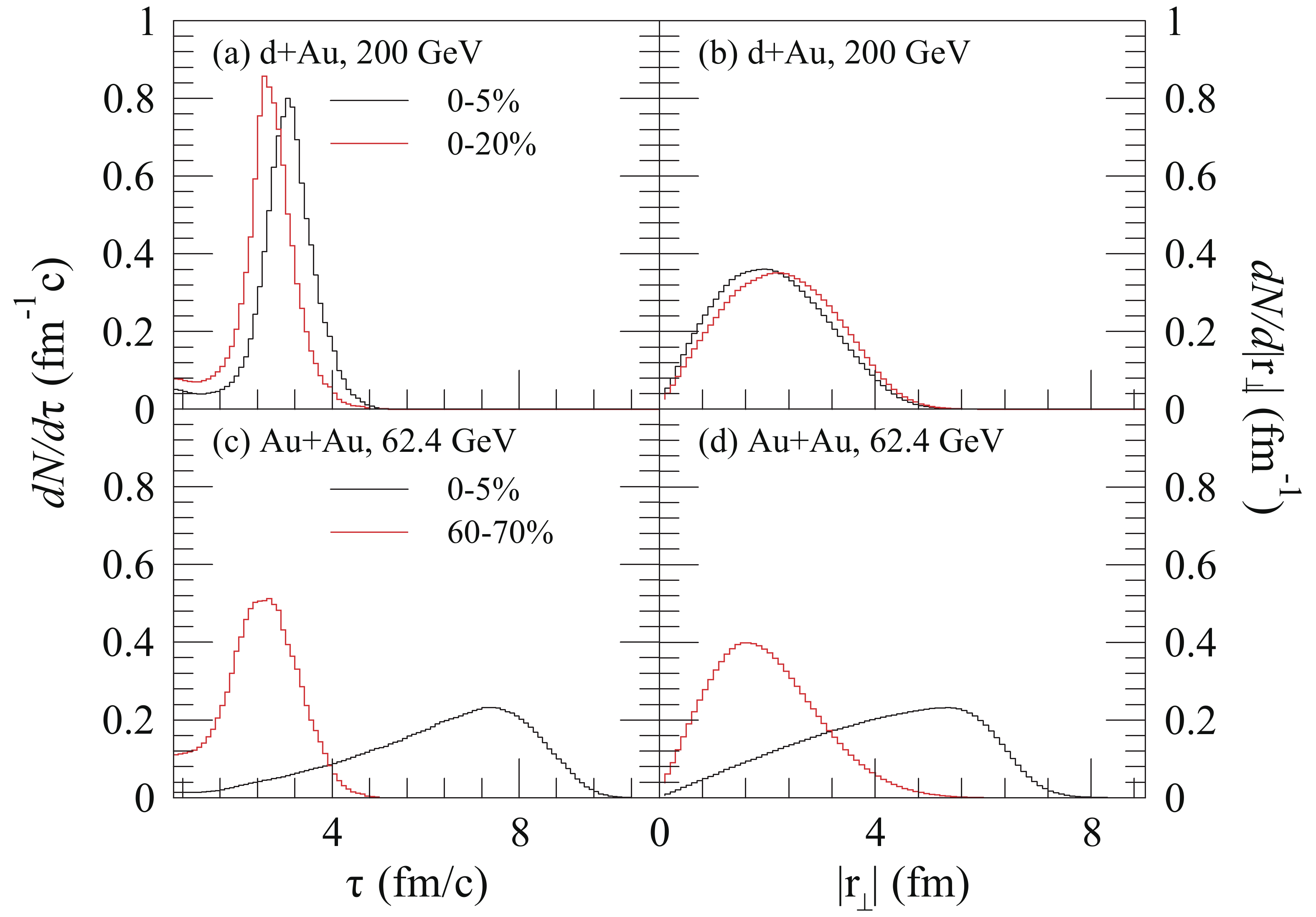
Figure 3. (color online) Normalized distributions of time and transverse coordinates of kaon freeze-out points in the
$ z = 0 $ plane for d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV (top panel) and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV (bottom panel), as in Fig. 2.In Table 1, we show some spatio-temporal properties of the kaon emission source. Here,
$ \bar{{\tau}} $ and$ \overline{|r_{\bot}|} $ are the average time and the average transverse radius of kaon freeze-out points in the$ z = 0 $ plane for a single event.$ \sigma_{\tau} $ and$ \sigma_{r} $ depict the standard deviation of the freeze-out time and transverse radius, respectively, for a single event:collision systems centrality $ \langle\,\bar{\tau}\,\rangle $ /(fm/c)

$ \langle\,\overline{|r_{\bot}|}\,\rangle $ /fm

$ \langle\,{\sigma_{\tau}}\,\rangle $ /(fm/c)

$ \langle\,{\sigma_{r}}\,\rangle $ /fm

d + Au (200 GeV) 0%–5% 3.02 2.14 0.66 0.91 d + Au (200 GeV) 0%–20% 2.59 2.31 0.58 0.87 d + Au (200 GeV) 20%–40% 2.03 2.62 0.47 0.75 Au+Au (62.4 GeV) 0%–5% 6.27 4.19 1.87 1.58 Au + Au (62.4 GeV) 50%–60% 2.87 2.20 0.84 0.99 Au + Au (62.4 GeV) 60%–70% 2.46 2.02 0.71 0.93 Table 1. Spatio-temporal properties of kaon emission source.
$ \begin{aligned} \sigma_{\tau} = \sqrt{\frac{1}{N}\sum_{i = 1}^{N}(\,{\tau}_{i}-\bar{{\tau}}\,)^{\,2}}, \end{aligned} $

(5) $ \begin{aligned} \sigma_{r} = \sqrt{\frac{1}{N}\sum_{i = 1}^{N}(\,{|{r_\bot}|_i}-\overline{|r_{\bot}|}\,)^{\,2}}, \end{aligned} $

(6) where
$ N $ is the total number of the freeze-out points for a single event,$ {\tau}_{i} $ and$ {|{r_\bot}|_i} $ are the space-time coordinates of the freeze-out point denoted by$ i $ .$ \langle \cdots \rangle $ in Table 1 denotes the average over events. The$ \langle\,\bar{\tau}\,\rangle $ and$ \langle\,\overline{|r_{\bot}|}\,\rangle $ are the average time and the average transverse radius, respectively, of kaon freeze-out points in the$ z = 0 $ plane for many events. The average time of kaon freeze-out points decreases from central to peripheral collisions in d + Au and Au + Au collisions. The collision of two nuclei occurs at the center of the transverse plane in the Au + Au collision, and the size of the source increases towards central collisions. Thus,$ \langle\,\overline{|r_{\bot}|}\,\rangle $ decreases from central to peripheral collisions in the Au + Au collision. However,$ \langle\,\overline{|r_{\bot}|}\,\rangle $ increases from central to peripheral collisions in the d + Au collision. This is because the collisions deviate from the center of the transverse plane with the decreasing collision centrality in the d + Au collision.$ \langle\,{\sigma_{\tau}}\,\rangle $ and$ \langle\,{\sigma_{r}}\,\rangle $ are the average width of time and space, respectively, of the freeze-out points for many events. They decrease with increasing collision centrality in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV. -
The BBC function is caused by the mass-shift due to the interactions between the particle and the medium, and it will be equal to 1 in the case of no mass-shift. In this study, the mass of kaons in the medium is treated as a parameter, and we assume that there is no mass-shift if the particle is not affected by the medium. The size of the systems of d + Au collisions and the peripheral Au + Au collisions are too small, and some particles may not be affected by the medium in these collision events. Therefore, the BBC results of
$ K^+ $ $ K^- $ are shown in two subsections. In section 3.1, we show the BBC results for all kaons with mass-shift. In turn, section 3.2 presents the BBC results for parts of all kaons with mass-shift. -
When all particles have a mass-shift, the BBC function averaged over event-by-event calculations for many events was defined as [15]
$ C({ k},-{ k}) = 1+\frac{\displaystyle\sum_{i = 1}^{N_E}|G_{si}({ k},-{ k})|^2}{ \displaystyle\sum_{i = 1}^{N_E}|G_{ci}({ k},{ k})|^2}, $

(7) where
$ N_E $ is the total event number.$ G_{ci}({ k},{ k}) $ and$ G_{si}({ k},-{ k}) $ are the chaotic and squeezed amplitudes, respectively, for a single event denoted by$ i $ . The chaotic amplitude$ G_{ci}(-{ k},-{ k}) $ is equal to$ G_{ci}({ k},{ k}) $ for the same event, and we use$ G_{ci}({ k},{ k}) $ uniformly in Eq. (7).In Fig. 4, we show the BBC functions of
$ K^+ $ $ K^- $ averaged over event-by-event calculations for central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. The BBC functions are shown in the$ k $ -$ m_* $ plane, where$ m_* $ is the kaon mass in the dense medium. If$ m_* $ is equal to the kaon mass in vacuum (494 MeV), there is no mass-shift, and the BBC functions of$ K^+ $ $ K^- $ become one (see Fig. 4). For d + Au collisions, the freeze-out temporal distribution of kaons is much narrower (see Fig. 2 and Fig. 3), and the temporal width parameter of the kaon emission source$ \langle\,{\sigma_{\tau}}\,\rangle $ is likewise very small (see Table 1). As is well known, a narrow temporal distribution may lead to a large BBC. The BBC functions of$ K^+ $ $ K^- $ for the collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV are much stronger than those for the collisions of Au + Au at$ \sqrt{s_{NN}} = 200 $ GeV and Pb + Pb at$ \sqrt{s_{NN}} = 2.76 $ TeV [15]. Hence, they are very likely to be observed experimentally. An observable signal of$ K^+ $ $ K^- $ BBC is also provided in the peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. For hydrodynamic sources, the BBC functions of$ K^+ $ $ K^- $ decrease with the increasing momentum$ k $ for a fixed$ m_* $ . This phenomenon is different from the results for the expanding source with the exponential decay emission time distribution [9,10,13,40,41]. This can be attributed to two factors: first, the BBC functions are affected by the emission time distribution of the particle [13-15], and second, the anisotropic flow also affects the BBC functions [41] (e.g., in Ref. [13], the BBC functions of$ K^+ $ $ K^- $ decrease with the increasing momentum$ k $ for a fixed$ m_* $ for the expanding source with the$ \alpha $ -stable Lévy emission time distribution).
Figure 4. (color online) BBC functions of
$ K^+ $ $ K^- $ averaged over event-by-event calculations for central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV (top panel) and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV (bottom panel).In Fig. 5, the BBC functions of
$ K^+ $ $ K^- $ are shown as a function of$ m_* $ at$ k = 200 $ MeV and$ k = 800 $ MeV for central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. For a fixed momentum, the BBC functions increase with the decreasing temporal width parameter$ \langle\,{\sigma_t}\,\rangle $ . -
The narrow temporal distribution corresponding to a small source may lead to a large BBC. However, if the source is too small, the particles may not be affected by the medium. Hence, we introduce a Gaussian factor
$ {\rm e}^{-\sigma_{r}^2/2\sigma_{c}^2} $ to describe the probability of the particles without a mass-shift. Here,$ \sigma_{c} $ is a spatial width cut parameter, and the probability of the particles with mass-shift is$ P(\sigma_r)\, = \,1-{\rm e}^{-\sigma_{r}^2/2\sigma_{c}^2} $ . In Fig. 6, we show the probability$ P(\sigma_r) $ as a function of$ \sigma_{r} $ with different$ \sigma_{c} $ . For the source with a certain$ \sigma_{r} $ , the probability decreases with the increasing cut parameter$ \sigma_{c} $ .
Figure 6. (color online) Probability of particles with mass-shift as a function of
$ \sigma_{r} $ for different spatial width cut parameter$ \sigma_{c} $ .The probability
$ P(\sigma_r) $ fluctuates among the events for a fixed cut parameter$ \sigma_{c} $ , because the width parameter$ \sigma_{r} $ of the source fluctuates among the events. The average probability,$ \langle\,P(\sigma_r)\,\rangle $ , of the kaons with mass-shift for central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV is shown in Table 2, where$ \langle \cdots \rangle $ depicts the average over events.$ \langle\,P(\sigma_r)\,\rangle $ :

$ \sigma_{c}\,=\,1\, $ fm

$ \sigma_{c}\,=\,1.5\, $ fm

$ \sigma_{c}\,=\,2\, $ fm

d + Au (200 GeV) 0%–5% 33.8% 16.9% 9.9% d + Au (200 GeV) 0%–20% 31.6% 15.7% 9.2% d + Au (200 GeV) 20%–40% 24.5% 11.9% 6.9% Au + Au (62.4 GeV) 0%–5% 71.3% 42.6% 26.9% Au + Au (62.4 GeV) 50%–60% 38.9% 19.9% 11.8% Au + Au (62.4 GeV) 60%–70% 34.9% 17.6% 10.4% Table 2. Average probability of kaons with mass-shift for central and peripheral collisions of d + Au at
$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV.When parts of all particles have a mass-shift, the BBC function averaged over event-by-event calculations for many events becomes
$ \begin{split}& C({ k},-{ k}) = \\ &\quad 1+\frac{\displaystyle\sum_{i = 1}^{N_E}(1-{\rm e}^{-\sigma_{r}^2/2\sigma_{c}^2})|G_{si}({ k},-{ k})|^2} {\displaystyle\sum_{i = 1}^{N_E}[(1-{\rm e}^{-\sigma_{r}^2/2\sigma_{c}^2})|G_{ci}({ k},{ k})|^2 +{\rm e}^{-\sigma_{r}^2/2\sigma_{c}^2}|G_{ci}^{0}({ k},{ k})|^2]}, \end{split}$

(8) where
$ G_{ci}^{0} $ is the chaotic amplitude when there is no mass shift.In Fig. 7, BBC functions of
$ K^+ $ $ K^- $ are shown as a function of$ m_* $ at$ k = 200 $ MeV and$ k = 800 $ MeV with various cut parameters$ \sigma_{c} $ in central and peripheral collisions of d+Au at$ \sqrt{s_{NN}} = 200 $ GeV. For a certain cut parameter$ \sigma_{c} $ , the probability of the kaons with mass-shift decreases with the increasing collision centralities (see Table 2), so the BBC functions are more suppressed in peripheral than in central collisions. A large cut parameter$ \sigma_{c} $ corresponds to a small probability of the kaons with mass-shift, and it leads to a small BBC (see Table 2 and Fig. 7). The BBC functions of$ K^+ $ $ K^- $ may be observable when only 9.9% of all kaons have a mass-shift in 0%–5% of d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV for$ \sigma_{c} = 2 $ fm (see Fig. 7 (c) and (f)).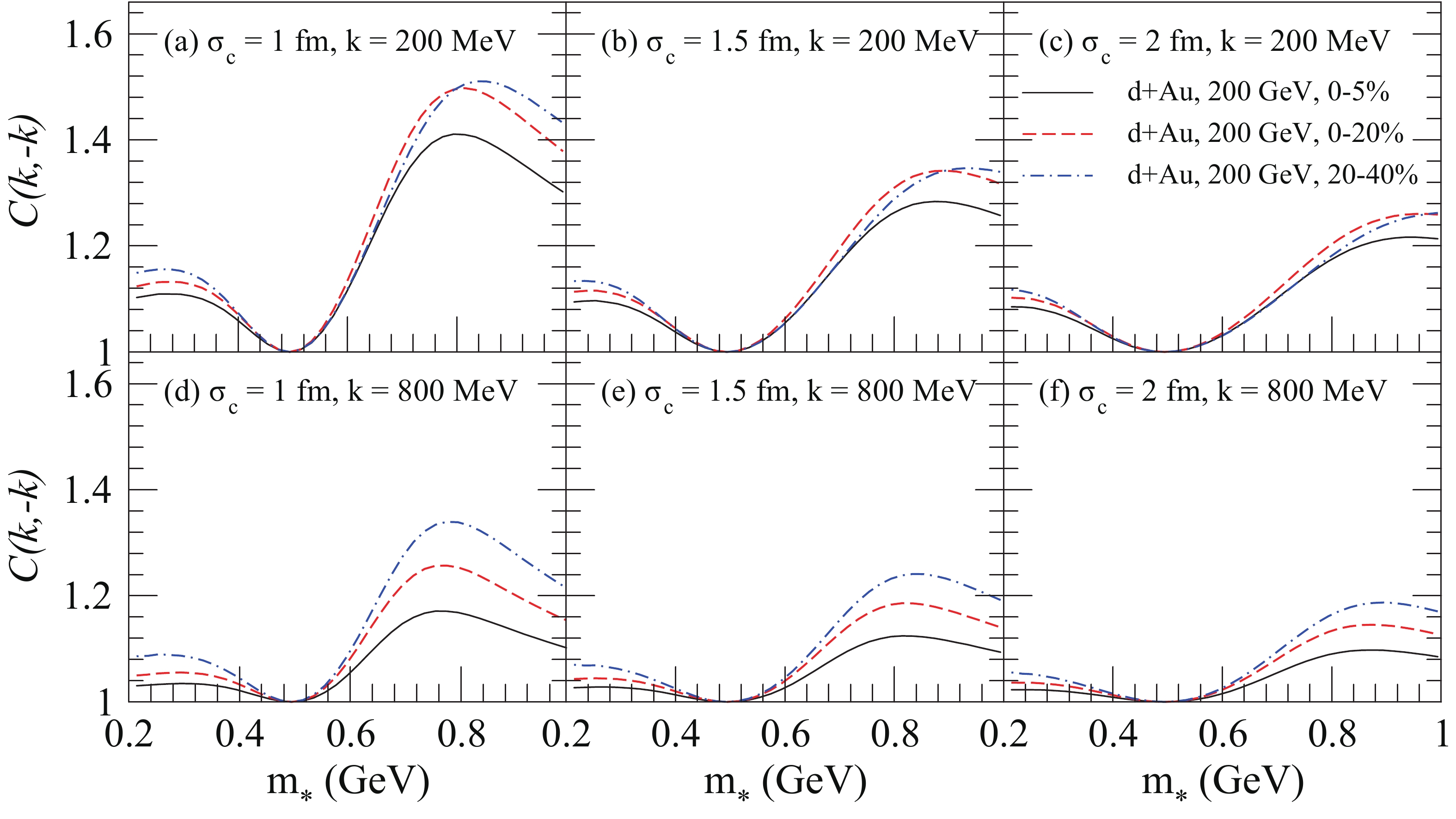
Figure 7. (color online) BBC functions of
$ K^+ $ $ K^- $ as a function of$ m_* $ at$ k = 200 $ MeV (top panel) and$ k = 800 $ MeV (bottom panel) with various cut parameters$ \sigma_{c} $ in central and peripheral collisions of d + Au at$ \sqrt{s_{NN}} = 200 $ GeV.In Fig. 8, we show the BBC functions of
$ K^+ $ $ K^- $ as a function of$ m_* $ at$ k = 200 $ MeV and$ k = 800 $ MeV with various cut parameters$ \sigma_{c} $ in central and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. The BBC functions of$ K^+ $ $ K^- $ decrease with the increasing cut parameter$ \sigma_{c} $ , because the probability of the kaons with mass-shift decreases with the increasing cut parameter. In peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV, the BBC functions of$ K^+ $ $ K^- $ may perhaps provide an observable signal. -
In high-energy heavy-ion collisions, the interactions between the particle and the dense medium may lead to a modification of the particle mass, and thus give rise to a squeezed BBC of the boson-antiboson. Investigations of the BBC in previous studies indicate that the BBC function
$ C({ k},-{ k}) $ is sensitive to the temporal distribution of the freeze-out points [9,10,13-16]. The BBC function will be larger for a narrow temporal distribution of the particles' freeze-out points [9,10,13,15].In this study, we focus on the observability of the BBC functions of
$ K^+ $ $ K^- $ in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and Au + Au collisions at$ \sqrt{s_{NN}} = 62.4 $ GeV using the VISH2+1 code [32,33] to simulate the evolution of particle-emitting sources. In comparison to a previous work [15], we select the freeze-out temperature by fitting the transverse momentum spectra of kaons. For all kaons that have a mass-shift, the BBC functions of$ K^+ $ $ K^- $ provide an observable signal in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. Considering that the systems of d + Au collisions and peripheral collisions of Au + Au are too small, the kaons may not be affected by the medium. Therefore, we introduce a Gaussian factor to describe the probability of the kaons with mass-shift and further study the BBC functions of$ K^+ $ $ K^- $ in parts of all kaons with mass-shift. The BBC functions of$ K^+ $ $ K^- $ may be observable when only about 10% of all kaons have a mass-shift in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV.In the calculations, a hydrodynamic model was used to simulate evolutions of the system and the effect of interactions in the hadronic phase on kaon transverse momentum spectra was not taken into account. Thus, the kinematic freeze-out temperature of kaons selected in this study is close to the chemical freeze-out temperature [42,43]. If the kinematic freeze-out temperature is significantly lower, the effect of interactions in the hadronic phase on the BBC functions needs to be considered. The momentum distribution of kaons may be changed after hadronic re-scattering [44]. In this case, the maxima of the squeezed correlations (for
$ { k}_1 = -{ k}_2 $ ) may be suppressed, and the slope of the squeezed correlation with respect to the angle between the momenta of the kaon and anti-kaon becomes smaller. The contribution of hadronic interactions on kaons is expected to be very small for small collision systems [45]. Hence, the BBC function of$ K^+ $ $ K^- $ may be observable in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV. Since the BBC function corresponds to the interactions between the particle and the dense medium, the successful detection of the BBC function may indirectly mark that the dense medium has formed in these collision systems. We suggest the measurement of the BBC function of$ K^+ $ $ K^- $ experimentally in d + Au collisions at$ \sqrt{s_{NN}} = 200 $ GeV and peripheral collisions of Au + Au at$ \sqrt{s_{NN}} = 62.4 $ GeV.
Squeezed back-to-back correlations of K +K −in d + Au collisions at ${\sqrt{{s_{NN}}}}$ =200 GeV and Au + Au collisions at ${\sqrt{{s_{NN}}}}$ = 62.4 GeV
- Received Date: 2019-02-26
- Available Online: 2019-07-01
Abstract: We investigate the squeezed back-to-back correlations (BBC) of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: