Chiral criticality and glue dynamics

Locating and searching for the QCD critical end point (CEP) has attracted increasing attention in recent years. Non-monotonic behavior of the kurtosis of the net proton multiplicity distribution, with the change of the collision energy, has been observed in the beam energy scan (BES) program at the Relativistic Heavy-Ion Collider (RHIC) [1–3]. This can be attributed to critical fluctuations near the CEP. To pin down this possibility and putatively resolve the existence and location of the CEP, reliable theoretical calculations and predictions are in high demand.

Relevant theoretical studies put the emphasis on different sides. The first class is devoted to the computations and studies of equilibrium bulk properties of the quark-gluon plasma, herein in particular the fluctuations and correlations of conserved charges. Related studies involve, for instance, the first principle lattice QCD simulations [4–8], where Ref. [9] provides a recent review, continuum functional approaches, e.g., the functional renormalization group (FRG) [10–12], Dyson-Schwinger equations [13–15], etc. These studies are concerned with equilibrium critical fluctuations arising from the CEP. In heavy-ion collisions, besides the critical fluctuations, non-critical fluctuations likewise play a significant role [16–18]. These include the participant or volume fluctuations for a given selection of the collision centrality, overall global conservation, acceptance cuts, etc. Furthermore, non-equilibrium critical fluctuations and their real-time evolution have attracted lots of attention in recent years [19–22]. Higher-order critical fluctuations have been shown to be quite different from their equilibrium values [19]. More recent developments in this direction are provided in Refs. [23, 24].

A promising approach to reveal the properties of the QCD chiral symmetry and its spontaneous dynamical breaking is to study the chiral order parameter field, usually referred to as the $ \sigma $-field, and investigate its higher-order cumulants of fluctuations directly, see e.g., Refs. [19, 25]. Beside the chiral symmetry and its breaking, however, the QCD is characteristic of the color confinement, whose information is encoded in the glue dynamics of the background field. Furthermore, the net proton number fluctuations, which are employed to search for the QCD CEP in the BES program at RHIC, are physical quantities with the degree of freedom typical of baryons, rather than quarks. Therefore, the interrelations between the glue dynamics and the $ \sigma $-field fluctuations require further investigation. In this work, by employing the QCD-enhanced Polyakov-quark-meson (PQM) effective model [10], we study the influence of the glue dynamics on the $ \sigma $-field fluctuations and compare it with the net baryon number fluctuations. The computations in this study are performed within the FRG approach, through which quantum and thermal fluctuations are encoded successively with the evolution of the renormalization group (RG) scale [26]. More details regarding the FRG and recent QCD-related progresses are, among others, provided in Refs. [10–12, 27–40].

This paper is organized as follows. In Sec. 2 we present a brief introduction about the FRG and present the low energy effective model employed in this work. Two different critical fluctuations, i.e., those related to the δ field and the net baryon number, respectively, are discussed in Sec. 3. In Sec. 4, we present our numerical results and discussions. Finally, a summary and conclusion are given in Sec. 5.

Starting from an initial ultraviolet (UV) cutoff scale $ \Lambda $, the quantum, thermal, and density fluctuations of different wavelengths are successively encoded within the FRG approach, with the RG scale k nearing the infrared (IR) regime. Thus, the quantum theory is resolved with $ k\rightarrow 0 $. This process is described by the Wetterich equation [26] as follows

where $ \Gamma_{k} $ is the scale-dependent effective action; $ t = \ln (k/\Lambda) $; the super fields $ \Phi $ consist of all field components of a theory, and the super trace runs over all degrees of freedom. Here, $ \Gamma_{k}^{(2)} $ is the second-order derivative of $ \Gamma_{k} $ with respect to fields, i.e.,

The regulator $ R_{k} $ suppresses quantum fluctuations of size larger than 1/k, while it leaves others unchanged.

Specifically, for the rebosonized QCD, the r.h.s of Eq. (1) is decomposed into the equation that follows as

where $ \Phi = (A, c, \bar c, q, \bar q, \phi) $, and the four terms on the r.h.s. relate to the gluon, ghost, quark, and hadronic degrees of freedom, respectively. Here, the $ G $s denote their propagators. More discussion on the rebosonized QCD within the FRG approach is provided by Refs. [27, 28, 31–33, 37, 41]. In this study, we refrain from solving the entire coupled set of equations, however these can be found in Ref. [41], where flow equations of the rebosonized QCD are investigated at finite temperature and non-vanishing chemical potential. Instead of evolving the flows from an UV cutoff scale $ \Lambda $ at the perturbative regime, such as $ \sim 10^2 $ GeV, we choose the initial scale $ \Lambda \sim 1 $ GeV, where the glue part, including the gluon and ghost, decouples from the matter part because of the large mass gap of the gluon [31, 32, 37, 41]. Thus, when the scale is below $ \sim 1 $ GeV, quantum fluctuations resulting from the gluon interactions are remarkably suppressed, and it is reasonable to separate the effective action into the glue and the matter parts, viz.,

where the glue part corresponds to the first two terms on the r.h.s. of Eq. (3), and the matter part consists of quarks and hadrons, respectively. In this study, we focus on mesons for the hadronic degrees of freedom.

We adopt the following formalism for the scale-dependent effective action of the matter, i.e.,

with the notation $ \displaystyle\int_{x} = \int_0^{1/T}{\rm d} x_0 \displaystyle\int {\rm d}^3 x $. $ Z_{q, k} $ and $ Z_{\phi, k} $ are the wave function renormalizations for the quark and meson, respectively. $ h_{k} $ is the Yukawa coupling of the scalar and pseudo-scalar channels. $ {T} $s are the generators of $ SU(N_{f}) $ in the flavor space with $ \mathrm{Tr}(T^{i}T^{j}) = \displaystyle\frac{1}{2}\delta^{ij} $, complemented with $ T^{0} = \displaystyle\frac{1}{\sqrt{2N_{f}}}{1}_{N_{f}\times N_{f}} $, with flavor number $ N_{f} = 2 $. $ \phi = (\sigma, {\pi}) $ is the meson field, and the effective potential $ V_{k}(\rho) $ with $ \rho = \phi^2/2 $ is $ O(4) $ invariant. The term linearly proportional to the sigma field, i.e., $ -c\sigma $, explicitly breaks the chiral symmetry, whose effects will be investigated in detail in the following.

In Eq. (5), we couple the quark field with the background gluon field, whose temporal component is non-vanishing at finite temperature. It is well known that this background gluon field, also called as the Polyakov loop in a slight transformation, implements the QCD confinement through the $ Z(3) $ symmetry and is indispensable to describe the QCD thermodynamics. Recent years have witnessed significant progress on the study of the Polyakov dynamics, as depicted in Ref. [42] and the references cited therein. Specifically, incorporation of the Polyakov dynamics and low energy effective models leads to widely used Polyakov-loop-extended chiral models, e.g., the PQM [43] and the Polyakov-Nambu-Jona-Lasinio model [44–46].

In this study, we do not directly solve the flow equation for $ \Gamma_{{{\rm glue}}, k} $ in Eq. (4); instead, the QCD-enhanced glue potential $ V_{\rm{{glue}}} $, which is a polynomial in the Polyakov loop and has been discussed in detail in Ref. [10], is employed. Therefore, the thermodynamical potential density reads

where $ \Gamma_{{{\rm matt}}, \, k = 0} $ is obtained through integrating its relevant flow equation beginning from the initial scale $ \Lambda $. Here, we do not enter into the details, and more discussion is provided in Ref. [10].

In this study, we focus on two kinds of critical fluctuations, both of which are important in the studies of the QCD phase transition and QCD phase structure. One is the fluctuations of the $ \sigma $ field, which is the chiral order parameter and has been studied widely in the literature, e.g., Refs. [19, 25, 47]; the other is the fluctuations of the net baryon number or the net proton number, which is a significant probe to search for the QCD critical point in the experiments of BES, as described in Ref. [3] and the references cited therein. More importantly, we put an emphasis on the influence of the glue dynamics on these two kinds of critical fluctuations.

The coefficient c with a non-vanishing value of the chiral symmetry breaking term in Eq. (5), on one hand, breaks the chiral symmetry explicitly and provides mass for the pions. On the other hand, it works as an external source for the sigma field. Therefore, the mean value and various cumulants of the sigma field could be obtained by differentiating the pressure $ p = -\Omega $ with respect to the coefficient c,

with $ \delta\sigma = \sigma-\langle \sigma \rangle $, the inverse temperature $ \beta = 1/T $ and the volume V, where the angle bracket denotes the ensemble average. For simplicity, we define

For comparison, we also calculate the baryon number fluctuations, which read

with $ \mu_B = 3\mu $.

To precede the presentation of the calculated results, we provide a brief description of the numerical calculations. In this study, we adopt the local potential approximation (LPA), i.e., $ Z_{q, k} = Z_{\phi, k} = 1 $ and $ \partial_t h_{k} = 0 $ in Eq. (5). Calculations beyond LPA are given in Refs. [10–12]. For the matter part, at the initial UV-cutoff scale $ \Lambda $, which is chosen to be 700 MeV throughout, the effective potential in Eq. (5) is symmetric and can be well approximated as follows

with $ \lambda_{\Lambda} = 1 $ and $ \nu_{\Lambda} = (0.523\text{ GeV})^2 $. These parameters, together with the Yukawa coupling h = 6.5 and the coefficient of explicit chiral symmetry breaking $c = 1.7\times $$ 10^{-3}\, \text{GeV}^3 $, yields hadronic observables at vacuum, which read the pion mass $ m_{\pi} = 135 $ MeV, the sigma mass $ m_{\sigma} = 436 $ MeV, the constituent quark mass $ m_{q} = 302 $ MeV, and the $ \pi $ decay constant, which is identical to the vacuum expected value of the sigma field in Eq. (7), i.e., $ f_{\pi} = \langle \sigma \rangle = 92.8 $ MeV. For the glue part, we employ the same QCD-enhanced glue potential as used in Refs. [10, 11], which incorporates the back-reaction effect of the matter sector on the glue dynamics and thus leads to the correct scaling of the temperature, further details of which are given in Ref. [48].

In Fig. 1 we show the first four orders of the fluctuations of the $ \sigma $ field, as defined in Eq. (10), as functions of $ T $ in units of $ T_c $. The computations are performed in the PQM and quark-meson (QM) effective models, aimed at illuminating the role of the glue dynamics in the fluctuations of the $ \sigma $ field, aided by their difference. For the convenience of comparison, the temperature is rescaled by their pseudo-critical temperature $ T_c $, which is determined by locating the maximal value of $ \partial \langle \sigma \rangle/\partial T $ in this study. The value of $ T_c $ is 183 MeV for the PQM and 154 MeV for the QM, respectively. Comparing $ \langle \sigma \rangle $ calculated in the PQM and QM, as shown in upper-left panel of Fig. 1, one observes that the crossover regime of the temperature in unit of $ T_c $ shrinks, when the glue dynamics is taken into account, as $ T_c $ for the PQM is relatively larger. This is easily understood and also expected in light of the physical implication of the Polyakov loop, which transforms the active degree of freedom at low temperature from quarks in the QM to baryons in the PQM. Therefore, higher temperature is needed to drive the event of the chiral phase transition [10, 46]. In fact, this statement is even clearer upon observation of the higher-order fluctuations of the $ \sigma $ field, for example the quadratic, cubic, and quartic fluctuations of the $ \sigma $ field, plotted in other panels of Fig. 1. We find that the fluctuations of the $ \sigma $ field obtained in the PQM and QM models are qualitatively similar, except for the crossover regime for the PQM, which is smaller than that in the QM in units of $ T_c $.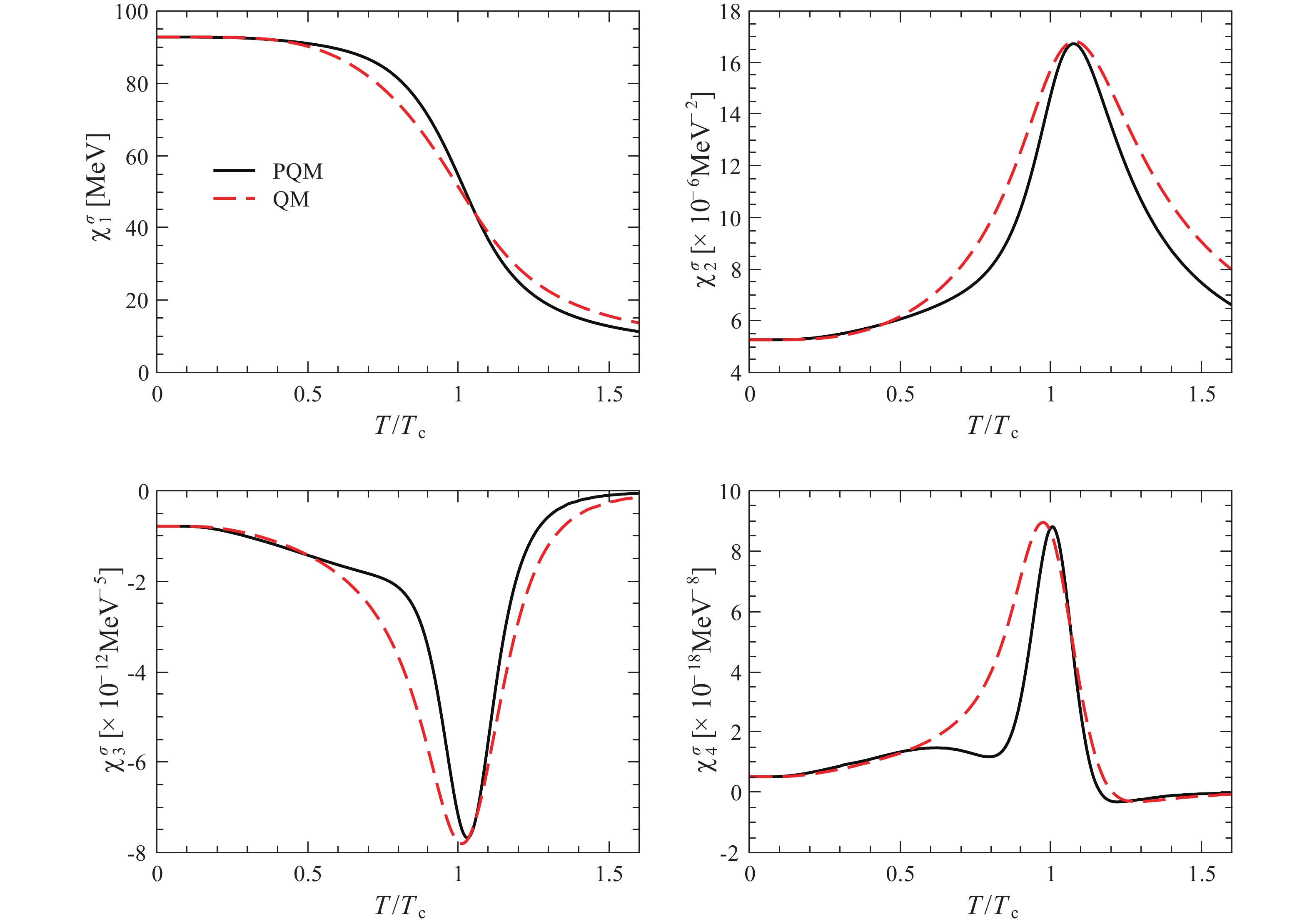

Figure 1.  (color online) Cumulants of the $ \sigma $-field distributions, i.e., Eq. (10), as functions of the temperature at vanishing chemical potential, calculated in the PQM and QM effective models.

Nevertheless, we should emphasize that the difference, discussed above regarding the $ \sigma $-field fluctuations obtained in PQM and QM, is only quantitative. Hence, this fails to be our concern. On the contrary, the $ \sigma $-field fluctuations calculated in these two effective models are in qualitative agreement with each other, if the insignificant quantitative difference is ignored. In another case, the $ \sigma $-field fluctuations are almost not influenced by the glue dynamics, and the minor impact is indirect, such as through the modified pseudo-critical temperature by the glue potential. This situation is different from the baryon number fluctuations discussed in the following, which are closely related to and affected directly by glue dynamics. This is reasonable, since the $ \sigma $ field is only related to the chiral property of the system, while it does not encode the information of color confinement.

We show $ \chi_4^{\sigma}/\chi_2^{\sigma} $ as a function of the temperature in Fig. 2. In the same way, we compare the results obtained in PQM and QM. The difference of the ratio between these two effective models seems slightly larger than that depicted in Fig. 1, and two peaks are detected on the curve for the PQM. However, only the second peak on the curve of PQM is relevant to the critical behavior, and the first wide bump resulting from the rapid change of the quartic $ \sigma $-field fluctuation in PQM, as shown in the lower-right panel of Fig. 1, is limited to a small region, and thus it leads to a stronger variance. Therefore, the first wide bump is not related to any critical behaviors. In summary, the qualitative behavior of the ratio $ \chi_4^{\sigma}/\chi_2^{\sigma} $ is likewise not affected by glue dynamics.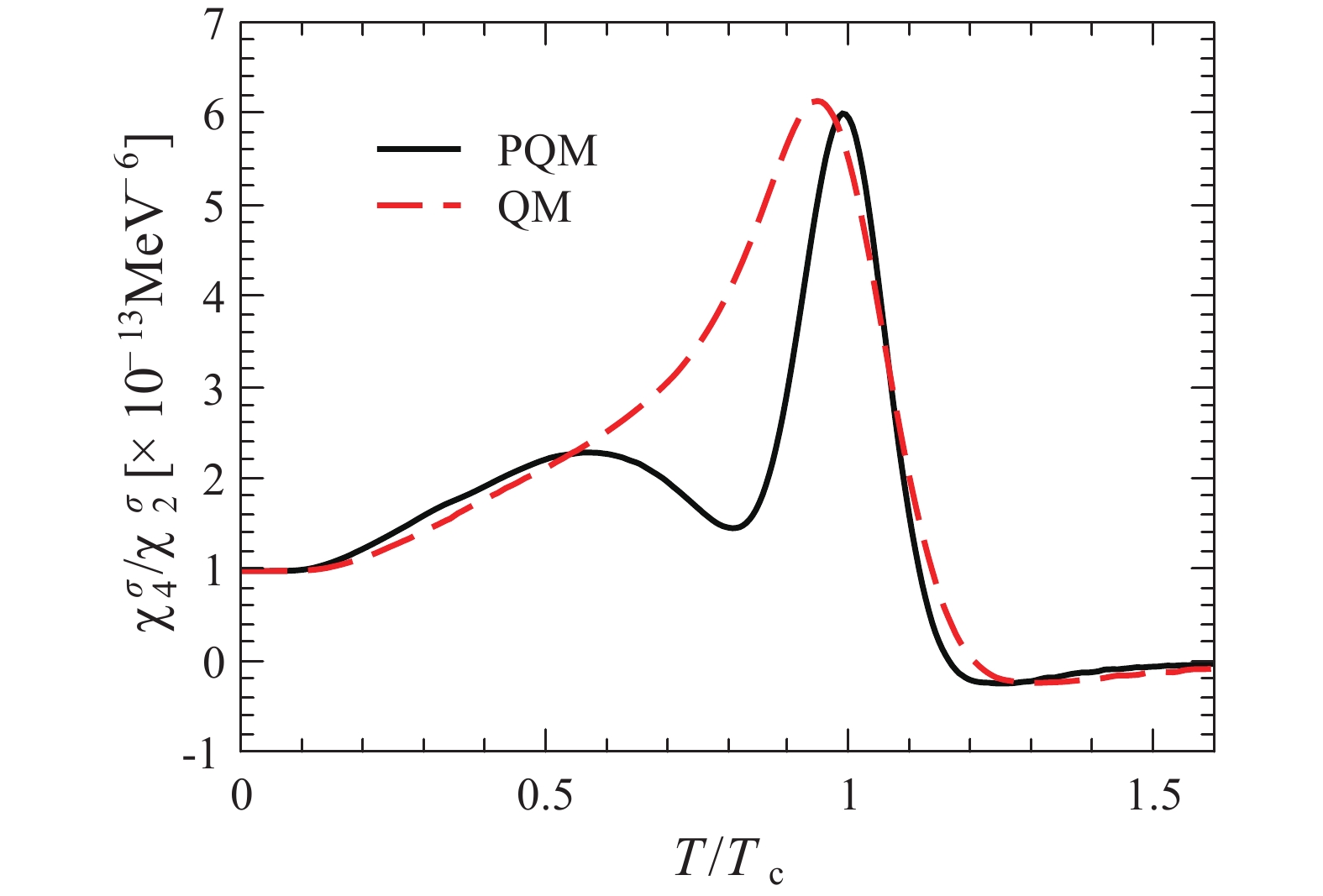

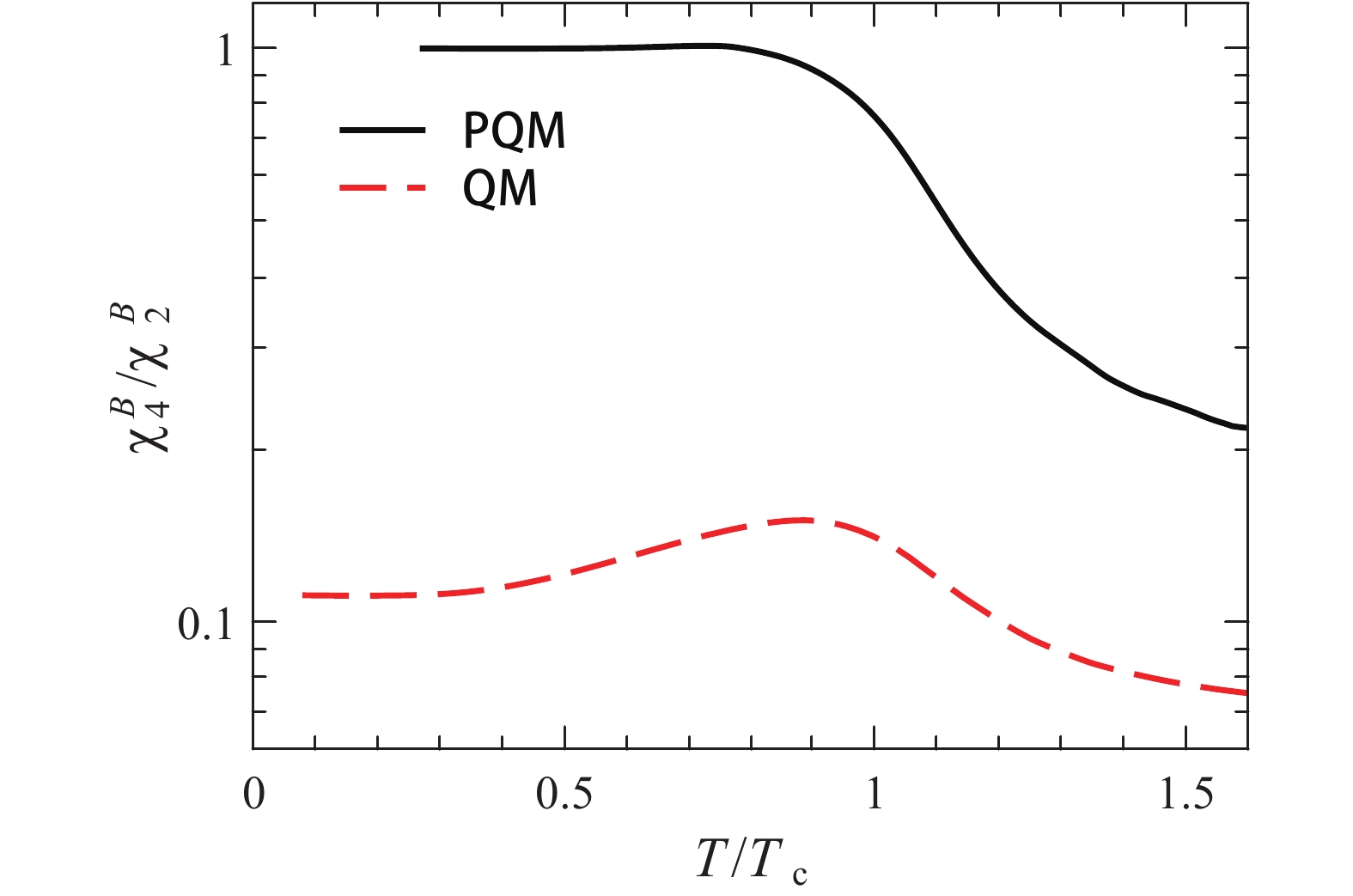
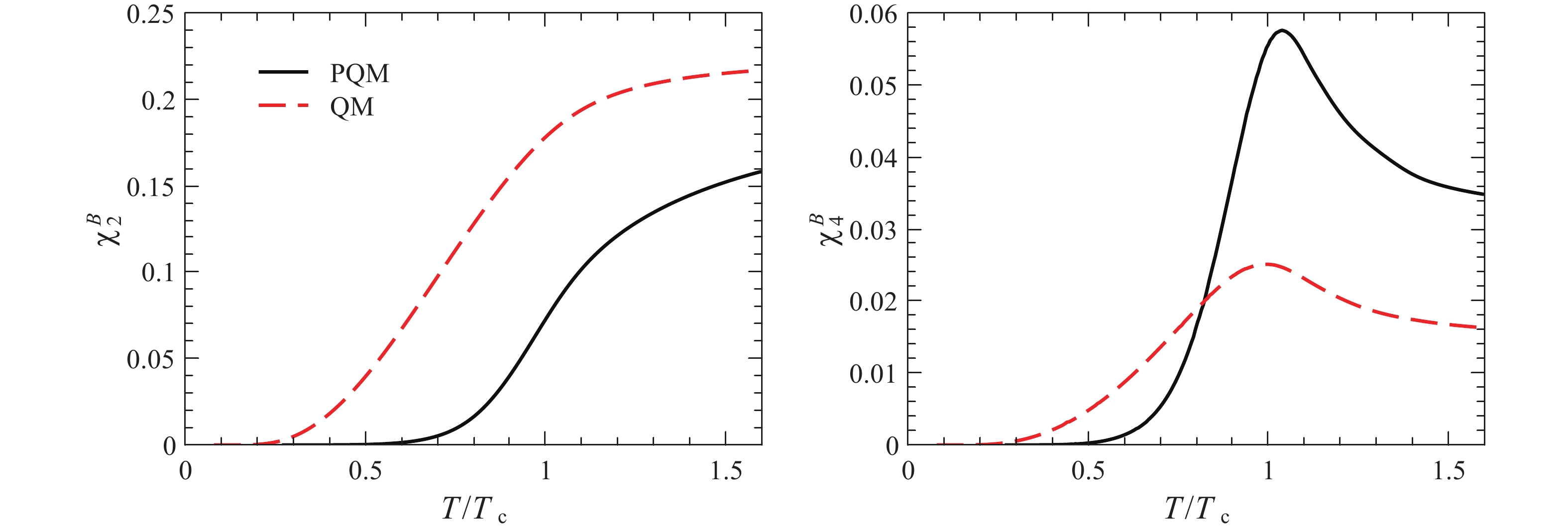
Figure 2.  (color online) $ \chi _4^\sigma /\chi _2^\sigma $ as a function of the temperature calculated in the PQM and QM effective models.

In the following, we present some results regarding the baryon number fluctuations calculated in the LPA. These results are not state-of-the-art, and in fact there are lots of calculations beyond the approximation of LPA, as depicted in Refs. [10–12]. The purpose of the computation of the baryon number fluctuations here is performed only to facilitate the comparison between these two kinds of fluctuations. In Fig. 3, we show the quadratic and quartic net baryon number fluctuations as functions of $ T $ obtained in the PQM and QM effective models. Unlike the $ \sigma $-field fluctuations, the baryon number fluctuations calculated in the PQM are remarkably different from those in QM. In fact, if one observes the kurtosis of the baryon number distribution, i.e., $ \chi_4^{B}/\chi_2^{B} $ in Fig. 4, this difference is immediately observed as qualitative, rather than quantitative. The baryon number fluctuation is not only sensitive to the chiral property, which is similar with the $ \sigma $-field fluctuation as for this point, but also is significantly influenced by the glue dynamics. The value of the ratio $ \chi_4^{B}/\chi_2^{B} $ is well known to represent the degree of freedom of the system at low temperature, viz., $ \chi_4^{B}/\chi_2^{B} \rightarrow $1 is relevant to the baryons, while $ \chi_4^{B}/\chi_2^{B} \rightarrow 1/9 $ is relevant to the quarks [10, 46], which corresponds exactly to results obtained in the PQM and QM effective models, respectively, as shown in Fig. 4. Therefore, the confinement information is encoded in the PQM model through glue dynamics, while the QM model does not include any confinement. The kurtosis of the net baryon number distribution calculated in the PQM effective model agrees well with lattice calculations, and more detailed discussions and comparison is given in Refs. [10–12]. Evidently, computations of the baryon number fluctuations performed with a theoretical approach only with the chiral symmetry and its dynamical breaking and without the glue dynamic, such as the QM effective model, are far from sufficient to account for the lattice results and the experimental measurement.

Figure 3.  (color online) Quadratic (left panel) and quartic (right panel) baryon number fluctuations defined in Eq. (11) as functions of the temperature at vanishing baryon chemical potential, calculated in the PQM and QM effective models.

Figure 4.  (color online) $ \chi _4^B/\chi _2^B$, i.e., the kurtosis of the net baryon number distribution, as a function of the temperature at vanishing baryon chemical potential, calculated in the PQM and QM effective models.

In this study, we have calculated the $ \sigma $-field fluctuations within the FRG approach in the PQM and QM effective models. Emphasis is put on the interrelation between the $ \sigma $-field fluctuations and the glue dynamics. We found that the $ \sigma $-field fluctuations are weakly influenced by glue dynamics, which contrasts remarkably in the case of the net baryon number fluctuations, that are strongly dependent on glue dynamics and involve the color confinement information.

What do our calculated results imply for current efforts of the search for the QCD CEP? We like to address this from both the theoretical and experimental aspects. Non-monotonic behavior of the kurtosis of the net proton number distribution varying with the collision energy has been observed in BES at RHIC [3]. Generally, the difference between the kurtosis of the proton number and that of the baryon number can be neglected. Thus, we assume that the kurtosis of the baryon number distribution is identical to that of the proton number distribution. To explain experimental observations and make reasonable predictions, a number of interesting theoretical scenarios and approaches have been proposed and investigated in detail, such as equilibrium critical fluctuations, equilibrium noncritical fluctuations, non-equilibrium evolution, etc. Whichever theoretical approach is applied, it is important that the confinement information is embedded in the theory, along with the chiral property. The $ \sigma $ field and its fluctuations alone are not sufficient to account for the baryon number fluctuations.

On the contrary, since the QCD CEP arises from the chiral symmetry and its spontaneous dynamical breaking, rather than from the confinement-deconfinement phase transition, it is also a good idea to employ other physical quantities to search for the CEP in the experiments, which are only sensitive to the chiral symmetry, and not affected by the color confinement. This could be, for instance, the electric charge fluctuations and some physical observables that are only connected to the chiral order parameter field.

Although the result and conclusion are based on the model calculation with vanishing chemical potential, it is possible to extend our conclusion and its implications by resorting to the Z(3) center symmetry of glue dynamics. This symmetry makes the kurtosis of the baryon number distribution in the PQM appear quite differently in comparison to that in the QM, as shown in Fig. 4. This symmetry is not dependent on the model calculation or on whether the chemical potential is finite or vanishing. Therefore, the glue dynamics can be assumed to still play a role near the CEP, which is partially confirmed in Ref. [11], where the kurtosis of the net proton number distribution at finite $ \mu $ is compared to experimental measurement.

We thank Yu-xin Liu for valuable discussions.