-
One of the objectives of jet physics is to explore the microscopic properties of hot-dense quantum chromodynamic (QCD) matter, quark-gluon plasma (QGP), generated in ultra-relativistic heavy-ion collisions [1-3]. Jets produced by partons from colliding nuclei in the early stage travel through the QCD matter carrying multi-scale physics evolution information. The interplay between elementary scattering, subsequent branching process, and strongly coupled parton-medium interactions can lead to the modification of jet shapes with respect to jet fragmentation in the absence of the medium. The jet structure modifications resulting from proton-proton (pp) collisions to heavy-ion collisions can be investigated in terms of a set of jet shape quantifications, which will shed light on the jet energy loss mechanism in the medium, color coherence, and fundamental medium properties.
Latest results from the LHC experiments conducted on charged particle nuclear modification factor measurement in a wide range of momenta exhibit sectionalized behavior that gives rise to an apparent soft and hard pQCD region [4]. The observations of more highly unbalanced di-jet with increasing event centrality [5], the suppression of inclusive jet yield by about a factor of two in central heavy-ion collisions relative to peripheral collisions, as well as the correlation of the jet suppression with missing transverse momentum [6-8] indicate that the jet energy redistributes within the jet in medium relative to the jet in vacuum, and that there is a non-zero fraction of jet energy loss especially at large angles relative to the jet axis. The fragmentation yield is found to decrease at intermediate
$ z $ and increase at small$ z $ in central collisions relative to peripheral collisions [9, 10]. The azimuthal di-hadron correlation excess yield is found to be more pronounced in the sub-leading jet, predominantly from several to 20 GeV arising from soft particles [11]. In [12], the jet shapes modifications are studied at small jet cone sizes ($ r<0.2 $ ) and found an inconsistent with a fully coherent energy loss picture. These results provide abundant inputs for theoretical calculations and phenomena modeling with regard to jet-medium interactions.In theory, most studies of the phenomena concerned with jet energy loss are based on pQCD, which can efficiently explain data at the intermediate momentum range, but is incapable of covering the entire kinematic range in the non-pQCD region [13, 14]. One important reason is the treatment of gluon radiation by assuming collinear radiation and model dependent on momentum exchange among the medium and parton dynamical evolution for leading order or next leading order contribution, especially for central
$ {\rm Pb+Pb} $ collisions [15]. Moreover, several physical mechanisms involve co-existence and competition of several effects when partons traverse the medium, such as recoil and non-recoil, coherence and de-coherence, depending on QCD local equilibrium temperature, medium density, path length, gluon formation time, and momentum exchange etc., which redistribute the parton energy at a relative larger angle with respect to its initial directions [16].Jet-medium interactions cover the entire kinematic range and include perturbative and non-perturbative effects at the LHC energies. It is essential to study the jet shape modification in various collision systems with a large set of jet shape quantities. In this study, the measurement of the jet shape observables, such as the fragmentation function
$ F(z) $ , relative momentum$ p_{T}^{\rm rel} $ , density of charged particles$ \rho(r) $ , jet angularity$ girth $ , jet momentum dispersion$ p_{T}^{\rm disp} $ , and the difference between leading and sub-leading constituent transverse momenta$ LeSub $ for proton-proton collisions at 0.9, 2.76, 5.02, 7, and 13 TeV, as well as for lead-lead collisions at 2.76 TeV and 5.02 TeV, are systematically studied by JEWEL [17]. One additional differential jet shape parameter of$ D_{girth} $ is proposed and studied at$ r<0.3 $ to investigate the jet shape evolution. -
Jet shape measurements have been suggested for the exploration of the microscopic evolution mechanism of parton-medium interaction in ultra-relativistic heavy-ion collisions. For different physical motivations, several jet shape observations have been proposed using jet constituents, overall jet-by-jet quantities, and jet cluster historical information. For example, the fragmentation function, missing
$ p_{T} $ method and jet-track angular correlations measurements using intra or inter-jet distributions are dedicated to investigating the longitudinal share of the energy within the jet and large angle radiations. The overall jet shape observations built on the jet-by-jet function of jet constituent four-momenta, such as jet mass, jet granularity, and jet momentum dispersion etc., could probe the jet energy loss dependence on large angle soft particle emission. Jet grooming measurements based on historical information of the jet cluster could locate the splitting phase space where medium-induced effects are expected [18, 19]. This study presents a jet shape investigation in$ {\rm Pb+Pb} $ and$ {\rm pp} $ collisions by inclusive constituents of the jet and jet-by-jet quantity to describe jet evolution and jet energy loss within QCD matter.In [20], ATLAS presented the fragmentation function and transverse profiles in
$ \sqrt{s} $ = 7 TeV$ {\rm pp} $ collisions in a wide jet momentum range of 25 GeV/c$ <p_{T, {\rm jet}}< $ 500 GeV/c and found discrepancies between various models and data. Fragmentation functions show a reduction yield at$ 0.04\leqslant z \leqslant 0.2 $ and an enhancement for$ z\leqslant 0.04 $ in$ \sqrt{s_{\rm NN}} =$ 2.76 TeV$ {\rm Pb+Pb} $ collisions by ATLAS [9]. This measurement was also conducted in ALICE [21] from di-hadron correlations in$ \sqrt{s} $ = 7 TeV$ {\rm pp} $ and$ \sqrt{s_{\rm NN}} $ = 5.02 TeV$ {\rm p+Pb} $ collisions, where no significant cold nuclear matter effect was observed. In [12, 22], the jet shape modifications were studied in small-radius jets to discriminate the relative quark and gluon jet fractions, which also suggested that the medium was able to resolve the jet structure at angular scales smaller than$ r = 0.2 $ . However, a detailed and systematic study is highly required to quantify the gluon induced fragmentation modifications, better constrain energy loss models, and isolate the quark and gluon jet fraction at the intermediate momentum range for multiple collision systems. In this study, the below observations are used.The jet fragmentation function
$ D_{i}^{h}(z,Q) $ is defined as the probability that a hadron carries a longitudinal momentum fraction$ z $ of$ p_{\rm jet} $ in the experiment.$ z $ is defined:$ z = \frac{\vec{p}_{\rm jet} \cdot \vec{p}_{\rm ch}}{|\vec{p}_{\rm jet}|^{2}} $

(1) which connects color partons and colorless hadrons to constrain QCD-motivated models from experiments. The quantity of
$ F(z, p_{T,{\rm jet}}) $ is measured as:$ F(z, p_{T, {\rm jet}}) = \frac{1}{N_{\rm jet}} \frac{{\rm d}N_{\rm ch}}{{\rm d}z}. $

(2) Here
$ N_{\rm ch} $ is the number of charged particles in the jet, and$ N_{\rm jet} $ is the number of selected jets to be used for normalization. Two additional quantities$ p_{T}^{\rm rel} $ and the density of charged particle$ \rho_{\rm ch} $ are also studied.$ p_{T}^{\rm rel} $ is the momentum of charged particles in a jet transverse to that of the jet's axis defined in Eq. (3), and its distribution$ f(p_{T}^{\rm rel}, p_{T, {\rm jet}}) $ is given in Eq. (4):$ p_{T}^{\rm rel} = \frac{|\vec{p}_{\rm ch}\times \vec{p}_{\rm jet}|}{|\vec{p}_{\rm jet}|}, $

(3) $ f(p_{T}^{\rm rel}, p_{T, \rm jet}) = \frac{1}{N_{\rm jet}} \frac{{\rm d}N_{\rm ch}}{{\rm d}p_{T}^{\rm rel}} . $

(4) The density of the charged particle
$ \rho_{\rm ch} $ in$ y-\phi $ space is measured as a function of angular distance$ r $ of charged particles from the jet axis, given by:$ \rho_{\rm ch}(r) = \frac{1}{N_{\rm jet}} \frac{{\rm d}N_{\rm ch}}{2\pi r{\rm d}r} . $

(5) As a complementary study, the jet-by-jet quantities, namely the first radial moment or angularity (or girth),
$ girth $ , the momentum dispersion,$ p_{T}^{\rm disp} $ , and the difference between the leading and sub-leading track transverse momentum,$ LeSub $ are also studied.$ girth $ and$ P_{T}^{\rm disp} $ are related to the moments of the so-called generalized angularities [23].$ LeSub $ is not an IRC-safe observable but indicates robustness against soft background particles contributions. The angularity is defined as$ g = \sum_{i \in \rm jet} \frac{p_{T,i}}{p_{T,{\rm jet}}} \Delta R_{{\rm jet},i}, $

(6) where
$ p_{T,i} $ is the transverse momentum of the$ i $ -th constituent and$ \Delta R_{\mathrm{jet},i} $ is the distance in ($ \eta $ ,$ \varphi $ ) space between constituent$ i $ and the jet axis. This shape is sensitive to the radial energy profile of the jet.The momentum dispersion
$ p_{T}^{\rm disp} $ is defined as:$ p_{T}^{\rm disp} = \frac{\sqrt{\sum_{i \in \rm jet} p_{T,i}^{2}}} {\sum_{i \in \rm jet} {p_{T,i}}}. $

(7) $ LeSub $ is defined as the difference of the leading track$ p_{T} $ and sub-leading track$ p_{T} $ ,$ LeSub = p_{T,{\rm track}}^{\rm {lead}}-p_{T,{\rm track}}^{\rm {sublead}}. $

(8) For jets with small radii r, it contributes to isolated pure energy loss effect from other medium effects and correlated background. Hence, the differential jet-by-jet quantity
$ D_{girth} $ is proposed, which is defined as jet's distribution of$ girth $ inside an annulus of inner radius$ r $ and outer radius$ r+\delta r $ around the jet axis, which is directly related to the jet energy topological structure and its evolution. -
In this study, JEWEL [17] is used to simulate jet production, QCD scale evolution, and re-scattering of jets in heavy-ion collisions based on pQCD. JEWEL describes the jet evolution and jet-medium interactions simultaneously and dynamically, based on leading-order matrix elements and the parton shower method. All partons belonging to partons showers initiated by hard scattered partons undergo collisions with thermal partons in the medium, leading to both elastic and radiative energy loss. Soft gluon radiation, recoil effect, and scattering processes are governed by formation time, which has been shown to agree with analytical calculations within the appropriate limits. The Landau-Migdal-Pomeranchuk (LPM) effect is included by generalizing the probabilistic formulation in the Eikonal limit to general kinematics. For the heavy-ion environment, the medium density profile is based on a longitudinally expanding Glauber overlap; the local temperature is sampled to determine the density of scattering centers and their momentum distribution. The initial time
$ \tau $ = 0.6 fm and temperature$ T_{i} $ = 0.4 GeV, the critical temperature$ T_{\rm C} $ = 170 MeV are fixed for central lead-lead collisions. Jets are reconstructed by using all final detectable charged and neutral particles with the anti-kt algorithm provided by the FastJet [24] package within$ |\eta|<2.0 $ and$ |\eta|<2.8 $ for the fragmentation distribution and jet-by-jet quantities measurements in separately. The analysis takes into account the recoil effect for heavy-ion collision, and the constituent subtraction method was used to remove the contribution of medium fragments from the parton energy. -
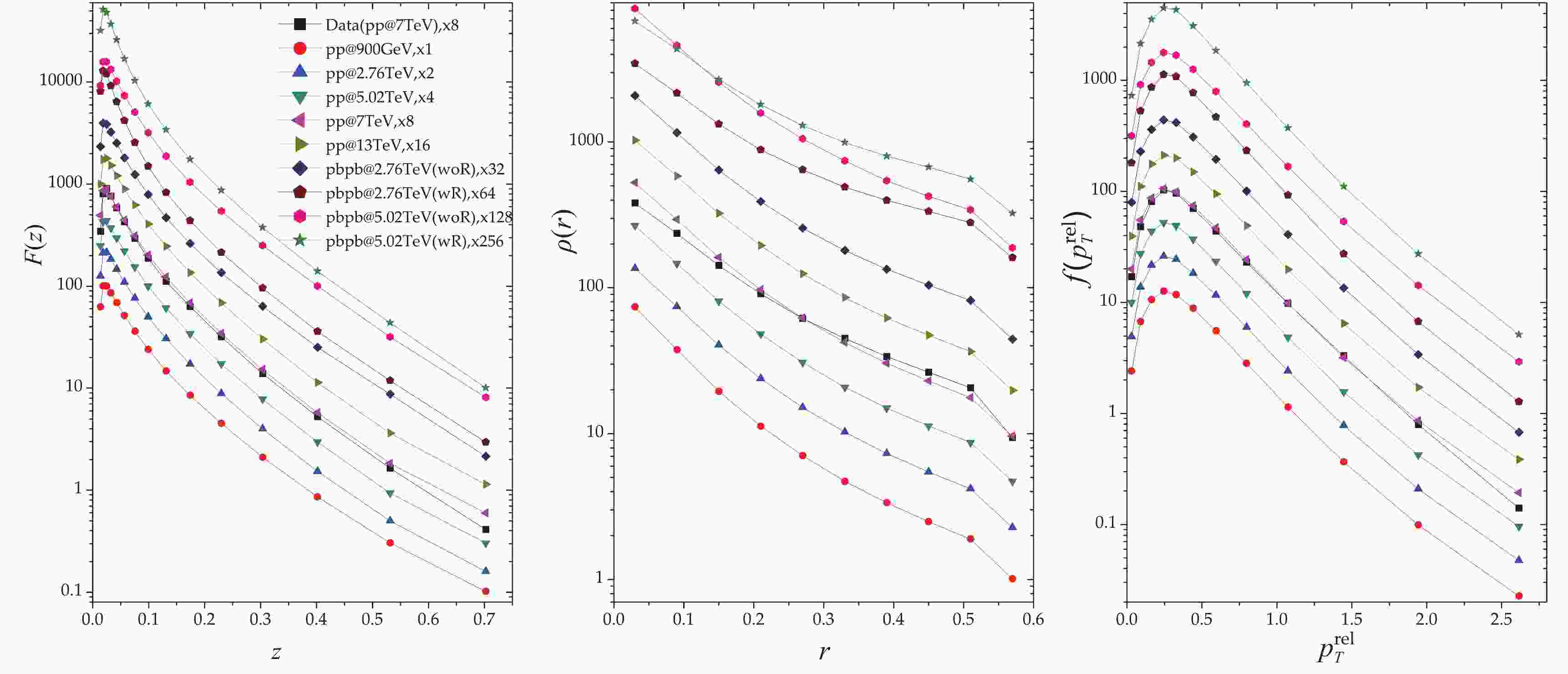
Figure 1 presents the fragmentation function distributions of
$ F(z) $ , relative momentum$ f(p_{T}^{\rm rel}) $ , and the density of charged particles$ \rho_{\rm ch}(r) $ for$ {\rm pp} $ collisions at$ \sqrt{s} $ = 0.9, 2.76, 5.02, 7, and 13 TeV and$ {\rm Pb+Pb} $ collisions at$ \sqrt{s_{\rm NN}} $ = 2.76 TeV and 5.02 TeV in the range of 25 GeV/c <$ p_{T,{\rm jet}}< $ 40 GeV/c simulated by JEWEL. The recoil effect is taken into account for$ {\rm Pb+Pb} $ collisions (referred to as$ wR $ for the recoil effect and$ woR $ for no recoil effect). The simulations are compared with data of$ {\rm pp} $ collisions at$ \sqrt{s} = $ 7 TeV.$ F(z) $ distributions indicate a strong enhancement at$ z<0.1 $ and a reduction at$ z>0.1 $ compared from$ {\rm pp} $ to$ {\rm Pb+Pb} $ collisions with the recoil effect. For$ {\rm pp} $ collisions and$ {\rm Pb+Pb} $ collisions without the recoil effect, the enhancement or reduction of$ F(z) $ depends on the collisional energy and participating nuclei.$ \rho(r) $ indicates the same performance that jet constituents spread to large jet-radius with the increase of the center-of-mass energy of collisions, and the medium effect is significant for the modification at relatively large angles. The$ \rho(r) $ distribution decreases exponentially with the jet-radius. The$ f(p_{T}^{\rm rel}) $ distribution is independent of the collisional energy, however it is strongly modified by QCD medium and exhibits an obvious increase in the approximate range of$ 0.3<r<1.0 $ .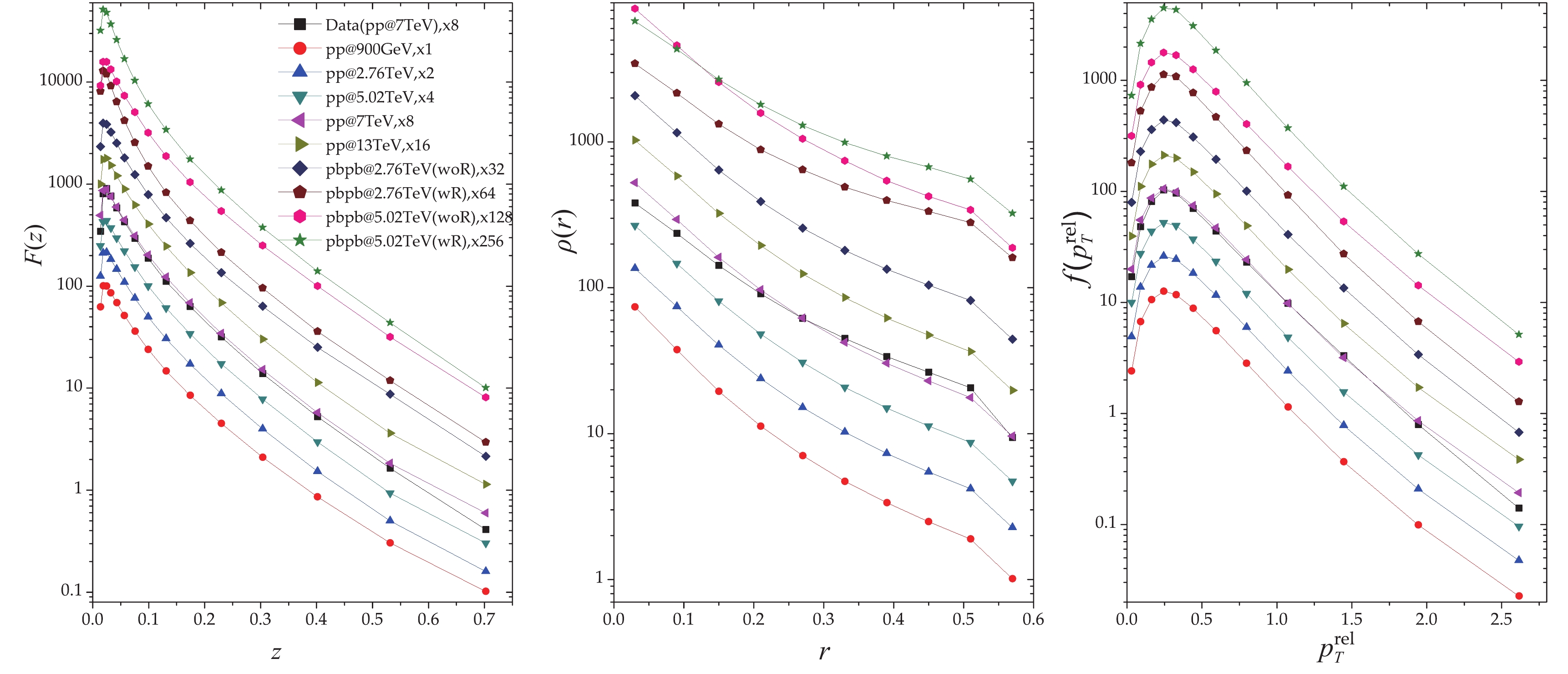
Figure 1. (color online)
$F(z)$ ,$\rho_{\rm ch}(r)$ , and$f(p_{T}^{\rm rel})$ distributions for$pp$ collisions at$\sqrt{s}$ = 900 GeV, 2.76 TeV, 5.02 TeV, 7 TeV, 13 TeV and${\rm Pb+Pb}$ collisions at$\sqrt{s_{\rm NN}}$ = 2.76 TeV and 5.02 TeV in the range of 25 GeV/c$<p_{T,{\rm jet}}<$ 40 GeV/c simulated by JEWEL and compared with data of${\rm pp}$ collisions at$\sqrt{s}$ = 7 TeV[20].To better illustrate the differences between the simulation and data, Figs. 2, 3, and 4 show the ratio plots with the reference data of
$ \sqrt{s} $ = 7 TeV$ {\rm pp} $ collisions for$ F(z) $ ,$ \rho(r) $ , and$ f(p_{T}^{\rm rel}) $ separately at four jet momentum intervals of [25,40] GeV/c, [40,60] GeV/c, [60,80] GeV/c and [80,110] GeV/c.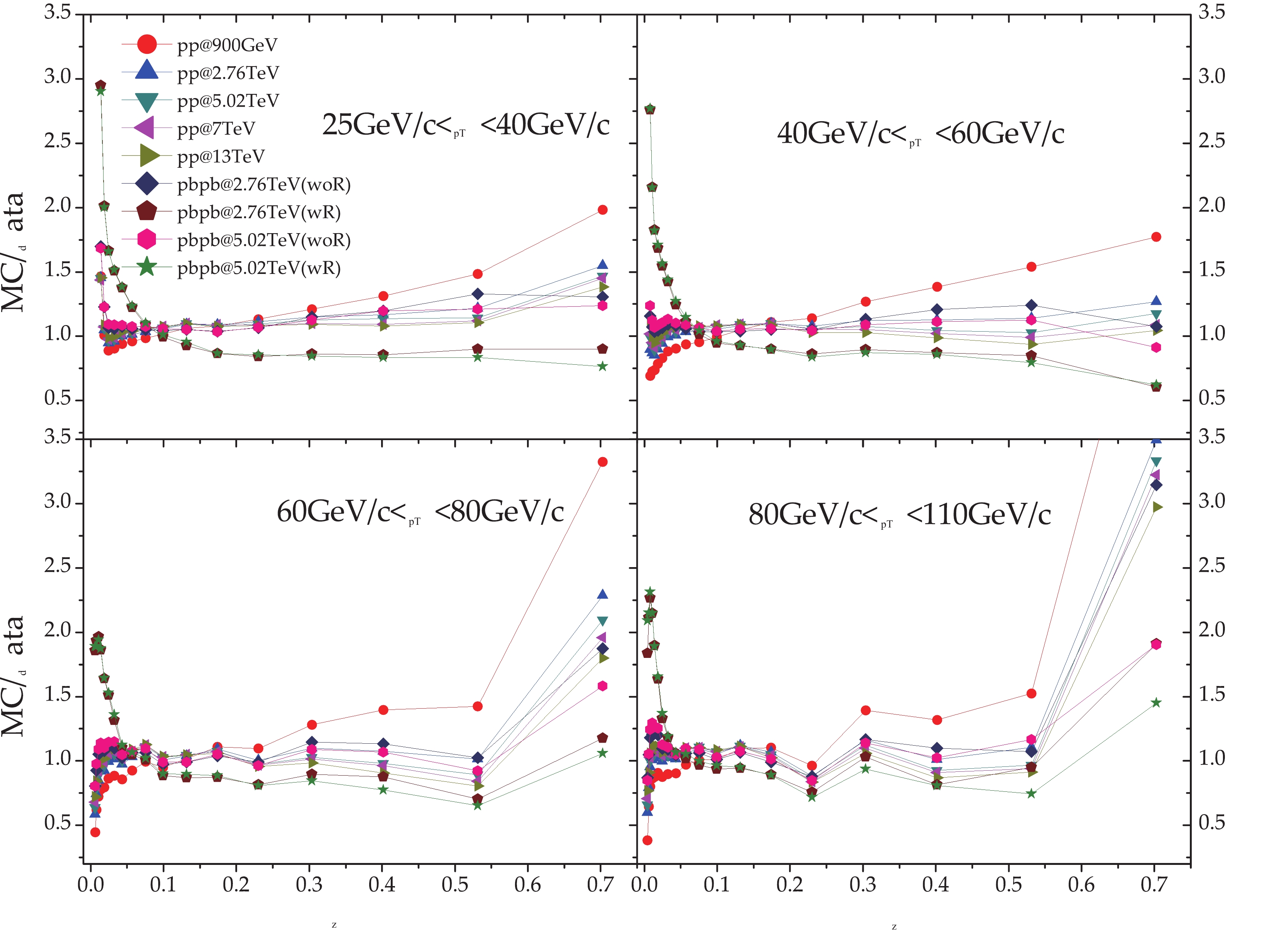
Figure 2. (color online) Ratio of simulations of
$F(z)$ for${\rm pp}$ collisions at$\sqrt{s}$ = 900 GeV, 2.76 TeV, 5.02 TeV, 7 TeV, 13 TeV and${\rm Pb+Pb}$ collisions at$\sqrt{s_{\rm NN}}$ = 2.76 TeV and 5.02 TeV by JEWEL to data of$\sqrt{s}$ = 7 TeV${\rm pp}$ collisions at four jet momentum intervals.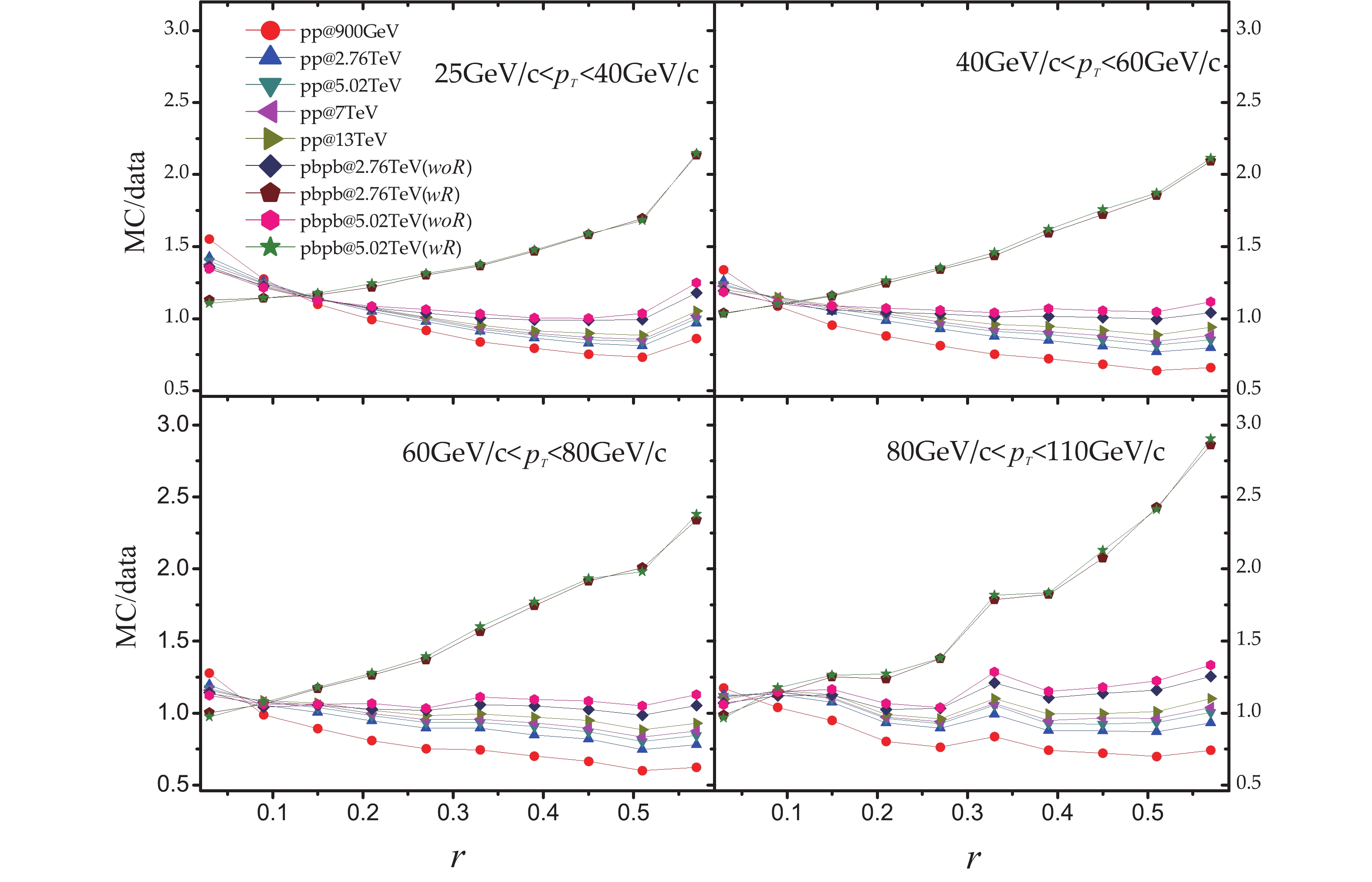
Figure 3. (color online) Ratio of simulations of
$\rho(r)$ for${\rm pp}$ collisions at$\sqrt{s}$ = 900 GeV, 2.76 TeV, 5.02 TeV, 7 TeV, 13 TeV and${\rm Pb+Pb}$ collisions at$\sqrt{s_{\rm NN}}$ = 2.76 TeV and 5.02 TeV by JEWEL to data of$\sqrt{s}$ = 7 TeV${\rm pp}$ collisions at four jet momentum intervals.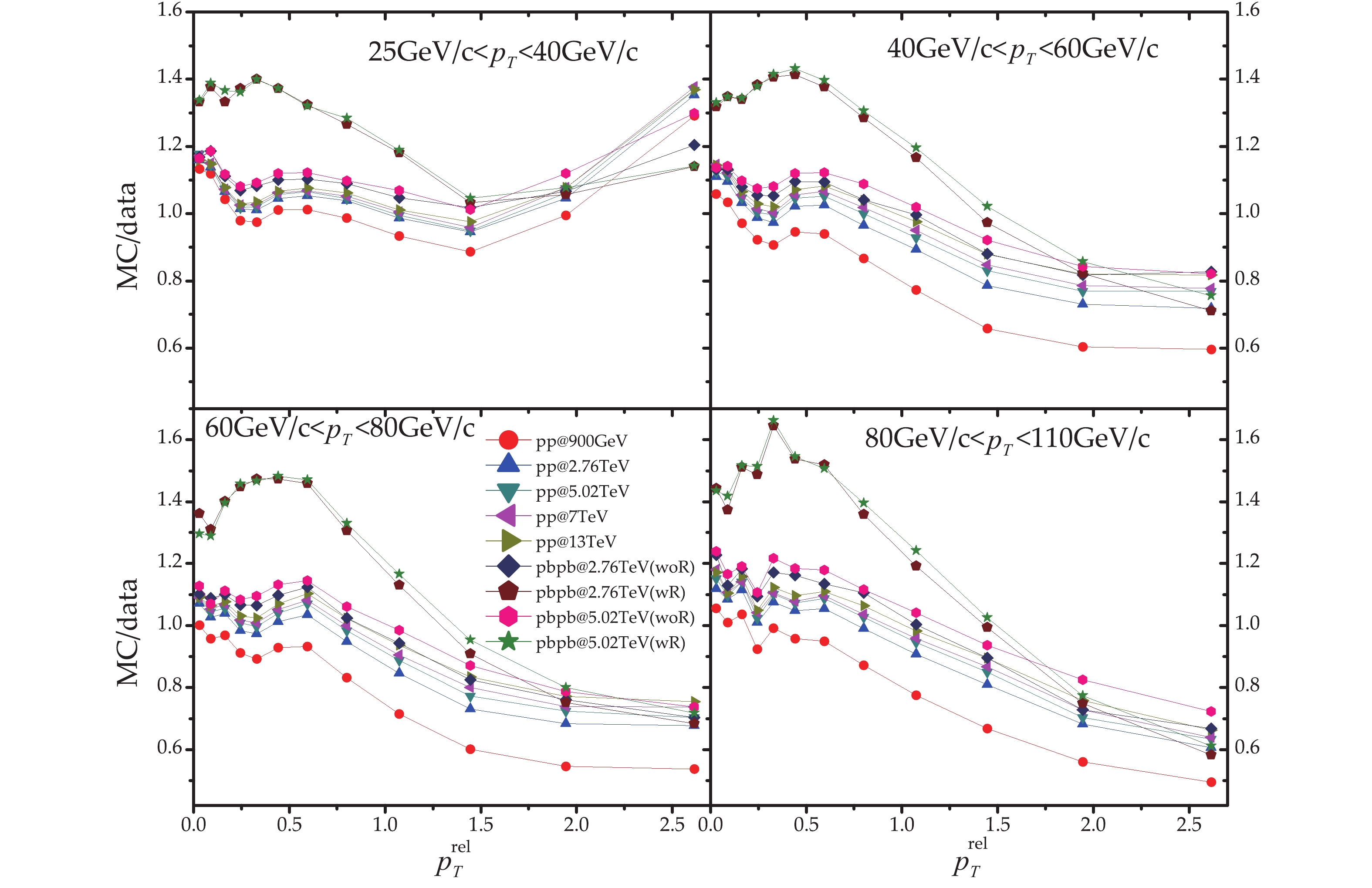
Figure 4. (color online) Ratio of simulations of
$f(p_{T}^{\rm rel})$ for${\rm pp}$ collisions at$\sqrt{s}$ = 900 GeV, 2.76 TeV, 5.02 TeV, 7 TeV, 13 TeV and${\rm Pb+Pb}$ collisions at$\sqrt{s_{\rm NN}}$ = 2.76 TeV and 5.02 TeV by JEWEL to data of$\sqrt{s}$ = 7 TeV${\rm pp}$ collisions at four jet momentum intervals.It's obvious that
$ F(z) $ in Fig. 2 is suppressed from$ {\rm Pb+Pb} $ to$ {\rm pp} $ collisions by the so-called nuclear modification factor of about 15% at$p_{T, {\rm jet}}\in$ [25,40] GeV/c and of about 10% at$p_{T, {\rm jet}}\in$ [80,110] GeV/c when$z>0.1$ . When$z<0.1$ , the nuclear modification factor increases by a factor of 2 to 3 with a decrease in$p_{T, {\rm jet}}$ . For$p_{T, {\rm jet}}>$ 60 GeV/c, the suppression increases at very low$z$ and then decreases when$z<0.01$ . For${\rm pp}$ collisions, the ratios are all enhanced at low$z<0.02$ and then kept almost at 1 for large$z$ and$p_{T, {\rm jet}}<$ 40 GeV/c, while for high momentum jets with$z<0.02$ , the ratio is suppressed by up to 50%. The fragmentation becomes harder for high$p_{T, {\rm jet}}$ and weak dependence on beam energies and medium effects.The nuclear modification factor of charged particle density
$ \rho(r) $ indicates a limited suppression in the small jet radius and a linear increase with the increase of the jet radius from$ {\rm pp} $ to$ {\rm Pb+Pb} $ collisions. The slope is about 2, which is the same level of increase in$ F(z) $ . Whereas for the$ {\rm pp} $ collisions, the ratio is almost constant and slightly differs with the center-of-mass energy.The weak dependence on the jet momentum
$ p_{T, {\rm jet}} $ and the center-of-mass energies of$ {\rm pp} $ collisions, as well as the strong dependence on the medium are observed in the ratio plot of$ f(p_{T}^{\rm rel}) $ in Fig. 4. The nuclear modification factor of$ p_{T}^{\rm rel} $ shows an enhancement up to 50% at low$p_{T}^{\rm rel}<0.5$ followed by a sharp decrease at larger$p_{T}^{\rm rel}$ . At very low$p_{T}^{\rm rel}$ in${\rm pp}$ collisions, a fluctuation in the curve may indicate a flow effect in${\rm pp}$ collisions, since$p_{T}^{\rm rel}$ and$\rho_{\rm ch}^{r}$ are directly related to the non-perturbative hadronization process controlled by perturbative QCD radiation. With the increase of$p_{T, {\rm jet}}$ , soft gluon radiation is important, as it will contribute to jet broadening and cause the mean value of$p_{T}^{\rm rel}$ to rise slowly.As demonstrated in [12], in the present study, these quantities are also dedicated to the study of smaller jet-radii (
$ r = 0.1, 0.12,... ,0.28, 0.30 $ ) to explore the medium effect and jet evolution. The$ {girth} $ at small jet-radii$ r<0.2 $ with different configurations is presented in Fig. 5. The trend obtained by simulation is similar to the data, although it could not efficiently reproduce the data. The angularity is the first radial moment of the jets, which is very sensitive to its radial energy profile. The girth distributions indicate that with the increase of jet-radius, the peak value of$ girth $ shifts to larger values.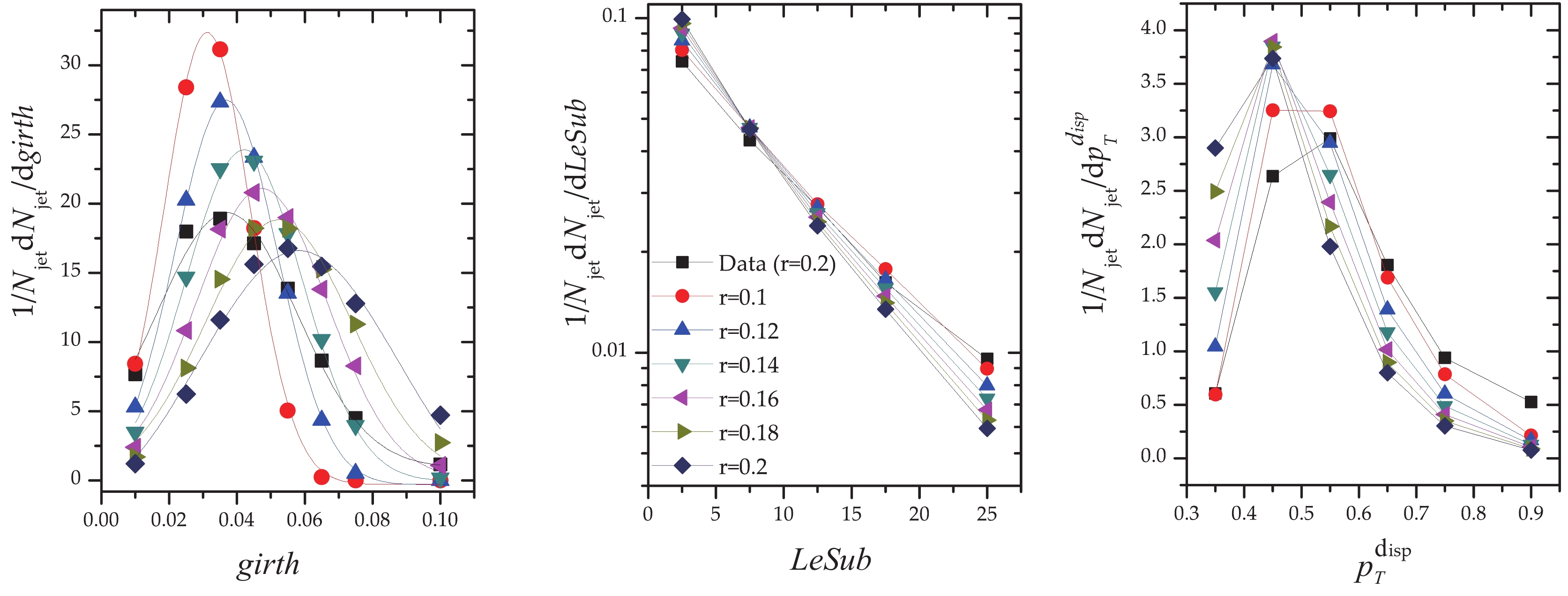
Figure 5. (color online) Jet shape distributions of
$girth$ (left),$LeSub$ (middle) and$P_{T}^{\rm disp}$ (right) in$0\sim 10$ % cental${\rm Pb+Pb}$ collisions at$\sqrt{S_{\rm NN}}$ =2.76 TeV in$p_{T,{\rm jet}}^{\rm ch}\in$ [40,60] GeV/c under different jet-radius cut selections by JEWEL, and the simulations are compared with data[12].Interestingly, the
$ LeSub $ distribution decreases exponentially with$ LeSub $ at different jet-radii. For small jet-radii, asymmetric parton splitting is more probable, while symmetric branching can be found at large jet-radii, which is directly related to the gluon and quark jet fraction. The momentum dispersion distribution shows that$ f(p_{T}^{\rm disp}) $ is a local maximum at$ P_{T}^{\rm disp} = 0.45 $ and then decreases with the increase of the jet radius at large$ P_{T}^{\rm disp} $ , implying a large energy fraction within smaller jet-radius.Figure 6 shows the differential
$ girth $ distribution in ~0%–10% of central${\rm Pb+Pb}$ collisions at$\sqrt{S_{\rm NN}}=$ 2.76 TeV in$p_{T, {\rm jet}}^{\rm ch}\in$ [40,60] GeV/c. It is found that the differential girth evolution from the small jet-radius interval to the larger behaves as a waveform, which attenuates and becomes flatter at larger values. Since the small radius$r$ jet shows larger jet energy loss and smaller granularity.$D_{girth}$ is sensitive to soft particles or the correlated background arising from hot QCD medium. This wave-like pattern and its evolution may potentially be used to investigate the medium properties, such as the coherence effect, medium density, and flow effect, etc.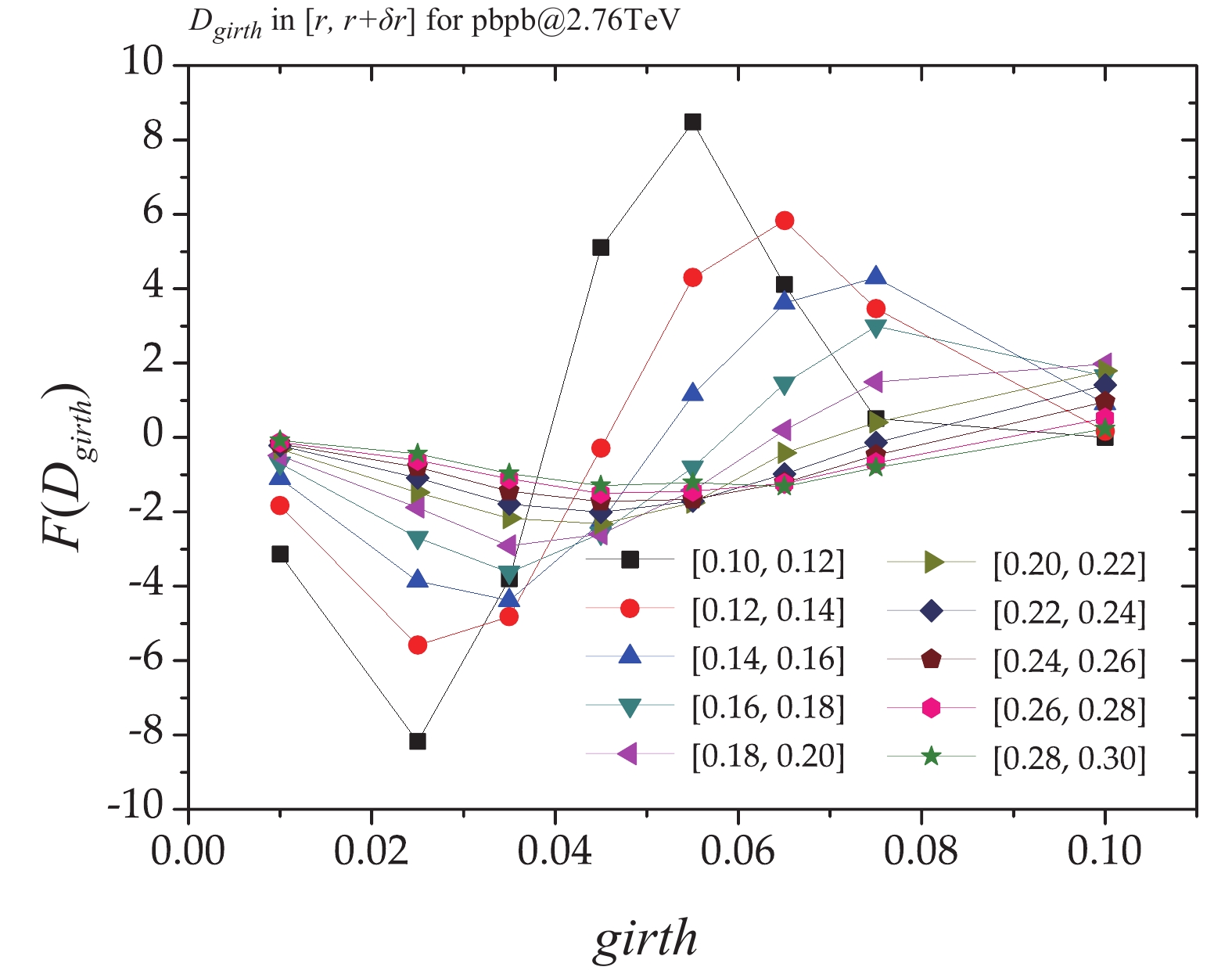
Figure 6. (color online) Differential
$girth$ distribution in 0%–10% of central${\rm Pb+Pb}$ collisions at$\sqrt{S_{\rm NN}}=$ 2.76 TeV in$p_{T,{\rm jet}}^{\rm ch}\in$ [40,60] GeV/c at jet radius of$[r,r+\delta r]$ by JEWEL.The comparison of differential
$ girth $ distribution between ~10% central${\rm Pb+Pb}$ collisions at$\sqrt{S_{\rm NN}}=$ 2.76 TeV and${\rm pp}$ collisions at$\sqrt{s}=$ 7 TeV in$p_{T,{\rm jet}}^{\rm ch}\in$ [40,60] GeV/c is plotted in Fig. 7 at three jet-radius intervals. It is apparent that the waveform in the${\rm pp}$ collision is ahead of${\rm Pb+Pb}$ collisions. This could explain why jet components propagate faster in vacuum than in medium. Furthermore, this observation has the potential to extract medium parameters and should be further investigated. -
A systematical study on jet shape modifications at LHC energies is presented in terms of numerous quantities,
$ F(z) $ ,$ p_{T}^{\rm rel} $ ,$ \rho_{\rm ch}(r) $ ,$ girth $ ,$ LeSub $ , and$ p_{T}^{\rm disp} $ by JEWEL. The study concludes that the medium effect is dominant for jet shape modifications, which has a weak dependence on the center-of-mass energy. Jet fragmentation is significantly enhanced at very low$ z<0.02 $ , and the fragmented jet constituents are linearly spread to larger jet-radii for$ p_{T}^{\rm rel}<1 $ . The differential girth is proposed and studied. The waveform attenuation phenomena is observed in$ f(p_{T}^{\rm rel}) $ ,$ girth $ , and$ D_{girth} $ distributions. The results of the$ D_{girth} $ distribution from$ {\rm pp} $ to$ {\rm Pb+Pb} $ indicate that the wave pattern in$ {\rm pp} $ collisions is ahead of the$ {\rm Pb+Pb} $ collisions at small jet-radius intervals, and thus Dgirth represents an excellent jet shape quantity to explore the relationship with medium density, jet energy loss, coherence effect, flow effect, etc.
Jet shape modification at LHC energies by JEWEL
- Received Date: 2018-12-27
- Accepted Date: 2019-02-24
- Available Online: 2019-05-01
Abstract: Jet shape measurements are employed to explore the microscopic evolution mechanisms of parton-medium interaction in ultra-relativistic heavy-ion collisions. In this study, jet shape modifications are quantified in terms of the fragmentation function






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: