-
The study of QCD at finite isospin density and the corresponding pion superfluid phase is related to the investigation of compact stars, isospin asymmetric nuclear matter, and heavy-ion collisions at intermediate energies. When the isospin chemical potential is larger than the pion mass
$ \mu_I>M_\pi $ , then the quark and antiquark form coherent pairs and condense on a uniform Fermi surface [1-23]. Inside the pion superfluid phase, a smooth crossover appears between the Bardeen-Cooper-Shrieffer (BCS) condensation of fermions with large and overlapped pairs and the Bose-Einstein condensation (BEC) of molecules with small and distinguished pairs [13, 24-27]. The equation of state for a pion superfluid with a large pion condensate [2, 8, 28] will be stiff and may be used to describe the massive compact stars.The NJL model [29-34], which is inspired by the BCS theory, describes well the quark pairing mechanisms. In this model, quarks are elementary particles, and mesons are quantum fluctuations. The fluctuations' contribution to the thermodynamics of the quark-meson system can be expressed at the mean field level for quarks and with the random phase approximation (RPA) for mesons, in terms of the bound states and scattering phase shifts of quark-antiquark pairs [35, 36]. This result appears to be more general than for application in the NJL model, as it resembles the Beth-Uhlenbeck formula for the second virial coefficient for a gas of non-relativistic particles [37, 38] and relativistic particles [39]. Recently, the relativistic approach was extended to describe the thermodynamics of color superconductivity by Blaschke et al. [40]. At finite isospin density, taking into account all possible channels of the bubble summation in the RPA, the NJL model successfully describes the pion superfluid phase, especially the Goldstone mode corresponding to the spontaneous breaking of isospin symmetry [13]. Previous studies of the meson mass spectra in the pion superfluid phase treat mesons as bound states [6, 7, 13, 17, 41-46]. These include the NJL model, linear
$ \sigma $ model, and LQCD simulations. However, in a medium where the meson mass exceeds two times the quark mass, the meson can decay into its constituent quark-antiquark pair. It is thus not a stable bound state, but rather a resonant state.In this paper, we study the quark-antiquark scattering phase shift and its relation to the meson spectral function in pion superfluid phase within frame of the NJL model. When isospin symmetry is spontaneously broken, the new eigenmodes of the superfluid system are no longer the ordinary mesons with fixed isospin quantum numbers, but their linear combinations. Such strong meson mixing makes it impossible to define the quark-antiquark scattering phase shift and the meson spectral function for a fixed isospin channel. However, the whole phase shift and spectral function can be defined, which is relevant to the thermodynamics of the quark-meson system. We will discuss the relations among the meson propagator pole, quark-antiquark scattering phase shift, and the meson spectral function in the NJL model in Section 2. Further, we show numerical calculations in normal and pion superfluid phases and analyze the physical mechanisms in Section 3. Finally, we provide a summary of this study in Section 4.
-
The Lagrangian density of the two-flavor NJL model at quark level is defined as follows [30-34]
$ {\cal{L}} = \bar \psi \left( {i{\gamma ^\mu }{\partial _\mu } - {m_0} + \mu {\gamma _0}} \right)\psi + G[{\left( {\bar \psi \psi } \right)^2} + {\left( {\bar \psi i{\gamma _5}\vec \tau \psi } \right)^2}]. $

(1) $ m_0 $ is the current quark mass, characterizing the explicit chiral symmetry breaking. The quark chemical potential$ \mu ={\rm diag}\left(\mu_u, \mu_d\right)={\rm diag}\left(\mu_B/3+\mu_I/2, \mu_B/3-\mu_I/2\right) $ is a matrix in the flavor space, with$ \mu_u $ and$ \mu_d $ as the u- and d-quark chemical potentials and$ \mu_B $ and$ \mu_I $ as the baryon and isospin chemical potentials. G is the four-quark coupling constant with dimension (GeV)−2 in the scalar/pseudoscalar channel, which controls the spontaneous breaking of chiral symmetry and isospin symmetry.$ \tau_i\ (i=1, 2, 3) $ are the Pauli matrices in the flavor space.At zero isospin chemical potential, the Lagrangian has the symmetry of
$ {SU}_I(2)\bigotimes {SU}_A(2) $ corresponding to isospin symmetry and chiral symmetry, respectively. At finite isospin chemical potential without pion condensation, the isospin symmetry$ {SU}_I(2) $ and chiral symmetry$ {SU}_A(2) $ are explicitly broken to$ U_I(1) $ and$ U_A(1) $ , respectively. Therefore, the chiral symmetry restoration at finite isospin chemical potential depict the degeneracy of$ \sigma $ and$ \pi_0 $ mesons only, while the charged pions$ \pi_\pm $ still behave differently.The order parameters for the spontaneous breaking of chiral and isospin symmetry are the chiral condensate
$ \langle\sigma\rangle $ and pion condensate$ \langle\pi\rangle $ ,$ \begin{array}{*{20}{l}} {\langle \sigma \rangle = \langle \bar \psi \psi \rangle, }\\ {\langle \pi \rangle = \sqrt 2 \langle \bar \psi i{\gamma _5}{\tau _ \pm }\psi \rangle } \end{array} $

(2) with
$ \tau_\pm =(\tau_1\pm i\tau_2)/\sqrt 2 $ .Assuming that both condensates are real, the quark propagator in mean-field approximation can be expressed as a matrix in the flavor space [13],
$ \begin{array}{*{20}{l}} {{{\cal{S}}^{ - 1}}\left( k \right) = \left( {\begin{array}{*{20}{l}} {{\gamma ^\mu }{k_\mu } + {\mu _u}{\gamma _0} - {M_q}} & {2iG\langle \pi \rangle {\gamma _5}}\\ {2iG\langle \pi \rangle {\gamma _5}} & {{\gamma ^\mu }{k_\mu } + {\mu _d}{\gamma _0} - {M_q}} \end{array}} \right)} \end{array} $

(3) with non-vanishing off-diagonal elements in the phase with isospin symmetry spontaneous breaking. Here, the chiral symmetry breaking is hidden in the effective quark mass
$ M_q=m_0-2G\langle\sigma\rangle $ . One can explicitly obtain the mean field quark propagator [13]$ \begin{array}{*{20}{l}} {{\cal{S}}\left( k \right) = \left( {\begin{array}{*{20}{l}} {{{\cal{S}}_{uu}}(k)} & {{{\cal{S}}_{ud}}(k)}\\ {{{\cal{S}}_{du}}(k)} & {{{\cal{S}}_{dd}}(k)} \end{array}} \right)} \end{array} $

(4) in terms of the four effective quark energies
$ E_ \mp ^ \pm = \sqrt {{{\left( {\sqrt {{{{ {k}}}^2} + M_q^2} \pm \frac{{{\mu _I}}}{2}} \right)}^2} + 4{G^2}{{\langle \pi \rangle }^2}} \mp \frac{{{\mu _B}}}{3}, $

(5) by applying the method of the massive energy projector [47].
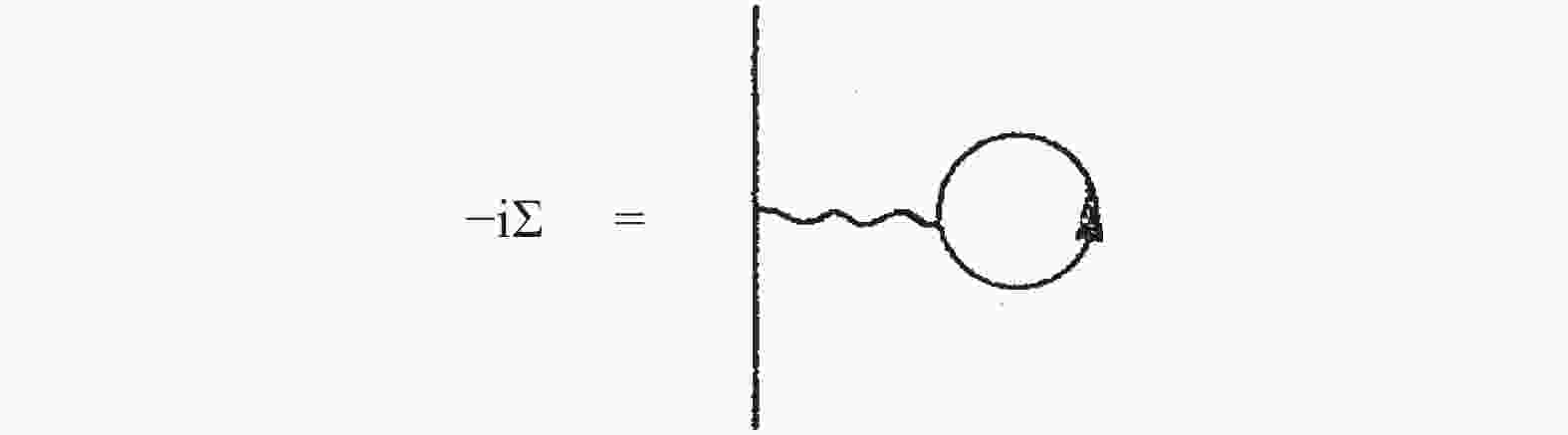
The ground state of the system is determined by the minimum thermodynamic potential, realized by solving the two gap equations[13, 31]
$ \begin{split} \langle \sigma \rangle =& - {N_{\rm c}}\int {\displaystyle\frac{{{{\rm d}^4}k}}{{{{(2\pi )}^4}}}} {\rm{T}}{{\rm{r}}_{\rm D}}\left[{{\rm i}{{\cal{S}}_{uu}}(k) + {\rm i}{{\cal{S}}_{dd}}(k)} \right], \\ \langle \pi \rangle =& {N_{\rm c}}\int {\displaystyle\frac{{{{\rm d}^4}k}}{{{{(2\pi )}^4}}}} {\rm{T}}{{\rm{r}}_{\rm D}}\left[{\left( {{{\cal{S}}_{ud}}(k) + {{\cal{S}}_{du}}(k)} \right){\gamma _5}} \right], \end{split} $

(6) which can be illustrated in Fig. 1. Here, the trace
$ {\rm{Tr}}_{\rm D} $ is in Dirac space, and the four momentums integral is defined as$ \int {\rm d}^4k/(2\pi)^4={\rm i}T\sum_n\int {\rm d}^3{ k}/(2\pi)^3 $ in Euclidean space with$ k_0={\rm i}\omega_n={\rm i}(2n+1)\pi T\ (n=0, \pm 1, \pm 2, \cdots) $ at finite temperature T. Obviously, the color degrees of freedom in the NJL model is trivial, and the trace in color space simply contributes a color factor$ N_{\rm c}=3 $ . At the chiral limit with vanishing current quark mass$ m_0=0 $ , the critical point of chiral symmetry restoration is determined by the first gap Eq. (6) at$ \langle \sigma \rangle=0 $ , and the pion superfluid phase with non-vanishing$ \langle\pi\rangle $ starts at$ \mu_I=0 $ . In the physical world with$ m_0\neq 0 $ , when there is no more strict chiral phase transition, the pion superfluid phase starts with$ \mu_I=M_\pi $ at T = 0 [13], where$ M_\pi $ is the pion mass in vacuum.
Figure 1. Hartree contribution to the self-energy for a particular interaction vertex in the NJL model.
The above treatment at the mean field level is clearly incomplete, as it omits the meson contribution, which should dominate the system at low temperature and chemical potential. In the NJL model, the meson modes are treated as quantum fluctuations above the mean field. The quark-antiquark scattering via meson exchange can be effectively expressed at the quark level in terms of quark bubble summation in RPA [30-36], shown in Fig. 2.
Considering all the possible quark bubbles between two interaction vertexes, the meson propagator can then be written as a matrix in the meson space
$ (\pi_+, \pi_-, \pi_0, \sigma) $ [13, 42],$ D(p) = \frac{{2G}}{{1 - 2G\Pi (p)}}, $

(7) where
$ p=(i\nu_n, { p}) $ is the meson four momentum with the Matsubara frequency$ \nu_n=2\pi nT $ , and$ \Pi(p) $ is the meson polarization matrix with elements$ {\Pi _{mn}}(p) = {\rm i}\int {\frac{{{{\rm d}^4}k}}{{{{(2\pi )}^4}}}} {\rm{Tr}}\left[{{\Gamma _m}{\cal{S}}(p + k)\Gamma _n^*{\cal{S}}(k)} \right] $

(8) with the meson vertexes
$ {\Gamma _m} = \left\{ {\begin{array}{*{20}{l}} 1 & {m = \sigma }\\ {{\rm i}{\tau _ + }{\gamma _5}} & {m = {\pi _ + }}\\ {{\rm i}{\tau _ - }{\gamma _5}} & {m = {\pi _ - }}\\ {{\rm i}{\tau _3}{\gamma _5}} & {m = {\pi _0}\;, } \end{array}} \right.\;\;\;\;\Gamma _m^* = \left\{ {\begin{array}{*{20}{l}} 1 & {m = \sigma }\\ {{\rm i}{\tau _ - }{\gamma _5}} & {m = {\pi _ + }}\\ {{\rm i}{\tau _ + }{\gamma _5}} & {m = {\pi _ - }}\\ {{\rm i}{\tau _3}{\gamma _5}} & {m = {\pi _0}\;.} \end{array}} \right. $

(9) In Eq. (8), the quark momentum integral is at finite temperature, and the trace runs across color, flavor, and spin degrees of freedom of quarks. The polarization matrix is symmetric with
$ \Pi_{mn}=\Pi_{nm} $ . In the normal phase with vanishing pion condensate$ \langle\pi\rangle=0 $ , the quark propagator is diagonal in the flavor space, and therefore all the off-diagonal elements of the polarization matrix$ \Pi $ in the meson space disappear automatically. In the pion superfluid phase, while there is no mixing between$ \pi_0 $ and other mesons,$ \Pi_{\pi_0\sigma} = \Pi_{\pi_0\pi_+} = \Pi_{\pi_0\pi_-} = 0 $ , the other three mesons$ \sigma, \pi_+ $ , and$ \pi_- $ are coupled to each other with nonzero elements$ \Pi_{\sigma\pi_+}, \Pi_{\sigma\pi_-}, \Pi_{\pi_+, \pi_-}\neq 0 $ [13, 42].Static meson properties, like mass and the meson contribution to the thermodynamics of the system [35, 36], are controlled by the determinant of the inverse meson propagator, which is a complex function and can be expressed in terms of a phase,
$ \begin{split} & \!\!\!\!\!{\rm{det}}\left[1-2G\Pi(\omega\pm {\rm i}\epsilon, { p})\right] = \left|{\rm{det}}\left[1-2G\Pi(\omega + {\rm i}\epsilon, { p})\right]\right|{\rm e}^{\mp {\rm i}\Phi}, \\ & \!\!\!\!\!\tan \Phi = -{\frac{{{\rm{Im}}\{{\rm{det}}\left[1-2G\Pi(\omega + {\rm i}\epsilon, { p})\right]\}}}{{{\rm{det}}\left[1-2G\Pi(\omega, { p})\right]}}}. \end{split} $

(10) Physically,
$ \Phi $ is the phase shift associated with the quark-antiquark scattering in the model. While the phase shift is controlled by the meson mass M around a pole of the propagator, which is determined by$ {\rm{det}}\left[1-2G\Pi(M, { p})\right]=0 $ , it is dominated by the background when the kinematics is away from the pole. In normal phase without pion condensate,$ \Phi $ can be explicitly separated into a meson part and a background part, and the latter is independent of the meson itself and determined by quark properties [36].The meson spectral function, which is also controlled by the complex structure of the meson propagator, is closely related to the quark-antiquark scattering phase shift. In the case without meson mixing, the spectral function for the meson m in the NJL model is conventionally defined as
$ \begin{split} \rho_m(\omega, { p}) = & -2{\rm{Im}} D_{mm}(\omega+{\rm i}\epsilon, { p})\\ =& -{\frac{{2G\sin \left(2\Phi_m(\omega, { p})\right)}}{{1-2G\Pi_{mm}(\omega, { p})}}} \end{split} $

(11) with the scattering phase shift for the meson m,
$ \tan \Phi_m = -{\frac{{{\rm{Im}}\left[1-2G\Pi_{mm}(\omega + {\rm i}\epsilon, { p})\right]}}{{1-2G\Pi_{mm}(\omega, { p})}}}. $

(12) In the pion superfluid phase with
$ \pi_+-\pi_--\sigma $ mixing, one can not separately define the spectral function for a fixed isospin channel. However, we can diagonalize the propagator matrix in Eq. (7), and calculate the spectral functions for their respective eigenstates. The analytical formula is too lengthy and too complicated to be shown here. Equivalently, we define the whole spectral function of the mixed mesons through the whole mixed meson propagator matrix,$ \begin{split} \rho(\omega, { p}) =& -2{\rm{Im}}\{{\rm{det}}D(\omega+{\rm i}\epsilon, { p})\}\\ =& -{\frac{{(2G)^3\sin \left(2\Phi(\omega, { p})\right)}}{{{\rm{det}} \left[1-2G\Pi(\omega, { p})\right]}}}, \end{split} $

(13) which is relevant to the scattering phase shift and the thermodynamics of the quark-meson system.
Accordingly, in any case, the meson spectral function is associated with both the meson pole depicted in the denominator and the quark-antiquark scattering phase shift in the numerator. This indicates that in the quark-meson plasma described by the NJL model, the meson spectral function is governed not only by meson characteristics but also by the quark properties.
-
Before performing numerical calculations, we first fix the parameters of the model. Since NJL model is non-renormalizable, it should be regularized. For simplicity, we choose a hard cutoff
$ \Lambda $ for the quark three-momentum. The three parameters$ \Lambda $ , G, and$ m_0 $ are fixed by fitting the physical quantities in vacuum: pion mass$ M_\pi=0.134 $ GeV, pion decay constant$ F_\pi=0.093 $ GeV, and the chiral condensate$\langle\sigma\rangle= $ $ 2(-0.25 \; {\rm{GeV}})^3 $ . The parameters we obtained are$ \Lambda=0.653 $ GeV, G = 4.93 GeV-2, and$ m_0=0.005 $ GeV [36].To gain some insight into the physical meaning of the "meson modes", we first examine the pole approximation to the inverse meson propagator
$ 1-2G\Pi(\omega, { p}) $ and the associated scattering phase shifts. For mesons in stable bound states, their masses$ M_m $ are determined by the poles of the meson propagator at vanishing three-momentum,$ {\rm{det}}\left[1-2G\Pi(M_m, {\bf 0})\right]=0. $

(14) Around the pole
$ \omega^2=E_m^2=M_m^2+{ p}^2 $ , we have$ 1-2G\Pi(\omega, { p})=(\omega^2-E^2_m) \times {{\rm{const}}}. $

(15) Taking the values
$ \omega \rightarrow \omega \pm {\rm i} \epsilon $ and inserting them into Eq. (10), the scattering phase shift is reduced to a simple step function,$ \Phi_m(\omega, { p})=\pi\Theta\left(\omega^2-E_m^2\right), $

(16) which gives a vanishing imaginary part of the determinant. The meson spectral function
$ \rho(\omega, { p}) $ becomes the$ \delta $ function located at the pole, and the meson contribution to the thermodynamic potential becomes the familiar function for an ideal meson gas,$ {\Omega _m} = \int {\frac{{{{\rm d}^3}{{p}}}}{{{{(2\pi )}^3}}}} \left[{\frac{{{E_m}}}{2} + T{\rm{ln}}\left( {1-{{\rm e}^{-{E_m}/T}}} \right)} \right]. $

(17) However, when the meson mass exceeds two times the quark mass, the meson can decay into its constituent quark-antiquark pair. Thus, this does not represent a stable bound state, but rather a resonant state. In this case, the pole is no longer on the real axis of the
$ \omega $ -plane, and the pole equation (14) should be regarded in its complex form in order to determine the resonant mass$ M_m $ and its associated width$ \Gamma_m $ that are defined through the relation$ {\rm{det}}\left[1-2G\Pi(M_m-{\rm i}\Gamma_m/2, {\bf 0})\right]=0. $

(18) In the normal phase without pion condensate, taking the approximation of the small width in comparison with the mass, we have [36, 48]
$ \Gamma_m \simeq \frac{m_0}{M_m M_q} {{\rm{Im}}} \frac{ (M_m-{\rm i}\epsilon)^2-\epsilon^2_m}{1-2G\Pi(M_m-{\rm i}\epsilon, {\bf 0})-m_0/M_q} $

(19) with
$ \epsilon_\pi=0 $ and$ \epsilon_\sigma= 2M_q $ .Around the complex pole
$ \omega^2=\left(M_m-{\rm i}\Gamma_m/2\right)^2+{ p}^2 $ , the imaginary part of the determinant can be considered as a constant, and the scattering phase shift satisfies$ \tan {\Phi _m}(\omega, {{p}}) = - \frac{{{M_m}{\Gamma _m}}}{{{\omega ^2} - \left( {E_m^2 - \Gamma _m^2/4} \right)}}. $

(20) The corresponding spectral function is of the form of Breit–Wigner distribution with width
$ \Gamma_m $ and approaches the$ \delta $ function in the limit$ \Gamma_m \rightarrow 0 $ .The meson masses
$ M_m $ and the associated widths$ \Gamma_m $ are displayed in Fig. 3 as functions of temperature at fixed isospin chemical potential. At$ \mu_I=0.1 $ GeV (upper panel), which is less than the critical value$ \mu_I=M_\pi $ of the pion superfluid, the system is in the normal phase without pion condensate at any temperature. Due to the explicit isospin symmetry breaking from$ SU_I(2) $ to$ U_I(1) $ at$ \mu_I\neq 0 $ , the degenerate pion mass$ M_\pi $ in vacuum splits into$ M_{\pi_+}, \ M_{\pi_-} $ , and$ M_{\pi_0} $ in medium. Thus, the explicit chiral symmetry breaking from$ SU_A(2) $ to$ U_A(1) $ at$ \mu_I\neq 0 $ reduces the degree of meson degeneration at high temperature: only the neutral mesons$ \sigma $ and$ \pi_0 $ become degenerate, while the charged pions$ \pi_+ $ and$ \pi_- $ still behave differently. Any pion is in its bound state at low temperature (especially in the pion superfluid phase) and starts to have nonzero width at the corresponding critical temperature of the Mott phase transition [49-51] where the pion energy is larger than the corresponding quark plus antiquark energies. The width increases monotonously with the temperature. The$ \sigma $ meson is always in the resonant state in the NJL model, whereas the width is rather small in the chiral symmetry breaking phase and increases rapidly when symmetry is gradually restored. Different from the case at$ \mu_I=0 $ where the three pions are degenerate, the meson mass splitting at$ \mu_I\neq 0 $ leads to different Mott phase transition points for different pions.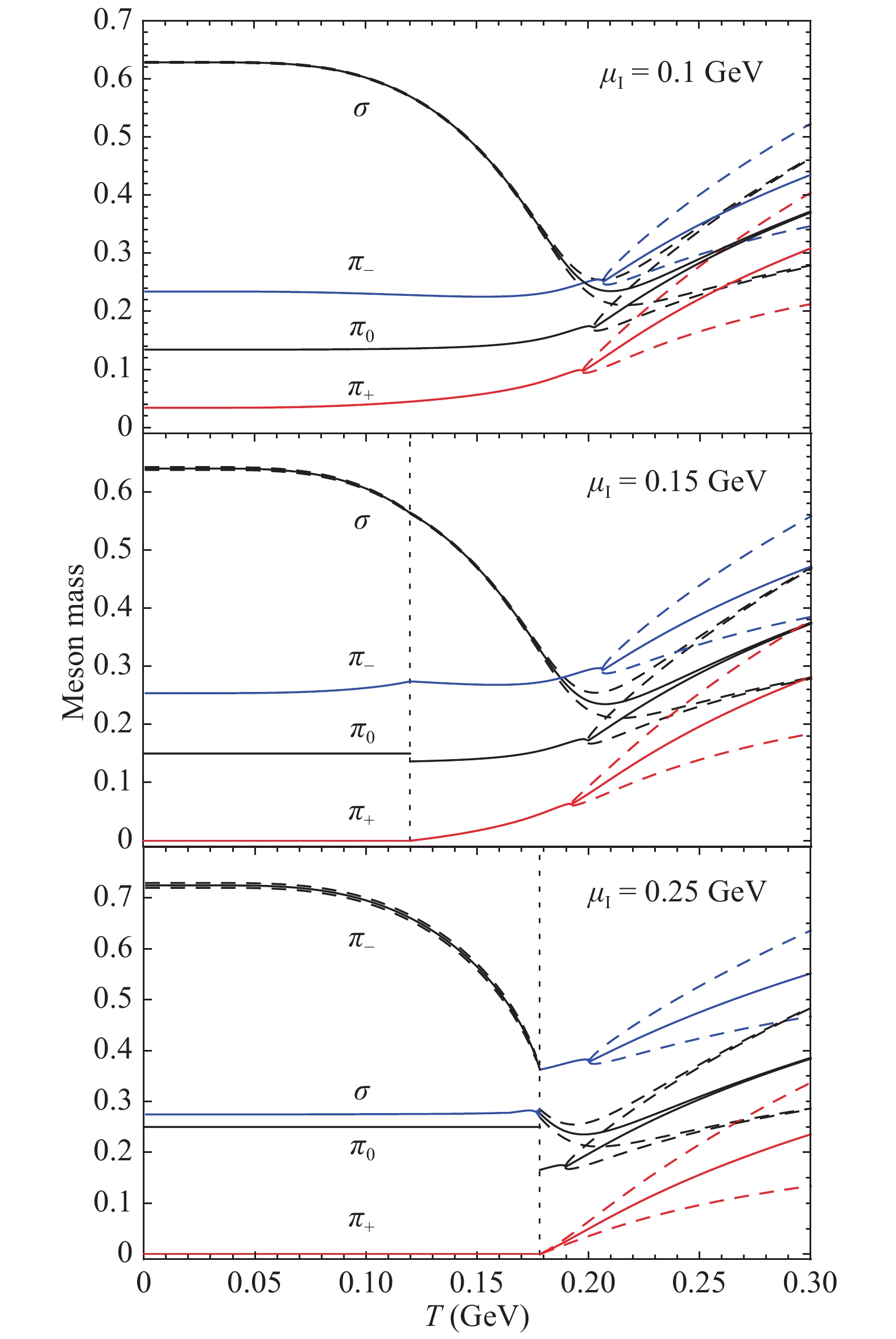
Figure 3. (color online) Meson masses
$ M_m(T) $ (solid lines) and their broadenings$ M_m(T)\pm\Gamma_m(T)/2 $ (dashed lines) at different isospin chemical potential$ \mu_I= $ 0.1 (upper panel), 0.15 (middle panel), 0.25 (lower panel) GeV and vanishing baryon chemical potential$ \mu_B=0 $ . The vertical dotted lines in the middle and lower panels separate the pion superfluid phase at low temperature from the normal phase at high temperature.In the normal phase with only chiral condensation, the quark propagator is diagonal and the summation of bubbles in RPA selects its specific channel by choosing the proper polarization function at each stage. Therefore, a meson mode, which is determined by the pole of the corresponding meson propagator, is only related to its own polarization function. However, when the isospin chemical potential exceeds the critical value
$ \mu_I=M_\pi $ , as depicted in the middle and lower panels of Fig. 3, then the system is in the pion superfluid phase at low temperature. The collective excitations of the system, determined by the pole Eq. (18), will in principle not be the original meson modes ($ \pi_+, \pi_-, \pi_0, \sigma $ ), but their linear combinations ($ c_{\pi_+}\pi_++c_{\pi_-}\pi_-+c_{\pi_0}\pi_0+c_\sigma\sigma $ ) [13, 42]. Due to this mixing, which is very strong at high$ \mu_I $ and low T, these new modes in the pion superfluid are no longer the eigenmodes of the isospin operator$ \hat I_3 $ . In the NJL model, from the explicit calculation of the polarization elements$ \Pi_{mn} $ ,$ \pi_0 $ decouples from the other mesons and is still an collective mode of the system, but the other three ($ \pi_+, \pi_-, \sigma $ ) are replaced by their linear combinations. Considering the fact that these new modes should return to the old modes at the critical point of pion superfluid, indicated by the vertical dotted lines in the middle and lower panels of Fig. 3, we still refer to these modes as$ \pi_+, \pi_-, \sigma $ according to the continuity. While the mixing is weak around the critical point, it becomes increasingly stronger at$ T\to 0 $ . For instance, at$ \mu_I=0.25 $ GeV, as shown in the lower panel of Fig. 3, the new mode$ \pi_- $ in the pion superfluid is dominated by the$ \pi_- $ component at$ T\to T_{\rm c} $ , but by the$ \sigma $ component at$ T\to 0 $ . Corresponding to the spontaneous isospin symmetry breaking, there exists a Goldstone mode in the pion superfluid. From the continuity at the critical point, we call it$ \pi_+ $ . While there is a small width associated with the new mode$ \sigma $ in the middle panel and$ \pi_- $ in the lower panel, the other new modes are in the bound states with$ \Gamma = 0 $ . The critical temperature starts with T = 0 at$ \mu_I=M_\pi $ and increases monotonously with$ \mu_I $ . In the normal phase at high temperature, any meson becomes a resonant state when its energy is beyond the quark + antiquark energies. The meson widths increase rapidly with temperature.For
$ \pi_0 $ meson, which decouples from the other three mesons, we can analytically derive$ M_{\pi_0}(T, \mu_I)=\mu_I $

(21) in the pion superfluid, by combining the pole equation
$ 1-2G\Pi_{\pi_0\pi_0}(M_{\pi_0}, {\bf 0})=0 $ and the gap equation for the pion condensate$ \langle\pi\rangle $ . However, the polarization$ \Pi_{\pi_0\pi_0} $ is not continuous at the critical point of pion superfluid in the case of nonzero temperature, leading to a jump of$ M_{\pi_0} $ from$ \mu_I $ in the pion superfluid phase to a lower value in the normal phase, as depicted by the jumps along the vertical dotted lines in the middle and lower panels of Fig. 3. When the temperature is high enough, the chiral symmetry is gradually restored, and the$ \sigma $ and$ \pi_0 $ masses approach to coincide.With the gap Eq. (6) for the chiral and pion condensates
$ \langle\sigma\rangle $ and$ \langle\pi\rangle $ , one can determine the phase boundaries of chiral restoration and pion superfluid in the NJL model. When chiral symmetry is explicitly broken with a nonzero current quark mass$ m_0 $ , there is no strict definition for the chiral symmetry restoration. The pseudo-critical temperature$ T_{{\rm pc}} $ is normally defined as the temperature at which the quark mass or chiral condensate has the maximum change, and we numerically have$ T_{{\rm pc}}=187 $ MeV with$ \mu_B=\mu_I=0 $ in the hard cutoff regularization scheme [36]. The critical temperature of the pion superfluid phase transition is determined by the condition$ \langle\pi\rangle=0 $ , see$ T_{\rm c} $ in Fig. 4. Taking the pole Eq. (14) in the normal phase, one can obtain the border between the meson bound and resonant states. The corresponding meson dissociation temperature is defined by the threshold where the pion mass is equal to the corresponding quark + antiquark mass, see$ T_{\rm d} $ in Fig. 4. The phase diagram of the pion superfluid in the plane of temperature and isospin chemical potential at vanishing baryon chemical potential is plotted in Fig. 4. The critical temperature$ T_{\rm c} $ and the$ \pi_0 $ dissociation temperature$ T_{\rm d} $ are displayed by solid and dashed lines, respectively. The two temperatures coincide when$ \mu_I $ is large enough. There are three phases in the plane: the pion superfluid phase in the region of$ T < T_{\rm c} $ , the normal phase with meson bound states in the region of$ T_{\rm c} < T < T_{\rm d} $ , and the normal phase without bound states in the region of$ T>T_{\rm d} $ . Since the thermal excitation of the pion condensate at the critical temperature$ T_{\rm c} $ are meson bound states at low$ \mu_I $ and resonant states or even quark and antiquark states at high$ \mu_I $ , there should be, in the pion superfluid phase, a crossover from Bardeen-Cooper-Schrieffer (BCS) state at high$ \mu_I $ to Bose-Einstein Condensation (BEC) state at low$ \mu_I $ [13, 24-27].
Figure 4. Phase diagram of pion superfluid in the
$ T-\mu_I $ plane at$ \mu_B=0 $ . The solid and dashed lines display the critical temperature$ T_{\rm c} $ of the pion superfluid and the dissociation temperature$ T_{\rm d} $ of the meson bound states, respectively.We now consider the quark-antiquark scattering phase shift in pole approximation. For all the numerical calculations for phase shifts and spectral functions shown in the following, we set the meson momentum
$ { p}=0 $ . At$ \mu_I=0 $ , pions are degenerate, in the bound state at low temperature and in the resonant state at high temperature. The pion phase shift$ \Phi_\pi(\omega) $ in the pole approximation is shown in Fig. 5 for the bound and resonant states. In vacuum at T = 0, the phase shift$ \Phi_\pi (\omega) $ is a step function. It is zero at$ \omega < M_\pi $ , then jumps suddenly from 0 to$ \pi $ at$ \omega=M_\pi $ , and keeps$ \pi $ at$ \omega > M_\pi $ . At T = 0.25 GeV, the pions are already in the resonant state, and the phase shift changes from the step function (16) to the smooth crossover (20). The rapid change is still around$ \omega=M_\pi= 0.28 $ GeV. While the phase shift can reach the limit$ \Phi_\pi=\pi $ at large enough$ \omega $ , it starts with a finite value$ \Phi_\pi\neq 0 $ at$ \omega=0 $ due to the finite width$ \Gamma_\pi $ .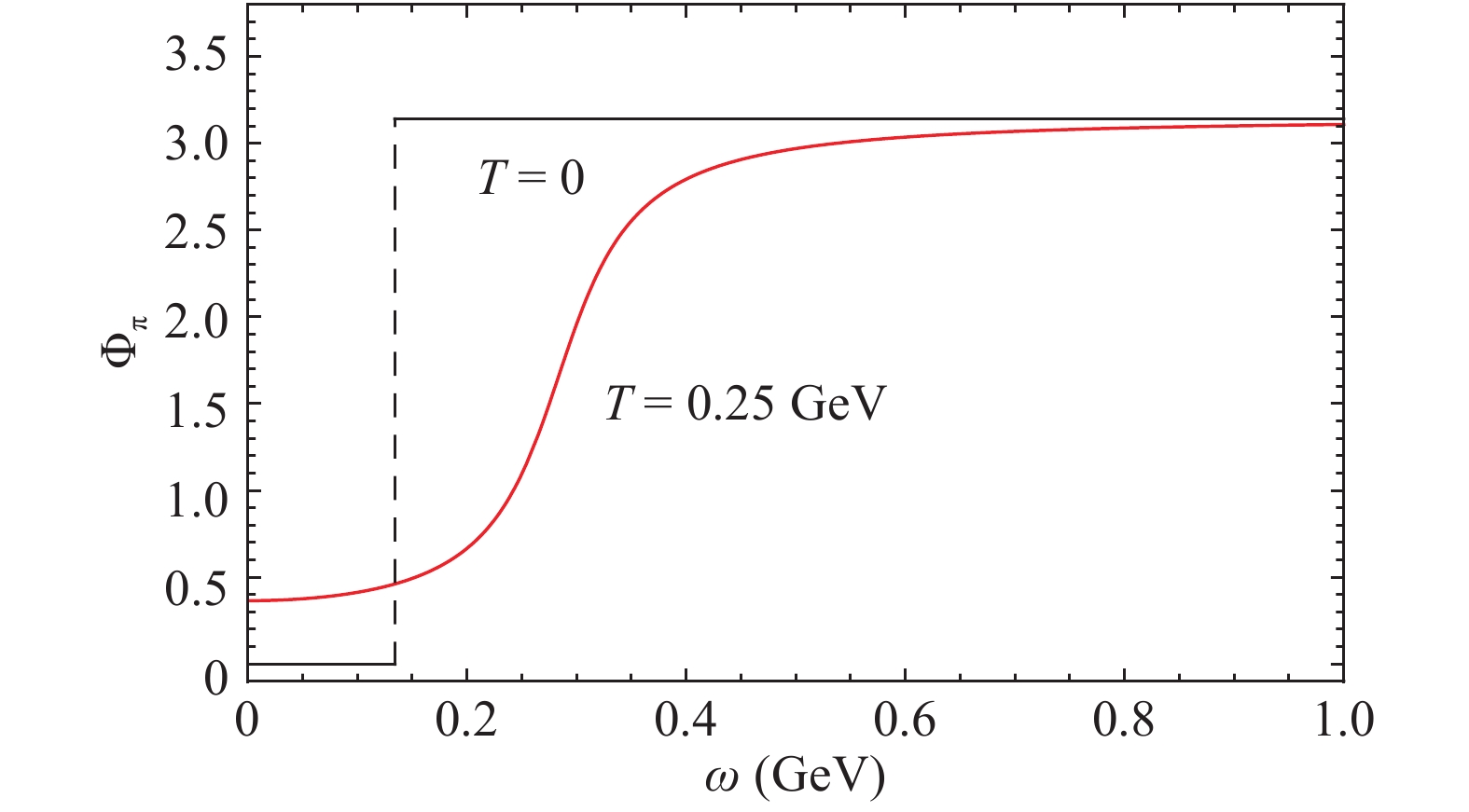
Figure 5. (color online) Pion phase shift
$ \Phi_\pi $ in the pole approximation as a function of pion energy$ \omega $ at vanishing chemical potentials and momentum$ \mu_I=\mu_B={ p}=0 $ . The two lines correspond to the bound state at T = 0 and resonant state at T = 0.25 GeV.However, the pole approximation is in principle insufficient for our calculation, since it is only valid for
$ \omega $ in the vicinity of the pole and should violently deviate from the original definition (10). Furthermore, it neglects the fact that the exact phase shift$ \Phi(\omega) $ must increase around the pole and then decrease in such a way that Levinson's theorem is fulfilled [35]. In our notation, this theorem reads$ \int_0^\infty {\rm d} \omega \frac{{{\rm d}\Phi }}{{{\rm d}\omega }} = 0. $

(22) Thus the pole approximation, which states that the phase shift starts with
$ \Phi=0 $ and ends with$ \Phi=\pi $ , is inconsistent with Levinson's theorem, and we therefore expect that a partial compensation to the meson spectral function$ \rho $ as calculated from (13) must arise when one performs a full calculation of the phase shift. In the following, we will perform the full calculations for the scattering phase shift and the spectral function.Fig. 6 shows the full scattering phase shift in normal phase at temperature T = 0, 0.2, 0.21, and 0.3 GeV and vanishing chemical potentials
$ \mu_B=\mu_I=0 $ . The full phase shift includes not only the meson part, which is controlled by the step function (16) or the crossover (20) around$\omega= $ $ M_m $ , but also a background part which starts at the threshold$ \omega_{th} = {\rm{Min}}(E^-_-+E^-_+)=2M_q $ and is independent of the meson properties, where$ E^-_\pm $ are the quasi particle energies defined in Eq. (5). Since the background part dominates the high energy region, we observe that the meson phase shifts coincide at high$ \omega $ domain in Fig. 6 and Fig. 7. It is the background part, which makes the full phase shift satisfy the Levinson's theorem (22): the phase shift starts with$ \Phi(\omega=0)=0 $ and ends with$ \Phi(\omega\to\infty)=0 $ , where in the large$ \omega $ region, the phase shift decreases and retains zero for$\omega>\omega_{{\rm max}}={\rm{Max}}(E^-_-+ $ $E^-_+)= 2\sqrt{M_q^2+\Lambda^2} $ . In the normal phase at$ \mu_I=0 $ , this has been explicitly proven [36].
Figure 6. (color online) Full scattering phase shifts
$ \Phi_m(\omega)\ (m=\pi, \sigma) $ in normal phase at T = 0, 0.2, 0.21, 0.3 GeV and$ \mu_B=\mu_I=0 $ .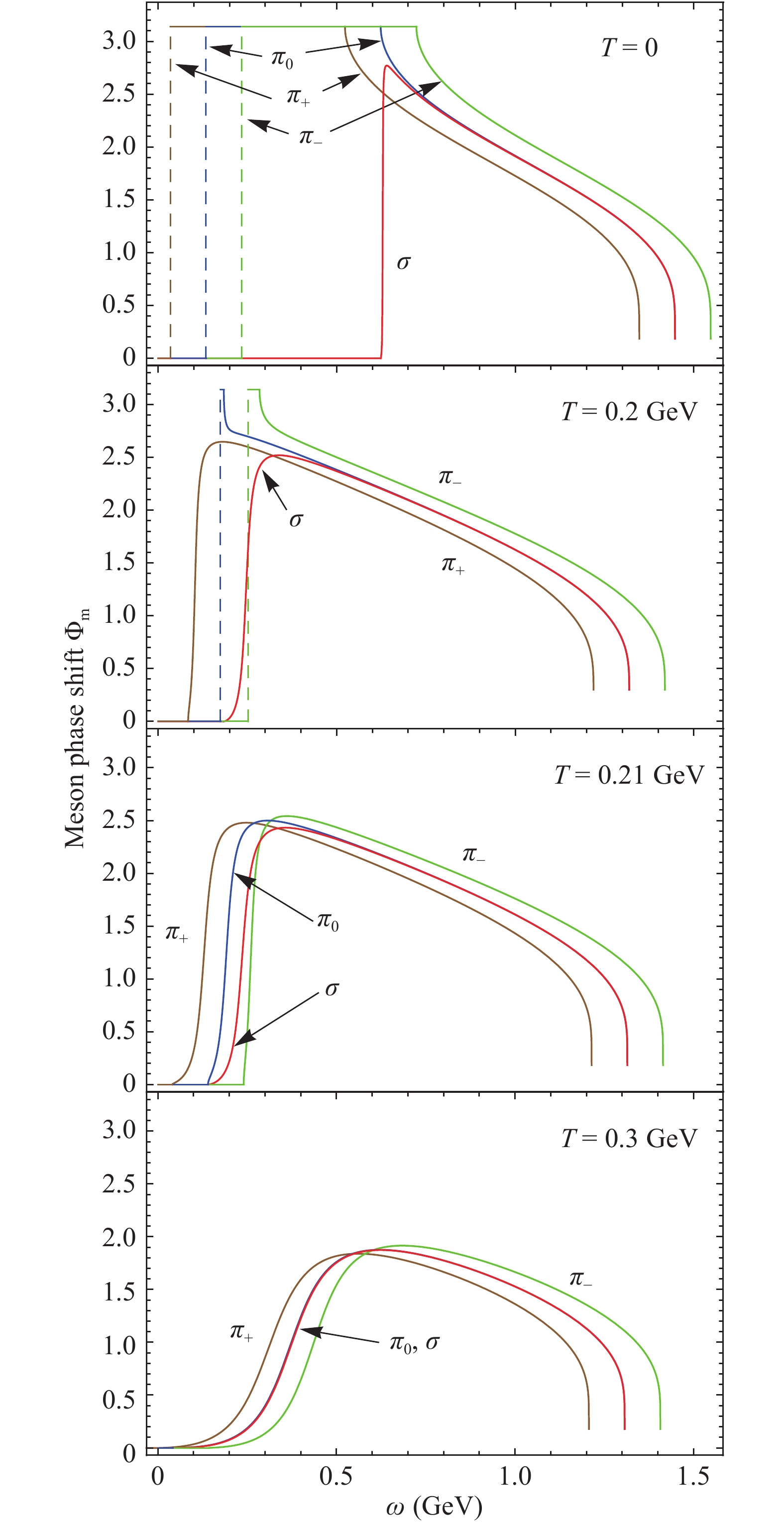
Figure 7. (color online) Full scattering phase shifts
$ \Phi_m(\omega)\ (m=\pi_+, \pi_-, \pi_0, \sigma) $ in normal phase at T = 0, 0.2, 0.21, 0.3 GeV,$ \mu_B=0 $ and$ \mu_I=0.1 $ GeV.In vacuum, with
$ T=\mu_B=\mu_I=0 $ , the degenerate pions are in a bound state, and the phase shift is given by the step function around the pion mass, after which it drops down continuously due to the background contribution. For sigma, its mass is slightly larger than two times the quark mass in the model, thus it is nearly a bound state. However, before the phase shift$ \Phi_\sigma $ reaches$ \pi $ at$ \omega=M_\sigma $ , the decreasing background component starts already at$\omega= $ $ 2M_q < M_\sigma $ . Therefore, the full phase shift can not reach$ \pi $ . Since the background contribution is meson-independent, the phase shifts for$ \pi $ and$ \sigma $ coincide at large$ \omega $ .At T = 0.2 GeV, which is below the critical temperature for the Mott phase transition of pions, the behavior of the phase shifts for pions and sigma is similar to that at T = 0. The pions are still in bound state with larger mass, their phase shift reaches
$ \pi $ at$ \omega=M_\pi $ and then decreases continuously, finally approaching zero at$ \omega_{\max} $ , due to the contribution from the background. The sigma becomes much lighter, however it remains in a resonant state with$ M_\sigma>2M_q $ . At T = 0.21 GeV, which is already larger than the critical temperature for the Mott phase transition of pions, both pions and sigma are in resonant states with$ M_\pi, \ M_\sigma >2M_q $ , and both phase shifts can not reach$ \pi $ . At T = 0.3 GeV, the chiral symmetry is well restored with a small quark mass, and all the mesons have almost the same mass. In this case, the phase shifts for pions and sigma coincide in the whole$ \omega $ region. Since the contribution from the background starts very early, the strong cancellation between the increasing meson part and the decreasing background part leads to a rather small phase shift.The full phase shifts at
$ \mu_I=0.1 $ GeV are shown in Fig. 7. Since$ \mu_I $ is less than the critical isospin chemical potential$ \mu_I=M_\pi $ , the isospin symmetry is explicitly broken, but the system remains in normal phase without pion condensate. The pions at low temperature are still in bound states, but with mass splitting. In vacuum with T = 0, the mass splitting is$ \Delta M_\pi=M_{\pi_0}-M_{\pi_+}=M_{\pi_-}-M_{\pi_0}=\mu_I $ . The continuous background contribution to$ \pi_+ $ starts at$ \omega_{th}={\rm{Min}}(E^-_-+E^-_+)=2M_q-\mu_I $ and ends at$\omega_{{\rm max}}={\rm{Max}}(E^-_-+ $ $ E^-_+)=2\sqrt{M_q^2+\Lambda^2}-\mu_I $ . Due to the meson independence of the background contribution, the phase shifts for the isospin neutral mesons$ \pi_0 $ and$ \sigma $ coincide at large$ \omega $ . After a shift of$ \omega\to\omega\pm\mu_I $ for$ \pi_+ $ and$ \pi_- $ , all the phase shifts coincide at large$ \omega $ . With increasing temperature, the$ \pi_+ $ meson first becomes a resonant state at T = 0.2 GeV and then immediately the other two pions$ \pi_0 $ and$ \pi_- $ obtain widths at T = 0.21 GeV. When the temperature is high enough, for instance at T = 0.3 GeV, all the scattering phase shifts coincide after proper shifts.In the pion superfluid phase, all four mesons are in bound or nearly bound states, as shown in Fig. 3. Since the meson
$ \pi_0 $ decouples from the other three mesons, its phase shift is similar to the one in the normal phase shown in Fig. 7. The only change is the location of the jump and the threshold for the continuous background contribution. Because of the mixing among$ \pi_+, \pi_- $ , and$ \sigma $ , one can not separately define their independent phase shifts. The whole phase shift for the three mixed mesons in pion superfluid is shown in Fig. 8 at finite isospin chemical potential and vanishing temperature and baryon chemical potential. The pion condensate dramatically changes the contribution from the continuous background. The first jump from 0 to$ \pi $ occurs at$ \omega=M_{\pi_+}=0 $ (note that$ \pi_+ $ is the Goldstone mode), and the second jump occurs at$\omega=M_{\pi_-}= $ $ 0.25 $ GeV for$ \mu_I=0.15 $ GeV (the upper panel), while$ \omega=M_\sigma=0.27 $ GeV for$ \mu_I=0.25 $ GeV (the lower panel), corresponding to the meson masses shown in Fig. 3. Before the third jump for the mode$ \sigma\ (\pi_-) $ at$ \omega=0.64\ (0.72) $ GeV, the continuous contribution from the background starts already, which partly cancels the third jump and leads to the non-monotonic behavior. The background contribution starts at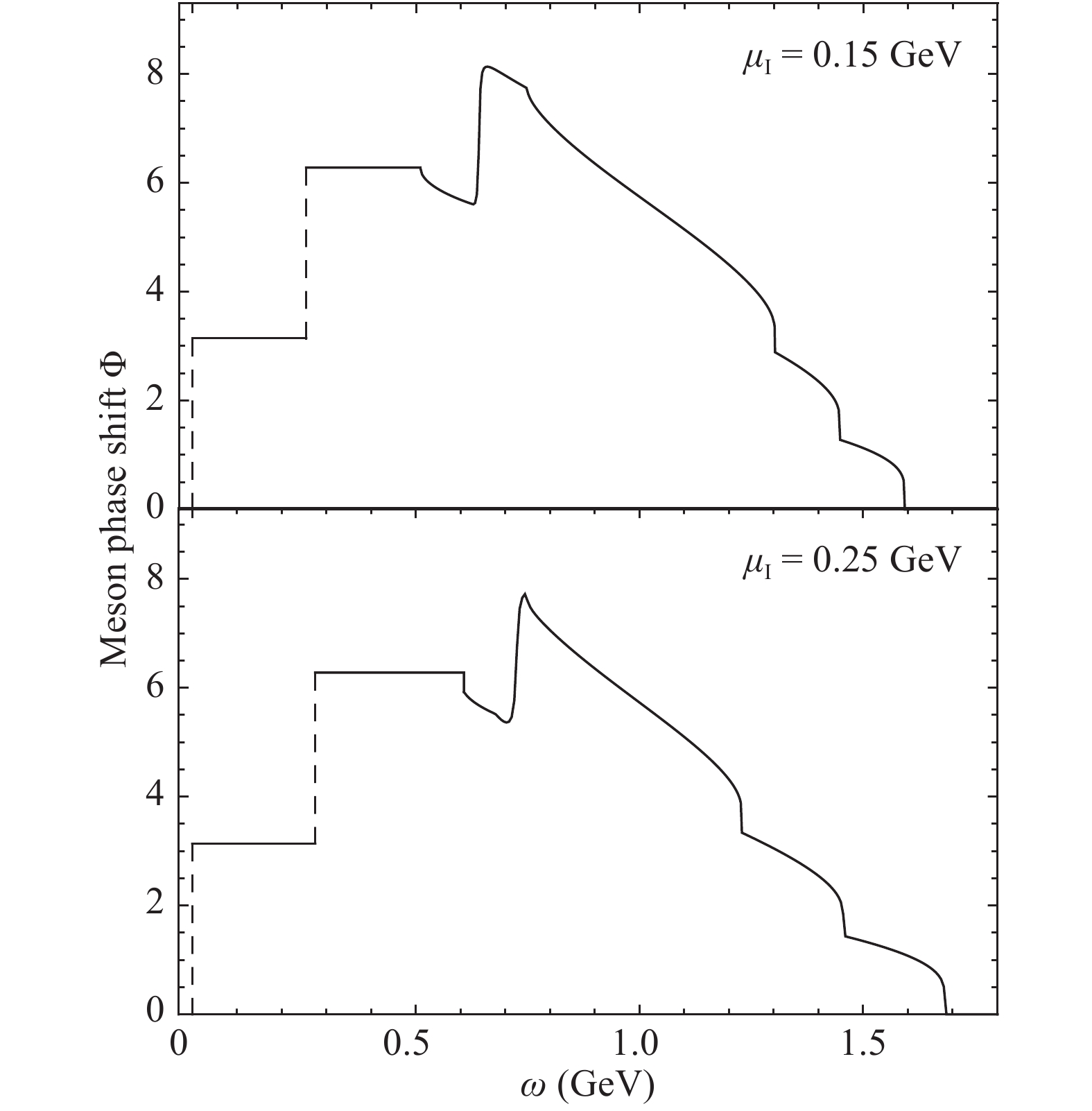
Figure 8. Whole quark-antiquark scattering phase shift
$ \Phi(\omega) $ in pion superfluid phase at$ \mu_I=0.15,\ 0.25 $ GeV and$ T=\mu_B=0 $ .$ \begin{split} {\omega _{{\rm th}}} =& {\rm{Min}}(E_ - ^ - + E_ + ^ - )\\ =& {\rm{Min}}\left( {2\sqrt {{{\left( {\sqrt {{{{k}}^2} + M_q^2} - \frac{{{\mu _I}}}{2}} \right)}^2} + 4{G^2}{{\langle \pi \rangle }^2}} } \right). \end{split} $

(23) For
$ M_q>\mu_I/2 $ , as in the upper panel of Fig. 8, the minimum is at vanishing quark momentum$ { k}=0 $ , and the threshold is$ \omega_{{\rm th}}=2\sqrt{\left(M_q-\mu_I/2\right)^2+4G^2\langle\pi\rangle^2} $ . For$ M_q < \mu_I/2 $ , as depicted in the lower panel of Fig. 8, the threshold is$ \omega_{{\rm th}}=4G\langle\pi\rangle $ , but with a finite quark momentum$ |{ k}|=\sqrt{\mu_I^2/4-M_q^2} $ . In the large$ \omega $ region of Fig. 8, the full phase shift drops down sequentially at the maximum values$ \begin{split} {\omega _{{\rm max}}} =& {\rm{Max}}(E_ - ^ \pm + E_ + ^ \pm )\\ =& \left\{ {\begin{array}{*{20}{l}} {2\sqrt {{{\left( {\sqrt {{\Lambda ^2} + M_q^2} - \frac{{{\mu _I}}}{2}} \right)}^2} + 4{G^2}{{\langle \pi \rangle }^2}} }\\ {2\sqrt {{\Lambda ^2} + M_q^2 + 4{G^2}{{\langle \pi \rangle }^2}} }\\ {2\sqrt {{{\left( {\sqrt {{\Lambda ^2} + M_q^2} + \frac{{{\mu _I}}}{2}} \right)}^2} + 4{G^2}{{\langle \pi \rangle }^2}}, } \end{array}} \right. \end{split} $

(24) which is consistent with the Levinson's theorem (22).
The meson spectral function
$ \rho_m $ in normal phase is shown in Fig. 9. In principle, any meson spectral function should contain a continuous part, due to the phase shift from the background. But, when the meson is in bound state, the contribution from the scattering phase shift is strongly suppressed by the meson pole, as indicated by the cancelation between the phase shift in the numerator and the pole in the denominator of Eq. (11). At T = 0, all three pions are in bound states, and their spectral functions are almost$ \delta $ functions located at the corresponding poles. Moreover, the contribution from the background phase shift is very small and can be neglected in comparison with the pole. Since$ \sigma $ is always in resonant state, its spectral function is already at a very small width in vacuum. However, the continuous phase shift, which is mainly on the right hand side of the pole, renders the spectral function no longer symmetric. With increasing temperature, the three pions will sequentially enter resonant states, and all the meson widths will increase continuously. When chiral symmetry is well restored, the$ \pi_0 $ and$ \sigma $ spectral functions coincide. Note that, the asymmetry of the spectral function becomes increasingly clear with increasing temperature.
Figure 9. (color online) Meson spectral functions
$ \rho_m(\omega)\ (m=\pi_+, \pi_-, \pi_0, \sigma) $ in normal phase at T = 0, 0.2, 0.21, 0.3 GeV,$ \mu_B=0 $ and$ \mu_I=0.1 $ GeV.In the pion superfluid phase, all the new meson modes
$ \pi_+, \pi_- $ , and$ \sigma $ are in or nearly in bound states, as shown in Fig. 3. Therefore, from the pole approximation, one may expect the full spectral function to be the sum of three$ \delta $ distributions at their pole positions. However, the strong mixing among them may enhance the phase shift contribution to the spectral function, especially when the enhancement is around a pole. The spectral function at$ \mu_I=0.15 $ GeV and$ T=\mu_B=0 $ is shown in Fig. 10. Considering the mixing effect on the scattering phase shift, we take here the absolute value of the spectral function in the pion superfluid. To focus on the dramatic change around the pole corresponding to the new mode$ \sigma $ at$ \omega=0.64 $ GeV, we have neglected in Fig. 10 the two$ \delta $ distributions around$ \omega=0 $ and 0.25 GeV corresponding to the Goldstone mode$ \pi_+ $ and$ \pi_- $ . The sudden drop of the scattering phase shift before the$ \sigma $ pole broadens the narrow$ \sigma $ spectrum and even splits the peak into two. This means that the pole approximation for the new mode$ \sigma $ in the pion superfluid is no longer a good approximation, even if the width shown in Fig. 3 is very narrow.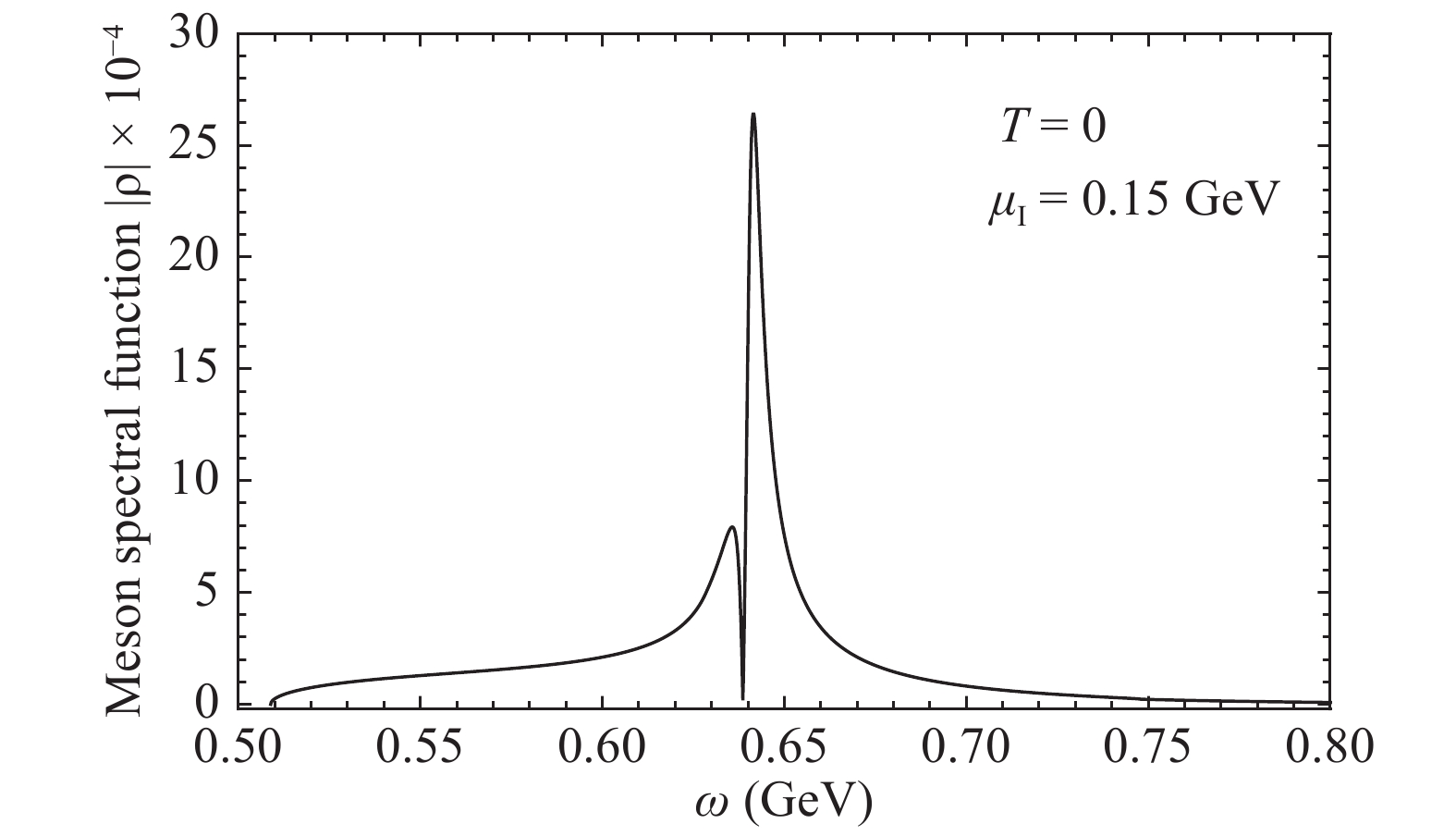
Figure 10. Meson spectral function
$ \rho(\omega) $ in the pion superfluid phase at$ \mu_I=0.15 $ GeV and$ T=\mu_B=0 $ . Only the part around the pole of the new mode$ \sigma $ is displayed, and the two$ \delta $ distributions at$ \omega=0 $ for the Goldstone mode$ \pi_+ $ and 0.25 GeV for$ \pi_- $ are not shown in the figure.We should point out that the broadening of the
$ \sigma $ spectrum in the pion superfluid phase is independent of the regularization scheme. Under the Pauli-Villars regularization scheme, one introduces the regularized quark masses$ m_i=\sqrt{m^2+a_i\Lambda^2} $ for$ i=0, 1, \cdots, N $ , and replaces$ m^2 $ in the quark energy$ E_\pm^\pm $ by$ m_i^2 $ and the momentum integration$ \int {\rm d}^3p F(E_\pm^\pm) $ by$ \int {\rm d}^3 p\sum_{i=0}^N c_iF(E^\pm_{\pm, i}) $ . The coefficients$ a_i $ and$ c_i $ are determined by constraints$ a_0=0 $ ,$ c_0=1 $ , and$ \sum_{i=0}^N c_im_i^{2L}=0 $ for$ L=0, 1, \cdots N-1 $ . Different from the hard cutoff scheme, in the Pauli-Villars scheme, the quark momentum runs formally from zero to infinity, and the divergence is removed by the cancelation among the subtraction terms. Applying the Pauli-Villars regularization scheme [28] with coupling constant G = 3.44 GeV-2, mass parameter$ \Lambda=1.127 $ GeV, and$ m_0=0.005 $ GeV. Fig. 11 depicts the spectral function around the new mode$ \sigma $ at$ \mu_I=0.15 $ GeV and$ T=\mu_B=0 $ . The wide and two-peak spectrum looks similar as in the hard cutoff scheme (Fig. 10), and it is a consequence of the mixing among the mesons in pion superfluid phase. The only difference is the location of the peak, which is around$ m_\sigma=0.48 $ GeV (the mass of new$ \sigma $ mode) in the Pauli-Villars regularization scheme and around$ m_\sigma=0.64 $ GeV in the hard cutoff scheme.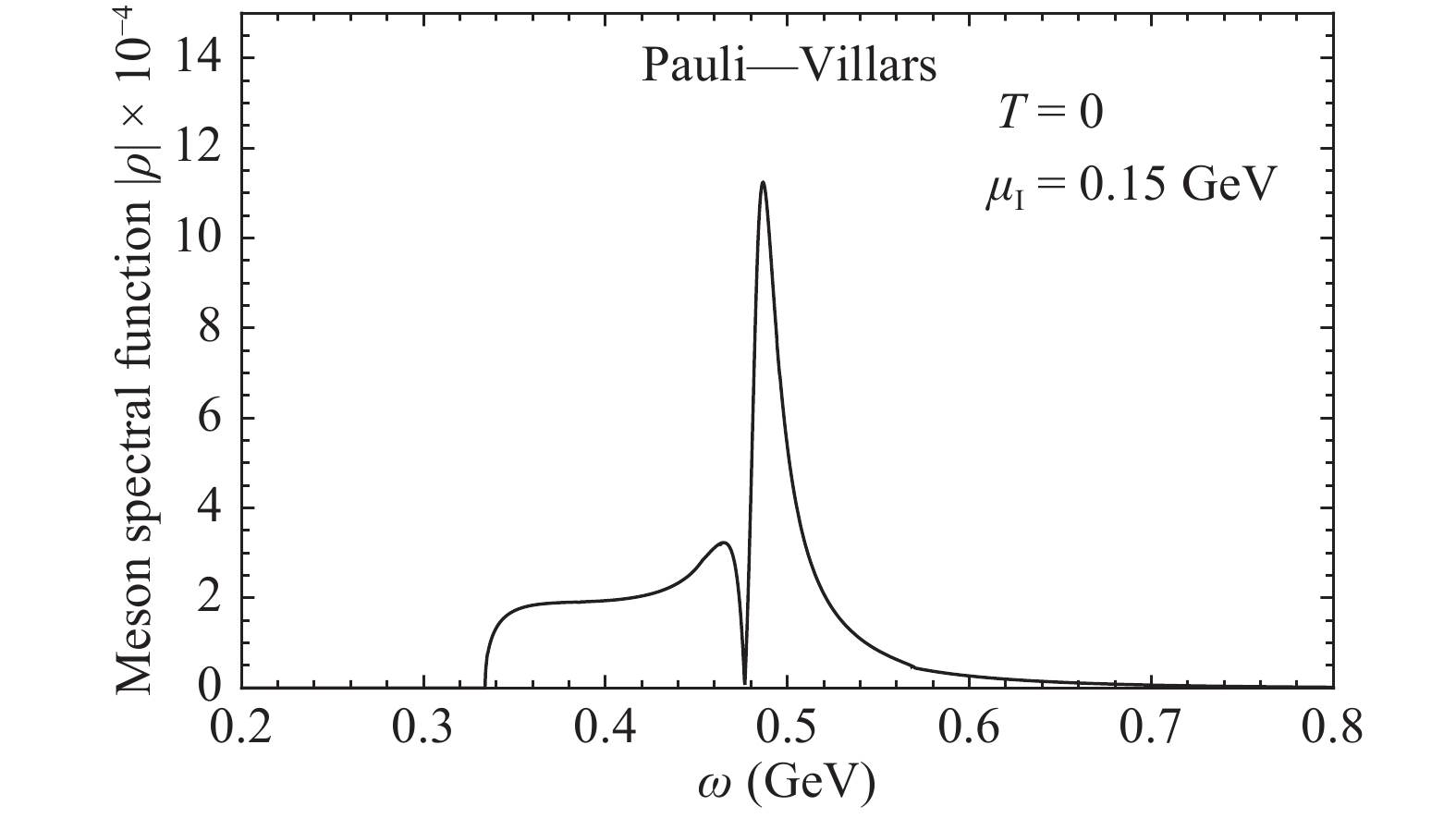
Figure 11. Meson spectral function
$ \rho(\omega) $ in the pion superfluid phase at$ \mu_I=0.15 $ GeV and$ T=\mu_B=0 $ , where only the part around the pole of the new mode$ \sigma $ is displayed as in Fig. 10. Here, we use the Pauli-Villars regularization scheme in the calculation, and the new mode$ \sigma $ has the mass$ m_\sigma=0.48 $ GeV. -
The quark-antiquark scattering phase shift is controlled by not only the meson bound or resonant state, which leads to a jump around the pole, but also the quarks as a background that is continuous and independent of meson properties. In the pion superfluid phase, the poles of the meson propagator are no longer located at the ordinary meson masses, and the phase shift is dramatically modified by meson mixing. As a result, the meson spectral function is strongly corrected when the change in the phase shift occurs around a pole. In the NJL model, the pole approximation for the new mode
$\sigma $ is no longer a good approximation due to its strong mixing with pions. The mixing in the pion superfluid enhances the width of the spectrum and even splits the peak into two. The fluctuations' contribution to the thermodynamics of the quark-meson systems at finite isospin chemical potential can be expressed in terms of the bound state and scattering phase shifts of quark-antiquark pairs, which will be reported in a future study.We all thank Prof. Pengfei Zhuang for the helpful discussion and contribution to the paper.
Quark-antiquark scattering phase shift and meson spectral function in pion superfluid
- Received Date: 2018-11-30
- Accepted Date: 2019-01-29
- Available Online: 2019-05-01
Abstract: We study the quark-antiquark scattering phase shift and meson spectral function in the pion superfluid described by the Nambu-Jona-Lasinio model. Meson mixing in the pion superfluid dramatically changes the full scattering phase shift and significantly broadens the spectral function of some collective modes.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF










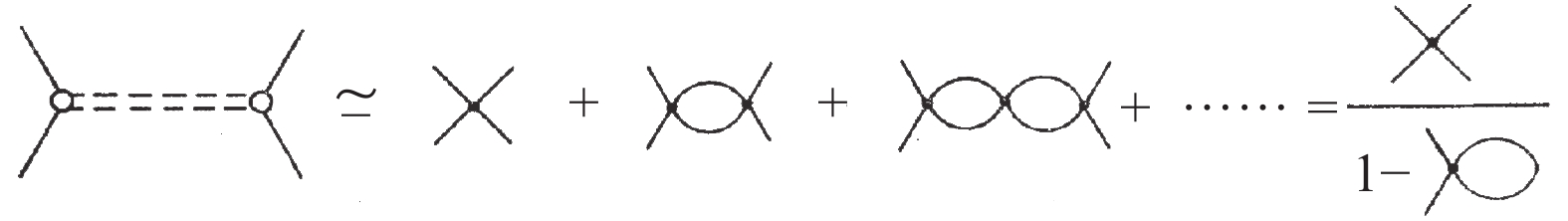



 DownLoad:
DownLoad: