-
The study of nuclear structure of neutron rich nuclei near the A = 130 mass region is fundamentally important for both nuclear physics and astrophysics. The classical N = 82 r-process waiting-point nuclide 130Cd was first identified by Kratz et al. in 1986 at CERN/ISOLDE [1]. The
$ \beta $ decay of the semi-magic nucleus 130Cd has been studied at the RIBF facility at the RIKEN Nishina Center, and the energy of the first excited 1+ state of 130In at 2120 keV was confirmed in Ref. [2]. The shell-model calculations produce the 1+ level by undervaluation of 550–750 keV [3, 4]. The obvious difference between shell model theory and experiment was improved by introducing monopole corrections to the employed Hamiltonian [5].The monopole interaction plays not only a significant role in the shell evolution owing to the monopole shift when valence nucleons occupy certain orbits [6], but also modifies the high core excitations in hole nuclei close to doubly magic 132Sn [7]. The core excitation is crucial for studying high energy levels in nuclei close to doubly magic 132Sn. For example, the 17/2+ level is well describedas a core-excited isomer with
$ T_{1/2}=630(60)ns $ in 131In [8]. Besides the core excitations, the$ \beta $ decay also plays an important role in nuclear physics, astrophysics and particle physics, and provides crucial information about the shell-model interaction and nuclear properties. The shell model calculations were performed to determine the half-lives and neutron-branching probabilities of the r-process waiting-point nuclei at the magic neutron number N = 82, and a good account of all experimentally known half-lives and Q-values is given for these N = 82 r-process waiting-point nuclei [5]. Recently, some frameworks found that the tensor force and particle-vibration coupling play important roles in the beta-decay calculations [9-11], which provide valuable improvements for further shell-model research.The doubly magic nuclei are very important for the study of nuclear structure. The prompt and delayed
$ \gamma $ -cascades in doubly magic 132Sn and its neighboring 131Sn have been studied at GAMMASPHERE using the 248Cm fission source [12]. By direct observation of single-particle states in odd-mass isotopes close to 132Sn, the doubly magic nature of 132Sn has been reconfirmed [13, 14]. As a strong signal of shell closure, the validity of the seniority has been predicted in earlier theoretical calculations and confirmed through experimental observation of 8+ seniority isomeric states in 126Pd, 128Pd and 130Cd [2, 15]. Further shell-model calculations are performed on these, and it was concluded that the shell closure persists at the neutron number N = 82 in the neutron-rich region [16]. For the neutron-rich nuclei close to 132Sn, the extended paring-plus-quadrupole model with monopole corrections (EPQQM) [17-20] provides a method to accurately describe both low-lying states and core excitations in a consistent manner [7, 16, 21].In the present work, the EPQQM are applied to the hole nuclei at the southwestern quadrant of 132Sn to study the monopole effects and core excited states by large-scale shell-model calculations. The model space consists of five neutron orbits (
$ 0g_{7/2}, 1d_{5/2}, 2s_{1/2}, 0h_{11/2}, 1d_{3/2} $ ) and four proton orbits ($ 0f_{5/2}, 1p_{3/2}, 1p_{1/2}, 0g_{9/2} $ ) with 78Ni as the closed core. In addition, two neutron orbits ($ 1f_{7/2} $ ,$ 2p_{3/2} $ ) above the N = 82 shell gap and two proton orbits ($ 0g_{7/2} $ ,$ 1d_{5/2} $ ) above the Z = 50 shell gap are included for allowing both proton and neutron core excitations. The proton (neutron) core excitations were restricted, such that only one proton (neutron) was allowed to excite across the Z = 50 (N = 82) shell gap. The single-particle energies and the two-body force strengths employed in the present work are consistent with our previous paper [21, 22]. The proton core excitations (PCE) are firstly discussed in the hole nuclei close to 132Sn. The monopole effects and neutron core excitations (NCE) will also be discussed in the present work. The$ \beta $ decays among 130Cd, 130In and 130Sn are studied with the quenching factor 0.7. The experimental data are obtained partly from the ENSDF database of NNDC On-line Data Service with cut-off dates of May 11, 2001, May 31, 2008, and May 31, 2008 for 130Sn, 130Cd, and 130In respectively. The shell-model code NUSHELLX@MSU is used for calculations [23]. -
With the proton-neutron (pn) representation, the EPQQM Hamiltonian [17-20] is given as follows:
$ \begin{split} H =& H_{\rm sp} + H_{P_0} + H_{P_2} + H_{QQ} + H_{OO} + H_{HH} + H_{\rm mc} \\ = & \displaystyle\sum_{\alpha, i} \varepsilon_a^i c_{\alpha, i}^\dagger c_{\alpha, i} - \displaystyle\frac{1}{2} \displaystyle\sum_{J=0, 2} \displaystyle\sum_{ii'} g_{J, ii'} \displaystyle\sum_{M} P^\dagger_{JM, ii'} P_{JM, ii'} \\ & - \frac{1}{2} \displaystyle\sum_{ii'} \displaystyle\frac{\chi_{2, ii'}}{b^4} \displaystyle\sum_M :Q^\dagger_{2M, ii'} Q_{2M, ii'}: \\ & - \displaystyle\frac{1}{2} \displaystyle\sum_{ii'} \displaystyle\frac{\chi_{3, ii'}}{b^6} \displaystyle\sum_M :O^\dagger_{3M, ii'} O_{3M, ii'}: \\ & - \displaystyle\frac{1}{2} \displaystyle\sum_{ii'} \displaystyle\frac{\chi_{4, ii'}}{b^8} \displaystyle\sum_M :H^\dagger_{4M, ii'} H_{4M, ii'}: \\ & + \displaystyle\sum_{a \leqslant c, ii'} k_{\rm mc}(ia, i'c) \displaystyle\sum_{JM}A^\dagger_{JM}(ia, i'c) A_{JM}(ia, i'c). \end{split} $

(1) Equation (1) includes the single-particle Hamiltonian (
$ H_{\rm sp} $ ), the J = 0 and J = 2 pairing ($ P_{0}^{\dagger}P_{0} $ and$ P_{2}^{\dagger}P_{2} $ ), the quadrupole-quadrupole ($ Q^{\dagger}Q $ ), the octupole-octupole ($ O^{\dagger}O $ ), the hexadecapole-hexadecapole ($ H^{\dagger}H $ ) terms, and the monopole corrections ($ H_{\rm mc} $ ). In the pn-representation,$ P^\dagger_{JM, ii'} $ and$ A^\dagger_{JM}(ia, i'c) $ are the pair operators, while$ Q^\dagger_{2M, ii'} $ ,$ O^\dagger_{3M, ii'} $ , and$ H^\dagger_{4M, ii'} $ are the quadrupole, octupole, and hexadecapole operators, respectively, where i (i') depict the indices for protons (neutrons). The parameters$ g_{J, ii'} $ ,$ \chi_{2, ii'} $ ,$ \chi_{3, ii'} $ ,$ \chi_{4, ii'} $ , and$ k_{\rm mc}(ia, i'c) $ are the corresponding force strengths, and b is the harmonic-oscillator range parameter. The two-body force strengths that suit the present particle-hole model space are listed in Table 1.ii' $ g_{0,ii'} $ 

$ g_{2,ii'} $ 

$ \chi_{2,ii'} $ 

$ \chi_{3,ii'} $ 

$ \chi_{4,ii'} $ 

pp 0.136 0.038 0.102 0.032 0.0015 nn 0.117 0.035 0.140 0.004 0.0008 pn 0 0 0.082 0 0.0009 Table 1. Two-body force strengths (in MeV) used in the present calculation.
In our previous papers, the monopole corrections of
$ M_c1\equiv k_{\rm mc}(\nu h_{11/2}, \nu f_{7/2})=0.52 $ MeV and$M_c2\equiv k_{\rm mc}(\pi g_{9/2}, $ $ \nu h_{11/2})= -0.4 $ MeV are employed to modify the N = 82 shell gap. The$ M_c2 $ is also necessary for obtaining the right ground state of 129Cd [22]. The$ M_c3\!\equiv\! k_{\rm mc}(\pi g_{9/2}, \nu g_{7/2})\!=\! $ −1.0 MeV is the new monopole correction introduced in the present work. As shown in Fig. 1, adding the monopole corrections of$ M_c1 $ and$ M_c2 $ has no influence on low-lying levels of 130Sn and 130Cd, while the$ M_c2 $ shifts up the 3+, 5+ and 1+ levels in 130In. The fact that the datum 1+ level at 2.120 MeV is much lower than the theoretical value in the present work is the experimental base for adding$ M_c3 $ . The orbit$ \pi g_{9/2} $ ($ \nu g_{7/2} $ ) is full of particles in the configuration of low-lying levels at 130Sn (130Cd), however the$ M_c3\equiv$ $ k_{\rm mc}(\pi g_{9/2}, \nu g_{7/2}) $ has effects only when the orbits$ \pi g_{9/2} $ and$ \nu g_{7/2} $ are both lacking particles, as in the 1+ level with a configuration of$ \pi g^{-1}_{9/2} \nu g^{-1}_{7/2} $ in 130In. Hence, the Hamiltonian including$ M_c3 $ has no effects on low-lying levels of 130Sn and 130Cd, however it significantly shifts down the 1+ level in 130In. This represents a neat reduction of the theoretical value and the corresponding datum. Unlike the addition of$ M_c1 $ and$ M_c2 $ to modify high core-excitations [7], the purpose of adding$ M_c3 $ is not for core excitation, as no effect was found on core excitations mentioned in the present work by adding$ M_c3 $ .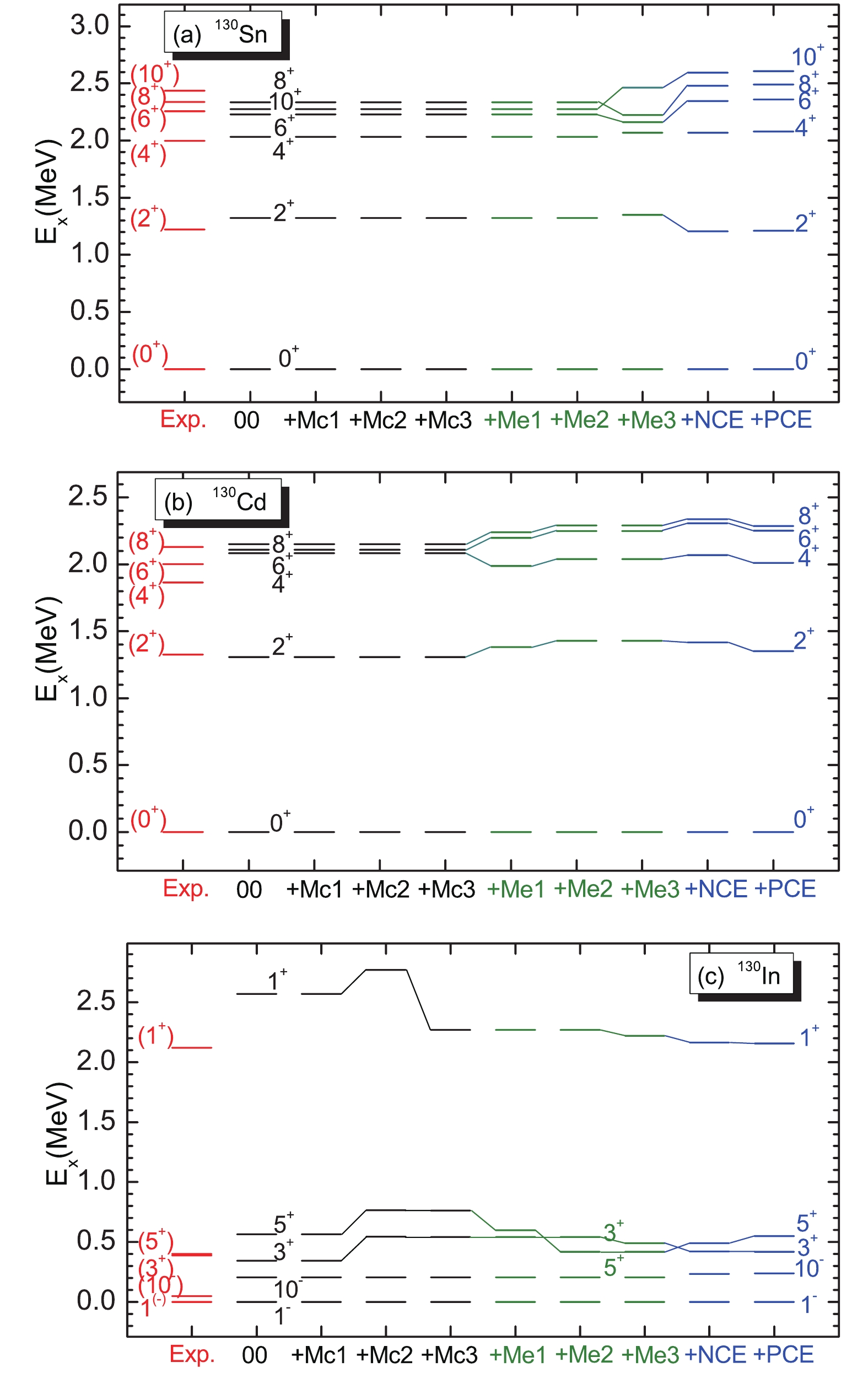
Figure 1. (color online) Effects of monopole corrections (
$ M_c $ ), matrix element ($ M_e $ ) modifications and allowing the neutron (proton) core excitations (NCE & PCE) in the low-lying levels of hole nuclei 130Sn, 130Cd and 130In in comparison with corresponding data. The$ M_c $ and$ M_e $ are added to the initial Hamiltonian (00) one by one, and their definition and value of the$ M_c $ and$ M_e $ are given in the text.The matrix element of J = 4 in the proton orbit
$ g_{9/2} $ is increased by –0.18 MeV to obtain the right order of 6+ and 8+ levels in 128Pd [16]. For simplified notation, this modification is marked as$ M_e1 $ . As shown in Fig. 1(a), although the$ M_e1 $ has no effects on the low-lying levels of 130Sn, it breaks the degeneracy in 4+, 6+, and 8+ levels of 130Cd, and also shifts down the 5+ level in 130In to close to the corresponding datum in the experiment. In the research of the A = 129 hole nuclei near 132Sn, two zero-value matrix elements were given new values in the Hamiltonian (marked as$ M_e2 $ ),$ \left< p_{1/2}, g_{9/2}, |V| p_{1/2}, g_{9/2}, \right>_{J=4}^{\pi} = $ 0.32 and$\left< p_{1/2}, g_{9/2},\right. $ $ \left.|V| p_{1/2}, g_{9/2}, \right> _{J=5}^{\pi}= -0.22 $ . The$ M_e2 $ has no effects on the low-lying levels of 130Sn, and little effect on 130Cd. It has obvious effects on shifting down the 5+ level in 130In. During the study of Sb isotopes in the particle-hole nuclei near 132Sn, the new modification is needed in the three interaction matrix elements (marked as$ M_e3 $ ) by the amount of$ \Delta \langle h_{11/2}, h_{11/2}|V|h_{11/2}, h_{11/2}\rangle^{\nu}= $ $-0.15, -0.15, +0.2 $ (MeV) for J = 6, 8, 10, respectively. Although the$ M_e3 $ is used in the northeastern quadrant of 132Sn [24], it also works well in the present hole-nuclei region. As shown in Fig. 1(a), the$ M_e3 $ not only breaks the degeneracy in 6+, 8+ and 10+ levels in 130Sn, but also gives the consistent order with experimental data.
HTML
1. Introduction
2. The Hamiltonian and modifications
-
The core excitations depict one of most important physics effects in the hole-nuclei region near 132Sn. In low-lying levels of 130Sn (Fig. 1(a)), including neutron core-excitations, the 2+ level is shifted down, and the 6+, 8+, and 10+ levels are lifted up. The model space allowing neutron core excitations keeps the level order consistent with the experimental (3+) and (5+) states in 130In. After adding these modifications to the Hamiltonian, we study the data in 130In [2] by the model space allowing both proton and neutron core excitations. As shown in Fig. 2(a), the low-lying states are accurately described by the new Hamiltonian with
$ M_c3 $ and$ M_e3 $ modifications. The 1+ level with 2.120 MeV is the main final state for the$ \beta $ decay of 130Cd that occurs in about 70% of all decays [2], and the theoretical one at 2.155 MeV is a perfect reproduction with the main configuration of$ \pi g^{-1}_{9/2} \nu g^{-1}_{7/2} $ .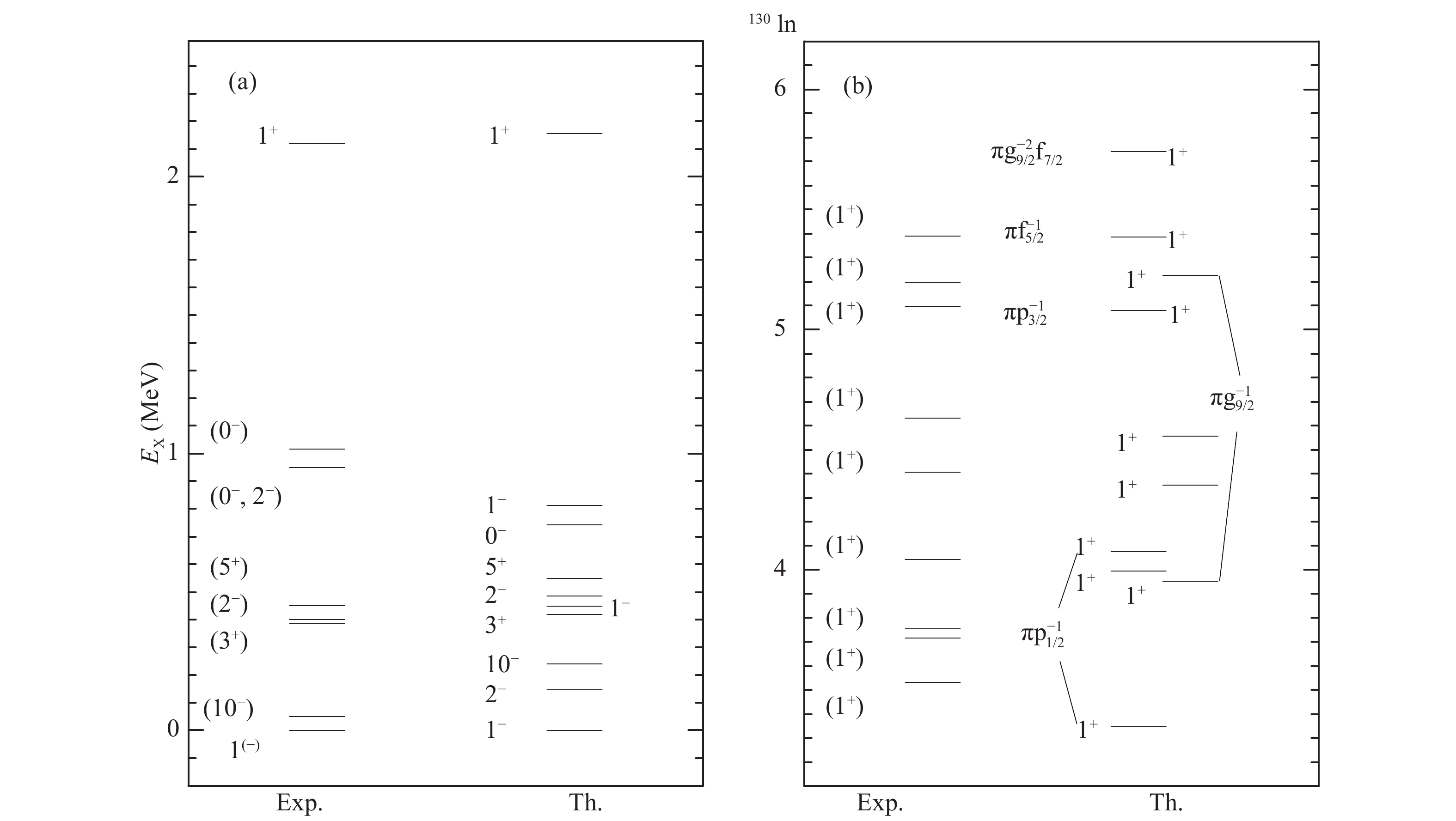
Figure 2. Level scheme of 130In under the Hamiltonian including
$ M_c3 $ and$ M_e3 $ in comparison with corresponding data. The proton configurations of 1+ levels in part (b) are provided. The experimental data are obtained from the ENSDF database of NNDC On-line Data Service with cut-off dates of May 11, 2001, May 31, 2008, and May 31, 2008 for 130Sn, 130Cd, and 130In respectively, with the exception of (2–), (1–, 2–), (0–) and (1+) levels in the energy interval 3.5–4.1 MeV [2].The 1+ levels exhibited in Fig. 2(b) are the core excitations. With the exception of the highest one near 6 MeV, which is the proton core excited state across the Z = 50 shell gap with configuration of
$ \pi g^{-2}_{9/2} g_{7/2} \nu d^{-1}_{3/2} $ , the others are the neutron core excitations across the N = 82 shell gap. Their main configurations are$ \pi g^{-1}_{9/2} \nu h^{-1}_{11/2}d^{-1}_{3/2} f_{7/2} $ ,$ \pi p^{-1}_{1/2} \nu h^{-2}_{11/2} f_{7/2} $ ,$ \pi p^{-1}_{3/2} \nu h^{-2}_{11/2} f_{7/2} $ , and$ \pi f^{-1}_{5/2} \nu h^{-2}_{11/2} f_{7/2} $ . Their proton configurations are marked in Fig. 2(b) for the purposes of differentiating between them. Fig. 3 shows the lowest core-excitations in 130In. The NCE states lie lower with the energy interval 2.0−4.1 MeV. The latest observed decays with the energy interval 3.5−4.3 MeV have a large overlap. The PCE states have the energy interval of 4.5−6.5 MeV, which spans the energy interval 5.2−5.6 MeV of the newly observed decays in 130In.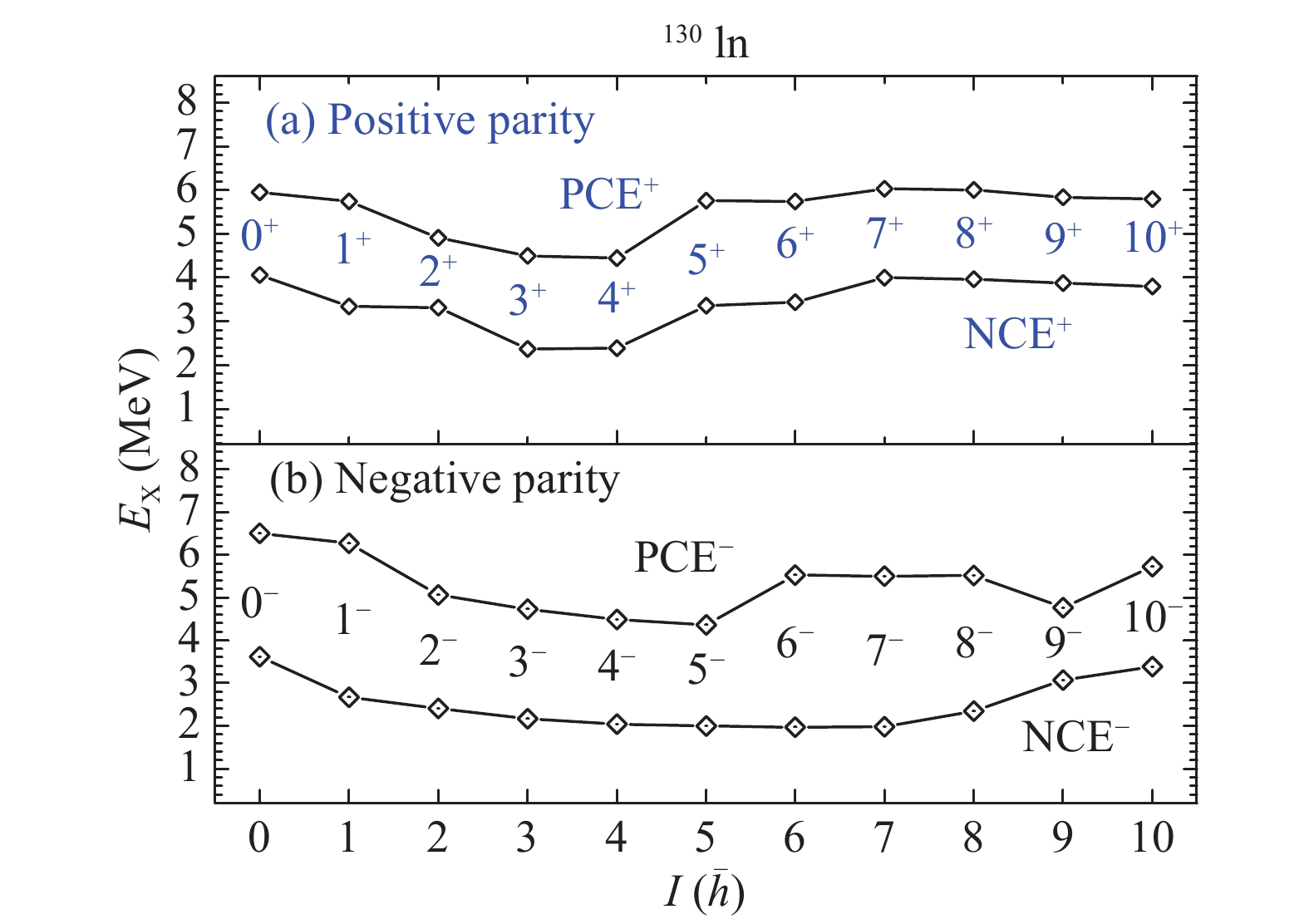
Figure 3. (color online) Neutron (proton) core-excited states in 130In. "I" is used to mark the level spin.
For the positive parity states of 130In in Fig. 3(a), the ones of NCE from 0+ to 7+ have the main configuration of
$ \pi p^{-1}_{1/2} \nu h^{-2}_{11/2} f_{7/2} $ , and the last three levels of 8+, 9+, and 10+ have the main configuration of$ \pi g^{-1}_{9/2} \nu h^{-1}_{11/2} d^{-1}_{3/2}f_{7/2} $ , while the 9+ and 10+ levels at 3.883 and 3.804 MeV, respectively, depict the yrast state in theory. The higher positive parity states of PCE also have two main configurations, the$ \pi p^{-1}_{1/2}g^{-1}_{9/2}g_{7/2} \nu h^{-1}_{11/2} $ is for the levels of 0+, 5+, 8+, 9+, and 10+, and the$ \pi g^{-2}_{9/2}g_{7/2} \nu d^{-1}_{3/2} $ is for the last six levels. The negative parity states of NCE only have a single configuration$ \pi g^{-1}_{9/2} \nu h^{-2}_{11/2} f_{7/2} $ , and the PCE with negative parity have the main configuration of$ \pi g^{-2}_{9/2}g_{7/2} \nu h^{-1}_{11/2} $ , except for the 1− level with configuration of$ \pi p^{-1}_{1/2}g^{-1}_{9/2}g_{7/2} \nu d^{-1}_{3/2} $ .As shown in Fig. 4, the energy interval in 130Sn is 3.8–5.4 MeV (5.7–7.7 MeV) for neutron (proton) core excitations, which is obviously higher than the one in 130In. For the neutron core excitations, the positive parity states have the main configuration of
$ \nu h^{-3}_{11/2} f_{7/2} $ , while the 8+ level is the lowest one with 3.824 MeV and the 10+ state is the highest one with 4.966 MeV. The negative parity levels have the main configuration of$ \nu h^{-2}_{11/2}d^{-1}_{3/2} f_{7/2} $ , while the lowest one is the 4− level at 3.793 MeV and the highest one is the 8− level at 5.253 MeV. The 5+, 7+, 9+, 0−, 1−, and 10− levels are the yrast states in theory. For the proton core excitations, the positive parity ones have the main configuration of$ \pi g^{-1}_{9/2} g_{7/2} \nu h^{-2}_{11/2} $ , while the 0+ (6+) level is the highest (lowest) one with 7.668 (5.765) MeV. The negative parity states of proton core excitations have two main configurations, which are$ \pi g^{-1}_{9/2} g_{7/2} \nu h^{-2}_{11/2} $ is for the levels of 0−, 7−, 8−, 9− and 10− and$ \pi p^{-1}_{1/2} g_{7/2} \nu h^{-1}_{11/2}d^{-1}_{3/2} $ for the levels from 1− to 6−.
Figure 4. (color online) Neutron (proton) core-excited states in 130Sn. "I" is used to mark the level spin.
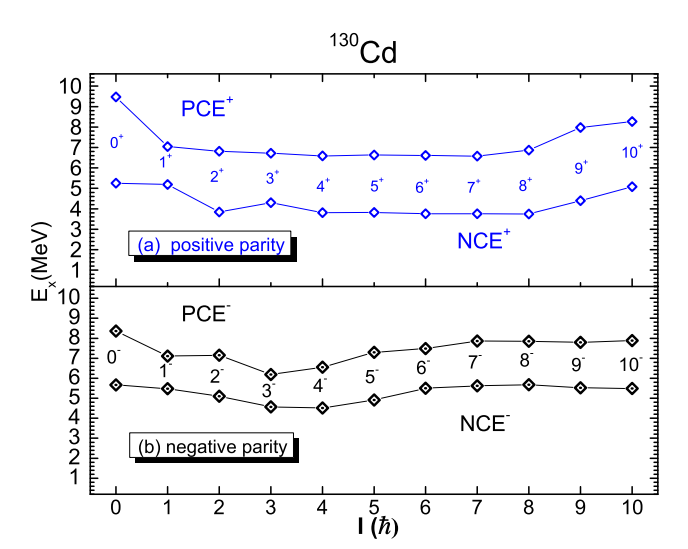
The proton core excitations in 130Cd (Fig. 5) have a much higher energy interval (6.2–9.5 MeV), where the main configuration is
$ \pi g^{-3}_{9/2} g_{7/2} $ for the positive parity and$ \pi p^{-1}_{1/2} g^{-2}_{9/2} g_{7/2} $ for the negative. The energy interval of neutron excitations is 3.7–5.7 MeV, while their main configuration is$ \pi g^{-2}_{9/2} \nu h^{-1}_{11/2} f_{7/2} $ for the positive parity levels. The negative parity of neutron core excitations have two main configurations,$ \pi g^{-2}_{9/2} \nu d^{-1}_{3/2} f_{7/2} $ for the levels from 2− to 5− and$ \pi p^{-1}_{1/2}g^{-1}_{9/2} \nu h^{-1}_{11/2} f_{7/2} $ for the others. The ten neutron core excitations of 3+, 5+, 7+, 9+, 10+, 0−, 1−, 8−, 9−, and 10− are the yrast states in theory.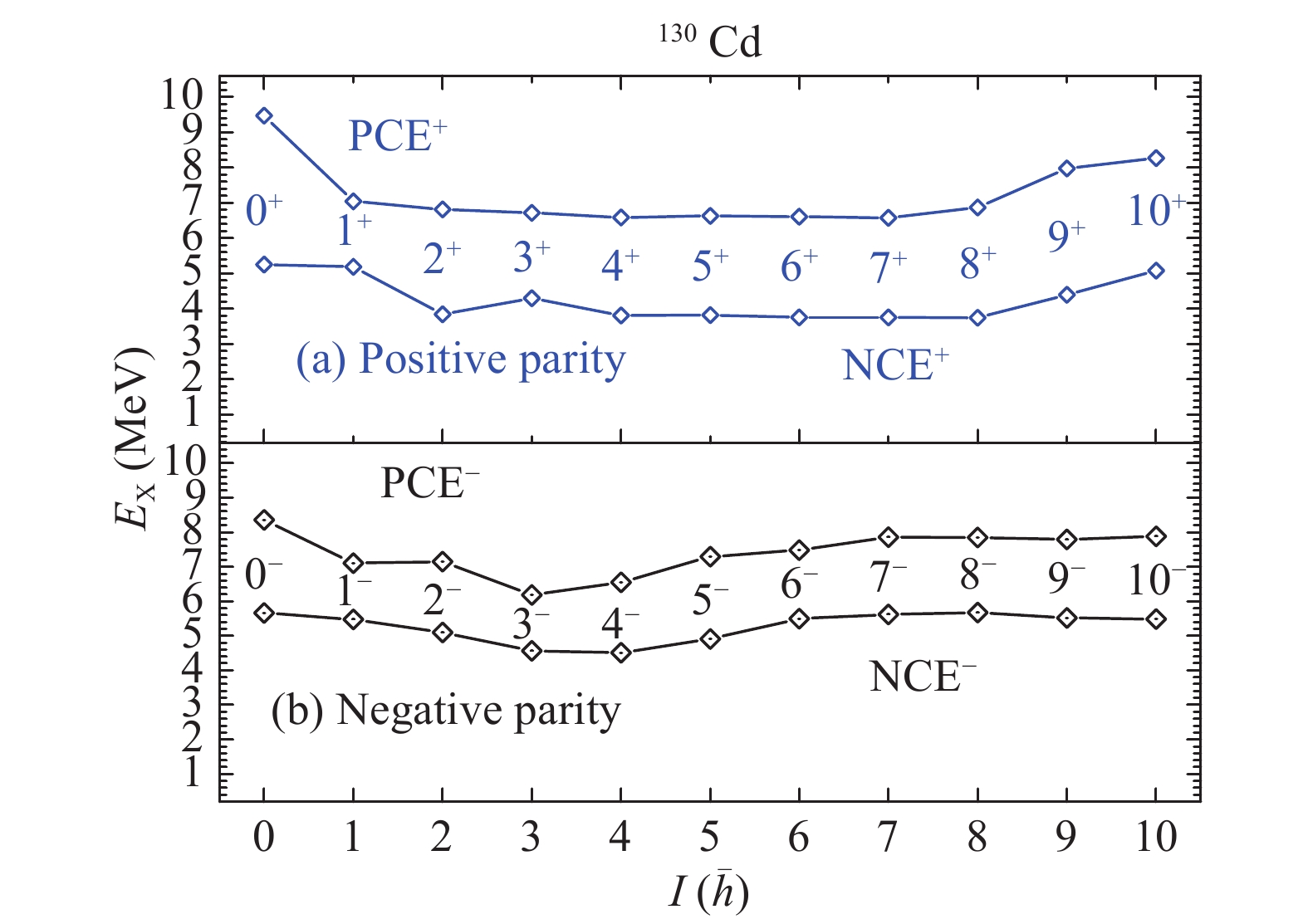
Figure 5. (color online) Neutron (proton) core-excited states in 130Cd. "I" is used to mark the level spin.
In contrast to electromagnetic transitions,
$ \beta $ decay accompanies charge-changing from one nucleus to another. The study of$ \beta $ decay shows the nature of both the weak interaction and the structure of nuclear wave functions. The$ \beta $ decays among the A = 130 nuclei of 130Cd, 130In and 130Sn are studied in the present work (Fig. 6). The quenching factor is selected as 0.7, and the theoretical results provide a good performance. The properties of the$ \beta $ decay in the classical N = 82 waiting point nucleus 130Cd play an important role in the calculations of the astrophysical r-process.
Figure 6. (color online)
$ \beta $ decay among the A = 130 nuclei of 130Cd, 130In and 130Sn. The effects of modifications$ M_c $ and$ M_e $ (added to the Hamiltonian one by one) on the value of the reduced Gamow-Teller transition probability (B(GT)) to (1+) with 2.120 MeV. Experimental data are obtained from the ENSDF database of NNDC On-line Data Service with cut-off dates of May 11, 2001, May 31, 2008, and May 31, 2008 for 130Sn, 130Cd, and 130In respectively.The Gamow-Teller transition from the (0+) ground state of 130Cd to the 1+ level with 2.120 MeV in 130In dominates about 70% of the
$ \beta $ decays in 130Cd. If only GT transitions are considered, this branching ratio is larger than 99% in the present work. The half-life of 130Cd is 36 ms, also dominated by this GT transition. The jj45pna interaction is used for comparison, and is in approximate accordance with our results. The contribution of the first forbidden transition is small, about 13% [25]. As shown in Fig. 6(a), by comparing with corresponded datum from ground state of 130Cd to the 1+ level with 2.120MeV in 130In, the theoretical logft value of the GT transition is smaller with the normal quenching factor (0.7). When 0.4 is used as quenching factor, the half-life of 130Cd will be efficiently reproduced. By Using the newly developed fully self-consistent proton-neutron quasiparticle random phase approximation (RQRPA), the half-life of 130Cd was well reproduced in comparison with experimental datum [26, 27].Note that the ground state of 130Cd is dominated by
$ \pi g^{-2}_{9/2} $ (about 80%), while the 1+ level with 2.120 MeV in 130In is dominated by$ \pi g^{-1}_{9/2} \nu g^{-1}_{7/2} $ . The GT transition is rather strong between these two configurations, so the logft value becomes rather small, and is very close to the super-allowed transition. Apart from this exception, the decay to the other 1+ states in 130In becomes more difficult with larger logft in both experiment and theory.By adding the above modifications to the Hamiltonian one by one, the effects of them on B(GT) to (1+) at 2.120 MeV are exhibited in Fig. 6(b). The three monopole corrections of
$ M_c1 $ ,$ M_c2 $ , and$ M_c3 $ have no effects on this B(GT), while the matrix modifications of$ M_e1 $ and$ M_e2 $ obviously exert an influence on it. The model space allowing neutron core excitations also decreases the value of B(GT) in Fig. 6. As a mother nucleus, the$ \beta $ decay from 130In forms the semi-magic nucleus 130Sn. Although the 9− and 2− states in 130Sn are located relatively high, there is less possibility for them to be core excitation states by comparing with the present calculations. More studies are expected to clarify the contribution of core excitation on the$ \beta $ decay in the southwestern quadrant of 132Sn.
-
In summary, the core excitations and the monopole effects are discussed in the neutron-rich hole nuclei close to 132Sn by large-scale shell-model calculations. The model space includes five neutron orbits (
$0g_{7/2}, 1d_{5/2}, $ $ 2s_{1/2}, 0h_{11/2}, 1d_{3/2} $ ) and four proton orbits ($0f_{5/2}, 1p_{3/2}, $ $ 1p_{1/2}, 0g_{9/2} $ ), while two neutron orbits ($ 1f_{7/2} $ ,$ 2p_{3/2} $ ) above the N = 82 shell gap and two proton orbits ($ 0g_{7/2} $ ,$ 1d_{5/2} $ ) above the Z = 50 shell gap are considered for allowing both proton and neutron core excitations. The main conclusions in the present work are the following.The monopole corrections and matrix element modifications employed in our previous papers are checked carefully by the odd-odd nucleus 130In and even-even nuclei of 130Sn and 130Cd. The new monopole effect of
$ M_c3 $ is found between the proton orbit$ g_{9/2} $ and neutron orbit$ g_{7/2} $ in hole-nuclei close to doubly magic 132Sn. The energy intervals of proton and neutron core excitations in 130In lie in the energy range of 4.5−6.5 MeV and 2.0−4.1 MeV, respectively. Neutron core excitations the high energy yrast states are found theoretically in the A = 130 nuclei of 130In, 130Sn and 130Cd. The$ \beta $ decay among these A = 130 nuclei are calculated in the present work. The dominant$ \beta $ decays in 130Cd, the Gamow-Teller transition to the 1+ level with 2.120 MeV in 130In is discussed in detail.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: