-
It is believed that Galactic cosmic rays (GCRs) with a wide energy range up to a few PeV originate from supernova remnants (SNRs) [1, 2]. Observationally, the entire spectrum of CRs observed from the Earth can be described by a rigidity-dependent power law with a spectral index of
$ s\approx 2.7 $ below the “knee” energy ($ \sim 10^{15.5} \rm eV $ ) [3]. Moreover, GCRs components can have different spectral indices$ s_i $ , i.e.,$ N_i(E)\propto E^{-s_i} $ , and cut-off energies. Particularly, recent data from numerous experiments show that the shape of the CR proton spectrum is not a single power law below the “knee”, and the same anomaly is observed for the helium spectrum. The PAMELA observations indicate that the proton spectral index$ s_{{\rm p}} \approx 2.85\; (2.67) $ below (above)$ 232_{-30}^{+35} $ GV, and the helium spectral index$ s_{{\rm He}} \approx 2.776\; (2.477) $ below (above)$ 243_{-31}^{+27} $ GV [4]. The AMS-02 observations show that$ s_{{\rm p}} \approx 2.849\; (2.716) $ below (above) 336 GV for protons [5] and$ s_{{\rm He}} \approx 2.780\; (2.661) $ below (above) 245 GV for helium nuclei [6]. From these measurements, two general conclusions can be deducted, namely that the CR spectra harden remarkably at a characteristic transition rigidity, and that the spectrum of CR helium nuclei is harder than that of CR protons.The spectral hardening behavior has been studied extensively, and many models have been proposed. In general, theoretical models that describe the hardening fall into three classes: acceleration mechanisms, properties of CR sources, and propagation effects. With respect to acceleration mechanism, it has been proposed that the spectral hardening may arise from non-linear diffusive shock acceleration (NLDSA), and hardening of the cosmic-ray spectrum mainly results from modification of gas flow in the shock precursor by the cosmic-ray pressure, and the hard energy spectrum of particles accelerated by reverse shocks makes the concavity more pronounced [7]. The higher the efficiency of the CR acceleration, the more pronounced is the concavity. For large efficiencies, the spectrum above a few GeV becomes as flat as
$ \propto $ $ E^{-1.5} $ . However, observations of$ \gamma $ -rays in SNRs both in GeV [8] and in TeV [9] bands demonstrate a considerable dispersion in the spectral index. Based on these observations, the source spectrum was assumed to have a slope with some distribution, such that the hardening can be reproduced [10]. Moreover, a possible physical explanation of the observed dispersion was provided [11]. Even when the CR spectrum at a source exhibits a simple power-law form, the superposition of two classes of CR sources [12] or nearby SNRs [13] can likewise be responsible for the observed spectral hardening. In addition, a recent crucial finding on GCRs indicates that the P/He ratio decreases steadily with rigidity [4, 6]. Therefore, the two-component particle distributions were proposed for the spectral anomaly [14]. This simple explanation provides a common interpretation for the single hardening spectra of protons and helium nuclei and the P/He ratio anomaly. Spectral hardening may also be attributed to the combination of cosmic-ray-induced turbulence and background turbulence [15, 16].The explanations mentioned above are based on the assumption that SNRs are the main contributors to CRs. Since CRs gain energy by repeatedly passing back and forth between upstream and downstream plasmas, the dynamical reaction of the accelerated particles must be taken into account. The model of diffusive shock acceleration (DSA) was improved by coupling the accelerated particle population, shock structure, and electromagnetic fluctuations, resulting in NLDSA (see Refs. [17-19] for recent reviews on the SNR-CR paradigm). In order to explain the shape of the cutoff at some maximum momentum, Caprioli [19] showed that the highest energy CRs escape from the upstream free escape boundary into the interstellar medium (ISM). Most of the shock-accelerated CRs, by energy content as well as number, are carried into the downstream region of the SNR. Bell [20] examined the fate of low energy CRs as they are advected downstream, and found that CRs below the “knee” can be divided into two populations, one consists of accelerated particles with energies above 200 GeV, which are released upstream by the SNR, and another includes the accelerated particles with energies below 200 GeV, which are advected into the interior of the SNR during expansion and then released from the SNR at the end of its life. We will assume this scenario into our following calculations, and propose another possible explanation of the spectral hardening of CR protons and helium nuclei with energies of approximately 200 GeV.
Throughout this paper, it is assumed that GCRs mainly originate from one single source or from one type of standard sources. Wherever the origin of GCRs is mentioned, it is referred to SNRs unless otherwise stated. This paper is organized as follows. In Section 2, we provide a brief review on the NLDSA model and the “two-populations” scenario. The results and discussion are given in Sections 3 and 4, respectively.
-
A full description of the revised NLDSA model can be found in Refs. [18, 19]. Here, we only provide a brief summary of the key ingredients for the sake of completeness.
In the shock frame, coordinate x is directed the shock from upstream to downstream with a shock located at
$ x = 0 $ . Physical quantities measured at upstream infinity, immediate upstream of the shock, and downstream are labeled with subscripts 0, 1, and 2, respectively.$ \tilde{u} = u+u_{{\rm A}} $ , where u is the plasma velocity, and$ u_{{\rm A}} $ is the Alfvén velocity. In this case, the distribution function of the ith accelerated particles$ f_{i} $ takes the form${f_{i}}(x,p) = {f_{{\rm{sh}},{i}}}(p){{\rm e}^{ - \int_x^0 {\rm d} x'\frac{{\tilde u(x')}}{{{\kappa _i}(x',p)}}}}\left[ {1 - \frac{{{W_i}(x,p)}}{{{W_{i,0}}(p)}}} \right],$

(1) where
${W_i}(x,p) = \int_x^0 {\rm d} x'\frac{{{u_0}}}{{{\kappa _i}(x',p)}}\exp \left( {\int_{x'}^0 {\rm d} x''\frac{{\tilde u(x'')}}{{{\kappa _i}(x'',p)}}} \right),$

(2) and
$ W_{i,0}(p) = W_{i}(p)|_{x = x_0} $ ,$ f_{{\rm {sh}}, i}(p) = f_{{\rm {sh}},{i}}(0, p) $ is the particle spectrum at the shock location, which is${f_{{\rm{sh}},{{i}}}}(p) = \frac{{{\eta _{{i}}}{n_0}{q_{{\rm{p}},{{i}}}}(p)}}{{4\pi p_{{\rm{inj}},{{i}}}^3}}\exp [ - \Lambda (p,{p_{{\rm{inj}},{{i}}}})]$

(3) with
$\Lambda (p,{p_{{\rm{inj}},{{i}}}}) = \int_{{p_{{\rm{inj}},{{i}}}}}^p {\frac{{{\rm d}p'}}{{p'}}} {q_{{\rm{p}},{{i}}}}(p')\left[ {{U_{{\rm{p}},{{i}}}}(p') + \frac{1}{{{W_{i,0}}(p')}}} \right],$

(4) where
$ \eta_{i} $ is the fraction of the ith particles crossing the shock injected in the acceleration process,$ n_{0} $ is upstream mass density,$ p_{{\rm inj}, {i}}\propto \xi_{\rm inj} $ is the injection momentum,$ \xi_{\rm inj} $ is the injection parameter,$ U_{{\rm p}, i}(p') $ is the mean velocity effectively felt by a particle with momentum p in the upstream region normalized to$ u_{0} $ , and$ q_{{\rm p}, i}(p') $ is the spectral slope relevant for a particle with momentum p.The non-linear effects of NLDSA can be summarized as follows:
(i) The dynamical reaction of accelerated particles. The effect was described in Ref. [21], where the slowing down of the upstream flow is significant due to the positive feedback of the pressure of accelerated particles or CRs. Thus, the normalized pressure of the accelerated particles
$ P_{{\rm CR}}(x) $ with a plasma density$ \rho_{0} $ can be estimated as${P_{{\rm{CR}}}}(x) = \frac{{4\pi }}{{3{\rho _0}u_0^2}}\sum\limits_i {\int_{{p_{{\rm{inj}},i}}}^\infty {\rm d} } p\;{p^3}u(x){f_i}(x,p).$

(5) (ii) The magnetic field amplification acts as a self-regulating mechanism of the acceleration process. This arises from the streaming instability of plasma flow. The normalized pressure of the magnetic field can be expressed as
${P_{\rm{B}}}(x) = \frac{2}{{25}}\frac{{{{[1 - U{{(x)}^{5/4}}]}^2}}}{{U{{(x)}^{3/2}}}},$

(6) where
$ U(x) = \tilde{u}(x)/u_{0} $ is the normalized fluid velocity for a particle. In the absence of a consistent kinetic theory for the CR-magnetic field interplay in the precursor, a constant magnetic field in the upstream be assumed, whose strength is given by the saturation at the shock from Eq. (6).The temporal evolutions of the radius and velocity of the SNR shock are derived at two stages: [22]
(1) Ejecta-dominated stage (
$ \tau = t/T_{\rm ST} \leqslant 1 $ ), where the radius and velocity of the SNR are given by${R_{{\rm{sh}}}}(t) \simeq 14.1{\tau ^{4/7}}\;\;{\rm{pc}},$

(7) ${V_{{\rm{sh}}}}(t) \simeq 4140{\tau ^{ - 3/7}}\;\;{\rm{km/s}},$

(8) (2) Sedov-Taylor stage (
$ \tau = t/T_{\rm ST} > 1 $ ) :${R_{{\rm{sh}}}}(t) \simeq 16.2{(\tau - 0.3)^{2/5}}\;\;{\rm{pc}},$

(9) ${V_{{\rm{sh}}}}(t) \simeq 3330{(\tau - 0.3)^{ - 3/5}}\;\;{\rm{km/s}},$

(10) where
$ T_{\rm ST} \simeq 309E_{51}^{-1/2}M_{\rm ej, \odot}^{5/6}n_{0}^{-1/3} $ yr is the starting time of the Sedov-Taylor stage [22], i.e.,$ T_{\rm ST} \simeq 1900 $ yr for$ n_0 = 0.01 $ cm−3. Here,$ E_{\rm 51} $ is the explosion energy in units of$ 10^{51} $ erg, and$ M_{\rm ej, \odot} = M_{\rm ej}/M_{\odot} = 1.4 $ is the ejecta mass in units of the solar mass. -
Following the above analysis, Caprioli [19] presented a semi-analytical solution of particle acceleration in non-linear shock waves with a free-escape boundary at an upstream location, which may explain the shape of the cutoff at some maximum momentum. Lin et al. [23] extended this conclusion to show that the knee feature of the observed H + He spectrum at high energy can be efficiently reproduced by using a “three components” scenario.
The first component consists of the particles that are advected in the downstream region. Taking the adiabatic loss into account, the energy
$ E(t) $ of a particle with energy$ E_{0} $ advected downstream at time$ t_{0} $ is$ E(t) = $ $ E_0(V_{\rm sh}(t)/V_{\rm sh}(t_0))^{2/3\gamma} $ ,$ \gamma = 5/3 $ is the ratio of specific heat. Hence, the particle numbers per unit energy are given by$\begin{split} {q_{{\rm{adv}},{{i}}}}({E_0}) =& \frac{{16{\pi ^2}}}{{{c^2}}}\int_{{T_i}}^{{T_f}} p R_{\rm sh}^2(t){E_0}{f_{{\rm{sh}},{{i}}}}(p)\frac{{{V_{{\rm{sh}}}}({t_0})}}{{{r_{{\rm{tot}}}}}} \\ &\times{\left( {\frac{{{V_{{\rm{sh}}}}(t)}}{{{V_{{\rm{sh}}}}({t_0})}}} \right)^{2/3\gamma }}{\rm d}t. \end{split}$

(11) Some particles are confined in the upstream region and then released from the SNR at the end of its life, which is referred to as the second component. The particle numbers per unit energy are
${q_{{\rm{conf}},{{i}}}}({E_0}) = \lambda \frac{{16{\pi ^2}}}{{{c^2}}}\int_{{T_i}}^{{T_f}} p R_{\rm sh}^2(t){E_0}{f_{{\rm{sh}},{{i}}}}(p)\frac{{{V_{{\rm{sh}}}}({t_0})}}{{{r_{{\rm{tot}}}}}}{\rm d}t.$

(12) Here,
$ \lambda $ represents the fraction of the particles confined by the upstream region in the acceleration process.The third component contains the particles that instantaneously escape around a maximum momentum
$ p_{{\rm max}}(t) $ from the upstream free escape boundary during the Sedov-Taylor stage with escape flux$ \Phi_{{\rm esc},{i}}(p) $ . Therefore, the particle numbers per unit energy are${q_{{\rm{esc}},{{i}}}}({E_0}) = \frac{{16{\pi ^2}}}{{{c^2}}}\int_{{T_i}}^{{T_f}} p R_{{\rm sh}}^2(t){E_0}\frac{{{\Phi _{{\rm{esc}},{{i}}}}(p)}}{{{r_{{\rm{tot}}}}}}{\rm d}t.$

(13) In this scenario, however, the resulting spectra for protons and helium nuclei at energies below the “knee” resemble power law trends, which are contradictory with the observed hardening spectra at rigidity ~200 GV. The distributions of particles both upstream and downstream of the shock are assumed to be proportional to the distribution of shock in this case. Although adiabatic loss was included, the maximum energy of the particles that are released into the ISM downstream from the shock is close to
$ 10^{5} $ GeV (see also Fig. 1 of Ref. [23] or Fig. 4 of Ref. [19]).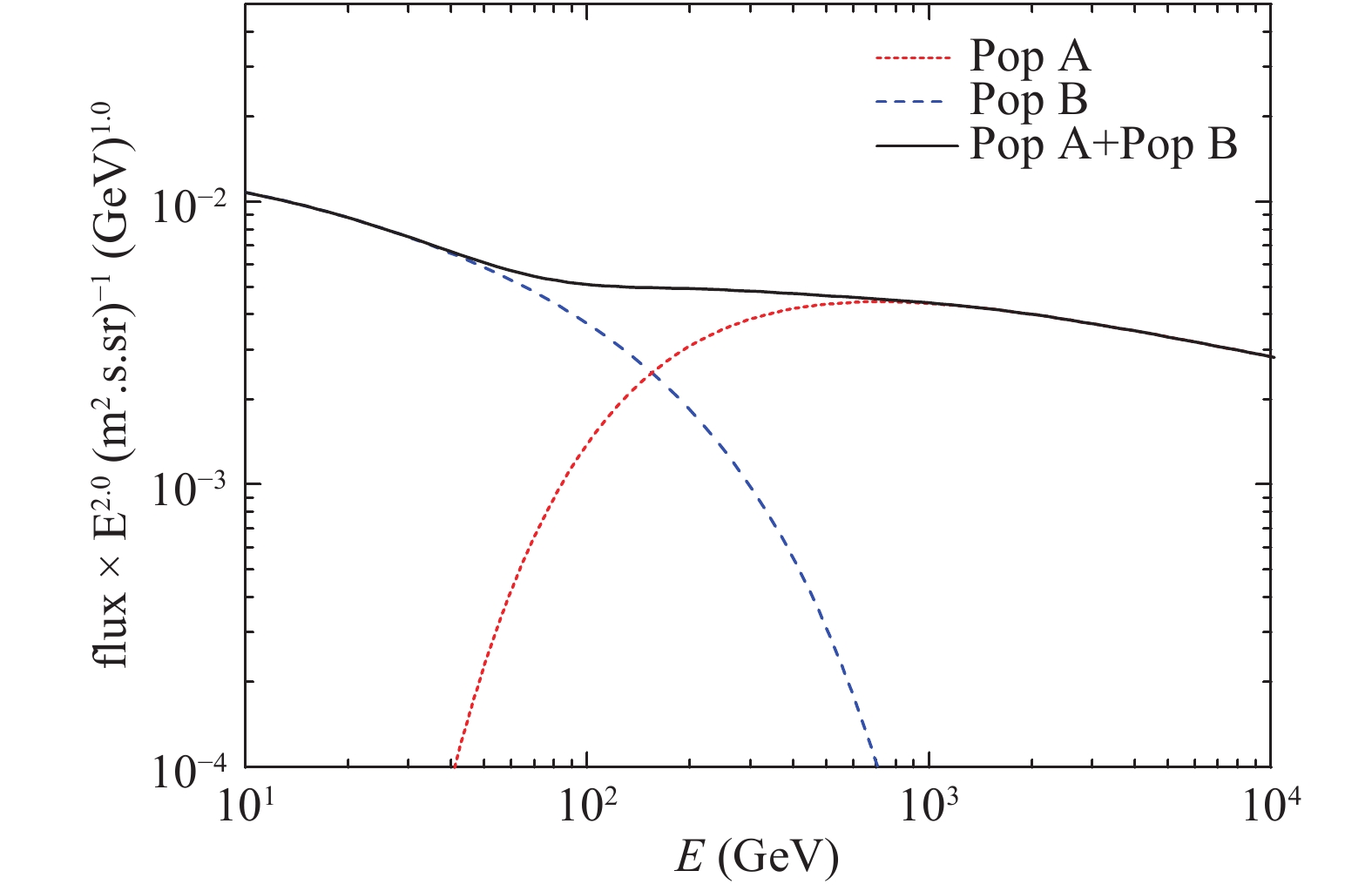
Figure 1. (color online) Injection spectrum of protons. The spectra of two populations (Pop A and Pop B) are presented by short-dashed and long-dashed lines, respectively. The solid line is the sum of populations A and B. Typical parameters of a benchmark SNR are
$E_{\rm 51} = 1\;{\rm{and}}\;$ $M_{\rm ej, \odot} = M_{\rm ej}/M_{\odot} = 1.4$ , and the parameters of the ISM are$n_0 = 0.01$ cm−3 and$B = 5\; $ μG. All quantities are calculated at the SNR ages of 10000 yr. The model parameters of NLDSA are$\lambda_{1} = 0.66$ ,$\lambda_{2} = 0.34$ and$\xi_{\rm inj} = 3.0$ .Unlike the scenario above, Bell [20] showed that the CR particles advected into the downstream region of shock may provide the GCRs component below ~200 GeV, and the maximum energy of these particles is determined by the escaping CR electric charge [24]. The magnetic field is generated by non-resonant hybrid (NRH) instability [25], and the CR streaming with an electric current density
$ j_{\rm CR} $ can drive the NRH instability. The condition for CR acceleration to PeV energies is that magnetic field be amplified strongly, which fixes the number of instability e-foldings in the range 5–10:$ \int\gamma_{\rm NRH,max}{\rm d}t\sim 5 $ , where$ \gamma_{\rm NRH,max} $ is the maximum NRH growth rate. Since$ \gamma_{\rm NRH, max} = 0.5 j_{\rm CR}\sqrt{\mu_{0}/\rho} $ , where$ \mu_{0} $ depicts the permeability of vacuum, the condition is that a CR electric charge$ Q_{\rm CR} = \int j_{{\rm CR}}{\rm d}t = 10\sqrt{\rho/\mu_{0}} $ per unit area must escape through a spherical surface surrounding the SNR to amplify the magnetic field and inhibit CR escape through that surface. By this argument, on the one hand, Bell [20] derived an estimation for the energy$ E_{\rm max,s} $ , which is the maximum CR energy at the shock:${E_{{\rm{max}},{\rm{s}}}} = 200n_{\rm e}^{1/2}E_{51}^{1/3}B_5^{4/3}\;\;{\rm{GeV}},$

(14) where the electron density is
$ n_{{\rm e}} = 0.1 $ cm−3, and$ B_5 $ is the magnetic field in units of 5 μG. For typical parameters of the SNR, the energy of CR particles released into the ISM from the interior of the SNR at the end of its life is less than$ \sim 200 $ GeV. On the other hand, Bell [24] showed that CR above 200 GeV can be produced efficiently by young SNRs and released into the Galaxy by escaping upstream of the shock. In summary, the Galactic CR population can be divided into two populations, and the transition region of the two CR populations is at about 200 GeV. Note that the Alfvén instability operates differently from the NRH instability and dominates in a different regime. However, its maximum growth rate is a numerical factor multiplicative of$ \gamma_{\rm NRH,max} $ , hence the argument above also applies to the Alfvén instability.Since the maximum CR energy
$ E_{\rm max,s} $ is about 200 GeV [20], the two components (Eq. (11) and Eq. (12)) should be reconsidered. The first component (see Eq. (11)) mainly contributes to CRs with an energy of$ \leqslant E_{\rm max,s} $ , and the second component (see Eq. (12)) mainly contributes to CRs with an energy of$ > E_{\rm max,s} $ . Therefore, both the equations can be recast as$\begin{split} {{q_{{\rm{adv}},{{i}}}}({E_0})} = &{{A_1} \times \frac{{16{\pi ^2}}}{{{c^2}}}\int_{{T_i}}^{{T_f}} p R_{{\rm sh}}^2(t){E_0}{f_{{\rm{sh}},{{i}}}}(p)\frac{{{V_{{\rm{sh}}}}({t_0})}}{{{r_{{\rm{tot}}}}}}}\\ &\times{ {{\left( {\frac{{{V_{{\rm{sh}}}}(t)}}{{{V_{{\rm{sh}}}}({t_0})}}} \right)}^{2/3\gamma }}{\rm d}t} \end{split}$

(15) $\begin{split} {{q_{{\rm{conf}},{{i}}}}({E_0})} =&{ {A_2} \times \frac{{16{\pi ^2}}}{{{c^2}}}\int_{{T_i}}^{{T_f}} p R_{{\rm sh}}^2(t){E_0}{f_{{\rm{sh}},{{i}}}}(p)}\\ &{ \times \frac{{{V_{{\rm{sh}}}}({t_0})}}{{{r_{{\rm{tot}}}}}}{\rm d}t,} \end{split}$

(16) with
${A_1} = {\lambda _1}\exp \left( { - \frac{{{E_0}}}{{{E_{{\rm{max}},{\rm{s}}}}}}} \right),\;\;{A_2} = {\lambda _2}\exp \left( { - \frac{{{E_{{\rm{max}},{\rm{s}}}}}}{{{E_0}}}} \right).$

For the sake of comparison with the scenario given by Bell [20], particles described by Eqs. (15) and (16) are defined as populations B and A, respectively. Here, we introduce two parameters in exponential form,
$ A_{1} $ and$ A_{2} $ , which also consist of fractional factors ($ \lambda_{1} $ and$ \lambda_{2} $ ), and$ E_{\rm max,s} = 200 $ GeV. For the population B, although the energy of particles advected downstream can be up to the ‘knee’ of CRs in the NLDSA model [19], Bell [20] showed that most of CRs released into the Galaxy from downstream have energies less than 200 GeV, and the number of particles with energies larger than 200 GeV in the center of the shock of SNR is relatively small. Hence, the resulting spectrum should be soft and the flux should be decreased at energies above 200 GeV. Most particles in population A have energies greater than 200 GeV. In order to give a reasonable description of the two populations, we use two parameters in exponential form to describe such characteristics of the spectra of Pop A and Pop B. In Fig. 1, we present the spectrum of protons injected into the ISM. The spectrum from the upstream is labeled with “Pop A”, the spectrum from downstream is labeled with “Pop B”. The solid line (Pop A + Pop B) represents the total injection spectrum. The hardening of spectrum is produced in this case. In contrast, since the distributions of particles in the advection component and the confined component are functions of the particle spectrum at the shock location$ f_{{\rm sh},i}(p) $ , we use$ \lambda_{1} $ and$ \lambda_{2} $ in Eqs. (15) and (16) to represent the fractions of the particles that comprise the advection component and the confined component, respectively, where$ \lambda_{1} + \lambda_{2} = 1 $ . The dependence of the CR proton flux as a function of energy for three different values of$ \lambda_{1} $ is shown in Fig. 2, demonstrating that the cross-over energy decreases with decrease of the factor$ \lambda_{1} $ .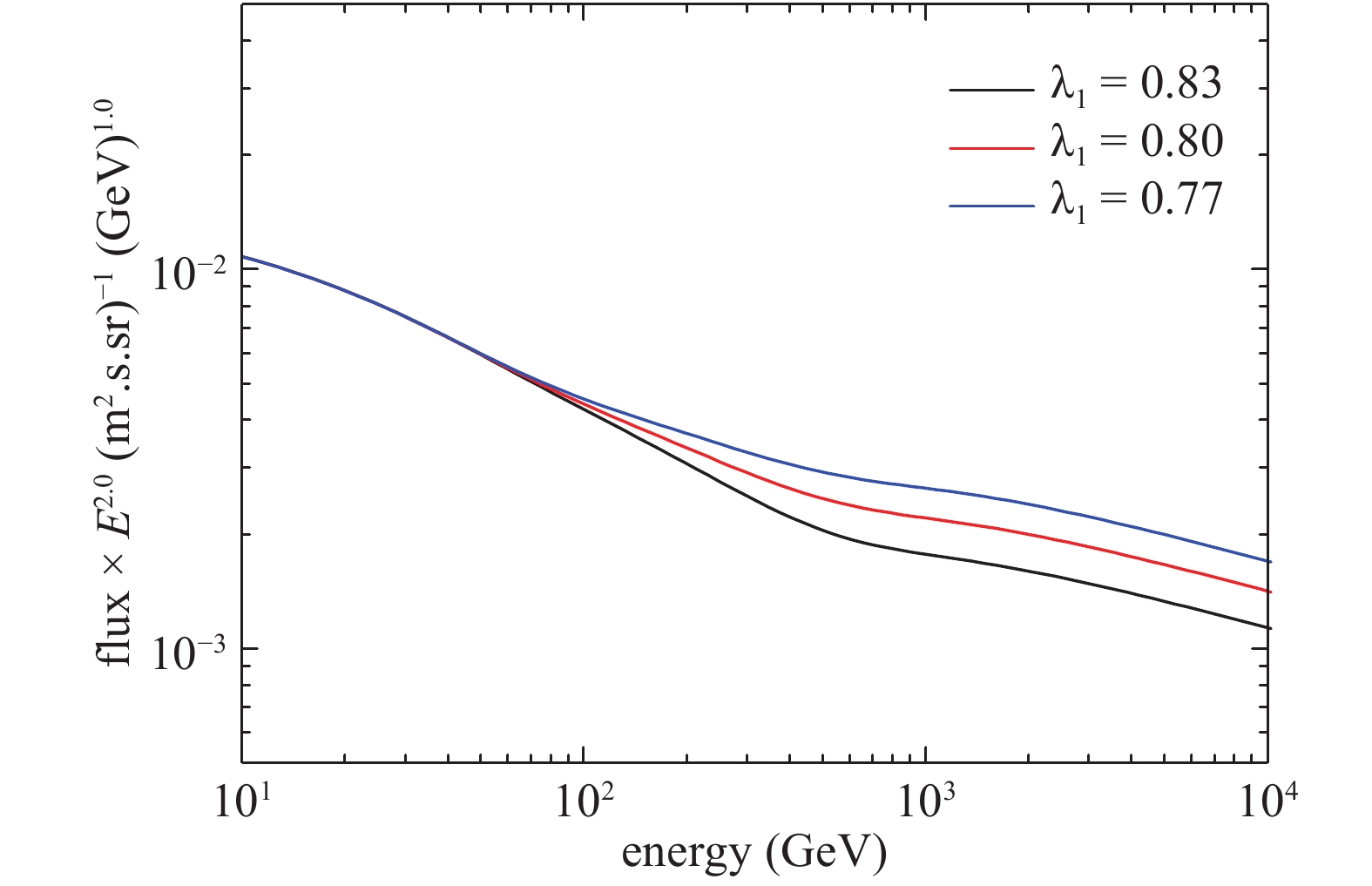
Figure 2. (color online) Cumulative proton spectra for three different values of
$\lambda_{1} = 0.83$ , 0.80 and 0.77. The curves are artificially normalized at the energy 10 GeV. Other parameters are the same as those in Fig. 1.A key parameter affecting the spectral shape of accelerated particles through NLDSA inside the SNR is the injection parameter
$ \xi_{\rm inj} $ . In Fig. 3, we show the cumulative proton spectra for various values of$ \xi_{\rm inj} $ . For the convenience of studying the tendency of these spectra, the curves are normalized artificially at the energy of 10 GeV. A larger$ \xi_{\rm inj} $ (smaller$ \eta_{i} $ ) leads to a flatter spectrum and more prominent hardening features.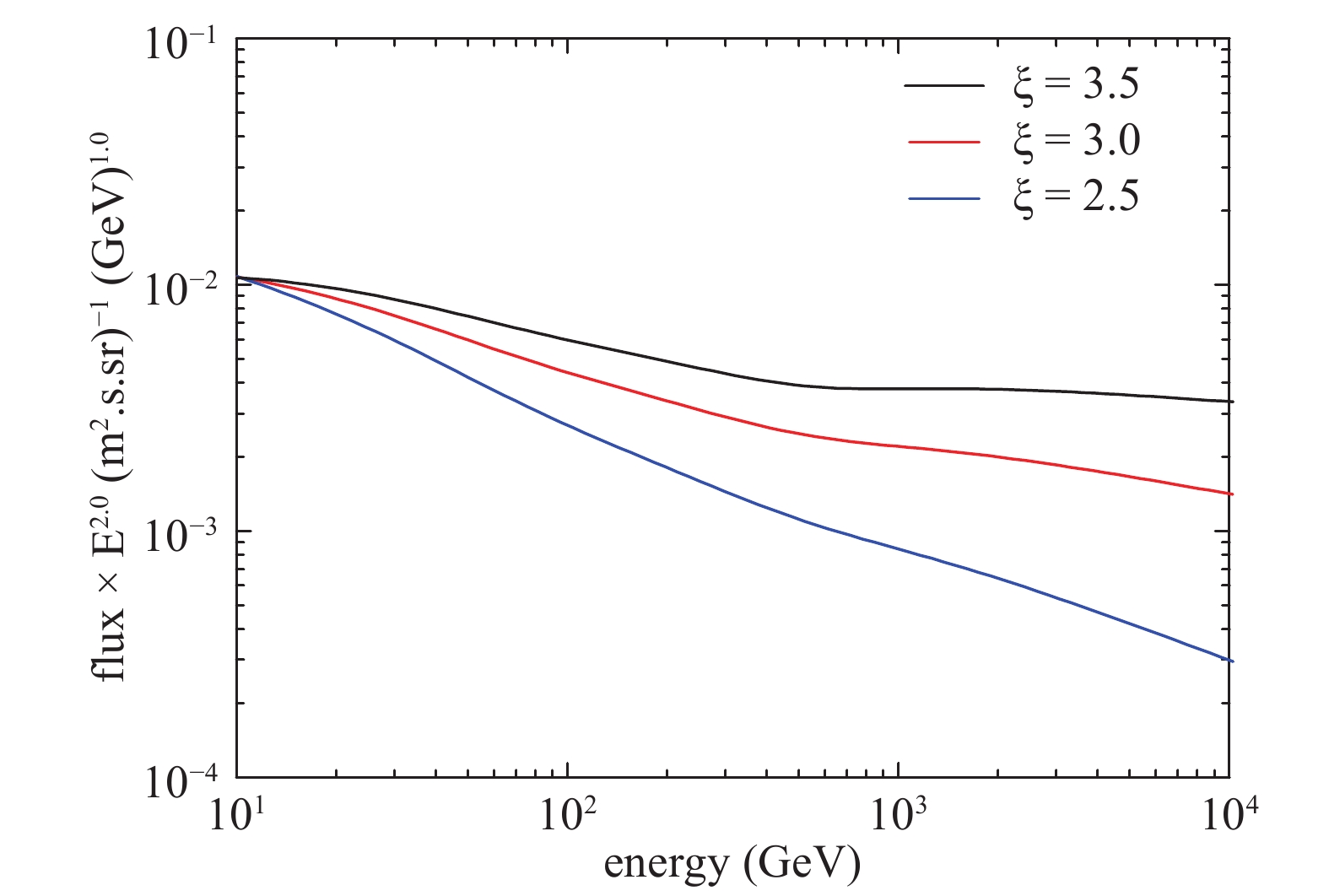
Figure 3. (color online) Cumulative proton spectra for three different values of
$\xi_{\rm inj} = 2.5$ , 3.0, and 3.5. Other parameters are the same as those in Fig. 1 except for$\lambda_{1} = 0.80$ . Note that the curves are artificially normalized at the energy of 10 GeV.Finally, the temporal evolution of CRs proton spectrum is illustrated in Fig. 4. Two earliest time-steps (300 yrs and 600 yrs) are in the ejecta-dominated stages, while the others are in the early, intermediate, and late Sedov-Taylar stages. The total CR flux grows rapidly during the early stage, and reaches saturation around ~20000 yr. More importantly, the cross-over energy moves towards lower energies with the aging of SNRs.

Figure 4. (color online) Cumulative proton spectra at different SNR ages. The parameters of NLDSA are
$\lambda_{1} = 0.80$ ,$\xi_{\rm inj} = 3.0$ , and other parameters are the same as those in Fig. 1. -
After escaping from SNRs, CRs supposedly propagate diffusively across the Galaxy. We calculate the spectra of protons and helium nuclei on the Earth by using the leaky box model, taking the relative abundance
$ \eta_{\rm He}/ \eta_{\rm H} = 0.26 $ into account. Both spectra below ~50 GeV$ \rm nucleon^{-1} $ are not considered, since both solar modulation and possible advection effects are significant at these energies [26].Under these assumptions, the energy spectrum
$ N_{{\rm obs}, i}(E) $ of the ith particles observed at the Earth can be expressed as [27]${N_{{\rm{obs}},i}}(E) \propto {q_i}(E){\left( {\frac{1}{{{\lambda _{{\rm{esc}},i}}}} + \frac{1}{{{\lambda _{{\rm{int}},i}}}}} \right)^{ - 1}},$

(17) where
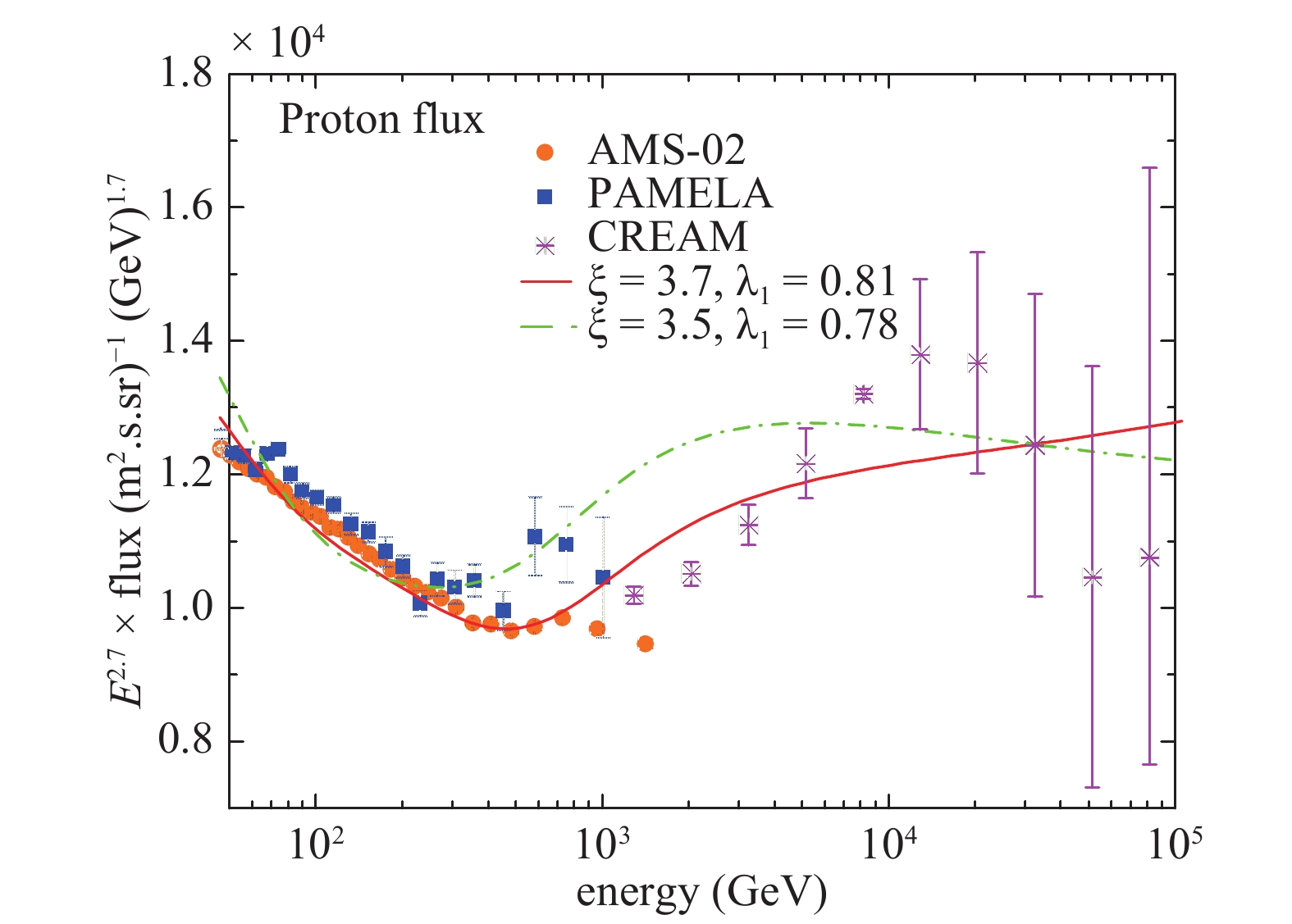
$ \lambda_{{\rm esc}, i} $ is the escape path length and$ \lambda_{{\rm esc}, i} = 7.3(R_i/$ $ 10\; {\rm GV})^{-\delta}\beta(p) $ g/cm2 with a function of the particle magnetic rigidity$ R_i = pc/Z_i $ where$ Z_i $ is the charge of the particle and c is the speed of light,$ \beta(p) $ is the dimensionless speed of a nucleus with a momentum p and$ \delta = 0.3 – $ 0.6 is chosen in order to reproduce the observed proton spectrum. The interaction length is$ \lambda_{{\rm int}, i} = \lambda_{0, i}(E/10\; \rm GeV)^{-\epsilon_i} $ , where$ \lambda_{0, \rm H} = 50 $ g·cm−2 and$ \lambda_{0, \rm He} = 21 $ g·cm−2,$ \epsilon_{\rm H} = 0.05 $ , and$ \epsilon_{\rm He} = 0.0416 $ . The difference between proton and helium spectra are probably related to the propagation effect.In Fig. 5, the calculated energy spectra of protons and the data observed by the AMS-02 [6], PAMELA [4], and CREAM [28] are shown. Two kinds of model parameters are used:
$ \xi = 3.7 $ ,$ \lambda_{1} = 0.81 $ ,$ \delta = 0.58 $ (red line for AMS-02), and$ \xi = 3.5 $ ,$ \lambda_{1} = 0.78 $ , and$ \delta = 0.58 $ (green line for PAMELA). The results show that the overlap of the two populations can naturally lead to a spectral hardening of the proton spectrum at$ \leqslant $ TeV energies, and this is in good agreement with the data of AMS-02 (the red line). However, when reproducing the data of the PAMELA, scenarios may become complicated (the green line). A similar hardening is also found in the helium spectrum (Fig. 6). -
In this paper, the spectral hardening of CR protons and helium nuclei at several hundred GeV has been investigated within the revised NLDSA model. Based on the work of Bell [20], in this study we assume that there are two populations (Pop A and Pop B) at the SNRs. The former consists of particles with energies above
$ \sim E_{\rm max, s} $ (see Eq. (14)) released upstream of the shock of SNR (see Eq. (16)), while the latter makes up those particles with energies below$ \sim E_{\rm max, s} $ released downstream of the shock of SNR (see Eq. (15)). The observed spectral hardening of CR protons and helium nuclei near approximately 200 GeV may be explained as a natural production of the overlap of the two populations at energies$ \leqslant $ TeV within a reasonable parameter range.For comparison with previous studies, functions
$ A_{1} $ and$ A_{2} $ are introduced in this paper. The exponential form provides an energy constraint close to the transition region to make the theory agree with observation. This exponential form is not unique. Since there is little literature discussing the actual spectral shape of populations A and B, especially at the cross-over energy, other functions have been used to replace the exponential form within$ A_{1} $ and$ A_{2} $ . These include the step function and the smooth-step function, however the resulting CR spectra perform poorly when compared with the observed data. Moreover, Bell. [20, 24] showed that population A can be produced by young SNRs and population B is related to the centers of older SNR. In other words, the different evolution history of the two populations may cause hardening of the final spectrum. In addition, the acceleration efficiency would affect our results, where a smaller acceleration efficiency leads to more prominent hardening features. It can be predicted that the cross-over energy moves towards low energies with aging of SNRs and reaches a saturation around ~20 kyr. A possible explanation of this feature might stem from the existence of CR bubbles at the centers of SNR, as shown by Chevalier [29].The observed CR helium spectrum was found to be more hardening than CR protons, and our model thus cannot reproduce the observed data given by CREAM [28], even when using the difference of interaction strengths. Obviously, such different interaction strengths are insufficient to account for total spectral hardening, such that it is possible that the anomaly relates to propagation properties in the Galaxy. In fact, the re-acceleration of CRs is one of the most likely candidates. Recent secondary cosmic ray Li, Be, and B observations of AMS-02 [30] strongly favor the occurrence of re-acceleration of cosmic rays during the propagation. These primary (or secondary) nuclei share almost identical spectra with each other. More importantly, there are spectral breaks of both primary and secondary nuclei at a few hundred GV, and the spectral indices of secondary nuclei are harder than those of primary nuclei. Another limitation of our model is the simplification of the injection processes of different compositions, without the effects of partial ionization and dust sputtering. Moreover, one has to keep in mind that the data of AMS-02 and CREAM for helium nuclei at 2~4 TeV are different. Future instruments (e.g. LHAASO [31-33], DAMPE [34, 35]) with high statistics and accurate measurements will be expected to clarify the spectral behaviors above TeV energies, and offer a final judgment between different theoretical models of the SNR.
Spectral hardening of cosmic ray protons and helium nuclei in supernova remnant shocks
- Received Date: 2018-10-24
- Accepted Date: 2019-01-22
- Available Online: 2019-05-01
Abstract: The observed hardening of the spectra of cosmic ray protons and helium nuclei is studied within the model of nonlinear diffusive shock acceleration of supernova remnants (SNRs). In this model, the injected particles with energies below the spectral " knee” are assumed to be described by two populations with different spectral indexes around 200 GeV. The high-energy population is dominated by the particles with energies above 200 GeV released upstream of the shock of SNR, and the low-energy population is attributed to the particles with energies below 200 GeV released downstream of the shock of SNR. In this scenario, the spectral hardening of cosmic ray protons and helium nuclei observed by PAMELA, AMS-02, and CREAM experiments can be reproduced.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: