-
Dynamical Chiral Symmetry Breaking (DCSB) is a very important feature of Quantum Chromodynamics (QCD). With the increases of temperature or/and chemical potential, there appears a phase transition from hadronic matter to a new phase, the quark-gluon plasma (QGP). This phase transition may occur in the relativistic heavy ion collisions at RHIC [1, 2] in the Brookhaven National Laboratory (BNL). It is believed that the phase transition is a crossover at high temperature and small chemical potential, while it is a first order phase transition at low temperature and large chemical potential. Thus, there possibly exists a critical end point (CEP) at finite temperature and chemical potential (see Refs. [3-6] and reference therein). Determining the existence of CEP and its location in the QCD phase diagram is one of the main goals of the heavy ion collision experiments. For this purpose, the second phase of the beam energy scan at RHIC will be performed between 2019 and 2020 [7, 8] , and we are optimistic that the experimental results could answer these questions. On the theoretical side, various non-perturbative QCD models and theories are considered, and the influence of various factors in the real experimental environment on the possible QGP production in heavy ion collisions are studied in the QCD phase diagram. For example, one needs to consider the effects of finite temperature, finite density and strong magnetic fields generated in the experiments on the possible CEP at finite temperature and chemical potential [3-5, 9-13]. It should be pointed out that many previous calculations of the QCD phase diagram are based on infinite thermodynamical systems without considering the QGP generated in the laboratory, i.e. that the so-called fireball is very limited in size. The volume of the smallest fireball produced in RHIC could be as small as (2 fm)3 [14], although its volume before freeze-out in Au-Au and Pb-Pb collisions ranges from 50 fm3 to 250 fm3 [14-16]. Since the fireballs produced in the laboratory are of finite size, the finite size effect on CEP must be considered in the second phase of the beam energy scan at RHIC.
The finite volume effects have attracted considerable theoretical attention in the past decades [17-20]. The current studies are based on the assumption that the effective Lagrangian of a finite (small) volume physical system is the same as the corresponding infinite physical system. Based on this assumption, different models are adopted for studying the finite volume effects on the QCD phase transition, for example, the Random Matrix Theory (RMT) [21-25], Quark-meson-model [26-31], (Polyakov-loop extended) Nambu-Jona-Lasinio (NJL) model [32-38], Dyson-Schwinger equations (DSEs) [39, 40], etc. Since the spatial size of the physical system is limited, it is necessary to select appropriate spatial boundary conditions. Usually, periodic or anti-periodic boundary conditions are adopted [20], which results in discretized momenta in spatial direction, as is the case with Matsubara frequency in imaginary temperature field theory. As an example, for a fermion in a finite volume, the quark momentum is discretized and the integral over all spatial momenta is replaced by a sum over discrete momentum modes. The discretized momentum depends on the selected anti-periodic boundary condition (APBC)
$\vec p_{\rm APBC}^2 = \frac{{4{\pi ^2}}}{{{L^2}}}\sum\nolimits_{i = 1}^3 {{{\left({n_i} + \frac{1}{2}\right)}^2}} ,{n_i} = 0, \pm 1, \pm 2\,...,$

(1) where L is the cubic volume size. It can be easily seen from the above equation that we must include the contribution of all frequency modes when considering the finite volume effects. If an infrared cutoff of the three-dimensional momentum is applied, the contribution of low-frequency modes is ignored. Similarly, if a three-dimensional ultraviolet momentum cutoff is used, the contribution of all high-frequency modes is neglected, which is, in principle, problematic. In addition, if the same boundary conditions in both spatial and temporal (temperature) directions are chosen in the Euclidean space, namely anti-periodic boundary conditions for fermion fields and periodic boundary conditions for boson fields, the discretizations in the spatial and temporal directions are physically equivalent [20].
As shown in the finite temperature field theory, the running couplings in Quantum Electrodynamics (QED) [41, 42] and QCD [43] depend on temperature. The following question then naturally arises: the effective Lagrangian of a finite volume system should, in principle, depend on the system size, similarly to a finite temperature system where it depends on temperature; so, how should an effective Lagrangian be constructed to reasonably reflect the finite volume effects? This is the motivation for this paper.
Before we introduce the effective Lagrangian of a finite volume system with spatial size effects, let us briefly review how we introduced in previous studies the temperature dependent effective Lagrangian in a finite temperature system. As is known, the quark propagator and gluon propagator satisfy their respective DSEs and they are coupled to each other. Therefore, the gluon propagator should depend on the temperature and/or chemical potential, which is also shown clearly in lattice simulations. However, in the framework of the usual DSEs, the gluon propagator is only used as phenomenological input, and the coupling between the gluon propagator and the quark propagator is not considered, as are not considered the effects of temperature and chemical potential on the gluon propagator. More specifically, in the framework of the NJL model, the coupling constant can be regarded as the inverse of a "static" gluon propagator, and the effect of the quark propagator on the "static" gluon propagator should be, in principle, included. The authors of Refs. [9, 11, 13, 44] considered the influence of quark feedback on the "static" gluon propagator through the operator product expansion (OPE) method, and obtained a modified NJL model with quark feedback. In the modified NJL model described in Refs. [9, 11, 13, 44], the coupling constant G in the NJL model is modified into
$ G_1+G_2\langle\bar\psi\psi\rangle $ , where G2 weighs the influence of quark feedback on the "static" gluon propagator (The physical mechanism for quark feedback is given in the appendix of Ref. [44] ). With an additional parameter that is introduced in the modified NJL model, it reflects better the relationship between the quark propagator and the gluon propagator, which is the basic requirement of QCD. More importantly, in the modified NJL model [44] one can fit better the lattice data at finite temperature, which reflects the fact that the introduction of quark feedback to study the chiral phase transition at finite temperature is physically reasonable. Since the discretization of spatial and temporal directions are physically equivalent in the Euclidean space, similarly to the imaginary temperature field theory, the effective coupling is temperature dependent, and it is possible to construct an effective coupling that also depends on the finite volume. Obviously, since the quark condensate depends on temperature and/or chemical potential, the effective coupling in the modified NJL model naturally depends on temperature and/or chemical potential. Based on the physical equivalence of spatial and temporal directions in the Euclidean space, we introduce the finite volume dependent effective Lagrangian using the same approach as in the finite temperature and finite chemical potential system.This paper is organized as follows: In Section 2, the modified NJL model with finite volume dependent coupling is introduced. The chiral phase transition in the modified NJL model is presented in Section 3, and the conclusion is given in Section 4.
-
As is well known, the NJL model is a low energy effective theory of QCD, which can describe the main features of non-perturbative QCD, e.g., Dynamical Chiral Symmetry Breaking. The Lagrangian of the usual two-flavor model is given by
${\cal L} = i\bar \psi /\!\!\!\!\partial \psi - m\bar \psi \psi + \frac{G}{{2{N_c}}}\left[ {{{\left( {\bar \psi \psi } \right)}^2} + {{\left( {\bar \psi {\gamma _5}\tau \psi } \right)}^2}} \right],$

(2) where m denotes the current quark mass of two-flavor light quark and G denotes the coupling constant. Then, the gap equation is given as
$M = m - \frac{G}{{{N_c}}}\langle \bar \psi \psi \rangle ,$

(3) where M denotes the constituent quark mass. Since this is an unrenormalizable theoretical model, a method of regularization is necessary. The commonly used NJL model generally uses a three-momentum cutoff in the momentum space to regularize the amount of divergence. It is important to note that this ultraviolet (UV) regularization of the (P)NJL model is not suitable for studying small volume effects. Equation (1) clearly shows that all frequency modes in momentum space contribute to the finite volume effects. If a UV cutoff (for example, three- momentum cutoff NJL model) is adopted, the contribution of high frequency modes would be ignored. If a simple infrared cutoff is adopted [34, 36, 38], the contribution of low frequency modes would be ignored. In our case, we have to abandon the commonly used three-momentum cutoff and instead use the proper-time regularization to study the finite size effects. This is because the proper-time regularization is not plagued by the UV momentum cutoff.
In this paper, the scheme of proper time regularization proposed by J. S. Schwinger [45] is adopted
$\frac{1}{{{p^2} + {m^2}}} = \int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s\;{\rm{exp}}\left[ { - s\left( {{p^2} + {m^2}} \right)} \right],$

(4) where
$ \Lambda $ denotes the ultraviolet cutoff. Thus, the gap equation (3) is given by$\begin{split} M =& m + 4G{N_f}M\int {\frac{{{{\rm{d}}^4}p}}{{{{(2\pi )}^4}}}} \int {\rm{d}} s{\rm{exp}}\left[ { - s\left( {{p^2} + {M^2}} \right)} \right]\\ =& m + \frac{M}{{3{\pi ^3}}}G\int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s{s^{ - 2}}{\rm{exp}}( - s{M^2}). \end{split}$

(5) At zero temperature, the normal NJL model reproduces well the properties of hadrons. However, in the case of finite temperature, the result can not recover lattice simulations. To fit the lattice simulations at finite temperature within the OPE method proposed in Refs. [10, 11, 13, 44], the coupling in the Lagrangian (2) is modified into
$G \to {G_1} + {G_2}( - \langle \bar \psi \psi \rangle ).$

(6) There are four parameters, G1, G2, m and
$ \Lambda $ available for fitting the results of lattice simulations at zero and finite temperatures. We stress that G1, G2 and$ \Lambda $ can reproduce the pion mass and decay constant, and$ G= G_1+G_2(-\langle\bar\psi\psi\rangle) $ at zero temperature. It is found that one additional parameter is required for fitting the lattice results at finite temperature [46, 47]. Therefore, the gap equation (3) is modified into$\begin{array}{l} M = m + \displaystyle\frac{M}{{3{\pi ^3}}}\left[ {{G_1} + {G_2}M/{\pi ^3}\int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s{s^{ - 2}}{\rm{exp}}( - s{M^2})} \right]\\ \;\;\;\;\;\;\;\;\displaystyle\times\int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s{s^{ - 2}}{\rm{exp}}\left( { - s{M^2}} \right). \end{array}$

(7) According to the finite temperature field theory, the gap equation at finite temperature is given by
$ \begin{split}M =& m \!+\! \frac{{MT}}{{\pi \sqrt \pi }}\left[ {{G_1} + {G_2}MT\frac{3}{{\pi \sqrt \pi }}\int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s{\theta _2}({{\rm e}^{ - 4{\pi ^2}{T^2}s}}){s^{ - 3/2}}{{\rm e}^{ - s{M^2}}}} \right] \\ &\times \int_{\frac{1}{{{\Lambda ^2}}}} {\rm{d}} s{\theta _2}({{\rm e}^{ - 4{\pi ^2}{T^2}s}}){s^{ - 3/2}}{{\rm e}^{ - s{M^2}}}.\quad\quad\quad\quad\quad\quad\quad\quad\quad(8) \end{split} $

Here,
$ \theta_2(x)= 2 x^{1/4}\sum_{n=0}^{\infty}x^{n(n+1)} $ . Thus, the coupling naturally depends on temperature. Considering the equivalence of spatial and temporal directions in the Euclidean space, the coupling constant should depend on the volume in a finite volume system. Therefore, we can directly extend the calculations in the above infinite thermodynamic system to a finite temperature and finite volume system.In principle, thermodynamical properties of a finite volume system depend not only on the size of the system but also on its geometric shape. In this paper, as an interesting attempt, we take a cubic box as the geometric shape of the system. We consider a cubic box with edge length L and anti-periodic boundary conditions in all spatial directions for a fermion, i.e.,
$\begin{array}{l} \psi ({x_0},{x_1},{x_2},{x_3}) = - \psi ({x_0},{x_1} + L,{x_2},{x_3}),\\ \psi ({x_0},{x_1},{x_2},{x_3}) = - \psi ({x_0},{x_1},{x_2} + L,{x_3}),\\ \psi ({x_0},{x_1},{x_2},{x_3}) = - \psi ({x_0},{x_1},{x_2},{x_3} + L). \end{array}$

Thus, the momentum is replaced by the discrete momenta
$ (p_1,p_2,p_3,p_4)\rightarrow ((2n_1+1)\pi/L,(2n_2+1)\pi/L,(2n_3+1)\pi/L, $ $(2n_4+1)\pi T) $ , where$ n_1,n_2,n_3,n_4 \in (-\infty,\infty) $ , and the momentum integral is replaced by a sum of discrete momenta with$\int {\frac{{{\rm{d}}{p^4}}}{{{{(2\pi )}^4}}}} \to \frac{T}{{{L^3}}}\sum\limits_{{n_1},{n_2},{n_3},{n_4} = - \infty }^\infty . $

The gap equation in a finite volume (cubic box) at finite temperature is given by
$\begin{split} &M = m + 4M{N_f}\\&\;\times\left\{ {{G_1} + {G_2}\displaystyle\frac{{24T}}{{{L^3}}}\int {\rm{d}} s{{\left[{\theta _2}\left({{\rm e}^{ - \frac{{4{\pi ^2}s}}{{{L^2}}}}}\right)\right]}^3}[{\theta _2}({{\rm e}^{ - 4{\pi ^2}{T^2}s}})]{\rm{exp}}( - s{M^2})} \right\}\\ &\;\times\left\{ {\displaystyle\frac{T}{{{L^3}}}\int {\rm{d}} s{{\left[{\theta _2}\left({{\rm e}^{ - \frac{{4{\pi ^2}s}}{{{L^2}}}}}\right)\right]}^3}[{\theta _2}({{\rm e}^{ - 4{\pi ^2}{T^2}s}})]{\rm{exp}}( - s{M^2})} \right\}. \end{split}$

(9) From Eq. (9), if we use anti-periodic boundary conditions for both spatial and temporal directions in the Euclidean space, it is easy to see that discretization of time and space are completely equivalent. Specifically, the effects of 1/L and T on the quark gap equation are mathematically equivalent. Thus, similarly to increasing the temperature, it can be expected that the chiral symmetry will be partially restored with decreasing the system size L.
-
With increase of temperature, a chiral phase transition appears. The quark condensate is adopted as an order parameter to describe the chiral phase transition,
$ - \langle \bar \psi \psi \rangle = {\rm{Tr}}S(p) = {N_f}{N_c}\int {\frac{{{{\rm{d}}^4}p}}{{{{(2\pi )}^4}}}} \frac{{4M}}{{{p^2} + {M^2}}}.$

As is known, there is a second order phase transition at finite temperature in the chiral limit, and a crossover beyond the chiral limit (m≠0). To locate the pseudo-critical temperature of the crossover, the thermal susceptibility is used
${\chi _T} = \frac{{\partial \langle \bar \psi \psi \rangle }}{{\partial T}},$

(10) and the pseudo-critical temperature is located at the peak of the susceptibility [48, 49].
In this paper, to perform numerical calculations, the parameters are chosen as follows:
$ \Lambda $ =990 MeV and m = 5.5 MeV, which are obtained by fitting the pion mass$ m_{\pi}=138 {\rm MeV} $ and the pion decay constant$ f_{\pi}= 93 {\rm MeV} $ [50]. Moreover, G1 = 22.3 GeV−2 and G2 = 0.5003 GeV−5, which are obtained by fitting the results of lattice simulations [47] in the infinite volume thermodynamical system, as shown in Fig. 1 [11].$ \sigma_n=(\langle\bar\psi\psi\rangle_T/\langle\bar\psi\psi\rangle_0) $ in Fig. 1 denotes the normalized quark condensate. From Fig. 1, it is found that the results fit well the lattice simulations at finite temperature, although there is only one more additional parameter. As the quark condensate depends on both the temperature and size of the finite volume system, the modified coupling naturally depends on the temperature and size.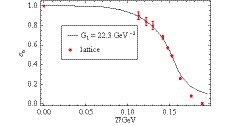
Figure 1. (color online) The results of the modified NJL model compared with the lattice simulations from Ref. [47].
Fig. 2 shows the quark condensate as a function of temperature for different system sizes. It is easy to see that the condensate decreases with smaller L at low temperatures. As spatial and temporal directions are equivalent, the decrease of size means increase of temperature, which enhances the fluctuations and leads to restoration of DCSB. With temperature increase, due to thermal fluctuations, DCSB is partially restored and the condensates of different sizes tend to be equal. For L = 4 fm, the condensate is almost the same as for an infinite thermodynamical system, which implies that systems larger than 4 fm can be regarded as infinite thermodynamical systems. This result agrees qualitatively with the results of different model calculations [27, 39].
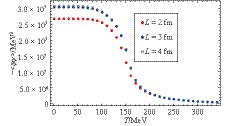
Figure 2. (color online) The quark condensate as a function of temperature in the modified NJL model.
As is known, the effective coupling decreases in the perturbative regime with increase of temperature [43]. However, in the strong coupling regime, this is not very clear. In our study, the influence of quark feedback is included in the modified NJL model and the effective coupling is divided into two parts: the first part, G1 , is independent of the system size and temperature, while the second,
$ G_2 \langle\bar\psi\psi\rangle $ , depends on the system size and temperature. In Fig. 3 , the system size dependent coupling is shown as a function of the system size at zero temperature. Clearly, the effective coupling decreases with decreasing size. Due to the equivalence of spatial and temporal directions in the Euclidean space, the decreasing system size leads to enhancement of fluctuations, so that, in principle, the effective coupling should decrease as the size decreases. It is known that, once the coupling constant is smaller than a critical coupling constant, the nontrivial solution of the gap equation cannot be found in the NJL model [51], which means that DCSB is partially restored. In Fig. 4 , the quark condensate is shown as a function of the system size at zero temperature. With decreasing system size, the quark condensate also decreases, and the chiral symmetry is partially restored. With increase of the system size L, the condensate tends to a constant when L > 4 fm, which means that a finite volume system can be regarded as equivalent to an infinite thermodynamical system. This is consistent with the conclusions we have obtained for the effective coupling as a function of spatial size.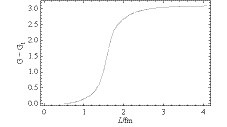
Figure 3. The system size dependent coupling as a function of the system size L at zero temperature.
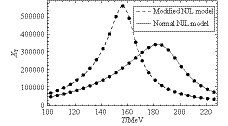
Let us now proceed to the calculations of thermal susceptibility. Since the effective coupling decreases with decreasing size of the system, the modified NJL model, when compared to the normal NJL, should result in a chiral phase transition for the same size L. In Fig. 5 and Fig. 6 , the susceptibilities for both models are shown for system sizes L = 3 fm and L = 2 fm, respectively. It is found that the susceptibilities have a smooth peak, which means that the transition is a crossover at a finite temperature. For L = 3 fm, the pseudo-critical temperature Tc = 156 MeV in the modified NJL model is smaller than in the normal NJL model, which is Tc = 181 MeV. As the size decreases, e.g. for L = 2 fm, the pseudo-critical temperature also decreases: in the modified NJL model it is Tc = 149 MeV, and Tc = 180 MeV in the normal NJL model. Therefore, the pseudo-critical temperature decreases in both models. This result agrees with the other model calculations [34, 35, 38]. The transition temperature in the modified NJL model is smaller than in the NJL model, which means that the quark feedback increases the fluctuations and reduces the transition temperature. In order to study the contribution of the quark feedback and of the anti-periodic boundary conditions on the pseudo-critical temperature, the susceptibilities in the modified and normal NJL models are shown in Fig. 6. From Fig. 6, it is easy to find that the pseudo-critical temperature of the chiral phase transition is due to both the modified effective coupling and the anti-periodic boundary conditions, and that the effect of the modified effective coupling is more pronounced. This further demonstrates the importance of introducing the effective coupling that is related to the spatial size. Specifically, for the case of an infinite volume, the modified NJL model reduces the critical temperature from Tc = 183 MeV to Tc = 156 MeV, and this critical temperature is even smaller than in the normal NJL model with L = 2 fm (Tc = 180 MeV). It is also found that the modified NJL model with anti-periodic boundary conditions further reduces the critical temperature (Tc = 149 MeV). The above calculations clearly show that the transition temperatures obtained by considering the size dependent effective Lagrangian are much smaller than the corresponding temperatures obtained with the size independent Lagrangian. We believe that this fact should be considered in the forthcoming second phase of the RHIC energy scan.
-
In principle, the effective Lagrangian of a finite volume thermodynamical system should be different from the infinite thermodynamical system. However, the studies of the finite volume effects are usually made on the basis of the effective Lagrangian of an infinite thermodynamical system with different boundary conditions [20]. In this paper, we tried to introduce an effective Lagrangian that naturally depends on the finite volume size. Specifically, within the usual framework of the NJL model, we obtained a modified NJL model with finite volume size dependence, by considering the quark feedback to the "static" gluon propagator. Based on this modified NJL model, we studied the chiral phase transition in finite volume and finite temperature systems, and compared the results with the normal NJL model. We found that quark feedback can reduce the temperature of crossover in a fixed system size. This implies that quark feedback is very large. To our knowledge, this is the first time that an effective Lagrangian has been used to analyze the effects of volume size on the chiral phase transition in a finite temperature and finite volume system. Due to the equivalence of spatial and temporal directions in the Euclidean space, a decrease of system size is equivalent to an increase of temperature. The effective coupling in the modified NJL model shows a decreasing behavior as the volume size decreases. In this paper, we only studied the chiral phase transition at finite temperature. To locate the CEP, this model must be extended to the case of finite chemical potential, which is the next step in our work.
Finite volume effects on the QCD chiral phase transition in the finite size dependent Nambu-Jona-Lasinio model
- Received Date: 2018-08-16
- Accepted Date: 2018-12-06
- Available Online: 2019-03-01
Abstract: The effective Lagrangian of a finite volume system should, in principle, depend on the system size. In the framework of the Nambu-Jona-Lasinio (NJL) model, by considering the influence of quark feedback on the effective coupling, we obtain a modified NJL model so that its Lagrangian depends on the volume. Based on the modified NJL model, we study the influence of finite volume on the chiral phase transition at finite temperature, and find that the pseudo-critical temperature of crossover is much lower than that obtained in the normal NJL model. This clearly shows that the volume dependent effective Lagrangian plays an important role in the chiral phase transitions at finite temperature.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: