-
The critical phenomena, occurring in the second or higher order phase transitions, displays several novel properties (e.g. universal power law divergence of some quantities, and scaling relations of different quantities), which are strongly related to the correlations of the fluctuations and cannot be described by mean field calculations at spatial dimension lower than four [1]. It was first experimentally observed in the carbon dioxide system [2], and has been studied well in other systems (see Ref. [3,4] for further details). In the field of nuclear physics, the progresses of relativistic heavy-ion collisions [5-7] have motivated a significant amount of research on the criticality of the critical end point (CEP) in quantum chromodynamics (QCD) phase transition (refer to Refs. [8, 9] for details). It is widely accepted that with the physical quark masses QCD, phase transition should be a continuous crossover at small baryon chemical potential, while it becomes a first-order transition for sufficiently large baryon number density. Between the two kinds, a second-order phase transition would occur at the CEP. Along with the criticality at CEP in
$ T-\mu $ plane with physical quark masses, the criticality of the chiral critical lines in the entire quark masses plane$ m_{u/d}-m_s $ has also attracted a significant amount of attentions [3,4,10-14] theoretically.In general, the main characteristics of a critical point are described by a set of critical exponents, which are related to the leading scaling behavior of certain quantities along certain axes. For example, conventionally, the standard thermodynamical critical exponents
$ (\alpha,\beta,\gamma,\delta) $ are defined as follows. The exponent$ \alpha $ is related to the leading power scaling of specific hea t$ C_\rho $ by$ C_\rho \sim|T-T_{\rm c}|^{-\alpha}, $

(1) as the critical point is approached along the first-order axis with a certain density
$ \rho $ . The exponent$ \beta $ is defined as$ \Delta\rho \sim(T_{\rm c}-T)^{-\beta}, $

(2) when the temperature
$ T $ approaches the critical temperature$ T_{\rm c} $ along the first-order line. Here,$ \Delta\rho $ is the the discontinuity of$ \rho $ across the first-order line. The exponent$ \gamma $ is defined as$ \chi_2 \sim(T-T_{\rm c})^{-\gamma}, $

(3) along the first-order axis, with
$ \chi_2\equiv \left(\displaystyle\frac{\partial\rho}{\partial\mu}\right)_{T} $ the baryon number susceptibility. The exponent$ \delta $ is defined as$ \rho-\rho_{\rm c} \sim(\mu-\mu_{\rm c})^{\frac{1}{\delta}}, $

(4) when
$ \mu $ approaches$ \mu_c $ , and the temperature is fixed to the critical temperature$ T_{\rm c} $ . Along with the definition from the thermodynamical quantities, the critical exponents can also be defined using the order parameters like chiral condensate [12, 15] and pion condensate [16]. Other than the above critical exponents related to the scaling behavior of static quantities, the critical exponents also describe the dynamical evolution when a system approaches the critical point; these are not discussed here. Using the renormalization group theory [17], the critical exponents are related to each other by the following equations:$ \alpha+2\beta+\gamma=2,\alpha+\beta(1+\delta)=2. $

(5) The mean field calculation show that
$ \alpha=0 $ ,$\beta=\displaystyle\frac{1}{2}$ ,$\gamma=1$ , and$\delta=3$ in three-dimensional (3D). Many research efforts have been made to go beyond the mean field approximation in order to study the critical behavior of QCD using different methods such as lattice simulations [18-22], Dyson-Schwinger equations [23, 24], functional renormalization group [16, 25],$ \epsilon $ expansion [10, 26]. In general, the lattice simulations are the most reliable method to study QCD. It is extracted from lattice simulations that$ \alpha\approx-0.213$ ,$\beta\approx 0.385$ ,$\gamma\approx 1.453$ ,$\delta\approx 4.824 $ for$ O(4) $ universality class [27-29] and$ \alpha\approx 0.110 $ ,$\beta\approx 0.327$ ,$\gamma\approx 1.237$ ,$\delta\approx 4.789$ for$Z(2) $ universality class [30]. However, when quark masses become small, lattice simulations become fairly expensive. Moreover, the sign problem makes it hard to obtain a reliable result for large baryon number density. Thus, it is necessary to investigate QCD phase transition using other methods to investigate the properties of QCD. The development of anti-de Sitter/conformal field theory correspondence (AdS/CFT) [31-33] provides a new method to deal with strong interacting systems such as QCD. Many research attempts have been made to build a realistic holographic QCD model to describe hadron physics [34-58], hot/dense QCD matter [59-76], etc. For near critical point physics in bottom-up holographic QCD, several groups have developed different models with CEP in the Einstein-Maxwell-Dilaton (EMD) system [76-80]. The static critical scaling near the CEP is investigated in [77], and it is shown to be$ \alpha=0$ ,$\beta\approx0.482$ ,$\gamma\approx0.942$ ,$\delta\approx3.035 $ , which are in agreement with the mean field results. Meanwhile, the dynamical critical exponents, which are related to the dynamical evolution of the system towards the critical point, are analyzed in [78-80]. Further, the critical exponents at chiral critical lines are given in [81]. Most studies provide a group of thermodynamical critical exponents that are similar to the mean field results. This might be owing to the suppression of quantum corrections by large$ N_c $ as noted in [77]. In the phenomenological sense, it is noteworthy to check if the critical behavior can be described beyond mean field level. Because if one tries to compare the holographic data to lattice simulations or experimental data, the value of$ N_c $ is not infinite in some scenarios. In this work, we follow the studies in [82, 83] and attempt to extract the critical exponents in a holographic QCD model with a CEP.The remainder of this paper is organized as follows. In Section 1, we provide a brief introduction of the critical phenomena and holographic method. In Section 2, we describe the EMD system, which we take as our basis. In Section 3, we present the results of our holographic QCD model. Finally, in Section 4, a short summary is provided.
-
As mentioned above, the EMD system provides a good basis to consider both finite temperature and finite chemical potential. By including a
$ U(1) $ gauge field, the chemical potential can be introduced in the system. In the framework of EMD system, the authors of [82] proposed a holographic QCD model with a CEP at$ T_{\rm c}=0.121 $ GeV,$\mu^B_{\rm c}=0.693 $ GeV. The model is shown to produce correct vector meson spectra as well as thermodynamical data. In [83], it is shown that the baryon number susceptibilities extracted in this model are comparable with the experimental data. Furthermore, the study demonstrates the close relationship between the location of the CEP and the location of the peak in baryon number susceptibilities. In this study, we attempt to examine the critical behavior near the CEP and check if it is possible to go beyond mean field level.First, for the compactness of this paper, we will briefly introduce the EMD system. From [82], the action is taken as
$ S=S_{\rm b}+S_{\rm m}, $

(6) $ S_{\rm b}=\frac{1}{16\pi G_5}\int {\rm d}^5x\sqrt{-g}\left[R - \frac{f(\phi)}{4}F^2-\frac{1}{2}\partial_\mu\phi\partial^\mu\phi-V(\phi)\right] , $

(7) $ S_{\rm m}=\frac{1}{16\pi G_5}\int {\rm d}^5x\sqrt{-g}\left[\frac{f(\phi)}{4}\left(F^2_V+F^2_{\tilde{V}}\right)\right]. $

(8) Here
$ S $ is the full action including the background part$ S_{\rm b} $ and the matter part$ S_{\rm m} $ ,$ g $ is the determinant of metric$ g_{\mu\nu} $ ,$ G_5 $ is the 5D Newton constant,$ \phi $ is the dilaton field,$ F, F_V, F_{\tilde{V}} $ are the strength tensor of gauge field dual to the baryon number current, isospin vector current, and axial-vector current, respectively. In general, if$ F,F_V,F_{\tilde{V}}=$ 0, it is reduced to the zero chemical potential case. If$ F \neq 0 $ , one could introduce baryon number chemical potential in the system, while for$ F_V \neq 0 $ the corresponding chemical potential related to isospin number can be introduced. In the present study, we focus on cases with finite baryon number densities and set$ S_{\rm m}=0 $ . The EMD system could describe glue-dynamics well. In [76], it is shown to describe the phase diagram in heavy quark limit well. Further, in Einstein-Dilaton system, it was shown that the glue ball spectral and the pure gluon thermodynamics could be described well [49, 75]. To take chiral dynamics into consideration, a direct method is to add the$ S_{\rm m} $ part. Further, similar to [82], one can add thechiral dynamics by adjusting the dilaton potential$ V(\phi) $ carefully. In some sense,$ S_{\rm m} $ part is replaced by the potential terms. In this work, we follow [82], and choose the latter approach.To consider gravity dual to QCD, we consider the following metric ansatz
$ {\rm d}s^2=\displaystyle\frac{{\rm e}^{2A(z)}}{z^2}\left[-h(z){\rm d}t^2+\frac{1}{h(z)}{\rm d}z^2+{\rm d}\vec{x}^{\;2}\right], $

(9) and consider the black hole solution. Inserting the metric ansatz into Eq.(7), one can derive the Einstein equation and simplify it as [82]
$ \phi^{\prime\prime}+\left( \frac{g^{\prime}}{g}+3A^{\prime}-\dfrac{3} {z}\right) \phi^{\prime}+\left( \frac{z^{2}e^{-2A}A_{t}^{\prime2}f_{\phi} }{2g}-\frac{e^{2A}V_{\phi}}{z^{2}g}\right) =0, $

(10) $ A_{t}^{\prime\prime}+\left( \frac{f^{\prime}}{f}+A^{\prime}-\dfrac{1} {z}\right) A_{t}^{\prime} =0, $

(11) $ A^{\prime\prime}-A^{\prime2}+\dfrac{2}{z}A^{\prime}+\dfrac{\phi^{\prime2}}{6} =0, $

(12) $ g^{\prime\prime}+\left( 3A^{\prime}-\dfrac{3}{z}\right) g^{\prime} -{\rm e}^{-2A}z^{2}fA_{t}^{\prime2} =0, $

(13) $ A^{\prime\prime}+3A^{\prime2}+\left( \dfrac{3g^{\prime}}{2g}-\dfrac{6} {z}\right) A^{\prime}-\dfrac{1}{z}\left( \dfrac{3g^{\prime}}{2g}-\dfrac {4}{z}\right) +\dfrac{g^{\prime\prime}}{6g}+\frac{{\rm e}^{2A}V}{3z^{2}g} =0. $

(14) In the above equations, there are undefined functions such as
$ A(z) $ ,$A_t(z)$ ,$f(z)$ ,$\phi(z)$ ,$V(\phi)$ ,$ f(\phi) $ , which should be input as the basis of the model. In general, there are different kinds of methods to deal with this issue as discussed in [49]. One can input$ V(\phi), f(\phi) $ as in Refs. [77] and solve$ A(z), \phi(z),A_t(z) $ numerically from the equations of motion. Another method is to input$ \phi(z),f(\phi) $ or$ A(z), f(\phi) $ and solve the rest; this method is usually called the "potential reconstruction approach" and is used in several works [75, 76, 84-88]. As analyzed in [85], the potential reconstruction approach could be considered as a good approximation of the fixing potential method. The qualitative picture of the thermodynamical quantities and phase transition structure are the same as in fixing potential method. Because it is convenient and the main features are maintained, we follow the study in [82] and use the potential reconstruction method.As in [82], we take
$ A(z) $ and$ f(z) $ as$ A(z)=-\frac{c}{3} z^2-b z^4, $

(15) $ f(\phi(z))={\rm e}^{c z^2-A(z)}. $

(16) Here,
$ b,c $ are model parameters, which are fixed from the meson spectra and sound speed data to be b= −6.25×$ 10^{-4} \;{\rm GeV}^4, c=0.227\;{\rm GeV}^2 $ . Requiring the boundary conditions at the horizon$ z=z_H $ and boundary$ z=0 $ $ A_t(z_H)=g(z_H)=0, $

(17) $ A(0)=-\sqrt{\frac{1}{6}}\phi(0), g(0)=1, $

(18) $ A_t(0)=\mu+\rho z^2+\cdots, $

(19) one can solve the remaining unknown functions, which are described in detail in [82]; the calculations are not repeated here. To study the thermodynamical properties, one can extract the baryon number density
$ \rho $ , entropy density$ s $ , and temperature$ T $ from the background solution as$ \rho=\frac{ c \mu }{1-{\rm e}^{c z_H^2}}, $

(20) $ s=2\pi \frac {{\rm e}^{3A(z_H)}}{z_H^3}, $

(21) $ \begin{split} T=&\displaystyle\frac{z_H^3 {\rm e}^{-3 A(z_H)}}{4 \pi \int_0^{z_H} y^3 {\rm e}^{-3 A(y)} {\rm {\rm d}}y}\left[1-\frac{2 c \mu ^2}{(1-{\rm e}^{c z_H^2})^2}\right. \\ &\times\left.\left( {\rm e}^{c z_H^2} \int_0^{z_H} y^3 {\rm e}^{-3 A(y)} {\rm d}y-\int_0^{z_H} y^3 {\rm e}^{c y^2-3 A(y)} {\rm d}y\right)\right]. \end{split} $

(22) From the above equations, one can obtain free energy by thermodynamical relations
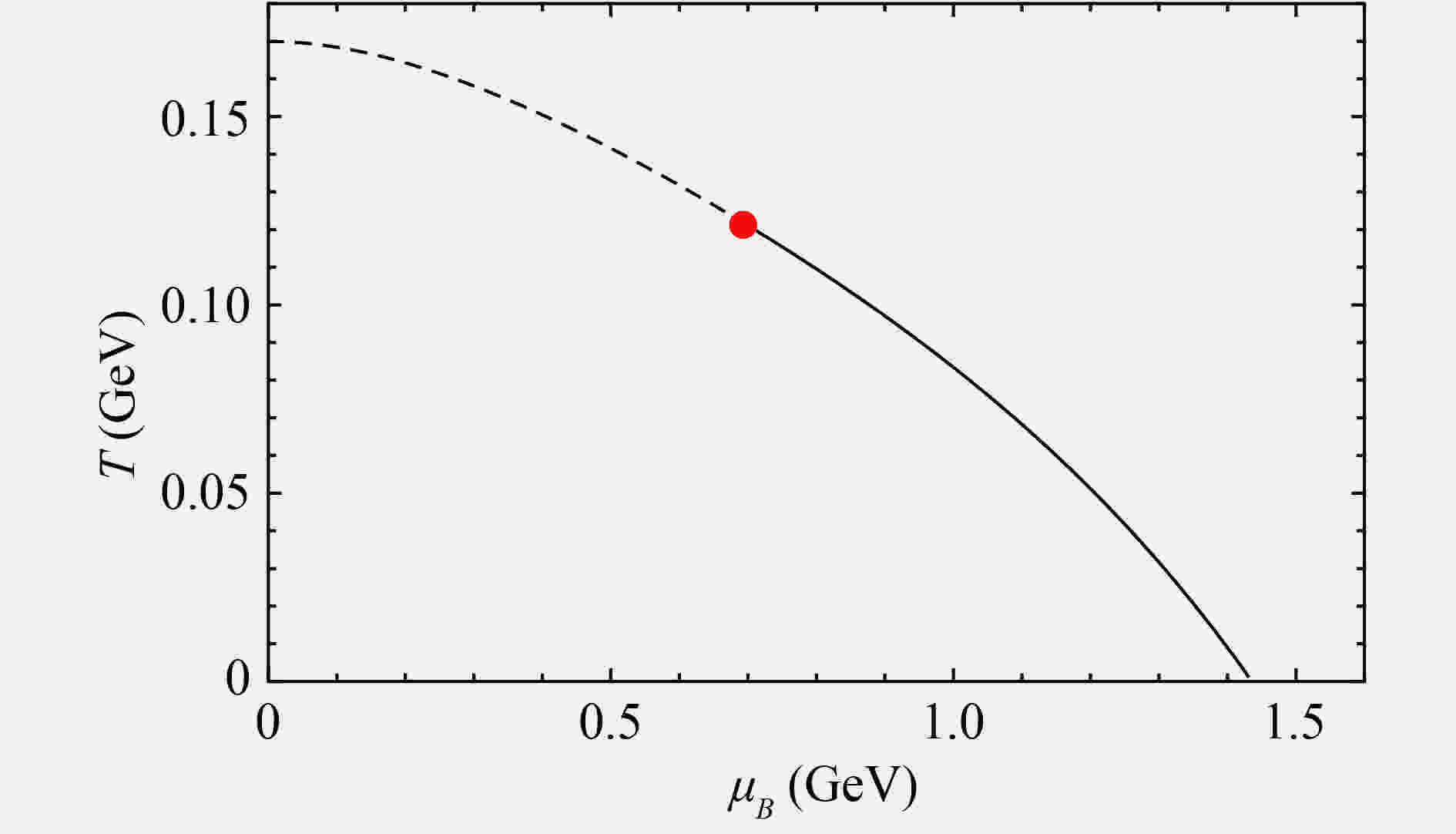
$ F=-\int [s{\rm d}T+\rho {\rm d}\mu] $ . It is found that at small chemical potential regions, there is only one solution for each temperature. The low-energy phase and high-energy phase are connected smoothly, which gives a crossover transition. Meanwhile, when the chemical potential is sufficiently large, there would be three branches of solutions in a short temperature region, showing a typical first-order transition. Minimizing the free energy, the transition temperature of the first-order phase transition can be determined. The phase transition line was determined as in Fig. 1, where we find a crossover line (the black dashed line) and a first-order line (the black solid line). The boundary of the crossover line and the first-order line is the CEP, which is located at$(T^{\rm c},\mu_B^{\rm c})= $ $ (0.121\;{\rm GeV},0.693\;{\rm GeV}) $ . In the next section, we focus on studying the near critical point behavior of this CEP.
Figure 1. Phase diagram in
${ T-\mu_B }$ plane from the holographic QCD model defined in Eqs. (15, 16) with${ b=-6.25\times 10^{-4}\; {\rm GeV}^4, c=0.227\;{\rm GeV}^2 }$ . At small chemical potential, the phase transition is a crossover (the black dashed line), while it turns to be first order one (the black solid line) at large chemical potential. The CEP (the red dot) locates at$ {(T^{\rm c},\mu_B^{\rm c})=(0.121\;{\rm GeV},0.693\;{\rm GeV}) }$ . -
Compared to the traditional method, holographic methods describe the system in a higher dimension. The fifth dimension in holographic QCD could be mapped to the energy scale, and the evolution of fields in the fifth dimension could be mapped to the running of couplings in the four-dimensional (4D) theory. Hence, one should expect the corrections from holographic methods to critical exponents given by the mean field theory. However, the studies in [77] showed that the corrections are suppressed in the holographic method. To verify this, we studied the near critical point behavior in an independent holographic model. In particular, in this section, we focused on extracting the critical exponents
$ (\alpha, \beta, \gamma, \delta) $ of the holographic model described in the previous section.First, we analyze the specific heat, which is defined as
$ C_\rho\equiv T\left(\displaystyle\frac{\partial s}{\partial T}\right)_{_\rho} $ . We fix the baryon number density and take the derivative of entropy density with respect to$ T $ . We find that$ C_\rho $ is a regular function of temperature at$ T=T_{\rm c} $ , as shown in Fig. 2. This indicates that the exponent$ \alpha $ defined in Eq. (1) would be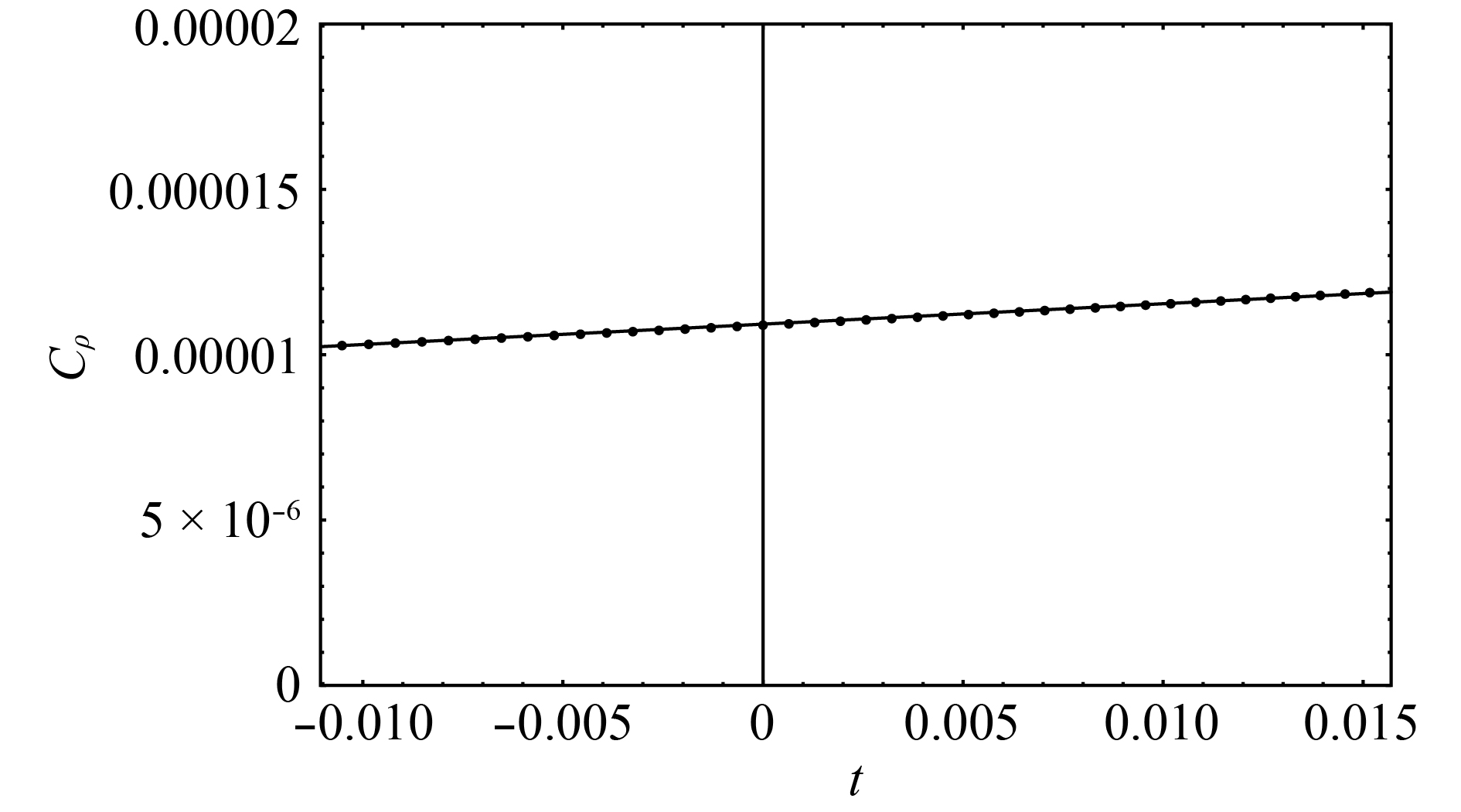
Figure 2. Specific heat
${ C_\rho} $ around the critical point along a line of constant${ \rho }$ , along the first-order axis. From this figure, we can see${ \alpha }$ = 0.$ \alpha = 0. $

(23) Then, we examine the critical behavior of the discontinuity of the baryon number density
$ \Delta \rho $ . It is easy to understand that near the crossover line in Fig. 1 the difference of$ \rho $ of the two sides should be zero. Therefore, we focus on the first-order line. Near the first order line, at a certain temperature, the density$ \rho $ is triple-valued function of the baryon chemical potential, as shown in Fig. 3(a). From Fig. 3(a), we can see that outside the range$ \mu_< < \mu < \mu_> $ the solution of equation of motion is single-valued, while inside this region it is triple-valued. Because the critical exponent$ \beta $ is defined along the first-order line, we have to determine the transition chemical potential. In principle, it should be done by minimizing the free energy, or equivalently from Maxwell's equal-area construction. Here, we use Maxwell's equal-area construction to determinate the transition point. Because we only want to study the critical exponent of$ \Delta\rho $ , we can simply consider$ \Delta\rho \equiv\rho_>-\rho_< $ on the first-order line. Under this convention, we show the log-log plot of$ (\log(t),\log(\Delta\rho)) $ in Fig. 3(b), with$ t \equiv(T-T_{\rm c})/T_{\rm c} $ . From this plot, we can see that the data points of$ (\log(t),\log(\Delta\rho)) $ lie almost in a straight line, showing the power low divergence of the critical behavior of$ \Delta\rho $ versus$ T-T_{\rm c} $ . From the linear fitting, we find that the slope of the straight line is approximately 0.54, which implies that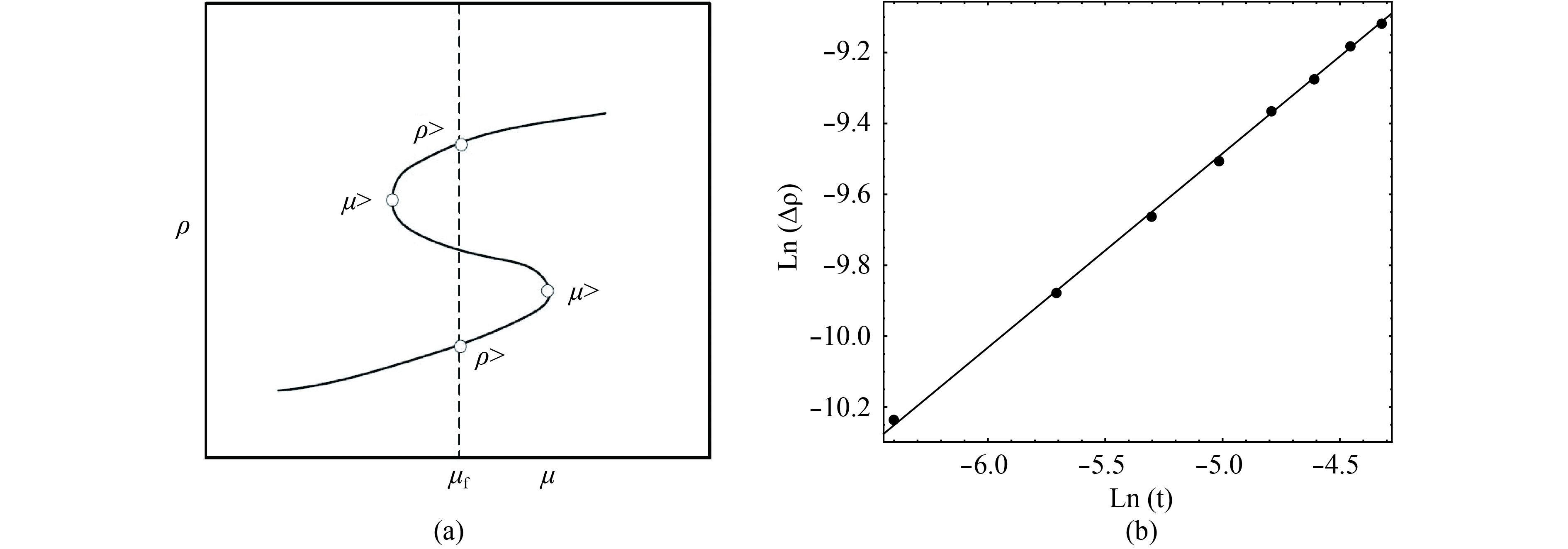
Figure 3. Discontinuity in the baryon number density on a log-log plot. The slope gives us a value
$ {\beta }$ = 0.54, here${ t\equiv(T-T_{\rm c})/T_{\rm c} }$ .$ \beta\approx 0.54, $

(24) which is in agreement with the mean field value
$ \beta=\displaystyle\frac{1}{2} $ in 3D.As defined in Eq. (2), the critical exponent comes from the baryon number susceptibility
$ \chi_2\equiv \left(\displaystyle\frac{\partial\rho}{\partial\mu}\right)_{T} $ . Taking the derivative of$ \rho $ with respective to$ \mu $ , we can extract$ \chi_2 $ from the results of$ \rho $ . The log-log plot of$ \chi_2 $ versus$ T $ is shown in Fig. 4. From the plot, we can see that$ \chi_2 $ diverges at the CEP$ t=0 $ . All the data points of$ (\log(t),$ $\log(\chi_2)) $ lie almost on a straight line. From the linear fitting, we obtain the slope of the straight line as 0.95, which implies that the critical exponent$ \gamma=1.05 $ .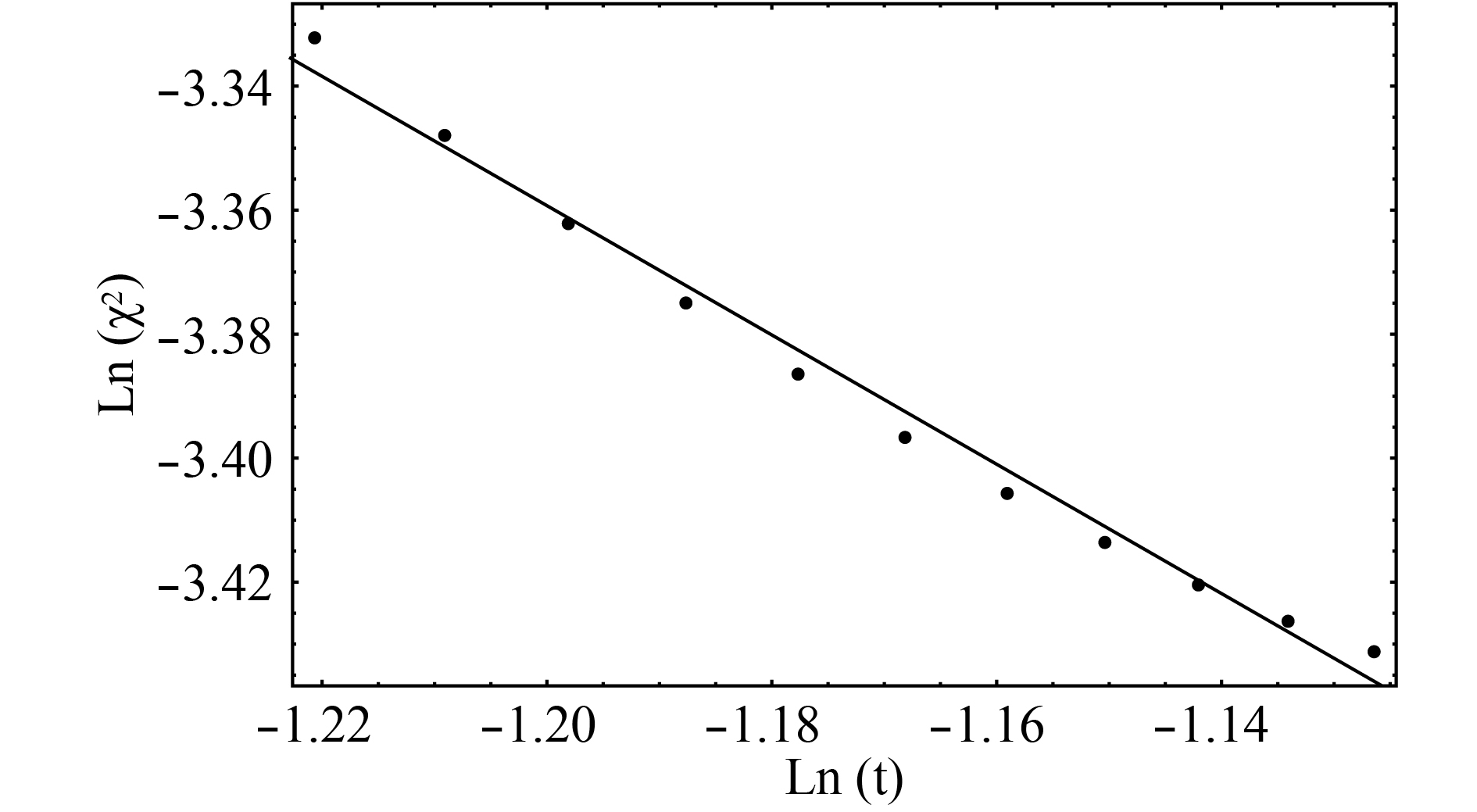
Figure 4. Baryon number susceptibility
${ \chi_2 }$ vs${t \equiv (T-T_{\rm c}) / T_{\rm c}}$ as the critical point is approached on a log-log plot. The slope of a best fit line through the data gives the value$ {\gamma= 1.05} $ .Taking
$ T=T_{\rm c}=0.121 $ GeV,$\mu=\mu_{\rm c}=0.693 $ GeV, we obtain$ \rho_{\rm c}=0.00004858 $ . Keeping$ T=T_{\rm c} $ and varying$ \mu $ , we can find that$ \rho $ changes correspondingly. The log-log plot of$ \rho-\rho_{\rm c} $ versus$ \mu-\mu_{\rm c} $ is given in Fig. 5. From the figure, we see that all the data points of$ (\log(\mu-\mu_{\rm c}),\log(\rho-\rho_{\rm c})) $ lie almost in a straight line, showing the leading power low of the critical behavior of$ \rho-\rho_{\rm c} $ versus$ \mu-\mu_{\rm c} $ . From the linear fitting, we find that the slope of the straight line is approximately 0.337, which implies that
Figure 5.
$ {\rho} $ approaches${ \rho_{\rm c} }$ as$ {\mu }$ approaches${ \mu_{\rm c} }$ on the critical isotherm on a log-log plot. The slope shows$ {\delta }$ = 2.97.$ \delta\approx 2.97, $

(25) which is in agreement with the mean field value
$ \delta=3 $ in 3D. -
We studied the critical behavior of hot and dense QCD matter in the holographic QCD model from [82], which could describe both the meson spectra quantitatively and phase diagram qualitatively. We extracted the specific heat
$ C_\rho $ , discontinuity of baryon number density$ \Delta\rho $ , baryon number sucesptibility$ \chi_2 $ , and baryon number density$ \rho $ near the critical point. We found that the specific heat is a regular function of$ T $ near the CEP, which indicates that$ \alpha=0 $ . Unlike the specific heat, the other three quantities diverge at the CEP. We obtained the log-log plot of these quantities and found that the numerical data lies almost in straight lines for the three quantities, which impies the leading power law of the critical scaling. From the linear fitting, we obtain the results$ \alpha=0 $ ,$\beta\approx $ 0.54,$\gamma=$ 1.05, and$\delta=2.97$ , which is almost the same as the 3D Ising mean field result, which shares the same critical exponents with a large variety of systems in the mean field level.The result is in agreement with the results from a previous study on different holographic models [78]. The current result is within the mean field approximation. However, in some sense, the holographic method could characterize the running coupling of the 4D theory. This might be owing to the large
$ N_{\rm c} $ suppression of the quantum corrections as mentioned in [77]. If we consider this problem from a more general Gauge/Gravity duality, going outside the limitation of the large$ N_{\rm c} $ in a phenomenological approach, there might be another possibility. The EDM system might only describe the pure glue system. Although, if the potential$ V(\phi) $ or other quantities are adjusted to incorporate the effects of chiral dynamics, only the interaction far away from the CEP are described well. Near the CEP, owing to the divergence of the correlation length, the contribution from the chiral dynamics might also be important①). Therefore, we might expect the correct couplings between the glue dynamics and the chiral dynamics could improve this problem. In fact, in our recent study, [89], we found that the running of the dilaton field with temperature would affect the chiral critical exponents in the soft-wall model. If the dilaton field does not depend on the temperature, the chiral critical exponents would be mean field result, while when the dilaton field exhibits critical scaling near the critical temperature, the chiral critical exponents would go beyond the mean field level (For further details, please refer to [89].) Therefore, we expect that if we correctly couple the two dynamics in a full system, correct critical behavior might be obtained.
Criticality of QCD in a holographic QCD model with critical end point
- Received Date: 2018-10-18
- Available Online: 2019-02-01
Abstract: The thermodynamics of strongly interacting matter near the critical end point are investigated in a holographic QCD model, which can describe the QCD phase diagram in






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: