-
To understand the confinement nature of QCD, it is crucial to study the spectral properties of quarkonia in hot and dense asymmetric hadronic matter. The in-medium properties of excited charmonium states
$ (\chi_c $ and$ \psi $ ) and open charm mesons (D and$ \bar D $ ) can alter the$ J/\psi $ production rate and its suppression in non-central heavy ion collisions [1, 2]. The suppression mechanism suggested by Matsui and Satz cannot fully explain recent experimental data, which exhibit non-trivial suppression [3-5]. Therefore, to understand the additional suppression mechanism, various other methods such as density dependent suppression and comover scattering have been proposed [3, 6, 7]. In addition to the temperature and density, it is believed that in non-central heavy ion collisions, such as in the large hadron collider (LHC) and in the relativistic heavy ion collider (RHIC), immense magnetic fields are generated, approximated on the order of$ eB $ ~$ 2-15 m_{\pi}^2 $ (1$ {{m}_{\pi}^2} $ =$ 2.818\times 10^{18} $ Gauss) [8-10]. The decay of the magnetic field does not occur immediately due to its interaction with residual matter. This is referred to as the chiral magnetic effect [9, 11-13]. According to Lenz's law, this magnetic field generates induced currents in remnant matter, which further generate the induced magnetic field that affects the relaxation time and electric conductivity of the medium, and eventually the decay of the external magnetic field [14-20]. This extended decay time allows higher charmonium and bottomonium states to interact with the magnetic field even in hot nuclear matter [19-23]. The presence of the magnetic field may induce modification of chiral condensates [24-27] in addition to quarkonia, which further has an impact on the properties of different mesons, such as the$ \rho $ [28], B [29, 30], and D meson [19, 31]. Significant observables are expected in future experiments, as in the compressed baryonic matter (CBM) of the FAIR collaboration, the Japan Proton Accelerator Research Complex (J-PARC) and Nuclotron-based Ion Collider Facility (NICA,), which may shed light on the medium modifications of charmonia and bottomonia with regard to the density, temperature, and magnetic field [32].To explain the QCD phase diagram in a non-perturbative region, various phenomenological models are proposed on the basis of the effective field theory, namely the Walecka model [33], Nambu-Jona-Lasinio (NJL) model [34], Polyakov loop extended NJL (PNJL) model [35-37], quark-meson coupling (QMC) model [38-43], Polyakov quark meson (PQM) model [44, 45], coupled channel approach [46-49], chiral
$ SU(3) $ model [21, 50-53], and QCD sum rules [54-59]. These models incorporate basic QCD properties such as trace anomaly and chiral symmetry. The Polyakov extended models [60, 61] and functional renormalization group (FRG) [62, 63] techniques incorporate thermal and quantum fluctuations near the critical temperature region. With these beyond mean field approximations, the critical point moves towards the larger chemical potential side [64, 65]. In previous studies, we investigated the magnetic field-induced in-medium properties of lowest charmonium states$ J/\psi $ and$ \eta_c $ using the QCDSR. We have shown that the mass-shift reflects the behavior of gluon condensates, which were incorporated from the chiral$ SU(3) $ model [21]. In the present study, we intend to investigate the effect of the external magnetic field on P-wave charmonium as well as S and P-wave bottomonium states at finite temperature and density. To this end, the non-perturbative mean field approximation is used, where the contributions from fluctuations are neglected. In this approximation, the contributions from the pseudoscalar and axial vector meson are neglected, as all meson fields are treated as classical fields [50, 51]. The chiral$ SU(3) $ model is vastly applied to investigate the in-medium properties of light mesons in nuclear and hyperonic matter [53, 66, 67]. To study the in-medium properties of heavy D and B mesons, this model is also generalized to$ SU(4) $ and$ SU(5) $ respectively [51, 52, 68, 69]. In this model, the scalar and tensorial gluon condensates are extracted in terms of the in-medium non-strange meson field$ \sigma $ , strange scalar meson field$ \zeta $ , scalar isovector meson field$ \delta $ , vector meson field$ \omega $ , vector-isovector meson field$ \rho $ , and dilaton field$ \chi $ [50]. In contrast, QCDSR, which represents a non-perturbative approach to investigate the confining nature of strong interactions, has also been used extensively to study the in-medium properties of heavy mesons [20, 22, 53, 54, 57-59, 70-73]. The open charm and bottomonium mesons have also been studied under the influence of a strong magnetic field [19, 29, 31].The in-medium properties of charmonia and bottomonia have been studied extensively in the literature [2, 20-23, 53, 71, 74-78]. Because of the interaction of gluon condensates in hadronic medium, the quarkonia undergo significant modifications. The P-wave charmonia with modified mass and decay width decays into
$ J/\psi $ and hence affects the production ratio$ N_{J/\psi}/N_{\chi_c} $ in nuclear matter, which further affects the suppression mechanism [76]. The medium modifications of masses and the decay width of$ {\chi_c}_0 $ and$ {\chi_c}_1 $ mesons in hot gluonic matter as a function of temperature has been studied using QCD sum rules [2]. In this study, the authors investigate the larger mass-shift and width broadening for the P-wave charmonium states as compared to lower states$ J/\psi $ and$ \eta_c $ [53, 73]. In Refs. [23, 77], using QCD second order stark effect, the in-medium properties of heavy charmonium states ($ \psi $ (3686) and$ \psi $ (3770)) were studied in the nuclear matter, and a significant mass-shift was observed. Moreover, in Ref. [20], authors have studied the effect of the magnetic field on the lowest charmonium states using QCD sum rules. The magnetic field-induced mass mixing of$ J/\psi $ and$ \eta_c $ has also been calculated under the QCD sum rules approach [22]. The mass-shift of bottomonia is studied by the unification of QCDSR and the maximum entropy method (MEM) in Ref. [71]. The bottomonia mass-spectra were calculated for different temperatures. In Ref. [78], authors investigated the mass-splitting by studying the mixing of pseudoscalar and vector charmonia and bottomina in the Cornell potential due to the background magnetic field. The mass modifications of the Upsilon$ \Upsilon $ bottomonium state has been studied using the chiral$ SU(3) $ model in the magentized nuclear matter at zero temperature, and it has been observed that the magnetic field effects are more prominent in the high density regime [75].The article is organized as follows: in the following section, we briefly describe the methodology to calculate the mass spectra of charmonia and bottomonia. In Section 3, we discuss the quantitative results of the present work. Finally, Section 4 provides the conclusion.
-
To study the effective mass of charmonium and bottomonium, we use the conjunction of QCDSR with the chiral
$ SU(3) $ model, which depicts the non-perturbative mechanism to study the confining nature of QCD [50, 54, 57, 59, 66]. In subsection 2.1, we briefly explain how gluon condensates are extracted from the chiral SU(3) model. The Borel sum rule and moment sum rule are explained in subsection 2.2. -
To describe nucleon-nucleon interactions, we employ an effective field theoretical approach, which is based on the non-linear realization of chiral symmetry [79-81] and broken scale invariance [50, 51, 66] in the presence of external magnetic field at finite temperature and density. These interactions are expressed in terms of the scalar fields
$ \sigma $ ,$ \zeta $ ,$ \delta $ ,$ \chi $ , and vector fields$ \omega $ and$ \rho $ in this model. The$ \rho $ and$ \delta $ fields are incorporated to introduce the effect of the isospin asymmetry in nuclear medium. Moreover, the dilaton$ \chi $ field is introduced to incorporate the trace anomaly property of QCD [50]. The Lagrangian density of the chiral$ SU(3) $ model with the mean-field approximation is given as$ {\cal L}_{\rm chiral} = {\cal L}_{\rm kin} + {\cal L}_{\rm vec} + \sum\limits_{ M = S,V}{\cal L}_{\rm MN} + {\cal L}_{\rm SB} + {\cal L}_0 . $

(1) In the above equation,
$ {\cal L}_{\rm kin} $ represents the kinetic energy term,$ {\cal L}_{\rm vec} $ depicts the mass of vector mesons through the interactions with scalar fields and carries the self-interaction quartic terms, and$ {\cal L}_{\rm MN} $ is the meson-nucleon interaction term, where S and V represent the pseudoscalar and vector mesons, respectively.$ {\cal L}_{\rm SB} $ describes the explicit chiral symmetry breaking, and$ {\cal L}_{0} $ describes spontaneous chiral symmetry breaking.The thermopotential
$ \Omega $ per unit volume in zero magnetic field can be written as [21, 82]$\begin{split} \frac{\Omega }{V} = &- \frac{{{\gamma _i}T}}{{{{(2\pi )}^3}}}\sum\limits_{i = n{\kern 1pt} ,p{\kern 1pt} } {\int {{{\rm d}^3}} } k \left \{ {\text{ln}}\left( {1 + {e^{ - \beta [E_i^ * (k) - \mu _i^*]}}} \right)\right. \hfill \\ & \left.+ {\text{ln}}\left( {1 + {e^{ - \beta [E_i^ * (k) + \mu _i^*]}}} \right)\right \} - {L_{\rm vec}} - {L_{\rm SB}} - {L_0} - {V_{\rm vac}}, \hfill \\ \end{split} $

(2) where the sum runs over the neutron and proton,
$ \gamma_i $ is spin degeneracy factor for nucleons;$ \mu^{*}_{i} = \mu_{i}-g_{\omega i}\omega-g_{\rho i}\tau_{3}\rho $ and$ E^{\ast}_i(k) = \sqrt{k^2+{m^{*}_{i}}^2} $ are the effective nucleon chemical potential and the effective single particle energy of nucleons, respectively. Moreover, the vacuum potential energy,$ {\cal{V}}_{\rm vac} $ is subtracted from the thermopotential to obtain zero vacuum energy.The Lagrangian density (Eq.(1)) in the presence of a magnetic field modifies as
$ {\cal L} = {\cal L}_{\rm chiral}+{\cal L}_{\rm mag}, $

(3) where
$ {\cal L}_{\rm mag} = -{\bar {\phi_i}}q_i \gamma_\mu A^\mu \phi_i -\frac {1}{4} \kappa_i \mu_N {\bar {\psi_i}} \sigma ^{\mu \nu}F^{\mu \nu} \phi_i -\frac{1}{4} F^{\mu \nu} F_{\mu \nu}. $

(4) In the above equation,
$ \phi_i $ is a wave function of the$ i^{th} $ nucleon, and the next term represents the interaction with the electromagnetic field tensor,$ F_{\mu \nu} $ . Further,$ \mu_N $ and$ k_i $ are the nuclear magneton and the anomalous magnetic moment of$ i^{th} $ nucleon, respectively. In this study, the magnetic field is chosen to be uniform and along the Z-axis. We discuss the interactions of the uncharged and charged particle with the uniform magnetic field in the following.In the presence of the uniform external magnetic field, the charged proton experiences the Lorentz force, hence the Landau quantization is applied. In this quantization, the transverse momenta of the proton are confined to the closed loops, namely Landau levels,
$ \nu $ , with,$ k_\perp^2 = 2 \nu |q_p| B $ , where$ \nu \geqslant 0 $ is a quantum number [83]. Thus, the integral transformation takes place as$ \int {{\rm d}^3}k \rightarrow \frac{|q_p| B}{(2\pi)^2} \sum_{\nu} \int_{0}^\infty {\rm d} k_\parallel \, , $ where$ k_\parallel $ depicts the longitudinal momenta. Here, the summation represents a sum over the discrete Landau levels,$ \nu = n+\frac{1}{2}-\frac{q_p}{|q_p|}\frac{s}{2} = 0, 1, 2, \cdots $ of the proton in the normal plane. Moreover, n is the orbital quantum number, and the quantum number s is$ -1 $ for spin down and$ +1 $ for spin up protons. The effective single particle energy of the proton is likewise modified as$ \tilde E^{p}_{\nu, s} = \sqrt{\left(k^{p}_{\parallel}\right)^{2}+ \left(\sqrt{m^{* 2}_{p}+2\nu |q_{p}|B}-s\mu_{N}\kappa_{p}B \right)^{2}} $ [84].With these modifications, the first term of the thermopotential (Eq.(2)) for the proton will be
$ \begin{split} \frac{{{\Omega _p}}}{V} =& - \frac{{T|{q_p}|B}}{{{{(2\pi )}^2}}}\left[ {\sum\nolimits_{\nu = 0}^{\nu _{max}^{(s = 1)}} {\int_0^\infty {\rm d} } {k_\parallel }\bigg\{ {\rm{ln}}\left( {1 + {e^{ - \beta [\tilde E_{\nu ,s}^p - \mu _p^*]}}} \right) }\right.\\&+ {\rm{ln}}\left( {1 + {e^{ - \beta [\tilde E_{\nu ,s}^p + \mu _p^*]}}} \right)\bigg\} { +\!\! \sum\nolimits_{\nu = 1}^{\nu _{max}^{(s = - 1)}} \!\!{\int_0^\infty \!{\rm d} } {k_\parallel }\bigg\{ {\rm{ln}}\left( {1 + {e^{ - \beta [\tilde E_{\nu ,s}^p - \mu _p^*]}}} \right)} \\&\left.+ {\rm{ln}}\left( {1 + {e^{ - \beta [\tilde E_{\nu ,s}^p + \mu _p^*]}}} \right)\bigg\} \right ]. \end{split}$

(5) In contrast, there is no Landau quantization for an uncharged neutron in the presence of an external magnetic field, therefore the integral
$ \int \frac{{\rm d}^3k}{(2\pi)^3} \, $ remains unmodified [83]. However, because of the non-zero anomalous magnetic moment$ k_n $ , the effective single particle energy of the neutron is modified as$ \tilde E^{n}_{s} \!\!=\!\!\!\! \sqrt{\left(k^{n}_{\parallel}\right)^{2} \!\!\!+\!\! \left(\!\!\sqrt{m^{* 2}_{n}\!+\!\left(k^{n}_{\bot}\right)^{2} }\!-\!\!s\mu_{N}\kappa_{n}B \right)^{2}} $ ,and hence, the first term of Eq.(2) for the neutron will be$ \frac{\Omega_n} {V} \!= \!-\frac{T} {(2\pi)^3} \sum\limits_{s = \pm 1} \int {\rm d}^3k\biggl\{{\rm ln} \left( 1\!+\!e^{-\beta [ \tilde E^{n}_{s} - \mu^{*}_{n} ]}\right) + {\rm ln}\left( 1\!+\!e^{-\beta [\tilde E^{n}_{s}+\mu^{*}_{n}]} \right) \}. $

(6) The net thermopotential in the presence of uniform external magnetic field can be expressed as
$ \frac{\Omega} {V} = \frac{\Omega_p} {V}+\frac{\Omega_n} {V} -{\cal L}_{\rm vec}- {\cal L}_{\rm SB} - {\cal L}_0 -{\cal{V}}_{\rm vac}. $

(7) By minimizing the thermopotential
$ \Omega/V $ with respect to the fields$ \sigma $ ,$ \zeta $ ,$ \delta $ ,$ \chi $ ,$ \rho $ , and$ \omega $ , the corresponding coupled equations of motion of these fields are determined and given as$ \begin{split} \frac{\partial (\Omega/V)}{\partial \sigma} = &k_{0}\chi^{2}\sigma-4k_{1}\left( \sigma^{2}+\zeta^{2} +\delta^{2}\right)\sigma-2k_{2}\left( \sigma^{3}+3\sigma\delta^{2}\right) \\ &-2k_{3}\chi\sigma\zeta -\frac{d}{3} \chi^{4} \bigg (\frac{2\sigma}{\sigma^{2}-\delta^{2}}\bigg ) +\left( \frac{\chi}{\chi_{0}}\right) ^{2}m_{\pi}^{2}f_{\pi}\\ & -\displaystyle\sum g_{\sigma i}\rho_{i}^{s} = 0, \end{split} $

(8) $ \begin{split} \frac{\partial (\Omega/V)}{\partial \zeta} = &k_{0}\chi^{2}\zeta-4k_{1}\left( \sigma^{2}+\zeta^{2}+\delta^{2}\right) \zeta-4k_{2}\zeta^{3}-k_{3}\chi\left( \sigma^{2}-\delta^{2}\right)\\ &-\frac{d}{3}\frac{\chi^{4}}{\zeta}+\left(\frac{\chi}{\chi_{0}} \right) ^{2}\left[ \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi}^{2}f_{\pi}\right] \\ &-\sum g_{\zeta i}\rho_{i}^{s} = 0 , \end{split} $

(9) $ \begin{split} \frac{\partial (\Omega/V)}{\partial \delta} =& k_{0}\chi^{2}\delta-4k_{1}\left( \sigma^{2}+\zeta^{2}+\delta^{2}\right) \delta-2k_{2}\left( \delta^{3}+3\sigma^{2}\delta\right)\\ &+2k_{3}\chi\delta \zeta + \frac{2}{3} d \chi^4 \left( \frac{\delta}{\sigma^{2}-\delta^{2}}\right) -\sum g_{\delta i}\tau_3\rho_{i}^{s} = 0 , \end{split} $

(10) $ \begin{array}{l} \displaystyle\frac{\partial (\Omega/V)}{\partial \omega} = \left (\frac{\chi}{\chi_{0}}\right) ^{2}m_{\omega}^{2}\omega+g_{4}\left(4{\omega}^{3}+12{\rho}^2{\omega}\right)-\sum g_{\omega i}\rho_{i}^{v} = 0 , \end{array} $

(11) $ \begin{array}{l} \displaystyle\frac{\partial (\Omega/V)}{\partial \rho} = \left (\frac{\chi}{\chi_{0}}\right) ^{2}m_{\rho}^{2}\rho+g_{4}\left(4{\rho}^{3}+12{\omega}^2{\rho}\right)-\sum g_{\rho i}\tau_3\rho_{i}^{v} = 0 , \end{array} $

(12) and
$ \begin{split} \frac{\partial (\Omega/V)}{\partial \chi} =& k_{0}\chi \left( \sigma^{2}+\zeta^{2}+\delta^{2}\right)-k_{3} \left( \sigma^{2}-\delta^{2}\right)\zeta \!+\! \chi^{3}\left[1 +{\rm {ln}}\left( \frac{\chi^{4}}{\chi_{0}^{4}}\right) \right] \\ & +(4k_{4}-d)\chi^{3} -\frac{4}{3} d \chi^{3} {\rm {ln}} \Bigg ( \bigg (\frac{\left( \sigma^{2} -\delta^{2}\right) \zeta}{\sigma_{0}^{2}\zeta_{0}} \bigg ) \bigg (\frac{\chi}{\chi_0}\bigg)^3 \Bigg )\\ & + \frac{2\chi}{\chi_{0}^{2}}\left[ m_{\pi}^{2} f_{\pi}\sigma +\left(\sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi}^{2}f_{\pi} \right) \zeta\right] \\ &-\frac{\chi}{{{\chi_0}^2}}(m_{\omega}^{2} \omega^2+m_{\rho}^{2}\rho^2) = 0 , \end{split} $

(13) respectively.
In the above equations,
$ f_K $ and$ f_\pi $ are the decay constants of K and$ \pi $ mesons, which also serve as order parameters of spontaneous symmetry breaking. The medium dependence of$ f_K $ and$ f_\pi $ in the present work is considered via equations$ f_K = - \frac{1}{2}(\sigma+\sqrt{2}\zeta) $

(14) and
$ f_\pi = -\sigma, $

(15) respectively. Moreover,
$ m_K $ and$ m_\pi $ are the masses of K and$ \pi $ mesons, respectively, and the additional parameters$ k_0, k_2 $ , and$ k_4 $ are fitted to reproduce the vacuum values of scalar$ \sigma $ ,$ \zeta $ , and$ \chi $ mesons and the remaining parameter$ k_1 $ is selected to generate the effective mass of nucleon at nuclear saturation density (around 0.$ 65 m_N $ ), while remaining parameter$ k_3 $ is constrained by$ \eta^\prime $ and$ \eta $ masses. The in-medium mass of nucleons is given as$ m_{i}^{*} = -(g_{\sigma i}\sigma + g_{\zeta i}\zeta + g_{\delta i}\tau_3 \delta) $ . Here,$ g_{\sigma i} $ ,$ g_{\zeta i} $ , and$ g_{\delta i} $ represent the coupling strengths of nucleons (i =$ n,p $ ) with$ \sigma $ ,$ \zeta $ , and$ \delta $ fields, respectively and are chosen to reproduce the vacuum mass of nucleons. The values of these different parameters used in the present work are listed in Table 1. Furthermore,$ \rho^{v}_{i} $ and$ \rho^{s}_{i} $ represent the number/vector and scalar densities of the$ i^{th} $ nucleon, respectively for the magnetic/non-magnetic case [21, 85-87]. The isospin asymmetry of the medium is defined by parameter$ \eta = (\rho^{v}_{n} -{\rho^{v}_{p}} )/2\rho_N $ , and$ \tau_3 $ denotes the third component of the isospin. The coupled Eq. (8) to Eq. (15) are solved simultaneously to obtain medium dependent values of different scalar and vector fields.$ \sigma_0 $ /MeV

$ \zeta_0 $ /MeV

$ \chi_0 $ /MeV

d $ \rho_0 $ /

$ {\rm fm}^{-3} $ 

−93.29 −106.8 409.8 0.064 0.15 $ k_0 $ 

$ k_1 $ 

$ k_2 $ 

$ k_3 $ 

$ k_4 $ 

2.53 1.35 −4.77 −2.77 −0.218 $ m_\pi $ /MeV

$ m_K $ /MeV

$ f_\pi $ /MeV

$ f_K $ /MeV

$ g_4 $ 

139 498 93.29 122.14 79.91 $ g_{\sigma N} $ 

$ g_{\zeta N } $ 

$ g_{\delta N } $ 

$ g_{\omega N} $ 

$ g_{\rho N} $ 

10.56 −0.46 2.48 13.35 5.48 Table 1. Values of various parameters.
The scalar gluon condensate
$ G_0 $ =$ \left\langle \frac{\alpha_{s}}{\pi} G^a_{\mu \nu} {G^a}^{\mu \nu} \right\rangle $ and tensorial gluon operator$ G_2 $ =$ \left\langle \frac{\alpha_{s}}{\pi} G^a_{\mu\sigma} {{G^a}_\nu}^{\sigma} \right\rangle $ can be expressed within the chiral SU(3) model in terms of scalar fields through following relation [53]$ G_0 \!=\! \frac{8}{9} \Bigg [(1 - d) \chi^{4} +\left( \frac {\chi}{\chi_{0}}\right)^{2} \left( m_{\pi}^{2} f_{\pi} \sigma + \left ( \sqrt {2} m_{K}^{2}f_{K} - \frac {1}{\sqrt {2}} m_{\pi}^{2} f_{\pi} \right ) \zeta \right) \Bigg ], $

(16) and
$ \begin{split} {G_2} = &\frac{{{\alpha _s}}}{\pi }\bigg [ - (1 - d + 4{k_4})({\chi ^4} - {\chi _0}^4) - {\chi ^4} \\ &\left. {\text{ln}}\left (\frac{{{\chi ^4}}}{{{\chi _0}^4}}\right ) + \frac{4}{3}d{\chi ^4}{\text{ln}}\left (\left (\frac{{\left( {{\sigma ^2} - {\delta ^2}} \right)\zeta }}{{\sigma _0^2{\zeta _0}}}\right ){\left (\frac{\chi }{{{\chi _0}}}\right )^3}\right)\right] \\ \end{split} $

(17) respectively. The value of d has been taken from the QCD beta function,
$ \beta_{\rm QCD} $ at the one loop level [50], with$ N_f $ flavors and$ N_c $ colors,$ \beta_{\rm QCD} = -\frac{11 N_c g^3}{48 \pi^2} \left(1-\frac{2N_f}{11 N_c}\right) +{\cal O}(g^5) . $

(18) In the limit, the quark mass term (second term) equals to zero, and the scalar gluon condensate given by Eq. (16) gets modified as
$ G_0 = \frac{8}{9} (1 - d) \chi^{4} . $

(19) -
In QCDSR, we employ two approaches, i.e., the Borel sum rules and the moment sum rules. The moment sum rules are derived using the operator product expansion (OPE) method, which is a non perturbative technique to define the product of fields as a sum over the same fields to resolve the difficulties arising from perturbative effects [54]. The Borel sum rules are derived from Borel transformations and OPE. These transformations are standard mathematical techniques to incorporate perturbative effects by summation of divergent asymptotic series [74]. The moment sum rule is a good tool to calculate heavy quark masses due to large separation of scale, nevertheless, Borel sum rules have several merits, i.e., better OPE convergence.
The current-current correlation function of heavy quark currents is given by [57]
$ \Pi^{\, J}(p) = i \int {\rm d}^4x {\rm e}^{{\rm i} p \cdot x} \langle T[j^{\, c}(x) j^{\, c {†}}(0)] \rangle , $

(20) with
$ \left\langle \right\rangle $ being the Gibbs average. In the above equation,$ p = ( E_0, \vec{p}) $ , is the four-momentum vector and symbol c represents the scalar$ (S) $ , vector$ (V) $ , pseudoscalar (P), and axial vector$ (A) $ mesons. These mesons currents are defined as$ j^{\, S} = \bar{q}q $ ,$ j^{\, V}_\mu = \bar{q} \gamma_\mu q $ ,$ j^{\, P} = \bar{q} \gamma_5 q $ , and$ j^{\, A}_\mu = (q_\mu q_\nu/q^2-g_{\mu \nu})\bar{q} \gamma^\nu \gamma_5 q $ with q as the heavy quark operator. -
We perform the Borel transformation [74] on the function
$ \Pi^{\, J}(p) $ by going into the deep Euclidean region ($ p^2 $ =$ E^2_0 $ = -$ \Omega^2\ll 0 $ ) to obtain a better radius of convergence. The transformed correlation function$ {\cal{M}}^J(M^2) $ can be written as$ { \cal{M}}^J(M^2) = \lim\limits_{\substack{\Omega^2/n \rightarrow M^2, \\ n,\Omega^2 \rightarrow \infty}} \frac{(\Omega^2)^{n+1}\pi}{n!}\left(-\frac{{\rm d}}{{\rm d}\Omega^2}\right)^n \tilde{\Pi}^J(\Omega^2). $

(21) At finite temperature and density of the medium and the correlation function can be expanded in terms of the dimension-4 scalar gluon condensate and twist-2 gluon operator, whose Borel transformation, using Eq. (21), will lead to
$ { {\cal{M}}^J(M^2) }= e^{-g}\pi A^J(g)[1+\alpha_s(M^2)a^J(g)+b^J(g)\phi_b +c^J(g)\phi_c], $

(22) In the above,
$ g = 4m_q^2/M^2 $ is a dimensionless scale parameter, where M depicts the Borel mass. Symbols$ A^J(g) $ ,$ a^J(g) $ ,$ b^J(g) $ , and$ c^J(g) $ are Borel transformed Wilson coefficients and are given in Ref. [74]. The first term is the leading order of OPE. The second term corresponds to the perturbative correction and the remaining two terms are associated with the medium modified scalar gluon condensate$ G_0 $ =$ \left\langle \frac{\alpha_{s}}{\pi} G^a_{\mu \nu} {G^a}^{\mu \nu} \right\rangle $ and tensorial gluon condensate$ G_2 $ =$ \left\langle \frac{\alpha_{s}}{\pi} G^a_{\mu\sigma} {{G^a}_\nu}^{\sigma} \right\rangle $ as$ \phi_{b} = \frac{4 \pi^{2}}{9} \frac{G_0 }{(4 m_{q}^{2})^{2}}, $

(23) and
$ \phi_{c} = \frac{4 \pi^{2}}{3(4 m_{q}^{2})^{2}}G_2 , $

(24) respectively, which are also the carrier of thermal effects of the medium. The
$ \alpha_{s} $ and$ m_{q} $ parameters are the running coupling constant and running quark mass, respectively. The condensate$ G_0 $ and$ G_2 $ appearing in the above equations are evaluated using Eqs. (16) and (17), respectively.In the QCDSR analysis, the dispersion integral is used to express the correlation function in terms of the spectral function. For finite temperature and density of the medium, the spectral function depicts the imaginary part of the correlation function [74]. Thus, we have following dispersion relation for the Borel sum rule,
$ { \cal{M}}^{{J}}(M^2) = \int_{0}^{\infty}{\rm d}s\,e^{-s/M^2}{\rm Im}\tilde{\Pi}^J(s). $

(25) In the above,
$ e^{-s/M^2} $ is an exponential weight factor, and s represents a continuum parameter.In Eq. (25), Im
$ \tilde{\Pi}^J(s) $ can be decomposed into the pole and the continuum part as$ {\rm{Im}}\tilde{\Pi}(s) = {\rm{Im}}\tilde{\Pi}^{{\rm pole}}(s) + {\rm{Im}}\tilde{\Pi}^{{\rm cont}}(s), $

(26) with the pole contribution under zero decay width approximation
$ {\rm{Im}}\tilde{\Pi}^{{\rm pole}}(s) = f_0\delta(s-{{m^*_{Q}}}^{2}), \quad \Gamma = 0, $

(27) where
$ f_0 $ is a strength parameter. The finite decay width is important in deconfined medium, whereas in the present work, we investigated the modification of masses of charmonium and bottomonium in nuclear medium, which is confined in nature [74]. In Ref. [88], using the zero width approximation, authors have studied the mass of light vector mesons$ \rho $ ,$ \omega $ , and$ \phi $ under finite temperature and density. The continuum contribution in Eq. (26) is defined in terms of a perturbative spectral function with a sharp threshold factor, i.e.,$ {\rm{Im}}\tilde{\Pi}^{{\rm cont}}(s) = \theta(s-s_0){\rm{Im}}\tilde{\Pi}^{J,{\rm{\rm pert}}}(s), $

(28) where
$ \theta(s-s_0) $ , is sharp threshold factor for the continuum, and the cut off parameter$ s_0 $ for the pole term is adjusted to reproduce the corresponding side of OPE and$ \tilde{\Pi}^{J,{\rm{pert}}}(s) $ perturbative spectral function for different meson currents [74]. Using Eq. (26) in (25), we have$ \begin{array}{l}{ \cal{M}}^{{J}}(M^2) = \displaystyle\int_{0}^{s_0}{\rm d}s\,e^{-s/M^2}{\rm{Im}}\tilde{\Pi}^{\rm pole}(s)+ \displaystyle\int_{0}^{\infty}{\rm d}s\,e^{-s/M^2}{\rm{Im}}\tilde{\Pi}^{\rm cont}(s) \\ \Rightarrow {\cal{M}}^{{J}}(M^2) = \displaystyle\int_{0}^{s_0}{\rm d}s\,e^{-s/M^2}{\rm{Im}}\tilde{\Pi}^{\rm pole}(s)+{\cal{M}}^{{\rm cont}}(M^2) \\ \Rightarrow {\cal{M}}^{{J}}(M^2) - {\cal{M}}^{{\rm cont}}(M^2) = \displaystyle\int_{0}^{s_0}{\rm d}s\,e^{-s/M^2}{\rm{Im}}\tilde{\Pi}^{\rm pole}(s). \end{array} $

(29) Differentiating both sides of above equation with respect to
$ 1/M^2 $ and taking ratio with Eq. (29) itself (to eliminate$ f_0 $ from the pole term from Eq. (27)), we obtain$\begin{split} &-\frac{ \dfrac{\partial}{\partial(1/M^2)} [{\cal{M}}^{{J}}(M^2) -{\cal{M}}^{{\rm cont}}(M^2)]} {{\cal{M}}^{{J}}(M^2) -{\cal{M}}^{{\rm cont}}(M^2)}\\ &= \frac{ \displaystyle \int_{0}^{s_0} {\rm d}s \, s\,e^{-s/M^2} {\rm{Im}}\tilde{\Pi}^{{\rm pole}}(s)} { \displaystyle \int_{0}^{s_0} {\rm d}s \, e^{-s/M^2} {\rm{Im}}\tilde{\Pi}^{{\rm pole}}(s)} = {{m^*_{Q}}}^{2}, \end{split}$

(30) where
$ {{m^*_{Q}}}^{2} $ is due to the use of Eq. (27) in the second term of Eq. (30). We solved above equation to evaluate the in-medium mass$ {{m^*_{Q}}} $ , of a given quarkonia as a function of Borel parameter$ M^2 $ . -
The
$ n^{th} $ moment$ M_n^J $ corresponds to the derivative of the correlation function, if one does not take the limit in Eq. (21),i.e.,$ \begin{split} M_n^J \equiv \left. { 1 \over n!} \left( {{\rm d} \over {\rm d} {E_0}^2} \right)^n \tilde{\Pi}^{J}({E_0}^2) \right|_{{E_0}^2 = -Q^2},= \frac{1}{\pi}\int_{4m_{q}^2}^{\infty}\frac{{\rm Im} \tilde{\Pi}^{J}(s)}{(s+Q^2)^{n+1}}{\rm d}s, \end{split} $

(31) at a fixed
$ Q^2 = 4m_c^2 \xi $ .Within QCDSR, using OPE, the moment can be expressed analytically as follows [58]
$ M_{n}^{J} (\xi) = A_{n}^{J} (\xi) \left[ 1 + a_{n}^{J} (\xi) \alpha_{s} + b_{n}^{J} (\xi) \phi_{b} + c_{n}^{J} (\xi) \phi_{c} \right], $

(32) where
$ A_n^J(\xi) $ ,$ a_n^J(\xi) $ ,$ b_n^J (\xi) $ , and$ c_n^J (\xi) $ are the Wilson coefficients for meson currents [2, 54], and$ \xi $ is the normalization scale. Hence, using$ \phi_b $ and$ \phi_c $ (Eqs. (23) and (24)) in the expression of$ M_{n}^{J} $ , the in-medium mass of the quarkonium states [21, 53, 57] can be written as$ {{m^*_{Q}}}^{2} \simeq \frac{M_{n-1}^{J} (\xi)}{M_{n}^{J} (\xi)} - 4 m_{q}^{2} \xi. $

(33) The in-medium mass-shift of quarkonium is given by
$ \Delta {{m^*_{Q}}} = {{m^*_{Q}}}-{{m_{Q}}}, $

(34) where
$ {{m_{Q}}} $ ($ Q = {\chi_c}_0(S) $ ,$ {\chi_c}_1(A),\eta_b(P), \Upsilon(V), {\chi_b}_0(S),{\chi_b}_1(A) $ ) is the vacuum mass of mesons. In the next section, we discuss the numerical results of the present work. -
The in-medium mass-shift of charmonia and bottomonia is calculated through two different QCDSR approaches using the in-medium scalar gluon condensate
$ G_0 $ and tensorial gluon condensate$ G_2 $ , in the presence of a uniform external magnetic field at finite temperature and density of asymmetric nuclear matter. We used the value of running charm (bottom) quark mass$ m_c(m_b) $ , and running strong coupling constant$ \alpha_s $ to be 1240 (4120) MeV and 0.21 (0.158), respectively. In addition, the chiral symmetry restoration at high temperature and magnetic field is also characterized by the in-medium$ f\pi $ and$ f_K $ decay constants. We have divided this discussion in two subsections. In subsection 3.1, we discuss the in-medium behavior of scalar fields$ \sigma $ ,$ \zeta $ ,$ \delta $ , and$ \chi $ as a function of the external magnetic field$ eB $ . The magnetic field induced gluon condensates and mass-shift of heavy quarkonia will be discussed in subsection 3.2. -
In the chiral
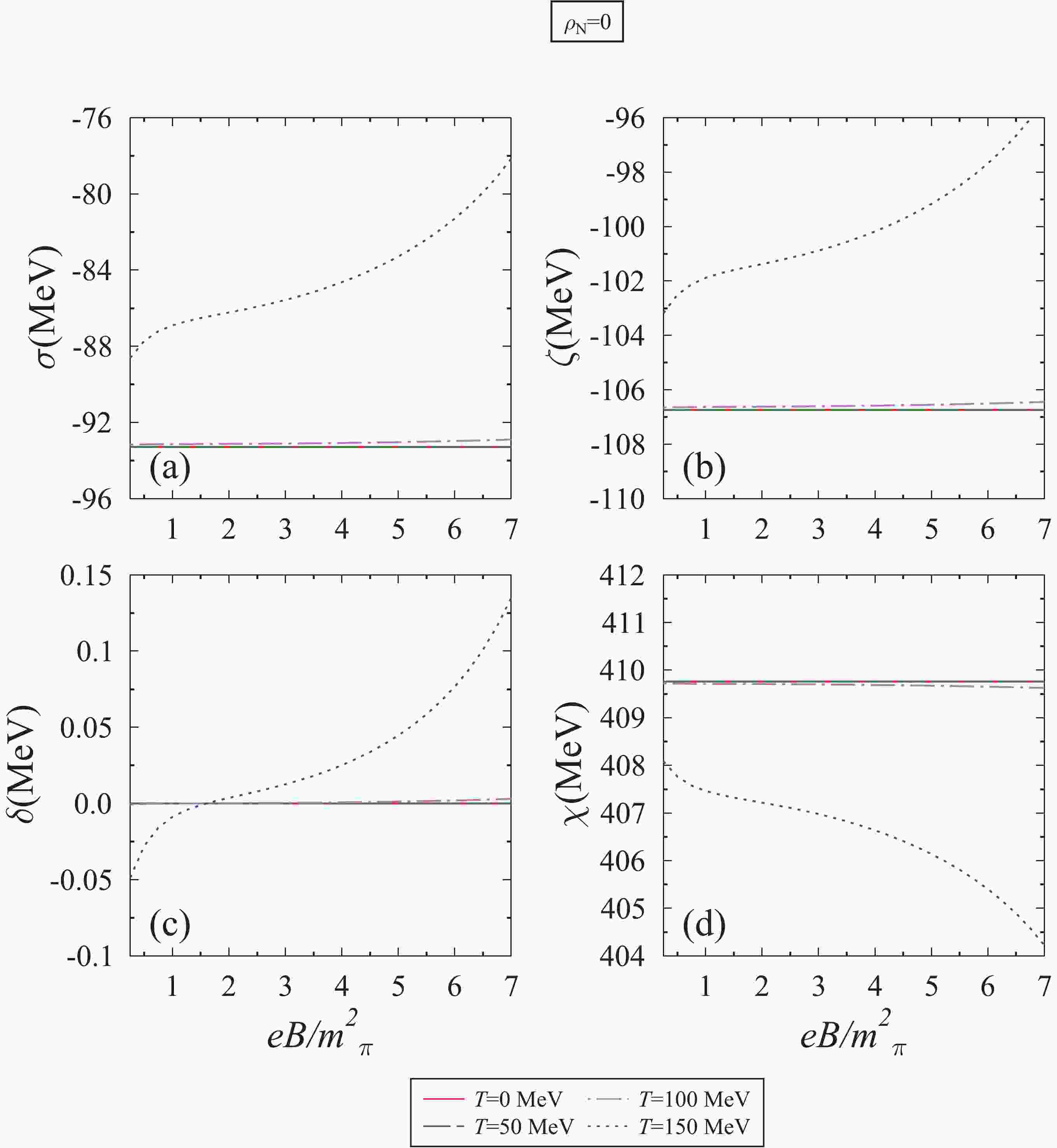
$ SU(3) $ model, the effect of the magnetic field is considered through the scalar density$ \rho^{s}_i $ , and vector density$ \rho^{v}_i $ , of the nucleons appearing in the scalar and vector field equations (8) to (11) [21]. In Fig.1, we plotted the variation of$ \sigma $ ,$ \zeta $ ,$ \delta $ , and$ \chi $ fields as a function of the magnetic field$ eB/{{m^2_{\pi}}} $ (1$ {{m^2_{\pi}}} $ =$ 5.48\times 10^{-2} $ GeV2 =$ 2.818\times 10^{18} $ Gauss), at nucleon density$ \rho_N $ = 0 and temperatures T = 0, 50, 100, 150 MeV. Here, e and$ {{m_{\pi}}} $ are the electric charge and mass of pion, respectively. As can be seen from this figure, the magnetic field affects the scalar fields negligibly for temperatures T = 0, 50, and 100 MeV. However, for T = 150 MeV, the magnitude of$ \sigma $ ,$ \zeta $ , and$ \chi $ field decreases as a function of the magnetic field. This is due to the fact that at higher temperature chiral symmetry restoration is considered and the different magnetic field strength rectifies the critical temperature, which is in accordance with the (inverse) magnetic catalysis process [11].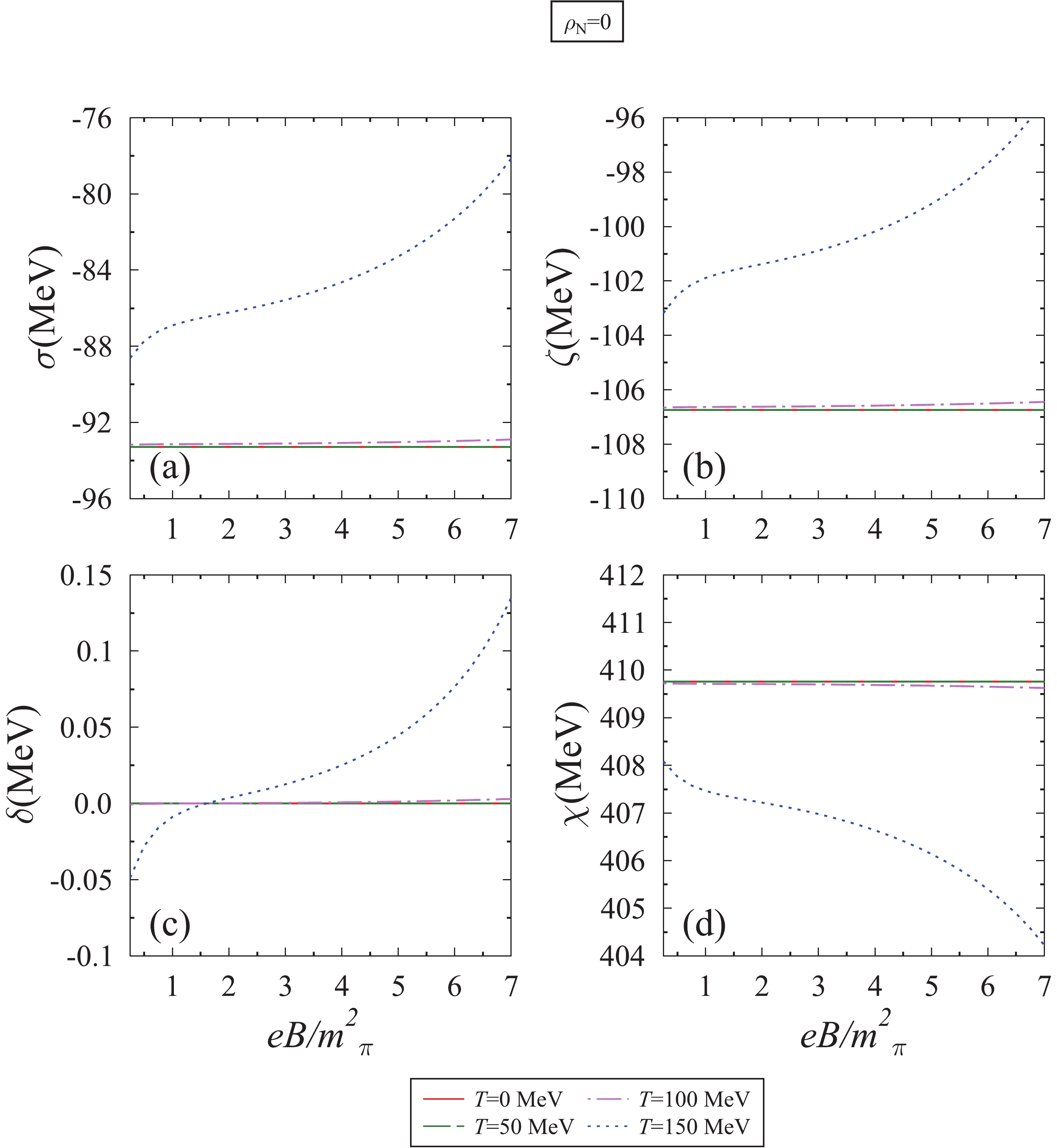
Figure 1. (color online) Scalar fields
$ \sigma $ ,$ \zeta $ ,$ \delta $ , and$ \chi $ plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ , for different values of temperature T, at nucleon density$ \rho_N = 0 $ .In Figs. 2 and 3, we plotted the scalar fields
$ \sigma $ ,$ \zeta $ ,$ \delta $ and$ \chi $ as a function of the magnetic field$ eB/{{m^2_{\pi}}} $ at different temperatures T, for nucleon density$ \rho_N $ =$ \rho_0 $ ($ 4\rho_0 $ ) and isospin asymmetry parameters$ \eta $ = 0 and 0.5. In Fig. 2, for symmetric nuclear matter ($ \eta = 0 $ ), the magnitude of$ \sigma $ and$ \zeta $ fields decreases with the increase in the magnetic field. The drop occurs in case of high density, as compared to low density. For example, the values of$ \sigma $ field at T = 0 and$ \rho_N $ =$ \rho_0 $ ($ 4\rho_0 $ ) are −49.38 (−25.71) MeV and −44.87 (−17.54) MeV for$ eB $ =$ {{m^2_{\pi}}} $ and 7$ {{m^2_{\pi}}} $ , respectively, and the values of$ \zeta $ fields are −75.51 (−72.72) MeV and −63.08 (−60.06) MeV. At finite density, the magnitude of scalar fields increase with the increase in the temperature of the medium. For example, at$ \rho_N $ =$ \rho_0 $ ($ 4\rho_0 $ ),$ \eta $ = 0, and$ eB $ = 4$ {{m^2_{\pi}}} $ the values of$ \sigma $ fields are −47.34 (−23.72), −52.20 (−26.21) and −51.84 (−27.72) MeV for T = 0,100 and 150 MeV, respectively and for$ \zeta $ field, these values are −74.23 (−62.23), −77.32 (−63.30) and −77.09 (−63.98) MeV. As discussed earlier, in the present model, the interaction of quarkonium with medium is expressed in terms of scalar fields, which incorporates the attractive interactions. The scalar fields are solved under different simultaneous conditions of the medium, such as density, magnetic field, temperature, and isospin asymmetry. In this framework, the effect of these physical parameters are introduced by the scalar and vector density of medium's constituents [21]. The scalar density increases with the increase in the number density of the medium, which results in the increase in the$ \sigma $ and$ \zeta $ field (magnitude decrease), whereas with the increase in temperature, the scalar density decreases, hence we obtain the opposite behavior of scalar fields [53]. The increase in the magnetic field increases the scalar density, and we observed an increase in the value of scalar fields. This may be due to inverse magnetic catalysis [11, 89], where the interaction of QCD medium with a strong magnetic field induces additional fermion-antifermion condensates with weak attractive interactions (analogous to BCS theory). Consequently, the net chiral condensates are enhanced, and the critical temperature decreases [90, 91].
Figure 2. (color online) Scalar field
$ \sigma $ and$ \zeta $ plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ , for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .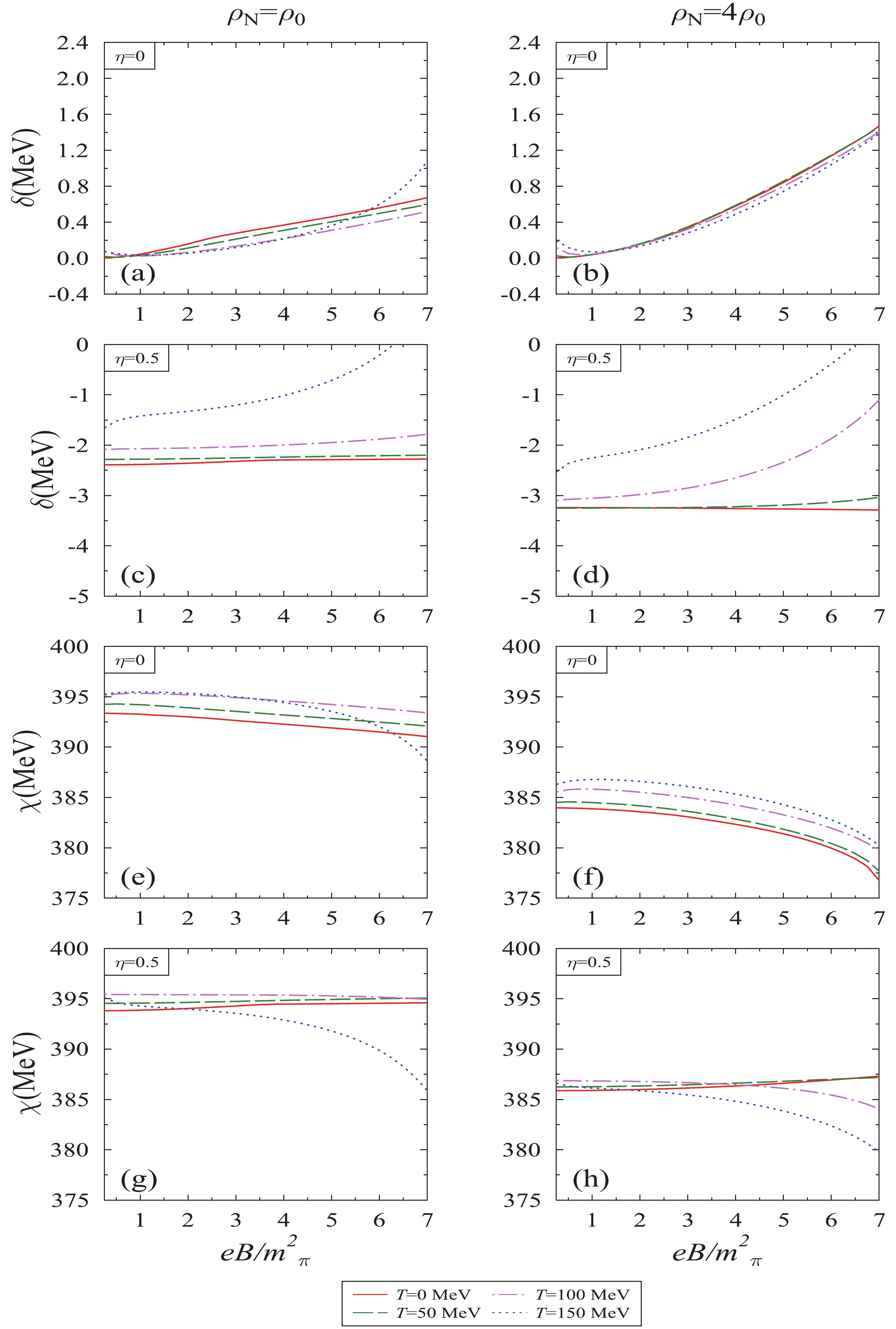
Figure 3. (color online) Scalar field
$ \delta $ and$ \chi $ plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ , for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .Considering the effects of isospin asymmetry in subplots (c), (d), (g), and (h), it is observed that at
$ \eta $ = 0.5 and$ \rho_N $ = 4$ \rho_0 $ , the magnitude of$ \sigma $ and$ \zeta $ field decreases (same as of symmetric matter case) with respect to$ eB $ for temperature T = 100 MeV and 150 MeV, whereas it increases for low temperatures such as T = 0 and 50 MeV. This is because in highly asymmetric matter, due to large number of neutrons, a significant difference in$ \rho^{s}_n $ and$ \rho^{s}_p $ is observed, which results in opposite behaviour of fields in low temperature. Moreover, for the same$ \eta $ , the temperature effect on$ \sigma $ and$ \zeta $ field becomes very small for high density with respect to the magnetic field. The above behavior is due to the competing effects between scalar densities$ \rho^{s}_n $ and$ \rho^{s}_p $ of the neutron and proton, as these densities exhibit temperature and magnetic field dependence [21, 53].In Fig. 3, the scalar fields
$ \delta $ and$ \chi $ are plotted as a function of the magnetic field. In subplots (a)–(d), the magnitude of the$ \delta $ field increases with respect to the magnetic field, and it varies more significantly at high density compared to low density. For$ \eta $ = 0, the non-zero value of$ \delta $ field is observed due to the inequality$ \rho^{s}_n $ $ \neq $ $ \rho^{s}_p $ , as for a finite magnetic field the Lorentz force effects become significant [21], which act on the neutron and proton in a different manner. Further, if we move towards higher asymmetry, the temperature and magnetic field effects on$ \delta $ field are more prominent. For example, at$ \rho_N $ = 4$ \rho_0 $ ,$ eB $ = 4$ {{m^2_{\pi}}} $ and$ \eta $ = 0 (0.5), the values of$ \delta $ field are 0.58 (−3.25), 0.54 (−2.64), and 0.48 (−1.48) MeV for T = 0, 100, and 150 MeV respectively, and for$ eB $ = 7$ {{m^2_{\pi}}} $ , these values change to 1.47 (−3.28), 1.40 (−1.10), and 1.38 (0.41) MeV. In subplots (e)–(h), the glueball field$ \chi $ is plotted, and thus for$ \eta $ = 0, the magnitude of the dilaton field decreases with an increase in the magnetic field. Here, the observed decrement is larger in the high density regime compared to low density regime. Furthermore, in pure neutron matter, the trend of the$ \chi $ field is exactly opposite as compared to symmetric medium at low temperature. For example, at$ \eta $ = 0.5,$ \rho_N $ =$ 4\rho_0 $ , and$ eB $ =$ 4{{m^2_{\pi}}} $ (7$ {{m^2_{\pi}}} $ ), the values of$ \chi $ fields are observed as 386 (387), 386 (384), and 385 (379) MeV for T = 0, 100, and 150 MeV, respectively. Whereas for$ \eta $ = 0 and the same parameters, the respective values are 382 (376), 384 (379), and 385 (379) MeV. This observed crossover is because the$ \chi $ field is solved along with$ \sigma $ and$ \zeta $ fields in coupled equations of motion, which as discussed earlier, contributes from the magnetic field induced scalar densities of the neutron and proton. -
In Fig. 4, We plotted the scalar and twist-2 gluon operator condensates with magnetic field for different values of nucleon density, temperature, and isospin asymmetry. Eqs. (16) and (17) indicate that the scalar and tensorial condensate depends on scalar fields. The former strongly depends on the
$ \chi $ field due to its fourth power dependence alone. Therefore, the behavior of the scalar condensate reflects the same functional dependence on the magnetic field and other parameters, as is the case with the$ \chi $ field. In the latter case,$ G_2 $ has a mixed fields dependence in every term and hence exhibits crossover behavior. Moreover, in the present investigation, we obtain a non-zero value for the twist-2 gluon operator$ G_2 $ , as the magnetic field breaks down the Lorentz symmetry by affecting the neutron and proton separately [21, 59]. In addition, in the high density regime, the value of$ G_2 $ decreases as compared to low density, however it follows the same trend with respect to the magnetic field. At high density, the values of$ G_2 $ increase with the increase in the magnetic field for symmetric nuclear matter, while they decrease for T = 0 and 50 MeV at$ \eta $ = 0.5. In the above discussion, scalar and tensorial gluon condensates are calculated using Eqs. (16) and (17), where we have considered the medium dependent value of decay constants$ f_\pi $ and$ f_K $ .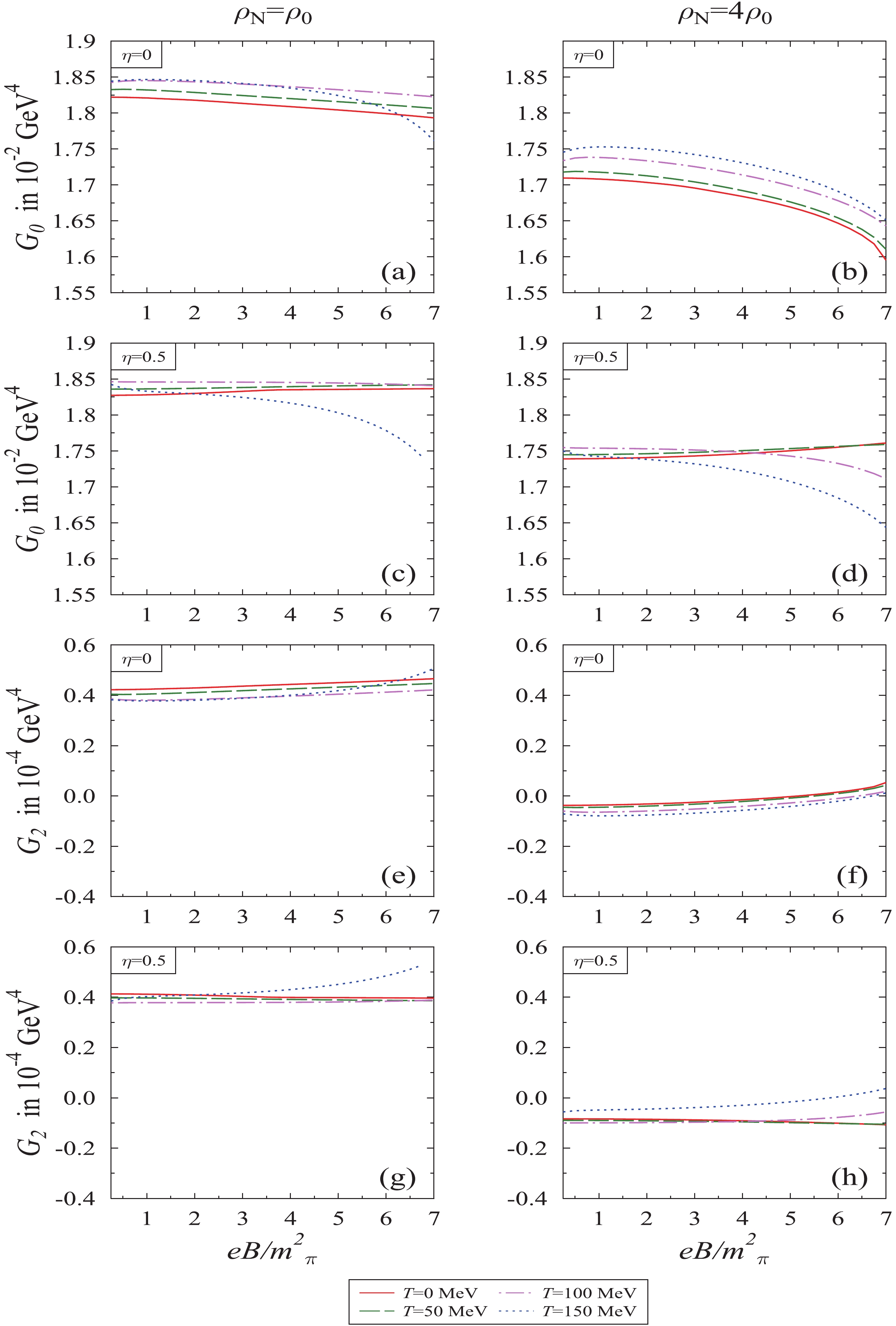
Figure 4. (color online) Scalar gluon condensate
$ G_0 $ and twist-2 gluon operator$ G_2 $ , describing trace and non-trace part of the energy momentum tensor, respectively, plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ , for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .These condensates are used as input in
$ \phi_b $ and$ \phi_c $ to calculate the effective mass and hence, in-medium mass-shift of quarkonia from Borel and the moment sum rule. In the former case, the threshold value$ s_0 $ is assumed to obtain the stability of the plot between the effective mass with respect to the Borel parameter$ M^2 $ . In this study, we have assumed its value to be 12.25 GeV2 and 114.91 GeV2 for charmonia and bottomnia, respectively [74]. To understand the implications from the OPE side, in Figs. 5 and 6, we plotted the OPE coefficients for the Borel sum rule with respect to the Borel parameter. In Fig. 5, for P-wave charmonia, we observed for a particular value of medium parameters ($ eB,T,\rho_N $ , and$ \eta $ ), the expansion coefficients of charmonia varies appreciably with the Borel parameter. However, in Fig. 6, for same parameters, the bottomonia expansion coefficients, such as$ b(g)\phi_b $ and$ c(g)\phi_c $ , are suppressed due to the term$ m_q^2 $ present in the expression of$ \phi_b $ and$ \phi_c $ , as the mass of bottom quark is very large. From both sum rules, the effective mass of the quarkonia decreases with the increase in the magnetic field, temperature, nucleon density, and isospin asymmetry. The observed mass-shift of the axial vector meson$ {\chi_c}_1 $ is larger than the scalar meson$ {\chi_c}_0 $ . In Fig. 7, we plotted the in-medium mass-shift (Borel sum rule) of$ {\chi_c}_0 $ and$ {\chi_c}_1 $ mesons as a function of the magnetic field for different values of isospin asymmetry, temperature, and nucleon density. In this figure, for$ \eta $ = 0, we noticed that the in-medium negative mass-shift increases more with the increase in the magnetic field. Considering the temperature effects, the magnitude of mass-shift is larger at zero temperature for both nucleon densities. It decreases with the increase in temperature, but follows the same functional dependence for the magnetic field. For highly asymmetric nuclear matter, at$ \rho_N $ = 4$ \rho_0 $ , the magnitude of in-medium mass-shift decreases with the increase in the magnetic field$ eB $ for T = 0 and 50 MeV, whereas for T = 100 and 150 MeV, the magnitude of mass-shift increases with the increase in magnetic field. The values of mass-shift of P-wave charmonia calculated from the Borel sum rule at$ eB $ = 3$ {{m^2_{\pi}}} $ and 7$ {{m^2_{\pi}}} $ are tabulated in Table 2. The crossover is a reflection of values of$ \phi_b $ and$ \phi_c $ , which are directly proportional to gluon condensates$ G_0 $ and$ G_2 $ , respectively. In Fig. 8, we have compared the mass-shift of P-wave charmonia obtained from the Borel sum rule as well as the moment sum rule as a function of the magnetic field and for fixed value of nucleon density, temperature, and isospin asymmetry parameter. For the moment sum rule, following our previous work for$ J/\psi $ and$ \eta_c $ mesons [21], in this article we work with$ \xi = 2.5 $ , since the Wilson coefficients for heavy quarkonia are larger than the S-wave [2]. We found that the magnitude of observed mass-shift of quarkonia is less for the Borel sum rule as compared to the moment sum rule. For example, in the moment sum rule, the values of$ {\chi_c}_0 $ mass-shift at$ \rho_N $ =$ 4\rho_0 $ and$ eB $ = 3$ {{m^2_{\pi}}} $ (7$ {{m^2_{\pi}}} $ ) with respect to vacuum are −67.70 (−86.51) and −62.55 (−76.47) MeV for T = 0 and 100 MeV, respectively, and for the$ {\chi_c}_1 $ meson mass-shift for same parameters are −77.90 (−71.98) MeV and −96.72 (−87.97) MeV. The difference in the mass-shift from two sum rules is because in the Borel sum rule for better perturbative expansion, the limit on the dispersion relation (see Eq.(21)) enters a deeper Euclidean region. In Ref. [2], the authors have reported the mass-shift of$ \chi_{c_0} $ and$ \chi_{c_1} $ as a function of$ T/T_c $ in zero magnetic field and observed that the effective masses of these mesons decrease with the increase in$ T/T_c $ .
Figure 5. (color online) OPE coefficients (charm) for scalar and axial vector current plotted as a function of Borel parameter
$ M^2 $ , for$ eB = 5{{m^2_{\pi}}} $ , T = 100 MeV, nucleon density$ \rho_N $ =$ 4\rho_0 $ , and isospin asymmetry parameter,$ \eta $ = 0.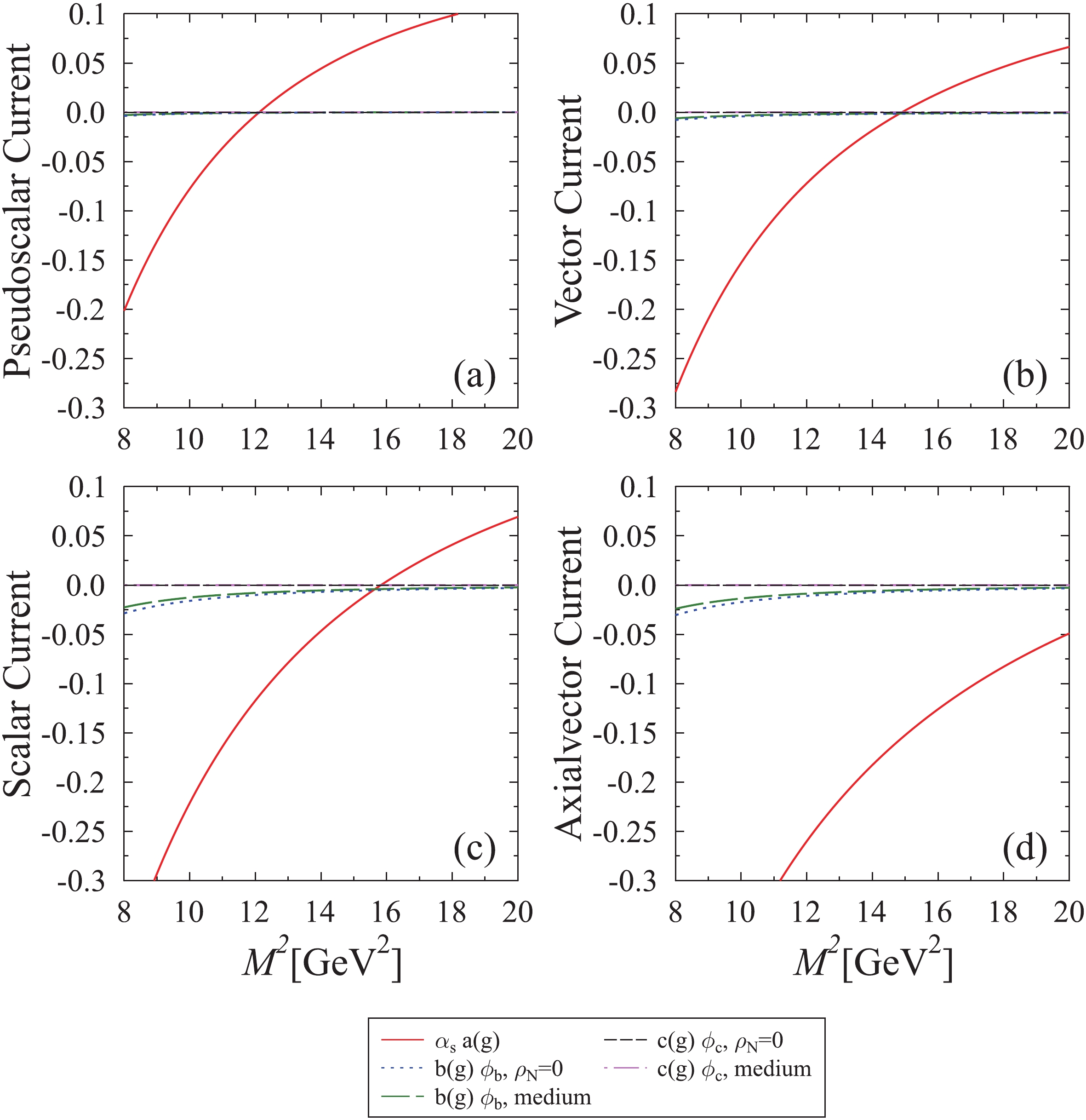
Figure 6. (color online) OPE coefficients (bottom) for pseudoscalar, vector, scalar, and axialvector current plotted as a function of Borel parameter
$ M^2 $ , for$ eB = 5{{m^2_{\pi}}} $ , T = 100 MeV, nucleon density$ \rho_N $ =$ 4\rho_0 $ , and isospin asymmetry parameter,$ \eta $ = 0.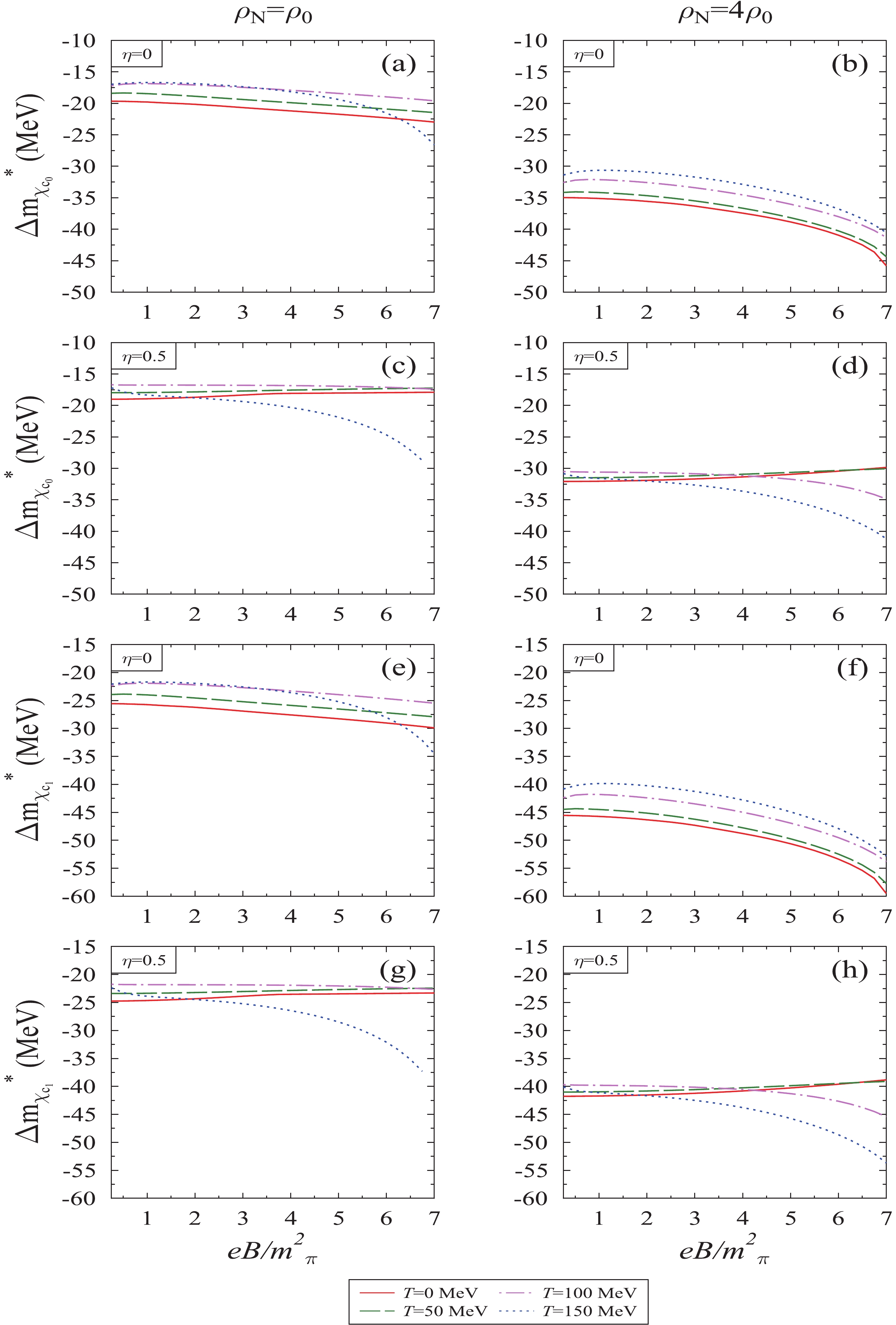
Figure 7. (color online) In-medium mass-shift of
$ {\chi_c}_0 $ and$ {\chi_c}_1 $ meson calculated from Borel sum rule plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .$\Delta m_Q$ 

$\eta=0$ 

$\eta=0.5$ 

$T=0$ 

$T=100$ 

$T=0$ 

$T=100$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

${\chi_c}_0$ 

$\Delta m_{Q_{30}}$ 

−20.66 −36.32 −17.44 −33.39 −18.34 −31.67 −16.79 −30.84 $\Delta m_{Q_{70}}$ 

−22.95 −45.79 −19.58 −41.27 −17.89 −29.84 −17.40 −34.85 ${\chi_c}_1$ 

$\Delta m_{Q_{30}}$ 

−26.88 −47.30 −22.69 −43.47 −23.86 −41.21 −21.83 −40.13 $\Delta m_{Q_{70}}$ 

−29.88 −59.49 −25.47 −53.80 −23.28 −38.81 −22.63 −45.39 Table 2. In the above table, we tabulate the effect of magnetic field on the mass-shifts of
${\chi_c}_0$ and${\chi_c}_1$ mesons from the Borel sum rule. Here,$\Delta m_{Q_{30}}$ represents the mass-shift between$eB$ = 3${{m^2_{\pi}}}$ and B = 0 (similar to$\Delta m_{Q_{70}}$ ). Further,$\rho_N$ and temperature$T$ are given in units of fm-3 and MeV, respectively.
Figure 8. (color online) In-medium mass-shift of
$ {\chi_c}_0 $ and$ {\chi_c}_1 $ meson plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ using different sum rules, for T = 0 and 100 MeV, nucleon density$ \rho_N $ =$ 4\rho_0 $ and isospin asymmetry parameter,$ \eta $ = 0.In Figs. 9 and 10, we plotted the in-medium magnetic field induced mass shift of bottomonia with respect to the magnetic field using the Borel sum rule. In Fig. 9, the mass-shift of pseudoscalar meson
$ \eta_b $ and vector meson$ \Upsilon $ is plotted, whereas in Fig. 10, the scalar meson$ \chi_{b_0} $ and pseudovector meson$ \chi_{b_1} $ is plotted. The mass-shift of bottomonia follows the same trend as for charmonia for different medium parameters. However, we found that the effect of medium characteristics on the mass of bottomonia is very small compared to the P-wave charmonia mass, whereas it is very close to the S-wave mass [21]. This is due to the presence of the square mass term in Eqs. (23) and (24), as discussed earlier. In the bottom sector, we see that the magnitude of mass-shift increase with the increase in nuclear density. The induced bottomonia mass-shifts are listed in Table 3. If we compare this Borel sum rule result with the moment sum rule results, we find that the obtained mass-shift from the Borel sum rule exhibits little difference compared to the moment sum rule. For example, in the moment sum rule, the values of$ \eta_b $ mass-shift at$ \rho_N $ =$ 4\rho_0 $ and$ eB $ = 3$ {{m^2_{\pi}}} $ (7$ {{m^2_{\pi}}} $ ) with respect to vacuum are −0.93 (−1.18) and −0.86 (−1.07) MeV for T = 0 and 100 MeV, respectively, and for the$ \Upsilon $ meson mass-shift for same parameters are −1.95 (−2.45) and −1.80 (−2.22) MeV. Similarly, the values of$ {\chi_b}_0 $ mass-shift at$ \rho_N $ =$ 4\rho_0 $ and$ eB $ = 3$ {{m^2_{\pi}}} $ (7$ {{m^2_{\pi}}} $ ) with respect to vacuum are −9.46 (−11.85) and −8.72 (−10.73) MeV for T = 0 and 100 MeV, respectively, and for the$ {\chi_b}_1 $ meson mass-shift for same parameters are −7.77 (−9.73) and −7.16 (−8.81) MeV. In the present study, we find negative mass shifts of charmonia and bottomonia under different conditions of the medium. We observe a large negative shift with respect to density, which compensates other different medium effects. In the heavy meson-nucleon scattering, the negative or positive sign of scattering length decides, whether the mass will increase or decrease in the medium. It is also observed that for both charmonium and bottomonium, the mass of P-wave states is larger than the S-wave states, and this is valid for both sum rules. These large induced mass shift is due to the derivatives (by$ 1/M^2 $ ) of the expansion coefficients of spin 1 states, which are larger than the spin 0 states for the same Borel parameter [74]. In Ref. [75], authors have calculated the in-medium mass-shift of Upsilon states in the presence of the magnetic field. In this article, for$ \eta $ = 0, at$ \rho_N $ =$ \rho_0 $ ($ 4\rho_0 $ ), the mass-shift of$ \Upsilon $ (1s) is calculated as −0.71 (−2.57) and −0.71 (−2.46) MeV for magnetic fields 4$ {{m^2_{\pi}}} $ and 8$ {{m^2_{\pi}}} $ , respectively, at zero temperature, which is consistent with our results. The QCDSR along with the maximum entropy method (MEM) has been applied to study the thermal effects on bottomonia in zero magnetic field [71]. In this study, the authors have investigated the dissociation of the excited state of bottomonia at a lower temperature than that of the ground state. In the presence of a strong external magnetic field, the heavy quark system also exhibits mixing effects, which is likewise confirmed by experiments [20, 22, 92, 93]. The magnetically induced mixing between$ J/\psi $ and$ \eta_c $ has been studied by QCD sum rules [22]. In these conditions, the radiative decay mode$ J/\psi $ $ \rightarrow $ $ \eta_c $ $ + $ $ \gamma $ , leads to an additional mass shift caused by mixing of these mesons (resonances). In this study, the authors found that the mixing effects generate repulsion and influence the mass shift. Moreover, to predict the actual mass shift of mesons, one has to consider mixing effects in both the phenomenological as well as the OPE side. In Ref. [20], authors found that the spectral properties of the$ \eta_c $ meson depend on the spectral properties of the$ J/\psi $ meson. Furthermore, in both articles, the authors found a small residual mass shift for charmonia as well. Within the present model, in the future, the mixing effect has to be included in the phenomenological aspect to isolate the mass shift.
Figure 9. (color online) In-medium mass-shift of
$ \eta_b $ and$ \Upsilon $ meson calculated from Borel sum rule plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ , for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .
Figure 10. (color online) In-medium mass-shift of
$ {\chi_b}_0 $ and$ {\chi_b}_1 $ meson calculated from the Borel sum rule plotted as a function of magnetic field$ eB/{{m^2_{\pi}}} $ for different values of temperature T, nucleon density$ \rho_N $ , and isospin asymmetry parameter,$ \eta $ .$\Delta m_Q$ 

$\eta=0$ 

$\eta=0.5$ 

$T=0$ 

$T=100$ 

$T=0$ 

$T=100$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

$\rho_0$ 

$4\rho_0$ 

${\Upsilon}$ 

$\Delta m_{Q_{30}}$ 

−1.77 −3.08 −1.49 −2.84 −1.57 −2.70 −1.44 −2.63 $\Delta m_{Q_{70}}$ 

−1.97 −3.86 −1.68 −3.50 −1.53 −2.55 −1.49 −2.96 ${\eta_b}$ 

$\Delta m_{Q_{30}}$ 

−1.18 −2.14 −0.99 −1.97 −1.04 −1.88 −0.95 −1.83 $\Delta m_{Q_{70}}$ 

−1.31 −2.68 −1.11 −2.42 −1.02 −1.78 −0.99 −2.06 ${\chi_b}_0$ 

$\Delta m_{Q_{30}}$ 

−4.96 −8.58 −4.20 −7.89 −4.41 −7.48 −4.04 −7.29 $\Delta m_{Q_{70}}$ 

−5.51 −10.81 −4.71 −9.77 −4.30 −7.06 −4.19 −8.23 ${\chi_b}_1$ 

$\Delta m_{Q_{30}}$ 

−5.02 −8.71 −4.23 −8.02 −4.45 −7.61 −4.07 −7.41 $\Delta m_{Q_{70}}$ 

−5.58 −10.94 −4.75 −9.90 −4.34 −7.18 −4.22 −8.36 Table 3. In the above table, we tabulate the effect of the magnetic field on mass-shifts of
$\eta_b$ ,$\Upsilon$ ,${\chi_b}_0$ , and${\chi_b}_1$ mesons from the Borel sum rule. Here,$\Delta m_{Q_{30}}$ represents the mass-shift between$eB$ = 3${{m^2_{\pi}}}$ and B = 0 (similar to$\Delta m_{Q_{70}}$ ). Further,$\rho_N$ and temperature$T$ are given in units of fm-3 and MeV, respectively. -
In the present study, we calculated the mass-shift of P-wave charmonium and S and P-wave bottomonium considering in-medium effects of order parameters of spontaneous symmetry breaking. The magnetic field induced mass-shift of P-wave charmonia is more prominent than that of S-wave charmonia [21], whereas the change in the mass-shift is significantly smaller for bottomonia. To calculate the effective mass, we used the unified approach of the chiral
$ SU(3) $ model and QCDSR. In the former, the medium effects are calculated in terms of$ \sigma $ ,$ \zeta $ ,$ \delta $ , and$ \chi $ mesonic fields, which are used further to calculate the in-medium scalar and tensorial gluon condensates. Using these gluon condensates as input in the QCDSR, the mass-shift of$ {{\chi_c}_0} $ ,$ {{\chi_c}_1} $ ,$ \eta_b $ ,$ \Upsilon $ ,$ {{\chi_b}_0} $ , and$ {{\chi_b}_1} $ mesons have been calculated. The temperature and magnetic field effects are introduced through the scalar density$ \rho^{s}_i $ , and vector density$ \rho^{v}_i $ of the$ i^{th} $ nucleon [21]. Moreover, we introduced the effect of isospin asymmetry by the incorporation of$ \delta $ and$ \rho $ fields, which are solved along with other mesonic fields employing the coupled equations of motion. Within QCDSR, we use two different sum rules approaches, i.e., the Borel sum rule and the moment sum rule. In this study, we have observed that from both sum rules, the effective mass of these mesons decreases with the increase in the magnetic field and nucleon density. The magnitude of in-medium mass-shift increases with the increase in the magnetic field for all temperatures except for pure neutron matter, where it increases for high temperatures, and decreases for low temperatures. Further, the decrease in the in-medium mass-shift of the above mesons is more relevant in the case of the high-density regime than low density. However, the magnitude of mass-shift observed from both sum rules is different. We observe a lower magnitude in the mass-shift with the Borel sum rule than with the moment sum rule. The Borel sum rule is more reliable than the moment sum rule, owing to the inclusion of deeper perturbative expansion terms and hence a better region of OPE convergence [74]. The calculated mass-shift can be used to study the in-medium decay of higher quarkonium states [2, 94] to lower quarkonium states for a better understanding of$ J/\psi $ suppression. This decay width can also be used to calculate experimental observables, such as the in-medium cross-section [95] in asymmetric heavy ion collision experiments.One of the author, Rajesh Kumar sincerely acknowledges the support towards this work from the Ministry of Science and Human Resources Development (MHRD), Government of India, via Institute fellowship of the National Institute of Technology Jalandhar.
Charmonia and bottomonia in asymmetric magnetized hot nuclear matter
- Received Date: 2019-06-23
- Accepted Date: 2019-09-26
- Available Online: 2019-12-01
Abstract: We investigate the mass-shift of P-wave charmonium (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: