-
Analysis of high-momentum transfer experiments suggests that 20 % of nucleons can form pairs in nuclei with high nucleon momentum due to short-range interaction [1−6]. Moreover, short-range correlated (SRC) pairs are strongly isospin-dependent, i.e., n-p pairs account for approximately 90 %, whereas p-p and n-n SRC pairs account for approximately 10 % [3, 6]. Because in neutron-rich nuclei the fractions of high-momentum protons and neutrons are inversely proportional to their relative fractions (
$ x_{p} $ or$ x_{n} $ ) in the nucleus [7, 8], neutrons move slower than protons on average.In recent years, the np dominance of SRC pairs has attracted much attention [9−18]. The high-momentum distribution of nucleons in neutron-rich nuclei is important for understanding the cooling rate and equation of state of neutron stars [19]. It has been demonstrated that the neutron excess in asymmetric nuclear matter or neutron stars (contains only about 5%−10% protons) could affect the distribution of high-momentum protons dramatically [8]. However, these studies mostly focus on issues such as how unalike fermions form such SRC pairs and the structure of protons and neutrons [20]. The proton transition momentum, i.e., starting point of
$ 1/k^{4} ,$ is seldom mentioned. Dose it start from its own Fermi momentum or the correlated majority neutron Fermi momentum? In symmetric nuclear matter, proton Fermi momentum is almost equivalent to that of neutrons [21]. However, in asymmetric nuclear matter or in neutron stars, neutron Fermi momenta are higher than those of protons [22]. High-energy electron-scattering experiments showed that the n-p SRC pairs have large relative momenta and small center-of-mass momenta in both balanced and imbalanced systems [3, 6], which means neutrons and protons should have almost identical momentum in the HMT. Thus, protons with$ 1/k^{4} $ distributions should not start from their own Fermi momenta.In this work, we will use nucleon transverse flow, isospin-dependent transverse flows, proton elliptic flow, and isospin-sensitive elliptic flows to study the proton transition momentum effect in semi-peripheral 40Ca + 40Ca,112Sn + 112Sn, and 197Au + 197Au collisions at an impact energy of 400 MeV/A. Moreover, the sensitivity of pion production to proton transition momentum is also studied at 200 MeV/A, 400 MeV/A, and 600 MeV/A beam energies with impact parameter
$ b = 6~{\rm fm} $ . -
In this work, we adopt the semi classical isospin-dependent Boltzmann-Uehling-Uhlenbeck (IBUU) transport model [23]. The nucleon density distribution is given by
$\begin{split} r = R(x_{1})^{1/3},\quad \cos\theta = 1-2x_{2},\quad \phi = 2\pi x_{3},\\ x = r\sin\theta \cos\phi, \quad y = r\sin\theta \sin\phi, \quad z = r\cos\theta, \end{split}$

(1) where
$ x_{1}, x_{2}, x_{3} $ are three independent random numbers, and R is the radius of the nucleus. The maximum nucleon momentum distribution reaches$ \lambda k_{F_{n,p}} = 2.75k_{F_{n,p}} $ [10], and$ \lambda $ is the high-momentum tail cutoff parameter. The nucleon momentum distribution in the high momentum tail (HMT) is given by following equation:$ n^{\rm HMT}(k) \propto 1/k^{4}, $

(2) where
$ n(k) = \left\{ {\begin{array}{*{20}{l}} {{C_1}},&{k\leqslant {k_{\rm F}};}\\ {{C_2}/{k^4},}&{{k_{\rm F}} < k < \lambda {k_{\rm F}},} \end{array}} \right.$

(3) and the proportion of nucleons in the HMT is kept at 20 %:
$ 4\pi\int_{k_{\rm F}}^{\lambda k_{\rm F}}n^{\rm HMT}(k)k^{2}{\rm d}k \bigg/4\pi \int_{0}^{\lambda k_{\rm F}}n(k)k^{2}{\rm d}k \simeq 20\%.$

(4) The number of protons in the HMT is
$ Z^{\rm HMT} = \frac{A}{2}4\pi\int_{k_{\rm F}}^{\lambda k_{\rm F}}n^{\rm HMT}(k)k^{2}{\rm d}k.$

(5) and the number of neutrons in the HMT is
$ N^{\rm HMT} = \frac{A}{2}4\pi\int_{k_{\rm F}}^{\lambda k_{\rm F}}n^{\rm HMT}(k)k^{2}{\rm d}k$

(6) with normalization condition
$ 4\pi\int_{0}^{\lambda k_{\rm F}}n(k)k^{2}{\rm d}k = 1.$

(7) The parameters
$ C_{1} $ and$ C_{2} $ in Eq. (3) can be determined from the above equations, A is the total number of nucleons, and$ k_{\rm F} $ is nucleon Fermi momentum.In this model, the isospin- and momentum-dependent mean-field single particle potential is used [18, 24]:
$ \begin{split} U(\rho,\delta,\vec{p},\tau) =& A_u(x)\frac{\rho_{\tau'}}{\rho_0}+A_l(x)\frac{\rho_{\tau}}{\rho_0}\\ &+B\left(\frac{\rho}{\rho_0}\right)^{\sigma}(1-x\delta^2)-8x\tau\frac{B}{\sigma+1}\frac{\rho^{\sigma-1}}{\rho_0^\sigma}\delta\rho_{\tau'}\\ &+\frac{2C_{\tau,\tau}}{\rho_0}\int {\rm d}^3\,\vec{p^{'}}\frac{f_\tau(\vec{r},\vec{p^{'}})}{1+(\vec{p}-\vec{p^{'}})^2/\Lambda^2}\\ &+\frac{2C_{\tau,\tau'}}{\rho_0}\int {\rm d}^3\,\vec{p^{'}}\frac{f_{\tau'}(\vec{r},\vec{p^{'}})}{1+(\vec{p}-\vec{p^{'}})^2/\Lambda^2}, \end{split} $

(8) where
$ \tau = 1/2 $ for neutron, and$ \tau' = -1/2 $ for proton.$ \rho_0 $ denotes saturation density, and neutron and proton densities are denoted by$ \rho_n $ and$ \rho_p,$ respectively.$ \delta = (\rho_n\!-\!\rho_p)/(\rho_n\!+\!\rho_p) $ is the isospin asymmetry. The parameter values$ A_u(x) $ = 33.037 − 125.34x MeV,$ A_l(x) $ = −166.963 + 125.34x MeV, B = 141.96 MeV,$ C_{\tau,\tau} =$ 18.177 MeV,$ C_{\tau,\tau'} = $ −178.365 MeV,$ \sigma = 1.265 $ , and$ \Lambda = 630.24 $ MeV/c are obtained by fitting empirical values of the saturation density$ \rho_{0} = 0.16~{\rm fm}^{-3} $ , effective mass$ m_{s}^{*} = 0.7 $ m, binding energy$ E_{0} = -16$ MeV, incompressibility$ K_{0} = 230 $ MeV, single-particle potential$ U_{0,\infty} = 75 $ MeV at infinitely large nucleon momentum at saturation density in symmetric nuclear matter, symmetry potential$ U_{\rm sym,\infty} = -100 $ MeV at infinitely large nucleon momentum, and symmetry energy$ E_{\rm sym}(\rho_{0}) = 30 $ MeV. The parameter x in the single particle potential is used to mimic different forms of the symmetry energy and can change with density while the empirical values remain unchanged [25]. The phase-space distribution function$ f_{\tau}(\vec{r},\vec{p}) $ is solved by following a test particle evolution on a lattice. The isospin-dependent reduced medium nucleon-nucleon scattering cross section is used for nucleon-nucleon collisions. More details about the above transport model can be found in Refs. [15, 16, 25]. -
Figure 1 presents the nulceon average kinetic energy distribution with different proton starting momentum points. In case A, the protons and neutrons in the HMT start from their respective Fermi momenta, while in case B, HMT nucleons start from the majority neutron momenta. It is found that the neutron average kinetic energy remains unchanged as one would expect in both two cases. However, when the changing proton momentum of the HMT from its own Fermi momentum to the correlated neutron Fermi momentum, the proton average kinetic energy changes from lower than the average neutron kinetic energy (
$ E^{p}_{\rm kin} < E^{n}_{\rm kin} $ ) to higher than the majority average kinetic energy ($ E^{p}_{\rm kin} > E^{n}_{\rm kin} $ ) in asymmetric nuclear matter, and the value of$ (E^{p}_{\rm kin}-E^{n}_{\rm kin}) $ becomes larger in a more neutron-rich system with xp = 40 %. Therefore, the dynamics of nuclear reactions would be affected by the proton transition momentum in the HMT.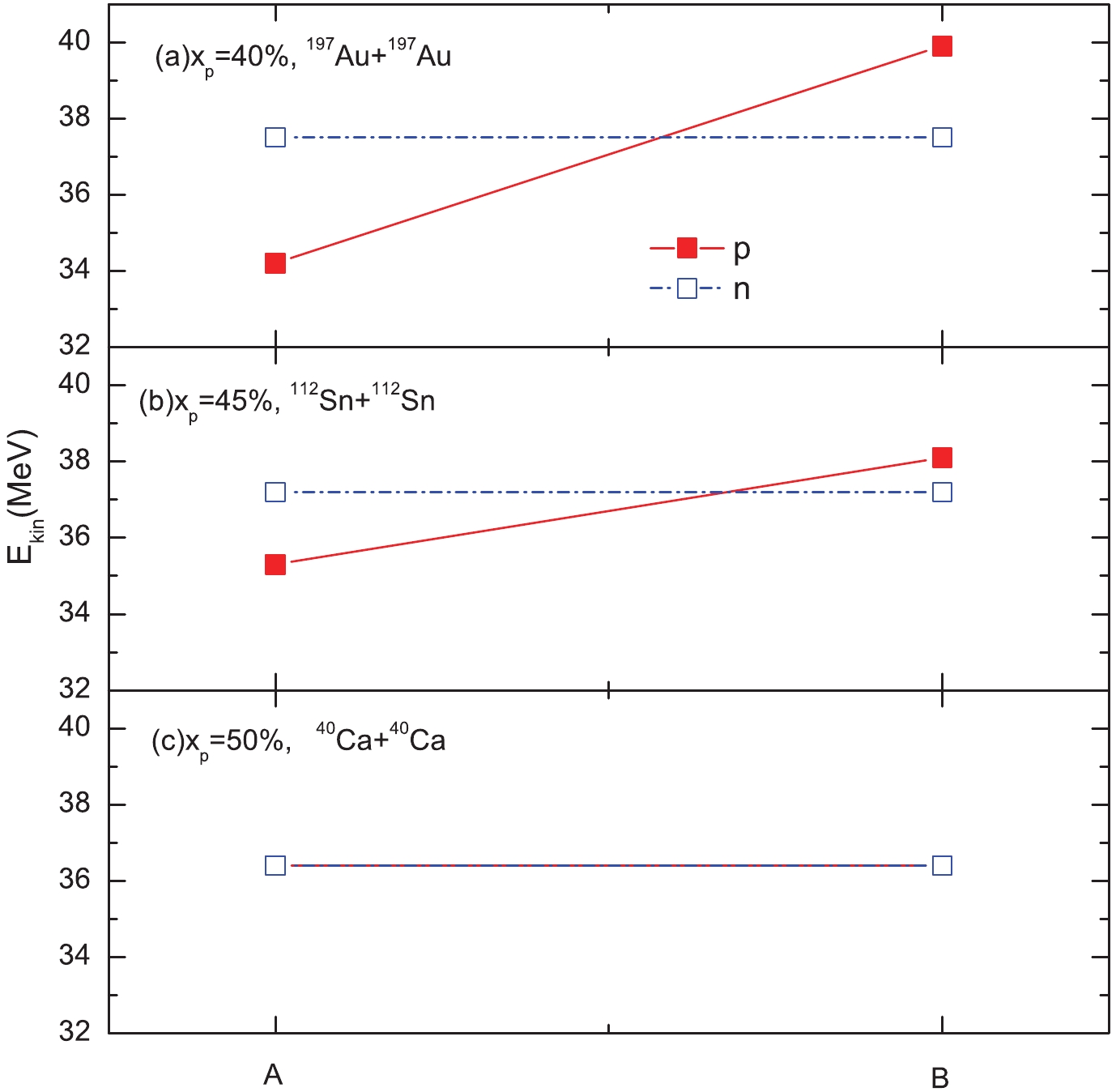
Figure 1. (color online) Distribution of neutron and proton average kinetic energy with different starting momentum points of the
$1/k^{4}$ distribution. In case A, the starting point is their respective Fermi momentum, while in case B, all nucleons start from the majority Fermi momentum.The proton (left panels (a)
$ \sim $ (c)) and neutron (right panels (d)$ \sim $ (e)) collective transverse flow as a function of reduced rapidity with different proton transition momenta of the HMT in reactions systems with xp = 40 %, xp = 45 %, and xp = 50 % is shown in Fig. 2. Nucleon collective transverse flow is [26−30]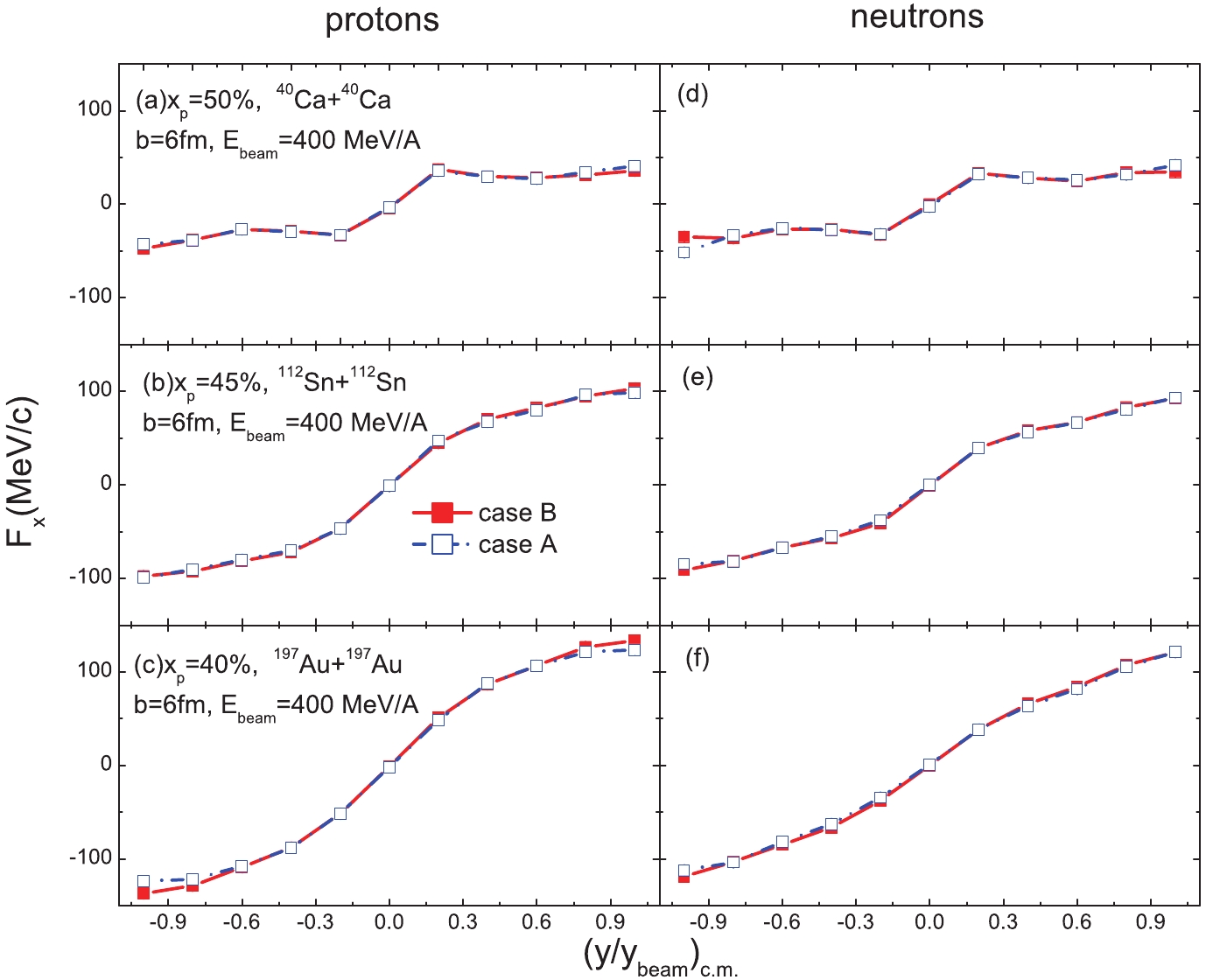
Figure 2. (color online) (left) Rapidity distribution of proton transverse flow for different proton starting momenta cases. (right) Same as left panel but for neutron transverse flow.
$ {F^{n,p}}(y) = \frac{1}{{{N_{n,p}}(y)}}\sum\limits_{i = 1}^{{N_{n,p}}(y)} {p_x^i} (y).$

(9) In the above equation,
$ p_{x}^{i} $ is the$ i{\rm th} $ particle’s transverse momentum in the reaction plane,$ N_{n,p}(y) $ is the number of free neutrons or protons at rapidity y. Here, a nucleon with local density less than$ \rho_{0}/8 $ was identified as free. From Fig. 2, it is found that the proton transition momentum has no effect on neutron transverse flow because the neutron starting momentum is unchanged in both cases. The proton transverse flow is in fact insensitive to the proton transition momentum of the HMT, and a slightly higher proton transverse flow is observed only when the proton fraction is xp = 40 %. This is because the nucleon high-momentum distribution roughly exhibits a$ C/k^{4} $ shape, and there are only a few protons with momenta higher than the Fermi momentum in the nucleus.We now explore the effect of proton transition momentum in the HMT using the isospin-dependent collective flows. The neutron to proton differential collective flow is defined as [31]
$ {F^{n - p}}(y) = \frac{1}{{N(y)}}\sum\limits_{i = 1}^{N(y)} {{p_{xi}}} (y){\tau _i}, $

(10) where
$ N(y) $ is the total number of free nucleons at the rapidity, and$ \tau_{i} $ is +1 for neutrons and −1 for protons. The difference between neutron and proton transverse flow is defined as${F^n}(y) - {F^p}(y) = \frac{1}{{{N_n}(y)}}\sum\limits_{i = 1}^{{N_n}(y)} {{p_{xi}}} (y) - \frac{1}{{{N_p}(y)}}\sum\limits_{i = 1}^{{N_p}(y)} {{p_{xi}}} (y). $

(11) Figure 3 gives the neutron to proton differential flow
$ F^{n-p}(y) $ (left panels) and the difference of neutron and proton transverse flow$ (F^{n}(y)-F^{p}(y)) $ (right panels) as a function of reduced rapidity in the 40Ca + 40Ca, 112Sn + 112Sn, and 197Au + 197Au systems with different proton starting momenta in the HMT. Panels (a) and (d) show that the proton transition momentum in the HMT has no effect on these two transverse flows in a symmetric system. This result is consistent with panel (c) of Fig. 1. For 197Au + 197Au collisions, the proton transition momentum effect could be found in panels (c) and (f), but this effect is not significant. However, in 112Sn + 112Sn collisions, these two isospin-dependent transverse flows almost have no proton momentum transition effect. This is because when the starting momentum point of protons starts from the majority neutron Fermi momentum, the average proton kinetic energy$ E^{p}_{\rm kin} $ is enhanced in small proton fraction$ x_{p} $ collisions. It is also found that in 197Au + 197Au collisions, the strength of$ (F^{n}(y)-F^{p}(y)) $ in case B is lower than that in case A because the neutron-proton correlation in the HMT causes a higher proton transverse flow.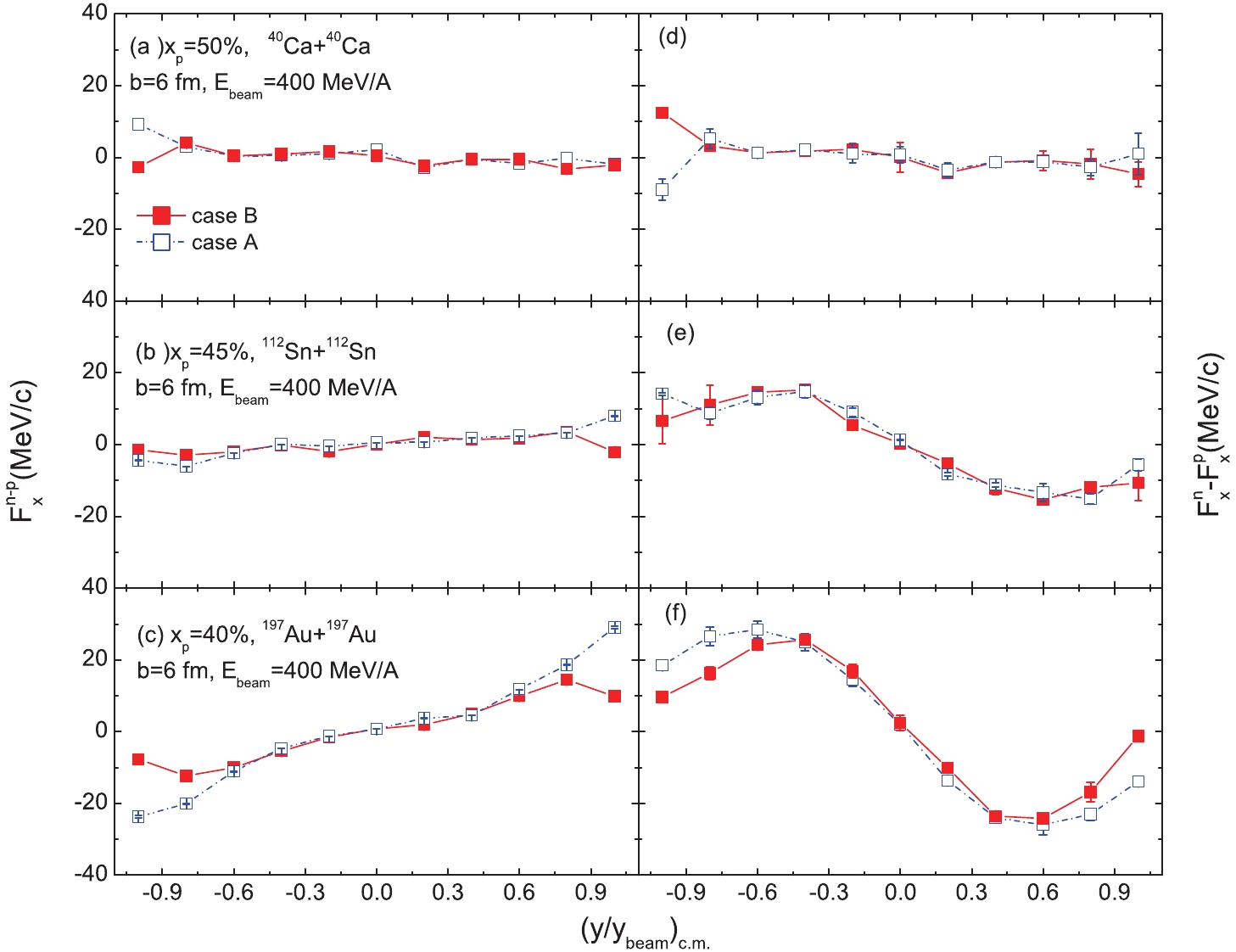
Figure 3. (color online) Neutron to proton differential transverse flow (left) and the difference of neutron and proton transverse flow (right) as a function of reduced rapidity with different proton starting momenta in the HMT.
Because neutrons would not be affected by the proton transition momentum, we will study the effects of proton transition momentum on proton elliptic flow and isospin-dependent elliptic flow. The nucleon elliptic flow that corresponds to the second Fourier coefficient can be expressed as [26, 32−36]
$ v_{2} = <\cos(2\phi)> = \left\langle \frac{p_{x}^{2}-p_{y}^{2}}{p_{x}^{2}+p_{y}^{2}}\right\rangle, $

(12) where
$ p_{x} $ is the nucleon transverse momentum in the reaction plane along the x axis, and$ p_{y} $ is the nucleon transverse momentum perpendicular to the reaction plane along the y axis. Similar to the neutron to proton differential flow, the neutron to proton differential elliptic flow is defined as$ v_{2}^{n-p} = \frac{N_{n}}{N}v_{2}^{n}-\frac{N_{p}}{N}v_{2}^{p}, $

(13) where N denotes the total number of nucleons, and
$ N_{n} $ and$ N_{p} $ are the numbers of neutrons and protons, respectively. The difference of neutron and proton elliptic flow, i.e.,$ (v_{2}^{n}-v_{2}^{p}),$ is also analyzed.In Fig. 4, we show the effects of proton transition momentum in the HMT on proton elliptic flow in collisions with proton fractions xp = 40 %, 45 %, and 50 %. It is seen that the effect of proton transition momentum on proton elliptic flow is generally small in 197Au + 197Au collisions and only slightly larger in the high-kineticenergy region. In 40Ca + 40Ca collisions, this effect disappearsbecause the majority average kinetic is almost equal to the minority average kinetic in symmetric nuclear matter.

Figure 4. (color online) Kinetic energy distribution of proton elliptic flow in semi-peripheral collisions at beam energy 400 MeV/A with different proton starting momenta.
Presented in Fig. 5 presents the neutron to proton differential elliptic flow (upper figure) and the difference of neutron and proton elliptic flow (lower figure) as a function of kinetic energy in collisions of 112Sn + 112Sn and 197Au + 197Au. A clear proton transition momentum effect is seen in the difference of neutron and proton elliptic flow (
$ v_{2}^{n}-v_{2}^{p} $ ) in a more neutron-rich reaction system, as shown in panel (d), while the neutron to proton differential elliptic flow ($ v_{2}^{n-p} $ ) is relatively less sensitive to the proton transition momentum except in the high-kinetic energy region, as shown in panel (c). We can also see that the proton high-momentum distribution$ 1/k^{4} $ point starting from the correlated neutron Fermi momentum causes small values of ($ v_{2}^{n}-v_{2}^{p} $ ) and ($ v_{2}^{n-p} $ ) due to neutron-proton correlations in the HMT. The nucleon elliptic flow is negative, and the absolute value of proton elliptic flow is larger than that of neutron elliptic flow [31]; this is the reason why the difference of neutron and proton elliptic flow ($ v_{2}^{n-p} $ ) is positive.
Figure 5. (color online) (upper) Kinetic energy distribution of neutron to proton differential elliptic flow with different proton starting momenta at an incident beam energy of 400 MeV/A in semi-peripheral 112Sn + 112Sn and 197Au + 197Au collisions. (lower) Same as upper panel but for the difference of neutron and proton elliptic flow.
It is well known that the
$ \pi^{-} $ meson is mainly from n-n collisions and$ \pi^{+} $ meson is mainly from p-p collisions; therefore, the$ \pi^{-}/\pi^{+} $ ratio can be used to extract important information about proton transition momentum in the HMT. Fig. 6 presents the beam energy distribution of the$ \pi^{-}/\pi^{+} $ ratio with different proton starting momenta in the HMT. In the 40Ca +40Ca reaction system, it is found that the$ \pi^{-}/\pi^{+} $ ratio becomes approximately constant around 1. This is because in the$ \Delta $ resonance model, the$ \pi^{-}/\pi^{+} $ ratio is approximately$ (5N^{2}\!\! +\!\! NZ)/(5Z^{2}\!\! +\!\! NZ)\! \approx \!(N/Z)^{2} $ [37], where N and Z are the total neutron and proton numbers in the participant region, respectively. This is also the reason why the value of$ \pi^{-}/\pi^{+} $ a shown in panel (b) and panel (c) increases as the proton proportion$ x_{p} $ decreases. Note that the proton starting momentum in the HMT starting from its own Fermi momentum gives a large value of$ \pi^{-}/\pi^{+} $ , while starting from the majority neutron Fermi momentum corresponds to a relatively small value of$ \pi^{-}/\pi^{+} $ in neutron-rich collisions. This is because much higher proton average kinetic energy collisions produce more$ \pi^{+},$ and the multiplicity of$ \pi^{-} $ remains the same if the neutron average kinetic energy remains unchanged.
Figure 6. (color online) Beam energy distribution of
$\pi^{-}/\pi^{+}$ ratio with beam impact parameter$b=6$ fm in 40Ca + 40Ca, 112Sn + 112Sn, and 197Au + 197Au collisions with different proton starting momenta in the HMT.From Fig. 6, it can be clearly seen that at incident beam energy 200 MeV/A, the effect of proton transition momentum on the
$ \pi^{-}/\pi^{+} $ ratio reaches its maximum. This effect decreases as beam energy increases as a result of the dominance of n-p correlations in nuclei at lower beam energies. Therefore, at around (and particularly below) the charged pion production threshold beam energies, the$ \pi^{-}/\pi^{+} $ ratio in heavy-ion collisions could be a probe of the proton transition momentum of the HMT in neutron-rich matter. -
In summary, in the framework of the IBUU transport model, proton transition momentum in the HMT was studied by nucleon transverse flows and elliptic flows in 40Ca + 40Ca,112Sn + 112Sn and 197Au + 197Au collisions at an incidentbeam energy of 400 MeV/A with impact parameter
$ b = 6~{\rm fm} $ . It was found that in neutron-rich reactions, the difference of neutron and proton elliptic flow is largely affected by the proton transition momentum, especially in the high-kinetic energy region. The neutron to proton differential elliptic flow, neutron to proton differential transverse flow, and the difference of neutron and proton transverse flow are less sensitive to the proton transition momentum. Thus, the difference of neutron and proton elliptic flow in the high-kinetic energy region provides a promising way to probe the proton high momentum distribution in nuclei in neutron-rich nuclear matter. The effect of proton transition momentum in the HMT on charged pion production was also studied. At beam energy 600 MeV/A, the$ \pi^{-}/\pi^{+} $ ratio shows no significant sensitivity to the proton transition momentum in asymmetric nuclear matter, while at 400 MeV/A and especially at 200 MeV/A, the ratio does have significant sensitivity. The above results may help us to further understand the nucleon momentum distributions in the HMT in asymmetric nuclear matter such as neutron stars.The authors thank Prof. Yong for useful discussions.
Isospin-sensitive observables as a probe of proton transition momentum in the HMT
- Received Date: 2019-07-10
- Available Online: 2019-11-01
Abstract: Based on the IBUU transport model, the effect of proton transition momentum on collective flows is studied in 40Ca + 40Ca,112Sn + 112Sn, and 197Au + 197Au collisions at an incident beam energy of 400 MeV/A with impact parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: