-
The
$ \beta - $ decay half-life is one of the most important weak interaction rates and is of great significance in both nuclear physics and astrophysics [1–5]. In nuclear physics, the$ \beta - $ decay half-life is a sensitive probe of nuclear structure, because it is mainly affected by the decay energy ($ Q $ value) and the transition matrix elements, both of which are determined by the nuclear structure. In astrophysics, the$ \beta - $ decay half-life is of great importance for nucleosynthesis (thus, element abundance in stars) and evolution of stars, because it determines by which route (the rapid neutron capture process (r-process), or the slow neutron capture process (s-process)) the heavier elements are produced in the Universe. It is believed that nuclei with atomic number less than iron are produced through thermonuclear reactions and about half of the heavier elements, referred to as neutron-rich nuclei heavier than iron, are made by the r-process, which is considered to occur in high temperature and high neutron density environment, although the actual site of the astrophysical r-process is still not known with certainty [6–8]. Recent works have confirmed the theoretical predictions that heavy nuclei are produced in r-processes during neutron star merging in the Universe [9–11], bringing new challenges for nuclear physics and astrophysics.As
$ \beta - $ decay half-life is a key quantity for nuclear structure and nucleosynthesis, theoretical studies of the$ \beta - $ decay half-life have been a hot topic in the past years. Since the first$ \beta - $ decay theory proposed by Fermi [12] in the 1930s, different models have been proposed to calculate the$ \beta - $ decay half-life. Some of these models are microscopic calculations in the framework of the interacting shell-model [13–15] or the quasiparticle random phase approximation (QRPA), on top of semi-empirical global models [16–20] or the Hartree-Fock-Bogoliubov method [21]. Because the microscopic calculations are very time consuming and model dependent, there exist several phenomenological methods. Sargent [22] proposed a fifth power law$ (T_{1/2}\propto E^{-5}) $ between the$ \beta - $ decay half-life and$ \beta - $ decay energy. Recently, we systematically analyzed the experimental data for$ \beta - $ decay half-life and found an exponential law for the$ \beta - $ decay half-life for nuclei far from stability, which is similar to the relation between the$ \alpha - $ decay half-life and decay energy [23–25]. The calculations with an empirical formula based on this exponential law reproduce the experimental data well.Most calculations mentioned above only consider the allowed transitions. Very recently, the forbidden transitions were included in the QRPA and shell-model calculations [26–30]. It was found in the shell-model calculations that the forbidden transitions become very important and must be considered for heavier r-process nuclei [26, 27, 30]. This was also confirmed by the QRPA calculations with interactions built on the various Hartree-Bogoliubov treatments, in which the forbidden transitions are included [28]. However, there are several problems in the present theoretical calculations: i) there is a lack of systematic studies of the contributions of allowed and first forbidden (FF) transitions to the total
$ \beta - $ decay half-life; ii) the microscopic calculations including the FF transitions are very time consuming; iii) it is hard to balance the contributions of allowed and forbidden transitions and hence of the quenching factor of the 8 matrix elements in the FF transitions. Therefore, systematical studies of the contributions of allowed and forbidden transitions are needed, and a reliable and fast formula for calculating the$ \beta - $ decay half-life is of great importance.Recent experimental measurements of the contribution of FF transitions to the
$ \beta^{-} $ -decay half-life focused mainly on heavy nuclei with mass number higher than 100 near the$ \beta- $ stable line [31–35]. In general, experimental data for neutron-rich nuclei are still very rare, especially in the region of heavy nuclei. As a result, one can not determine the full FF contribution in a given nucleus using the existing data due to the unknown spin or parity of certain energy levels. For example, the uncertainty of the FF contributions for nuclei$ ^{104}{\rm Tc} $ ,$ ^{105}{\rm Mo} $ and$ ^{175}{\rm Er} $ [36] is about 50%. Thus, developing a reliable and simple formula for predicting the FF contribution is of great significance.In this paper, we first systematically investigate the experimental branching ratios of the first forbidden transitions, and propose an empirical relation for predicting the branching ratios. Based on this relation, we propose a new formula for calculating the nuclear
$ \beta^{-} - $ decay half-life which includes the forbidden transitions. -
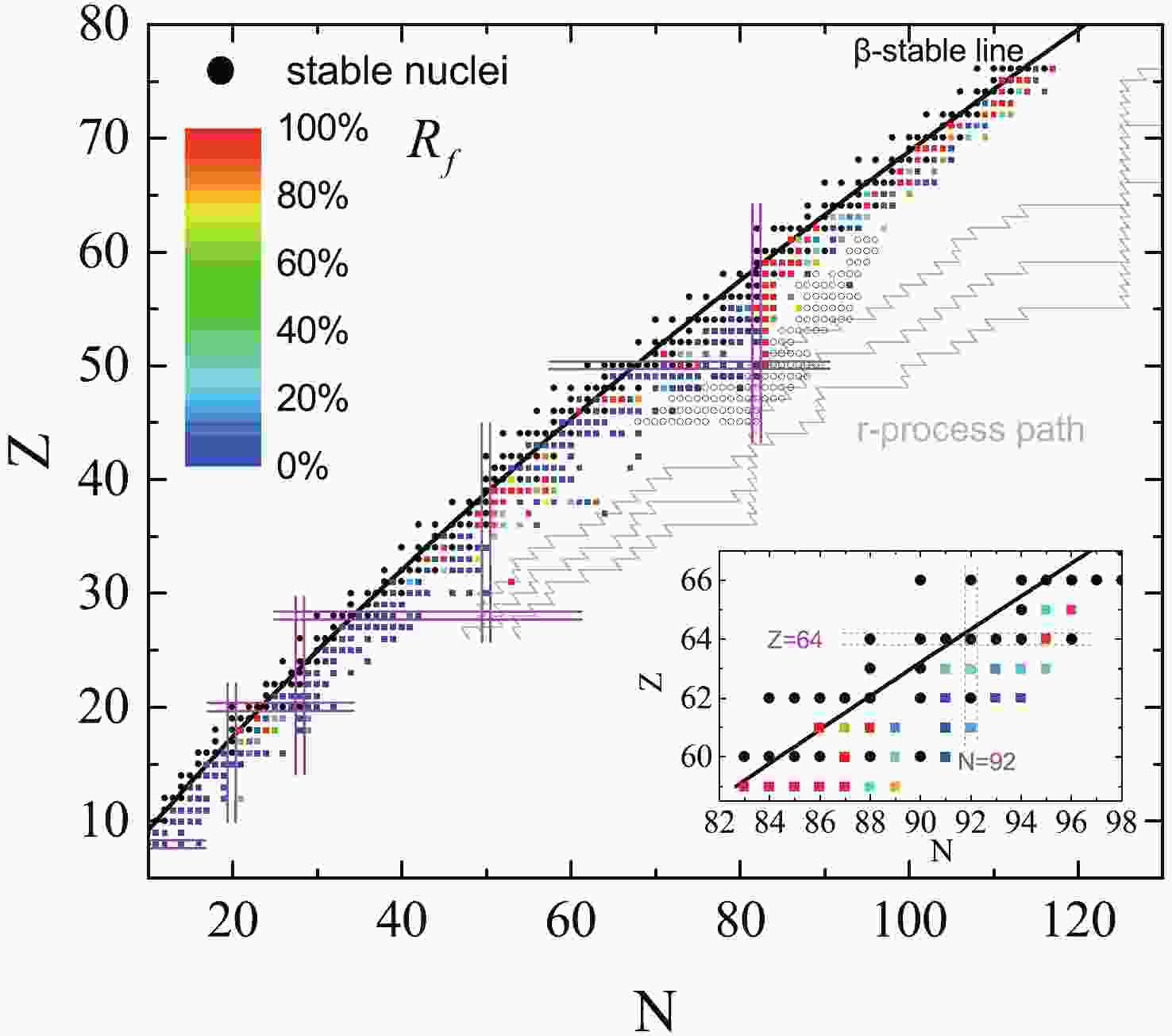
We plot the available experimental data for the total branching ratios of the first forbidden transitions in Fig. 1. In the experimental data for the total branching ratios [36], there is generally an unknown contribution in a given nucleus because of the unknown spin or parity of certain energy levels. Therefore, we plot only those nuclei where the unknown contribution is less than 10% . One can see from Fig. 1 that the contribution of first forbidden transitions for most nuclei is small (less than 20%). This shows that for most nuclei the allowed transitions are the main contribution and that the FF transitions can be neglected. However, one can see in Fig. 1 that there are three regions where the FF contribution is larger than 30%. In these regions, the FF contribution in nearly half of the nuclei is close to 100%. Obviously, the FF contribution is non-negligible and must be included in the calculations of the
$ \beta^{-} - $ decay half-life.
Figure 1. (color online) The experimental branching ratios (
$ R_f$ ) for the FF transitions (in percentage) as a function of the proton (Z) and neutron (N) numbers. Experimental data for 368 plotted nuclei are taken from the database of Nuclear Structure and Decay Data (NuDat) of National Nuclear Data Center (NNDC) [36].$ R_f$ for the nuclei around the subshell closure$ N = 92$ is shown in the inset. Magenta solid lines indicate the positions of closed proton and neutron shells. Black solid dots and open circles denote stable nuclei and 130 nuclei used for fitting Eq. (17), respectively. The three r-process paths are from Ref. [37].We can identify three regions, where the FF contribution is comparable to allowed transitions, the light nuclei region, the medium nuclei region and the heavy nuclei region. In Fig. 1, one can see that the light nuclei region contains nuclei with
$ 20<N<30 $ and$ 11<Z<20 $ . For nuclei$ {}^{\; 39}_{\; 18} {\rm Ar} _{21}^{}$ ,$ {}^{\; 42}_{\; 18}{\rm Ar} _{24}^{}$ and$ {}^{\; 42}_{\; 19}{\rm K} _{23}^{}$ in this region, the FF contribution is nearly 100%. Also, there are five nuclei in this region whose FF contributions are more than 30%. Recent shell-model calculations in the$ sd+pf+sdg $ valence space were used to study the$ \beta^{-} - $ decay half-life of nuclei in this region, and they showed that the FF transitions have a non-negligible contribution to the half-life [27]. The medium nuclei region contains nuclei with$ 30<Z<43 $ and$ 40<N<64 $ . It can be seen that the FF contribution in most nuclei in this region is more than 20%, while 15 nuclei with nearly a 100% FF contribution are located in the region$ N>50 $ . This implies that the FF transitions are also non-negligible and must be considered in calculations of the$ \beta^{-} - $ decay half-life. Our previous shell-model calculations including FF transitions for the waiting point nuclei around N = 50 also showed that the contribution of FF transitions is non-negligible [26]. For eight nuclei with Z = 46, 47, 50 and 51 near the β-stable line, the FF contribution is close to 100%. In Fig. 1, one can see that besides the light and medium nuclei regions, there is another region ($ N > 82 $ ), where the FF contribution is very large, and the fraction of nuclei with significant FF contribution is much higher than in the light and medium regions. In particular, for the nuclei with$ 82<N<88 $ , the FF contribution of 21 nuclei, for which experimental data is available, is nearly 100%. In the region$ 98<N<115 $ , the FF contribution of most nuclei close to the β-stable line is nearly 100%.In the inset of Fig. 1, we show the FF contributions around the subshell closure N = 92 close to the β-stable line. In general, the first forbidden transitions and the allowed transitions for the nuclei in the inset are of equal importance. The FF contribution in nuclei located around
$ {}^{154}_{\; 62} {\rm Sm}_{92}^{}$ decreases to the minimum, which is close to 0. However, the FF contributions in the region$ 82<N<88 $ increase towards the maximum, which is close to 100%.We systematically study the
$ \beta ^{-} $ -decay half-life of nuclei in the inset of Fig. 1, in which the allowed and first forbidden transitions are experimentally known. It is found that the branching ratios of first forbidden transitions for these nuclei can be described by the following formula, which will be discussed later.$ {R_f} = 100 - \left(h_0 + {h_1}{e^{ - \textstyle\frac{{{(Z-62)^2+(N - 92)^2}}}{{17}}}}\right), $

(1) where
$ h_0 $ and$ h_1 $ are parameters, and Z and N are the proton and neutron numbers of the parent nuclei. With a least-squares fit of the available experimental data for the nuclei in the inset of Fig. 1, we obtain the following parameters in Eq. (1):$ h_0 = 0 $ ,$ h_1 = 98 $ . The average deviation for the 27 nuclei in the inset, which has the form:$ \Delta = \frac{1}{n}\sum\limits_{i = 1}^n | {\log _{10}}R_{f{{\rm cal}}}^i - {\log _{10}}R_{f{{\rm exp}}}^i|, $

(2) is 0.20, where n is the number of nuclei in the fit. To see how the formula reproduces the experimental branching ratios, we show the ratio of the theoretical prediction to the experimental data in Fig. 2. It is seen from Fig. 2 that the experimental data are reproduced reasonably well for most cases. Hence, the formula for the branching ratio seems reliable and could be used to predict the relative contributions of the allowed and forbidden transitions. This is very important as it allows to quantify the contribution of forbidden transitions, and hence to study the quenching factor for the 8 matrix elements in the forbidden transitions, and even the quenching of allowed transitions.

Figure 2. Logarithm of the ratio
$ {R_{f{{\rm cal}}}}/{R_{f{{\rm exp}}}}$ between$ R_f$ calculated with Eq. (1) and the experimental value, versus the neutron number of the parent nuclei.It is worthwhile to discuss the physics behind Eq. (1). According to Fermi's theory of β-decay, the partial half-life
$ T_{1/2} $ is obtained by$ {T_{1/2}} = \frac{{\ln 2}}{\lambda }, $

(3) where the decay constant λ has the form:
$ \begin{split} \lambda = & \frac{1}{{2{\pi ^3}}}\frac{{m_e^5{c^4}}}{{{\hbar ^7}}}\int_1^{{w_0}} C(w)F(Z,R,w)(w^{2}-1)^{1/2} \\&\times w{{({w_0} - w)}^2} {\rm d}w. \end{split} $

(4) In Eq. (4),
$ C(w) $ is the shape factor depending on the electron energy w in units of electron mass,$ w_{0} $ is the maximum available electron energy, also in electron mass units, and$ F(Z,R,w) $ is the Fermi function that corrects the phase space integral for the Coulomb distortion of the electron wave function near the nucleus, which is a function of the nucleus radius R, proton number Z and w [38–40]. For the GT decay, the shape factor does not depend on the electron energy, and for the$ \beta^{-} $ -decay it has the form$ C(w) = B( {\rm GT}^{-}) $ . For the first forbidden (FF) transition, the shape factor$ C(w) $ has the form:$ C(w) = k + k_{a}w + \frac{{k_{b}}}{w} + k_{c}{w^2}, $

(5) where the coefficients k,
$ k_{a} $ ,$ k_{b} $ , and$ k_{c} $ depend on the FF nuclear matrix elements [41]. For the GT decay, replacing$ C(w) $ in Eq. (4) with$ C(w) = B( {\rm GT}^{-}) $ , one can obtain the decay constant for allowed transitions [42]$ {\lambda _a} = {a}{(2R)^{ - {\alpha ^2}{Z^2}}}{e^{\alpha Z\pi }} {\left(\frac{{w_{0}m_{e}c{^2}}}{c}\right)^{5 - {\alpha ^2}{Z^2}}}B( {\rm GT}^{-}), $

(6) where a is constant. For simplicity, Eq. (6) can be written in the following form:
$ {\lambda _a} = {d_1}{w_0^{5 - {\alpha ^2}{Z^2}}}, $

(7) where the coefficient
$ d_1 $ represents all terms in Eq. (6) except the term$ {w_0}^{5-\alpha^2 Z^2} $ . For FF transitions, in analogy with GT transitions, one can obtain the form:$ \begin{split} {\lambda _f} = {b_{ - 1}}{w_0^{4 - {\alpha ^2}{Z^2}}} + {b_0}{w_0^{5 - {\alpha ^2}{Z^2}}}+ {b_1}{w_0^{6 - {\alpha ^2}{Z^2}}} + {b_2}{w_0^{7 - {\alpha ^2}{Z^2}}}, \end{split} $

(8) where the coefficients
$ b_{-1} $ ,$ b_0 $ ,$ b_1 $ , and$ b_2 $ contain the term$ {(2Rm_{e}c)^{ - {\alpha ^2}{Z^2}}}{e^{\alpha Z\pi }} $ and the respective matrix elements.If we ignore the forbidden transitions higher than the first order, the branching ratio of the allowed transition
$ R_{a} $ can be written as:$ R_{a} = \frac{{{\lambda _a}}}{{{\lambda _a} + {\lambda _f}}}, $

(9) where
$ \lambda _f $ is the decay constant of the first forbidden transition. One can obtain the following expression by combining Eq. (7), Eq. (8) and Eq. (9)$ R_{a} = \frac{1}{{{c_{ - 1}}/w_0 + {c_0} + {c_1}w_0 + {c_2}{w_0^2}}}, $

(10) where the coefficients
$ c_{ - 1} $ ,$ c_0 $ ,$ c_1 $ and$ c_2 $ contain only some constants and matrix elements.One can use Eq. (10) to calculate the branching ratios of the allowed transitions if we know the expression for
$ w_0 $ . To achieve this goal, we plot the ratio$ w_0/(bN+c) $ (b and c are parameters) as a function of the neutron number N in Fig. 3(a) and Fig. 3(b). It can be seen from the two panels that the ratio has a minimum value around the shell (N = 82) and subshell closures (N = 92). To consider the shell correction, we use the form$ w_0 = (bN+c)(1-S) $ to describe$ w_0 $ empirically, where S represents the shell correction described by the Gaussian function [24]. The expression for$ w_0 $ including the proton number Z and the neutron number N can be written as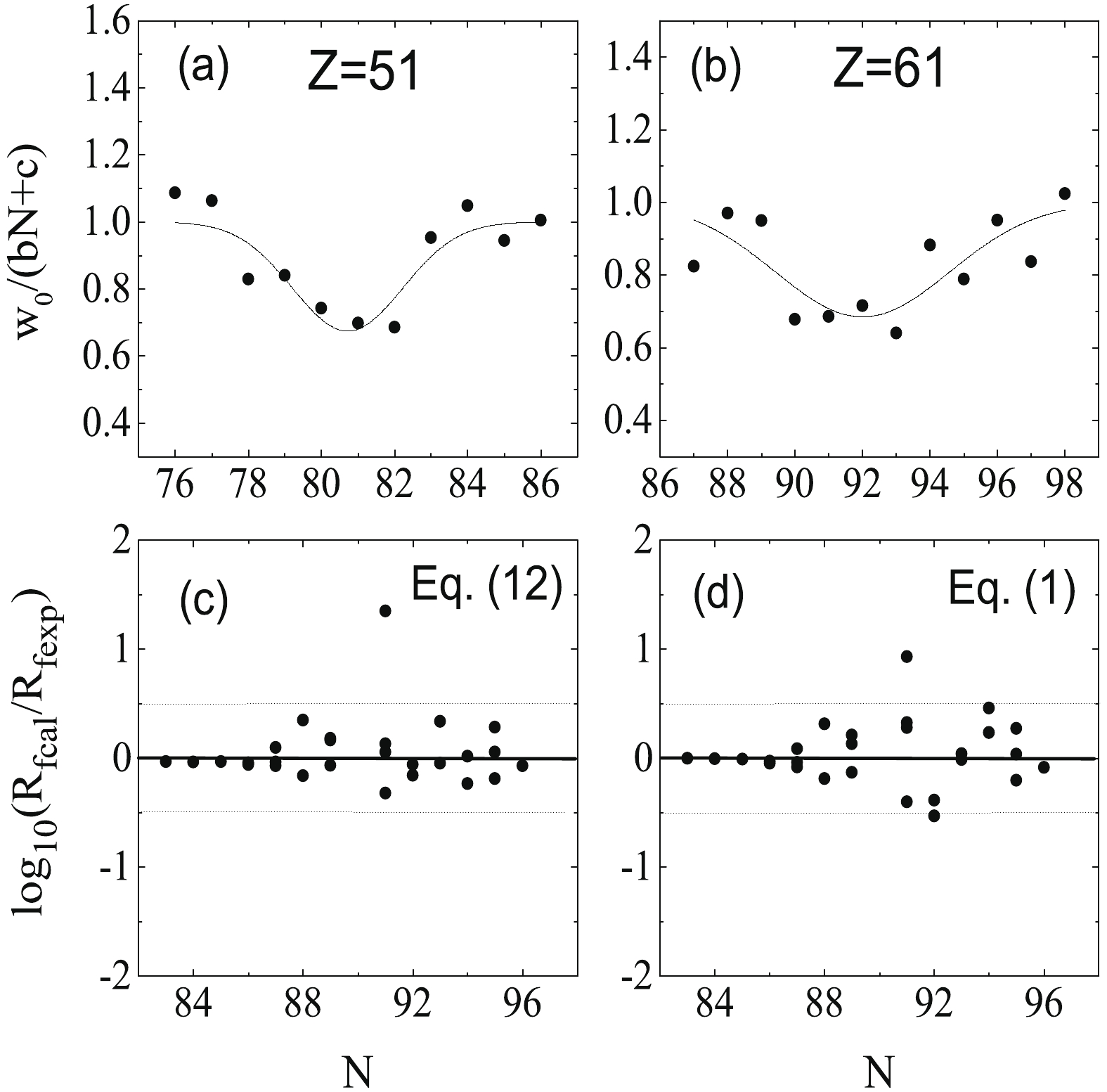
Figure 3. (a and b) Ratio between
$ w_0$ and$ (bN+c)$ versus the neutron number for the Z = 51 and Z = 61 isotopic chains. (c and d) Logarithm of the ratio$ {R_{f{{\rm cal}}}}/{R_{f{{\rm exp}}}}$ between$ R_f$ calculated respectively with Eq. (12) and Eq. (1) and the experimental data, versus the neutron number of the parent nuclei around Z = 62.$ {w_0}{(Z,N)} = ({b_3}ZN + {b_4}N + {b_5}Z + {b_6})(1 - S), $

(11) where
$ \{b_i|i = 3-6\} $ are parameters. Substituting Eq. (11) into Eq. (10) and fitting the experimental data for$ R_a $ for the nuclei around the subshell N = 92, we obtain the expression for$ R_a $ including the parameters:$ \begin{split} {R_{{a}}} =& \frac{{100}}{{10.05/{w_0} + 10.54 - 5.67{w_0} + 0.68w_0^2}},\\ {w_0} =& ( -0.02ZN + 1.42N + 1.68Z\\ &-106) \left(1- 0.60e^{- \textstyle\frac{{(Z - 62)^2 + (N - 92)^2}}{30}}\right). \end{split} $

(12) For
$ w_{0}>1 $ , Eq. (12) is replaced by a Gaussian function similar to the Gaussian function in Eq. (1). It is very convenient to calculate the branching ratios with Eq. (1). For simplicity, we take Eq. (1) to fit the experimental data for$ R_a $ . A comparison between the experimental data for$ R_f $ and the results calculated by Eq. (12) and Eq. (1) are shown in Fig. 3(c) and Fig. 3(d), respectively. It is seen from the two panels that Eq. (12) describes reasonably well the experimental data, similar to Eq. (1), which indicates that Eq. (12) can be replaced by Eq. (1) around the subshell N = 92. Although Eq. (12) can be regarded as equivalent to Eq. (1) around N = 92, there is a difference in the region away from N = 92, as Eq. (12) is still a function of the decay energy, while Eq. (1) becomes a constant in this case. However, it was observed that when$ w_0 $ is larger than$ w_0 = 11 $ [36] for the nucleus$ {}^{161}_{\; 62}{\rm Sm}_{99}^{} $ , Eq. (12) varies slowly. This shows that Eq. (12) can be replaced by Eq. (1) far from the subshell N = 92. It should be noted that the branching ratios calculated with Eq. (1) for Z=62 and N=92 (obtained by fitting the experimental data) have a small deviation from the subshell closures Z=64 and N=92. Therefore, for simplicity of calculation, we take in this paper Eq. (1) for calculations of the$ \beta ^{-} $ -decay half-life and the FF contribution instead of Eq. (12).The first forbidden transitions in Fig. 1 were discussed theoretically in [28]. In particular, heavy nuclei beyond the shell closure at N = 82, with N = 83, 84, and 85 and Z = 59, have large FF contributions: 100%, 99%, 97% given by Eq. (1), which are very close to the experimental values: 100%, 100%, 99%, respectively. This suggests that the FF contribution is significantly larger after the shell closure at
$ N = 82 $ .As shown in Table 1, protons and neutrons of these parent nuclei fill the
$ sdg $ and$ pfh $ shells, respectively. The ground state parity of odd A parent nuclei is opposite to that of their daughter nuclei, and the ground state parity of odd-odd and even-even nuclei is negative and positive, respectively. As a consequence, the contributions of forbidden transitions are larger for nuclei dominated by transitions from ground state to ground state. It is also seen in Table 1 that there are no allowed transitions between the ground states of parent nuclei and daughter nuclei. Moreover, when the parity of every excited state of daughter nuclei is opposite to the ground state parity of parent nuclei, or the transition order is higher than the first forbidden, then the contribution of allowed transitions is 0. This case is denoted by the blank space in the fifth column in Table 1. The decay energies become smaller for the GT transitions from the ground state to excited states of daughter nuclei, resulting in a lower contribution of allowed transitions. As$ R_f $ > 90% for the nuclei shown in Table 1, the contributions of allowed transitions are less than 10%.Parent Nuclei Daughter $J\pi_{gs}$ 

Maximum $R_{f}$ (%)

Daughter $J\pi$ , E(level)

Daughter $E_a$ /MeV

$Q_{gs}$ /MeV

${}^{134}_{\; 51}$ Sb

$_{83}^{}$ (

$0^{-}$ )

$0^{+}$ 

97.6 ( $0^{+}$ ; g.s.)

8.91 ${}^{135}_{\; 52}$ Te

$_{83}^{}$ (

$7/2^{-}$ )

$7/2^{+}$ 

62 ( $7/2^{+}$ ; g.s.)

4.46 6.40 ${}^{137}_{\; 54}$ Xe

$_{83}^{}$ (

$7/2^{-}$ )

$7/2^{+}$ 

67 ( $7/2^{+}$ ; g.s.)

1.87 4.68 ${}^{137}_{\; 55}$ Cs

$_{82}^{}$ (

$7/2^{+}$ )

$3/2^{+}$ 

94.7 ( $11/2^{-}$ ; 0.66 MeV)

1.69 ${}^{138}_{\; 55}$ Cs

$_{83}^{}$ (

$3^{-}$ )

$0^{+}$ 

44 ( $3^{+}$ ; 2.45 MeV)

2.88 5.89 ${}^{139}_{\; 55}$ Cs

$_{84}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

85 ( $7/2^{-}$ ; g.s.)

1.62 4.72 ${}^{139}_{\; 56}$ Ba

$_{83}^{}$ (

$7/2^{-}$ )

$7/2^{+}$ 

70 ( $7/2^{+}$ ; g.s.)

2.83 ${}^{140}_{\; 56}$ Ba

$_{84}^{}$ (

$0^{+}$ )

$3^{-}$ 

40 ( $1^{-}$ ; 0.04 MeV)

1.56 ${}^{140}_{\; 57}$ La

$_{83}^{}$ (

$3^{-}$ )

$0^{+}$ 

43.9 ( $3^{+}$ ; 2.41 MeV)

2.46 4.27 ${}^{141}_{\; 57}$ La

$_{84}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

98.12 ( $7/2^{-}$ ; g.s.)

2.21 3.01 ${}^{141}_{\; 58}$ Ce

$_{83}^{}$ (

$7/2^{-}$ )

$5/2^{+}$ 

69.7 ( $7/2^{+}$ ; 0.15 MeV)

1.09 ${}^{143}_{\; 58}$ Ce

$_{85}^{}$ (

$3/2^{-}$ )

$7/2^{+}$ 

48.2 ( $3/2^{+}$ ; 0.35 MeV)

1.97 ${}^{144}_{\; 58}$ Ce

$_{86}^{}$ (

$0^{+}$ )

$0^{-}$ 

76.5 ( $0^{-}$ ; g.s.)

0.83 ${}^{142}_{\; 59}$ Pr

$_{83}^{}$ (

$2^{-}$ )

$0^{+}$ 

96.3 ( $0^{+}$ ; g.s.)

2.08 2.67 ${}^{143}_{\; 59}$ Pr

$_{84}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

100 ( $7/2^{-}$ ; g.s.)

1.45 ${}^{144}_{\; 59}$ Pr

$_{85}^{}$ (

$0^{-}$ )

$0^{+}$ 

97.9 ( $0^{+}$ ; g.s.)

2.19 3.51 ${}^{145}_{\; 59}$ Pr

$_{86}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

97.6 ( $7/2^{-}$ ; g.s.)

2.32 ${}^{146}_{\; 59}$ Pr

$_{87}^{}$ (

$2^{-}$ )

$0^{+}$ 

45 ( $0^{+}$ ; g.s.)

1.19 4.76 ${}^{147}_{\; 60}$ Nd

$_{87}^{}$ (

$5/2^{-}$ )

$7/2^{+}$ 

80.2 ( $5/2^{+}$ ; 0.09 MeV)

1.41 ${}^{147}_{\; 61}$ Pm

$_{86}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

99.99 ( $7/2^{-}$ ; g.s.)

0.74 ${}^{165}_{\; 66}$ Dy

$_{99}^{}$ (

$7/2^{+}$ )

$7/2^{-}$ 

83 ( $7/2^{-}$ ; g.s.)

0.49 1.80 ${}^{166}_{\; 66}$ Dy

$_{100}^{}$ (

$0^{+}$ )

$0^{-}$ 

97 ( $1^{-}$ ; 0.08 MeV)

0.43 1.00 ${}^{166}_{\; 67}$ Ho

$_{99}^{}$ (

$0^{-}$ )

$0^{+}$ 

49.9 ( $2^{+}$ ; 0.08 MeV)

1.66 2.37 ${}^{169}_{\; 68}$ Er

$_{101}^{}$ (

$1/2^{-}$ )

$1/2^{+}$ 

55 ( $1/2^{+}$ ; g.s.)

0.86 ${}^{170}_{\; 69}$ Tm

$_{101}^{}$ (

$1^{-}$ )

$0^{+}$ 

81.9 ( $0^{+}$ ; g.s.)

1.48 ${}^{171}_{\; 69}$ Tm

$_{102}^{}$ (

$1/2^{+}$ )

$1/2^{-}$ 

98.04 ( $1/2^{-}$ ; g.s.)

0.61 ${}^{172}_{\; 69}$ Tm

$_{103}^{}$ (

$2^{-}$ )

$0^{+}$ 

36 ( $2^{+}$ ; 0.08 MeV)

1.15 2.39 ${}^{173}_{\; 69}$ Tm

$_{104}^{}$ (

$1/2^{+}$ )

$5/2^{-}$ 

76 ( $1/2^{-}$ ; 0.40 MeV)

1.81 Table 1. Experimental data [36] for
$ \beta^{-}$ -decay and nuclear properties of 28 parent nuclei with$ R_{f}$ >90%, and of their daughter nuclei. Ground state spin and parity of parent and daughter nuclei are shown in the first and second columns, respectively. Spin and parity of the energy level of daughter nuclei with maximum$ R_{f}$ decay branch (3rd column) with a transition from the ground state of parent nuclei to energy level of daughter nuclei are listed in the fourth column. The fifth column denotes the lowest excited energy of daughter nuclei with allowed decay from ground state of parent nuclei to excited state of daughter nuclei. In the fifth column, the blanks denote the case without allowed transitions from ground state of parent nuclei to energy levels of daughter nuclei.In summary, the reasons why the FF contributions are important in heavy nuclei with cross-shell transitions are as follows: 1) there are no allowed transitions from ground state to ground state and energy levels of some daughter nuclei; 2) the allowed transitions to the excited states of the other daughter nuclei are suppressed due to the reduced decay energies. For light nuclei, neutrons and protons fill mainly the orbits with the same parity, thus the decay is dominated by allowed transitions. Based on a systematical analysis of the experimental data, we identified, for the first time, the regions where the FF contributions are important. The underlying physics is also illustrated. This is helpful for the calculations and predictions of the
$ \beta ^{-} $ -decay half-life. Conversely, one can also extract the nuclear structure information from the branching ratios of FF transitions in an unknown region of the nuclei chart. -
According to the above discussion, the FF contribution is more important [26–30, 43] for heavy nuclei and must be considered in
$ \beta ^{-} $ -decay half-life calculations. Using the relation between the total half-life$ T_t $ and the partial half-life$ T_a $ for the allowed transitions and$ T_f $ for the FF transitions, one can obtain the expression:$ \ln {T_t} = \ln {T_a} + \ln (R_{a}/100). $

(13) In principle,
$ T_{a} $ could be obtained from Eq. (6) [42], from which one can get$ \begin{split} \ln {T_a} = & {a_0} + {a_1}{\alpha ^2}{Z^2} + ({\alpha ^2}{Z^2} - 5) \ln Q - \alpha Z \pi \\& + \frac{1}{3}{\alpha ^2}{Z^2}\ln A, \end{split} $

(14) where
$ a_0 $ and$ a_1 $ are parameters,$ Q = {w_0}{m_e}{c^2} $ for a transition from ground state to ground state, and A is the mass number. It was shown in Refs. [24, 42] that the paring effects and the shell effects are important for$ \beta ^{-} $ -decay half-life. With these effects included, Eq. (14) can be written as$ \begin{split} \ln {T_a} = & {a_0} + {a_1}{\alpha ^2}{Z^2} + ({\alpha ^2}{Z^2} - 5) \ln (Q - {a_2}\delta ) \\& - \alpha Z \pi + \frac{1}{3}{\alpha ^2}{Z^2}\ln A + S(Z,N), \end{split} $

(15) where
$ a_2 $ is a parameter,$ \delta = (-1)^{N}+(-1)^{Z} $ denotes the even-odd staggering caused by the pairing effect on β-decay Q value, and$ S(Z,N) $ is the shell correction factor.Eq. (13) is a strict definition, while Eq. (15) is an empirical formula based on the assumption that
$ \beta^{-} $ -decays in the r-process nuclei are dominated by the allowed transitions from ground state to ground state. For nuclei with a larger FF contribution, Eq. (15) underestimates the$ \beta^{-} $ -decay half-life. Therefore, when one uses Eq. (15) to calculate$ T_a $ , additional correction related to$ R_a $ should be included. The empirical Eq. (13) can then be written as:$ \ln {T_t} = \ln {T_a} + \ln (k R_{a}+d). $

(16) where
$ T_a $ is calculated using Eq. (15), and k and d are parameters. The reason for expanding$ \ln(R_a/100) $ in Eq. (13) into$ \ln(k{R_a}+d) $ is that when$ {R_a} $ is close to 0, the correction term approaches negative infinity. Also, when$ {R_a} $ is close to 0, small errors in the evaluation of$ {R_a} $ result in big differences in the obtained half-life. Therefore, choosing the form$ \ln(k{R_a}+d) $ is more reliable in practice.Substituting Eq. (15) and Eq. (1) in Eq. (16), and fitting to the experimental data allows to obtain the various parameters. Because the simplified Eq. (1) is more practical than Eq. (12) and describes reasonably well the experimental data, we replace
$ {R_a} $ in Eq. (16) by Eq. (1) instead of Eq. (12). To avoid mixing of the contributions of allowed and FF transitions in the fitting, we choose first the nuclei with the main allowed transition to determine the parameters of$ \ln {T_a} $ , and then fit the nuclei with big FF contribution to determine the$ {R_a} $ part. Due to the absence of experimental data for FF contributions in neutron-rich nuclei, we choose the fit region using the FF predictions in Ref. [28]. It was shown in this paper that neutron-rich nuclei in the region$ Z>40 $ and$ N<82 $ have a large contribution of allowed transitions, while the nuclei in the region$ N>82 $ are dominated by FF transitions. In these two regions, the experimental data for$ \beta ^{-} $ -decay half-life of 130 nuclei are selected to determine the parameters of$ \ln {T_a} $ and$ {R_a} $ by least-squares fitting. Another reason for choosing these neutron-rich nuclei is that the theoretical errors become larger in Eq. (15) due to the smaller Q values near the β-stable line [42], so that we chose those nuclei that are as far as possible from the β-stable line to reduce the errors. The position of the chosen 130 nuclei in the nuclear chart is shown in Fig. 1.We now substitute Eq. (15) and Eq. (1) in Eq. (16) and follow the fitting procedure described in the previous paragraph to get the formula for the
$ \beta ^{-} $ -decay half-life and its parameters:$ \begin{split} \ln {T_t} =& {a_0} + ({\alpha ^2}{Z^2} - 5)\ln (Q - {a_2}\delta ) - \alpha Z\pi \\ &+ {a_1}{\alpha ^2}{Z^2} + \frac{1}{3}{\alpha ^2}{Z^2}\ln A + S(Z,N)\\ & + \ln (k{R_a} + d),\\ S(Z,N) =& {a_3}{e^{{ - \textstyle\frac{{{{(Z - 50)}^2} + {{(N - 82)}^2}}}{{20}}}}} + {a_4}{e^{ - \textstyle\frac{{{{(Z - 58)}^2} + {{(N - 82)}^2}}}{{19}}}},\\ \ln (k{R_a} + d)\! =\!& \ln \left({a_5} + {a_6}{e^{ - \textstyle\frac{{{{(Z - 47)}^2} \!+\! {{(N - 80)}^2}}}{{56}}}}\! + \!{a_7}{e^{ - \textstyle\frac{{{{(Z - 57)}^2} + {{(N - 94)}^2}}}{{127}}}}\right), \end{split} $

(17) where
$ \{a_i|i = 0-7\} $ are parameters, listed in Table 2 for convenience. It should be noted that the Gaussian centers for$ R_a $ in Eq. (17) are different from those in Eq. (1). The Gaussian center in Eq. (1) is determined by fitting to the experimental data for nuclei close to the β-stable line, while the fitting range for Eq. (17) is far from the β-stable line. In addition, the fitting zone includes the magic numbers N = 82, Z = 50 and 58. The shell effects on half-life are described by the term$ S(Z,N) $ [24, 42] in Eq. (17).$a_0$ 

$a_1$ 

$a_2$ 

$a_3$ 

$a_4$ 

$a_5$ 

$a_6$ 

$a_7$ 

6.92 26.10 −0.94 3.14 2.73 2.69 −2.31 −2.41 Table 2. The eight parameters of Eq. (17) obtained by the least-squares fit of the experimental
$ \beta^{-}$ -decay half-life for 130 heavy nuclei.To test the reliability of Eq. (17), the average deviation ∆ is calculated by
$ \Delta = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\log }_{10}}T_{{{\rm cal}}}^i - {{\log }_{10}}T_{{{\rm exp}}}^i} \right|}. $

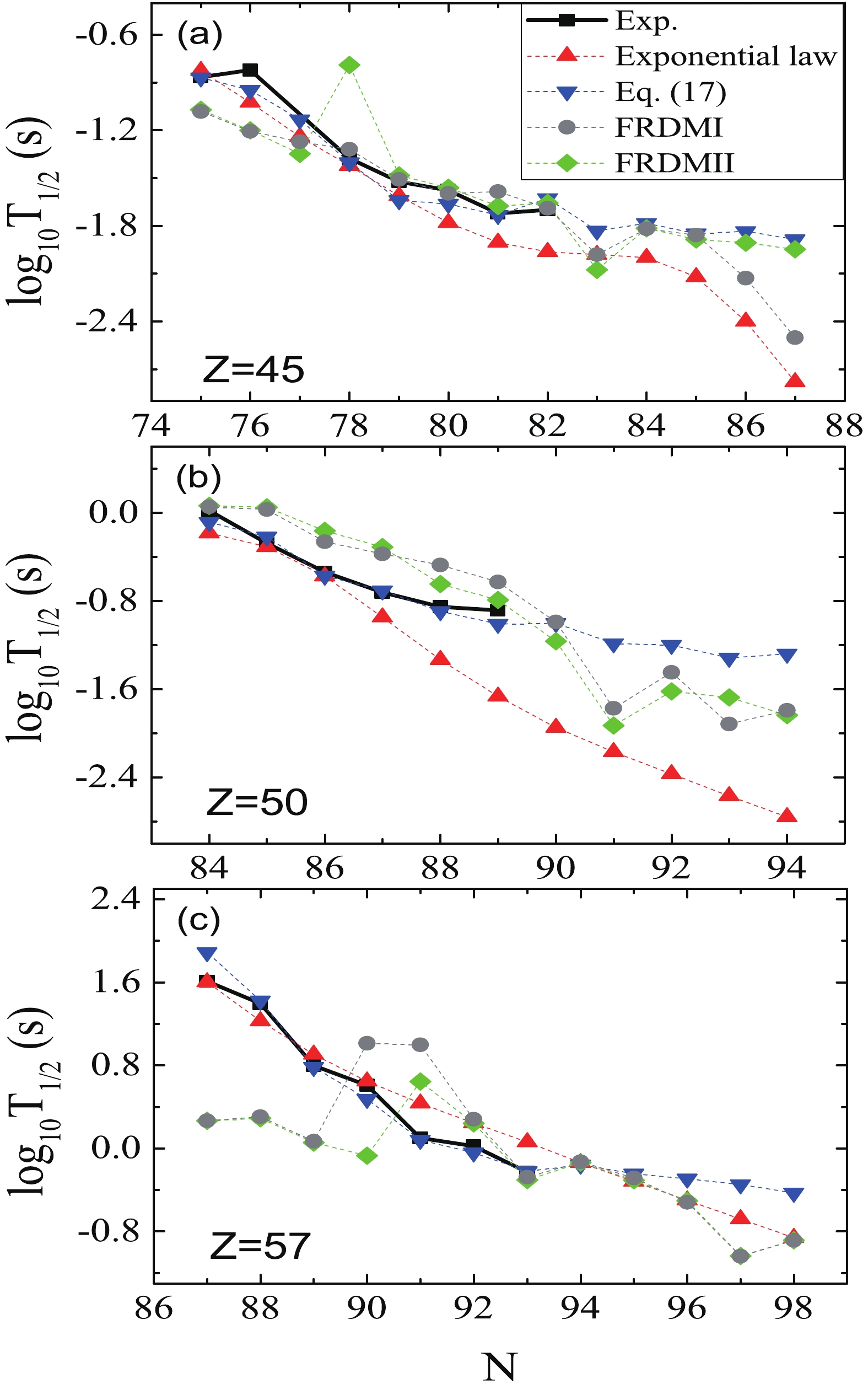
(18) The calculated average deviation of Eq. (17) is 0.12, which means that the average deviation between the experimental data and the calculated half-lives after including FF transitions is a factor of 1.32. To compare with this work, we use the exponential formula [24] to fit the experimental data of the 130 nuclei which were used to determine the parameters of Eq. (17). The results for some nuclei are illustrated in Fig. 4. Microscopic theoretical calculations are also listed in the figure for comparison. Also, to demonstrate the extrapolating power of Eq. (17), we use Eq. (17) and the Q values from Ref. [20] to predict the
$ \beta ^{-} $ -decay half-lives in Fig. 4. The deviation between the calculated and experimental Q values [20] are 8% for the nuclei shown in Fig. 4. It can be seen from this figure that the results of this work, which include the FF transitions, are much closer to the experimental data than the others. From Fig. 4, it can be seen that Eq. (17) predicts larger values than the other models, and that they decrease more slowly with increasing neutron number. For the Z = 45 isotopic chain, our results are closer to FRDMII calculations than the other models. In general, the largest difference is between this work and the exponential law [24], especially for the Z = 50 isotopic chain. Predictions of all models are closest for the Z = 57 isotopic chain. It should be noted that Eq. (17) has only two additive parameters, while there are 6 parameters in the exponential formula [24]. Our results are also very close to the previous shell-model calculations that include FF contribution. For example, the calculated$ \beta^{-}- $ decay half-lives using Eq. (17) for$ {}^{128}_{\; 46}{\rm Pd}_{82}^{} $ and$ {}^{127}_{\; 45}{\rm Rh} _{82}^{} $ are 43 ms and 23 ms, and are very close to the experimental values of$ 35\pm3 $ ms and$ 20_{ - 7}^{ + 20} $ ms, and the shell-model results of 47.25 ms and 27.98 ms [26].Both the formula for the FF branching ratio (Eq. (1)) and Eq. (17) can reproduce the experimental data reasonably well. The extrapolating power of Eq. (17) was shown in Fig. 4. It is also important to discuss the extrapolating power of the formula for the FF branching ratio. We recall that Eq. (1) contains the Gaussian function with a center at
$ {}^{154}_{\; 62}{\rm Sm} _{92}^{} $ . However,$ R_a $ in Eq. (17) is based on Eq. (1) with different Gaussian centers. Accordingly, we can examine the Gaussian functions for$ R_a $ in Eq. (17) to discuss the extrapolation power of the formula for the FF branching ratio.The Gaussian functions for
$ {R_f} $ ($ {R_f} = 100-{R_a} $ ) in Eq. (17) are$ \begin{split} {R_f} =& 100 - \left({h_2} + {h_3}{e^{ - \textstyle\frac{{{{(Z - 47)}^2} + {{(N - 80)}^2}}}{{56}}}} + {h_4}{e^{ - \textstyle\frac{{{{(Z - 57)}^2} + {{(N - 94)}^2}}}{{127}}}}\right), \end{split} $

(19) where
$ {h_2} $ ,$ {h_3} $ and$ {h_4} $ are parameters which are not equal to$ {a_5} $ ,$ {a_6} $ and$ {a_7} $ in Eq. (17).$ {a_5} $ ,$ {a_6} $ and$ {a_7} $ include contributions of parameters k and d, which are unrelated to$ {R_f} $ , and hence k and d need to be excluded to obtain a realistic expression for$ {R_f} $ . There are only about ten nuclei with available experimental data for$ {R_f} $ around$ {}^{127}_{\; 47} {\rm Ag} _{80}^{}$ and$ {}^{151}_{\; 57}{\rm La} _{94}^{} $ [36], which is not enough to determine reliably the parameters in Eq. (19) by least-squares fitting. Therefore, we also include the theoretical data for$ {R_f} $ for 84 nuclei,$ Z = 47 $ , 57 isotopes and$ N = 80 $ , 94 isotones, from Ref. [28]. Finally, the values of$ {h_2} $ ,$ {h_3} $ and$ {h_4} $ , obtained by the least-squares fit of the experimental and theoretical data for$ {R_f} $ , are$ {h_2} = 35 $ ,$ {h_3} = 59 $ and$ {h_4} = 10 $ .Before using Eq. (19) to calculate
$ {R_f} $ , it is necessary to define its application region, which can be determined from Eq. (12). The theoretical expression for the branching ratio Eq. (12) was obtained by fitting the experimental data for heavy nuclei with cross-shell transitions. For nuclei without cross-shell transitions, the contribution of the terms related to$ w_0 $ in Eq. (12) can be in principle neglected. As a consequence, in this case$ R_a $ of Eq. (12) should be approximately constant, and equal to 100. With these limitations, the proposed Eq. (17) and Eq. (19) are not applicable to nuclei with$ Z>40 $ and$ 50<N<70 $ . In addition, Eq. (19) includes Gaussian functions whose application is limited to the region around their centers. Therefore, Eq. (19), and even Eq. (17), are mainly applicable to the region around$ {}^{127}_{\; 47} {\rm Ag} _{80}^{}$ and$ {}^{151}_{\; 57} {\rm La} _{94}^{}$ , which does not include other major shell closures, except for magic numbers$ Z = 50 $ and$ N = 82 $ .Within its application region and with the parameters of Eq. (19), we obtain results similar to the RQRPA results [28]: i) the FF contribution is around 60% in the region
$ 50<Z<63 $ and$ 90<N<100 $ around$ {}^{151}_{\; 57} {\rm La} _{94}^{}$ ; ii) the allowed transitions are dominant in the region$ 43<Z<52 $ and$ 75<N<85 $ around$ {}^{127}_{\; 47}{\rm Ag} _{80}^{} $ .Concerning the ability of Eq. (19) to reproduce
$ R_f $ shown in Fig. 1, there are in general large differences between the experimental data for$ R_f $ and the values calculated using Eq. (19). For example, the calculated FF contribution for several nuclei around$ {}^{127}_{\; 47} {\rm Ag} _{80}^{}$ is about 10%, which is close to the experimental values (less than 20%) [36]. However, there is a difference of about 15%-80% between the experimental data and calculations in the region$ 70<N<84 $ and$ Z>50 $ . Around$ {}^{127}_{\; 47} {\rm Ag} _{80}^{}$ and$ {}^{151}_{\; 57}{\rm La}_{94}^{} $ , more experimental data for neutron-rich nuclei are needed to constrain the parameters of Eq. (19) and to test its ability to reproduce the FF contributions. -
Based on the theory of
$ \beta- $ decay and the analysis of experimental data, we propose a new formula for the contribution of the first forbidden (FF) transitions for the nuclei around$ N = 92 $ and near the β-stable line. Also, another formula, which includes the contribution of FF transitions, is proposed for calculating the nuclear$ \beta^{-} $ -decay half-life. Both formulas give reasonable description of the experimental data. For the neutron-rich nuclei region$ 43<Z<63 $ and$ 75<N<100 $ , centered at$ {}^{127}_{\; 47}{\rm Ag} _{80}^{} $ and$ {}^{151}_{\; 57}{\rm La}_{94}^{} $ , the FF branching ratios calculated with RQPRA could be fitted well by the formula for the FF contribution. However, because of limited experimental data for the branching ratios of unstable nuclei, the fit parameters in this formula are not fully constrained. As a result, the formula for the$ \beta^{-} $ -decay half-life is more suitable for calculations of half-lives than of the branching ratios of forbidden transitions. For the latter, more studies are necessary. The formula for the half-life is the first empirical formula which incorporates the contribution of the first forbidden transitions. This formula is useful for predicting$ \beta^{-} $ -decay half-life in nuclear structure studies, as well as for nucleosynthesis calculations in stars.
The contribution of the first forbidden transitions to the nuclear β−-decay half-life
- Received Date: 2019-03-01
- Accepted Date: 2019-08-16
- Available Online: 2019-11-01
Abstract:





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: