-
After the discovery of the Higgs boson [1, 2], the focus of high energy physics turned to the study of its detailed properties. While the Higgs measurements at the Large Hadron Collider (LHC) could reach a precision level of about 5%~10% [3] (except for the Higgs trilinear coupling), precision measurements of Higgs couplings could benefit from the cleaner environment of a future
$ e^+e^- $ collider. Among several proposals, the Circular Electron Positron Collider (CEPC) in China [4, 5] is proposed to run as a Higgs factory at 240 GeV, which maximizes the$ e^+e^-\to HZ $ cross-section, producing at least a million Higgs bosons over a period of 7 years.Apart from the Higgs boson, the top quark could play an equally important role in the electroweak symmetry breaking mechanism [6]. By virtue of its large mass, it is often thought of as a window to new physics. Producing top quark pairs at a lepton collider would, however, require a minimum center-of-mass energy of about
$ 2m_{\rm top}\approx $ 345 GeV, beyond the currently planned CEPC energy. While an energy upgrade above the$ t\bar t $ threshold remains an option, an interesting question to ask is whether we could still learn something about the top quark at an energy below the production threshold. One possibility, for instance, would be to study virtual top quarks, which appear in almost all electroweak processes due to quantum corrections [7–9].In this work, we study a different possibility: instead of producing pairs of top quarks on shell, single top quark can be produced in association with a light quark. The process
$ e^+e^-\to t(\bar t)j $ is possible with$ E_{\rm cm} = 240 $ GeV. This process is highly suppressed by the Glashow-Iliopoulos-Maiani (GIM) mechanism [10] in the Standard Model (SM), but if physics beyond SM exists and gives rise to the so called top quark flavor-changing neutral (FCN) interactions, this production mode could happen via an s-channel Z or photon, or via a contact four-fermion FCN interaction. The top quark FCN couplings have been searched for at the LHC, Tevatron, LEP2 and HERA experiments [11–52]. Currently, the best constraints of the two-fermion FCN couplings come from the LHC [15, 24, 34, 39, 40], while the four-fermion contact interactions have received much less attention, even though they are indispensable for a complete description of FCN couplings, and are also motivated by the explicit models beyond SM [53–56]. Interestingly, it was shown that the best sensitivity for the$ eetq $ contact interactions is still given by the LEP2 experiments, despite its much lower integrated luminosity [53, 57]. LHC and LEP2 thus provide complementary constraints of the theory space spanned by the two types of FCN interactions. This immediately implies that a future$ e^+e^- $ collider could further improve our knowledge of the top quark flavor properties. The goal of this paper is to study the prospects of top FCN couplings at CEPC, to demonstrate that a similar complementarity is expected between CEPC and the high-luminosity LHC (HL-LHC), and to provide input for CEPC experiments. Similar prospects have been provided previously for TESLA, FCC-ee, and CLIC [58–60], but only the CLIC report [60] has considered the four-fermion interactions.The paper is organized as follows. In Section 2, we describe the theory background with focus on the two-fermion FCN and four-fermion
$ eetq $ FCN interactions, and their different sensitivities at a hadron collider and a$ e^+e^- $ collider. In Section 3, we give the details of our simulation and our analysis strategy. In Section 4, we present our results and discuss possible improvements. Section 5 is devoted to our conclusion. Some additional results can be found in Appendix A. -
FCN interaction of the top quark is highly suppressed by the GIM mechanism. The branching ratios for two-body top FCN decays in SM are of the order of
$ 10^{-12} $ –$ 10^{-15} $ [61–63]. Any hint for such processes would thus immediately point to physics beyond SM. A wide variety of limits have been set on these couplings. For example, flavor changing decay modes$ t\to qZ $ and$ t\to q\gamma $ were searched for at the Tevatron by CDF [11–13] and D0 [14], and at the LHC by ATLAS [15–19] and CMS [20–22]. At the LHC,$ t\to qH $ was also searched for [23–32]. Direct top production,$ pp\to t $ , was considered at the Tevatron by CDF [33], and at the LHC by ATLAS [34–36], while a similar production with an additional jet in the final state was considered by D0 [37, 38] and CMS [39]. Single top production in association with a photon and a Z were searched for by CMS [40] and ATLAS [41]. At LEP2,$ e^+e^-\to tj $ was investigated by all four collaborations [42–47], while at HERA, the single-top$ e^-p\to e^-t $ production was considered by ZEUS [48, 49] and H1 [50–52]. The most constraining limits were recently collected and summarized in Table 33 of Ref. [57]. The sensitivities in terms of the two-body branching ratios are roughly of the order$ 10^{-4} $ to$ 10^{-3} $ , approaching the expected values from typical new physics models [64].A complete and systematic description of the top quark FCN couplings based on the Standard Model Effective Field Theory (SMEFT) [65–67] was discussed and documented in the LHC TOP Working Group note [68]. The idea is that starting from the Warsaw basis operators [69], one defines linear combinations of Wilson coefficients that give independent contributions in a given measurement. For the
$ e^+e^-\to tj $ process, the relevant basis operators are the following two-fermion operators:$ O_{\varphi q}^{1(ij)} = (\varphi^\dagger i\!\!\overleftrightarrow{D}_\mu\varphi) \left( \bar q_i \gamma^\mu q_j \right), $

(1) $ O_{\varphi q}^{3(ij)} = (\varphi^\dagger i\!\!\overleftrightarrow{D}^I_\mu\varphi) \left( \bar q_i \gamma^\mu \tau^I q_j \right), $

(2) $ O_{\varphi u}^{(ij)} = (\varphi^\dagger i\!\!\overleftrightarrow{D}_\mu\varphi) \left( \bar u_i \gamma^\mu u_j \right), $

(3) $ O_{uW}^{(ij)} = \left( \bar q_i\sigma^{\mu\nu}\tau^I u_j \right)\tilde \varphi W_{\mu\nu}^I, $

(4) $ O_{uB}^{(ij)} = \left( \bar q_i\sigma^{\mu\nu} u_j \right)\tilde \varphi B_{\mu\nu}, $

(5) where
$ \varphi $ is the Higgs doublet,$ \tilde\varphi = i\sigma_2\varphi $ ,$ \tau^I $ is the Pauli matrix,$ B_{\mu\nu} $ and$ W_{\mu\nu}^I $ are the$ U(1)_Y $ and$ SU(2)_L $ gauge field strength tensors,$ (\varphi^\dagger i\!\!\overleftrightarrow{D}_\mu\varphi)\!\equiv\! i\varphi^\dagger\left( D_\mu\!\!-\!\!\overleftarrow{D}_\mu \right)\varphi $ , and$ (\varphi^\dagger i\!\!\overleftrightarrow{D}_\mu\varphi)\!\equiv\! $ $ i\varphi^\dagger\left( \tau^ID_\mu-\overleftarrow{D}_\mu \tau^I\right)\varphi $ . The following four-fermion basis operators are also relevant:$ O_{lq}^{1(ijkl)} = \left( \bar l_i \gamma_\mu l_j \right) \left( \bar q_k \gamma^\mu q_l \right), $

(6) $ O_{lq}^{3(ijkl)} = \left( \bar l_i \gamma_\mu \tau^I l_j \right) \left( \bar q_k \gamma^\mu \tau^I q_l \right), $

(7) $ O_{lu}^{(ijkl)} = \left( \bar l_i \gamma_\mu l_j \right) \left( \bar u_k \gamma^\mu u_l \right), $

(8) $ O_{eq}^{(ijkl)} = \left( \bar e_i \gamma_\mu e_j \right) \left( \bar q_k \gamma^\mu q_l \right), $

(9) $ O_{eu}^{(ijkl)} = \left( \bar e_i \gamma_\mu e_j \right) \left( \bar u_k \gamma^\mu u_l \right), $

(10) $ O_{lequ}^{1(ijkl)} = \left( \bar l_i e_j \right)\varepsilon \left( \bar q_k u_l \right), $

(11) $ O_{lequ}^{3(ijkl)} = \left( \bar l_i \sigma_{\mu\nu} e_j \right)\varepsilon \left( \bar q_k \sigma^{\mu\nu} u_l \right), $

(12) where
$ i,j,k,l $ are flavor indices. For the four-fermion operators, only the$ i = j = 1 $ components are relevant for the$ e^+e^-\to t(\bar t)j $ process. Other operators such as$O_{u\varphi}^{(ij)}\equiv $ $ \left( \varphi^\dagger\varphi \right)\left( \bar q_iu_j\tilde\varphi \right) $ and$ O_{uG}^{(ij)} \equiv \left( \bar q_i\sigma^{\mu\nu} T^a u_j \right)\tilde \varphi G_{\mu\nu}^a $ could lead to FCN couplings$ tqH $ and$ tqg $ , but they cannot be probed in the single top channel. The following linear combinations of Wilson coefficients can be defined as independent degrees of freedom that enter this process:Two-fermion degrees of freedom:
$ c_{\varphi q}^{-[I](3+a)}\equiv {}_{\Re}^{[\Im]}\! \left\{ C_{\varphi q}^{1(3a)} - C_{\varphi q}^{3(3a)} \right\}, $

(13) $ c_{\varphi u}^{[I](3+a)}\equiv {}_{\Re}^{[\Im]}\! \left\{ C_{\varphi u}^{1(3a)} \right\}, $

(14) $ c_{uA}^{[I](3a)}\equiv \left\{ c_WC_{uB}^{(3a)}+s_WC_{uW}^{(3a)} \right\}, $

(15) $ c_{uA}^{[I](a3)}\equiv \left\{ c_WC_{uB}^{(a3)}+s_WC_{uW}^{(a3)} \right\}, $

(16) $ c_{uZ}^{[I](3a)}\equiv \left\{ -s_WC_{uB}^{(3a)}+c_WC_{uW}^{(3a)} \right\}, $

(17) $ c_{uZ}^{[I](a3)}\equiv \left\{ -s_WC_{uB}^{(a3)}+c_WC_{uW}^{(a3)} \right\}. $

(18) Four-fermion eetq degrees of freedom:
$ c_{lq}^{-[I](1,3+a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lq}^{1(113a)}-C_{lq}^{3(113a)} \right\}, $

(19) $ c_{eq}^{[I](1,3+a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{eq}^{(113a)} \right\}, $

(20) $ c_{lu}^{[I](1,3+a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lu}^{(113a)} \right\}, $

(21) $ c_{eu}^{[I](1,3+a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{eu}^{(113a)} \right\}, $

(22) $ c_{lequ}^{S[I](1,3a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lequ}^{1(113a)} \right\}, $

(23) $ c_{lequ}^{S[I](1,a3)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lequ}^{1(11a3)} \right\}, $

(24) $ c_{lequ}^{T[I](1,3a)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lequ}^{3(113a)} \right\}, $

(25) $ c_{lequ}^{T[I](1,a3)}\equiv {}_{\Re}^{[\Im]}\!\left\{ C_{lequ}^{3(11a3)} \right\}, $

(26) where quark generation indices (
$ a = 1,2 $ ) and lepton generation indices are enclosed in parentheses. An I in the superscript represents the imaginary part of the coefficient, denoted by$ \Im $ on the right hand side, while without I only the real part is taken, represented by$ \Re $ on the right hand side. In total, one collects the following 28 real and independent degrees of freedom for each a (and thus 56 in total):$ \begin{array}{*{20}{c}} c_{\varphi q}^{-(3+a)} \!\!&\!\! c_{uZ}^{(a3)} \!\!& \!\!c_{uA}^{(a3)} \!\!& \!\! c_{lq}^{-(1,3+a)} \!\!&\!\! c_{eq}^{(1,3+a)}\!\! & \!\! c_{lequ}^{S(1,a3)} \!\!&\!\! c_{lequ}^{T(1,a3)} \\ c_{\varphi u}^{(3+a)} \!\!&\!\!c_{uZ}^{(3a)} \!\!& \!\!c_{uA}^{(3a)} \!\!& \!\! c_{lu}^{(1,3+a)} \!\!&\!\! c_{eu}^{(1,3+a)}\!\! & \!\! c_{lequ}^{S(1,3a)} \!\!&\!\! c_{lequ}^{T(1,3a)} \\ c_{\varphi q}^{-I(3+a)} \!\!& \!\!c_{uZ}^{I(a3)}\!\! &\!\! c_{uA}^{I(a3)} \!\!& \!\! c_{lq}^{-I(1,3+a)}\!\!& \!\!c_{eq}^{I(1,3+a)} \!\!& \!\! c_{lequ}^{SI(1,a3)} \!\!& \!\!c_{lequ}^{TI(1,a3)} \\ c_{\varphi u}^{I(3+a)} \!\!&\!\! c_{uZ}^{I(3a)} \!\!&\!\! c_{uA}^{I(3a)} \!\!& \!\! c_{lu}^{I(1,3+a)} \!\!&\!\! c_{eu}^{I(1,3+a)}\!\! & \!\! c_{lequ}^{SI(1,3a)} \!\!&\!\! c_{lequ}^{TI(1,3a)} \end{array} $

(27) Among the seven columns, the first three come from the two-fermion operators.
$ c^-_{\varphi q} $ and$ c_{\varphi u} $ give rise to$ tqZ $ coupling with a vector-like Lorentz structure, while$ c_{uA} $ and$ c_{uZ} $ give rise to the$ tq\gamma $ and$ tqZ $ dipole interactions. The last four come from the$ eetq $ four-fermion operators.$ c^-_{lq} $ ,$ c_{lu} $ ,$ c_{eq} $ , and$ c_{eu} $ coefficients give rise to interactions between two vector currents, while$ c^S_{lequ} $ and$ c^T_{lequ} $ to interactions between two scalar and two tensor currents, respectively. We note that the first two rows are CP-even while the last two rows are CP-odd. The first and the third rows involve a left-handed light quark, while the second and the fourth rows involve a right-handed light quark. The interference between coefficients from different rows in the limit of massless quarks vanishes for this reason. Furthermore, the signatures of the degrees of freedom in the first row are identical to those in the third row, and similarly the second row is identical to the fourth row. This is due to the absence of an SM amplitude that interferes with the FCN coefficients, which leads to cross-sections that are invariant under a change of phase:$ c_i+c^I_ii\to {\rm e}^{{\rm i}\delta} (c_i+c^I_ii) $ . It is therefore sufficient to focus on the degrees of freedom in the first two rows, and in the rest of the paper we will refer to them simply as coefficients. We also note that the$ e^+e^-\to tj $ signal of the coefficients from the first two rows are similar, up to a$ \theta\to \pi-\theta $ transformation of the scattering angle in the$ tj $ production. The decay of the top quark, however, breaks this similarity. This is because the two coefficients produce left-handed and right-handed top quarks respectively, while the lepton momentum from the top decay is correlated with the top helicity. This leads to a difference in signal efficiencies between the first two rows.Two-fermion FCN interactions in the first three columns are considered in almost all experimental searches. Four-fermion FCN interactions, on the other hand, have unduly been neglected. They were proposed in Ref. [70], and searched for at LEP2 by the L3 and DELPHI collaborations [45, 47], but the three-body decays through four-fermion FCN interactions have never been searched for at the Tevatron or LHC, except for the lepton-flavor violating case. As for the prospects at future
$ e^+e^- $ colliders, four-fermion couplings were also neglected in the studies of single top at TESLA and FCC-ee [58, 59], although the recent CLIC yellow report has included them [60]. However, the four-fermion operators are indispensable for a complete characterization of the top quark flavor properties. They could arise, for example, in the presence of a heavy mediator coupling to one top quark and one light quark, or in the cases where the equation of motion (EOM) is used to remove redundant two-fermion operators in terms of the basis operators. Their existence also guarantees the correctness of the effective description when particles go off-shell or in loops, see [53] for a detailed discussion. The three-body decay$ t\to cf\bar f $ was calculated in several explicit models [54–56], giving a further motivation for considering the$ tcll $ contact operators. Ref. [71] recast the LHC constraints of$ t\to qZ $ to provide bounds. Finally, the lepton-and-quark-flavor violating top decay through contact interactions was studied in [72], and recently searched for by the ATLAS collaboration [73].An interesting fact about the
$ eetq $ four-fermion FCN interaction is that the most stringent limits are still coming from the LEP2 experiments. In Ref. [57], a global analysis based on the current bounds was performed within the SMEFT framework. The result clearly showed that the LHC is more sensitive to the two-fermion operator coefficients, while LEP2 is more sensitive to the four-fermion ones. Hence, their results are currently complementary in the full parameter space, as demonstrated in Fig. 59 in Section 8.1 of Ref. [57]. The complementarity persists even with HL-LHC (see Fig. 59 right of Ref. [57]), despite an order of magnitude difference between the LEP2 and HL-LHC luminosities. Clearly, this implies that an$ e^+e^- $ collider with higher luminosity could continue to provide valuable information about the top FCN interactions, and explore the parameter space which will not be covered by the HL-LHC.The difference in sensitivities between the two types of colliders can be understood as follows. The two-fermion operators can be searched for at the LHC by the flavor-changing decay of the top quark, but the same decay through a four-fermion operator is a three-body decay and will be suppressed by an additional phase space factor. As an illustration, the decay rates of
$ t\to ce^+e^- $ through$ c_{\varphi u} $ ,$ c_{uZ} $ and$ c_{eu} $ are$ 8.1\times 10^{-5} $ ,$ 2.4\times10^{-4} $ GeV and$ 3.2\times10^{-6} $ GeV , respectively, for$ c/\Lambda^2 = 1 $ TeV−2. Furthermore, the$ e^+e^- $ mass spectrum is a continuum, and thus the best sensitivity requires a dedicated search without a mass window cut (see discussions in Refs. [53, 71]). Searching for four-fermion operators in single top channels at a hadron collider suffers from the same phase-space suppression. The situation in an$ e^+e^- $ collider is, however, different. The two-fermion operators can be searched for through single top$ e^+e^-\to Z^*/\gamma^* \to tj $ (or through top decay if the center-of-mass energy allows for top quark pair production, though typically the former has a better sensitivity [58]). In the case of a four-fermion operator, instead of a suppression effect, the production rate is actually enhanced due to the fact that there is one less propagator than in the two-fermion case. As an illustration, the single top production cross-section at$ E_{\rm cm} = 240 $ GeV for$ c_{\varphi u} $ ,$ c_{uZ} $ and$ c_{eu} $ are 0.0018 pb, 0.020 pb and 0.12 pb, respectively, for$ c/\Lambda^2 = 1 $ TeV−2, and this enhancement effect increases with energy. The comparison of the two cases is illustrated in Fig. 1. Another advantage of a lepton collider is that one can reconstruct the missing momentum. This is not relevant for the problem at hand, but could be important for setting bounds on four-fermion operator with neutrinos, see Ref. [74].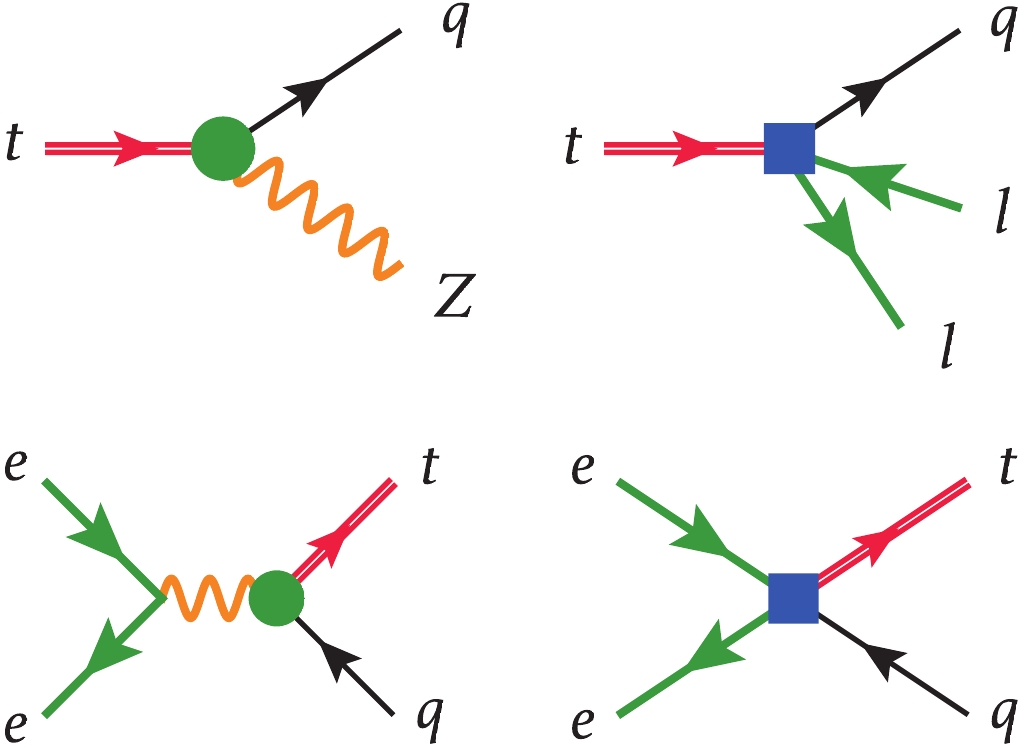
Figure 1. (color online) (top) The flavor-changing decay at the LHC. The four-fermion operator contribution is suppressed by an additional phase space factor compared with the two-fermion contribution. (bottom) The flavor-changing single top at a
$e^+e^-$ collider. The four-fermion operator contribution is enhanced due to one less s-channel propagator than in the two-fermion case. Green dots and blue squares represent two- and four-fermion operator insertions. -
To study the prospects of top FCN couplings, we consider the scenario of CEPC running with a center-of-mass energy
$ E_{\rm cm} = 240 $ GeV and an integrated luminosity of 5.6 ab−1. We simulate the signal and background at leading order with parton shower by MADGRAPH5_AMC@NLO [75] and PYTHIA8 [76, 77]. The signal is generated with the UFO model [78, 79], DIM6TOP, which follows the LHC TopWG EFT recommendation [68] and is available at https://feynrules.irmp.ucl.ac.be/wiki/dim6top. The detector level simulation is performed with DELPHES with the default CEPC card [80]. Jets are reconstructed using the FASTJET package [81] with the anti-$ k_t $ algorithm [82] with a radius parameter of 0.5. Automatic calculation for QCD corrections of processes involving only two-fermion FCN operators were developed in Ref. [83] (see also Refs. [84–92] where the results for the other top flavor-changing channels have been presented). The corrections for four-fermion operators were given in the appendix of Ref. [53]. The sizes are below 20%, corresponding to less than 10% change in the coefficients, and therefore we neglect these corrections in this work. The dominant background comes from the W-pair and Z-pair production, and we do not expect a significant change at the next-to-leading order in QCD.We consider the semi-leptonical top quark decays. The signal final state is
$ bjl\nu $ , where j is an up or charm quark jet. The dominant background is$ qq'l\nu $ , with one light or charm quark jet misidentified as a b-jet. A large fraction comes from the W pair production with one W decaying hadronically and the other leptonically, while the diagrams with only one W resonance decaying leptonically also make an important contribution. We thus take into account the full contribution from the$ e^+e^-\to Wq\bar q' $ process with W decaying leptonically. Adding all the diagrams from$ e^+e^-\to l\nu q\bar q' $ does not make a sizable change to the background [58], and so they are not taken into account. Another source of background comes from$ b\bar bll $ and$ c\bar cll $ , where one of the jets is mistagged and one of the leptons is missed by the detector. This is included in our simulation, but the contribution is subdominant. Selected diagrams for the signal and background are shown in Fig. 2.
Figure 2. (color online) Selected Feynman diagrams for the signal (top) and background (bottom). Green dots and blue squares represent two- and four-fermion operator insertions. Red double lines represent top quark propagators.
Based on the expected signature of the signal process, we select events with exactly one charged lepton (electron or muon) and at least two jets. The charged lepton must have
$ p_{\rm{T}}>10 $ GeV and$ |\eta|<3.0 $ . All jets are required to have$ p_{\rm{T}}>20 $ GeV and$ |\eta|<3.0 $ . Exactly one jet should be b-tagged. If more than one non-b-tagged jet is present, the one with the highest$ p_{\rm{T}} $ is selected as the up or charm quark jet candidate. We have chosen a b-tagging working point with 80% efficiency for b-jets and a mistagging rate of 10% (0.1%) from c-jets (light jets) [93]. A missing energy greater than 30 GeV is also required due to the presence of a neutrino. The W boson candidate is reconstructed from the charged lepton and the missing energy. The top quark candidate is reconstructed by combining the W boson candidate with the b-jet.At the parton level, we expect the non-b-tagged jet from the signal to have
$ E_j = \dfrac{s-m_{\rm top}^2}{2\sqrt{s}}\approx 58\ {\rm{GeV}} $ . For the background, if the contribution comes from the diboson production (e.g. Fig. 2 down left), we expect the dijet mass to peak at$ m_W = 80.4 $ GeV. The contribution from the non-resonant diagrams (e.g. Fig. 2 down right) cannot, however, be neglected and gives rise to a continuum spectrum in the dijet mass distribution. At the reconstruction level, it turns out that the energy of the non-b-tagged jet$ E_j $ , the invariant mass of the b-jet and the non-b-tagged jet$ m_{jj} $ , and the invariant mass of the top quark candidate$ m_{\rm top} $ are the most useful variables to discriminate the signal from background. In Fig. 3, we plot these variables at the reconstruction level, for the background as well as for the signals from the two typical operator coefficients,$ c_{uZ} $ and$ c_{eq} $ , for illustration.
Figure 3. (color online) Signal and background at the reconstruction level. Distributions of
$m_{\rm top}$ ,$E_j$ , and$m_{jj}$ are shown for signals from$c_{uZ}^{(23)}$ and$c_{eq}^{(1,3+2)}$ .As our baseline analysis, we impose the following kinematic cuts at the reconstruction level
$ E_j< 60\ {\rm{GeV}}\,, $

(28) $ m_{jj}>100 \ {\rm{GeV}}\,, $

(29) $ m_{\rm top}<180 \ {\rm{GeV}}\,. $

(30) These cuts are motivated by Fig. 3. The expected number of background events after event selection is about 1400 with an integrated luminosity of 5.6 ab−1, corresponding to a statistical uncertainty of about 2.7%. We assume that the systematic uncertainty will be under control below this level. The impact of the systematic uncertainty can be easily estimated, e.g. a 3% systematic uncertainty will weaken the bound of the cross-section by a factor of about 1.5, which corresponds to a factor of 1.2 on the value of the coefficients. In the rest of the paper we simply ignore the systematic effects. We will see that this simple baseline scenario already allows to obtain reasonable sensitivities.
In the absence of any FCN signal, the 95% confidence level (CL) upper bound of the fiducial cross-section is
$ 0.0134 $ fb. Alternatively, the 5$ \sigma $ discovery limit of the signal cross-section, determined by$ S/\sqrt{B} = 5 $ , is a function of the integrated luminosity$ L_{\rm{int}} $ :$ \sigma = \frac{5\sqrt{\sigma_{B}}}{\sqrt{L_{\rm{int}}}} = \frac{2.51\ {\rm{fb}}}{\sqrt{L_{\rm{int}}/{\rm{fb}}^{-1}}}. $

(31) The cross-section is a quadratic function of the operator coefficients. Including the interference effects, such a function has 28 independent terms for the 7 coefficients in each row of Eq. (27). These terms for the first two rows are the same as those for the last two rows, because they only differ by a CP phase which would never show up in the cross-section (without any possible interference with SM). Thus, only 56 independent terms need to be determined for the first two rows for each a. We sample the parameter space by 56 points and simulate the fiducial cross-section for each of them. The results are fitted by the following form:
$ \sigma = \sum\limits_{a = 1,2} {\frac{{{{(1\;{\rm{TeV}})}^4}}}{{{\Lambda ^4}}}} \left( {\overrightarrow {C_1^a} \cdot {{M}}_{\bf{1}}^{{a}} \cdot {{\overrightarrow {C_1^a} }^T} + \overrightarrow {C_2^a} \cdot {{M}}_{\bf{2}}^{{a}} \cdot {{\overrightarrow {C_2^a} }^T}} \right), $

(32) where
$ \vec{C}_{1,2} $ denote the vectors formed by the coefficients in the first and second rows of Eq. (27). a is the light quark generation.$ {{M}}_{1,2}^a $ are$ 7\times7 $ matrices. The above result allows to convert the upper bound and discovery limit of the cross-section into a 56-dimensional coefficient space.We have verified the relations between signatures from different rows in Eq. (27): the 1st (2nd) and the 3rd (4th) rows always give the same signatures; the 1st (3rd) and the 2nd (4th) rows at the production level are identical up to a
$ \theta\to \pi-\theta $ transformation in the production angle, but differ if the top decays. In Appendix A, a comparison between the signals from$ c_{uZ}^{(23)} $ ,$ c_{uZ}^{(32)} $ and$ c_{uZ}^{I(23)} $ are shown in Fig. A1. A comparison between the signals from$ c_{eq}^{(1,3+2)} $ ,$ c_{eu}^{(1,3+2)} $ and$ c_{eq}^{I(1,3+2)} $ are shown in Fig. A2.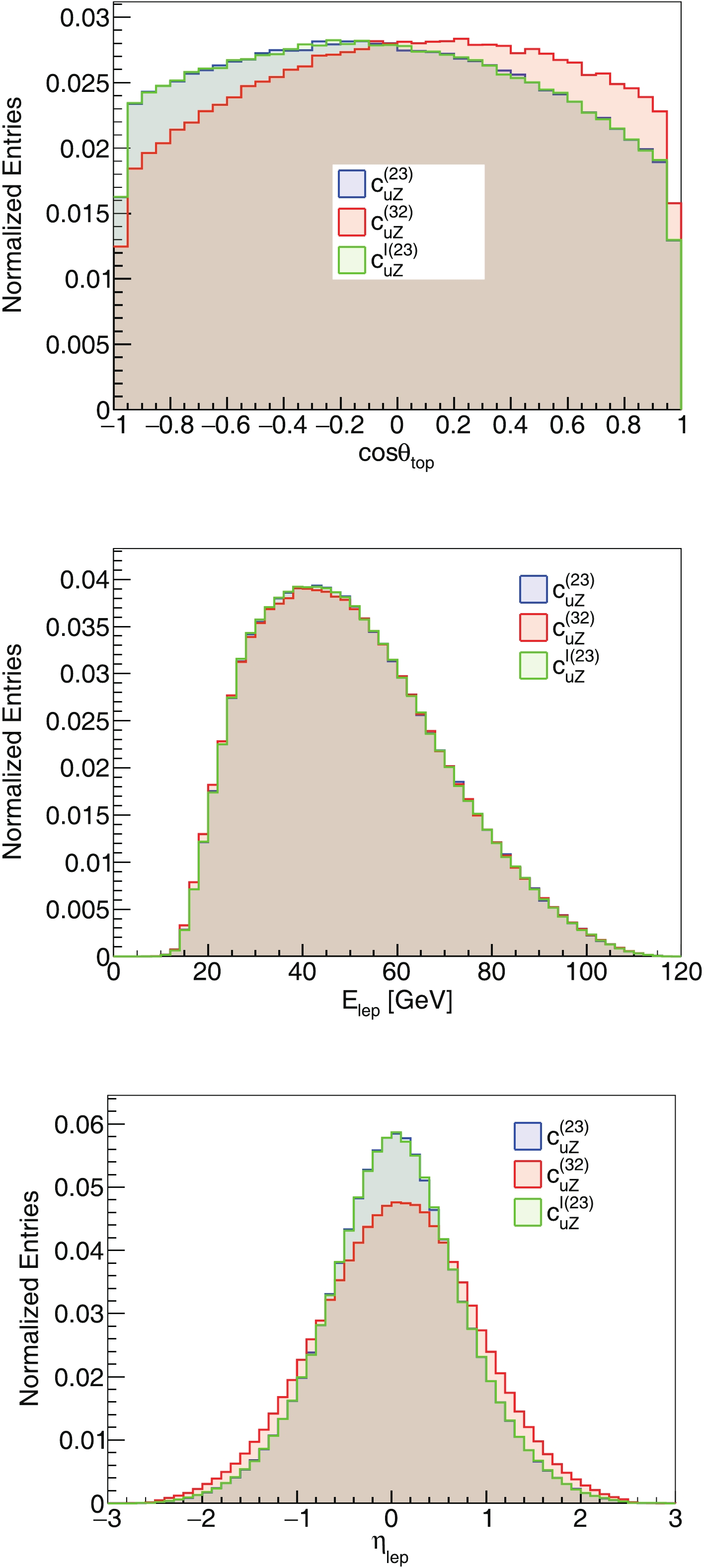
Figure A1. (color online) Signals from
$c_{uZ}^{(23)}$ ,$c_{uZ}^{(32)}$ and$c_{uZ}^{I(23)}$ at the parton level. Distributions of the scattering angle, the lepton energy, and the lepton pseudorapidity are compared.
Figure A2. (color online) Signals from
$c_{eq}^{(1,3+2)}$ ,$c_{eu}^{(1,3+2)}$ and$c_{eq}^{I(1,3+2)}$ at the parton level. Distributions of the scattering angle, the lepton energy, and the lepton pseudorapidity are compared.Our baseline analysis could be improved by exploiting additional features of the signal with a template fit. One possibility is to make use of heavy flavor tagging. The operators with
$ a = 2 $ , requiring a tagged c-jet in the signal definition, could largely suppress the background, as most background comes from events with one charm quark and one strange quark in the final state, with the charm mistagged as a b. The clean environment of CEPC allows a precise determination of the displaced vertices and excellent capability of c-jet tagging [5]. We assume a working point with a 70% tagging efficiency for c-jets and 20% (12%) mistagging rate from b-jets (light jets) [93]. To constrain the coefficients with$ a = 2 $ , we require a c-jet in the signal definition, while to constrain the$ a = 1 $ coefficients we veto the events with a c-jet, although the latter is not expected to significantly change the sensitivity as most background events do not have an extra c-jet except the one that fakes the b-jet. Another useful information is the angular distribution of the single top, which is determined by the specific Lorentz structure of the operator. In Fig. 4 , we show the distribution of the top scattering angle from all 7 coefficients in the first row at the parton level and the reconstruction level. The scattering angle$ \theta $ is defined as the angle between the momentum of the$ e^+ $ beam and t or$ \bar t $ . The distributions for the top and anti-top are related by$ \theta\to\pi-\theta $ , and this is illustrated by comparing the first two plots in Fig. 4. Furthermore, this holds even for the reconstructed top and anti-top candidates from the background due to the CP symmetry. For this reason, we consider the observable$ c = Q_l\times\cos\theta $ , i.e. the lepton charge times the cosine of the scattering angle. The discrimination power of this observable is illustrated in the right plot of Fig. 4, at the reconstruction level. We perform a template fit by further dividing the signal region into 4 bins, defined as$ c\in(-1,-0.5) $ ,$ [-0.5,0) $ ,$ [0,0.5) $ , and$ [0.5,1) $ . To construct a$ \chi^2 $ fit, we take$ \sqrt{B} $ in each bin as the experimental uncertainty. The smallest number of events in one bin is 24 even after requiring a c-jet, and so the Gaussian distribution is a good approximation. We simulate the Gaussian fluctuation in all bins by generating a large number of pseudo-measurement samples and compute the average$ \chi^2 $ for each point in the coefficient space. Our 95% CL bound is determined by$ \left<\chi^2\right><9.49 $ .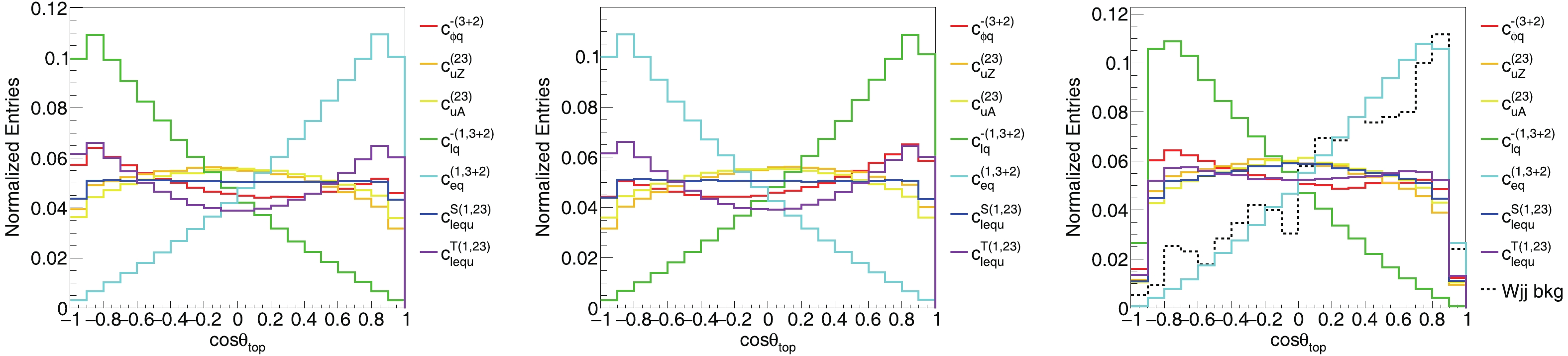
Figure 4. (color online) Scattering angle from the signals of the seven coefficients in the first row of Eq. (27).
$\theta_{\rm top}$ is defined as the angle between the momentum of the$e^+$ beam and t or$\bar t$ . (left) parton level, for top production. (middle) parton level, for anti-top production. (right) reconstruction level, for top production, including the background. -
Following our baseline analysis, the 95% CL limits of the individual coefficients in the first row are given in Fig. 5, where they are compared with the current limits from LHC+LEP2 and with the HL-LHC projection. FCC-ee projection at the center-of-mass energy of 240 GeV is given in Ref. [59], but only for the 3 two-fermion coefficients, and we show them in the same plot. Note that Ref. [71] suggested that the current signal region of the
$ t\to ql^+l^- $ decay mode, designed for the search of$ t\to qZ $ mode, can be extended by including the “off-shell” region with$ \left|m_{l^+l^-}-m_Z\right|>15 $ GeV. This could lead to HL-LHC prospects that are slightly better than Fig. 5 for some of the four-fermion coefficients. The CLIC bounds, on the other hand, are only available with higher center-of-mass energy runs and are not shown in the plot. For example, the expected limits of the four-fermion coefficients from a 380 GeV run with an integrated luminosity of 500 fb−1, are about a factor of$ 3\sim4 $ better than those from CEPC, due to the higher beam energy and beam polarization [60].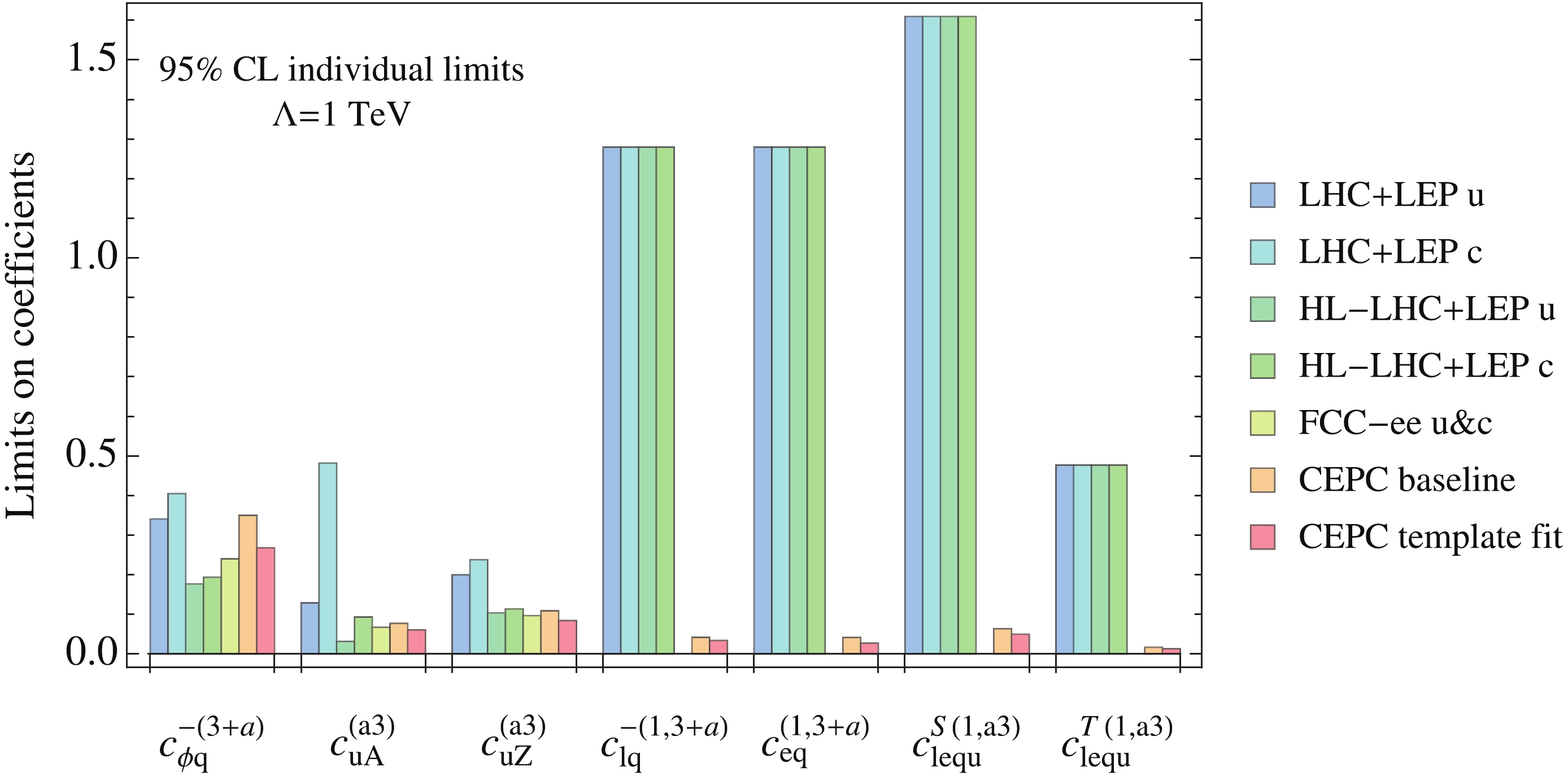
Figure 5. (color online) The 95% CL limits of the individual coefficients in the first row of Eq. (27) as expected from CEPC, compared with the existing LHC+LEP2 bounds and the projected limits from HL-LHC+LEP2 and FCC-ee with 3 ab−1 luminosity at 240 GeV (only for the first three coefficients), see Refs. [57, 59]. The results for both generations
$a = 1,2$ are displayed. The orange column “CEPC baseline” is the expected limit following our baseline analysis, which applies to both flavors (a = 1,2). The red column “CEPC template fit” uses c-jet tagging for signal definition and only applies to$a = 2$ operators.Looking at the 3 two-fermion coefficients on the left, the limits are either weaker than or comparable to HL-LHC. Still, we emphasize that even in this case the CEPC measurement provides an important consistency check with the existing results. The most interesting result, however, is the improvement of the other four four-fermion coefficients. As expected, we see that they are 1~2 orders of magnitude better than the current limits and the combination of HL-LHC and LEP2. Similar results are observed for the second row operators and are displayed in Fig. A3 in Appendix A. In Fig. 6 , we show the two-dimensional bound of the two-fermion coefficient
$ c_{\varphi q}^{-(3+a)} $ and the four-fermion coefficient$ c_{eq}^{(1,3+a)} $ , compared with LHC, HL-LHC, and LEP2. Clearly, a large fraction of the currently allowed parameter space will be probed by CEPC. A similar plot for the operators in the second row of Eq. (27) is given in Fig. A4 in Appendix A.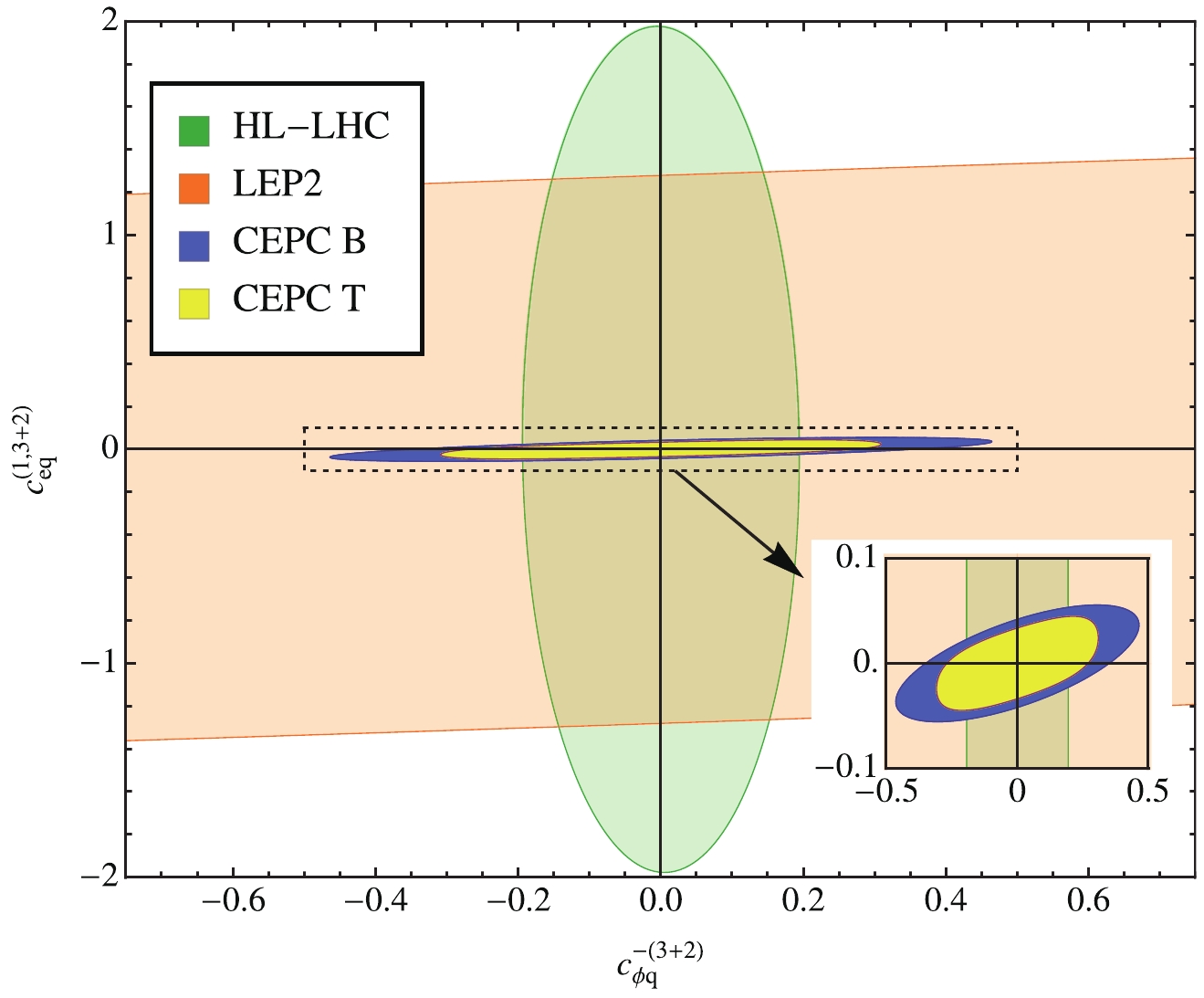
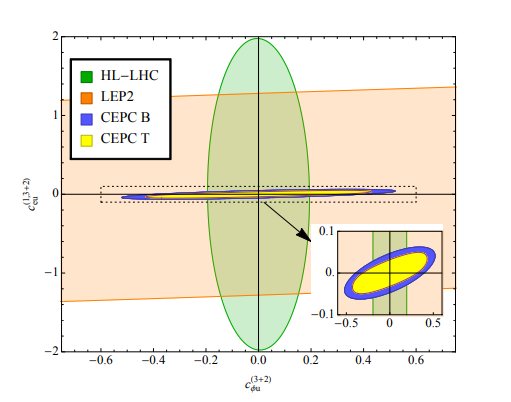
Figure 6. (color online) Two-dimensional bound of the two-fermion coefficient
$c_{\varphi q}^{-(3+2)}$ and the four-fermion coefficient$c_{eq}^{(1,3+2)}$ at 95% CL. Other operators are fixed to 0. The allowed regions from HL-LHC and LEP2 are similar to Fig. 59 in Section 8.1 of Ref. [57], except that there all coefficients are marginalized over. The blue region (“CEPC B”) is the bound expected from CEPC following our baseline analysis. The yellow region (“CEPC T”) is obtained with a template fit approach, see the discussion in Section 4.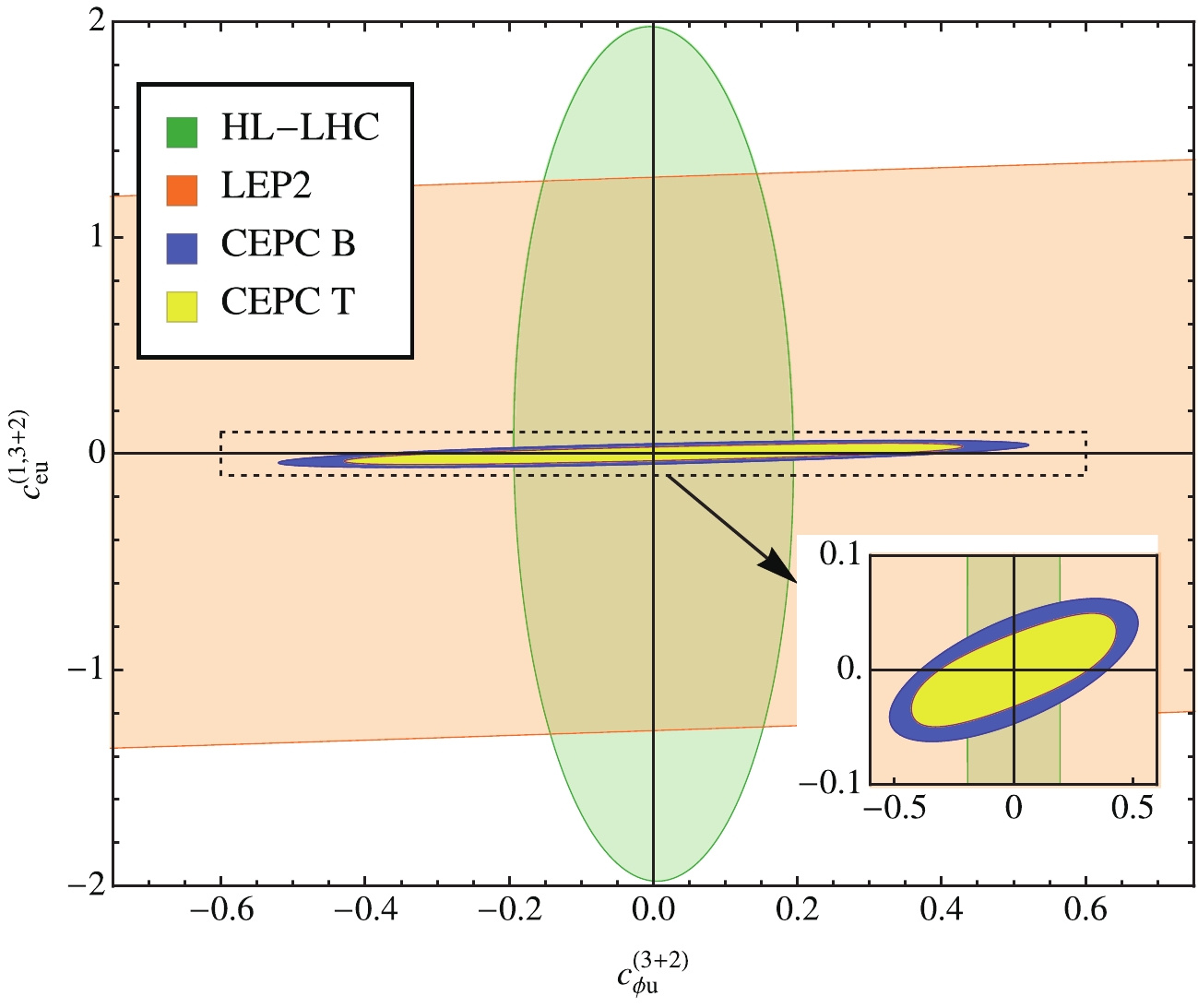
Figure A4. (color online) Two-dimensional bounds on a two-fermion coefficient
$c_{\varphi u}^{-(3+2)}$ and a four-fermion coefficient$c_{eu}^{(1,3+2)}$ , at the 95% CL. Other operators are fixed at 0. The allowed regions from HL-LHC and LEP2 are similar to Fig. 59 in Section 8.1 of Ref. [57], except for that there all coefficients are marginalized over. The blue region (“CEPC B”) is the bound expected from the CEPC, following our baseline analysis. The yellow region (“CEPC T”) is obtained with a template fit approach, see more discussions in Section 4.In Fig. 7 we plot the discovery limits of the seven coefficients in the first row of Eq. (27) in terms of
$ \Lambda/\sqrt{c} $ , as a function of integrated luminosity. The scale is roughly that of new physics, assuming that the coupling is of the order of one. The plot shows that new physics at a few TeV leading to four-fermion FCN interactions can be discovered already at an early stage of CEPC running. The improvement with luminosity is, however, less significant. Note that the two curves corresponding to$ c_{eq}^{(1,3+2)} $ and$ c_{lq}^{-(1,3+2)} $ overlap with each other. This is because they give rise to four-fermion couplings that only differ in the chirality of the electron fields, and thus have the same rate in the signal region defined by our baseline analysis. The results for the coefficients of the second row are given in Appendix A, Fig. A5, where a similar degeneracy between$ c_{eu}^{(1,3+2)} $ and$ c_{lu}^{(1,3+2)} $ can be observed.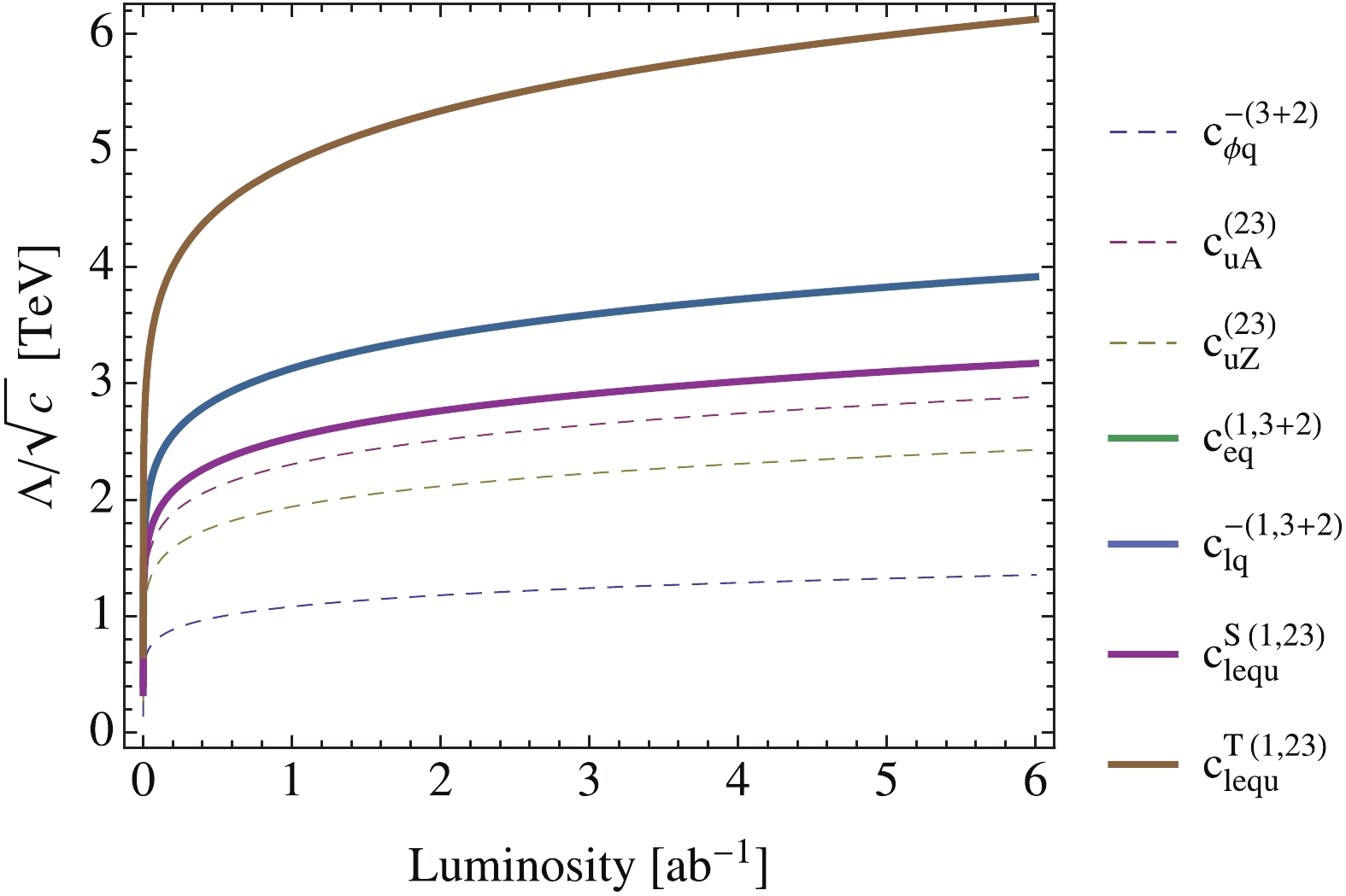
Figure 7. (color online) The five-sigma discovery limit of
$\Lambda/\sqrt{c}$ , which is roughly the scale of new physics, for the coefficients in the first row of Eq. (27), as a function of the integrated luminosity of CEPC.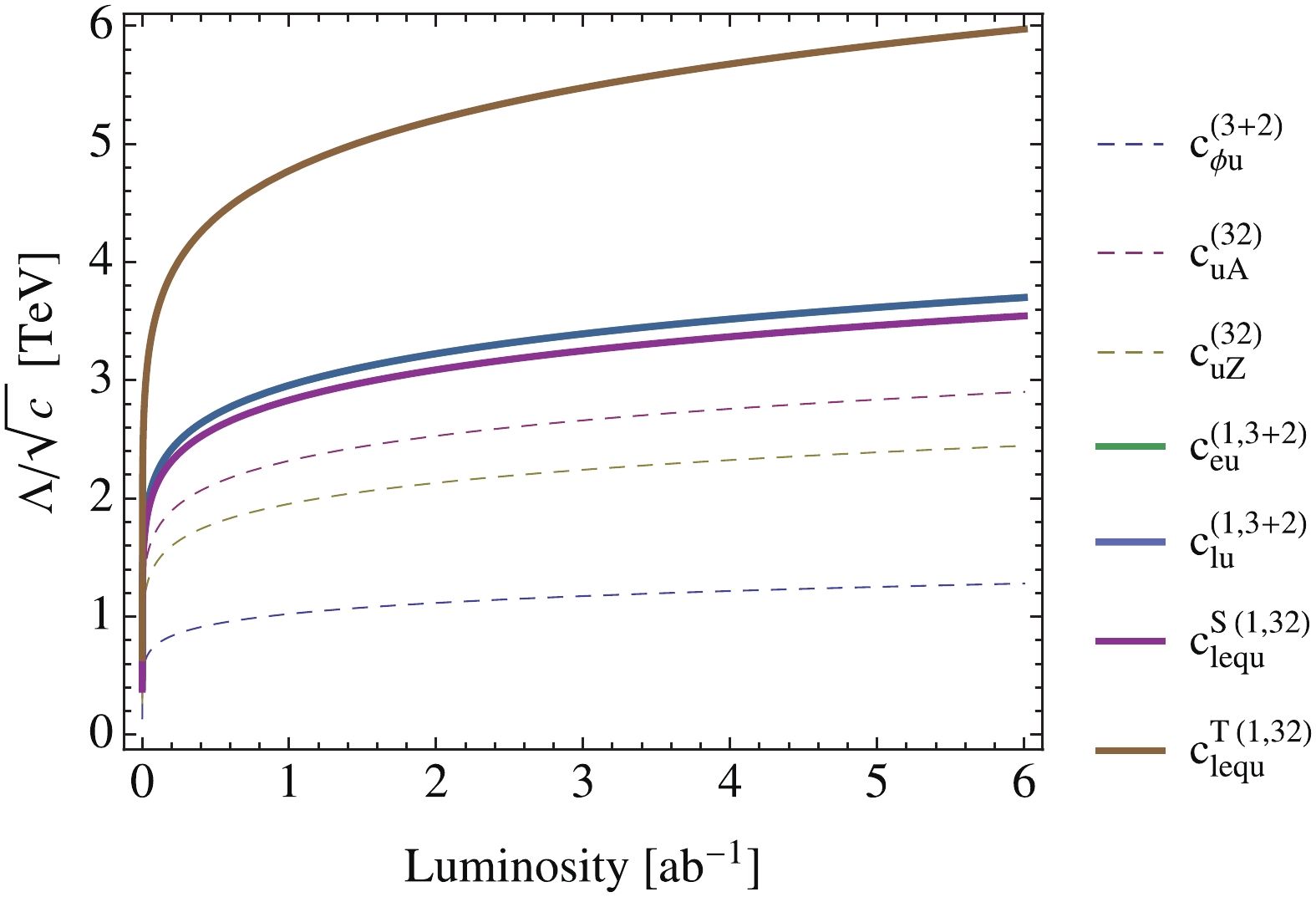
Figure A5. (color online) Five-sigma discovery limit of
$\Lambda/\sqrt{c}$ , which is roughly the scale of new physics, for coefficients in the second row of Eq. (27), as function of integrated luminosity at the CEPC.The template fit method described in the previous section leads to two-fold improvements. First, if SM is assumed, the 95% CL limits of the operator coefficients for
$ a = 2 $ are improved. This is mostly due to the c-tagging requirement. The results are shown in Fig. 5 (red columns), and in Fig. 6 (the yellow region), where the improvements are seen clearly. The same effects on the other four-fermion operators are displayed and compared in Fig. 8. The second improvement is from the discrimination power between the different kinds of signals, which comes from both the angular distribution and the c-tagging information. This is particularly important when an excess is found, in which case we need to understand the FCN operator that leads to it. The baseline approach can only give the overall magnitude of the flavor-changing effects, while the template fit helps to pin down the actual form of the operator. This is illustrated in Fig. 9, where we consider two hypothetical scenarios, with$ c_{eq}^{(1,3+a)} = c_{lq}^{-(1,3+a)} = 0.05 $ , and$ c_{lequ}^{S(1,a3)} = 0.065 $ ,$ c_{lequ}^{T(1,a3)} = 0.025 $ ($ \Lambda = 1 $ TeV). These values are consistent with the current bounds, but are around the sensitivity expected at CEPC. Assuming that the other coefficients vanish, with the baseline approach we are able to identify the overall flavor-changing effect, but not the value of each coefficient. The allowed region in the two-dimensional parameter space is a ring, giving no information about the actual form of new physics. The template fit, on the other hand, can pinpoint with more precision the value of each coefficient. This holds also for the$ a = 1 $ case, even though the precision is slightly worse. A four-fold degeneracy shows up in the first scenario. This is because the overall sign of the coefficients does not have a visible effect (due to the absence of SM interference), and the relative sign between$ c_{eq}^{(1,3+a)} $ and$ c_{lq}^{-(1,3+a)} $ cannot be observed because the two operators do not interfere. In the second case, this is reduced to a two-fold degeneracy. This is because the interference between$ c_{lequ}^{S(1,a3)} $ and$ c_{lequ}^{T(1,a3)} $ is proportional to$ \cos\theta $ , so the opposite sign can be excluded by the angular distribution. In fact, due to the shape of the background (see Fig. 4 right), the template fit has a better discrimination power when$ c_{lequ}^{S(1,a3)} $ and$ c_{lequ}^{T(1,a3)} $ have opposite signs. This effect can be seen even with the SM hypothesis, see the right plot in Fig. 8. The discrimination between$ a = 1 $ and$ a = 2 $ operators is also possible with the help of c-tagging. This is demonstrated in Fig. 10, where we consider three hypothetical scenarios, with$ \left(c_{lq}^{-(1,3+1)},\right. \left.c_{lq}^{-(1,3+2)}\right) =$ $ (0,0.05),\ (0.05,0) $ , and$ (0.35,0.35) $ . By using events with and without a c-jet, we can resolve the light-quark flavor involved in the FCN coupling with some precision. This is unlike LHC, where one has to combine the production and decay measurements to disentangle the two light-quark flavors in the flavor-changing signal by using the fact that the production channel depends on the light-quark parton distribution function.
Figure 8. (color online) Two-dimensional limits of the four-fermion coefficients, at 95% CL, under the SM hypothesis, with the other coefficients turned off. The template fit approach improves the sensitivity.

Figure 9. (color online) Two-dimensional limits of the four-fermion coefficients, at 95% CL, with the other coefficients turned off. Two hypotheses are considered. (left)
$c_{eq}^{(1,3+a)} = c_{lq}^{-(1,3+a)} = 0.05$ . (right)$c_{lequ}^{S(1,a3)} = 0.065$ ,$c_{lequ}^{T(1,a3)} = 0.025$ . Both points are labeled by a black dot in the plots. The template fit helps to pinpoint the coefficients. Better precision is obtained for operators involving a charm-quark (i.e.$a = 2$ ).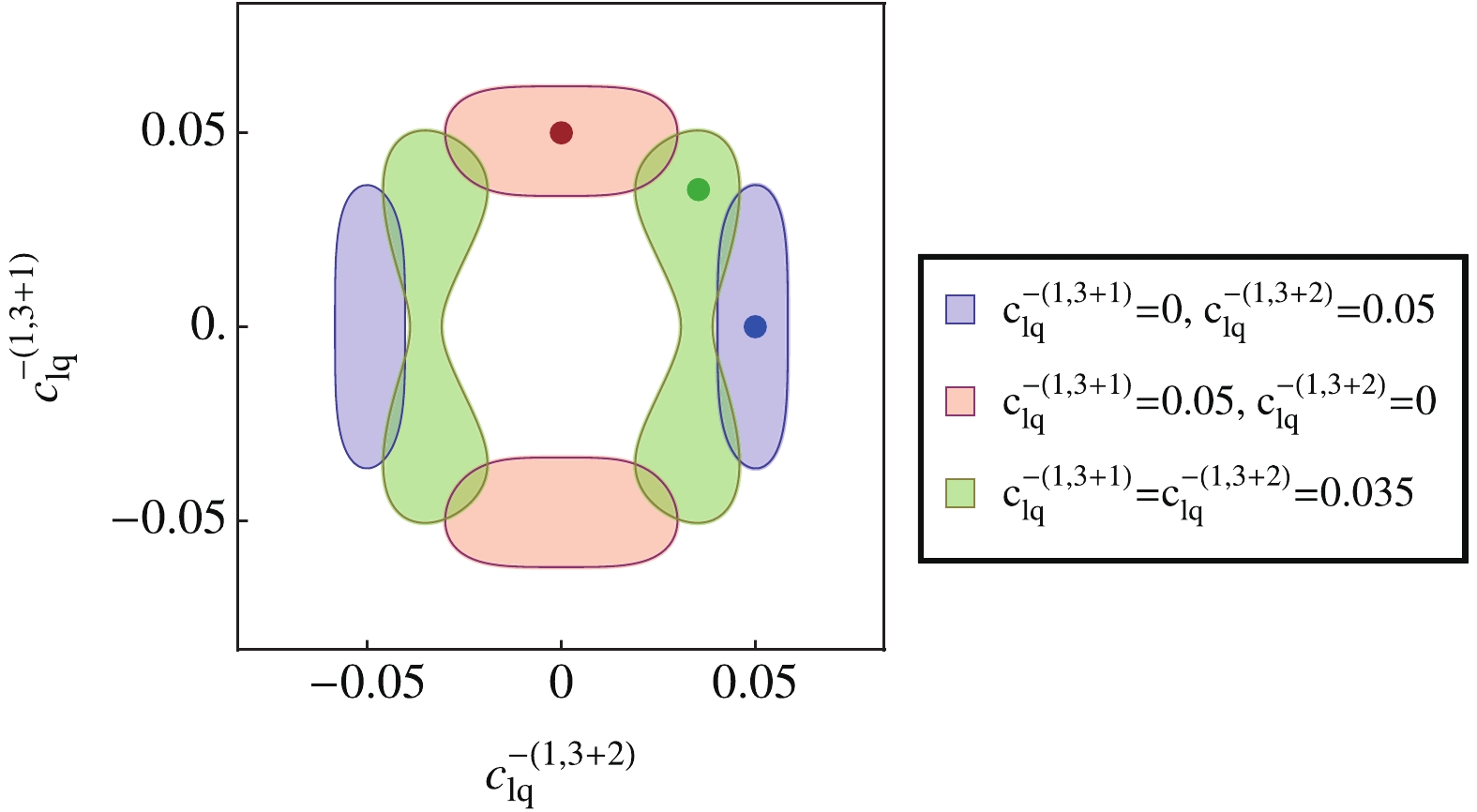
Figure 10. (color online) Two-dimensional limits of the
$c_{lq}^{-(1,3+a)}$ coefficients with$a = 1$ and$a = 2$ , at 95% CL. The other coefficients are turned off. Three hypotheses are considered. The template fit helps to identify the light-quark flavor involved in the FCN coupling.As an additional remark, we note that a flat direction exists between the three coefficients
$ c_{\varphi q}^{-(3+a)} $ ,$ c_{lq}^{-(1,3+a)} $ and$ c_{eq}^{(1,3+a)} $ , which cannot be constrained by a single run at 240 GeV. A second working point with larger energy would be useful to lift the degeneracy, as the two-fermion and four-fermion contributions depend differently on energy. All other directions can be constrained simultaneously at 240 GeV.A more comprehensive study can further improve these results in several aspects. The QCD correction of the four-fermion operators can be implemented in the analysis, although we expect the correction to be similar to the two-fermion case. Kinematic features of the signals from different operators can be fully exploited by using a multivariate analysis. Alternatively, one could also construct the covariant matrix directly, following the statistically optimal observable [94, 95], which in theory guarantees the best sensitivity. However, the nonlinear form of the cross-section in the parameter space and the non-analytic nature of the detector effects need to be carefully dealt with. The same approach has been used to study the FCN couplings at the CLIC [60], where the detector effects were taken into account by an efficiency parameter. Finally, useful information may also come from the study of flavor changing decay of the top quark, depending on the possibility of an energy upgrade above the 350 GeV threshold, which in addition could also provide access to the Higgs and gluon FCN couplings. We defer these studies to a future work.
-
The CEPC collider, proposed as a Higgs factory, is also an ideal machine to study the flavor properties of the top quark. The FCN interactions of the top quark can be searched for in the single top production
$ e^+e^-\to tj $ . The results from the LEP2, Tevatron and LHC experiments suggest that a future lepton collider would provide the best sensitivity for the four-fermion$ eetq $ FCN interactions, complementary to a hadron collider which mainly constrains the two-fermion FCN interactions. In this work, we derived the expected sensitivity at CEPC, with an energy of 240 GeV and integrated luminosity of 5.6 ab-1 , of the full set of 56 FCN operators that are relevant for the$ e^+e^-\to tj $ channel, and showed that an improvement of about 1-2 orders of magnitude of the four-fermion FCN couplings could be expected. Our main results are displayed in Figs. 5 and 6, where one can clearly see that a large fraction of the currently allowed FCN parameters could be tested at CEPC. We also showed that the capability of c-jet tagging at CEPC further improves the sensitivity for the flavor-changing couplings between the top and charm quarks. In case a signature is established, we showed that kinematic observables could be used to pinpoint the values of the coefficients, which in turn would give information about the new physics behind the discovery.Note added: After this work was posted on arXiv, Ref. [96] appeared, where the authors discussed the expected limits of the four-fermion coefficients at the Large Hadron-Electron Collider. The results are of the same order of magnitude as what we gave in Figs. 5 and A3.

Figure A3. (color online) The 95% CL limits on individual coefficients in the second row of Eq. (27), expected from the CEPC, compared with the existing LHC+LEP2 bounds, and the projected limits from HL-LHC+LEP2 and from FCC-ee with 3 ab-1 luminosity at 240 GeV (only for the first three coefficients), see Refs. [57, 59]. Results for both generations
$ a = 1,2 $ are displayed. The orange column "CEPC baseline" is the expected limits following our baseline analysis, which applies to both flavors (a = 1,2). The red column "CEPC template fit" uses the c-jet tagging in its signal definition and only applies to$ a = 2 $ operators.We would like to thank M. Chala, B. Fuks, G. Durieux, Z. Liang and H.-S. Shao for helpful discussions and suggestions.
-
Here, we list some additional results mentioned in the previous sections. In Figs. A1 and A2, we compare the signals from
$ c_{uZ}^{(23)} $ ,$ c_{uZ}^{(32)} $ ,$ c_{uZ}^{I(23)} $ , and from$ c_{eq}^{(1,3+2)} $ ,$ c_{eu}^{(1,3+2)} $ ,$ c_{eq}^{I(1,3+2)} $ , illustrating the relations between the coefficients in different rows of Eq. (27). In Fig. A3, we show the individual limits and prospects for the coefficients from the second row of Eq. (27), similar to Fig. 5. In Fig. A4, we present the two-dimensional bound of the two-fermion coefficient$ c_{\varphi u}^{-(3+2)} $ and the four-fermion coefficient$ c_{eu}^{(1,3+2)} $ , similar to Fig. 6. Finally, in Fig. A5, we show the discovery limits of the coefficients of the second row of Eq. (27), similar to Fig. 5.
Probing the top quark flavor-changing couplings at CEPC
- Received Date: 2019-06-20
- Accepted Date: 2019-09-06
- Available Online: 2019-11-01
Abstract: We propose to study the flavor properties of the top quark at the future Circular Electron Positron Collider (CEPC) in China. We systematically consider the full set of 56 real parameters that characterize the flavor-changing neutral interactions of the top quark, which can be tested at CEPC in the single top production channel. Compared with the current bounds from the LEP2 data and the projected limits at the high-luminosity LHC, we find that CEPC could improve the limits of the four-fermion flavor-changing coefficients by one to two orders of magnitude, and would also provide similar sensitivity for the two-fermion flavor-changing coefficients. Overall, CEPC could explore a large fraction of currently allowed parameter space that will not be covered by the LHC upgrade. We show that the c-jet tagging capacity at CEPC could further improve its sensitivity to top-charm flavor-changing couplings. If a signal is observed, the kinematic distribution as well as the c-jet tagging could be exploited to pinpoint the various flavor-changing couplings, providing valuable information about the flavor properties of the top quark.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: