-
Electromagnetic signals are the major messengers that carry physical information of celestial bodies. In 2015, the first gravitational wave event has been directly detected by the advanced LIGO detector [1]. This gravitational wave signal was produced by the merging of a binary black hole system, which according to the most popular models, has no electromagnetic counterpart. Not long after the first GW event was revealed, another GW event, GW170817, has been detected by the advanced LIGO detector [2]. GW 170817 was produced by the merging of a binary neutron star system. The corresponding electromagnetic counterparts were detected by several instruments [3–9]. These observations opened the era of multi-messenger astronomy. The gravitational waves also provide another approach to test the cosmology [10–14]. The relative arrival time between the GW signals of GW170817 and its EM counterparts has been used to constrain the Lorentz invariance violation [15–19].
In astronomy,
$\gamma$ -ray bursts (GRBs) are extremely energetic explosions and frequently observed phenomena. For recent reviews, see e.g. Refs. [20, 21]. GRBs are widely believed to be produced by the gravitational collapse of massive stars (long GRBs) [22, 23] or the merging of compact binary systems such as binary neutron stars and neutron star – black hole systems (short GRBs) [24, 25]. Except for the production of gravitational waves and electromagnetic signals, these two mechanisms may also produce high energy neutrinos [26]. The energy of GRB neutrinos depend on the sites and mechanisms that produced neutrinos, which can be in a wide range from MeV to EeV [21, 27, 28]. For example, Bahcall & Mészáros [29] showed that inelastic collisions between differentially streaming protons and neutrons in the fireball model can produce 5 – 10 GeV neutrinos. The photomeson interactions of accelerated protons in GRB jet can produce TeV neutrinos [30]. The proton-photon interaction in the GRB emission region can produce PeV neutrinos [27, 31, 32]. In a highly relativistic jet, the produced neutrinos can reach the EeV range [33, 34]. Moreover, the GRB central engine is expected to produce copious MeV neutrinos [35]. Neutrinos only participate weak and gravitational interactions. They are less affected by intergalactic media than photons. According to the standard model of particle physics, neutrinos never decay and approximately propagate at the speed of light. Therefore, neutrinos are excellent messengers for astronomical observations.The foundation of the IceCube Neutrino Observatory makes the detection of high energy neutrino possible [36]. The data of the IceCube have already been used to search for high energy neutrino emission from GRBs [37, 38]. The three messengers, i.e., gravitational waves, electromagnetic signals, and neutrinos originated from the same GRB, are expected to be detected in the coming future. The combined observations would shed light on the long-existing central engine mystery of GRBs. There are two typical models of GRB prompt radiation, i.e., the hot fireball model [25, 39] and the magnetic jet model [40]. One difference between these two models is the energy budget. In the hot fireball model, the energy is mainly carried by baryons, while in the magnetic jet model the energy is mainly carried by the Poynting flux. Therefore, the electron density in the magnetic jet model is several orders of magnitude lower than that in the hot fireball model [41, 42]. Neutrinos may change from one flavor to another when they propagate through the region with high electron density, which is known as the Mikheyev-Smirnov-Wolfenstein (MSW) effect [43]. The matter effect of high energy neutrinos has been discussed in Ref. [44]. In this study, we will analyse the matter effect on high energy neutrinos in the hot fireball model. Since the MSW effect depends on electron density alone, the path of neutrino propagation can be used to constrain the electron distribution in GRB outflow and hence shed new light on the GRB emission mechanism.
Neutrino oscillations [45] provide important physical information of neutrinos, such as the mass-squared difference of neutrinos. The electron density of the hot fireball model varies dramatically, so the coherent effect of neutrino oscillations disappear if it propagates through a region with high electron density [46]. If one observed the coherent effect of neutrino oscillations for the high energy neutrino, it must emit from the region where its electron density is low enough such that the MSW effect can be ignored. However, typical distance scale between the source of GRB and the earth is Gpc, which is much larger than the neutrino oscillation lengths even for ultra high energy neutrinos. Therefore, neutrino oscillations for the neutrino emitted from GRB will not be observed. The signals of merging of a binary neutron star system possibly propagate close to gravitational source and their path undergoes a deflection [47]. The strongly lensed gravitational wave signals and their electromagnetic counterpart have been used to test the Lorentz invariance violation [47–49]. Strongly lensed neutrinos can revive neutrino oscillations. This is because the relative length between different paths may comparable to the neutrino oscillation length. Therefore, the interference between neutrinos propagating along different paths may occur [50]. Such neutrinos interference will provide information on the neutrino mass.
In this study, we investigate the matter effect and discuss the interference effect of strongly lensed neutrinos emitted from GRBs. This paper is organized as follows. In Section 2, we first give a brief introduction to the neutrino oscillations and the MSW effect. Then, we present the relation between neutrino flavor ratio and electron density distribution of the hot fireball model. In Section 3, we discuss the neutrino oscillations in the strongly lensed system. We take a typical strong lensing system to calculate the survival probability of neutrinos and discuss the probability to use the lensed neutrinos to distinguish the neutrino mass hierarchy. Finally, conclusions and remarks are given in Section 4.
-
Neutrino oscillation experiments show that neutrinos must be massive. The flavor eigenstates
$|\nu_\alpha\rangle$ of neutrinos can be mixed via the Maki-Nakagawa-Sakata (MNS) matrix V as follows [51]$|\nu_\alpha\rangle = \sum\limits_k V^\ast_{\alpha k} |\nu_k\rangle\; ,$

(1) where
$|\nu_k\rangle$ denotes the mass eigenstates of neutrinos. The propagation of the state$|\nu_k\rangle$ is described by a form of plane wave$|\nu_k(t,\vec{x})\rangle = \exp(-{\rm i}\Phi_k)|\nu_k\rangle\; .$

(2) Here, the phase
$\Phi_k$ is a solution of Klein-Gordon equation. In flat spacetime, it is of the form$\Phi_k = E_k t-\vec{p}_k\cdot \vec{x},$

(3) where
$E_k$ and$\vec{p}_k$ denote the energy and momentum of mass eigenstates$|\nu_k(t,\vec{x})\rangle$ , respectively. In this study, we only consider two flavor neutrinos ($\nu_e$ and$\nu_\mu$ ). The flux of tau neutrino ($\nu_\tau$ ) can be neglected according to GRBs model [52]. In this simplified case, the probability that neutrino produced as$|\nu_e\rangle$ at source is detected as$|\nu_e\rangle$ is given as [45]$\begin{split} P_{ee}\equiv|\langle\nu_e|\nu_e(s)\rangle|^2 = &1-\sin^2 2\theta\sin^2\left(\frac{\Phi_1-\Phi_2}{2}\right)\\ = &1-\sin^2 2\theta\sin^2\left(\frac{\Delta m^2 L}{4E}\right), \end{split}$

(4) where L denotes the distance between the source of neutrinos and the detector,
$\theta$ and$\Delta m^2$ denote the neutrino mixing angle and mass-squared difference, respectively.When neutrinos propagate through a massive region with high electron density, the electron neutrino will be scattered by electrons. Such effect can be evaluated by the effective Hamiltonian of neutrinos, and the effective potential is given as
$\mathcal{V} = \sqrt{2}G_{\rm F} n_{\rm e}$ [45], where$n_{\rm e}$ denotes number density of electron and$G_{\rm F}$ denotes Fermi constant. In a hot fireball model of GRBs, the number density of electron satisfies power-law distribution [20]$ n_{\rm e} = n_0\left(\frac{r}{r_0}\right)^{-N}, $

(5) where
$r_0$ is the base radius of the GRBs outflow,$n_0$ is the electron density at$r_0$ , and N is the power-law index.$N = 3$ or$N = 2$ , depending on whether the outflow is in the accelerating or coasting phase, and$r_0$ is assumed to be approximately$10^7$ cm. For a typical long GRBs of isotropic equivalent luminosity$L = 10^{51}$ erg/s and saturated Lorentz factor$\eta = 100$ , the initial electron density is estimated to be$n_0\approx 10^{26}$ ${\rm cm}^{-3}$ in the hot fireball model. In the magnetic jet model of GRBs, the initial electron density is about three orders of magnitude lower than the one in the hot fireball model [41, 42]. Therefore, the matter effect on the neutrinos can be used to distinguish the two models.Since the number density of electron in hot fireball model varies dramatically, the neutrinos propagate non-adiabatically through such media. In this case, the coherent effect of neutrino oscillations vanishes, and the averaged survival probability of electron neutrinos is given by the following formula [46]
$ P_{ee} = \frac{1}{2}+\left(\frac{1}{2}-\Theta(A-\Delta m^2\cos2\theta)P_c\right)\cos2\theta\cos2\theta_m(r_i), $

(6) where the effective neutrino mixing angle
$\theta_m(r_i)$ in matter at neutrino production point$r_i$ , and it is given as$ \tan2\theta_m = \frac{\Delta m^2\sin2\theta}{\Delta m^2\cos2\theta-A}, $

(7) $\Theta$ is the heaviside step function, and the parameter A is defined as$A\equiv \sqrt{2}G_{\rm F} n_{\rm e} E$ . In formula (6),$P_c$ represents the crossing probability between two instantaneous mass eigenstates, and it is of the form [46]$ P_c = \frac{\exp(-\pi\gamma F/2)-\exp(-\pi\gamma F/2\sin^2\theta)}{1-\exp(-\pi\gamma F/2\sin^2\theta)}, $

(8) where
$ F = \,_2F_1\left(\frac{N+1}{2N},\frac{2N+1}{2N};2;-\tan^22\theta\right) $

(9) is the hypergeometric function, and the adiabaticity parameter
$\gamma$ is defined as$ \gamma\equiv\frac{\Delta m^2\sin^2 2\theta}{2E\cos2\theta}\left(\left|\frac{{\rm d}n_{\rm e}}{n_{\rm e}{\rm d}r}\right|_{r_s}\right)^{-1}. $

(10) Here, the subscript
$r_s$ Eq. (10) denotes that this quantity is evaluate at resonant point, which is determined by$A(r_s) = \Delta m^2\cos2\theta$ .In the upper panel of Fig. 1 and Fig. 2, we plot the , and the crossing probability will approach
$\cos^2\theta$ if the neutrino energy is sufficiently high. In such high energy limit, the minimum value of$P_{ee}$ is just the resonant point and equals 0.5.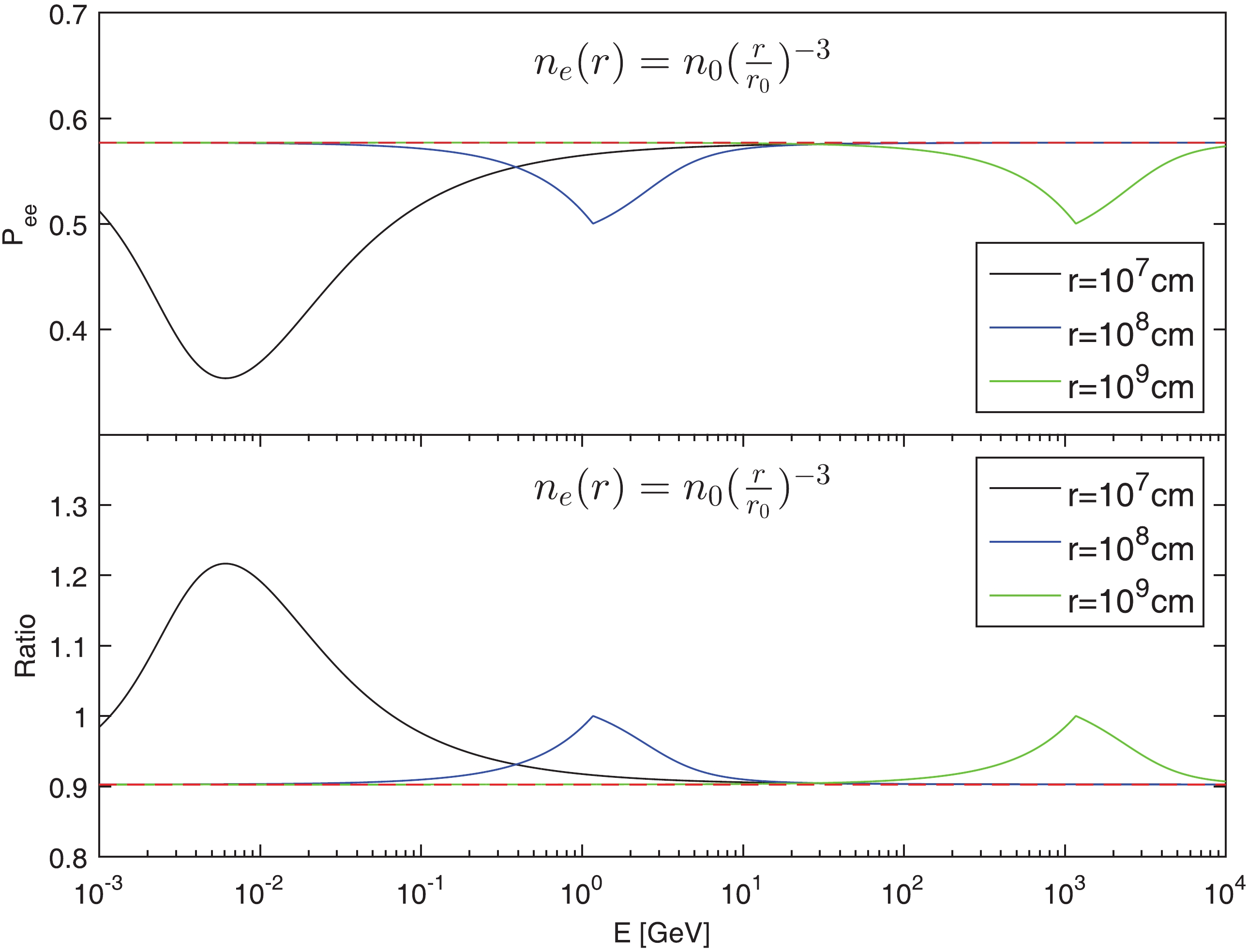
Figure 1. (color online)
$P_{ee}$ and ratio versus E relations in$n_{\rm e}\propto r^{-3}$ case. The red-dashed line in each panel represents the classical result.
Figure 2. (color online) The
$P_{ee}$ and ratio versus E relations in the$n_{\rm e}\propto r^{-2}$ case. The red-dashed line in each panel represents the classical result.High energy neutrinos are produced via the decays of charged pions (and kaons) followed by the decays of muons [45]. The neutrino flavor ratio
$\phi_e:\phi_\mu:\phi_\tau = 1:2:0$ is a good approximation, where the neutrino flux is defined as$\phi_\alpha = \phi_{\nu_\alpha}+\phi_{\bar{\nu}_\alpha}$ for ($\alpha = e,\mu,\tau$ ). However, the neutrino flavor ratio depends on the shape of the energy spectrum [52, 53]. For example, the neutrinos flavor ratio should be$\phi_e:\phi_\mu:\phi_\tau = 1:1.86:0$ if the neutrino fluxes with spectrum$\propto E^{-2}_\nu$ [52]. In hot fireball model of GRBs, the positron can be neglected. Thus, the matter effect for the anti neutrino can be ignored. In this study, we only consider the flavor ratio for neutrinos. In the lower panel of Fig. 1 and Fig. 2, we plot the flavor ratio versus E relation at different radius r. The initial flavor ratio is assumed to be$R_0 = \phi_{\nu_e}^0:\phi_{\nu_\mu}^0 = 1:2$ . The value of the initial flavor ratio will affect the magnitude of the peak of curve in the lower panel of Fig. 1 and Fig. 2, if$R_0\neq1:1$ . -
The gravitational effects on the propagation and oscillations of neutrinos are an interesting topic that has been extensively discussed in the literature [50, 54, 55]. In the reference given above, the evolution of mass eigenstates
$|\nu_k\rangle$ in curved spacetime still satisfies Eq. (2), the only change is the phase$\Phi_k$ , which is given as a covariant form$ \Phi_k = \int p_\mu^{(k)}{\rm d}x^\mu, $

(11) where
$p_\mu^{(k)} = m_k g_{\mu\nu}\displaystyle\frac{{\rm d}x^\nu}{{\rm d}s}$ , and$g_{\mu\nu}$ and${\rm d}s$ are the metric tensor and the line element, respectively. Schwarzschild spacetime is a good approximation for describing the spacetime of gravitational lensing system. Substituting the Schwarzschild metric into Eq. (11), one can obtain the phase for non-radial propagation neutrinos [50]$ \Phi_k = \frac{m_k^2(r_A+r_B)}{2E}\left(1-\frac{b^2}{2r_A r_B}+\frac{2GM}{r_A+r_B}\right), $

(12) where M is the mass of the gravitational source, b denotes the impact parameter,
$r_A$ and$r_B$ denote the distance between source and lens and the distance between lens and detector, respectively. One can find from Eq. (12) that the gravitational effect is considerable only for strong gravitational environment. In most gravitational systems, the distance or the source from the detector on earth,$X\equiv r_A+r_B$ , is of the order of Gpc, hence the gravitational effect on phase can be ignored.In a strong lensing system, neutrinos emitted from the source can propagate along two different paths (denoted as the long path L and short path S for convenience). Then, the evolution of flavor eigenstates
$|\nu_e(s)\rangle$ is given as$\begin{split} |\nu_e(s)\rangle =& C\sum\limits_{ {\rm path} = L,S}\cos\theta\exp(-{\rm i}\Phi_1^{ {\rm path}})|\nu_1\rangle\\&+\sin\theta\exp(-{\rm i}\Phi_2^{ {\rm path}})|\nu_2\rangle,\end{split} $

(13) where C is the normalization constant. By making use of the Eqs. (12) and (13), one can obtain the survival probability of strongly lensed electron neutrinos [50]
$ 1-P_{ee} = P_1+P_2, $

(14) where
$ \begin{split} P_1 =& \sin^2 2\theta\sin^2\left[\frac{\Delta m^2X}{4E}\left(1-\frac{\sum b^2}{4r_A r_B}\right)\right]\\&\times\cos\left(\frac{m_1^2X}{4E}\frac{\Delta b^2}{2r_Ar_B}\right)\cos\left(\frac{m_2^2X}{4E}\frac{\Delta b^2}{2r_Ar_B}\right)\; , \end{split}$

(15) and
$ P_2 = \sin^2 2\theta\sin^2\left(\frac{\sum m^2X}{4E}\frac{\Delta b^2}{4r_Ar_B}\right)\sin^2\left(\frac{\Delta m^2X}{4E}\frac{\Delta b^2}{4r_Ar_B}\right). $

(16) Here, we have defined
$\sum b^2\equiv b_L^2+b_S^2$ ,$\Delta b^2\equiv b_L^2-b_S^2$ , and$\sum m^2\equiv m_1^2+m_2^2$ in the above equations. The term$P_1$ in Eq. (14) represents the interference between the two mass eigenstates propagating along the same path, the term$P_2$ represents the interference between the mass eigenstates propagating along different paths.In strong lensing system, the typical scale of
$\Delta b$ is kpc, and the typical scale of X is Gpc. Therefore, the oscillation effect appears for$P_2$ if the energy of neutrinos reaches$\rm PeV$ . However, even for such high energy neutrinos, X is far larger than$4E/\Delta m^2$ . The term$\sin^2\left[\displaystyle\frac{\Delta m^2X}{4E}\left(1-\displaystyle\frac{\sum b^2}{4r_A r_B}\right)\right]$ should be averaged over many rounds of oscillations. The observed average survival probability of strongly lensed electron neutrinos should be$ 1-\bar{P}_{ee} = \bar{P}_1+P_2, $

(17) where
$ \bar{P}_1 = \frac{1}{2}\sin^2 2\theta\cos\left(\frac{m_1^2X}{4E}\frac{\Delta b^2}{2r_Ar_B}\right)\cos\left(\frac{m_2^2X}{4E}\frac{\Delta b^2}{2r_Ar_B}\right)\; , $

(18) unlike the neutrino oscillations of single path (4), the average survival probability of strongly lensed electron neutrinos (17) depends on both the neutrino mass-squared differences and the sum of neutrino mass-squared. Therefore, the coherent effect of strongly lensed neutrinos could determine the mass of neutrinos.
In the lower panels of Fig. 3 and Fig. 4, we show the
$\bar{P}_{ee}$ versus E relation in the normal hierarchical case ($m_1\ll m_2<m_3$ ) and inverted hierarchical case ($m_3\ll m_1<m_2$ ) [56], respectively. In the normal hierarchical case,$\sum m^2\simeq\Delta m^2$ . Then, the evolution of$\bar{P}_{ee}$ is mastered by a single wave number$\Delta m^2/4E$ . In the inverted hierarchical case,$\sum m^2\ll\Delta m^2$ . Then,$\bar{P}_{ee}$ evolves as a wave packet. These facts can be found directly from Fig. 3 and Fig. 4. GRBs can be a source of$\rm PeV$ neutrinos [21]. As a frequently observed astronomical phenomenon, the strongly lensed high energy neutrinos are likely to be detected in the future, which will carry the information of neutrino mass. In the calculation, the lens parameters are taken to be that of a typical strong lensing system HST14176+5226 [48]: the redshift of source$z_s = 3.4$ , the redshift of lensing plane$z_l = 0.809$ , Einstein ring radius$\theta_E = 1.489''$ , the misalignment angle$\beta = 0.13''$ . The distance are calculated in the flat$\Lambda$ CDM model with parameters$\Omega_M = 0.3$ ,$\Omega_\Lambda = 0.7$ and$H_0 = 70\; {\rm km\; s^{-1}\; Mpc^{-1}}$ .
Figure 3. Normal hierarchical case:
$\Delta m^2\approx m_2^2\approx 7.53\times $ $10^{-5}\; {\rm eV}^2,$ $m_1^2\approx 0$ [56].
Figure 4. Inverted hierarchical case:
$m_1\approx m_2\approx 0.05\; {\rm eV}$ ,$\Delta m^2\approx 7.53\times$ $ 10^{-5}\; {\rm eV}^2$ [56]. -
Neutrinos produced from GRBs carry important information on the GRB emission region. In this study, we calculated the matter effect on high energy neutrinos in the hot fireball model of GRBs. The electron density in the magnetic jet model of GRB is sufficiently lower than the one in the hot fireball model. Once the matter effect on high energy neutrinos has been observed, it can be used to distinguish these two models. The average survival probability and flavor ratio of neutrinos that produced at massive region with high electron density has been calculated. The electron density in hot fireball model satisfies power-law distribution [20]. The ratio of resonant neutrino energy for different spherical shell r gives the information on power index N.
In the standard internal shock model, GRBs occur at a distance from the central engine of
$r\sim 10^{13}$ cm or more. This is because below this distance, the optical depth is too large such that the photons cannot escape from the jet. However, neutrinos can occur at a significantly smaller radius before the emission of photons. The matter effect is noticeable only for the neutrinos produced at small radii (where the electron density is large enough). At radius$r\sim 10^{13}$ cm or more, the electron density is small, so the matter effect is undetectable. For the progenitors of long GRBs, the death of massive stars is the leading model. According to this model, the electron density in the envelope around massive star also follows the power-law distribution that is the same with Eq. (5) [30]. In our study, we assume that the electrons obey the general power distribution along the line-of-sight, in regardless of whether they are produced in the GRB outflow or pre-exist in the envelope before the photon emission of GRBs.GRBs could produce
$\rm PeV$ neutrinos [21]. We have calculated the coherent effect for strongly lensed$\rm PeV$ neutrinos, which was first suggested by Ref. [50]. The interference between the mass eigenstates propagating along different paths plays an important role for strongly lensed neutrino oscillations. The average survival probability of strongly lensed electron neutrinos depends on both the neutrino mass-squared difference and the mass-squared summation. Therefore, strongly lensed neutrinos could be used to determine the neutrino mass.We would like to thank prof. S. Zhou for helpful discussions.
Matter effects and coherent effect of neutrinos produced from ${{\gamma}}$ -ray bursts
- Received Date: 2019-05-20
- Available Online: 2019-10-01
Abstract: Neutrinos produced from






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: