-
Since the Large Hadron Collider (LHC) announced the discovery of a scalar-like resonance [1, 2], many subsequent measurements confirmed that it is the Higgs particle, the last brick of the Standard Model (SM) [3]. Among these measurements, the generic Higgs coupling to vector gauge bosons presented the largest (~ 7%) deviation from the SM prediction, but its experimental error is so big (±56%) that the good agreement with SM still stands. Both the unexplained phenomena, like the dark matter, and the theoretical issues like the hierarchy (naturalness) problem, still need extensions of SM. The interaction between the Higgs scalar and vector gauge bosons is a key ingredient for the underlying nature of spontaneous breaking of electroweak gauge symmetry. In addition to the suggested experiments of kinematic distributions at LHC Run2 [4, 5] and high-luminosity run [6], future Higgs factories are under considerations, such as the International Linear Collider (ILC) in Japan [7], the Circular Electron Positron Collider (CEPC) in China [8, 9], and Future Circular Collider (FCC-ee) in Europe [10]. Along these lines, many pre-analyses have been made to unveil the nature of the gauge boson and Higgs couplings [11, 12]. Future lepton colliders will accumulate events with full kinematics and less background at high luminosity, which will enable precision tests in the Higgs sector. Hence, it becomes indispensable to unfold and use the event shapes in the experimental data to explore the subtleties of the Higgs properties.
Theoretically, the effective field theory (EFT) provides a natural framework. A comprehensive study usually lists the relevant higher dimension operators and constrains their Wilson coefficients separately [13-15]. Since the EFT operators are defined by the interaction bases before gauge symmetry breaking, all effective HVV couplings
$ (VV = ZZ,Z\gamma,WW $ or$ \gamma\gamma) $ become unavoidable after symmetry breaking when compared to experiments at the electroweak scale. An alternative approach is to start from phenomenological parameters defined by mass eigenstates as a convenient bridge between EFT and experiments, but at a price of losing the direct map to the underlying operators [16-20]. Many works have been done theoretically for the LHC experiments to demonstrate how these phenomenological parameters can be constrained using the distribution of the polarization angle [21-23].In lepton colliders, the Higgs will be produced via strahlung [24, 25] in association with the Z gauge boson (mainly via off-shell Z), so that at a given luminosity the events via HZZ vertex will undoubtedly play a more important role due to larger statistics and lower experimental uncertainties than
$ HWW,\; H\gamma\gamma $ or$ HZ\gamma $ . In order to connect the HZZ event shape to the phenomenological parameters, we followed the strongly interacting light Higgs (SILH) scenario [16, 26, 27], without any modifications in the underlying theory. Further developments were described in [28], where only four phenomenological parameters are used as HZZ couplings. Since the present designs of the circular electron positron colliders and of the ILC are based on a center-of-mass energy around 240 GeV, it is necessary to perform the detailed sensitivity study of the Higgs production for a specific detector design.In this work, we investigate the polarization angle of the Z decays associated with Higgsstrahlung, as well as the azimuthal angle of the Z decays. Our work is focused on the physics parameters that are extracted from the angular distributions, and on the sensitivity study, which relies on the characteristics of detector design and on the systematical errors of the experiment. A comprehensive study would certainly be helpful at this stage, although the
$ HZZ $ ,$ HZ\gamma $ and$ HWW $ events will have to be analyzed separately by the experiments.The paper is organized as follows: In Section 2, analytical formulas for the angular distribution and CP-violation terms for the Z to 2 lepton decays affected by the new coupling
$ HZZ $ are presented. Section 3 gives the numerical limit of the sensitivity of new physics parameters at CEPC. A summary is given in Section 4. -
The generic effective Hamiltonian in the
$ HZZ $ sector is written as [27]$ \begin{split} {\cal L}_{HZZ} =& -\frac{{1}}{4}g_{1}Z_{\mu\nu}Z^{\mu\nu}h-g_{2}Z_{\nu}\partial_{\mu}Z^{\mu\nu}h \\&+ g_{3}Z_{\mu}Z^{\mu}h-\frac{{1}}{4}{\widetilde{g}} Z_{\mu\nu}{\widetilde{Z}}^{\mu\nu}h , \end{split} $

(1) where
$ Z_{\mu\nu} = \partial_{\mu}Z_{\nu}-\partial_{\nu}Z_{\mu} $ and$ {\widetilde{Z}}_{\mu\nu} = \frac{1}{2}\epsilon_{\mu\nu\rho\sigma}Z^{\rho\sigma} $ . The effective Feynman rule can be derived from Eq (1) as$ \begin{split} V_{\mu\nu} =& {\rm i}g_{\mu\nu}[ g_0 + g_{3}+g_{2}(p_{3}^{2}+p_{2}^{2})+g_{1}(p_{2}\cdot p_{3})] \\&- {\rm i}[\frac{1}{2}g_{1}(p_{3}^{\mu}p_{2}^{\nu}+p_{2}^{\mu}p_{3}^{\nu})+g_{2}(p_{2}^{\mu}p_{2}^{\nu}+p_{3}^{\mu}p_{3}^{\nu}) \\&- {\widetilde{g}}\epsilon_{\mu\nu\rho\sigma}p_{3}^{\rho}p_{2}^{\sigma}]. \end{split}$

(2) In this parameterization,
$ g_0 = e M_Z /(c_w s_w ) $ is the HZZ coupling in the Standard Model. Taking the convention of [28],$ g_3 $ is a small number in units of$ g_0 $ , while$ g_1, g_2, {\tilde g} $ are small numbers in units of$ e^2 /( g_0 s^2_w c^4_w ) $ , so that the interaction is consistent with the dimension of mass. The new type of couplings$ g_1, g_2, {\tilde g} $ should be smaller than one in SM, since most experimental data are consistent with SM. The number of free parameters in new physics is then reduced from 12 to only 4 [28], while keeping a sufficiently general structure for the interaction between the Higgs and vector bosons. In contrast to the$ \kappa_Z $ parametrization [29], which has only one parameter, these four parameters are effective for revealing the details of potential new physics.We will focus only on the real Z that is produced in association with the Higgs boson. It decays into a pair of leptons, either
$ e^- e^+ $ or$ \mu^-\mu^+ $ , since they are the particles with the highest detection efficiency and carry the polarization message of a Z boson. Even in lepton colliders it will be hard to tag the electric charge of jets, and we have to choose between the electron or muon as the spin analyzer at a price of reduced statistics. The kinematics of this process is illustrated in Fig. 1. Obviously, the above mentioned new physics coupling of$ HZZ $ beyond SM may make the$ e^+ e^- \to Z^* \to HZ $ cross-section different from SM. Furthermore, the complicated new physics structure in Eq. (2) may also change the polarization fraction of the Z boson, making the angular distribution of the final lepton pairs different from SM.In the Standard Model, the off-shell photon can also contribute to the strahlung production via the for a given design of a lepton collider. In this regard, we do not need to worry about the constraint of the
$ \gamma^* ZH $ coupling on the electric dipole moment (EDM) of electron [30, 31].The momenta and helicities of the incoming (anti-) electron and outgoing bosons are defined as:
$ e^- (p_1 , \sigma_1 ) + e^+ ( p_2, \sigma_2) \rightarrow Z( k, \lambda ) + H( q ) , $

(3) where
$ \sigma_{1,2} = +\displaystyle\frac{1}{2}, -\displaystyle\frac{1}{2} $ and$ \lambda = -1, 0, +1 $ . The invariant amplitude for the Higgs production is$\begin{split} {\cal M}^\lambda =& {\bar v}(p_1) ( v_e I + a_e \gamma_5 ) \gamma_{\tau} u( p_2 )\\&\times P^{\tau\mu} V_{\mu\nu} ( k + q , k ) \epsilon^{\lambda,\nu} , \end{split}$

(4) where
$ P^{\tau\mu} $ is the propagator of the virtual Z boson in unitary gauge, and the polarization vector$ \epsilon^\lambda (k) $ of the real Z is$ \begin{split}\epsilon^{\pm,\mu} =& (0, \cos\vartheta, \mp I, -\sin\vartheta)/\sqrt 2, \\ \epsilon^{0,\mu} =& (k, E_z \sin\vartheta, 0, E_z \cos\vartheta)/M_z , \end{split}$

(5) where
$ E_Z $ is the energy of the Z boson.In the rest frame of the real Z, the decay (helicity) amplitude is written as [32]
$ D_{\lambda,\tau} ( k^2 , \vartheta, \varphi ) = \sqrt {k^2 } ( v_f + \tau a_f ) d^\tau_\lambda ( \vartheta, \varphi) , $

(6) where
$ \tau $ is the helicity of the spin analyzer in the Z decay, and$ d^\tau_\lambda ( \vartheta, \varphi) $ is the usual$ \displaystyle\frac{1}{2}- $ representation of the rotation group. There is also a Breit-Wigner factor, but it is left out as it is an overall factor. The scatting angle$ {\hat \vartheta} $ , polarization angle$ \vartheta $ and azimuthal angle$ \varphi $ are defined in Fig. 1. -
The differential cross-section for Higgs production in the Born approximation reads
$ \begin{split} \frac{ {\rm d} \sigma }{ {\rm d} \cos {\hat \vartheta} {\rm d} \cos\vartheta {\rm d}\varphi } =& K \sum\limits_\tau D^{*}_{\lambda ' ,\tau} \rho^{ \lambda ' \lambda } D_{\lambda,\tau} \\ =& K \sum\limits_\tau {\bar {\sum\limits_{\sigma_1, \sigma_2} } } D^{*}_{\lambda ' ,\tau} { {\cal M}^{\lambda '}}^{\dagger} {\cal M}^\lambda D_{\lambda,\tau} . \end{split} $

(7) The kinetic factor K reads:
$ K = \frac{ \beta }{ 128 s \left| s- m^2_Z \right| ^2 } \frac{ | { p}_l | }{ 32 \pi^3 M_Z^2 \Gamma_Z} , $

(8) where
$ \beta = {( 1 + m^4_Z/s^2 + m^4_H/s^2 - 2m^2_Z/s - 2m^2_H/s -} $ ${ 2 m^2_Z m^2_H/s^2 ) }^{1/2} $ , with s the center-of-mass energy squared, and$ | { p}_l | $ the momentum of the lepton which is the Z spin analyzer. The definition of spin matrix$ \rho^{ \lambda ' \lambda } $ respects the fact that no beam polarization is expected from the incoming leptons in CEPC. In the case of longitudinal beam polarizations in a linear collider like ILC, a detailed study was published in [17, 32].After integration in the phase space, the total cross-section is:
$ \sigma = K \frac{ 128 \pi C_{l{\bar l}} \; s\; }{ 9 } Q , $

(9) where
$ Q = ( g^2_0 + 2 g'_3{g_0} ) (E^2_Z + 2 m^2_Z) + \frac{1}{2} g_1 g_0 \beta^2 E_Z s^{3/2}. $

(10) The SM coupling
$ C_{l{\bar l}} = \left( a^2_e + v^2_e \right) \left(a^2_f+ v^2_f \right) $ for the leptonic final states of Z will be defined by the experiment. Since new physics couplings are a small perturbation of the SM couplings, we only keep the leading order linear terms. It is interesting that the anomalous couplings appear as a combination:$ g '_3 = 2 g_2 ( s + m^2_Z ) + g_3 + g_1 \sqrt{s} E_Z. $

(11) This relation further reduces the number of free parameters to three,
$ g_1 $ ,$ g '_3 $ and$ {\tilde g} $ . We would also like to point out that this relation takes place at the level of the amplitude of ZH associated production, so it can be regarded as a new parametrization for analyzing the Higgsstrahlung channel. To isolate the$ g_2 $ contribution, one has to investigate the decay channel Higgs into Z pair, whose yield seems relatively small, and is an independent issue beyond the scope of this work. -
Although there are only three effective couplings left, one can not distinguish their contribution by the total cross-section measurement only. Different kinds of new physics will give more information on the angular distributions of the decay products of the Z boson, which characterize its polarization fractions. The polar angle distribution of the outgoing lepton is derived as
$ \begin{split} \frac{ {\rm d} \sigma }{ \sigma {\rm d} \cos\vartheta } =& \frac{3 M_Z^2 }{ 8 ( a^2_f+ v^2_f )\; Q }\\&\times \left\{ \left[ \left( g^2_0 + 2 { g '_3}{g_0 } \right) \frac{E_Z^2}{M_Z^2}+ g_1 g_0 \frac{ \beta^2 E_Z s^{3/2}}{2M_Z^2} \right] \right.\\& \times\left.\Gamma^0 (\vartheta)+ \left(g^2_0+ 2 {g '_3}{g_0} \right) [ \Gamma^- (\vartheta) + \Gamma^+ (\vartheta) ] \right \} , \end{split}$

(12) where
$ \Gamma^\lambda (\vartheta) $ is the normalized partial width of the Z boson in the$ \lambda $ helicity state, defined as$ \begin{split} \Gamma^\pm (\vartheta) =& \frac{1}{2} M_Z^2 \left[ \left(a_f^2+v_f^2\right) ( \cos 2\vartheta +3 )\right.\\&\left. + 8\; \pm\; a_f v_f \cos\vartheta \right] \end{split} $

(13) $ \begin{array}{l} \Gamma^0 (\vartheta) = 2 M_Z^2 \left(a_f^2+v_f^2\right) \sin^2\vartheta . \end{array} $

(14) The fraction of each spin polarization, characterized by the distribution of the polarization angle
$ \vartheta $ , is obtained by integrating out the scatting angle$ {\hat \vartheta} $ . In principle, the final lepton coupling$ a_f, v_f $ may receive extra contributions if anomalous$ Z l \bar{l} $ interaction is included. Since CEPC proposes a better option, a Z-factory run to explore this possibility, we keep in this work$ a_f, v_f $ as in SM . It is interesting to note that the fraction of transverse polarization can be increased if the integration in scattering angle is performed in a reduced interval, for example, in a forward region defined by$ | \cos {\hat \vartheta} | > \cos \displaystyle\frac{\pi}{4} $ ,$ \begin{split} \frac{ {\rm d} \sigma }{ \sigma {\rm d} \cos\vartheta }\bigg|_{fwd} =& \frac{3 M_Z^2 }{ 128 ( a^2_f+ v^2_f )\; Q } \times \{ 2 ( 8-5\sqrt{2} )\\ &\times \left [ ( g^2_0 + 2 { g '_3}{g_0 } ) \frac{E_Z^2}{M_Z^2} + g_1 g_0 \frac{ \beta^2 E_Z s^{3/2}}{2M_Z^2} \right ] \Gamma^0 (\vartheta) \\&+ ( 16 - 7\sqrt{2} ) (g^2_0+ 2 {g '_3}{g_0} ) \\&\times [ \Gamma^- (\vartheta) + \Gamma^+ (\vartheta) ] \}. \end{split}$

(15) It is obvious that the contribution from
$ \Gamma^\pm (\vartheta) $ is enhanced by a factor of 3.3 in the forward region. In the experiments, this polarization distribution, together with the total cross-section, will be used to fit the parameters$ g_1 $ and$ g '_3 $ . -
Up to now, all the analyses are independent of the CP violation term
$ {\widetilde{g}} $ in the effective Hamiltonian of Eq. (1), which characterizes the CP violating effects in new physics beyond the Standard Model. We need to study the azimuthal angle$ \varphi $ dependence of the Z boson decays in order to study CP violation effects:$ \frac{ {\rm d} \sigma }{ \sigma {\rm d} \varphi} = \frac{ 1}{2 \pi } - \frac{ M_Z^2}{4 \pi Q} {g_0} \left\{ ( g_0 + 2 {g '_3} ) \cos{2\varphi} +{\tilde g} s \beta \sin{2\varphi} \right\}. $

(16) Here, the first two terms are background from SM, and CP violation appears in the third term, with the
$ \sin2\varphi $ dependence of the signal against the background of$ \cos 2\varphi $ .There is no
$ \sin\varphi $ term in the above equation. However, it can be recovered by breaking the symmetry in decay angle$ \vartheta $ integration,$ 0\to \pi/2 $ or$ \pi/2 \to \pi $ , at a price of$ \cos\varphi $ background in SM$ \begin{split} \frac{ {\rm d} \sigma }{ \sigma {\rm d} \varphi}\bigg |_{\vartheta \gtrless \pi/2 } =& \frac{ 1}{2 \pi }- \frac{ M_Z^2}{ 4 \pi Q} {g_0} \left\{ ( g_0 + 2 {g '_3} ) \cos{2\varphi} + {\tilde g} s \beta \sin{2\varphi}\right\} \\ & \pm \frac{ 3 a_e v_e M_Z } { 16 Q(v^2_e + a^2_e )} g_0 \left\{ \left[ 2( g_0 - 2 {g '_3} ) {E_Z} + g _1 \beta^2 s^{3/2} \right]\right.\\&\times\left. \cos{\varphi} + {\tilde g} s E_Z \sin\varphi \right\}. \end{split} $

(17) One can see from Fig. 2 that the distribution with
$ \sin\varphi $ reveals the CP violation as breaking of the height equality of the two peaks, while the$ \sin 2\varphi $ term makes a phase shift with respect to CP conserving SM background. -
At future Higgs factories, millions of Higgs events are expected, which will give signals of new physics, or at least provide constraints for new physics, presented in the form of Eq. (2). For example, the circular electron positron collider may deliver a luminosity of
$ 5000~{\rm fb}^{-1} $ at center-of-mass energy$ E = 240 ~{\rm GeV} $ . In the conceptual design report [8], the exclusive channel$ e^-e^+ \to ZH \rightarrow$ $ l^+ l^- b {\bar b} $ is investigated with phase space cuts:•
$ p_l \geqslant 18 ~{\rm GeV} $ ,$ p_b \geqslant 20~ {\rm GeV} $ ,•
$ | \cos\vartheta_l | \leqslant 0.98 , | \cos\vartheta_b | < 0.98 $ ,•
$ | M_{l^+ l^-} - M_Z | < 15~ {\rm GeV} , | M_{b{\bar b}} - M_H | < 12~ {\rm GeV} $ .Furthermore, CEPC simulations provided the expected performance for:
• lepton identification efficiency: 85%
• bottom jet tagging efficiency: 75%.
We adopt tighter cuts on the phase space and particle tagging (identification), so that the background (mainly ZZ production) can be suppressed to such a level that it can be ignored. At least, its contamination can be well estimated and subtracted in future experiments.
Before Higgs factory data and details of systematical studies become available, we perform Monte Carlo simulations and compare the new physics contribution with SM. Based on the histograms of angular distributions in SM, a Pearson
$ \chi^2 $ is defined for the event number in each bin based on the hypothesis of new physics. When the parameters$ g_1 $ ,$ g'_3 $ and$ {\tilde g} $ are sufficiently small, the effects of new physics are hidden by the (mainly statistical) SM errors (reflected in$ \chi^2 $ ) , so that the limits of sensitivity can be estimated accordingly.Instead of making additional assumptions or including more complicated procedures, we assume that the systematical errors are at the same level as the statistical ones, so that the sensitivity limits estimated in following subsections are conservative. Optimized and reliable sensitivity limits should be left to the actual data analysis using experimental input.
-
Using the above mentioned cuts, we scanned the new physics parameters
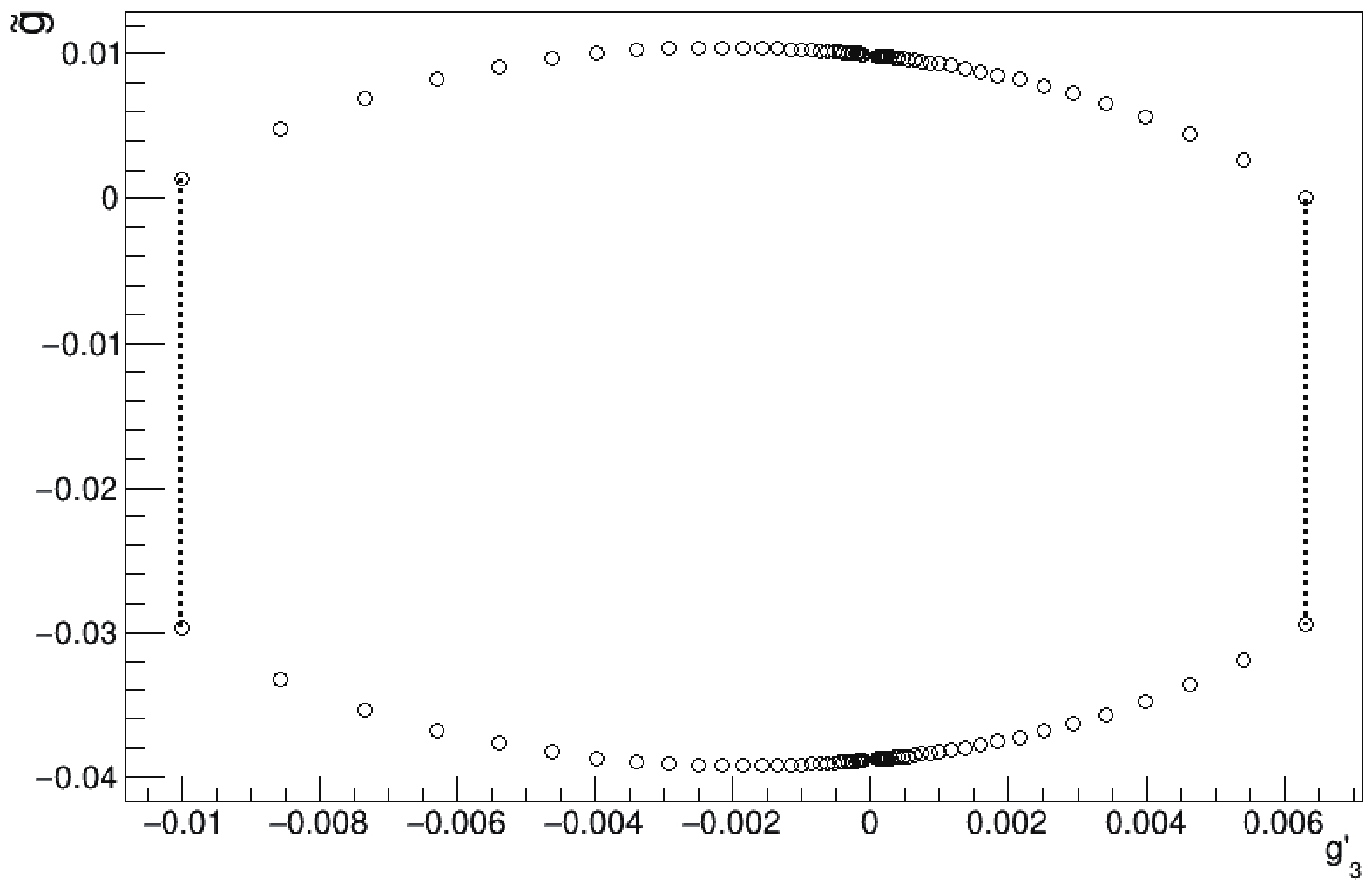
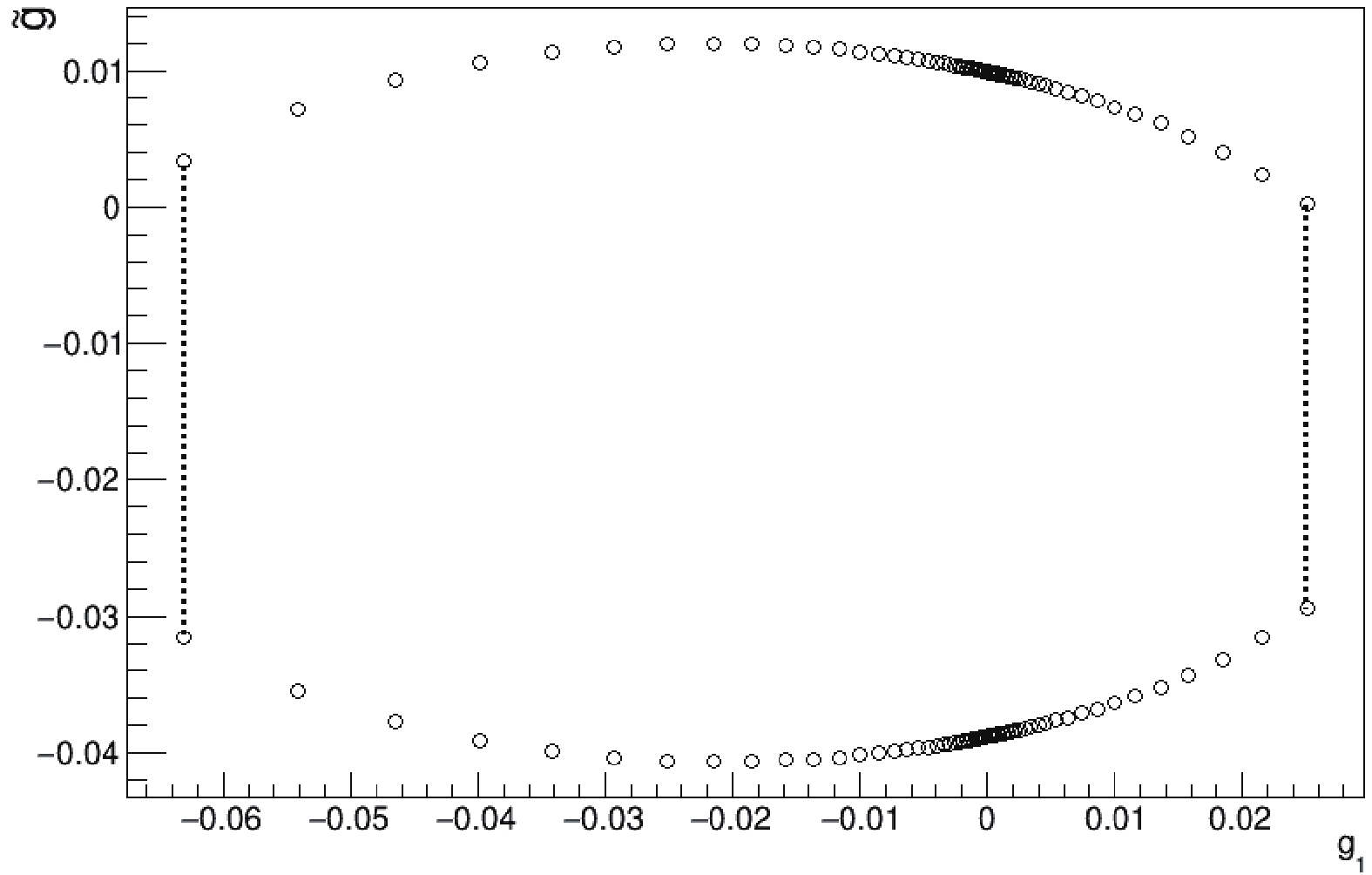
$ ( g_1 , g'_3 ) $ simultaneously. Their sensitivity limits occur when$ \Delta \sigma / \sigma \geqslant \sqrt{2}/ \sqrt{N_{evt}} $ , where$ N_{evt} $ is the observed number of events (signal) in$ ZH \rightarrow l^+ l^- b {\bar b} $ , as shown in Fig. 3. The new physics parameters$ ( g_1 , g'_3 ) $ inside the parallelogram will be difficult to distinguish from SM within experimental errors. It can be seen that CEPC can set limits at$ | g'_3| \leqslant 0.015 $ and$ |g_1| \leqslant 0.035 $ .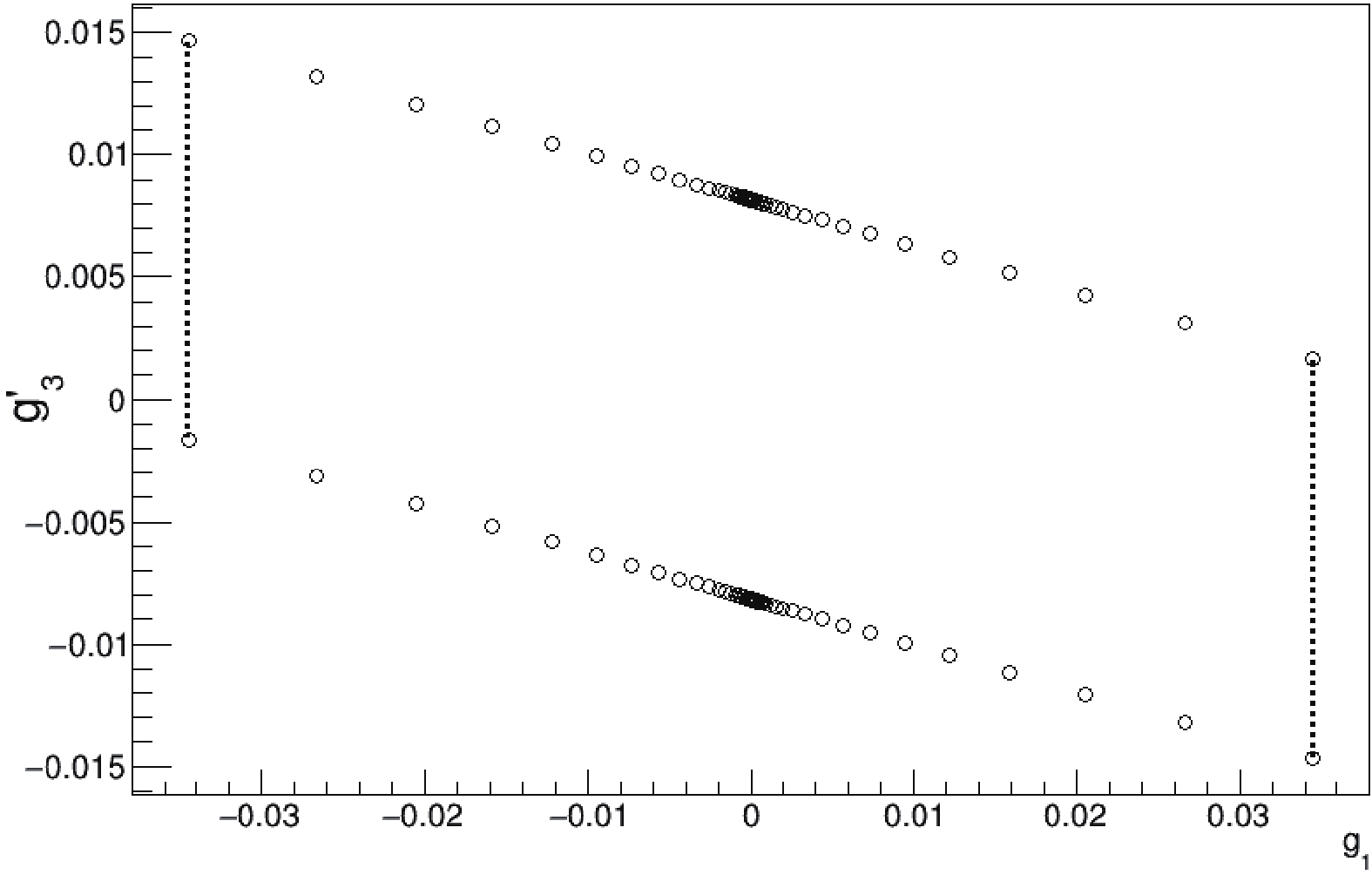
Figure 3. New physics sensitivity limits from the total cross-section measurements. The parameters inside the parallelogram are difficult to distinguish from the Standard Model within experimental errors.
One may also set lower limits
$ | g'_3| \leqslant 0.005 $ and$ |g_1| \leqslant 0.015 $ , by discarding systematical errors and relaxing event selection.On the other hand, the reconstruction of the recoil Z boson leads to an inclusive analysis with Higgs decaying to anything other than the
$ b {\bar b} $ final states. In this case, a tighter limit can be set with about three times larger statistics. In such a reconstruction, it is possible to reduce the dependence on invisible Higgs decays, but the details are beyond the scope of this paper. -
With the planned luminosity and the analysis outlined at the beginning of this section, we study the sensitivity to new physics using the polarization angle distribution, given in Eq. (12) and (15). The expected event number distribution with the polarization angle
$ \vartheta $ is shown in Fig. 4, with blue points for Eq. (12) and black points for Eq. (15). The polarization angle distribution will be different from the black plot in Fig. 4 if only the forward region of the decay angle is taken into account, as in Eq. (15). Since it comes with lower statistics (only half of the number of events), it is omitted in the present analysis until there is better input for experimental systematics.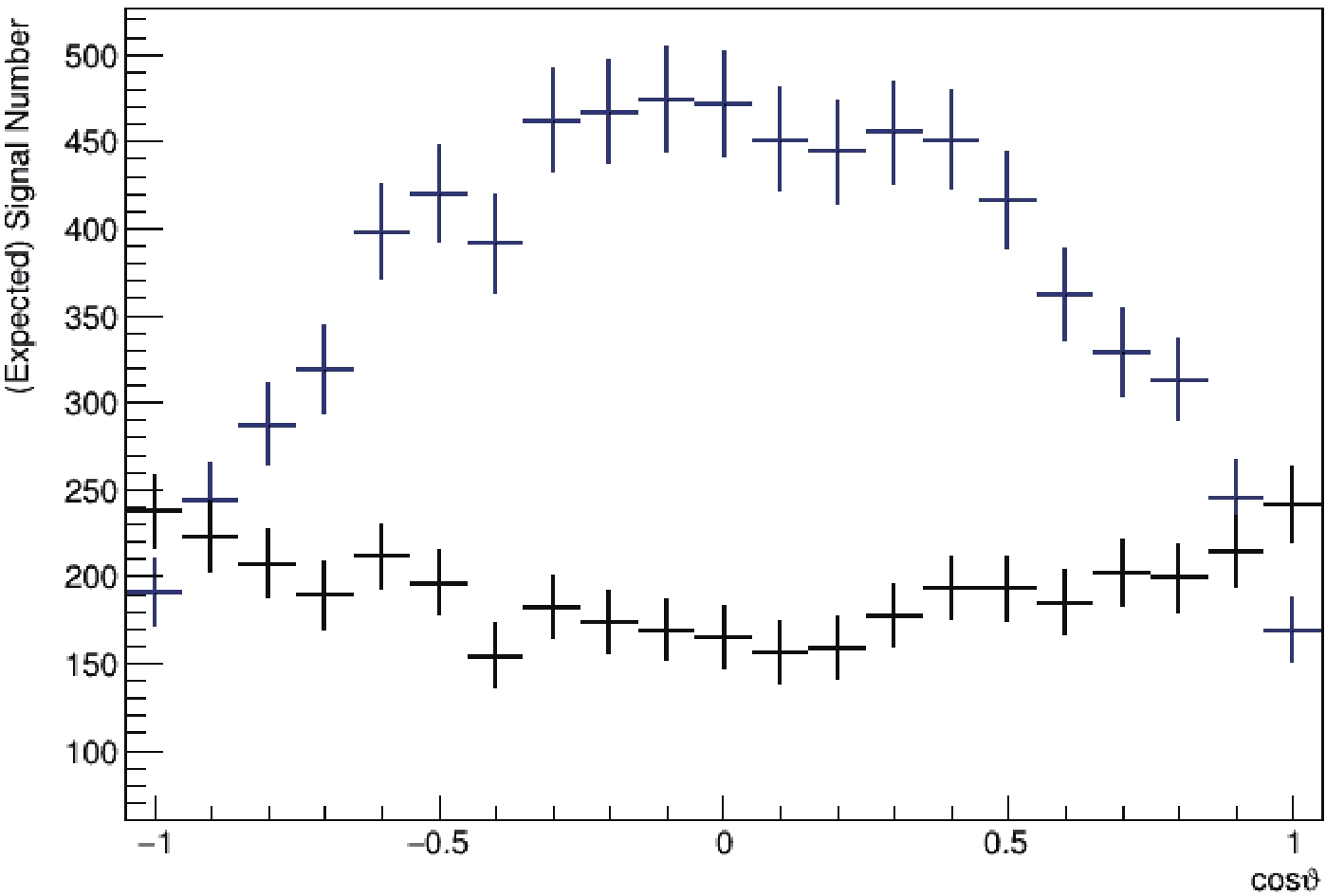
Figure 4. (color online) Expected event number distribution with the polarization angle
$ \vartheta $ , blue for Eq. (12) and black for Eq. (15).We show the experimental limits from polarization angle distributions for new physics parameters
$ g_1 $ and$ g'_3 $ in Fig. 5. The parameter region inside the blue lines is indistinguishable from the Standard Model. We also plot the limits from the cross-section study in Fig. 3. Fig. 5 shows that the two limiting regions overlap, which means that the sensitivity limits are further restricted to the meshed region. The polarization angle distribution will anyway be helpful since it will constrain new physics from a different direction than the cross-section. It is also worth to point out that in Eq. (12) the polarization angle distribution is normalized by the cross-section. This means that there is less dependence on the uncertainties from Higgs production or decay, because the actual analysis is done solely by fitting the shape. As a result, the HZZ couplings are better determined.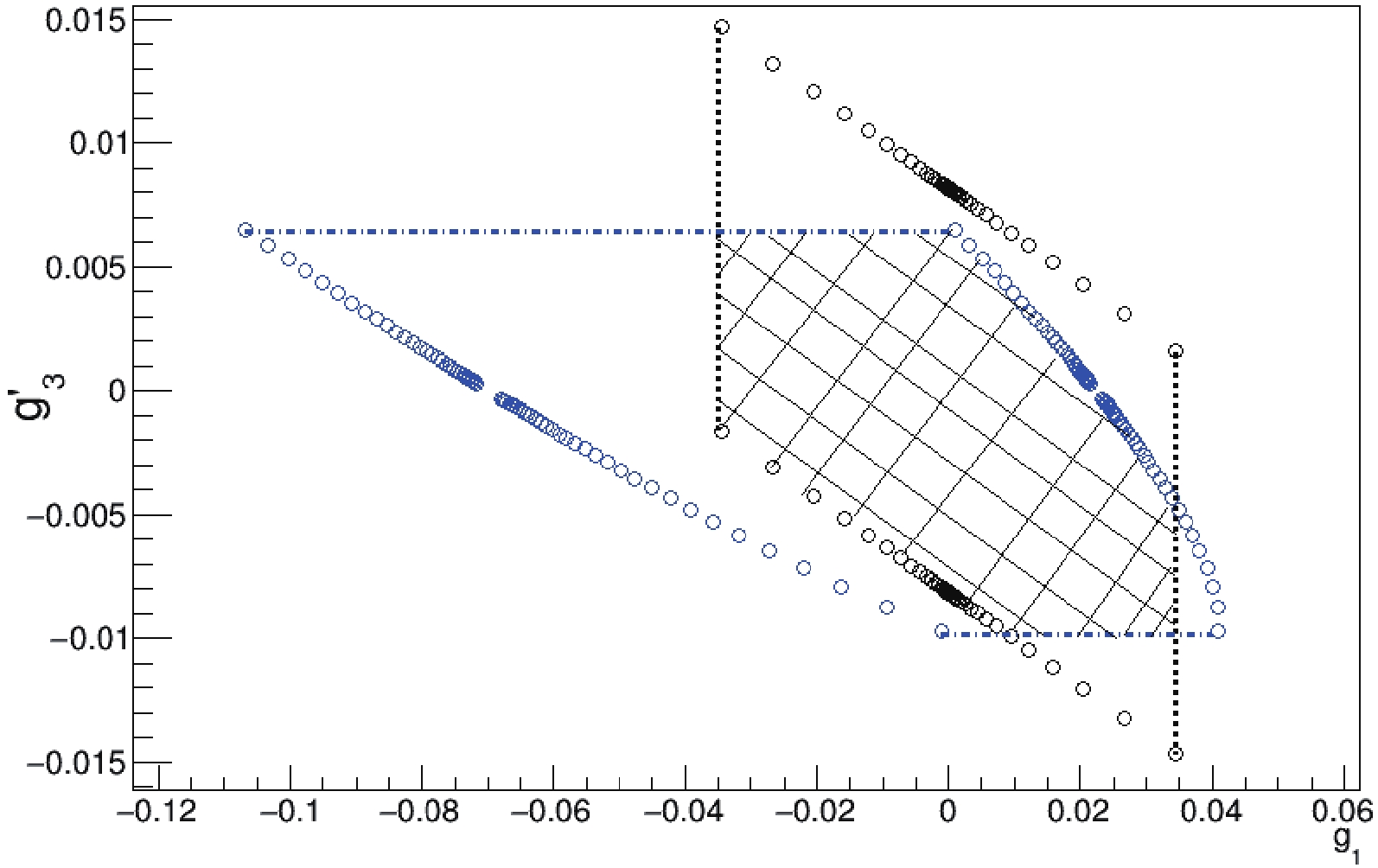
Figure 5. (color online) Limits from the polarization angle, with no sensitivity to new physics in the region delimited by the blue line. The region delimited by the black line is from Fig. 3. The overlap of two regions is the meshed region.
-
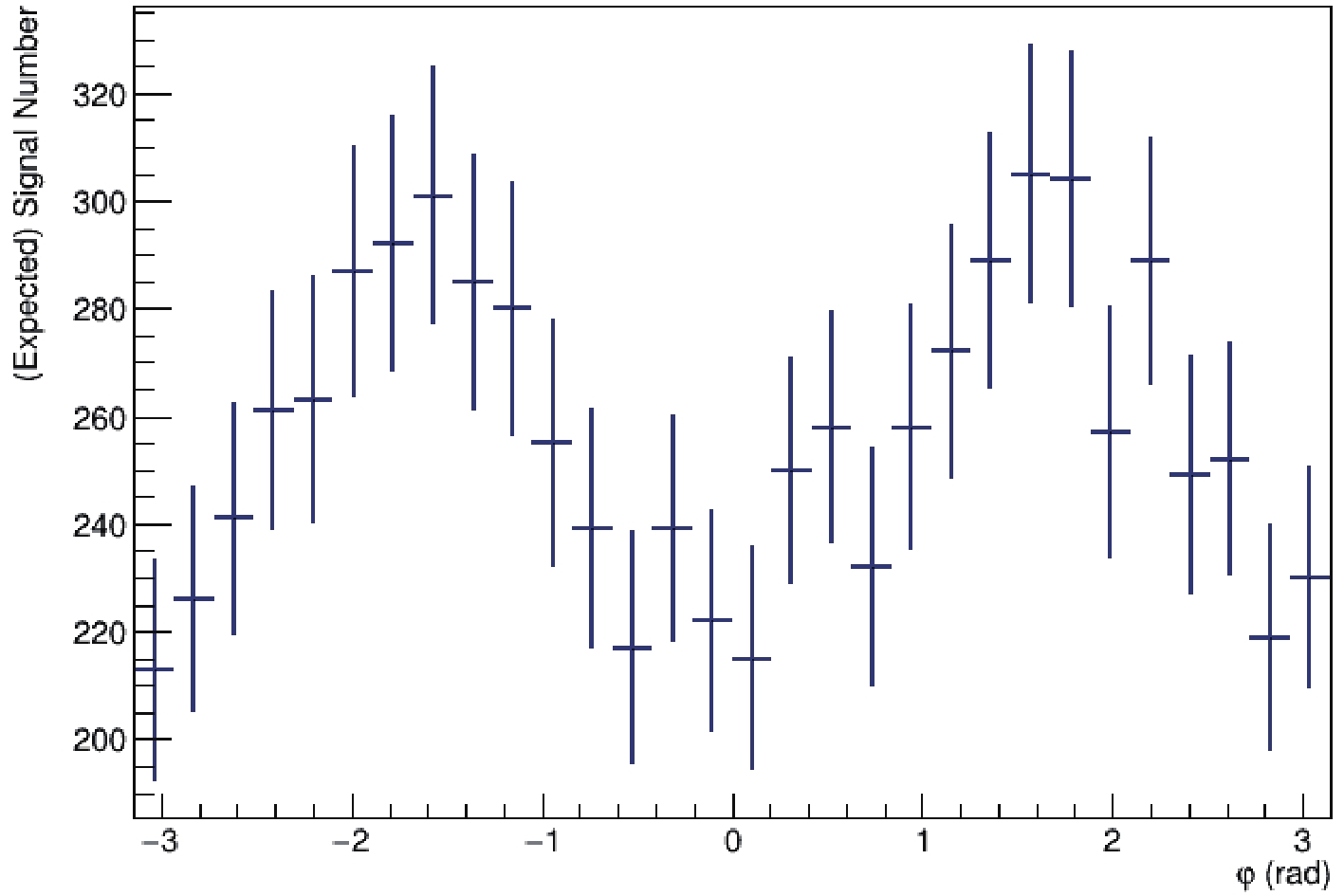
Using Eq. (16), we show the expected event number distribution with the azimuthal angle
$ \varphi $ in Fig. 6, where CP violation effect may appear. Without loss of generality, only one of the new physics parameters$ g_1 $ or$ g'_3 $ is scanned at a time together with the CP violation parameter$ \tilde g $ .Again, the forward region defined in Eq. (17) is omitted in the present analysis due to its lower statistics. After a careful study of the background, we derive the experimental limit for
$ \tilde g $ in correlation with$ g'_3 $ , shown in Fig. 7. The correlation sensitivity of$ \tilde g $ and$ g_1 $ is shown in Fig. 8. These figures indicate that the experimental sensitivity limit for$ \tilde g $ is$ -0.04 \sim 0.01 $ . -
We have studied the sensitivity to new physics in the
$ e^+ e^- \rightarrow HZ $ process at a future Higgs factory. On the basis of measurements of the cross-sections and angular distributions, we set the experimental limits for the dimension-6 operators of the effective field theory in a model independent way. In particular, using the azimuthal angle distribution of the Z boson decays, we found that a future Higgs factory could set a stringent limit on the CP violation effective operators in new physics, with the$ {\tilde g} $ sensitivity limit of$ -0.04 \sim 0.01 $ . Our study showed that a future electron positron collider is an ideal machine for the search of new physics signals.We thank Prof. CP-Yuan and Dr. Yan Bin for useful discussions, we would like to thank Prof. Gong Bin for illuminating comments.
Sensitivity study of anomalous HZZ couplings at a future Higgs factory
- Received Date: 2019-05-28
- Available Online: 2019-10-01
Abstract: We study the sensitivity of constraining the model independent HZZ coupling based on the effective theory up to dimension-6 operators at a future Higgs factory. Using the current conceptual design parameters of the Circular Electron Positron Collider, we give the experimental limits for the model independent operators given by the total Higgsstrahlung cross-section and the angular distribution of Z boson decays. In particular, we give the very small sensitivity limit for the CP violation parameter






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: