Study of excited D and D_s mesons in a relativized quark model

Quantum Chromodynamics (QCD) is experimentally well established theory of strong interaction of quarks and gluons. However, describing rich spectrum of hadrons from the first principle is still challenging due to non-perturbative nature of QCD at low energy. Considering this difficulty, many models and theoretical approaches have been adopted to calculate hadron properties. The quark model, where applicable, is considered to be a convenient tool. According to the quark model, a conventional meson is a bound state of a quark and an antiquark. The model predicts that a meson can have only certain specific values of $ J^{PC} $. The mesons with $ J^{PC} $ differing from quark-model values are called exotic mesons. In 1993 an exotic meson in the light quark sector having $ J^{PC} $ = 1^-+, was observed by the VES Collaboration [1]. After that, many exotic mesons have been observed. Theoretically, exotic mesons could be glueball, tetra quark or hybrid mesons. It is noted that $ J^{PC} $ value of these mesons can be allowed or forbidden by the quark model. Lattice QCD successfully describes these exotics [2−6]. Phenomenological models also provide good description of the properties of exotic mesons [7−14]. In open flavour mesons where quark and antiquark have different flavours, C parity no longer remains a good quantum number. In this case states are identified by their $ J^P $ values only. The states having the same $ J^P $ value are mixed. Indeed, all $ J^P $ states are mixed except 0⁺ and 0^-. Mixing is either the spin mixing or the S-D mixing. We will discuss it in detail in Sec. III. Incorporating mixing, where needed, we study the properties of hybrid as well as conventional mesons in open charm meson sector specifically charmed (D) mesons and charmed strange ($ D_s $) mesons.

Gluonic field plays a dominant role in binding quarks. In conventional mesons, the gluonic field is in the ground state while for hybrid mesons, it is in the excited state. We are particularly interested in studying the $ \Pi_u $ state, where gluonic field is in its first excited state. We use the leading Born-Oppenheimer approximation (LBO) for calculating the spectrum of hybrid mesons. In this approximation, a hybrid meson is treated as a diatomic molecule in which quarks and gluons are considered as nuclei and electron respectively. There are two steps involved in applying LBO approximation. In the first step the static potential energy of gluons is determined by treating quark antiquark spatially fixed, and in the second step the motion of quarks is restored through using this potential in Schrödinger wave equation. Parity of hybrid meson is $ \varepsilon(-1)^{L+\Lambda+1} $, where $ \Lambda $ is magnitude of the projection of total angular momentum of gluonic field onto the molecular axis. For $ \Pi_u $ potential, in which gluonic field is in its first excited state, $ \Lambda=1 $ and $ \varepsilon=\pm1 $ [2, 3].

Experimentally immense data is available in D and $ D_s $ meson domain. First two charmed mesons ($ D^0 $ and $ D^\pm $) were discovered in Mark I experiments in 1976 [15, 16]. Their $ J^P $ is 0^-. $ D^0 $ and $ D^\pm $ have masses $ 1864.83\pm0.05 $ MeV and $ 1869.58\pm0.09 $ MeV respectively. One year later, first charmed strange meson ($ D_s^{\pm} $) of $ J^P $ = 0^-, was observed in DASP Collaboration [17]. Mass of $ D_s^{\pm} $ is 1968.34 ± 0.07 MeV [18]. In the same experiment $ D_s^{*\pm} $ meson was also discovered having mass $ 2112.1\pm0.4 $ MeV and $ J^P=1^- $. Now we have data for more than twenty well recognized states. Information of their masses, $ J^P $ values and dozens of their decay modes are available in the Particle Data Group [18]. Side by side, a lot of work has been done to calculate their masses and other properties. By using Schrödinger-like wave equation in relativistic dynamics, spectrum and wave functions of D and $ D_s $ mesons are calculated in Ref. [19−22]. In Ref. [20], strong and radiative transitions are also reported. Ref. [23, 24] implemented Dirac formalism to calculate spectrum, radiative transitions, decay constant and leptonic decay width of $ D_s $ and D meson system respectively. In Ref. [25], spectra and wave functions of D and $ D_s $ mesons are obtained by using Bethe-Salpeter equation. Ref. [26] computed the spectra of heavy-light meson with the help of QCD motivated relativistic quark model. They investigated Regge trajectories too. By using the Dirac Hamiltonian, Ref. [27] computed the mass spectra, wave functions and hadronic transitions of heavy-light mesons. They also added leading order corrections in $ 1/m_{c,b} $. In Ref. [28], spectrum of D and $ D_s $ mesons is calculated by using Wilson twisted mass lattice QCD. Ref. [21, 22] discretized the relativistic wave equation using Cornell potential (Coulomb plus linear potential). After calculating the masses and wavefunctions of mesons by diagonalizing the resultant Hamiltonian matrix, the spin dependent part of the Hamiltonian is added perturbatively. Since states with different principal quantum numbers can also have same $ J^P $. Thus several principal quantum numbers collectively contribute in one mixed state (either spin mixed or S-D mixed). In Ref. [21, 22] the contribution of two to three principal quantum numbers is included to describe a mixed state. Another limitation of their work is that the perturbative effects of spin dependent potential are included in the masses but not in the wave function. This is understandable because first order perturbative correction to wave function involves a sum over all possible internal states which is extremely difficult to calculate. We adopted the same approach to solve the relativistic wave equation as did in Ref. [21, 22] with the improvements that address the limitations of approach of Ref. [21, 22]. Instead of including spin dependent part of the Hamiltonian perturbatively, we also include spin dependent terms in the Hamiltonian matrix. For this purpose we developed a system of coupled equation for mixed states. Since we are solving the coupled equations nonperturbatively, we are not restricted to include the contribution of only two to three principal quantum numbers to describe a mixed state. Two charmed strange mesons named $ D^*_{s0}(2317)^{\pm} $ and $ D_{s1}(2460)^{\pm} $ attract special attention as the observed values of their masses are much lower than the quark model predictions. Attempts have been made to describe them through alternative models [29−32]. A lot of work is done in literature to identify the nature of these mesons. In some literature [33, 34] these states are interpreted as tetraquarks, while in some places $ D^*_{s0}(2317)^{\pm} $ and $ D_{s1}(2460)^{\pm} $ are taken as $ DK $ and $ DK^{*} $ molecule states respectively [35, 36]. In Refs. [37, 38], these states are well described by including coupled-channel effects. Ref. [37] suggests that these states are the mixtures of bare $ c\bar{s} $ core and $ D^{(*)}K $ component. In Refs. [20−22, 39], these states have been studied as conventional mesons. The exact structure of these particles is still an open question in hadron physics.

In this work, we calculate masses, wave functions and radiative transitions of conventional as well as hybrid D and $ D_s $ mesons incorporating spin and S-D mixing effects on spectrum and wave function. Unlike previous works, we solve Schrödinger-type equation using full semi-relativistic Hamiltonian with spin-dependent part. This allows us to study both spin and S-D mixing without using perturbation theory.

Roadmap of our work is the following: In Sec. II, we describe our potential model for conventional and hybrid mesons. We use an extended version of the famous GI model. For the hybrid mesons, we add the potential model of gluonic excitation which we suggested in our previous work. In this paper we improve the parameter fitting of our proposed gluonic excited potential model by considering the latest lattice data [6]. In Sec. III, the phenomena of state mixing are examined. We distinguish two categories of mixed states. We also discuss the effects of spin dependent part of the potential model on the spectrum. In Sec. IV, we describe our relativistic wave equation. We explicitly describe how we calculate masses and wave functions of mesons using relativistic wave equation. State mixing effects in the Hamiltonian matrix are discussed too. Radiative transitions of charmed and charmed strange mesons are reviewed in Sec. V. In the last section we report our results and concluding remarks based on our calculations.

Phenomenological potential models are found very successful in describing various properties of heavy quark mesons especially mass [19−25, 40−43]. Among the suggested models, the GI model [19] is considered to be the most famous one. In this work, we have used it with some modifications.

Conventional D and $ D_s $ meson is a bound state of a heavy quark (Q = c) and a light antiquark ($ \bar{q} = \bar{u} $/$ \bar{d} $, $ \bar{s} $). Potential model for a conventional meson $ V_{Q\bar{q}}(r) $ is

where r is inter-quark distance. The first term of the potential model, called Coulomb term, is calculated by one gluon exchange diagram in perturbation theory. It determines the behaviour of potential at small distances. $ \alpha_s(r) $ is a strong running coupling constant of QCD. We use its following parameterization [19],

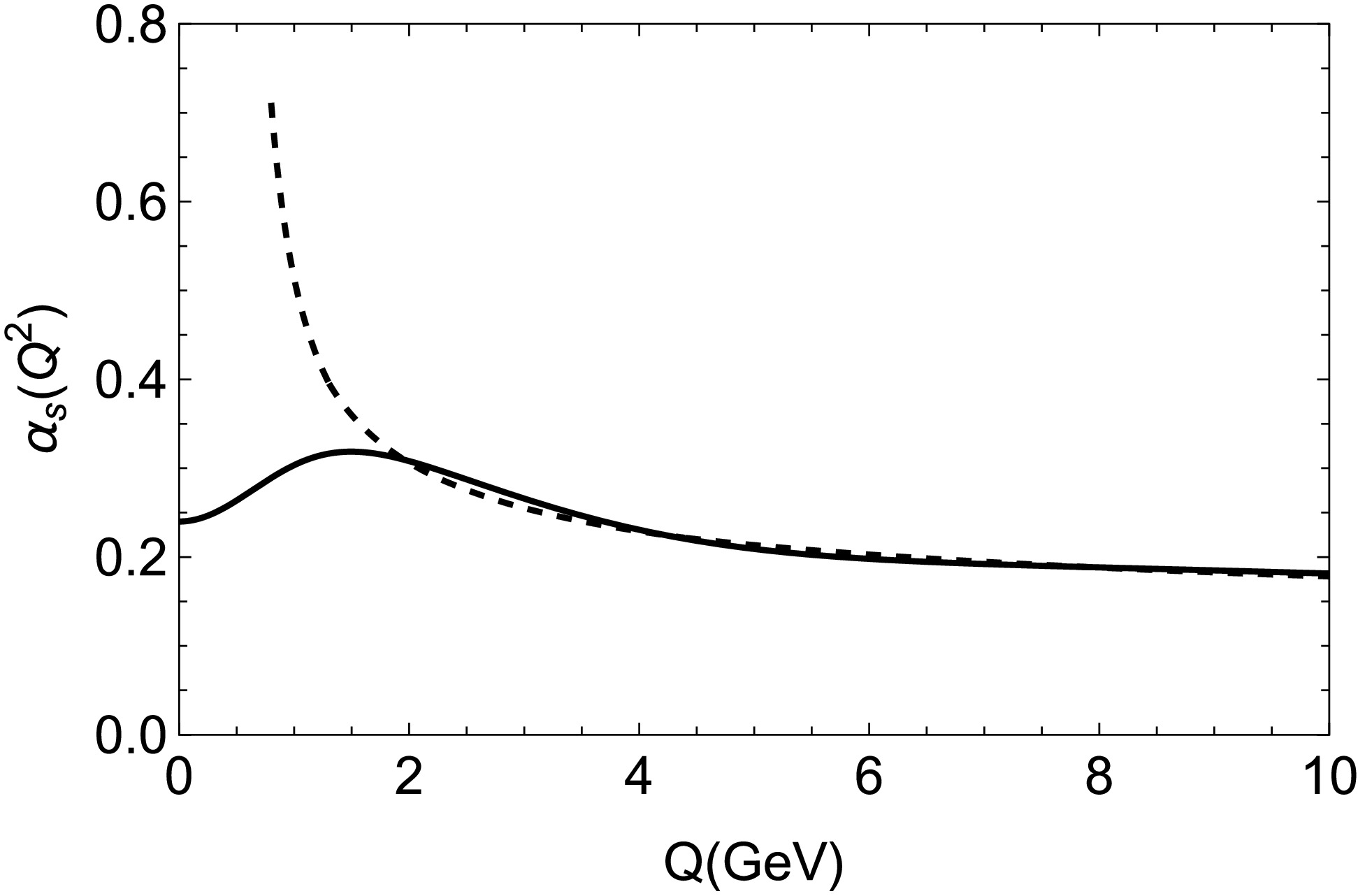
where $ \alpha_k^{\;,}s $ and $ \gamma_k^{\;,}s $ are free parameters. In this work we take $ \gamma_1 $ = $ \dfrac{1}{2} $, $ \gamma_2 $ = $ \dfrac{\sqrt{10}}{2}\; $ and $ \gamma_3 $ = $ \dfrac{\sqrt{1000}}{2}\; $ from Ref. [19]. With this choice of $ \gamma $'s, $ \alpha_2 $ and $ \alpha_3 $ control the shape of running coupling at small distance (large $ Q^2 $), where it is already fixed by pQCD. This allows us to fix $ \alpha_2=0.16 $ and $ \alpha_3=0.20 $ by fitting with 2-loop running coupling. Consequently, parameter $ \alpha_1 $ (or $ \alpha_s^c\equiv\alpha_1+\alpha_2+\alpha_3 $), which control the shape of running coupling in infrared region, is treated as a free parameter which is to be fixed by spectroscopy [19, 44]. Comparison of $ \alpha_s(Q^2) $ of the parametrized model with our fitted value of $ \alpha_s^c=0.24 $ and pQCD 2-loop result is shown in Fig. 2.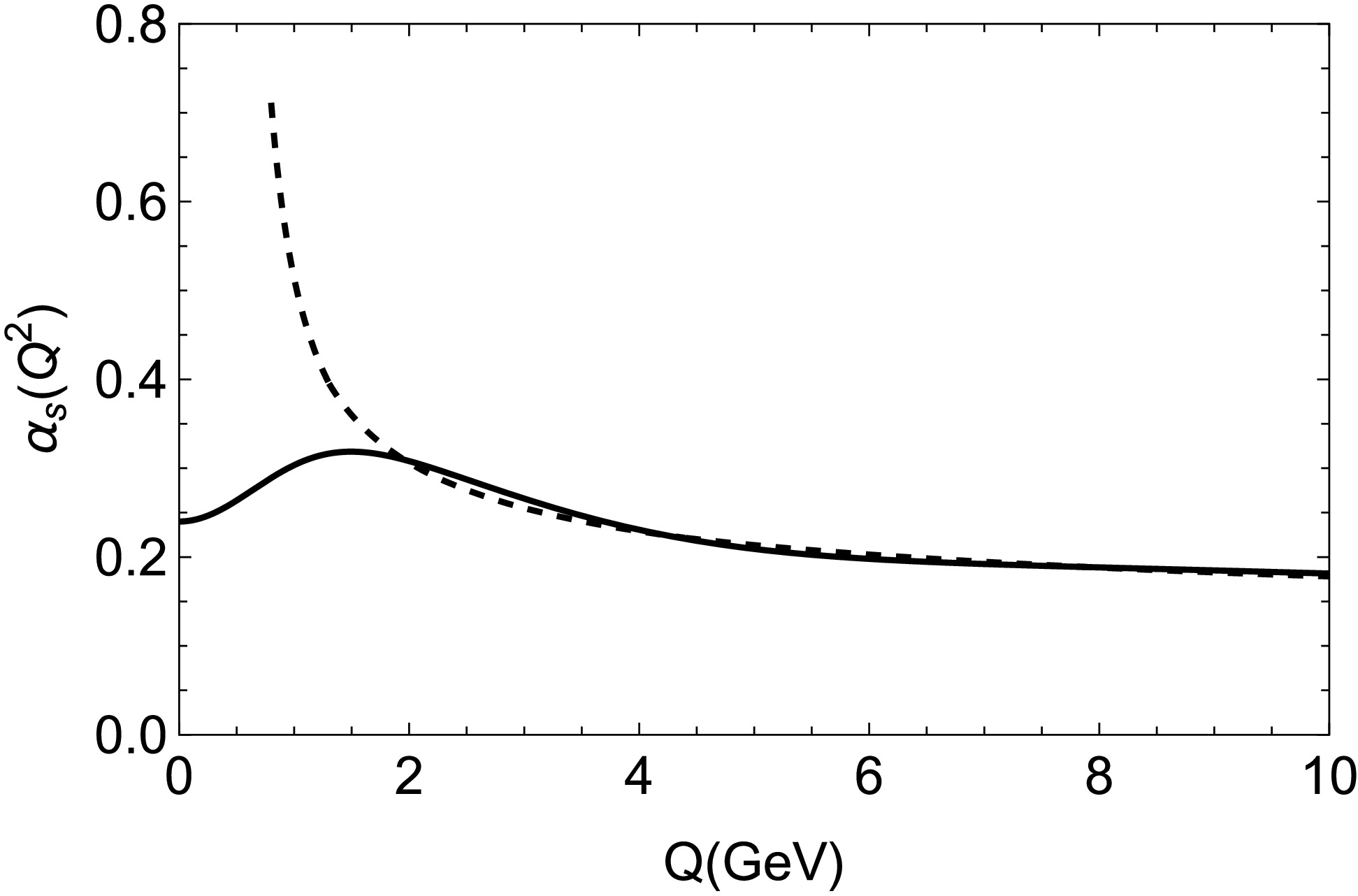

Figure 2.  Conventional charmed mesons spectrum.

Figure 1.  Strong running coupling constant in momentum space. Solid curve represent data taken from parametrize model and dotted curve represent data from QCD perturbative calculations up to two loop corrections.

The second term of the potential is the confinement term dominating at large distances and b is the string tension, determined by fitting the spectrum. The third term c of the potential model is also taken as a free parameter. The last part of the potential model, the spin dependent term $ V_{spin-dep}(r) $, is defined as following

where $ V_{hyp}(r) $ is spin-spin contact hyperfine interaction [43]. It is defined as

where $ \langle {{\bf{S}}_{\bf{Q}}\cdot{\bf{S}}_{\bar{{\bf{q}}}}} \rangle $ = $ \dfrac{S(S+1)}{2}-\dfrac{3}{4} $. In Ref. [19] parameter $ \sigma $ is

Numerical values of parameters $ \sigma_0 $ and $ s_0 $ are determined by fitting the spectrum. In Eq. (3), $ V_T(r) $ is tensor term defined as

where T is tensor operator,

The tensor operator has nonvanishing matrix elements only between $ L>0 $ and spin triplet states. Diagonal Hamiltonian matrix entries of tensor operator are [43]

To study S-D mixed states we also need following off diagonal matrix element of the tensor operator

where $ L^{'} = L $ + 2. In Eq. (3), $ V_{so}(r) $ is spin-orbit interaction term. It consists of two parts, such that

Here $ V_{sov}(r) $ is spin-orbit vector part

and $ V_{sos}(r) $ is spin-orbit scalar part of spin-orbit interaction term

For diagonal Hamiltonian matrices, $ \langle {{\bf{L}}\cdot{\bf{S}}_{\bf{Q}}} \rangle $ = $ \langle {{\bf{L}}\cdot{\bf{S}}_{\bar{\bf{q}}}} \rangle $ = $ \dfrac{\langle {{\bf{L}}\cdot{\bf{S}}} \rangle}{2} $, where $ \langle {{\bf{L}}\cdot{\bf{S}}} \rangle $ is

To study spin mixed states, we need following matrix element of the $ \langle {{\bf{L}}.{\bf{S}}_{\bf{Q}}} \rangle $ and $ \langle {{\bf{L}}.{\bf{S}}_{\bar{\bf{q}}}} \rangle $ operators:

The form of the spin dependent part of the potential model is extracted from the leading order perturbation theory in the non-relativistic approximation. However, this is not good approximation, especially for light quark in heavy light meson. Due to the presence of light quark in charmed and charmed strange meson, it is intimately important to incorporate relativistic effects. These effects modify the potential in two different ways [19]: First, quark antiquark separation (r) become smeared over a distance of order of inverse quark mass. By introducing the smearing function [19], smearing over $ 1/r^3 $ terms in spin dependent part of the potential model is incorporated. Smearing also eliminates the instability in the solution of the relativistic wave equation which occurs at short distances due to $ 1/r^3 $ term in spin dependent potential model, and makes the solution stable even at short distances. The second way to incorporate relativistic effects is to make potential model momentum dependent. Momentum dependence in a spin dependent term can effectively be incorporated by introducing multiple constant factors. This is done only for light quark, for heavy quark momenta drop out. Since momentum dependence modifies each spin interaction term in a different way, so we are required to take multiple constant ($ \epsilon_i $) interaction dependent, where i=1, 2, 3 and 4 is for hyperfine term, tensor term, spin orbit vector term and spin orbit scaler term respectively. We combine these constants into light mass and define interaction dependent mass as [21, 22], $ \tilde{m}_{qi} = \tilde{m}_{q}\epsilon_i $. Numerical values of these parameters are obtained by fitting the spectrum. It noted that since we are treating $ m_q $ as a free parameter, therefore, we must take of $ \epsilon_1=1 $.

In hybrid mesons, the gluonic field is in its excited state. In this case, quark antiquark potential can be written as following

where $ V_{Q\bar{q}}(r) $ is the potential for conventional mesons appearing in Eq. (1). $ V_g(r) $ is the potential energy difference between the ground and the first excited state of gluonic field. Our proposed model of $ V_g(r) $ is [45],

Numerical values of parameters A, B, $ \nu $ and $ \mu $ are determined by fitting the model with recent lattice data taken from Fig. 2 of Ref. [6]. The parameters are estimated by minimizing the $ \chi^{2} $ function using a global numerical optimization algorithm. Our improved fitted values of A, B, $ \nu $ and $ \mu $ are 3.0552 GeV, 0.9369 GeV, 0.3881 and $ -0.0025 $ respectively. There is no physical motivation for using above model for fitting gluon potential except that it provides a nice fit to the lattice data.

In D and $ D_s $ meson, charge conjugation is not a conserved quantum number, and states are described only by their $ J^P $ values. States having the same value of $ J^P $ can mix. Except 0^- and 0⁺ all possible values of $ J^P $ have mixed states. State mixing is categorized into two types, S-D mixing and spin mixing.

It is mixing of spin triplet states $ (^3L_{J} \leftrightarrow {}^3L'_{J}) $ having different values of orbital angular momentum (L, L') and same value of total angular momentum J=L+1=L'-1, so that L'=L+2. $ {}^3S_1 $ and $ {}^3D_1 $ states have the same values of $ J^P $, therefore, they are mixed. Similarly $ {}^3P_2 \leftrightarrow {}^3F_2 $, $ {}^3D_3 \leftrightarrow {}^3G_3 $, $ {}^3F_4 \leftrightarrow {}^3H_4 $, $ {}^3G_5 \leftrightarrow {}^3I_5 $ and so on, all are referred as S-D mixed states. S-D mixing occurs due to the tensor operator in the potential model, as this operator does not conserve orbital angular momentum.

The spin-orbit interaction term in the potential model does not conserve total spin of quark and antiquark. It causes mixing between spin triplet and spin singlet states $ ({}^1L_{L} \leftrightarrow {}^3L_{L}) $, for which $ J=L $. In this case, possible combinations of mixed states are $ {}^1P_1 \leftrightarrow {}^3P_1 $, $ {}^1D_2 \leftrightarrow {}^3D_2 $, $ {}^1F_3 \leftrightarrow {}^3F_3 $, $ {}^1G_4 \leftrightarrow {}^3G_4 $, $ {}^1H_5 \leftrightarrow {}^3H_5 $ and so on.

In studying the charmed and charmed strange mesons relativistic effects should be incorporated due to the presence of light quark. We use the relativistic wave equation to study the bound states of charmed and charmed strange mesons [19]. The Schrödinger-type equation in relativistic dynamics is

where $ \psi({\bf{r}}) $ and E are wave function and energy of meson respectively. H is effective Hamiltonian of meson:

where $ {\bf{p}} $ is center-of-mass momentum of quark such that $ {\bf{p}} = {\bf{p}}_Q = -{\bf{p}}_{\bar{q}} $. $ {\bf{p}}_Q $ and $ {\bf{p}}_{\bar{q}} $ are momenta of quark and antiquark. $ m_Q $ and $ m_{\bar{q}} $ are mass of heavy quark (i.e., charm quark) and light antiquark respectively. $ V({\bf{r}}) $ is the effective potential of bound state of quark antiquark system, discussed in Sec. II. We assumed our potential is central potential, i.e., $ V({\bf{r}})\equiv V(r) $. For conventional mesons $ V(r) $ = $ V_{Q\bar{q}}(r) $ (appearing in Eq. (1)) and for hybrid mesons $ V(r) $ = $ V_{hybrid}(r) $ (appearing in Eq. (15)).

A conventional meson is a bound state of a quark and an antiquark. When the distance between them is large enough, the wave function vanishes. We assume the distance at which the wave function vanishes is R. In order to solve Eq. (17), we find matrix representation of relativistic Hamiltonian H using spherical Bessel function as basis. The diagonalization of the Hamiltonian matrix yields $ \psi({\bf{r}}) $ and E. For unmixed state (i.e., 0^-, 0⁺) radial wave function is

where $ c_i^{\;,}s $ are expansion coefficients, $ j_l $ is the spherical Bessel function and $ a_{i} $ is $ i^{th} $ root of the spherical Bessel function such that $ j_{l}(a_{i}) = 0 $. In this basis the Eq. (17) reduces to Ref. [22]

where $ N_{li}^{2} $ is radial integral of the spherical Bessel function give by

In Eq. (20), the Hamiltonian matrix has the order N × N. By diagonalising the Hamiltonian matrix, we get N eigenvalues and eigenfunctions. Each eigenvalue and eigenfunction is associated with a particular value of the radial quantum number. For each eigen vector the resultant radial wave function is obtained from Eq. (19). In case of mixed states, $ \psi({\bf{r}}) $ is combination of two states. For spin mixed states, $ \psi({\bf{r}}) $ is

where $ a_i $ is zeroth roots of the spherical Bessel function corresponding to L orbital angular momentum. $ c_i^{(1)} $ and $ c_i^{(2)} $ are expansion coefficients associated to $ \lvert{{}^1L_L}\rangle_{\hat{r}} $ state and $ \lvert{{}^3L_L}\rangle_{\hat{r}} $ state respectively, which are defined as:

Where $ C_{m_s} $ is Clebsch-Gorden coefficient. In mixed states the Eq. (17) is reduced to two coupled equations. For spin mixed states the equations are:

In this case the Hamiltonian matrix H can be expressed through four N × N matrices $ H_{11} $, $ H_{12} $, $ H_{21} $, and $ H_{22} $ as following

$ H_{11} $ and $ H_{12} $ are read off from Eq. (25), and $ H_{21} $ and $ H_{22} $ from Eq. (26). The kinetic energy of mesons contributes only to diagonal Hamiltonian matrices ($ H_{11}, H_{22} $). $ \langle {V} \rangle_{11} $, $ \langle {V} \rangle_{12} $, $ \langle {V} \rangle_{21} $ and $ \langle {V} \rangle_{22} $ are potential energy matrix elements of $ H_{11} $, $ H_{12} $, $ H_{21} $ and $ H_{22} $ respectively. The definition of the potential energy matrix elements is mentioned in Table 1. It is noted that mixing of the states occurs due to off-diagonal Hamiltonian matrices ($ H_{12}, H_{21} $). For spin mixed state, contribution to $ \langle {V} \rangle_{12} $ and $ \langle {V} \rangle_{21} $ come through spin-orbit terms of the potential energy.

Potential energy matrix elements	Spin mixed state	S-D mixed state
$ \langle {V} \rangle_{11} $	$ \langle {{}^1L_L} | {V} | {{}^1L_L}\rangle $	$ \langle {{}^3L_J} | {V} | {{}^3L_J}\rangle $
$ \langle {V} \rangle_{12} $	$ \langle {{}^1L_L} | {V_{so}} | {{}^3L_L}\rangle $	$ \langle {{}^3L_J} | {V_{T}} | {{}^3L'_J}\rangle $
$ \langle {V} \rangle_{21} $	$ \langle {{}^3L_L} | {V_{so}} | {{}^1L_L}\rangle $	$ \langle {{}^3L'_J} | {V_{T}} | {{}^3L_J}\rangle $
$ \langle {V} \rangle_{22} $	$ \langle {{}^3L_L} | {V} | {{}^3L_L}\rangle $	$ \langle {{}^3L'_J} | {V} | {{}^3L'_J}\rangle $

Table 1.  The definition of potential energy matrix elements for spin and S-D mixed states.

In S-D mixed states, $ \psi({\bf{r}}) $ is

where $ a_i $ and $ a_i' $ are zeroth roots of the spherical Bessel function corresponding to L and L' orbital angular momentum respectively. In S-D mixed states, $ c_i^{(1)} $ and $ c_i^{(2)} $ are expansion coefficients associated to $ \lvert{{}^3L_J}\rangle_{\hat{r}} $ state and $ \lvert{{}^3L'_J}\rangle_{\hat{r}} $ state respectively, which are defined as:

For S-D mixed states, we have following set of equations:

Once again these equations can be used to define Hamiltonian matrix H in terms of four N × N matrices $ H_{11} $, $ H_{12} $, $ H_{21} $ and $ H_{22} $. It is noted that for S-D mixed states, contribution to $ \langle {V} \rangle_{12} $ and $ \langle {V} \rangle_{21} $ comes through tensor operator of the potential.

Our numerical results also depend upon the order of the matrix N. We observe that for a large value of N, dependency is negligible. In our calculations we take N = 50 and R=25 GeV^-1. Numerical values of quark masses and other parameters of the conventional potential model are extracted from fitting the spectrum to experimentally known states. We used 14 experimentally well-established states for fitting. The states that we used for fitting parameter values are mentioned in Table 2. For fitting the spectrum, we used the differential evolution method [46]. Differential evolution (DE) is a stochastic global optimization algorithm. In consecutive independent trials, DE successfully converged to the global minimum of the function. 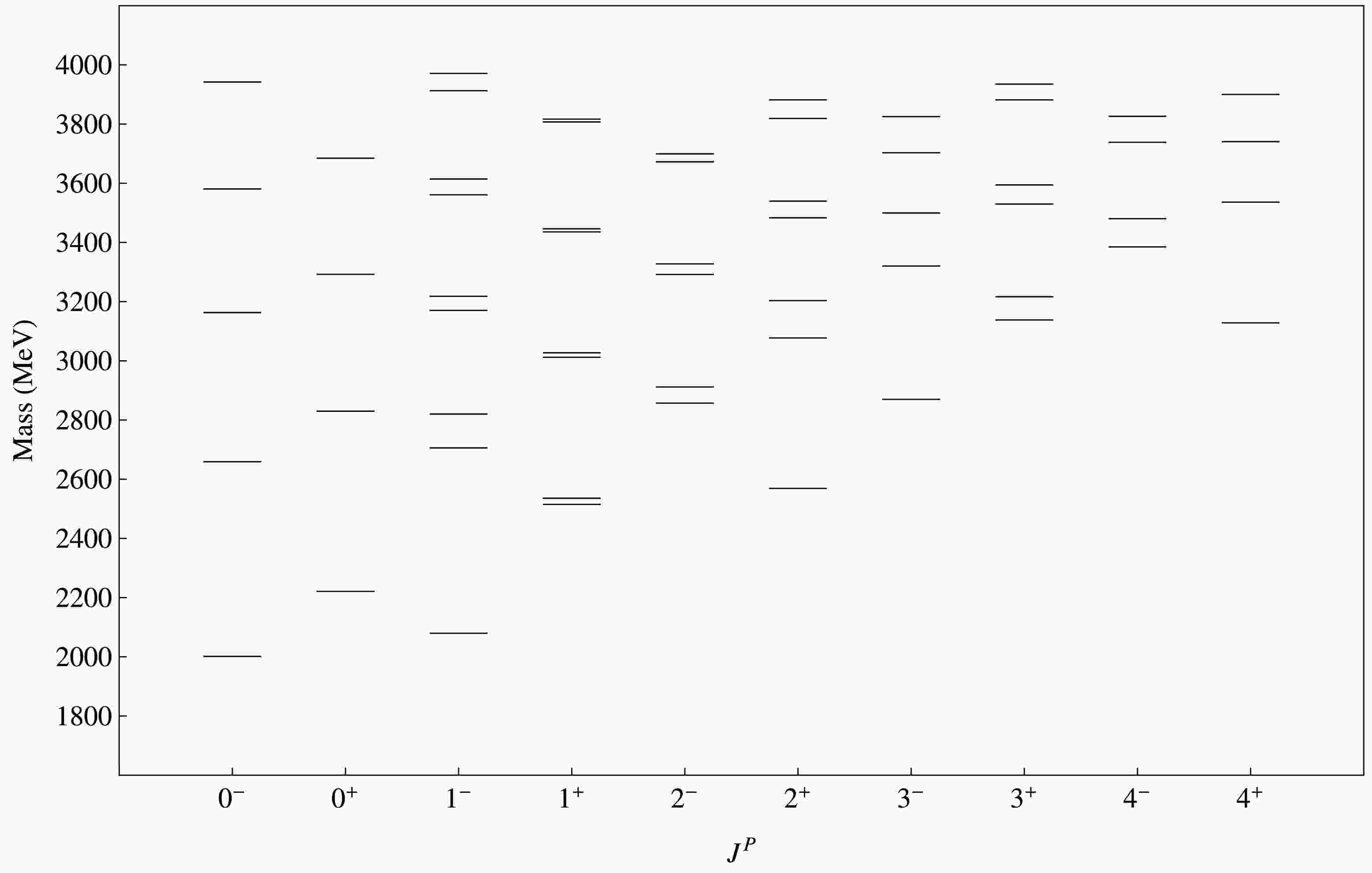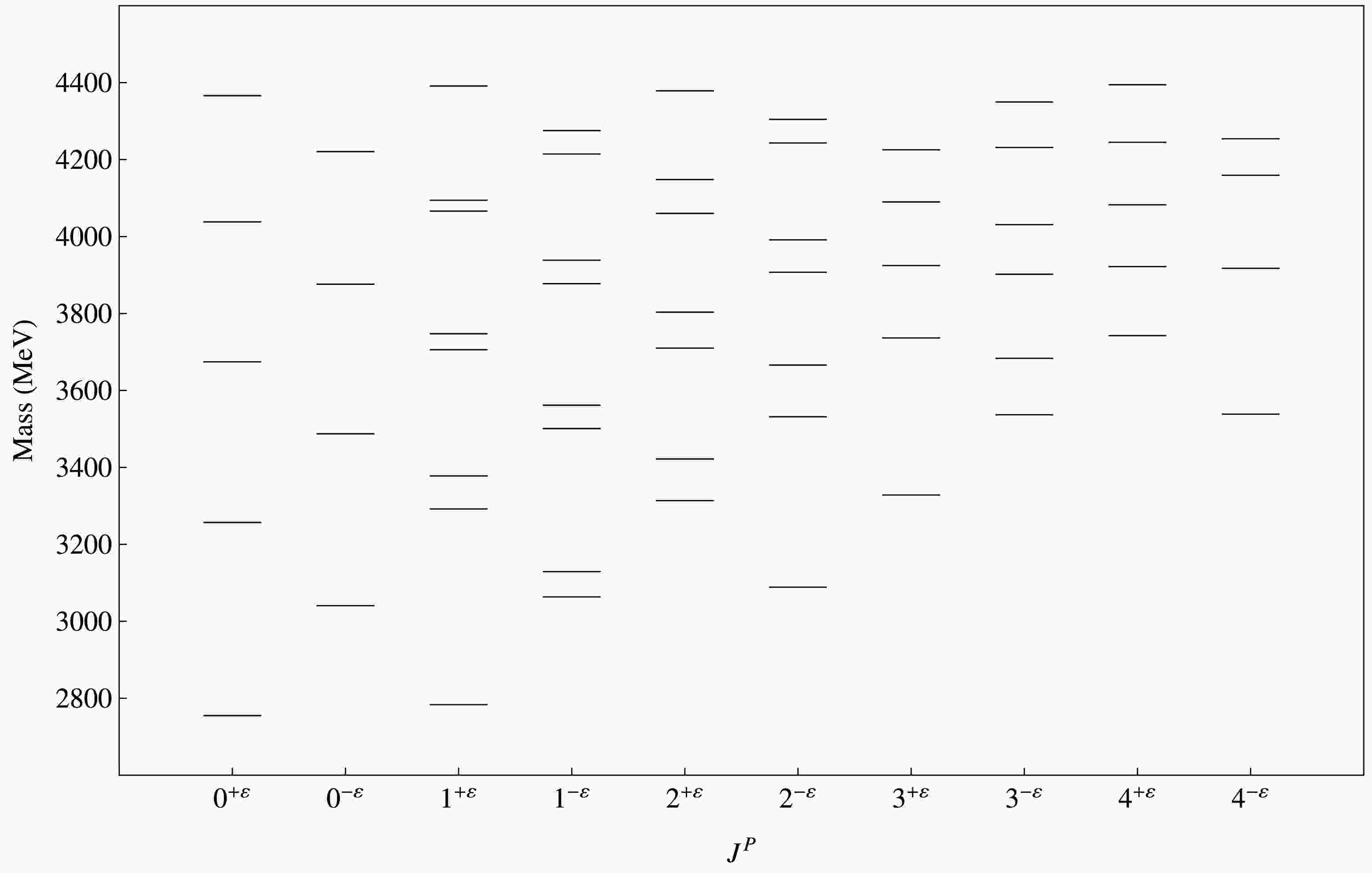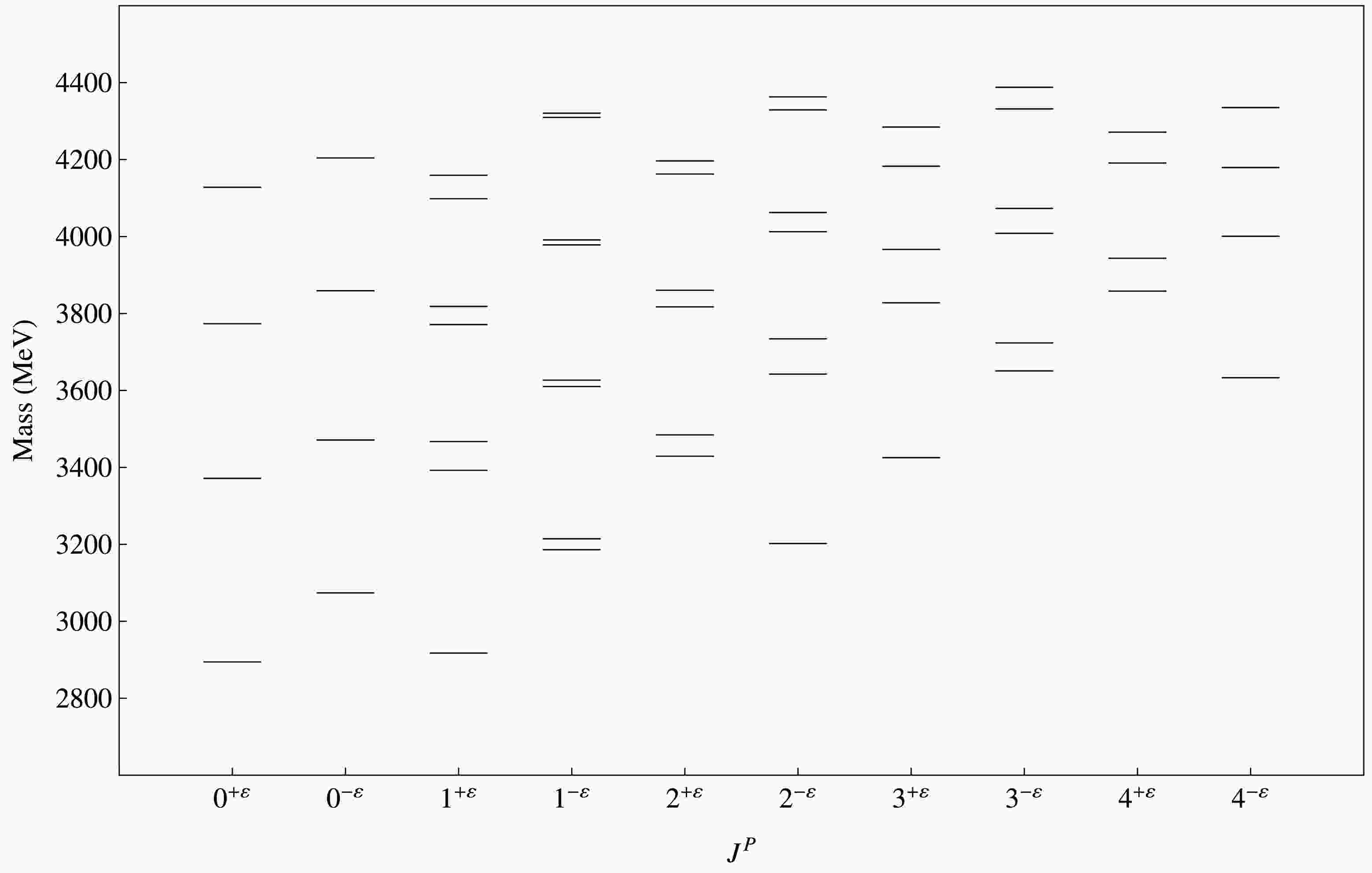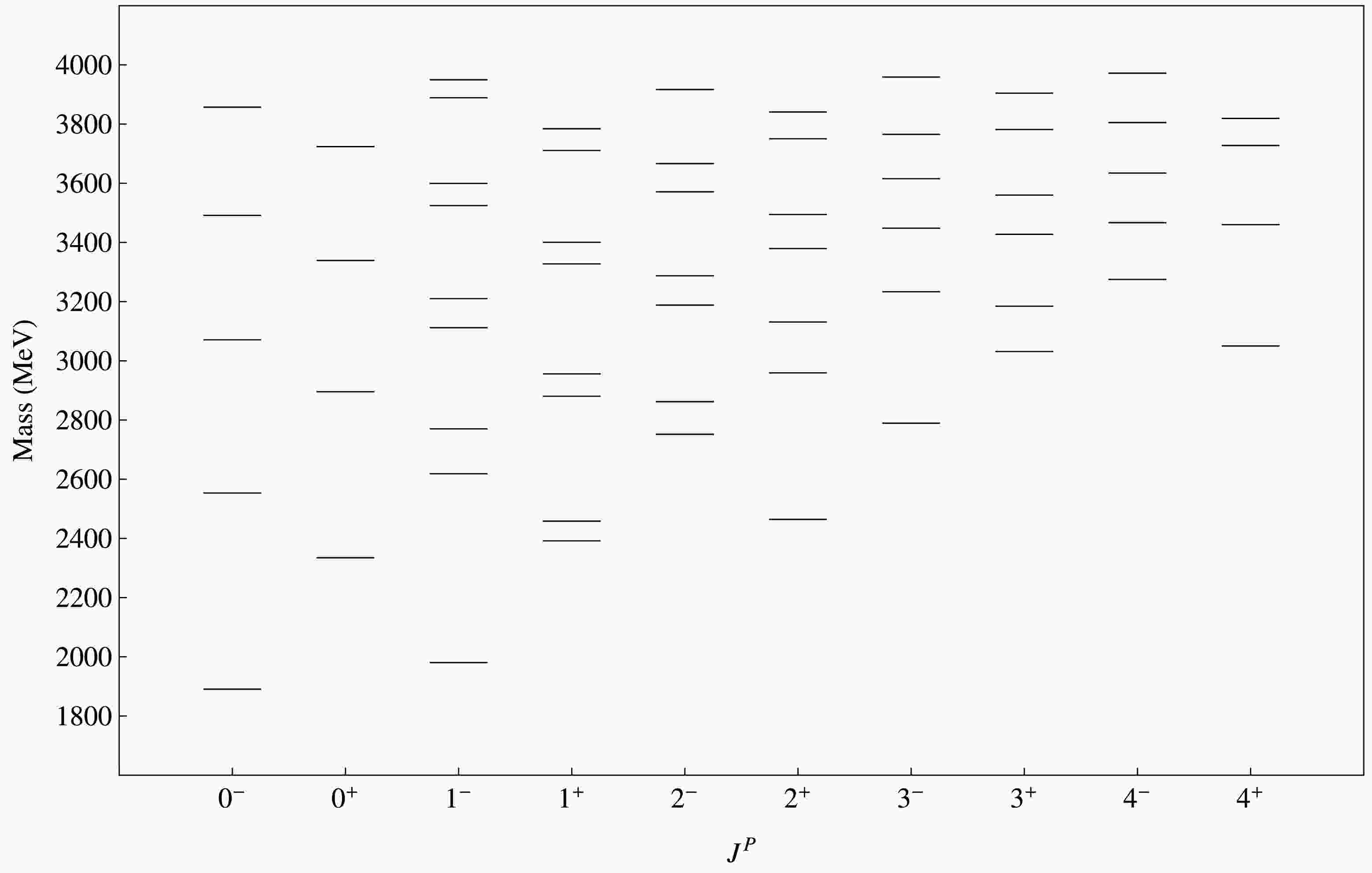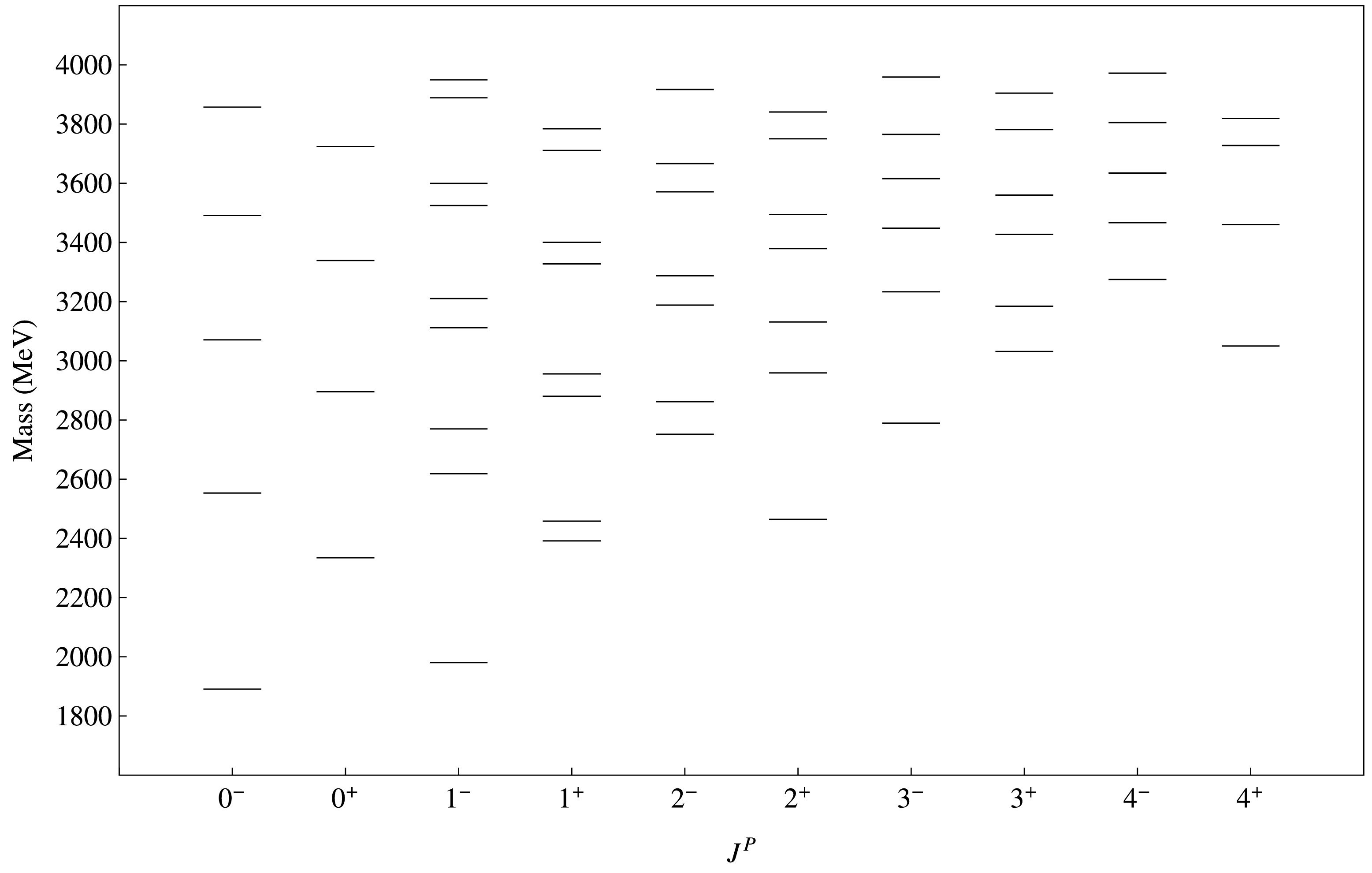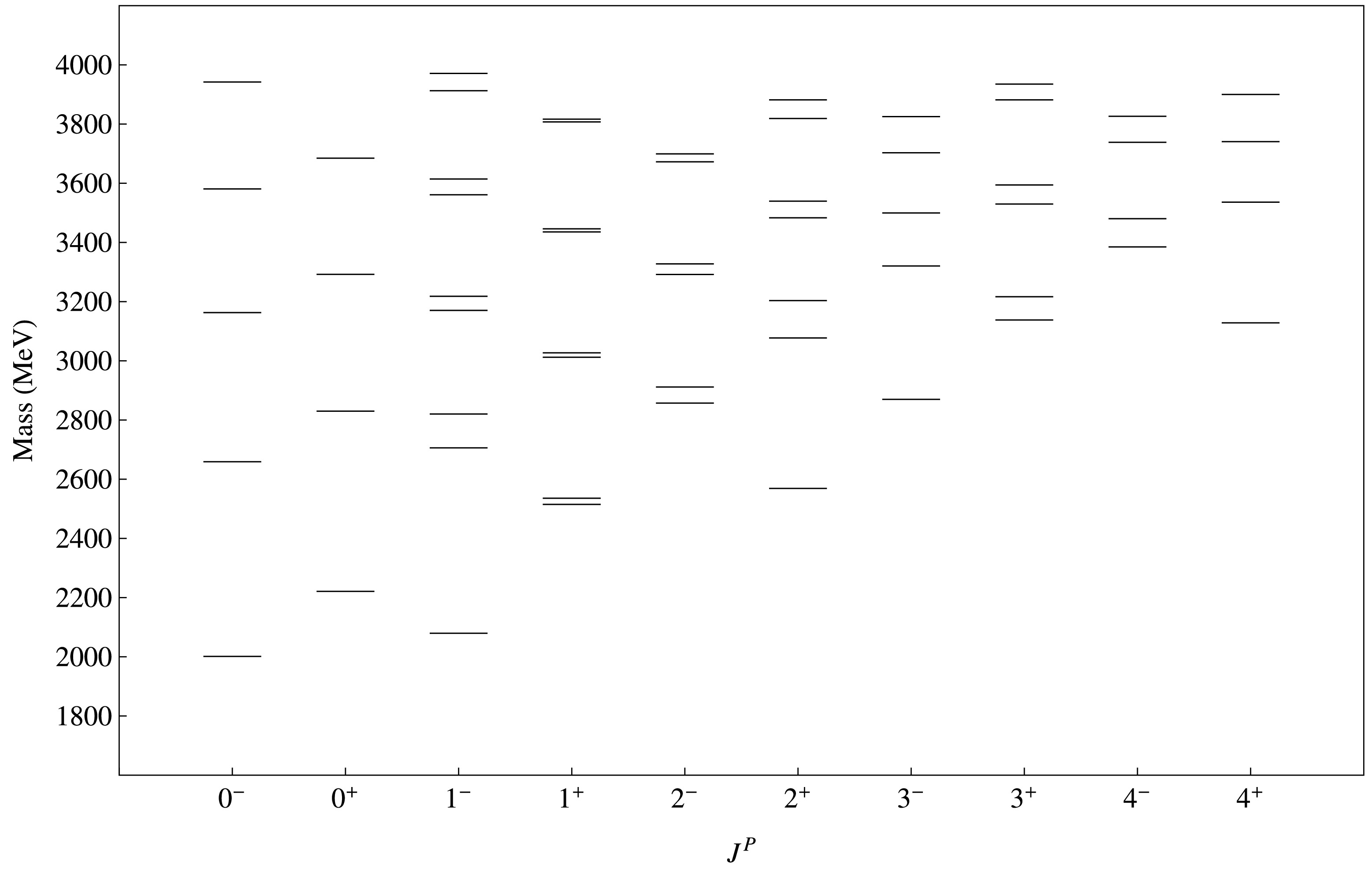By minimizing the $ \chi^{2} $ function using the DE algorithm, we find out the best fit values of parameters. Our fitted values of parameters are: $ m_{c} $ = 1.47 ± 0.01 GeV, $ m_{u/d} $ = 0.020 ± 0.001 GeV, $ \tilde{m}_{u/d} $ = 0.430 ± 0.001 GeV, $ m_{s} $ = 0.336 ± 0.007 GeV, $ \tilde{m}_{s} $ = 0.5967 ± 0.00046 GeV, $ \alpha_s^{c} $ = 0.240 ± 0.025, b = 0.211 $ \pm 0.002 \ {\rm{GeV}}^2 $, c = -0.4321 ± 0.0041 GeV, $ \sigma_0 $ = 0.5221 ± 0.013 GeV, $ s_0 $ = 0.91 ± 0.15, $ \epsilon_2 $ = 1.5 ± 0.59, $ \epsilon_3 $ = 1.5 ± 0.1, $ \epsilon_4 $ = 1.31 ± 0.14. Our predicted spectra of conventional charmed and charmed strange mesons is given in Fig. 2 and Fig. 3. In Fig. 4 and Fig. 5, we present our calculated spectrum of hybrid charmed mesons and hybrid charmed strange mesons. Comparison of our calculated spectrum of conventional D and $ D_s $ mesons with other works is given in Tables 2 and 3.

Meson	$ J^P $	Our Mass Results	GI Model[20]	[22]	[39]	PDG[18]
Charmed strange mesons:
$ D_s^\pm $	0-	2001.36	1979	1963	1964	1968.35 ± 0.07
$ D_s^{*\pm} $	1-	2079.63	2129	2103	2102	2112.2 ± 0.4
$ D_{s1}(2536)^\pm $	1+	2535.92	2556	2533	2510	2535.11 ± 0.06
$ D_{s2}^*(2573) $	2+	2569.18	2592	2573	2548	2569.1 ± 0.8
$ D_{s1}^*(2700)^\pm $	1-	2706.22	2732	2709	2680	2714 ± 5
$ D_{s1}^*(2860)^\pm $	1-	2820.59	2899	2803	2771	2859 ± 27 [48, 49]
$ D_{s3}^*(2860)^\pm $	3-	2869.84	2917	2853	2816	2860 ± 7
Charmed mesons:
$ D^0 $	0-	1890.66	1877	1867		1864.83 ± 0.05
$ D^*(2007)^0 $	1-	1980.63	2041	2004		2006.85 ± 0.05
$ D_0^*(2300)^{0} $	0+	2334.64	2399	2302		2343 ± 10
$ D_1(2430)^{0} $	1+	2458.56	2456	2415		2412 ± 9
$ D_1(2420)^0 $	1+	2391.87	2467	2429		2422.1 ± 0.6
$ D_2^*(2460)^{0} $	2+	2464.39	2502	2468		$ 2461.1_{-0.8}^{+0.7} $
$ D_3^*(2750) $	3-	2789.59	2833	2754		2763.1 ± 3.2

Table 2.  Comparison of our calculated spectrum (in MeV) of conventional D and $ D_s $ mesons with other works.

Figure 3.  Conventional charmed strange mesons spectrum.

Figure 4.  Hybrid charmed mesons spectrum.

Figure 5.  Hybrid charmed strange mesons spectrum.

Meson	$ J^P $	Our Results	GI Model[20]	[22]	[39]	Exp. Data
Charmed strange mesons:
$ D_{s0}^*(2590)^+ $	0-	2659	2673	2582	2557	2591±9 [47]
$ D_{sJ}^*(3040)^\pm $	1+, 2+	3026.94, 3077.36				$ 3044_{-9}^{+31} $ [49]
Charmed mesons:
$ D_0(2550)^0 $	0-	2553.34	2581	2483		2549 ± 19 [50, 51]
$ D_1^*(2600)^0 $	1-	2618.66	2643	2613		2627 ± 10 [51−53]
$ D_2(2740)^0 $	2-	2752.03	2816	2737		2747 ± 6 [53, 54]
$ D_1^*(2760)^0 $	1-	2770.32	2817	2785		2781 ± 22 [55]
$ D(3000)^0 $	3+, 3-, 4-	3184.76, 3233.29, 3275.27				3214 ± 60 [52, 54]

Table 3.  Comparison of our calculated spectrum (in MeV) of conventional D and $ D_s $ mesons with others works and experimental data.

Radiative transitions play a vital role in the identification of meson states. E1 radiative partial width between initial and final mesons in non-relativistic quark model is [56]

where $ \alpha $ = $ \dfrac{1}{137}\; $ is electromagnetic fine structure constant, $ \omega $ is photon energy, $ \lvert{n^{2S+1}L_J}\rangle $ is initial meson state, $ \lvert{n'^{2S'+1}L'_{J'}}\rangle $ is final meson state, $ E_f $ is the energy of final meson state and $ M_i $ is mass of initial meson. $ C_{fi} $ is angular momentum matrix element defined as

where $ \begin{Bmatrix}.&.&.\\.&.&. \end{Bmatrix}\; $ is a 6-j symbol. In Eq. (33), $ \langle {e_Q} \rangle $ is

Here $ m_c $ and $ m_{q} $ are constituent mass of charm quark and constituent mass of light (q) quark respectively. For D meson, q = u/d whereas for $ D_s $ meson q = s. $ e_{\overline{c}}$ = -2/3 is electric charge of anti-charm quark in units of $ |e| $. $ e_u $ = +2/3, $ e_d$ = -1/3 and $ e_s$ = -1/3 are electric charge of up, down and strange quark respectively in units of $ |e| $.

Matrix elements $ \langle {n'^{2S'+1}L'_{J'}} | {r} | {n^{2S+1}L_J}\rangle $ are calculated using the relativistic quark model wave functions obtained in Sec. IV. In E1 transitions, relativistic corrections are implicitly included due to the contribution of spin dependent interactions in the Hamiltonian.

M1 radiative partial width for S-wave meson bound state is [20]

where $ j_0 $ is the spherical Bessel function. Electromagnetic transitions are sensitive to the internal structure of mesons, particularly in mixed states. A mixed state is a combination of two states, only that state(s) contributes to E1 and M1 transitions, which fulfill the selection rules of these transitions. For calculating decay width of M1 transitions of conventional S-wave meson bound state, selection rules of M1 transitions and Eq. (28) implies that in this case only $ 1^{-}\leftrightarrow 0^{-} $ transition allowed further only $ ^{3}S_{1} $ component of 1^-1 state contributes to decay width. To calculate decay width of E1 transitions of conventional meson bound states ($ L<3 $), selection rules of E1 transitions and Eqs. (22, 28) indicate that only four transitions contribute, i.e., $ 1^{+}\leftrightarrow 0^{-} $, $ 1^{-}\leftrightarrow 0^{+} $, $ 1^{-}\leftrightarrow 1^{+} $ and $ 2^{-}\leftrightarrow 1^{+} $. In $ 1^{+}\leftrightarrow 0^{-} $ transition, only $ {}^{1}P_1 $ component of 1⁺ state fulfil selection rule of E1 transitions. In $ 1^{-}\leftrightarrow 0^{+} $ transition both components of 1^-1 state participate. In $ 1^{-}\leftrightarrow 1^{+} $, both components of the initial and final states take part except the $ {}^{1}P_{1} $ component of 1⁺ state. Finally, in $ 2^{-}\leftrightarrow 1^{+} $ transition both components of the initial and final states contribute.

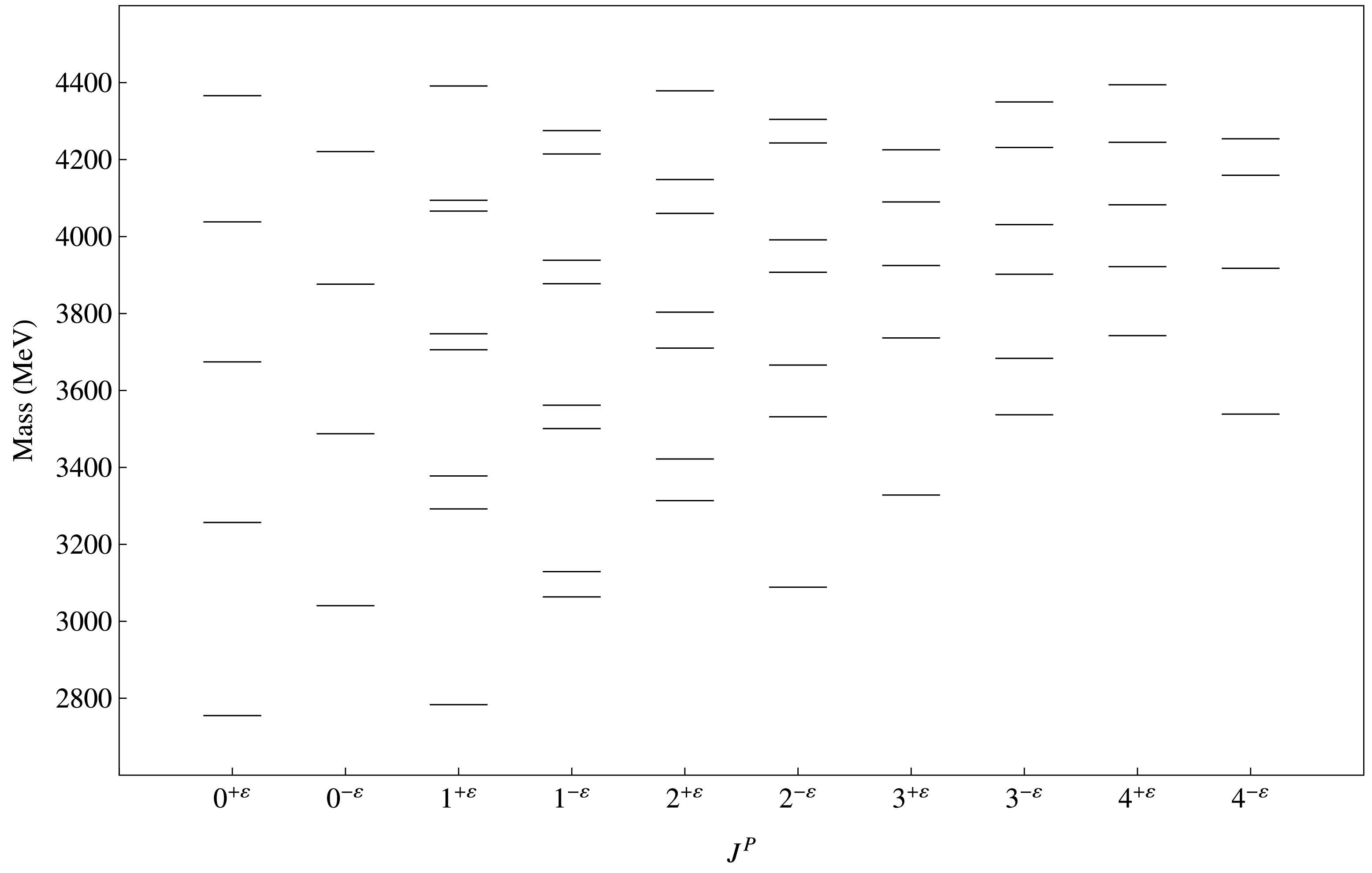
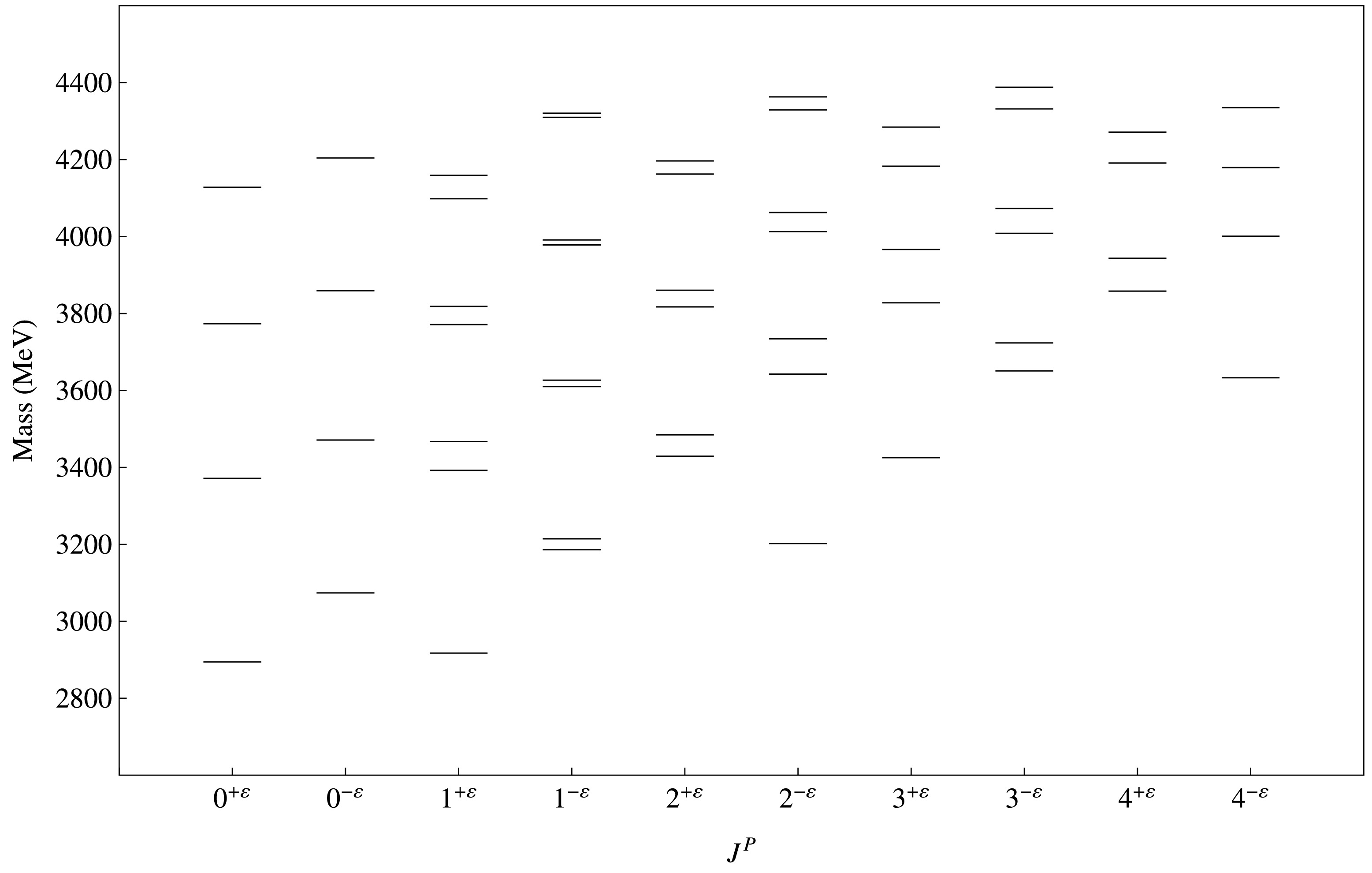
In this work we present a rich spectrum of conventional and hybrid charmed and charmed strange mesons. States having the same value of $ J^P $ are mixed. We have incorporated both spin and S-D mixing through the off-diagonal matrix elements of the Hamiltonian. In Fig. 2 to 5, state mixing phenomena are explicitly visualized by the spectrum pattern. Ref. [20] include spin mixing effects although they ignore S-D mixing in their calculations. In Ref. [22], spin dependent Hamiltonian part is added perturbatively after solving the eigenequation. In this work, we use the complete Hamiltonian (including spin dependent part) in the eigenequation. This allows us to study both spin and S-D mixing effects without resorting to perturbation theory.

Our calculated spectrum of conventional D and $ D_s $ mesons is reported in Table 4 with increasing order of value of mass. n is number of eigenvalues associated with specific value of $ J^P $. For unmixed states, it is visible that 0⁺ ($ {}^3P_0 $) states have larger mass as compared to 0^- ($ {}^1S_0 $) states due to spin and orbital excitation. In the case of S-D mixed states, higher orbital excited states (e.g., 2⁺, $ {}^3P_2 \leftrightarrow {}^3F_2 $) have large mass compared to lower one (e.g., 1^-, $ {}^3S_1 \leftrightarrow {}^3D_1 $). Same is observed for spin singlet and spin triplet mixed states. States with higher orbital excitations (e.g., 2^-, $ {}^1D_2 \leftrightarrow {}^3D_2 $) have large mass in comparison to lower orbital excited states (e.g., 1⁺, $ {}^1P_1 \leftrightarrow {}^3P_1 $). We also compare our calculated spectrum of conventional D and $ D_s $ mesons with experimental results and other works in Tables 2 and 3. Our results have good agreement with other works as well as with experimental data. We used meson states in Table 2 for fitting the parameters value. Table 3 shows the efficiency of our results. In Table 3, we identify $ D_{sJ}^*(3040)^\pm $ and $ D(3000)^0 $ as 1⁺ and 3^- state. We tentatively identify $ D_{sJ}^*(3040)^\pm $ and $ D(3000)^0 $ as 2⁺ and 3⁺ state. Possibility of $ D(3000)^0 $ could be 4^- state. Since the nature of $ D^*_{s0}(2317)^{\pm} $ and $ D_{s1}(2460)^{\pm} $ states are not clear as discussed in Sec. I, we do not include these states in the fitting procedure. Moreover, we do not find any good match to these states in conventional as well as hybrid mass spectrum. This result is consistent with hitherto exotic nature of $ D_{s0}^*(2317) $ and $ D_{s1}(2460) $ mesons.

$ J^P $	n	D Meson	$ D_s $ Meson
$0^-$	1	1890.66	2001.36
	2	2553.34	2659.00
	3	3070.94	3162.90
	4	3491.35	3581.01
$0^+$	1	2334.64	2221.26
	2	2895.60	2830.25
	3	3339.03	3292.43
	4	3723.79	3684.70
$1^-$	1	1980.63	2079.63
	2	2618.66	2706.22
	3	2770.32	2820.59
	4	3111.91	3170.35
	5	3210.21	3218.06
	6	3524.85	3561.34
	7	3599.51	3614.62
	8	3888.75	3912.91
$1^+$	1	2391.87	2514.83
	2	2458.56	2535.92
	3	2880.36	3012.05
	4	2955.80	3026.94
	5	3327.55	3435.81
	6	3400.51	3446.24
	7	3710.89	3807.50
	8	3784.40	3816.56
$2^-$	1	2752.03	2857.35
	2	2862.13	2911.54
	3	3188.32	3292.05
	4	3287.53	3327.83
	5	3571.28	3672.60
	6	3666.60	3699.38
	7	3916.99	4014.94
	8	4008.79	4037.37
$2^+$	1	2464.39	2569.18
	2	2959.26	3077.36
	3	3131.47	3203.58
	4	3379.56	3483.48
	5	3494.62	3539.61
	6	3750.46	3819.04
	7	3840.78	3881.70
	8	4086.20	4130.11
$3^-$	1	2789.59	2869.84
	2	3233.29	3320.75
	3	3448.43	3499.65
	4	3615.56	3702.96
	5	3765.23	3825.09
	6	3959.01	4053.21
	7	4075.86	4114.68
	8	4274.05	4363.43
$3^+$	1	3031.60	3138.04
	2	3184.76	3216.67
	3	3427.33	3529.81
	4	3560.11	3594.36
	5	3781.48	3881.76
	6	3904.52	3935.16
	7	4105.19	4203.53
	8	4222.14	4248.79
$4^-$	1	3275.27	3385.16
	2	3466.85	3480.50
	3	3634.65	3738.40
	4	3804.95	3826.51
	5	3971.98	4073.56
	6	4125.85	4149.44
	7	4278.55	4376.37
	8	4424.86	4445.97
$4^+$	1	3050.12	3128.49
	2	3460.14	3536.36
	3	3727.59	3740.77
	4	3819.37	3900.19
	5	4021.00	4050.96
	6	4144.89	4230.53
	7	4303.97	4357.16
	8	4445.31	4534.66

Table 4.  Our calculated conventional D and $ D_s $ meson masses (in MeV) for $ J^P = 0^- $, 0⁺, 1^-, 1⁺, 2^-, 2⁺, 3^-, 3⁺, 4^- and 4⁺.

In Table 5, we report our computed masses of hybrid D and $ D_s $ mesons. For hybrid candidates, parity condition is different to that for conventional mesons; this is due to the excited gluonic field contribution as discussed in Sec. I. It is observed that hybrid states have greater masses comparative to that of conventional ones. This happen due to gluonic excitations in $ \Pi_u $ states. In Table 6 and Table 7 we have reported our calculated E1 transitions of conventional to conventional and hybrid to hybrid mesons respectively. We also present M1 transitions of conventional to conventional and hybrid to hybrid mesons in Table 8 and Table9 respectively. We observed that the decay width of $ D^0(c\bar{u}) $ states is large as compared to $ D^\pm(c\bar{d}) $ states except few states in M1 transitions. In Table 10, we compare our calculated radiative decay width of conventional mesons with other works and experimental results. Our results are consistent with other works except for a few states of $ D^0 $ mesons. We expect our predicted results will be useful in detection of new charmed and charmed strange mesons.

$ J^P $	n	Hybrid D Meson	Hybrid $ D_s $ Meson
$0^{+\varepsilon}$	1	2755.01	2894.34
	2	3256.86	3371.39
	3	3674.27	3773.52
	4	4038.16	4128.21
$0^{-\varepsilon}$	1	3040.45	3073.69
	2	3487.44	3471.19
	3	3876.36	3858.93
	4	4220.98	4204.41
$1^{+\varepsilon}$	1	2783.31	2917.32
	2	3291.98	3392.35
	3	3377.88	3467.12
	4	3705.86	3771.09
	5	3747.28	3818.40
	6	4066.32	4098.38
	7	4094.33	4159.38
	8	4391.27	4406.70
$1^{-\varepsilon}$	1	3063.57	3186.10
	2	3129.03	3214.35
	3	3501.03	3610.14
	4	3561.83	3626.80
	5	3877.47	3978.27
	6	3938.51	3991.02
	7	4214.71	4309.78
	8	4275.42	4320.49
$2^{+\varepsilon}$	1	3313.71	3429.11
	2	3422.03	3484.54
	3	3710.06	3817.38
	4	3803.52	3860.47
	5	4060.25	4162.55
	6	4148.00	4196.43
	7	4378.76	4476.95
	8	4462.95	4504.55
$2^{-\varepsilon}$	1	3088.68	3202.11
	2	3531.70	3642.38
	3	3666.11	3734.10
	4	3907.27	4012.51
	5	3991.32	4062.51
	6	4243.29	4329.07
	7	4304.42	4363.03
	8	4550.91	4612.00
$3^{+\varepsilon}$	1	3328.26	3425.32
	2	3736.37	3827.75
	3	3924.76	3966.53
	4	4089.99	4182.79
	5	4225.45	4284.57
	6	4409.37	4503.65
	7	4512.24	4572.02
	8	4703.77	4797.78
$3^{-\varepsilon}$	1	3536.73	3650.73
	2	3683.47	3723.53
	3	3902.08	4008.45
	4	4030.85	4073.06
	5	4231.61	4331.70
	6	4349.85	4387.91
	7	4534.57	4619.30
	8	4645.99	4671.07
$4^{+\varepsilon}$	1	3742.56	3858.08
	2	3921.79	3943.51
	3	4082.66	4191.13
	4	4244.97	4271.20
	5	4394.41	4497.79
	6	4544.24	4572.21
	7	4683.88	4783.46
	8	4824.56	4852.37
$4^{-\varepsilon}$	1	3538.36	3633.01
	2	3917.60	4000.87
	3	4159.43	4179.46
	4	4254.05	4335.09
	5	4446.62	4483.56
	6	4560.83	4641.67
	7	4715.93	4763.97
	8	4845.22	4927.05

Table 5.  Our calculated hybrid D and $ D_s $ meson masses (in MeV) for $ J^P $ = $ 0^{-\varepsilon} $, $ 0^{+\varepsilon } $, $ 1^{-\varepsilon} $, $ 1^{+\varepsilon} $, $ 2^{-\varepsilon} $, $ 2^{+\varepsilon} $, $ 3^{-\varepsilon} $, $ 3^{+\varepsilon} $, $ 4^{-\varepsilon} $ and $ 4^{+\varepsilon} $.

Transition	initial state $ nJ^{P} $	final state $ nJ^{P} $	$ \Gamma_{e1} $(D meson) ($ c\bar{u} $, $ c\bar{d} $)	$ \Gamma_{e1} $($ D_s $ meson)
$0^- \rightarrow 1^+\gamma$	$20^-$	$11^+$	91.149, 3.457	0.4176
		$21^+$	75.435, 1.9573	0.2435
	$30^-$	$11^+$	210.5, 5.8748	0.3448
		$21^+$	226.65, 5.8811	0.2216
		$31^+$	432.72, 11.228	1.049
		$41^+$	109.09, 2.8305	0.697
$0^+ \rightarrow 1^-\gamma$	$10^+$	$11^-$	728.01, 19.4031	0.0859
	$20^+$	$11^-$	184.37, 4.8241	2.0001
		$21^-$	545.88, 14.164	0.2027
		$31^-$	35.948, 0.9328	0.0002
	$30^+$	$11^-$	47.770, 1.2456	0.3441
		$21^-$	290.88, 7.5475	1.6971
		$31^-$	407.65, 10.577	1.6964
		$41^-$	748.15, 19.413	0.5871
		$51^-$	158.37, 4.1092	0.162
$1^- \rightarrow 0^+\gamma$	$21^-$	$10^+$	43.527, 1.1612	1.9786
	$31^-$	$10^+$	628.92, 16.779	3.8272
	$41^-$	$10^+$	776.18, 20.707	0.1186
		$20^+$	604.83, 16.136	2.8181
	$51^-$	$10^+$	49.96, 1.3328	0.2344
		$20^+$	604.83, 16.136	2.8181
$1^- \rightarrow 1^+\gamma$	$21^-$	$11^+$	82.384, 2.7702	0.4364
		$21^+$	73.119, 1.8973	0.291
	$31^-$	$11^+$	497.36, 14.921	1.6613
		$21^+$	463.44, 12.025	1.263
	$41^-$	$11^+$	1028.9, 28.573	0.9155
		$21^+$	1016.9, 26.386	0.5979
		$31^+$	383.55, 9.9521	0.6226
		$41^+$	133.93, 3.4751	0.4148
	$51^-$	$11^+$	234.27, 6.4414	0.5734
		$21^+$	244.65, 6.3481	0.3518
		$31^+$	1126.6, 29.234	1.1176
		$41^+$	585.33, 15.188	0.7807
$1^+ \rightarrow 0^-\gamma$	$11^+$	$10^-$	847.18, 20.415	3.4365
	$21^+$	$10^-$	886.97, 23.498	3.7954
	$31^+$	$10^-$	0.123, 0.0032	0.1012
		$20^-$	443.01, 11.495	2.1211
	$41^+$	$10^-$	0.7203, 0.0189	0.0009
		$20^-$	764.76, 19.844	2.7341
$1^+ \rightarrow 1^-\gamma$	$11^+$	$11^-$	638.97, 14.809	2.2145
	$21^+$	$11^-$	851.13, 22.510	2.526
	$31^+$	$11^-$	80.893, 2.1169	0.4596
		$21^-$	313.77, 8.1415	1.8567
		$31^-$	4.6457, 0.1205	0.3447
	$41^+$	$11^-$	106.76, 2.7914	0.5276
		$21^-$	622.18, 16.144	2.2821
		$31^-$	20.975, 0.5442	0.4659
$1^+ \rightarrow 2^-\gamma$	$31^+$	$12^-$	65.085, 1.6888	0.5529
		$22^-$	0.2119, 0.0055	0.1558
	$41^+$	$12^-$	238.29, 6.1831	0.8464
		$22^-$	26.278, 0.6818	0.2738
	$51^+$	$12^-$	1.3736, 0.0356	0.1362
		$22^-$	5.0118, 0.13	0.1717
		$32^-$	181.45, 4.7082	0.998
		$42^-$	5.0814, 0.1318	0.4126
	$61^+$	$12^-$	2.6022, 0.0675	0.2015
		$22^-$	0.6375, 0.0165	0.2359
		$32^-$	554.7, 14.393	1.3456
		$42^-$	99.485, 2.5814	0.5961
$2^- \rightarrow 1^+\gamma$	$12^-$	$11^+$	1324.5, 40.073	5.3991
		$21^+$	1235.9, 32.0705	4.27
	$22^-$	$11^+$	2821.6, 81.961	8.0433
		$21^+$	2692.4, 69.861	6.5345
	$32^-$	$11^+$	135.6, 3.736	0.0116
		$21^+$	154.87, 4.0186	0.0318
		$31^+$	1541.9, 40.008	4.8947
		$41^+$	746.69, 19.375	3.7323
	$42^-$	$11^+$	167.93, 4.589	0.0259
		$21^+$	194.43, 5.045	0.0352
		$31^+$	3316.8, 86.062	6.8996
		$41^+$	2019.9, 52.411	5.3872

Table 6.  Partial widths for E1 decays (in KeV) of conventional D and $ D_s $ mesons.

Transition	initial state $ nJ^{P} $	final state $ nJ^{P} $	$ \Gamma_{e1} $(hybrid D meson) ($ c\bar{u} $, $ c\bar{d} $)	$ \Gamma_{e1} $(hybrid $ D_s $ meson)
$0^{+\varepsilon} \rightarrow 1^{-\varepsilon}\gamma$	$20^{+\varepsilon}$	$11^{-\varepsilon}$	261.12, 6.7754	1.059
		$21^{-\varepsilon}$	81.811, 2.1228	0.6407
	$30^{+\varepsilon}$	$11^{-\varepsilon}$	57.046, 1.4802	0.2516
		$21^{-\varepsilon}$	60.926, 1.5809	0.2588
		$31^{-\varepsilon}$	385.99, 10.016	1.5485
		$41^{-\varepsilon}$	117.44, 3.0472	1.0873
$0^{-\varepsilon} \rightarrow 1^{+\varepsilon}\gamma$	$10^{-\varepsilon}$	$11^{+\varepsilon}$	618.71, 16.054	0.4149
	$20^{-\varepsilon}$	$11^{+\varepsilon}$	387.02, 10.0423	1.9049
		$21^{+\varepsilon}$	264.43, 6.8614	0.0996
		$31^{+\varepsilon}$	63.071, 1.6365	0.00002
	$30^{-\varepsilon}$	$11^{+\varepsilon}$	6.5882, 0.1709	0.2337
		$21^{+\varepsilon}$	251.11, 6.5156	1.8328
		$31^{+\varepsilon}$	153.29, 3.9775	2.48
		$41^{+\varepsilon}$	301.26, 7.817	0.3068
		$51^{+\varepsilon}$	158.79, 4.1204	0.0377
$1^{+\varepsilon} \rightarrow 0^{-\varepsilon}\gamma$	$21^{+\varepsilon}$	$10^{-\varepsilon}$	199.35, 5.3184	1.3168
	$31^{+\varepsilon}$	$10^{-\varepsilon}$	511.52, 13.646	2.395
	$41^{+\varepsilon}$	$10^{-\varepsilon}$	3.2826, 0.0876	0.0766
		$20^{-\varepsilon}$	231.81, 6.1844	2.0572
	$51^{+\varepsilon}$	$10^{-\varepsilon}$	16.243, 0.4333	0.2632
		$20^{-\varepsilon}$	417.04, 11.126	2.48
$1^{+\varepsilon} \rightarrow 1^{-\varepsilon}\gamma$	$21^{+\varepsilon}$	$11^{-\varepsilon}$	222.27, 5.7673	0.7543
		$21^{-\varepsilon}$	85.868, 2.2281	0.4825
	$31^{+\varepsilon}$	$11^{-\varepsilon}$	436.29, 11.3207	1.7273
		$21^{-\varepsilon}$	229.88, 5.9648	1.2476
	$41^{+\varepsilon}$	$11^{-\varepsilon}$	71.744, 1.8616	0.4743
		$21^{-\varepsilon}$	61.15, 1.5867	0.3914
		$31^{-\varepsilon}$	303.65, 7.8791	0.8211
		$41^{-\varepsilon}$	115.48, 2.9963	0.5718
	$51^{+\varepsilon}$	$11^{-\varepsilon}$	132.82, 3.4463	0.1873
		$21^{-\varepsilon}$	113.01, 2.9322	0.156
		$31^{-\varepsilon}$	374.27, 9.7114	1.452
		$41^{-\varepsilon}$	174.23, 4.5208	1.0843
$1^{-\varepsilon} \rightarrow 0^{+\varepsilon}\gamma$	$11^{-\varepsilon}$	$10^{+\varepsilon}$	420.74, 10.917	1.4283
	$21^{-\varepsilon}$	$10^{+\varepsilon}$	714.93, 18.551	1.8474
	$31^{-\varepsilon}$	$10^{+\varepsilon}$	21.638, 0.5615	0.000008
		$20^{+\varepsilon}$	350.18, 9.0864	1.3169
	$41^{-\varepsilon}$	$10^{+\varepsilon}$	23.361, 0.6062	0.0033
		$20^{+\varepsilon}$	652.03, 16.918	1.6334
$1^{-\varepsilon}\rightarrow 1^{+\varepsilon}\gamma$	$11^{-\varepsilon}$	$11^{+\varepsilon}$	462.52, 12.001	1.4309
	$21^{-\varepsilon}$	$11^{+\varepsilon}$	827.38, 21.468	1.8929
	$31^{-\varepsilon}$	$11^{+\varepsilon}$	163.51, 4.2426	0.5119
		$21^{+\varepsilon}$	265.17, 6.8805	1.2207
		$31^{+\varepsilon}$	49.942, 1.2959	0.473
	$41^{-\varepsilon}$	$11^{+\varepsilon}$	196.41, 5.0965	0.577
		$21^{+\varepsilon}$	543.57, 14.104	1.5197
		$31^{+\varepsilon}$	158.73, 4.1187	0.6515
$1^{-\varepsilon} \rightarrow 2^{+\varepsilon}\gamma$	$31^{-\varepsilon}$	$12^{+\varepsilon}$	251.90, 6.5361	1.0387
		$22^{+\varepsilon}$	22.292, 0.5784	0.3843
	$41^{-\varepsilon}$	$12^{+\varepsilon}$	549.57, 14.26	1.3888
		$22^{+\varepsilon}$	116.31, 3.0179	0.5716
	$51^{-\varepsilon}$	$12^{+\varepsilon}$	12.435, 0.3227	0.0632
		$22^{+\varepsilon}$	30.026, 0.7791	0.1367
		$32^{+\varepsilon}$	377.98, 9.8075	1.5399
		$42^{+\varepsilon}$	38.496, 0.9989	0.6371
	$61^{-\varepsilon}$	$12^{+\varepsilon}$	1.709, 0.0443	0.0708
		$22^{+\varepsilon}$	18.596, 0.4825	0.1541
		$32^{+\varepsilon}$	860.24, 22.321	2.0341
		$42^{+\varepsilon}$	211.48, 5.4873	0.9093
$2^{+\varepsilon} \rightarrow 1^{-\varepsilon}\gamma$	$12^{+\varepsilon}$	$11^{-\varepsilon}$	872.62, 22.642	3.3811
		$21^{-\varepsilon}$	373.06, 9.6801	2.3478
	$22^{+\varepsilon}$	$11^{-\varepsilon}$	2390.7, 62.033	6.0388
		$21^{-\varepsilon}$	1386.2, 35.968	4.5079
	$32^{+\varepsilon}$	$11^{-\varepsilon}$	74.05, 1.9214	0.0924
		$21^{-\varepsilon}$	74.711, 1.9386	0.0787
		$31^{-\varepsilon}$	736, 19.097	3.0566
		$41^{-\varepsilon}$	284.58, 7.3841	2.3242
	$42^{+\varepsilon}$	$11^{-\varepsilon}$	57.592, 1.4944	0.0451
		$21^{-\varepsilon}$	66.767, 1.7324	0.0386
		$31^{-\varepsilon}$	2063.6, 53.545	5.1521
		$41^{-\varepsilon}$	1143.8, 29.679	4.0959

Table 7.  Partial widths for E1 decays (in KeV) of hybrid D and $ D_s $ mesons.

Transition	initial state $ nJ^{P} $	final state $ nJ^{P} $	$ \Gamma_{m1} $(D meson) ($ c\bar{u} $, $ c\bar{d} $)	$ \Gamma_{m1} $($ D_s $ meson)
$ 0^- \rightarrow 1^-\gamma $	$ 20^- $	$ 11^- $	11.097, 7.4747	2.184
	$ 30^- $	$ 11^- $	0.1487, 6.2222	2.3694
		$ 21^- $	22.198, 10.062	2.9894
		$ 31^- $	98.771, 1.2647	0.209
	$ 40^- $	$ 11^- $	0.1319, 1.566	0.5123
		$ 21^- $	25.08, 18.489	5.9304
		$ 31^- $	248.86, 10.857	0.1343
		$ 41^- $	16.733, 7.8301	3.7441
		$ 51^- $	68.052, 0.0079	2.0575
$ 1^- \rightarrow 0^-\gamma $	$ 11^- $	$ 10^- $	23.648, 0.6064	0.0665
	$ 21^- $	$ 10^- $	127.55, 17.5012	4.0203
		$ 20^- $	2.5479, 0.0644	0.0042
	$ 31^- $	$ 10^- $	2085, 19.985	7.9164
		$ 20^- $	4.8418, 0.19	0.0919
	$ 41^- $	$ 10^- $	112.9, 17.719	1.622
		$ 20^- $	82.281, 10.879	1.9332
		$ 30^- $	0.6405, 0.0163	0.00001
	$ 51^- $	$ 10^- $	1350, 0.9538	5.1259
		$ 20^- $	42.254, 1.3827	2.8697
		$ 30^- $	7.1297, 0.123	0.004

Table 8.  Partial widths for M1 decays (in KeV) of conventional D and $ D_s $ mesons.

Transition	initial state $ nJ^{P} $	final state $ nJ^{P} $	$ \Gamma_{m1} $(hybrid D meson) ($ c\bar{u} $, $ c\bar{d} $)	$ \Gamma_{m1} $(hybrid $ D_s $ meson)
$ 0^{+\varepsilon} \rightarrow 1^{+\varepsilon}\gamma $	$ 20^{+\varepsilon} $	$ 11^{+\varepsilon} $	22.206, 9.4979	2.1082
	$ 30^{+\varepsilon} $	$ 11^{+\varepsilon} $	8.4751, 10.6	2.2568
		$ 21^{+\varepsilon} $	14.759, 6.9874	2.1905
		$ 31^{+\varepsilon} $	2.6918, 1.303	0.5497
	$ 40^{+\varepsilon} $	$ 11^{+\varepsilon} $	9.428, 5.1214	0.7265
		$ 21^{+\varepsilon} $	21.874, 16.759	4.8863
		$ 31^{+\varepsilon} $	13.313, 3.7718	0.6848
		$ 41^{+\varepsilon} $	12.489, 5.5476	2.5828
		$ 51^{+\varepsilon} $	10.924, 2.235	1.2671
$ 1^{+\varepsilon} \rightarrow 0^{+\varepsilon}\gamma $	$ 11^{+\varepsilon} $	$ 10^{+\varepsilon} $	0.2161, 0.0056	0.0003
	$ 21^{+\varepsilon} $	$ 10^{+\varepsilon} $	53.308, 7.458	1.1989
		$ 20^{+\varepsilon} $	0.4085, 0.0105	0.0002
	$ 31^{+\varepsilon} $	$ 10^{+\varepsilon} $	425.28, 17.191	2.2738
		$ 20^{+\varepsilon} $	12.745, 0.2962	0.0171
	$ 41^{+\varepsilon} $	$ 10^{+\varepsilon} $	60.381, 11.716	0.9809
		$ 20^{+\varepsilon} $	46.49, 6.0773	0.9054
	$ 51^{+\varepsilon} $	$ 10^{+\varepsilon} $	760.03, 29.874	2.861
		$ 20^{+\varepsilon} $	234.39, 9.8806	1.5053
		$ 30^{+\varepsilon} $	2.5875, 0.0632	0.0022

Table 9.  Partial widths for M1 decays (in KeV) of hybrid D and $ D_s $ mesons.

Mode	Our Results	GI Model [20]	[57]	[58]	[39]	PDG [18]
Charmed strange mesons
$ D_s^{*\pm} \rightarrow D_s^{\pm}\gamma $	0.0665	1.03	2.39	1.12		< 1776.5
$ D_{s1}(2536)^\pm \rightarrow D_s^{\pm}\gamma $	3.7954	9.23	61.2	37.7	3.53
$ D_{s1}(2536)^\pm \rightarrow D_s^{*\pm}\gamma $	2.526	9.61	9.21	5.74	4.74
Charmed mesons ($ c\bar{u} $)
$ D^*(2007)^{0} \rightarrow D^{0}\gamma $	23.648	106				< 741
$ D_0^{*}(2300)^{0} \rightarrow D^{*}(2007)^{0}\gamma $	728.01	288
$ D_1(2430)^{0} \rightarrow D^{0}\gamma $	847.18	640
$ D_1(2420) \rightarrow D^{0}\gamma $	886.97	156
$ D_1(2430)^{0} \rightarrow D^{*}(2007)^{0}\gamma $	638.97	82.8
$ D_1(2420) \rightarrow D^{*}(2007)^{0}\gamma $	851.13	386
Charmed mesons ($ c\bar{d} $)
$ D^*(2010)^{\pm}\rightarrow D^{\pm}\gamma $	0.6064	10.8				≈ 1.334
$ D_0^{*} \rightarrow D^{*}(2010)^{\pm}\gamma $	19.4031	30
$ D_1 \rightarrow D^{\pm}\gamma $	20.415	66
$ D_1^{'}\rightarrow D^{\pm}\gamma $	23.498	16.1
$ D_1 \rightarrow D^{*}(2010)^{\pm}\gamma $	14.809	8.6
$ D_1^{'} \rightarrow D^{*}(2010)^{\pm}\gamma $	22.51	39.9

Table 10.  Comparison of our calculated radiative decay partial widths (in KeV) with other works. $ D_1 $ and $ D_1^{'} $ are mixed states ($ J^P = 1^+ $) of charmed mesons.