Valence quark distributions of pions: insights from Tsallis entropy

Parton distribution functions (PDFs) are key components of the quantum chromodynamics (QCD) collinear factorization theorem, in which scattering processes can be factorized into long-distance physics and short-distance hard scattering cross sections. PDFs are employed in long-distance physics and are defined as the probability density for finding a parton with a longitudinal momentum fraction x at a resolution scale of $ Q^2 $. In contrast to the hard scattering cross sections that can be calculated in perturbative QCD, PDFs have non-perturbative properties. Therefore, determining the PDFs of a hadron is a significant challenge in theoretical studies. In recent years, investigating the PDFs of a pion meson has been of great interest, for instance, the latest calculations in Ref. [1] and references therein. A pion, consisting of two valence quarks, is the lightest hadron, which is the Nambu-Goldstone boson of dynamical chiral symmetry breaking [2, 3]. In addition, a pion is the most important mediated particle of interactions between hadrons, such as the mediated particle of nuclear force proposed in Ref. [4]. As a result, the study of the internal structures of pions is beneficial to understand both dynamical chiral symmetry breaking and non-perturbative QCD.

The x-dependence of parton density functions at a low resolution scale is typically described by parameterizations of the non-perturbative input and its parameters are obtained by fitting observables to experimental data. However, compared to nucleon PDFs, existing knowledge of pion PDFs is limited owing to the scarcity of experimental data. However, many theoretical studies on pion PDFs have focused on determining the quark distribution, including the chiral-quark model [5−8], constituent quark model [9−11], basis light-front quantization (BLFQ) [12, 13], light-front holographic QCD (LFHQCD) [14], QCD sum rule [15], Dyson-Schwinger equation (DSE) [16−19], lattice QCD (LQCD) [20], and maximum entropy method (MEM) [21, 22]. The gluon distribution of a pion has been investigated using holographic QCD [23], DSE [16, 17, 24, 25], and LQCD [1]. Notably, Ref. [25] presents a comparison between LQCD and DSE. These two methods demonstrated good agreement, providing valuable insights into the origins of hadron masses. Furthermore, the pion structure function or PDFs have been predicted using the NJL model [26−31]. In addition, data-driven approaches have been used to investigate pion distribution functions (see Ref. [32] and references therein). Collectively these efforts enhance understanding of the internal structure of pions.

Among the various models, the MEM offers a simple but efficient approach for determining pion valence quark distributions [21]. It has been proposed as an alternative to conventional global fits for extracting PDFs [33]. In information theory, entropy serves as a quantitative measure of uncertainty and has gained increasing significance in physical theories. It is essential to emphasize that parton distributions are not direct experimental observables; rather, they represent probabilistic constructs. Consequent- ly, these distributions are fundamentally linked to the principles of information entropy. The relationship be-tween entropy and the gluon distribution has been notably explored by Kharzeev et al. [34]. Furthermore, the maximum entropy principle, as articlated by Jaynes [35], plays a pivotal role in establishing probability distributions that minimally incorporate external biases. The core premise of the MEM is to derive the most unbiased distribution possible based on the available information. In parton distribution studies, the MEM has proved particularly advantageous in scenarios where information derived from QCD calculations is limited [33].

In the MEM, the known properties of the hadron serve as testable information, while the valence quark distributions are determined by maximizing entropy. In Ref. [21], the MEM was first employed to model the non-perturbative input associated with pions. Using a very low resolution probe, valence constituents dominate in the quark-parton model. Based on the Von Neumann entropy, which satisfies the additivity property, the entropy of valence quark distributions at an initial scale of $ Q^2_0 $ is defined as follows:

With this entropy, the valence quark distribution is well described when the momentum contributed from gluons is nonzero. However, Eq. (1) is obtained under the ansatz that the interaction between valence quarks is negligible. It is more reasonable to describe the internal structure of a pion in terms of non-extensive entropy because the valence quarks are correlated. Tsallis entropy is a type of non-extensive entropy [36−38] and is defined as follows:

where $ p(x) $ is the probability distribution function and the index q represents the correlation strength of a system. When $ q\rightarrow 1 $, Eq. (2) is reduced to Von Neumann entropy as follows:

Tsallis entropy satisfies pseudo-additivity, which is represented as follows:

Tsallis entropy is a one-parameter extension of the Von Neumann entropy; therefore, it is more applicable and flexible for the description of a system with long-range correlation. In this study, we employ Tsallis entropy to determine the valence quark distributions of pions based on the MEM. Our results indicate that the correlation between valence quarks plays an important role in describing the valence quark distributions of pions.

The remainder of this paper is organized as follows. In Sec. II, we briefly introduce a naive non-perturbative input for valence quarks of pions and the definition of the MEM with Tsallis entropy. In Sec. III, based on the simplified version of the modified Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) evolution with GLR-MQ-ZRS corrections, the results from the MEM are compared with the experimental data and other models. The conclusions are then presented in Sec. IV.

At a very low resolution scale, for a $ \pi ^ + $ meson, it is reasonable to consider that the dominant components are the up valence quark and the down valence anti-quark. At the initial scale $ Q^2_0 $, the widely used parameterized form of valence quarks can be expressed as follows [21]:

This parameterization can describe well both the Regge behavior at a small x and the counting rule at a large x. Here, $ A_{\pi} $, $ B_{\pi} $, and $ C_\pi $ are undetermined parameters. In Eq. (5), we assume that the isospin symmetry has not been broken and the mass difference between $ u_\nu $ and $ \bar{d}_\nu $ is negligible; therefore, the distributions of $ u_\nu $ and $ \bar{d}_\nu $ are identical [21]. In addition, the distributions in Eq. (5) must satisfy the valence sum rule as follows:

The momentum sum rule is expressed as follows:

where g indicates the presence of gluons or sea quarks in a pion in addition to the valence quarks. The g value shoud be nonzero to obtain a better fit to the pion valence quark distribution as the sea quarks and the gluons can not be ignored, even at the initial scale [21]. The parameters $ Q_0^2 $ and g exhibit a strong dependence on each other. At extremely low values of $ Q_0^2 $, dressed valence quarks can be regarded as the sole effective degrees of freedom. When moving to relatively higher scales, the evolution process promptly generates distributions of sea quarks and gluons through quark splitting mechanisms. However, the determination of the initial scale value $ Q_0^2 $ remains contentious, as discussed in Ref. [21]. Consequently, g is treated as a fitting parameter.

Given the constraints expressed in Eqs. (6) and (7), the number of the undetermined parameters in Eq. (5) is reduced from three to one. To determine the remaining parameter, the MEM with Tsallis entropy is used. For the quark system, as defined in Eq. (2), the entropy for $ u_\nu $ or $ \bar{d}_\nu $ is as follows:

where $ v(x) $ is the valence quark distribution function and the q is a free parameter. Hence, at a low resolution scale where valence quarks are predominant, the entropy of the $ \pi^+ $ system is defined as follows:

According to the maximum entropy principle, the optimal non-perturbative input in Eq. (5) has the largest entropy. Therefore, the remaining free parameter in Eq. (5) is determined by taking maximum entropy. However, q is still an undetermined parameter derived from Tsallis entropy. To estimate the value of q, the valence quark distributions must be evolved to a high $ Q^2 $ and compared with the experimental data. The $ Q^2 $-dependence of PDFs can be determined using the well-known DGLAP evolution equation [39−41]. However, the linear DGLAP equation is valid only for a moderate x and large $ Q^2 $. Furthermore, only parton splitting is considered in the DGLAP equation, which gives rise to the destruction of unity or the Froissart bound [42]. To address this issue, the parton recombination effect should be considered. This effect is first considered by the Gribov-Levin-Ryskin-Mueller-Qiu (GLR-MQ) equation [43, 44] and its solution has been investigated in detail in recent years [45−48]. Based on the time-ordered perturbation theory (TOPT), Zhu, Ruan, and Shen (ZRS) reconsidered the parton recombination process [49−51] and obtained the modified DGLAP evolution equations with GLR-MQ-ZRS corrections, which satisfy the momentum conservation rule [50]. As the dominant effect is the recombination of gluon-gluon [52], in this study, we utilize modified DGLAP equations with simplified GLR-MQ-ZRS corrections, expressed as

for valence quark distributions,

for the sea quark distributions, and

for the gluon distribution. Here, R is the correlation radius of two gluons, $ \Sigma $ is the singlet quark distribution, $ P_{ij} $ is the splitting kernel functions [40, 52], and $ P_{gg\to g} $ and $ P_{gg\to \bar{q}} $ are the gluon-gluon recombination kernels [52].

The running coupling $ \alpha_{s} $ is a fundamental component in the formulation of the evolution equations. In recent calculations of continuum Schwinger methods, a infrared-safe parametrization of saturating $ \alpha_{s} $ was proposed [17]. This saturating $ \alpha_{s} $ was used to investigate the nucleon structure, which provides a unified description across the entire $ Q^2 $ range [53]. As our evolution proceeds from an extremely low scale to a high scale, we employed infrared-safe couplings to eliminate the divergent problem of $ \alpha_{s} $ at a low scale. This saturating $ \alpha_{s} $ is expressed as follows [17]:

$ \gamma_{m}=4/[11-(2/3)n_{f}],\; \Lambda_{{\rm{QCD}}}=0.234\; {\rm{GeV}},\; a_{0}=0.104\; {\rm{GeV}}^{2},\; a_{1}=0.0975\;{\rm{GeV}}^{2},\; b_{0}=0.121\; {\rm{GeV}}^{2} $, and $ n_{f} $ is the number of flavors. The above evolution equations and saturating $ \alpha_{s} $ are used to determine the pion PDFs.

In this section, we describe the use of the MEM with Tsallis entropy to determine the valence quark distributions and the use of modified DGLAP equations with the simplified GLR-MQ-ZRS corrections to perform the $ Q^2 $ evolution for comparisons with the experimental data. As the determination of the initial scale value $ Q^2_0 $ remains a subject of debate, it is treated as a fitting parameter. Simultaneously, parameter g is designated as a free parameter to account for contributions from sea quarks and gluons at the initial scale value $ Q^2_0 $.

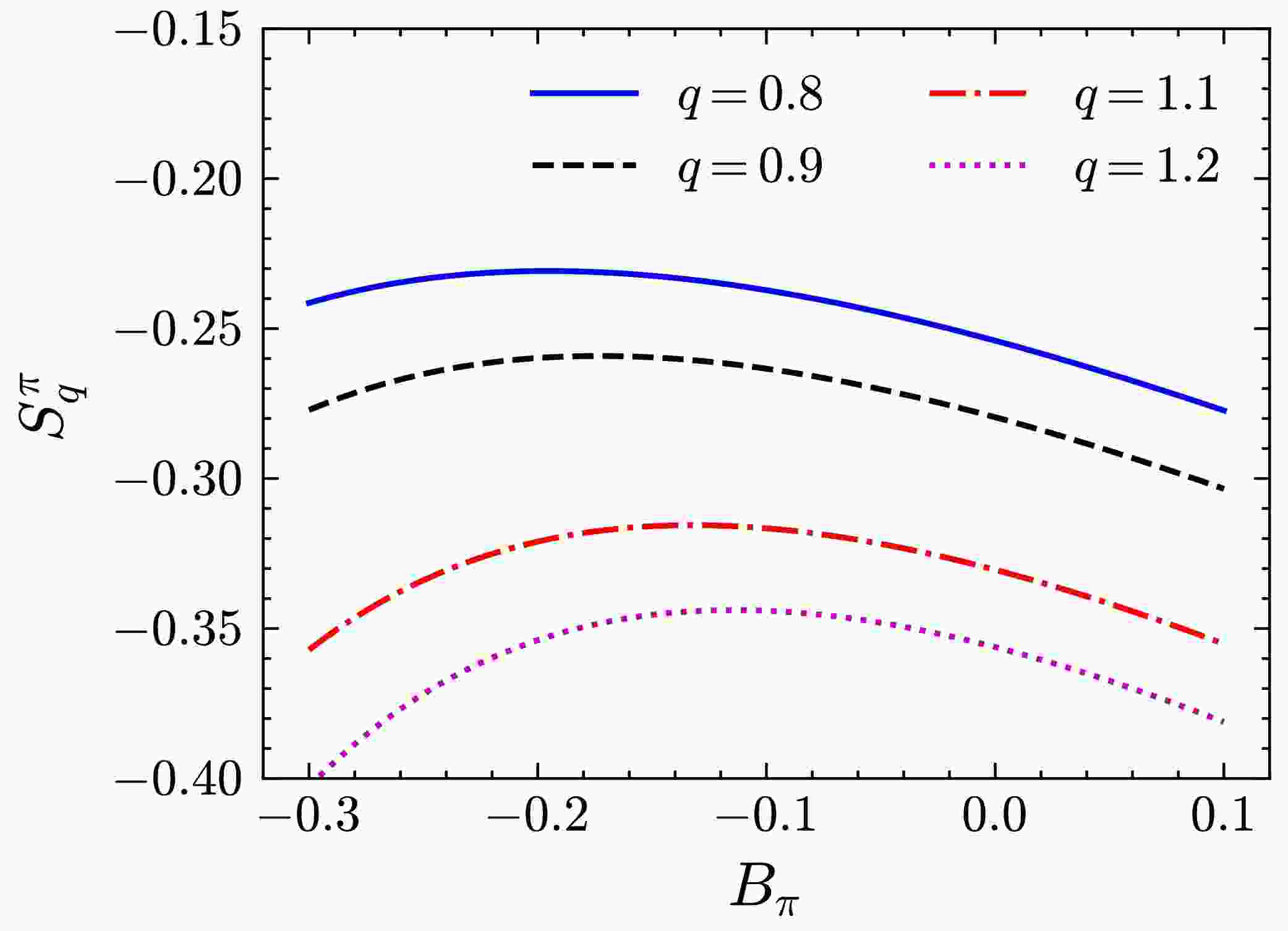
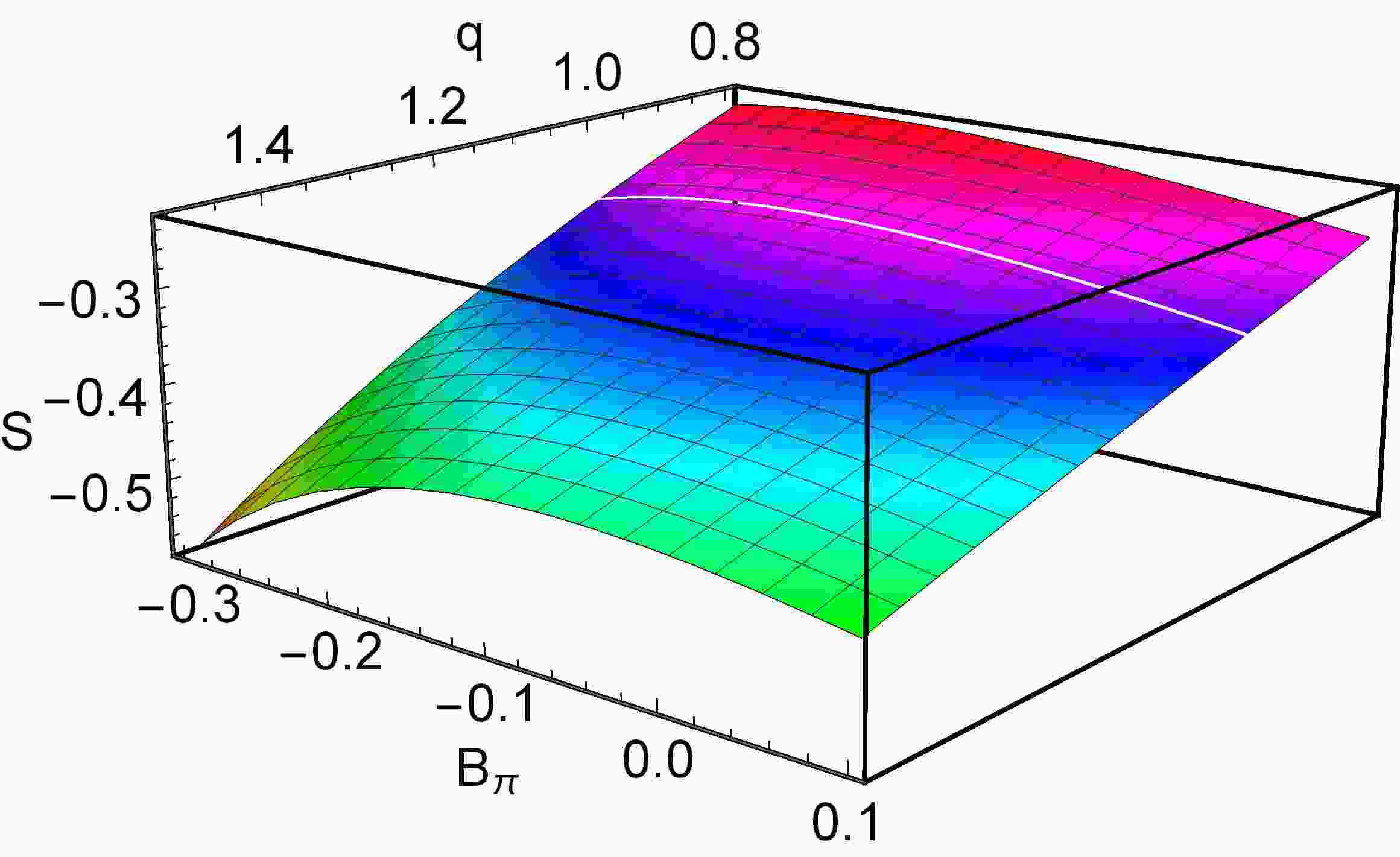
The Tsallis entropy for a pion as a function of $ B_\pi $ and q is shown in Fig. 1. As shown in Fig. 1, $ S_q^\pi $ monotonically decreases as q increases, while the maximum entropy is in the $ B_\pi $ direction. Therefore, it is physically realizable to determine the valence quark distributions based on the MEM with Tsallis entropy.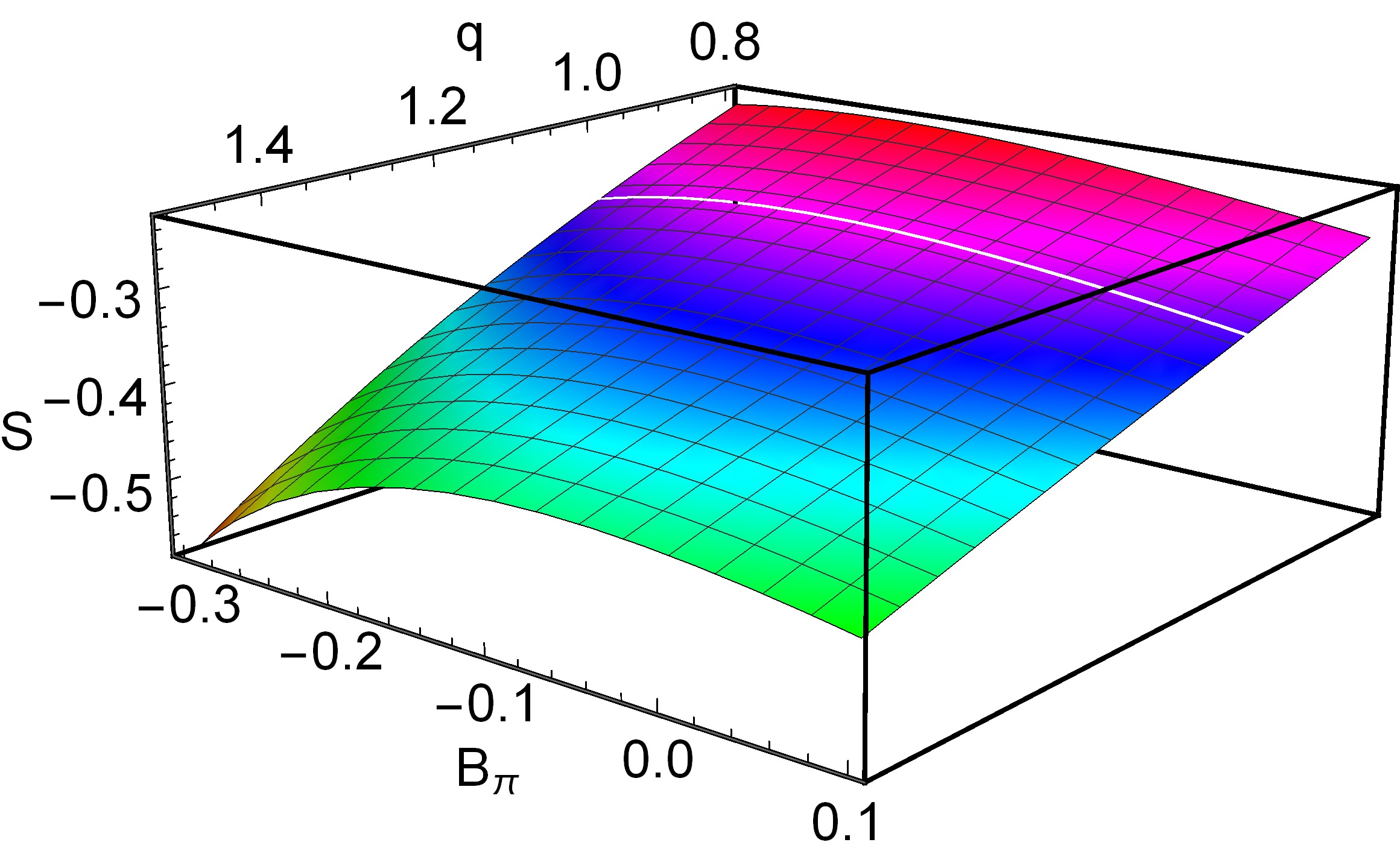

Figure 1.  (color online) Tsallis entropy of the valence quark non-perturbative input as a function of $ B_\pi $ and q.

To more effectively illustrate the relationship between entropy and the undetermined parameters, a simple approach is tentatively adopted by fixing $ g = 0.295 $ ($ Q^2_0=0.26\,{\rm{GeV}}^2 $), which is consistent with the global fit presented in GRS99 [54]. Fig. 2 presents the results for the Tsallis entropy as a function of $ B_\pi $ at various values of q at the initial scale. The undetermined parameters are related to entropy, and these parameters can be determined using maximum entropy principles. However, as q remains unknown, it must be obtained by fitting experimental data. Furthermore, the unfixed initial scale $ Q^2_0 $ exhibits a strong correlation with g; thus, q, g, and $ Q^2_0 $ are treated as fitting parameters from this point.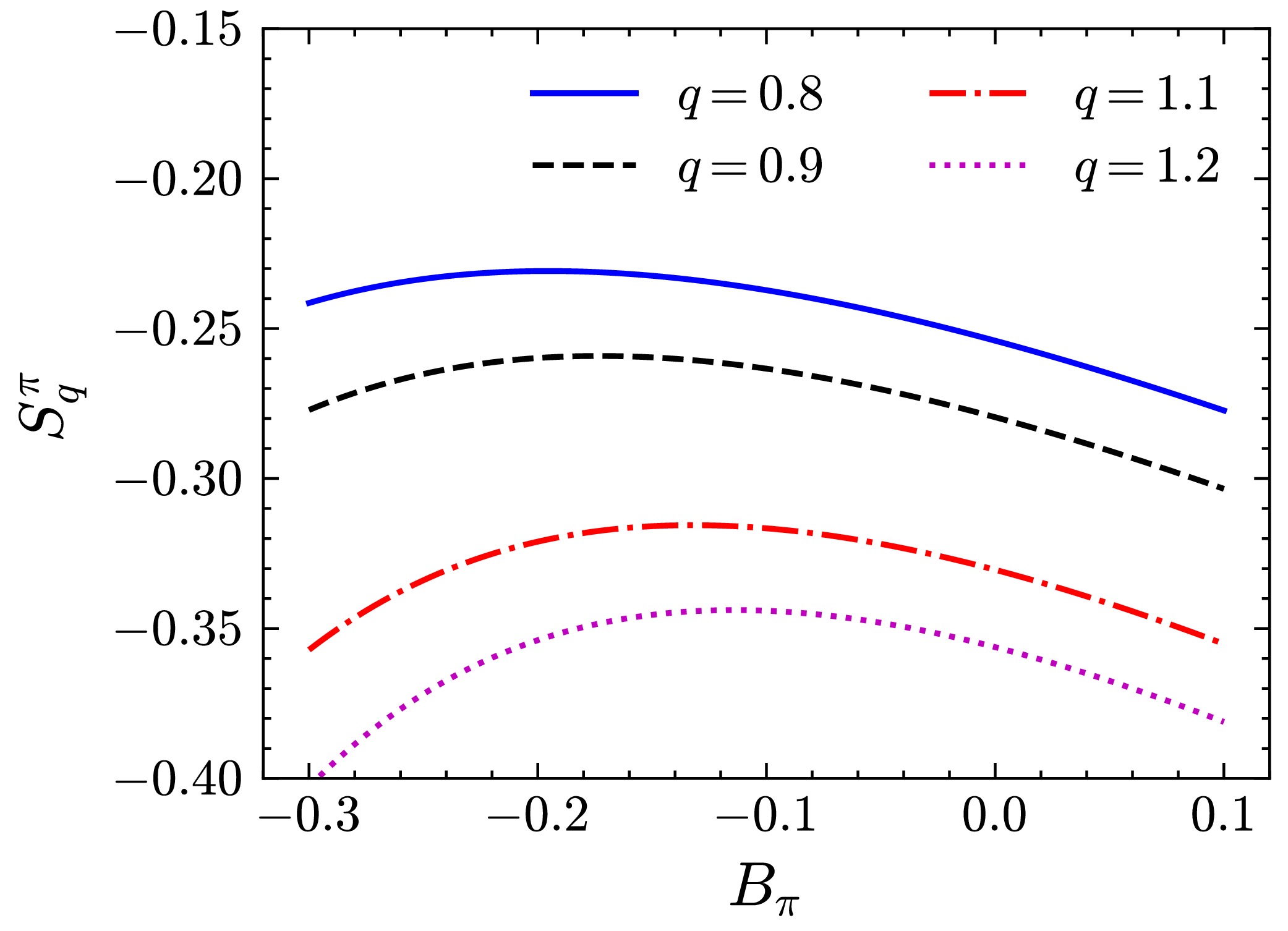

Figure 2.  (color online) Dependence of the Tsallis entropy of valence quarks on $ B_\pi $ at $ q=0.8 $ (blue solid curve), $ q=0.9 $ (black dashed curve), $ q=1.1 $ (red dot-dashed curve), and $ q=1.2 $ (pink dotted curve) at the initial scale.

To obtain the optimal value of parameters, the valence quark distribution functions at $ Q^2=20\; {\rm{GeV}}^2 $ are calculated using the modified DGLAP equation. The obtained $ Q^2 $ dependent valence quark distributions are compared with experimental data from E615 [55] (Fit-A). The parameters from Fit-A are listed in the first row of Table 1. As shown in Table 1, $ Q_0^2 = 0.093 $ and $ g = 0 $ yield the minimum value of $ \chi^2 $. This demonstrates that dressed valence quarks can be regarded as effective degrees of freedom at extremely low-energy scales. The corresponding optimal value of q is 0.915 which deviates from unity, indicating that the correlation between valence quarks plays an important role in the investigation of pion valence quark distributions.

	$Q^2_0$	g	q	A	B	C	D	$\chi^2$/d.o.f
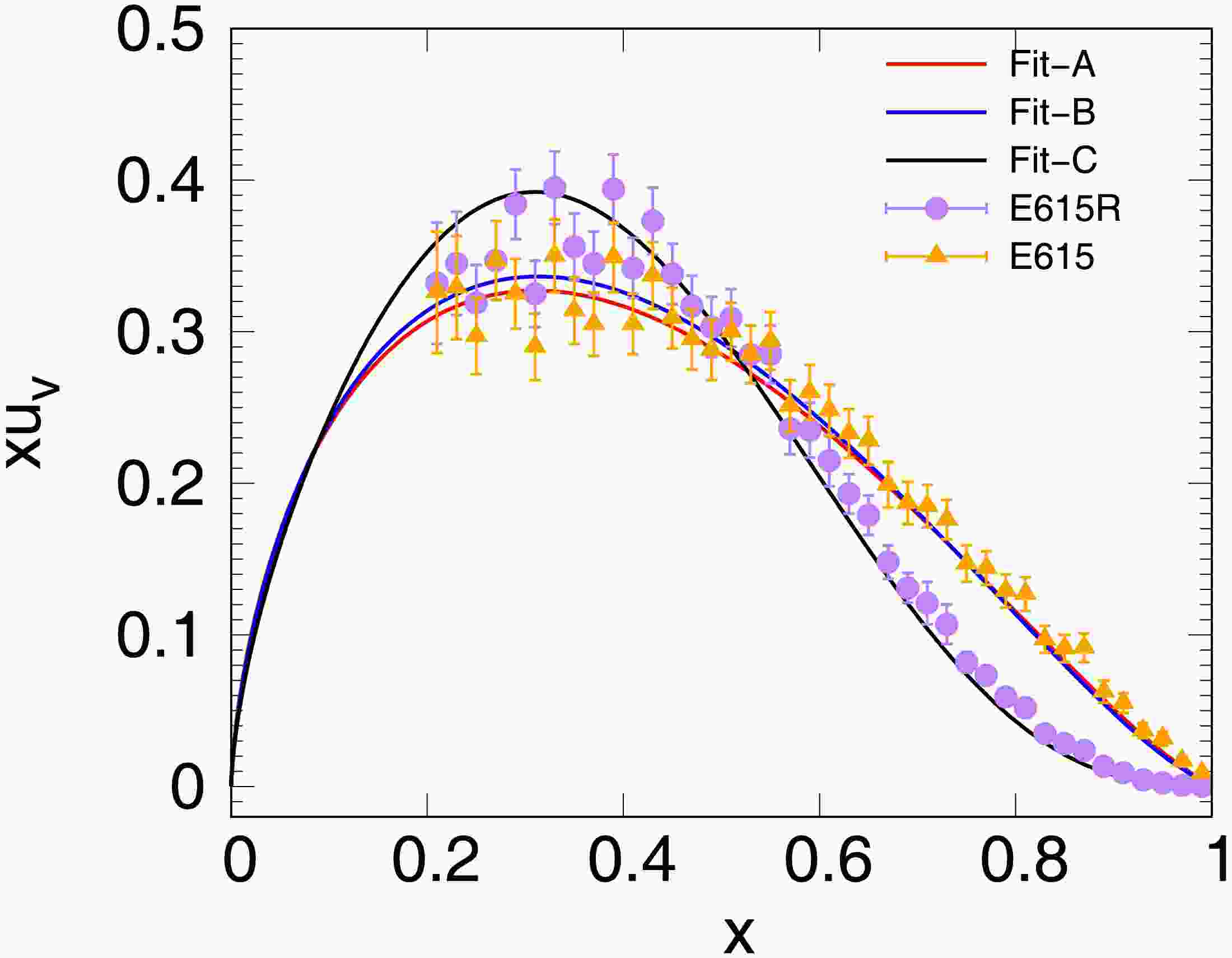
Fit-A	0.093	0.0	0.915	1.012	0.006	0.006	−	0.680
Fit-B	0.096	0.0	0.917	1.153	0.072	0.121	0.151	0.638
Fit-C	0.142	0.180	0.928	0.724	−0.132	1.932	24.171	1.445

Table 1.  Results from fitting the MEM to the E615 data [55] and the reanalyzed E615 data [56].

Fig. 3 shows the up valence quark distribution function at $ Q^2=20\; {\rm{GeV}}^2 $, obtained by performing the modified DGLAP evolution with the initial distribution in Eq. (5). In Fig. 3, the red line shows that the valence quark distribution function from Fit-A exhibits a good agreement with the E615 data [55]. It should be noted that the E615 data were reanalyzed in Ref. [56], resulting in a significantly softer valence distribution at large-x. Utilizing this modified dataset (E615R), we conducted a fitting using Eq. (5). However, we found that the fitting was inadequate. This may be attributed to the simplicity of the functional form, which requires an additional factor to suppress the valence quark distribution. Consequently, we refitted the experimental data by employing the same valence quark distribution form as that utilized in Ref. [56].

Figure 3.  (color online) Predicted up valence quark distribution function presented in comparison with the E615 data [55] and E615R data [56] at a scale of $ Q^2=20\; {\rm{GeV}}^2 $.

Using Eq. (14), we conducted fittings for the data from E615 (Fit-B) and E615R (Fit-C). As demonstrated by the blue and black lines in Fig. 3, Fit-B and Fit-C effectively characterized the E615 and E615R data, respectively. The last two rows of Table 1 show that, compared with the fit to E615, the fit to E615R yields a higher g value, which yields a softer quark distribution at the initial $ Q^2 $. It is important to note that when employing various distribution functions from different models to describe the $ J/\psi $ production data, it was observed that the $ J/\psi $ data tend to favor a higher gluon distribution [57]. Table 1 demonstrates an interesting result, that is, in the three sets of fitting results, the q values all deviate significantly from unity, which indicates that the consideration of the correlation between valence quarks is reasonable.

To test this outcome, we calculated the moments of the valence quark distributions, which have been well calculated using LQCD and other models [14, 17, 20, 21, 28, 58]. The moments of the momentum fraction of the valence quark distribution are defined as follows:

where n is the order of the moment. The lowest three nontrivial moments of the valence quark distribution at $ Q^2=4\; {\rm{GeV}}^2 $ are listed in Table 2, which shows that the predictions are consistent with the results from different models.

	$\langle x \rangle$	$\langle x^2 \rangle$	$\langle x^3 \rangle$
QCD analyses [58]	0.23	0.099	0.055
DSE [17]	0.24	0.094	0.047
LQCD [20]	0.213	0.101	0.0061
LFHQCD [14]	0.233	0.103	0.056
NJL model [28]	0.236	0.103	0.057
Von Neumann entropy [21]	0.24	0.10	0.057
This work, Fit-A	0.238	0.105	0.058
This work, Fit-B	0.242	0.106	0.059
This work, Fit-C	0.233	0.091	0.044

Table 2.  First three moments of the valence quark momentum distributions at $Q^2=4\; {\rm{GeV}}^2$ in comparision with those from QCD analyses [58], DSE [17], LQCD [20], LFHQCD [14], NJL model [28], and Shannon [21].

In this study, we investigate two distinct functional forms of initial non-perturbative input for valence quark distributions at a low resolution scale $Q^2_0$. The parameters are determined using two well-established constraints: the valence sum rule and the momentum sum rule, along with the MEM with Tsallis entropy. By comparing the $Q^2$-dependent valence quark distributions derived from the modified DGLAP equations, which includes GLR-MQ-ZRS corrections, to experimental data, we find that our results exhibit good agreement with both the E615 and E615R datasets when utilizing the input specified in Eq. (14). Additionally, the moments of the valence quark distributions are calculated and found to be consistent with the results from different models at $ Q^2=4\,{\rm{GeV}}^2 $.

In information theory, entropy is utilized as a metric for quantifying uncertainty. The concept of entropy is applicable and useful in determining the internal structure of a hadron as the detailed information of the valence quark distribution is unknown. By imposing constraints from well-known properties, the MEM aims to maximize entropy to ensure unbiased inference of the probability distribution. In the MEM, the Tsallis entropy demonstra-tes a powerful ability in determining pion valence quark distributions. The value of q deviates from unity, which indicates that the valence quarks correlate even at a low $ Q^2 $.