-
The exploration of new physics is an active field in particle physics, aiming to go beyond the limitations of the Standard Model (SM) and address mysteries such as dark matter, dark energy, and neutrino mass. In this context, the supersymmetry theory (SUSY) [1−3], grand unified theory (GUT) [4−6], extra dimension theory, and related extended theories [7−11] are popular frameworks for the research on new physics. Additional gauge particles are predicted along with the new gauge group involved. The detection of the
$ W^\prime $ particle is an important goal in new physics models. Recently, the CDF experiment group at Fermilab, through precise measurements of the W boson mass, found deviations from the expectations of the Standard Model [12]. The W mass anomaly can be explained within the 3-3-1 model, in which the$ W^\prime $ particle exists [13].The
$ W^\prime $ particle was mainly proposed to address some of the limitations and mysteries of the Standard Model. It is a hypothetical particle beyond the predictions of the Standard Model, resulting from new theories and models. The properties of the$ W^\prime $ particle are characterized by different predictions in different models. The origin and background of the$ W^\prime $ particle are closely related to the electroweak symmetry breaking and Higgs mechanism. In the Standard Model, W and Z bosons acquire masses through the Higgs mechanism. If the$ W^\prime $ particle exists, it may involve a relatively more complex mode of symmetry breaking. Therefore, the existence of the$ W^\prime $ particle may point to new phenomena, such as the aforementioned GUT and extra dimension theory, which provide possible frameworks to explain the properties of the$ W^\prime $ particle and its interactions with other particles. The alternative left-right model is an attractive approach resulting from GUT symmetry breaking. It explains neutrino masses and dark matter candidates. We choose the alternative left-right model to study$ W^\prime $ . In this model, the$ W^\prime $ particle allows for the existence of light masses, and its mass is influenced by the coupling constants. The ratio of$ M_{W^\prime}/M_{Z^\prime} $ depends on the right-handed coupling constant$ g_R $ . The model introduces an S symmetry, which provides theoretical stability for the new neutral fermions and Higgs particles, which can serve as dark matter candidates [14, 15]. Simultaneously, the model avoids flavor-changing neutral currents, which allows for the charged bosons to be light. One can study the interactions of$ W^\prime $ with the Standard Model particles and further explore the dark matter interactions with the$ W^\prime $ particle as a mediator. Overall, the exploration of the$ W^\prime $ particle is an exciting field in particle physics. It may reveal clues to new physics [16−23] and provides the key to a deeper understanding of the universe. In the coming years, we aim to further explore the$ W^\prime $ particle in future colliders.In this paper, we first introduce relevant research related to
$ W^\prime $ particles. Then, we focus on building the model proposed in this study and the current mass constraints on the$ W^\prime $ particle. Subsequently, we investigate the process$ \mu^+ \mu^-\to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ at a future muon collider. Finally, a brief summary is provided. -
The exploration of new physics is an active field in particle physics, aiming to go beyond the limitations of the Standard Model (SM) and address mysteries such as dark matter, dark energy, and neutrino mass. In this context, the supersymmetry theory (SUSY) [1−3], grand unified theory (GUT) [4−6], extra dimension theory, and related extended theories [7−11] are popular frameworks for the research on new physics. Additional gauge particles are predicted along with the new gauge group involved. The detection of the
$ W^\prime $ particle is an important goal in new physics models. Recently, the CDF experiment group at Fermilab, through precise measurements of the W boson mass, found deviations from the expectations of the Standard Model [12]. The W mass anomaly can be explained within the 3-3-1 model, in which the$ W^\prime $ particle exists [13].The
$ W^\prime $ particle was mainly proposed to address some of the limitations and mysteries of the Standard Model. It is a hypothetical particle beyond the predictions of the Standard Model, resulting from new theories and models. The properties of the$ W^\prime $ particle are characterized by different predictions in different models. The origin and background of the$ W^\prime $ particle are closely related to the electroweak symmetry breaking and Higgs mechanism. In the Standard Model, W and Z bosons acquire masses through the Higgs mechanism. If the$ W^\prime $ particle exists, it may involve a relatively more complex mode of symmetry breaking. Therefore, the existence of the$ W^\prime $ particle may point to new phenomena, such as the aforementioned GUT and extra dimension theory, which provide possible frameworks to explain the properties of the$ W^\prime $ particle and its interactions with other particles. The alternative left-right model is an attractive approach resulting from GUT symmetry breaking. It explains neutrino masses and dark matter candidates. We choose the alternative left-right model to study$ W^\prime $ . In this model, the$ W^\prime $ particle allows for the existence of light masses, and its mass is influenced by the coupling constants. The ratio of$ M_{W^\prime}/M_{Z^\prime} $ depends on the right-handed coupling constant$ g_R $ . The model introduces an S symmetry, which provides theoretical stability for the new neutral fermions and Higgs particles, which can serve as dark matter candidates [14, 15]. Simultaneously, the model avoids flavor-changing neutral currents, which allows for the charged bosons to be light. One can study the interactions of$ W^\prime $ with the Standard Model particles and further explore the dark matter interactions with the$ W^\prime $ particle as a mediator. Overall, the exploration of the$ W^\prime $ particle is an exciting field in particle physics. It may reveal clues to new physics [16−23] and provides the key to a deeper understanding of the universe. In the coming years, we aim to further explore the$ W^\prime $ particle in future colliders.In this paper, we first introduce relevant research related to
$ W^\prime $ particles. Then, we focus on building the model proposed in this study and the current mass constraints on the$ W^\prime $ particle. Subsequently, we investigate the process$ \mu^+ \mu^-\to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ at a future muon collider. Finally, a brief summary is provided. -
Research on the grand unified theory (GUT) is widely popular, originating from the symmetry breaking of the
$ E_6 $ group [24, 25]. The groups of$ S O(10) \times U(1) $ and$ S U(3) \times S U(3) \times S U(3) $ are two of the many subgroups of the$ E_6 $ group, where the classical left-right symmetric model arises from the$ S O(10) \times U(1) $ group structure [26, 27]. The alternative left-right model (ALRM) [10, 28] discussed in this study results from the breaking chain of the$ S U(3) \times S U(3) \times S U(3) $ subgroup.The quantum numbers and representations selected for the fermionic field content of the ALRM are inspired by heterotic superstring models [10]. With the largest subgroup
$ S U(3)_C \times S U(3)_L \times S U(3)_H $ of$ E_6 $ , there is a total of 27 representations to display the particles:$ 27 = (3,3,1)+(\bar{3},1,\bar{3})+(1,\bar{3},3)\equiv q+\bar{q}+l. $

(1) The alternative left-right model is based on the
$ S U(3)_C \times S U(2)_L \times S U(2)_{R^\prime} \times U(1)_{B-L} \times S $ gauge group. In this context, the$ S U(3)_C $ group represents the symmetry group of the strong interaction, corresponding to the strong force that binds quarks together.$ S U(2)_L $ is the symmetry of the weak interaction for left-handed particles.$ S U(2)_{R^\prime} $ is the symmetry of the weak interaction for right-handed particles and S is a discrete symmetry imposed to distinguish between scalar and dual scalar fields. Initially, the gauge and global symmetry group$ S U(2)_{R^\prime} \times U(1)_{B-L} \times S $ of ALRM is broken to produce the hypercharge$ U(1)_Y $ . The symmetry breaking is achieved through the$ S U(2)_{R^\prime} $ doublet of scalar fields$ \chi_R $ , which are charged under S. To maintain left-right symmetry, an$ S U(2)_L $ doublet of scalar fields$ \chi_L $ is introduced. However, unlike$ \chi_R $ ,$ \chi_L $ does not couple with S. The electroweak symmetry is further broken down to electromagnetism through a bidoublet Higgs field that carries charges under both$ S U(2)_L $ and$ S U(2)_{R^\prime} $ , but has no$ B-L $ quantum numbers. This Higgs field is non-trivial under both$ S U(2)_L $ and$ S U(2)_{R^\prime} $ transformations but does not affect the$ B-L $ symmetry [11]. We represent it using a more intuitive process as follows:$\begin{aligned}& S U(2)_{L} \times S U(2)_{R^\prime} \times U(1)_{B-L}\times S \xrightarrow{\langle\chi_{R}\rangle} S U(2)_{L}\\&\quad \times U(1)_{Y} \xrightarrow{\langle\Phi\rangle,\langle\chi_{L}\rangle} U(1)_{EM}.\end{aligned} $

(2) The particles of ALRM along with the corresponding field representation are listed in Table 1.
Fields $ S U(3)_C \times S U(2)_L \times S U(2)_{R^\prime} \times U(1)_{B-L} $ 

S Fermions $ Q_L=\left( \begin{array}{c} u\\ d \end{array} \right)_L $ 

$ \left( \begin{array}{c} 3,2,1,+\frac{1}{6} \end{array} \right) $ 

$ 0 $ 

$ Q_R=\left( \begin{array}{c} u\\ d^\prime \end{array} \right)_R $ 

$ \left( \begin{array}{c} 3,1,2,+\frac{1}{6} \end{array} \right) $ 

$ -\frac{1}{2} $ 

$ d^\prime_L $ 

$ \left( \begin{array}{c} 3,1,1,-\frac{1}{3} \end{array} \right) $ 

$ -1 $ 

$ d_R $ 

$ \left( \begin{array}{c} 3,1,1,-\frac{1}{3} \end{array} \right) $ 

0 $ L_L=\left( \begin{array}{c} \nu\\ e \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,2,1,-\frac{1}{2} \end{array} \right) $ 

$ 0 $ 

$ L_R=\left( \begin{array}{c} n\\ e \end{array} \right)_R $ 

$ \left( \begin{array}{c} 1,1,2,-\frac{1}{2} \end{array} \right) $ 

$ +\frac{1}{2} $ 

$ n_L $ 

$ \left( \begin{array}{c} 1,1,1,0 \end{array} \right) $ 

$ +1 $ 

$ \nu_R $ 

$ \left( \begin{array}{c} 1,1,1,0 \end{array} \right) $ 

0 Higgs $ \Phi=\left( \begin{array}{c} \phi_1^0 \phi_1^+\\ \phi_2^- \phi_2^0 \end{array} \right)_R $ 

$ \left( \begin{array}{c} 1,2,2^*,0 \end{array} \right) $ 

$ -\frac{1}{2} $ 

$ X_L=\left( \begin{array}{c} \chi_L^+\\ \chi_L^0 \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,2,1,+\frac{1}{2} \end{array} \right) $ 

$ 0 $ 

$ X_R=\left( \begin{array}{c} \chi_R^+\\ \chi_R^0 \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,1,2,+\frac{1}{2} \end{array} \right) $ 

$ +\frac{1}{2} $ 

Table 1. Field content of the ALRM and respective quantum numbers.
Under the S symmetry, there are some odd S symmetry particles: scotinos
$ n_L $ ,$ n_R $ , exotic quarks$ d_L^{\prime} $ ,$ d_R^{\prime} $ , gauge boson$ W^\prime $ , and scalar particles. The Yukawa Lagrangian of ALRM is expressed as$\begin{aligned}[b] {\cal{L}}_{Y} =\;& \bar{Q}_{L} Y^{q} \tilde{\Phi} Q_{R} + \bar{Q}_{L} Y_{L}^{q} \chi_{L} d_{R} + \bar{Q}_{R} Y_{R}^{q} \chi_{R} d_{L}^{\prime}\\& + \bar{L}_{L} Y^{\ell} \Phi L_{R} + \bar{L}_{L} Y_{L}^{\ell} \tilde{\chi}_{L} \nu_{R} + \bar{L}_{R} Y_{R}^{\ell} \tilde{\chi}_{R} n_{L} + h.c.,\end{aligned} $

(3) where Y is a
$ 3\times3 $ matrix of Yukawa couplings, with subscripts L and R representing the left-handed and right-handed coupling matrices respectively, and superscripts q and l representing the quarks and leptons in the model. The vacuum expectation values (vevs) of the scalar fields are expressed as$ \begin{aligned}[b]&\langle \Phi \rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0&0\\ 0&k \end{array}} \right),\quad \left\langle {{\chi _L}} \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0\\ {{v_L}} \end{array}} \right),\\& \left\langle {{\chi _R}} \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0\\ {{v_R}} \end{array}} \right).\end{aligned} $

(4) The masses of the gauge bosons are generated through the left-right symmetry breaking the Higgs mechanism. The masses of the charged bosons are
$\begin{aligned}[b]& M_{W} = \frac{1}{2} g_L \sqrt{k^2 + v_L^2} \equiv \frac{1}{2} g_L v, \quad \text{and} \\& M_{W^\prime} = \frac{1}{2} g_R \sqrt{k^2 + v_R^2} \equiv \frac{1}{2} g_R v^\prime .\end{aligned} $

(5) However, because
$ \langle\phi_1^0\rangle = 0 $ , the produced charged bosons will not mix, which means that the$ W^{\prime\pm} $ and$ W^\pm $ particles will maintain their respective characteristics and will not convert into each other.The mass squared matrix of the neutral gauge bosons in the
$ \{W_{L\mu}^3 $ ,$ W_{R\mu}^3 $ ,$ B_\mu\} $ basis is$ ({\cal{M}}_V^0)^2 = \frac{1}{4}\left( {\begin{array}{*{20}{c}} {g_{B - L}^2(v_L^2 + v_R^2)}&{ - {g_{B - L}}{g_L}v_L^2}&{ - {g_{B - L}}{g_R}v_R^2}\\ { - {g_{B - L}}{g_L}v_L^2}&{g_L^2{v^2}}&{ - {g_L}{g_R}{k^2}}\\ { - {g_{B - L}}{g_R}v_R^2}&{ - {g_L}{g_R}{k^2}}&{g_R^2{{(v')}^2}} \end{array}} \right), $

(6) where
$ g_L,g_R $ and$ g_{B-L} $ are the gauge coupling constants of$ S U(2)_L,S U(2)_{R^\prime} $ and$ U(1)_{B-L} $ [29]. The matrix can be diagonalized through three rotations that mix B,$ W^3_L $ , and$ W^3_R $ bosons into the massless photon A and massive Z and$ Z' $ states:$ \begin{aligned}[b]\left( {\begin{array}{*{20}{c}} {{B_\mu }}\\ {W_{L\mu }^3}\\ {W_{R\mu }^3} \end{array}} \right) =\;& \left( {\begin{array}{*{20}{c}} {\cos {\phi _W}}&0&{ - \sin {\phi _W}}\\ 0&1&0\\ {\sin {\phi _W}}&0&{\cos {\phi _W}} \end{array}} \right)\\&\left( {\begin{array}{*{20}{c}} {\cos {\theta _W}}&{ - \sin {\theta _W}}&0\\ {\sin {\theta _W}}&{\cos {\theta _W}}&0\\ 0&0&1 \end{array}} \right)\\&\left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos {\zeta _W}}&{ - \sin {\zeta _W}}\\ 0&{\sin {\zeta _W}}&{\cos {\zeta _W}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{A_\mu }}\\ {{Z_\mu }}\\ {{{Z'}_\mu }} \end{array}} \right),\end{aligned} $

(7) where the
$ \phi_W $ rotation mixes the B and$ W^3_R $ bosons into the hypercharge boson B, generated by the breaking of$ S U(2)_{R'} \times U(1)_{B-L} $ into$ U(1)_Y $ .$ \theta_W $ represents the usual electroweak mixing, and the$ \zeta_W $ rotation is related to the strongly constrained$ Z-Z' $ mixing. The mass of the charged$ W^\prime $ boson is indirectly constrained by the mass ratio$ M_{W^\prime}/M_{Z'} = c_{\phi W} $ [10], so the constraint of$ M_{W^\prime} $ is weaker than that of the LRSM.In recent years, many research groups (such as the ATLAS Collaboration and CMS Collaboration) have been actively exploring the experimental constraints on the mass of the
$ W^\prime $ particle, achieving a great deal of results [30−38]. Below are some of the latest research findings on the mass constraints of$ W^\prime $ :CMS Sequential Standard Model [35] $ W^\prime\to e^-\nu $ 

$ M_{W^\prime}\geq 5.3 $ TeV

Left-Right Symmetric Model [36] $ W^\prime\to e^- N $ 

$ M_{W^\prime}\geq 4.7 $ TeV

$ W^\prime\to \mu^- N $ 

$ M_{W^\prime}\geq 5.0 $ TeV

ATLAS Sequential Standard Model ( $ g_L=g_R $ ) [37]

$ W^\prime\to \tau^-\nu $ 

$ M_{W^\prime}\geq 5.0 $ TeV

Sequential Standard Model ( $ g_L\neq g_R $ ) [37]

$ W^\prime\to \tau^-\nu $ 

$ M_{W^\prime}\geq 3.5\sim5.0 $ TeV

Left-Right Symmetric Model [38] $ W^\prime\to e^- n_e $ 

$ M_{W^\prime}\geq 4.8 $ TeV

$ W^\prime\to \mu^- n_{\mu} $ 

$ M_{W^\prime}\geq 5.0 $ TeV

Table 2. Mass constraints for
$ W^\prime $ from LHC.1. Bounds from CMS: The CMS Collaboration has searched for
$ W^\prime $ and heavy neutrino$ N_R $ with the signature of observing high transverse masses of the$ \tau- $ lepton and missing transverse momentum at the LHC with$ \sqrt{s} = 13 $ TeV, corresponding to an integrated luminosity of$ 35.9\ {\rm fb}^{-1} $ . The mass bound of$ W^\prime $ is$ M_{W^\prime}\geq 4.0 $ TeV, with the right-handed coupling equal to the SM coupling [34]. However, depending on the coupling in the non-universal$ G(221) $ model, the bound of the heavy$ W^\prime $ bosons is$ M_{W^\prime}\geq 1.7\sim3.9 $ TeV [34]. Within the framework of the Sequential Standard Model, a$ W^\prime $ boson with mass less than 5.3 TeV is excluded from the combined results of electron decay channels at the LHC with$ \sqrt{s} = 13 $ TeV [35]. The CMS Collaboration used data from Run 2 at the LHC to obtain constraints on the mass of the$ W^\prime $ boson, leveraging the Left-Right Symmetric Model at$ \sqrt{s} = 13 $ TeV. According to the assumption that the right-handed neutrino masses are equal to half the$ W^\prime $ mass, the mass of$ W^\prime $ is excluded at 95% confidence level up to 4.7 and 5.0 TeV for the electron and muon channels, respectively [36].2. Bounds from ATLAS: The ATLAS Collaboration has searched for
$ W^\prime $ by observing at high transverse masses of the$ \tau- $ lepton and missing transverse momentum at the LHC with$ \sqrt{s} = 13 $ TeV, corresponding to an integrated luminosity of$ 138\ {\rm fb}^{-1} $ . The present mass bounds of$ W^\prime $ is$ M_{W^\prime}\geq 5.0 $ TeV in the Sequential Standard Model, with the right-handed coupling equal to the SM coupling [37]. According to the assumption that the coupling in the non-universal coupling implies$ g_L\neq g_R $ , the mass of$ W^\prime $ is excluded at 95% confidence level up to$ 3.5 \sim 5.0 $ TeV for the τ channel in the Sequential Standard Model. For an integrated luminosity of$ 80\ {\rm fb}^{-1} $ , the mass of$ W^\prime $ is excluded at 95% confidence level up to 4.8 and 5.0 TeV for the electron and muon channels, respectively, in the Left-Right Symmetric Model [38].The constraints on the
$ W^\prime $ particle mentioned above arise from the analysis of LHC data by various experimental groups using different models. Most current experimental results for$ W^\prime $ particles are primarily obtained through the exploration of single production channels. Even when considering the pair production of$ W^\prime $ , the constraints on it become weaker. Therefore, we decided to investigate the properties of$ W^\prime $ particles by exploring the signals of their pair production at a muon collider. This issue is closely related to our studied model. Most of the experimental results available today are based on sequential models or the classical left-right symmetric model. In these models, the decay products of the newly introduced additional charged bosons are Standard Model particles (leptons or quarks). The mass of the$ W^\prime $ boson is experimentally expected to be at least approximately 5.0 TeV, owing to constraints from its dilepton decay channel at the LHC. However, in our study of the ALRM, the decay process of the$ W^\prime $ boson couples to the quark-exotic quark and charged lepton-scotino final states, which is a consequence of the discrete symmetry. In this model, we treat the scotino particle as a dark particle, which is unobservable. As a result, most of the experimental findings do not provide a good reference for ALRM. The value of the right-handed coupling constant$ g_R $ has a significant impact on the constraints of the$ W^\prime $ particle mass. When the value of$ g_R $ is relatively small, the lower limit of the$ W^\prime $ mass might be smaller. In the ALRM adopted in this study, the allowed range of$ g_R $ for the coupling with right-handed gauge bosons is$ 0.37 \sim 0.765 $ , where the lower limit comes from the theoretical restriction that$ g_R/g_L $ must be larger than tan$ \theta_W $ [39, 40], and the upper limit comes from the phenomenological specification of$ g_R $ [10]. -
Research on the grand unified theory (GUT) is widely popular, originating from the symmetry breaking of the
$ E_6 $ group [24, 25]. The groups of$ S O(10) \times U(1) $ and$ S U(3) \times S U(3) \times S U(3) $ are two of the many subgroups of the$ E_6 $ group, where the classical left-right symmetric model arises from the$ S O(10) \times U(1) $ group structure [26, 27]. The alternative left-right model (ALRM) [10, 28] discussed in this study results from the breaking chain of the$ S U(3) \times S U(3) \times S U(3) $ subgroup.The quantum numbers and representations selected for the fermionic field content of the ALRM are inspired by heterotic superstring models [10]. With the largest subgroup
$ S U(3)_C \times S U(3)_L \times S U(3)_H $ of$ E_6 $ , there is a total of 27 representations to display the particles:$ 27 = (3,3,1)+(\bar{3},1,\bar{3})+(1,\bar{3},3)\equiv q+\bar{q}+l. $

(1) The alternative left-right model is based on the
$ S U(3)_C \times S U(2)_L \times S U(2)_{R^\prime} \times U(1)_{B-L} \times S $ gauge group. In this context, the$ S U(3)_C $ group represents the symmetry group of the strong interaction, corresponding to the strong force that binds quarks together.$ S U(2)_L $ is the symmetry of the weak interaction for left-handed particles.$ S U(2)_{R^\prime} $ is the symmetry of the weak interaction for right-handed particles and S is a discrete symmetry imposed to distinguish between scalar and dual scalar fields. Initially, the gauge and global symmetry group$ S U(2)_{R^\prime} \times U(1)_{B-L} \times S $ of ALRM is broken to produce the hypercharge$ U(1)_Y $ . The symmetry breaking is achieved through the$ S U(2)_{R^\prime} $ doublet of scalar fields$ \chi_R $ , which are charged under S. To maintain left-right symmetry, an$ S U(2)_L $ doublet of scalar fields$ \chi_L $ is introduced. However, unlike$ \chi_R $ ,$ \chi_L $ does not couple with S. The electroweak symmetry is further broken down to electromagnetism through a bidoublet Higgs field that carries charges under both$ S U(2)_L $ and$ S U(2)_{R^\prime} $ , but has no$ B-L $ quantum numbers. This Higgs field is non-trivial under both$ S U(2)_L $ and$ S U(2)_{R^\prime} $ transformations but does not affect the$ B-L $ symmetry [11]. We represent it using a more intuitive process as follows:$\begin{aligned}& S U(2)_{L} \times S U(2)_{R^\prime} \times U(1)_{B-L}\times S \xrightarrow{\langle\chi_{R}\rangle} S U(2)_{L}\\&\quad \times U(1)_{Y} \xrightarrow{\langle\Phi\rangle,\langle\chi_{L}\rangle} U(1)_{EM}.\end{aligned} $

(2) The particles of ALRM along with the corresponding field representation are listed in Table 1.
Fields $ S U(3)_C \times S U(2)_L \times S U(2)_{R^\prime} \times U(1)_{B-L} $ 

S Fermions $ Q_L=\left( \begin{array}{c} u\\ d \end{array} \right)_L $ 

$ \left( \begin{array}{c} 3,2,1,+\frac{1}{6} \end{array} \right) $ 

$ 0 $ 

$ Q_R=\left( \begin{array}{c} u\\ d^\prime \end{array} \right)_R $ 

$ \left( \begin{array}{c} 3,1,2,+\frac{1}{6} \end{array} \right) $ 

$ -\frac{1}{2} $ 

$ d^\prime_L $ 

$ \left( \begin{array}{c} 3,1,1,-\frac{1}{3} \end{array} \right) $ 

$ -1 $ 

$ d_R $ 

$ \left( \begin{array}{c} 3,1,1,-\frac{1}{3} \end{array} \right) $ 

0 $ L_L=\left( \begin{array}{c} \nu\\ e \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,2,1,-\frac{1}{2} \end{array} \right) $ 

$ 0 $ 

$ L_R=\left( \begin{array}{c} n\\ e \end{array} \right)_R $ 

$ \left( \begin{array}{c} 1,1,2,-\frac{1}{2} \end{array} \right) $ 

$ +\frac{1}{2} $ 

$ n_L $ 

$ \left( \begin{array}{c} 1,1,1,0 \end{array} \right) $ 

$ +1 $ 

$ \nu_R $ 

$ \left( \begin{array}{c} 1,1,1,0 \end{array} \right) $ 

0 Higgs $ \Phi=\left( \begin{array}{c} \phi_1^0 \phi_1^+\\ \phi_2^- \phi_2^0 \end{array} \right)_R $ 

$ \left( \begin{array}{c} 1,2,2^*,0 \end{array} \right) $ 

$ -\frac{1}{2} $ 

$ X_L=\left( \begin{array}{c} \chi_L^+\\ \chi_L^0 \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,2,1,+\frac{1}{2} \end{array} \right) $ 

$ 0 $ 

$ X_R=\left( \begin{array}{c} \chi_R^+\\ \chi_R^0 \end{array} \right)_L $ 

$ \left( \begin{array}{c} 1,1,2,+\frac{1}{2} \end{array} \right) $ 

$ +\frac{1}{2} $ 

Table 1. Field content of the ALRM and respective quantum numbers.
Under the S symmetry, there are some odd S symmetry particles: scotinos
$ n_L $ ,$ n_R $ , exotic quarks$ d_L^{\prime} $ ,$ d_R^{\prime} $ , gauge boson$ W^\prime $ , and scalar particles. The Yukawa Lagrangian of ALRM is expressed as$\begin{aligned}[b] {\cal{L}}_{Y} =\;& \bar{Q}_{L} Y^{q} \tilde{\Phi} Q_{R} + \bar{Q}_{L} Y_{L}^{q} \chi_{L} d_{R} + \bar{Q}_{R} Y_{R}^{q} \chi_{R} d_{L}^{\prime}\\& + \bar{L}_{L} Y^{\ell} \Phi L_{R} + \bar{L}_{L} Y_{L}^{\ell} \tilde{\chi}_{L} \nu_{R} + \bar{L}_{R} Y_{R}^{\ell} \tilde{\chi}_{R} n_{L} + h.c.,\end{aligned} $

(3) where Y is a
$ 3\times3 $ matrix of Yukawa couplings, with subscripts L and R representing the left-handed and right-handed coupling matrices respectively, and superscripts q and l representing the quarks and leptons in the model. The vacuum expectation values (vevs) of the scalar fields are expressed as$ \begin{aligned}[b]&\langle \Phi \rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0&0\\ 0&k \end{array}} \right),\quad \left\langle {{\chi _L}} \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0\\ {{v_L}} \end{array}} \right),\\& \left\langle {{\chi _R}} \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0\\ {{v_R}} \end{array}} \right).\end{aligned} $

(4) The masses of the gauge bosons are generated through the left-right symmetry breaking the Higgs mechanism. The masses of the charged bosons are
$\begin{aligned}[b]& M_{W} = \frac{1}{2} g_L \sqrt{k^2 + v_L^2} \equiv \frac{1}{2} g_L v, \quad \text{and} \\& M_{W^\prime} = \frac{1}{2} g_R \sqrt{k^2 + v_R^2} \equiv \frac{1}{2} g_R v^\prime .\end{aligned} $

(5) However, because
$ \langle\phi_1^0\rangle = 0 $ , the produced charged bosons will not mix, which means that the$ W^{\prime\pm} $ and$ W^\pm $ particles will maintain their respective characteristics and will not convert into each other.The mass squared matrix of the neutral gauge bosons in the
$ \{W_{L\mu}^3 $ ,$ W_{R\mu}^3 $ ,$ B_\mu\} $ basis is$ ({\cal{M}}_V^0)^2 = \frac{1}{4}\left( {\begin{array}{*{20}{c}} {g_{B - L}^2(v_L^2 + v_R^2)}&{ - {g_{B - L}}{g_L}v_L^2}&{ - {g_{B - L}}{g_R}v_R^2}\\ { - {g_{B - L}}{g_L}v_L^2}&{g_L^2{v^2}}&{ - {g_L}{g_R}{k^2}}\\ { - {g_{B - L}}{g_R}v_R^2}&{ - {g_L}{g_R}{k^2}}&{g_R^2{{(v')}^2}} \end{array}} \right), $

(6) where
$ g_L,g_R $ and$ g_{B-L} $ are the gauge coupling constants of$ S U(2)_L,S U(2)_{R^\prime} $ and$ U(1)_{B-L} $ [29]. The matrix can be diagonalized through three rotations that mix B,$ W^3_L $ , and$ W^3_R $ bosons into the massless photon A and massive Z and$ Z' $ states:$ \begin{aligned}[b]\left( {\begin{array}{*{20}{c}} {{B_\mu }}\\ {W_{L\mu }^3}\\ {W_{R\mu }^3} \end{array}} \right) =\;& \left( {\begin{array}{*{20}{c}} {\cos {\phi _W}}&0&{ - \sin {\phi _W}}\\ 0&1&0\\ {\sin {\phi _W}}&0&{\cos {\phi _W}} \end{array}} \right)\\&\left( {\begin{array}{*{20}{c}} {\cos {\theta _W}}&{ - \sin {\theta _W}}&0\\ {\sin {\theta _W}}&{\cos {\theta _W}}&0\\ 0&0&1 \end{array}} \right)\\&\left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos {\zeta _W}}&{ - \sin {\zeta _W}}\\ 0&{\sin {\zeta _W}}&{\cos {\zeta _W}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{A_\mu }}\\ {{Z_\mu }}\\ {{{Z'}_\mu }} \end{array}} \right),\end{aligned} $

(7) where the
$ \phi_W $ rotation mixes the B and$ W^3_R $ bosons into the hypercharge boson B, generated by the breaking of$ S U(2)_{R'} \times U(1)_{B-L} $ into$ U(1)_Y $ .$ \theta_W $ represents the usual electroweak mixing, and the$ \zeta_W $ rotation is related to the strongly constrained$ Z-Z' $ mixing. The mass of the charged$ W^\prime $ boson is indirectly constrained by the mass ratio$ M_{W^\prime}/M_{Z'} = c_{\phi W} $ [10], so the constraint of$ M_{W^\prime} $ is weaker than that of the LRSM.In recent years, many research groups (such as the ATLAS Collaboration and CMS Collaboration) have been actively exploring the experimental constraints on the mass of the
$ W^\prime $ particle, achieving a great deal of results [30−38]. Below are some of the latest research findings on the mass constraints of$ W^\prime $ :CMS Sequential Standard Model [35] $ W^\prime\to e^-\nu $ 

$ M_{W^\prime}\geq 5.3 $ TeV

Left-Right Symmetric Model [36] $ W^\prime\to e^- N $ 

$ M_{W^\prime}\geq 4.7 $ TeV

$ W^\prime\to \mu^- N $ 

$ M_{W^\prime}\geq 5.0 $ TeV

ATLAS Sequential Standard Model ( $ g_L=g_R $ ) [37]

$ W^\prime\to \tau^-\nu $ 

$ M_{W^\prime}\geq 5.0 $ TeV

Sequential Standard Model ( $ g_L\neq g_R $ ) [37]

$ W^\prime\to \tau^-\nu $ 

$ M_{W^\prime}\geq 3.5\sim5.0 $ TeV

Left-Right Symmetric Model [38] $ W^\prime\to e^- n_e $ 

$ M_{W^\prime}\geq 4.8 $ TeV

$ W^\prime\to \mu^- n_{\mu} $ 

$ M_{W^\prime}\geq 5.0 $ TeV

Table 2. Mass constraints for
$ W^\prime $ from LHC.1. Bounds from CMS: The CMS Collaboration has searched for
$ W^\prime $ and heavy neutrino$ N_R $ with the signature of observing high transverse masses of the$ \tau- $ lepton and missing transverse momentum at the LHC with$ \sqrt{s} = 13 $ TeV, corresponding to an integrated luminosity of$ 35.9\ {\rm fb}^{-1} $ . The mass bound of$ W^\prime $ is$ M_{W^\prime}\geq 4.0 $ TeV, with the right-handed coupling equal to the SM coupling [34]. However, depending on the coupling in the non-universal$ G(221) $ model, the bound of the heavy$ W^\prime $ bosons is$ M_{W^\prime}\geq 1.7\sim3.9 $ TeV [34]. Within the framework of the Sequential Standard Model, a$ W^\prime $ boson with mass less than 5.3 TeV is excluded from the combined results of electron decay channels at the LHC with$ \sqrt{s} = 13 $ TeV [35]. The CMS Collaboration used data from Run 2 at the LHC to obtain constraints on the mass of the$ W^\prime $ boson, leveraging the Left-Right Symmetric Model at$ \sqrt{s} = 13 $ TeV. According to the assumption that the right-handed neutrino masses are equal to half the$ W^\prime $ mass, the mass of$ W^\prime $ is excluded at 95% confidence level up to 4.7 and 5.0 TeV for the electron and muon channels, respectively [36].2. Bounds from ATLAS: The ATLAS Collaboration has searched for
$ W^\prime $ by observing at high transverse masses of the$ \tau- $ lepton and missing transverse momentum at the LHC with$ \sqrt{s} = 13 $ TeV, corresponding to an integrated luminosity of$ 138\ {\rm fb}^{-1} $ . The present mass bounds of$ W^\prime $ is$ M_{W^\prime}\geq 5.0 $ TeV in the Sequential Standard Model, with the right-handed coupling equal to the SM coupling [37]. According to the assumption that the coupling in the non-universal coupling implies$ g_L\neq g_R $ , the mass of$ W^\prime $ is excluded at 95% confidence level up to$ 3.5 \sim 5.0 $ TeV for the τ channel in the Sequential Standard Model. For an integrated luminosity of$ 80\ {\rm fb}^{-1} $ , the mass of$ W^\prime $ is excluded at 95% confidence level up to 4.8 and 5.0 TeV for the electron and muon channels, respectively, in the Left-Right Symmetric Model [38].The constraints on the
$ W^\prime $ particle mentioned above arise from the analysis of LHC data by various experimental groups using different models. Most current experimental results for$ W^\prime $ particles are primarily obtained through the exploration of single production channels. Even when considering the pair production of$ W^\prime $ , the constraints on it become weaker. Therefore, we decided to investigate the properties of$ W^\prime $ particles by exploring the signals of their pair production at a muon collider. This issue is closely related to our studied model. Most of the experimental results available today are based on sequential models or the classical left-right symmetric model. In these models, the decay products of the newly introduced additional charged bosons are Standard Model particles (leptons or quarks). The mass of the$ W^\prime $ boson is experimentally expected to be at least approximately 5.0 TeV, owing to constraints from its dilepton decay channel at the LHC. However, in our study of the ALRM, the decay process of the$ W^\prime $ boson couples to the quark-exotic quark and charged lepton-scotino final states, which is a consequence of the discrete symmetry. In this model, we treat the scotino particle as a dark particle, which is unobservable. As a result, most of the experimental findings do not provide a good reference for ALRM. The value of the right-handed coupling constant$ g_R $ has a significant impact on the constraints of the$ W^\prime $ particle mass. When the value of$ g_R $ is relatively small, the lower limit of the$ W^\prime $ mass might be smaller. In the ALRM adopted in this study, the allowed range of$ g_R $ for the coupling with right-handed gauge bosons is$ 0.37 \sim 0.765 $ , where the lower limit comes from the theoretical restriction that$ g_R/g_L $ must be larger than tan$ \theta_W $ [39, 40], and the upper limit comes from the phenomenological specification of$ g_R $ [10]. -
In this section, we investigate the properties of
$ W^\prime $ in terms of pair production through different processes at a future μ collider. A μ collider is a proposed lepton collider with great potential; related contents can be found in references [41−44]. We chose the process$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ as our main subject in this study. Before delving into the specifics of this process, we first explore all the decay branching ratios of the$ W^\prime $ particle within this model, which will help us identify the main decay channels of$ W^\prime $ and analyze their various properties. -
In this section, we investigate the properties of
$ W^\prime $ in terms of pair production through different processes at a future μ collider. A μ collider is a proposed lepton collider with great potential; related contents can be found in references [41−44]. We chose the process$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ as our main subject in this study. Before delving into the specifics of this process, we first explore all the decay branching ratios of the$ W^\prime $ particle within this model, which will help us identify the main decay channels of$ W^\prime $ and analyze their various properties. -
In ALRM, similar to the Standard Model, gauge bosons can decay into leptons or quarks. Owing to the presence of a larger number of new particles in this model, the decay channels of the
$ W^\prime $ boson are more complicated than those of the gauge particles in the Standard Model. The main decay channels of the$ W^\prime $ particle are included in Fig. 1. Owing to the large mass of the$ W^\prime $ particle, it can decay into a wider array of final states. The masses of the new particles involved are set as$ M_{d^\prime ,n_e} = 300 $ GeV,$ M_{s^\prime ,n_\mu} = 500 $ GeV, and$ M_{t^\prime ,n_\tau} = 700 $ GeV.The coupling strength of the
$ W^\prime $ particle decaying into all generations of leptons (e, μ, τ) was set to the same value for simplicity in this study. When the$ W^\prime $ particle mass is less than 2 TeV, the decay branching ratio of the first generation light quarks is the largest. The decay branching ratio of the third generation increases with the$ W^\prime $ particle mass. For a mass of$ W^\prime $ larger than 3 TeV, the decay branching ratios of quark channels tend to similar values of approximately 0.25. Meanwhile, the decay branching ratio of the electron channel is approximately 0.06, while the muon and tau channels are slightly below 0.05.The decay process of
$ W^\prime $ also involves flavor-changing processes, but their decay branching ratios are less than 0.01 in our studied parameter spaces. Thus, they are not represented in Fig. 1. Interesting studies on the flavor-changing processes can be found in [45−47]; these processes lie beyond the scope of this study. -
In ALRM, similar to the Standard Model, gauge bosons can decay into leptons or quarks. Owing to the presence of a larger number of new particles in this model, the decay channels of the
$ W^\prime $ boson are more complicated than those of the gauge particles in the Standard Model. The main decay channels of the$ W^\prime $ particle are included in Fig. 1. Owing to the large mass of the$ W^\prime $ particle, it can decay into a wider array of final states. The masses of the new particles involved are set as$ M_{d^\prime ,n_e} = 300 $ GeV,$ M_{s^\prime ,n_\mu} = 500 $ GeV, and$ M_{t^\prime ,n_\tau} = 700 $ GeV.The coupling strength of the
$ W^\prime $ particle decaying into all generations of leptons (e, μ, τ) was set to the same value for simplicity in this study. When the$ W^\prime $ particle mass is less than 2 TeV, the decay branching ratio of the first generation light quarks is the largest. The decay branching ratio of the third generation increases with the$ W^\prime $ particle mass. For a mass of$ W^\prime $ larger than 3 TeV, the decay branching ratios of quark channels tend to similar values of approximately 0.25. Meanwhile, the decay branching ratio of the electron channel is approximately 0.06, while the muon and tau channels are slightly below 0.05.The decay process of
$ W^\prime $ also involves flavor-changing processes, but their decay branching ratios are less than 0.01 in our studied parameter spaces. Thus, they are not represented in Fig. 1. Interesting studies on the flavor-changing processes can be found in [45−47]; these processes lie beyond the scope of this study. -
Next, we focus on the process of
$ W^\prime $ decay into a pair of light leptons, i.e.,$ \mu^+\mu^-\to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ . Although the branching ratios for quark final states are significantly larger than those for lepton final states in previous studies, we chose the latter as the target process in this part for the following reasons. First, the final charged leptons as free particles can be measured more easily than the quarks at colliders. Second, the right-handed neutrinos produced can be considered as candidates for dark matter, leading to the large missing transverse momentum as a signature. Finally, in our chosen decay chains, the couplings of$ W^\prime $ and leptons without quarks are included, which is advantageous for the study of$ W^\prime $ and leptons interactions. All of our results were obtained through Monte Carlo simulations [48, 49]. -
Next, we focus on the process of
$ W^\prime $ decay into a pair of light leptons, i.e.,$ \mu^+\mu^-\to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ . Although the branching ratios for quark final states are significantly larger than those for lepton final states in previous studies, we chose the latter as the target process in this part for the following reasons. First, the final charged leptons as free particles can be measured more easily than the quarks at colliders. Second, the right-handed neutrinos produced can be considered as candidates for dark matter, leading to the large missing transverse momentum as a signature. Finally, in our chosen decay chains, the couplings of$ W^\prime $ and leptons without quarks are included, which is advantageous for the study of$ W^\prime $ and leptons interactions. All of our results were obtained through Monte Carlo simulations [48, 49]. -
Figure 2 shows the cross-section distribution of the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process with the right-handed coupling constant$ g_R $ . The plot in Fig. 2 (a) shows the cross section for different collision energies of 3, 6, and 10 TeV (represented by red, green, and yellow solid lines, respectively). In the ALRM model, the mass of the$ W^\prime $ boson is determined by the coupling constant$ g_R $ and a vacuum expectation value obtained from Eq. (5). When the vacuum expectation value is fixed, there is a one-to-one correspondence between the right-handed coupling constant$ g_R $ and the mass of the$ W^\prime $ particle. Therefore, we added coordinate axes for both$ g_R $ and$ M_{W^\prime} $ parameters in the figure. The vacuum expectation value is fixed at 6.5 TeV in this figure. When the collision energy is 3 TeV, the cross section rapidly decreases for$ g_R = 0.45 $ , with the mass of the$ W^\prime $ boson close to 1.5 TeV, given that it is approaching the threshold for$ W^\prime $ pair production. When$ g_R $ reaches its maximum of 0.765, the corresponding mass of the$ W^\prime $ boson produced is approximately 2.4 TeV, which means that the$ W^\prime $ bosons can be on shell produced with a collision energy of 6 or 10 TeV in the complete studied parameter spaces. The cross section at a collision energy of 6 TeV or 10 TeV shows a trend of first rising and then falling with increasing values of$ g_R $ . These phenomena are due to the dual impact of$ g_R $ and mass of$ W^\prime $ .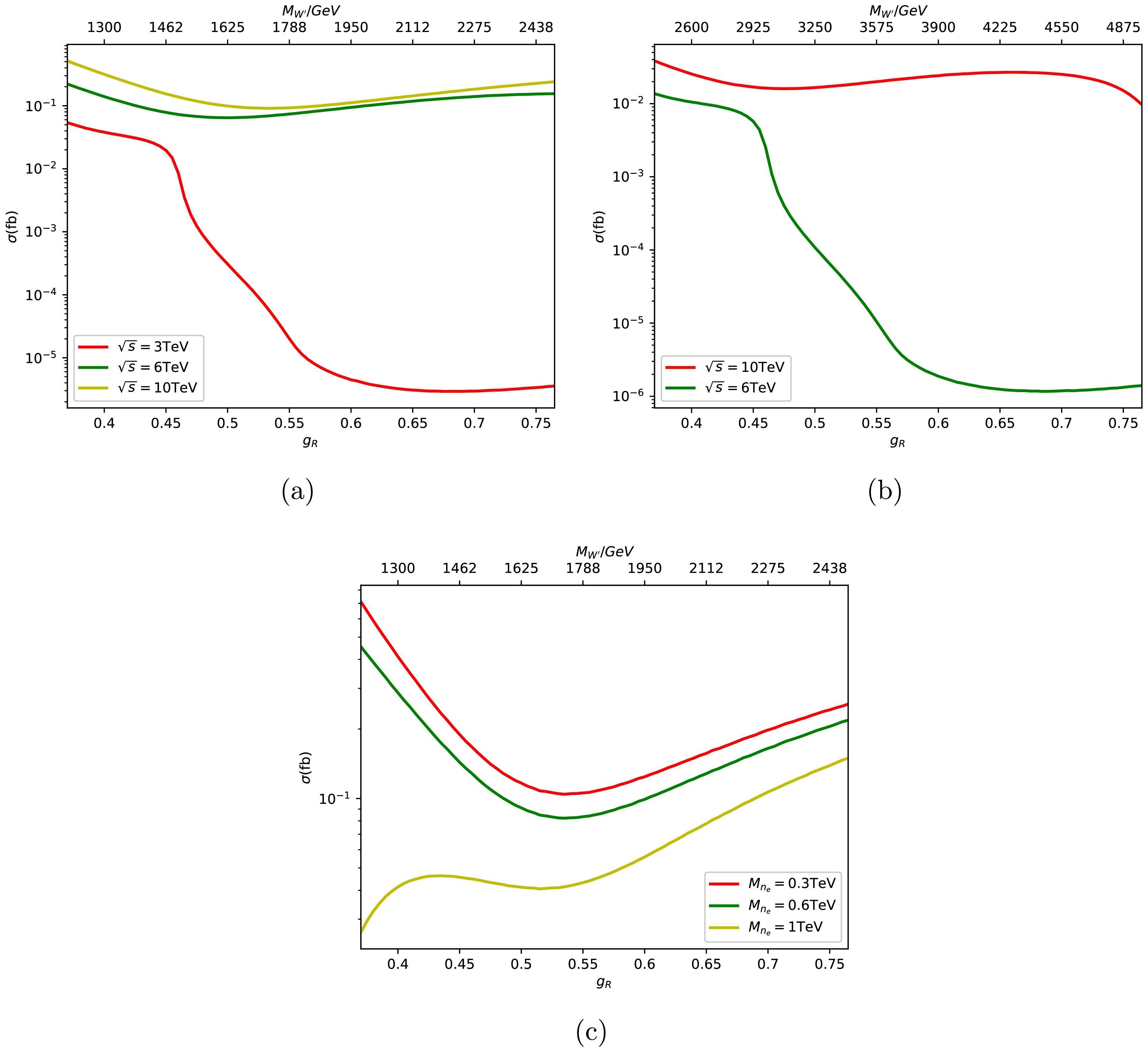
Figure 2. (color online) Cross section for the process
$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ versus different couplings in (a) and (b); (c) shows the cross section of the same process versus different values of$M_{n_e}$ for$\sqrt{s}=10$ TeV.The plot in Fig. 2 (b) also shows the cross section for the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process at collision energies of 6 and 10 TeV for different values of$ g_R $ . The differences between (a) and (b) result from different vacuum expectation values of the Higgs field, which leads to different$ W^\prime $ particle masses for the same coupling constant$ g_R $ . The vacuum expectation value is fixed at 13 TeV in Fig. 2 (b). Figure 2 (c) shows the cross section of the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process at a collision energy of 10 TeV for different neutrino mass scenarios (the red, green, and yellow solid lines represent the cross sections for neutrino masses of 0.3, 0.6, and 1 TeV, respectively). In this plot, the vacuum expectation value also remains at 6.5 TeV. When the neutrino mass is 0.3 (1) TeV, the cross section is approximately 0.41 (0.041)$ {\rm fb} $ for$ g_R = 0.4 $ and 0.24 (0.14)$ \rm fb $ for$ g_R = 0.75 $ . The neutrino mass has a significant impact on the cross section in the process of leptonic decaying channels.The polarization of the initial state particles can have a significant impact on the production of
$ W^\prime $ pairs. Figure 3 (a) shows that the cross section varies for different polarizations of the initial muons through the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process under a collision energy of 10 TeV and$ m_{W^\prime} = 2 $ TeV. The polarization varies from fully left-handed ($ P_{\mu} = -100 $ ) to fully right-handed ($ P_{\mu} = 100 $ ); some typical values are shown in the plots. Each curve in Fig. 3 represents a fixed polarization state of the$ \mu^- $ particle, with the polarization degree of the$ \mu^+ $ particle varying along the x-axis. The lines in Fig. 3 (a) reveals an important physics phenomenon. When the polarization of$ \mu^- $ is fixed, the cross section varies with the polarization of$ \mu^+ $ in different ways. When the polarization of$ \mu^- $ is 100, the cross section continuously decreases with the positive increase of$ \mu^+ $ polarization. When the polarization of$ \mu^- $ is$ -100 $ , the trend of the cross section continuously increases. Therefore, it provides the maximum and minimum values of the cross section in this process for the polarization conditions$ (P_{\mu^+},P_{\mu^-}) = (-100,100) $ and$ (P_{\mu^+},P_{\mu^-}) = (-100,-100) $ . In particular, when the$ \mu^- $ particles are fully polarized ($ P_{\mu^-} = \pm100 $ ), the trends in the plot become more pronounced, providing important clues about the characteristics of particle interactions under extreme polarization conditions. This is crucial for future studies on signal production enhancement.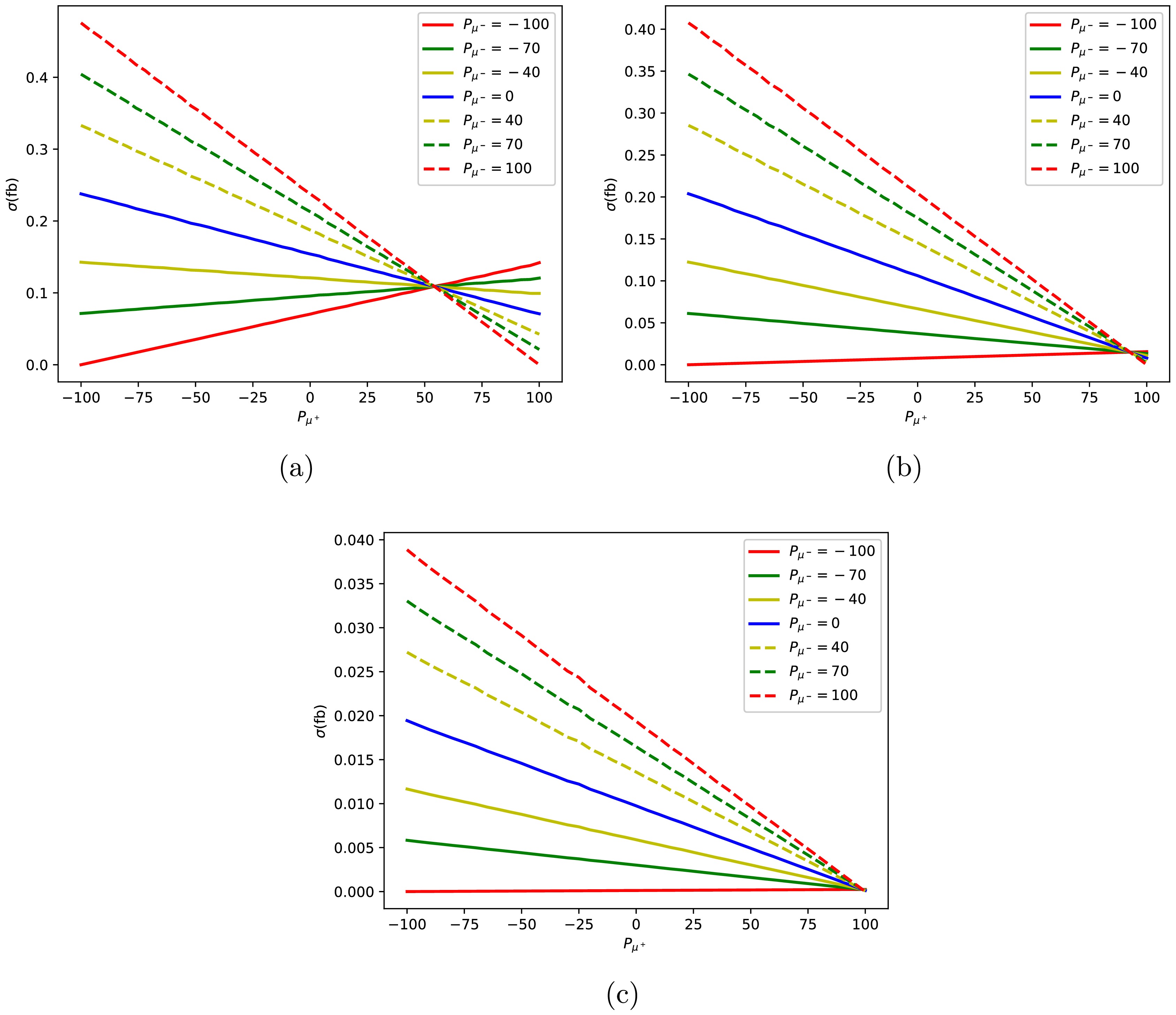
Figure 3. (color online) Cross-section distributions of the
$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ process for various initial state polarizations and$M_{W^\prime}=2$ TeV (a),$M_{W^\prime}=3.5$ TeV (b), and$M_{W^\prime}=5$ TeV (c) at a 10 TeV muon collider.Figures 3 (b) and (c) show the same distribution as that of (a) but for
$ M_{W^\prime} = 3.5 $ and 5 TeV. When the mass of$ W^\prime $ increases, the cross section changes significantly for$ P_{\mu^-}< 0 $ . When$ P_{\mu^-} $ equals$ -40 $ , the cross section for$ M_{W^\prime} $ at 2 TeV increases gradually with the positive polarization of$ \mu^+ $ , but for$ M_{W^\prime} $ at 3.5 TeV, the cross section exhibits a decreasing trend. It is important to note that when$ M_{W^\prime} $ takes values of 3.5 and 5 TeV and$ P_{\mu^-} = -100 $ , the cross section continuously increases with the positive polarization of$ \mu^+ $ , but the increase is relatively small. -
Figure 2 shows the cross-section distribution of the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process with the right-handed coupling constant$ g_R $ . The plot in Fig. 2 (a) shows the cross section for different collision energies of 3, 6, and 10 TeV (represented by red, green, and yellow solid lines, respectively). In the ALRM model, the mass of the$ W^\prime $ boson is determined by the coupling constant$ g_R $ and a vacuum expectation value obtained from Eq. (5). When the vacuum expectation value is fixed, there is a one-to-one correspondence between the right-handed coupling constant$ g_R $ and the mass of the$ W^\prime $ particle. Therefore, we added coordinate axes for both$ g_R $ and$ M_{W^\prime} $ parameters in the figure. The vacuum expectation value is fixed at 6.5 TeV in this figure. When the collision energy is 3 TeV, the cross section rapidly decreases for$ g_R = 0.45 $ , with the mass of the$ W^\prime $ boson close to 1.5 TeV, given that it is approaching the threshold for$ W^\prime $ pair production. When$ g_R $ reaches its maximum of 0.765, the corresponding mass of the$ W^\prime $ boson produced is approximately 2.4 TeV, which means that the$ W^\prime $ bosons can be on shell produced with a collision energy of 6 or 10 TeV in the complete studied parameter spaces. The cross section at a collision energy of 6 TeV or 10 TeV shows a trend of first rising and then falling with increasing values of$ g_R $ . These phenomena are due to the dual impact of$ g_R $ and mass of$ W^\prime $ .
Figure 2. (color online) Cross section for the process
$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ versus different couplings in (a) and (b); (c) shows the cross section of the same process versus different values of$M_{n_e}$ for$\sqrt{s}=10$ TeV.The plot in Fig. 2 (b) also shows the cross section for the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process at collision energies of 6 and 10 TeV for different values of$ g_R $ . The differences between (a) and (b) result from different vacuum expectation values of the Higgs field, which leads to different$ W^\prime $ particle masses for the same coupling constant$ g_R $ . The vacuum expectation value is fixed at 13 TeV in Fig. 2 (b). Figure 2 (c) shows the cross section of the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process at a collision energy of 10 TeV for different neutrino mass scenarios (the red, green, and yellow solid lines represent the cross sections for neutrino masses of 0.3, 0.6, and 1 TeV, respectively). In this plot, the vacuum expectation value also remains at 6.5 TeV. When the neutrino mass is 0.3 (1) TeV, the cross section is approximately 0.41 (0.041)$ {\rm fb} $ for$ g_R = 0.4 $ and 0.24 (0.14)$ \rm fb $ for$ g_R = 0.75 $ . The neutrino mass has a significant impact on the cross section in the process of leptonic decaying channels.The polarization of the initial state particles can have a significant impact on the production of
$ W^\prime $ pairs. Figure 3 (a) shows that the cross section varies for different polarizations of the initial muons through the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process under a collision energy of 10 TeV and$ m_{W^\prime} = 2 $ TeV. The polarization varies from fully left-handed ($ P_{\mu} = -100 $ ) to fully right-handed ($ P_{\mu} = 100 $ ); some typical values are shown in the plots. Each curve in Fig. 3 represents a fixed polarization state of the$ \mu^- $ particle, with the polarization degree of the$ \mu^+ $ particle varying along the x-axis. The lines in Fig. 3 (a) reveals an important physics phenomenon. When the polarization of$ \mu^- $ is fixed, the cross section varies with the polarization of$ \mu^+ $ in different ways. When the polarization of$ \mu^- $ is 100, the cross section continuously decreases with the positive increase of$ \mu^+ $ polarization. When the polarization of$ \mu^- $ is$ -100 $ , the trend of the cross section continuously increases. Therefore, it provides the maximum and minimum values of the cross section in this process for the polarization conditions$ (P_{\mu^+},P_{\mu^-}) = (-100,100) $ and$ (P_{\mu^+},P_{\mu^-}) = (-100,-100) $ . In particular, when the$ \mu^- $ particles are fully polarized ($ P_{\mu^-} = \pm100 $ ), the trends in the plot become more pronounced, providing important clues about the characteristics of particle interactions under extreme polarization conditions. This is crucial for future studies on signal production enhancement.
Figure 3. (color online) Cross-section distributions of the
$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ process for various initial state polarizations and$M_{W^\prime}=2$ TeV (a),$M_{W^\prime}=3.5$ TeV (b), and$M_{W^\prime}=5$ TeV (c) at a 10 TeV muon collider.Figures 3 (b) and (c) show the same distribution as that of (a) but for
$ M_{W^\prime} = 3.5 $ and 5 TeV. When the mass of$ W^\prime $ increases, the cross section changes significantly for$ P_{\mu^-}< 0 $ . When$ P_{\mu^-} $ equals$ -40 $ , the cross section for$ M_{W^\prime} $ at 2 TeV increases gradually with the positive polarization of$ \mu^+ $ , but for$ M_{W^\prime} $ at 3.5 TeV, the cross section exhibits a decreasing trend. It is important to note that when$ M_{W^\prime} $ takes values of 3.5 and 5 TeV and$ P_{\mu^-} = -100 $ , the cross section continuously increases with the positive polarization of$ \mu^+ $ , but the increase is relatively small. -
The angular distribution of the final particle is an important observable for the study of the properties of the
$ W^\prime $ boson. The formula for the angular distribution is$ \cos\theta = \frac{{{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}} \cdot {{\boldsymbol{p}}_{{\boldsymbol{i}}}}}{|{{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}}|\cdot |{{\boldsymbol{p}}_{{\boldsymbol{i}}}} |}, $

(8) where
$ {{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}} $ and$ {{\boldsymbol{p}}_{{\boldsymbol{i}}}} $ are the three momenta of the final and initial particles, respectively.In this study, the influence of angular distribution variables has been mainly analyzed by focusing on two aspects: the spin polarization of the incident particles and the variation of coupling constants [50], which are essentially the result of the combined action of angular momentum conservation and chirality rules. First, changes in the spin polarization state of incident particles affect the polarization direction of intermediate-state particles. This leads to a preference for a specific direction in the decay process of intermediate particles into final-state particles. Therefore, different polarization states will influence the angular distribution of the final-state particles. Second, the change in angular distribution is caused by the chiral asymmetry of the coupling strength, which is related to the right-handed coupling
$ g_R $ and different vacuum expectation values in the model. The V-A structure of the gauge interaction in the model leads to coupling differences between left-handed and right-handed particles, resulting in an asymmetric production process of final-state particles.Figure 4 (a) shows the effects of different values of the coupling constant
$ g_R $ on the angular distributions between$ \mu^- $ and$ e^- $ particles of the process$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ , with a vacuum expectation value of 6.5 TeV. For the unpolarized initial state, the coupling constant$ g_R $ has a significant impact on the angular distribution of the final-state particles. In Fig. 4 (a), when the value of the right-handed coupling constant$ g_R $ is 0.37, the angular distribution becomes symmetric. Note also the evident increase in the asymmetry of the angular distribution of the final-state particles as the coupling constant increases. When the right-handed coupling constant is 0.765, the cross section clearly enhances, with cosθ approaching unity.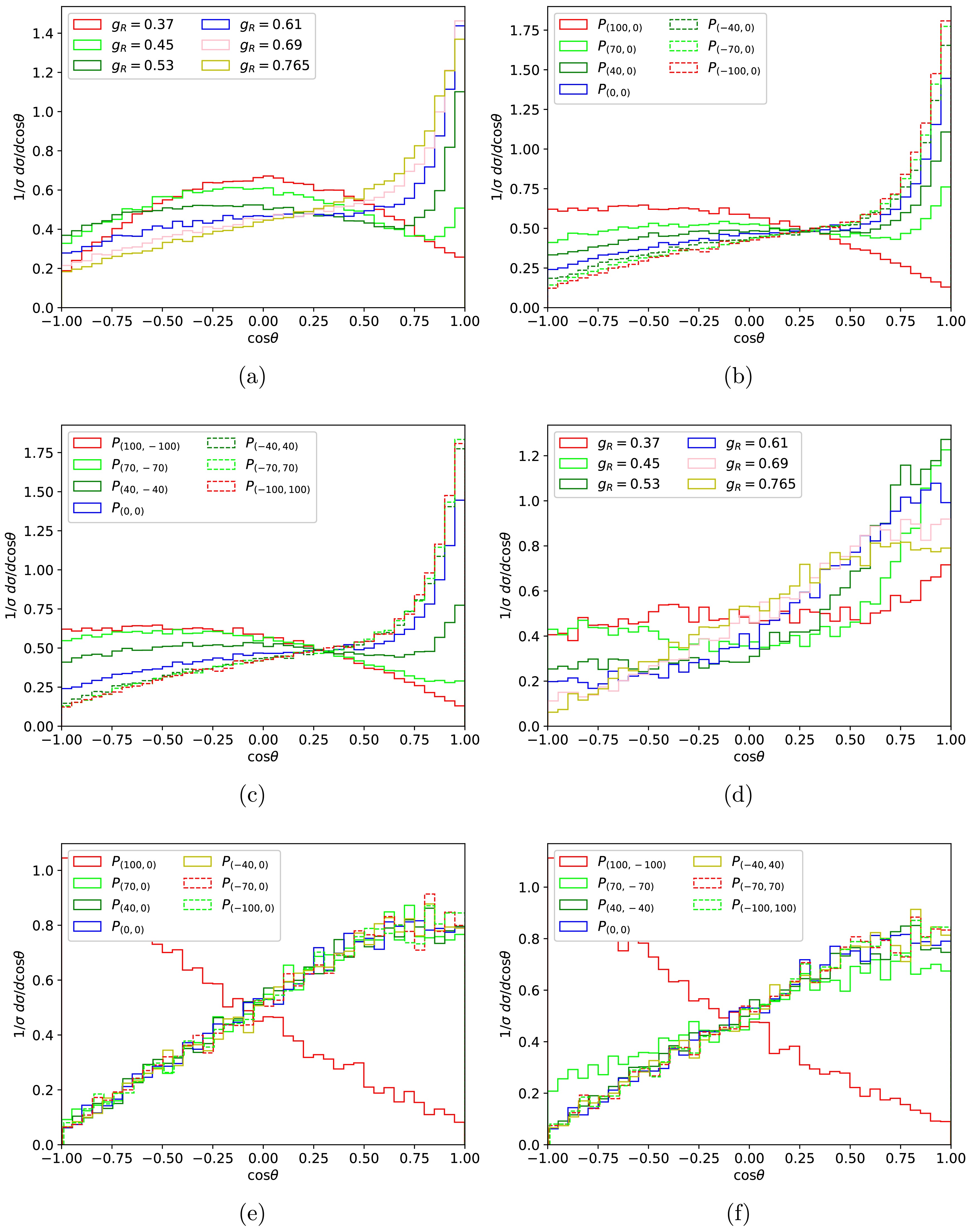
Figure 4. (color online) Angular distributions between
$\mu^-$ and$e^-$ of the unpolarized and polarized processes$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to $ $ e^+ e^- n_e \bar{n}_e$ for a collision energy of 10 TeV. The vacuum expectation is 6.5 TeV in (a) and 13 TeV in (d). The mass of$W^\prime$ is fixed at 2 TeV in (b) and (c) for$g_R=0.65$ , and$M_{W^\prime}=5$ TeV,$g_R=0.765$ in (e) and (f).Figure 4 (b) shows the impact of polarization of the initial
$ \mu^- $ on the final electron angular distributions. As the polarization strength increases, the changes in the angular distributions become more pronounced. Figure 4 (c) shows the angular distributions resulting from polarization of both initial$ \mu^- $ and$ \mu^+ $ . Note that, compared to Fig. 4 (b), polarizing both particles to the same extent on the basis of Fig. 4 (b) does not have a significant impact on the angular distribution.Figure 4 (d) also shows the angular distributions of final-state electrons with unpolarized initial particles for a vacuum expectation value of 13 TeV. Figures 4 (e) and (f) show the angular distributions of the final-state particles under polarized condition when the
$ W^\prime $ mass is 5 TeV. The results show that the angular distributions tend to the same shapes for various initial polarizations except for the case of values of$ P_{\mu^+} $ extremely close to 100.The mass of
$ W^\prime $ has a significant effect on the angular distribution of final electrons from the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process, as shown in Fig. 5. The mass of$ W^\prime $ was set at 2, 3.5, and 5 TeV for a collision energy of 10 TeV. The asymmetry of the angular distribution becomes more evident with the increase of the$ W^\prime $ mass. Moreover, the angular distributions tend to consistency as the mass of$ W^\prime $ increases to the threshold of$ W^\prime $ pair production. Note also that the effects of different$ g_R $ values are suppressed as the$ W^\prime $ mass increases.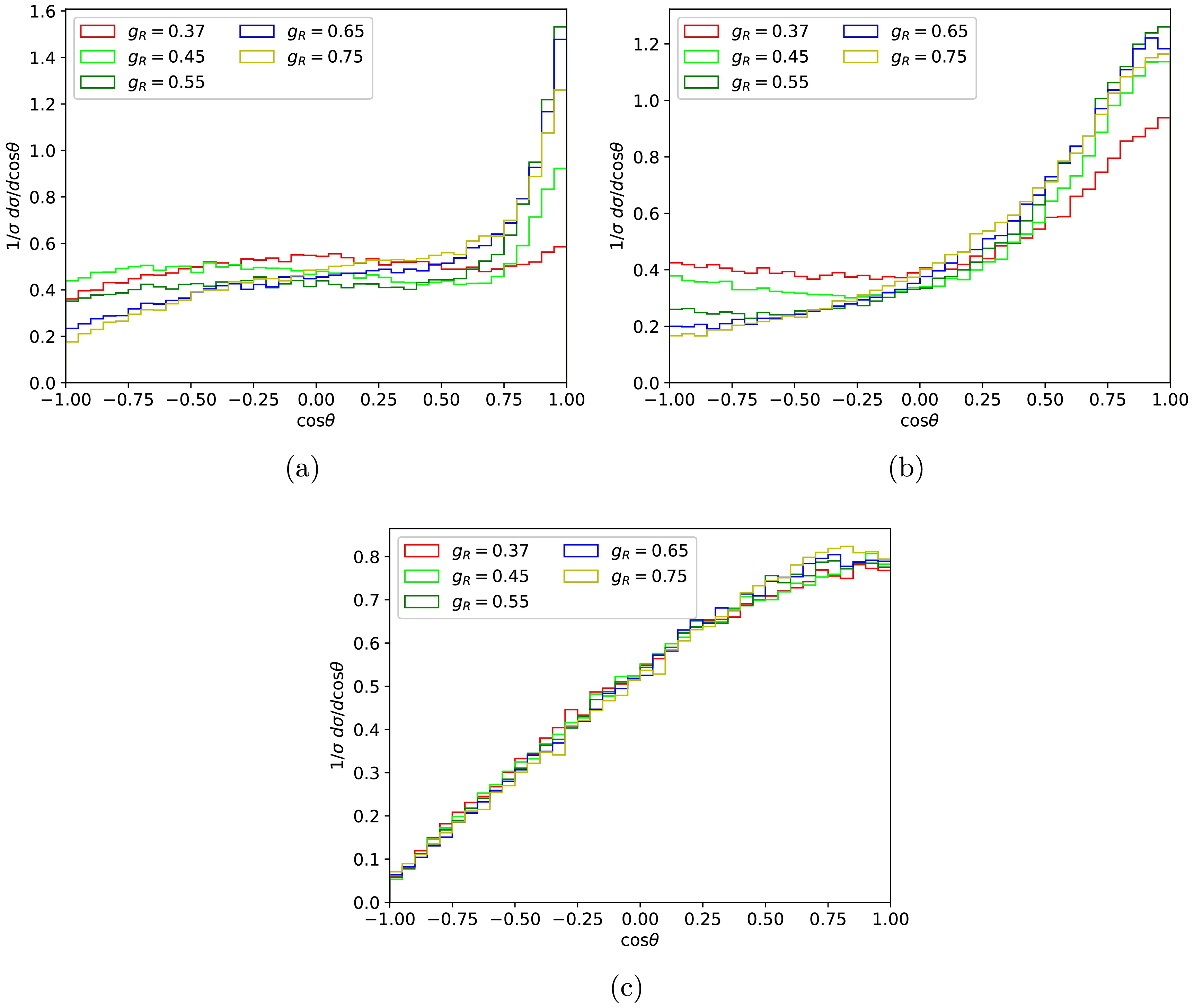
Figure 5. Angular distributions between
$\mu^-$ and$e^-$ of the unpolarized processes$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ corresponding to a collision energy of 10 TeV for$M_{W^\prime}=$ 2 TeV (a), 3.5 TeV (b), and 5 TeV (c), respectively.Forward-backward asymmetry is a specific aspect of angular distribution that describes the difference in emission probabilities of particles in the forward (
$ \cos\theta \geq 0 $ ) and backward ($ \cos\theta < 0 $ ) hemispheres. We define the formula for$ A_{FB} $ as$ A_{FB} = \frac{\sigma(\cos\theta\geq 0)-\sigma(\cos\theta<0)}{\sigma(\cos\theta\geq 0)+\sigma(\cos\theta<0)}. $

(9) A key aspect of this study concerning angular distribution is related to establishing a relationship between
$ A_{FB} $ and the coupling constants of the$ W^\prime $ particle. When a large number of background processes are present in the process, they can interfere with the variation characteristics of the signal process. Additionally, regarding the background information mentioned above, in the significance calculation process, the three background processes we mentioned are$ \mu^+ \mu^- \to W^+ W^- \to e^+ e^- \nu_e \bar{\nu}_e, \mu^+ \mu^- \to Z Z \to e^+ e^- \nu_e \bar{\nu}_e, \mu^+ \mu^- \to Z \nu_m \bar{\nu}_m,(Z \to e^+ e^-) $ . When the cut conditions mentioned in the paper are satisfied, the signal process can be completely separated from the background processes. At this point, the background has little effect on the angular distribution. Therefore, based on the complete separation of the signal process, we only simulated the angular distribution of the final-state particles of the signal process.Table 3 presents the forward-backward asymmetry of final electrons in the process
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ for various right-handed couplings and polarization of initial states. The asymmetry was 0.005 (0.37) for$ g_R = 0.37 $ (0.765) and a fixed vacuum expectation value of 6.5 TeV. The asymmetry varies from$ -0.24 $ to$ 0.42 $ with polarizations from$ P_{\mu^+} = 100 $ to$ P_{\mu^+} = -100 $ . Comparing the results of the second and third columns, one can find that the inversed polarization of$ \mu^- $ has little influence on the asymmetries.$ g_R $ 

$ A_{FB} $ 

$ P_{(P_{\mu^+},P_{\mu^-})} $ 

$ A_{FB} $ 

$ P_{(P_{\mu^+},P_{\mu^-})} $ 

$ A_{FB} $ 

$ 0.37 $ 

$ 0.005 $ 

$ (100,0) $ 

$ -0.24 $ 

$ (100,-100) $ 

$ -0.24 $ 

$ 0.45 $ 

$ -0.043 $ 

$ (70,0) $ 

$ 0.0016 $ 

$ (70,-70) $ 

$ -0.18 $ 

$ 0.53 $ 

$ 0.034 $ 

$ (40,0) $ 

$ 0.14 $ 

$ (40,-40) $ 

$ 0.013 $ 

$ 0.61 $ 

$ 0.21 $ 

$ (-40,0) $ 

$ 0.34 $ 

$ (-40,40) $ 

$ 0.39 $ 

$ 0.69 $ 

$ 0.31 $ 

$ (-70,0) $ 

$ 0.39 $ 

$ (-70,70) $ 

$ 0.41 $ 

$ 0.765 $ 

$ 0.37 $ 

$ (-100,0) $ 

$ 0.42 $ 

$ (-100,100) $ 

$ 0.42 $ 

Table 3. Forward-backward asymmetry under different conditions for
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n_e} $ . The vacuum expectation value is fixed at 6.5 TeV in the first column, and$ M_{W^\prime} $ is 2 TeV in the second and third columns. -
The angular distribution of the final particle is an important observable for the study of the properties of the
$ W^\prime $ boson. The formula for the angular distribution is$ \cos\theta = \frac{{{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}} \cdot {{\boldsymbol{p}}_{{\boldsymbol{i}}}}}{|{{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}}|\cdot |{{\boldsymbol{p}}_{{\boldsymbol{i}}}} |}, $

(8) where
$ {{\boldsymbol{p}}_{{\boldsymbol{f}}}^{\bf{*}}} $ and$ {{\boldsymbol{p}}_{{\boldsymbol{i}}}} $ are the three momenta of the final and initial particles, respectively.In this study, the influence of angular distribution variables has been mainly analyzed by focusing on two aspects: the spin polarization of the incident particles and the variation of coupling constants [50], which are essentially the result of the combined action of angular momentum conservation and chirality rules. First, changes in the spin polarization state of incident particles affect the polarization direction of intermediate-state particles. This leads to a preference for a specific direction in the decay process of intermediate particles into final-state particles. Therefore, different polarization states will influence the angular distribution of the final-state particles. Second, the change in angular distribution is caused by the chiral asymmetry of the coupling strength, which is related to the right-handed coupling
$ g_R $ and different vacuum expectation values in the model. The V-A structure of the gauge interaction in the model leads to coupling differences between left-handed and right-handed particles, resulting in an asymmetric production process of final-state particles.Figure 4 (a) shows the effects of different values of the coupling constant
$ g_R $ on the angular distributions between$ \mu^- $ and$ e^- $ particles of the process$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ , with a vacuum expectation value of 6.5 TeV. For the unpolarized initial state, the coupling constant$ g_R $ has a significant impact on the angular distribution of the final-state particles. In Fig. 4 (a), when the value of the right-handed coupling constant$ g_R $ is 0.37, the angular distribution becomes symmetric. Note also the evident increase in the asymmetry of the angular distribution of the final-state particles as the coupling constant increases. When the right-handed coupling constant is 0.765, the cross section clearly enhances, with cosθ approaching unity.
Figure 4. (color online) Angular distributions between
$\mu^-$ and$e^-$ of the unpolarized and polarized processes$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to $ $ e^+ e^- n_e \bar{n}_e$ for a collision energy of 10 TeV. The vacuum expectation is 6.5 TeV in (a) and 13 TeV in (d). The mass of$W^\prime$ is fixed at 2 TeV in (b) and (c) for$g_R=0.65$ , and$M_{W^\prime}=5$ TeV,$g_R=0.765$ in (e) and (f).Figure 4 (b) shows the impact of polarization of the initial
$ \mu^- $ on the final electron angular distributions. As the polarization strength increases, the changes in the angular distributions become more pronounced. Figure 4 (c) shows the angular distributions resulting from polarization of both initial$ \mu^- $ and$ \mu^+ $ . Note that, compared to Fig. 4 (b), polarizing both particles to the same extent on the basis of Fig. 4 (b) does not have a significant impact on the angular distribution.Figure 4 (d) also shows the angular distributions of final-state electrons with unpolarized initial particles for a vacuum expectation value of 13 TeV. Figures 4 (e) and (f) show the angular distributions of the final-state particles under polarized condition when the
$ W^\prime $ mass is 5 TeV. The results show that the angular distributions tend to the same shapes for various initial polarizations except for the case of values of$ P_{\mu^+} $ extremely close to 100.The mass of
$ W^\prime $ has a significant effect on the angular distribution of final electrons from the$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process, as shown in Fig. 5. The mass of$ W^\prime $ was set at 2, 3.5, and 5 TeV for a collision energy of 10 TeV. The asymmetry of the angular distribution becomes more evident with the increase of the$ W^\prime $ mass. Moreover, the angular distributions tend to consistency as the mass of$ W^\prime $ increases to the threshold of$ W^\prime $ pair production. Note also that the effects of different$ g_R $ values are suppressed as the$ W^\prime $ mass increases.
Figure 5. Angular distributions between
$\mu^-$ and$e^-$ of the unpolarized processes$\mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e$ corresponding to a collision energy of 10 TeV for$M_{W^\prime}=$ 2 TeV (a), 3.5 TeV (b), and 5 TeV (c), respectively.Forward-backward asymmetry is a specific aspect of angular distribution that describes the difference in emission probabilities of particles in the forward (
$ \cos\theta \geq 0 $ ) and backward ($ \cos\theta < 0 $ ) hemispheres. We define the formula for$ A_{FB} $ as$ A_{FB} = \frac{\sigma(\cos\theta\geq 0)-\sigma(\cos\theta<0)}{\sigma(\cos\theta\geq 0)+\sigma(\cos\theta<0)}. $

(9) A key aspect of this study concerning angular distribution is related to establishing a relationship between
$ A_{FB} $ and the coupling constants of the$ W^\prime $ particle. When a large number of background processes are present in the process, they can interfere with the variation characteristics of the signal process. Additionally, regarding the background information mentioned above, in the significance calculation process, the three background processes we mentioned are$ \mu^+ \mu^- \to W^+ W^- \to e^+ e^- \nu_e \bar{\nu}_e, \mu^+ \mu^- \to Z Z \to e^+ e^- \nu_e \bar{\nu}_e, \mu^+ \mu^- \to Z \nu_m \bar{\nu}_m,(Z \to e^+ e^-) $ . When the cut conditions mentioned in the paper are satisfied, the signal process can be completely separated from the background processes. At this point, the background has little effect on the angular distribution. Therefore, based on the complete separation of the signal process, we only simulated the angular distribution of the final-state particles of the signal process.Table 3 presents the forward-backward asymmetry of final electrons in the process
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ for various right-handed couplings and polarization of initial states. The asymmetry was 0.005 (0.37) for$ g_R = 0.37 $ (0.765) and a fixed vacuum expectation value of 6.5 TeV. The asymmetry varies from$ -0.24 $ to$ 0.42 $ with polarizations from$ P_{\mu^+} = 100 $ to$ P_{\mu^+} = -100 $ . Comparing the results of the second and third columns, one can find that the inversed polarization of$ \mu^- $ has little influence on the asymmetries.$ g_R $ 

$ A_{FB} $ 

$ P_{(P_{\mu^+},P_{\mu^-})} $ 

$ A_{FB} $ 

$ P_{(P_{\mu^+},P_{\mu^-})} $ 

$ A_{FB} $ 

$ 0.37 $ 

$ 0.005 $ 

$ (100,0) $ 

$ -0.24 $ 

$ (100,-100) $ 

$ -0.24 $ 

$ 0.45 $ 

$ -0.043 $ 

$ (70,0) $ 

$ 0.0016 $ 

$ (70,-70) $ 

$ -0.18 $ 

$ 0.53 $ 

$ 0.034 $ 

$ (40,0) $ 

$ 0.14 $ 

$ (40,-40) $ 

$ 0.013 $ 

$ 0.61 $ 

$ 0.21 $ 

$ (-40,0) $ 

$ 0.34 $ 

$ (-40,40) $ 

$ 0.39 $ 

$ 0.69 $ 

$ 0.31 $ 

$ (-70,0) $ 

$ 0.39 $ 

$ (-70,70) $ 

$ 0.41 $ 

$ 0.765 $ 

$ 0.37 $ 

$ (-100,0) $ 

$ 0.42 $ 

$ (-100,100) $ 

$ 0.42 $ 

Table 3. Forward-backward asymmetry under different conditions for
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n_e} $ . The vacuum expectation value is fixed at 6.5 TeV in the first column, and$ M_{W^\prime} $ is 2 TeV in the second and third columns. -
We ran Monte Carlo simulations [48, 51−53] to simulate collisions for signal and background processes, focusing on the di-lepton processes. In our simulations, we paid attention to the signal process with
$ W^\prime $ pair production as an intermediate state,$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e. $

(10) The main background processes include the production of
$ ZZ $ ,$ WW $ particles and the VBF process directly constituted by Z and neutrinos. The background processes are$ \mu^+ \mu^- \to W^+ W^- \to e^+ e^- \nu_e \bar{\nu}_e, $

(11) $ \mu^+ \mu^- \to Z Z \to e^+ e^- \nu_e \bar{\nu}_e, $

(12) $ \mu^+ \mu^- \to Z \nu_m \bar{\nu}_m,(Z \to e^+ e^-). $

(13) Here, the left-handed and right-handed neutrinos cannot be directly detected in the colliders. We treat them as missing transverse energy.
The signal-to-noise ratio is a measure of the strength of a signal relative to the level of background noise. Another approach to compare the signal and backgrounds is the significance. These two values can be expressed as
$ S/B = \frac{\sigma_{S}}{\sigma_{B}},\; \; S/\sqrt{B} = \frac{\sigma_{S}\times I}{\sqrt{\sigma_{B}\times I}}, $

(14) where
$ \sigma_{S} $ represents the cross section of the signal and$ \sigma_{B} $ represents the cross section of the backgrounds. I represents the integrated luminosity of the collider, which was set to$ 10~{\rm ab}^{-1} $ in this study.To distinguish the signal from the backgrounds, we show some kinematic distributions in Fig. 6. The collision energy was set to 10 TeV and
$ m_{W^\prime} = 2 $ TeV. Here,$ P_T $ represents the transverse momentum of the final-state electrons in Fig. 6 (a); η is the pseudo-rapidity of electrons in Fig. 6 (b). Another important parameter is α in Fig. 6 (c), which is the azimuthal angle of the final-state electrons calculated from the angle between the two charged leptons in the transverse plane; it is is defined as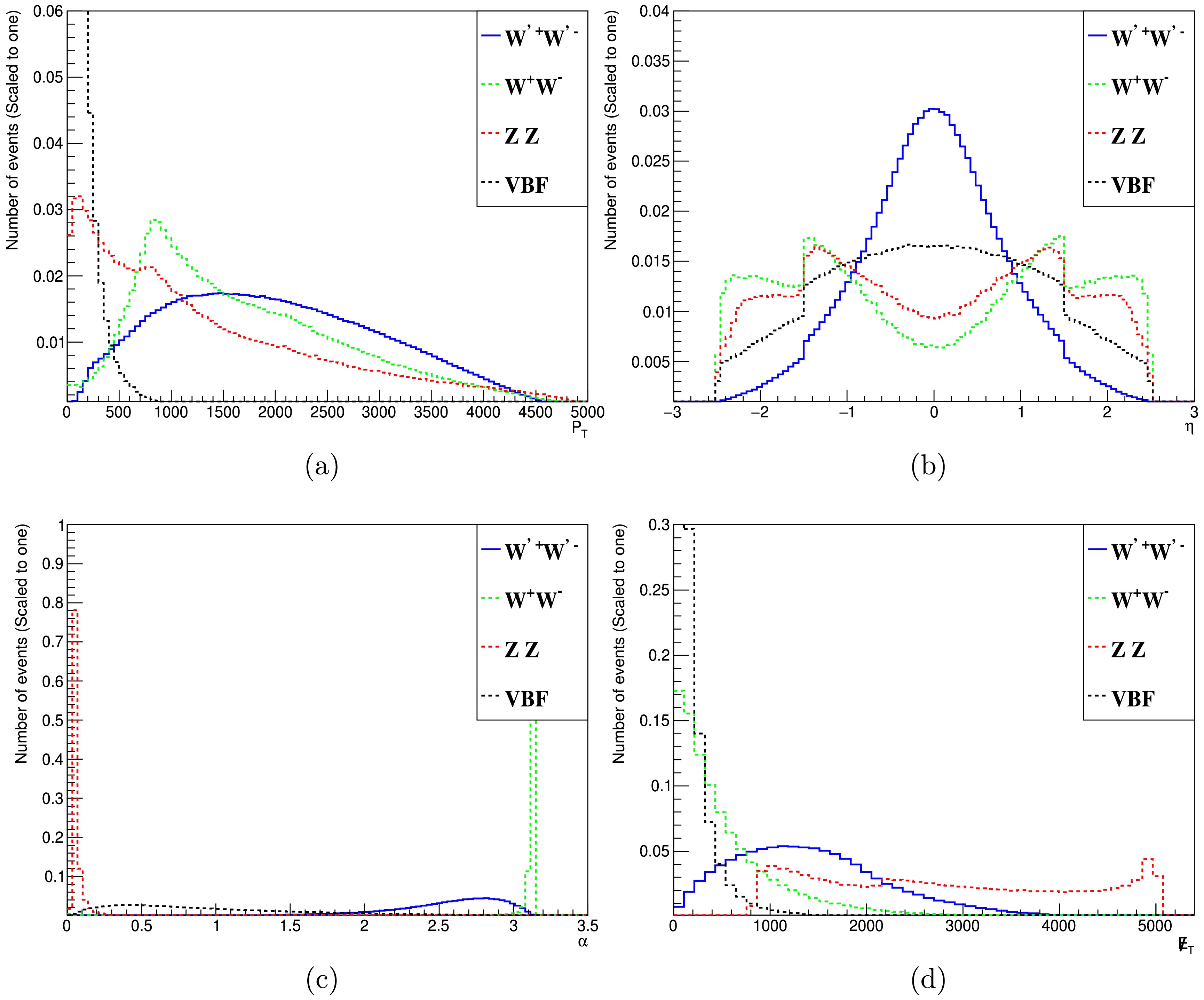
Figure 6. (color online) Kinematic distributions of the final particles for the signal and background processes before the cuts; (a), (b), and (c) represent the transverse momentum
$ P_T $ , pseudo-rapidity η, and correlated angle α between the two charged particles in the final state, respectively, and (d) represents the missing transverse energy$ \not {E}_T $ .$ \cos\alpha = \frac{{{\boldsymbol{p}}_{{\boldsymbol{e}}^+}^{\bf{*}}} \cdot {{\boldsymbol{p}}_{{\boldsymbol{e}}^-}}}{|{{\boldsymbol{p}}_{{\boldsymbol{e}}^+}^{\bf{*}}}|\cdot |{{\boldsymbol{p}}_{{\boldsymbol{e}}^-}} |}, $

(15) where
$ p_e $ denote the three-momentum vectors of the electrons in the relevant frame. The different distributions shown in Fig. 6 (c) between the signal process and background processes are determined by the kinematic characteristics of the collision process. The two background processes with distinct differences are those with intermediate states of Z bosons and W boson pairs, whose Feynman diagrams correspond to the t-channel and$ s/t $ -channels [54], respectively. For large collision energies,$ W/Z $ will be highly boosted, which will cause a distribution featuring a sharp peak. Concerning the large mass of the intermediate particle of$ W^\prime $ in the signal process as well as the heavy neutrino mass, the boost effects will be small, leading to much flatter distributions in the signal process. The last one in Fig. 6 (d) is$ \not {E}_T $ , which represents the transverse energy carried away by the neutrinos. From these distributions, we can determine the discrepancies between the signal and background processes.We searched for
$ W^\prime $ pair production by setting different masses of 2, 4.5, and 4.8 TeV at a collision energy of 10 TeV. Different cuts were applied to enhance the significance. The results are comprehensively listed in Table 4. The basic cuts are defined by setting a number of final-state electrons of two, and both of them are charge conjugates with transverse momentum$ P_T>10 $ GeV. When the cuts on the final-state electrons are set as$ P_T>400 $ GeV and$ 0.5< \alpha<3.1 $ , the signal-to-noise ratio reaches 17 and the significance reaches 101.62 for 2 TeV$ W^\prime $ . When the$ W^\prime $ mass is up to 4.5 TeV, the cuts change to$ 600<P_T<3700 $ GeV and$ 0.5< \alpha<3 $ . The signal-to-noise ratio is 9.47 and the significance value is 28.91. The results for$ m_{W^\prime} = 4.8 $ TeV correspond to cuts of$ 600<P_T< 3500 $ GeV and$ 0.5< \alpha<3 $ . The signal-to-noise ratio is 5.42 and the significance value is 16.35. For a mass of$ W^\prime $ close to 5 TeV and a threshold of pair production for collision energy of 10 TeV, the cross section decreases sharply with increasing mass, leading to an evident decrease of the significance.$ m_{W^\prime} $ 

Cut range $ \sigma_{WW} $ 

$ \sigma_{ZZ} $ 

$ \sigma_{VBF} $ 

$ \sigma_{S} $ 

$ S/\sqrt{B} $ 

$ S/B $ 

2 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.066 $ 

$ 0.0015 $ 

$ 0.98 $ 

$ P_T>400 $ GeV

$ 0.058 $ 

$ 0.00087 $ 

$ 0.31 $ 

$ 0.061 $ 

$ 0.16 $ 

$ 10.02 $ 

$ 0.5< \alpha<3.1 $ 

$ 0.0036 $ 

$ 0 $ 

$ 0 $ 

$ 0.061 $ 

$ 17 $ 

$ 101.62 $ 

4.5 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.0095 $ 

$ 2.1\times 10^{-4} $ 

$ 0.14 $ 

$ 600<P_T<3700 $ GeV

$ 0.047 $ 

$ 0.00056 $ 

$ 0.089 $ 

$ 0.0091 $ 

$ 0.066 $ 

$ 2.45 $ 

$ 0.5< \alpha<3 $ 

$ 0.00093 $ 

$ 0 $ 

$ 0 $ 

$ 0.0088 $ 

$ 9.47 $ 

$ 28.91 $ 

4.8 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.0053 $ 

$ 1.2\times 10^{-4} $ 

$ 0.079 $ 

$ 600<P_T<3500 $ GeV

$ 0.046 $ 

$ 0.00054 $ 

$ 0.089 $ 

$ 0.0051 $ 

$ 0.038 $ 

$ 1.38 $ 

$ 0.5< \alpha<3 $ 

$ 0.00091 $ 

$ 0 $ 

$ 0 $ 

$ 0.0049 $ 

$ 5.42 $ 

$ 16.35 $ 

Table 4. Signal-to-noise ratio and significance after cuts for masses of
$ W^\prime $ of 2, 4.5, and 4.8 TeV and a collision energy of 10 TeV; the integrated luminosity of the collider was set as$ 10~ {\rm ab^{-1}} $ . The unit of σ is$ \rm fb $ . -
We ran Monte Carlo simulations [48, 51−53] to simulate collisions for signal and background processes, focusing on the di-lepton processes. In our simulations, we paid attention to the signal process with
$ W^\prime $ pair production as an intermediate state,$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e. $

(10) The main background processes include the production of
$ ZZ $ ,$ WW $ particles and the VBF process directly constituted by Z and neutrinos. The background processes are$ \mu^+ \mu^- \to W^+ W^- \to e^+ e^- \nu_e \bar{\nu}_e, $

(11) $ \mu^+ \mu^- \to Z Z \to e^+ e^- \nu_e \bar{\nu}_e, $

(12) $ \mu^+ \mu^- \to Z \nu_m \bar{\nu}_m,(Z \to e^+ e^-). $

(13) Here, the left-handed and right-handed neutrinos cannot be directly detected in the colliders. We treat them as missing transverse energy.
The signal-to-noise ratio is a measure of the strength of a signal relative to the level of background noise. Another approach to compare the signal and backgrounds is the significance. These two values can be expressed as
$ S/B = \frac{\sigma_{S}}{\sigma_{B}},\; \; S/\sqrt{B} = \frac{\sigma_{S}\times I}{\sqrt{\sigma_{B}\times I}}, $

(14) where
$ \sigma_{S} $ represents the cross section of the signal and$ \sigma_{B} $ represents the cross section of the backgrounds. I represents the integrated luminosity of the collider, which was set to$ 10~{\rm ab}^{-1} $ in this study.To distinguish the signal from the backgrounds, we show some kinematic distributions in Fig. 6. The collision energy was set to 10 TeV and
$ m_{W^\prime} = 2 $ TeV. Here,$ P_T $ represents the transverse momentum of the final-state electrons in Fig. 6 (a); η is the pseudo-rapidity of electrons in Fig. 6 (b). Another important parameter is α in Fig. 6 (c), which is the azimuthal angle of the final-state electrons calculated from the angle between the two charged leptons in the transverse plane; it is is defined as
Figure 6. (color online) Kinematic distributions of the final particles for the signal and background processes before the cuts; (a), (b), and (c) represent the transverse momentum
$ P_T $ , pseudo-rapidity η, and correlated angle α between the two charged particles in the final state, respectively, and (d) represents the missing transverse energy$ \not {E}_T $ .$ \cos\alpha = \frac{{{\boldsymbol{p}}_{{\boldsymbol{e}}^+}^{\bf{*}}} \cdot {{\boldsymbol{p}}_{{\boldsymbol{e}}^-}}}{|{{\boldsymbol{p}}_{{\boldsymbol{e}}^+}^{\bf{*}}}|\cdot |{{\boldsymbol{p}}_{{\boldsymbol{e}}^-}} |}, $

(15) where
$ p_e $ denote the three-momentum vectors of the electrons in the relevant frame. The different distributions shown in Fig. 6 (c) between the signal process and background processes are determined by the kinematic characteristics of the collision process. The two background processes with distinct differences are those with intermediate states of Z bosons and W boson pairs, whose Feynman diagrams correspond to the t-channel and$ s/t $ -channels [54], respectively. For large collision energies,$ W/Z $ will be highly boosted, which will cause a distribution featuring a sharp peak. Concerning the large mass of the intermediate particle of$ W^\prime $ in the signal process as well as the heavy neutrino mass, the boost effects will be small, leading to much flatter distributions in the signal process. The last one in Fig. 6 (d) is$ \not {E}_T $ , which represents the transverse energy carried away by the neutrinos. From these distributions, we can determine the discrepancies between the signal and background processes.We searched for
$ W^\prime $ pair production by setting different masses of 2, 4.5, and 4.8 TeV at a collision energy of 10 TeV. Different cuts were applied to enhance the significance. The results are comprehensively listed in Table 4. The basic cuts are defined by setting a number of final-state electrons of two, and both of them are charge conjugates with transverse momentum$ P_T>10 $ GeV. When the cuts on the final-state electrons are set as$ P_T>400 $ GeV and$ 0.5< \alpha<3.1 $ , the signal-to-noise ratio reaches 17 and the significance reaches 101.62 for 2 TeV$ W^\prime $ . When the$ W^\prime $ mass is up to 4.5 TeV, the cuts change to$ 600<P_T<3700 $ GeV and$ 0.5< \alpha<3 $ . The signal-to-noise ratio is 9.47 and the significance value is 28.91. The results for$ m_{W^\prime} = 4.8 $ TeV correspond to cuts of$ 600<P_T< 3500 $ GeV and$ 0.5< \alpha<3 $ . The signal-to-noise ratio is 5.42 and the significance value is 16.35. For a mass of$ W^\prime $ close to 5 TeV and a threshold of pair production for collision energy of 10 TeV, the cross section decreases sharply with increasing mass, leading to an evident decrease of the significance.$ m_{W^\prime} $ 

Cut range $ \sigma_{WW} $ 

$ \sigma_{ZZ} $ 

$ \sigma_{VBF} $ 

$ \sigma_{S} $ 

$ S/\sqrt{B} $ 

$ S/B $ 

2 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.066 $ 

$ 0.0015 $ 

$ 0.98 $ 

$ P_T>400 $ GeV

$ 0.058 $ 

$ 0.00087 $ 

$ 0.31 $ 

$ 0.061 $ 

$ 0.16 $ 

$ 10.02 $ 

$ 0.5< \alpha<3.1 $ 

$ 0.0036 $ 

$ 0 $ 

$ 0 $ 

$ 0.061 $ 

$ 17 $ 

$ 101.62 $ 

4.5 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.0095 $ 

$ 2.1\times 10^{-4} $ 

$ 0.14 $ 

$ 600<P_T<3700 $ GeV

$ 0.047 $ 

$ 0.00056 $ 

$ 0.089 $ 

$ 0.0091 $ 

$ 0.066 $ 

$ 2.45 $ 

$ 0.5< \alpha<3 $ 

$ 0.00093 $ 

$ 0 $ 

$ 0 $ 

$ 0.0088 $ 

$ 9.47 $ 

$ 28.91 $ 

4.8 TeV Basic Cut $ 0.062 $ 

$ 0.0016 $ 

$ 44.93 $ 

$ 0.0053 $ 

$ 1.2\times 10^{-4} $ 

$ 0.079 $ 

$ 600<P_T<3500 $ GeV

$ 0.046 $ 

$ 0.00054 $ 

$ 0.089 $ 

$ 0.0051 $ 

$ 0.038 $ 

$ 1.38 $ 

$ 0.5< \alpha<3 $ 

$ 0.00091 $ 

$ 0 $ 

$ 0 $ 

$ 0.0049 $ 

$ 5.42 $ 

$ 16.35 $ 

Table 4. Signal-to-noise ratio and significance after cuts for masses of
$ W^\prime $ of 2, 4.5, and 4.8 TeV and a collision energy of 10 TeV; the integrated luminosity of the collider was set as$ 10~ {\rm ab^{-1}} $ . The unit of σ is$ \rm fb $ . -
Extra charged gauge bosons beyond the Standard Model have long been a topic of interest. Future muon colliders, with their high center-of-mass energies, offer a significant advantage in discovering heavy particles. In this study, we chose the ALRM model to study the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process and explore the properties of$ W^\prime $ . In this process, we examined the cross-section distribution, angular distribution, and forward-backward asymmetry for polarized and unpolarized scenarios of$ W^\prime $ particles at different masses.We conducted an in-depth study of the cross-section distribution of the process
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ at different collision energies. This cross section reaches 0.2$ \rm fb $ in a 10 TeV collider, which is correlated with the combined effects of$ g_R $ and$ W^\prime $ mass. We also investigated the angle distributions of the initial-state muon and final-state electron for different$ W^\prime $ masses. With a fixed$ W^\prime $ mass, the asymmetry of the angular distribution gradually strengthens as$ g_R $ increases. With the same coupling strength, the changes in$ W^\prime $ mass also greatly affect the angular distribution, but the overall trend remains consistent. We also investigated the cross-section and angular distributions for polarized initial state conditions. When the$ \mu^- $ polarization is different, the distributions of cross section also show significant changes for a$ W^\prime $ mass lower than half the collision energy. However, the polarization has little impact on the angular distributions when the$ W^\prime $ mass is close to the threshold of pair production, except for the case of$ P_{\mu^+} $ extremely close to 100. The forward-backward asymmetry defined from the angular distribution is an effective observable to study the interaction of$ W^\prime $ coupling to leptons. We also searched for$ W^\prime $ pair production at a muon collider with backgrounds of$ ZZ $ ,$ WW $ , and VBF processes. After applying suitable kinematic cuts, the significance exceeded$ 5 \sigma $ for the$ W^\prime $ boson with a mass of 4.8 TeV at 10 TeV muon colliders. The study of extra gauge particles is an important part of the new physics beyond the Standard Model. Searches for the pair production of$ W^\prime $ at future muon colliders will provide new perspectives for new physics models. -
Extra charged gauge bosons beyond the Standard Model have long been a topic of interest. Future muon colliders, with their high center-of-mass energies, offer a significant advantage in discovering heavy particles. In this study, we chose the ALRM model to study the
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ process and explore the properties of$ W^\prime $ . In this process, we examined the cross-section distribution, angular distribution, and forward-backward asymmetry for polarized and unpolarized scenarios of$ W^\prime $ particles at different masses.We conducted an in-depth study of the cross-section distribution of the process
$ \mu^+ \mu^- \to W^{\prime +} W^{\prime -} \to e^+ e^- n_e \bar{n}_e $ at different collision energies. This cross section reaches 0.2$ \rm fb $ in a 10 TeV collider, which is correlated with the combined effects of$ g_R $ and$ W^\prime $ mass. We also investigated the angle distributions of the initial-state muon and final-state electron for different$ W^\prime $ masses. With a fixed$ W^\prime $ mass, the asymmetry of the angular distribution gradually strengthens as$ g_R $ increases. With the same coupling strength, the changes in$ W^\prime $ mass also greatly affect the angular distribution, but the overall trend remains consistent. We also investigated the cross-section and angular distributions for polarized initial state conditions. When the$ \mu^- $ polarization is different, the distributions of cross section also show significant changes for a$ W^\prime $ mass lower than half the collision energy. However, the polarization has little impact on the angular distributions when the$ W^\prime $ mass is close to the threshold of pair production, except for the case of$ P_{\mu^+} $ extremely close to 100. The forward-backward asymmetry defined from the angular distribution is an effective observable to study the interaction of$ W^\prime $ coupling to leptons. We also searched for$ W^\prime $ pair production at a muon collider with backgrounds of$ ZZ $ ,$ WW $ , and VBF processes. After applying suitable kinematic cuts, the significance exceeded$ 5 \sigma $ for the$ W^\prime $ boson with a mass of 4.8 TeV at 10 TeV muon colliders. The study of extra gauge particles is an important part of the new physics beyond the Standard Model. Searches for the pair production of$ W^\prime $ at future muon colliders will provide new perspectives for new physics models.
Extra charged gauge boson W′ in Alternative Left-Right Model at future muon collider
- Received Date: 2025-04-22
- Available Online: 2025-12-15
Abstract: The study of extra charged gauge bosons beyond the Standard Model has always been of great interest. Future muon colliders will have a significant advantage in discovering exotic particles. In this paper, by studying the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF







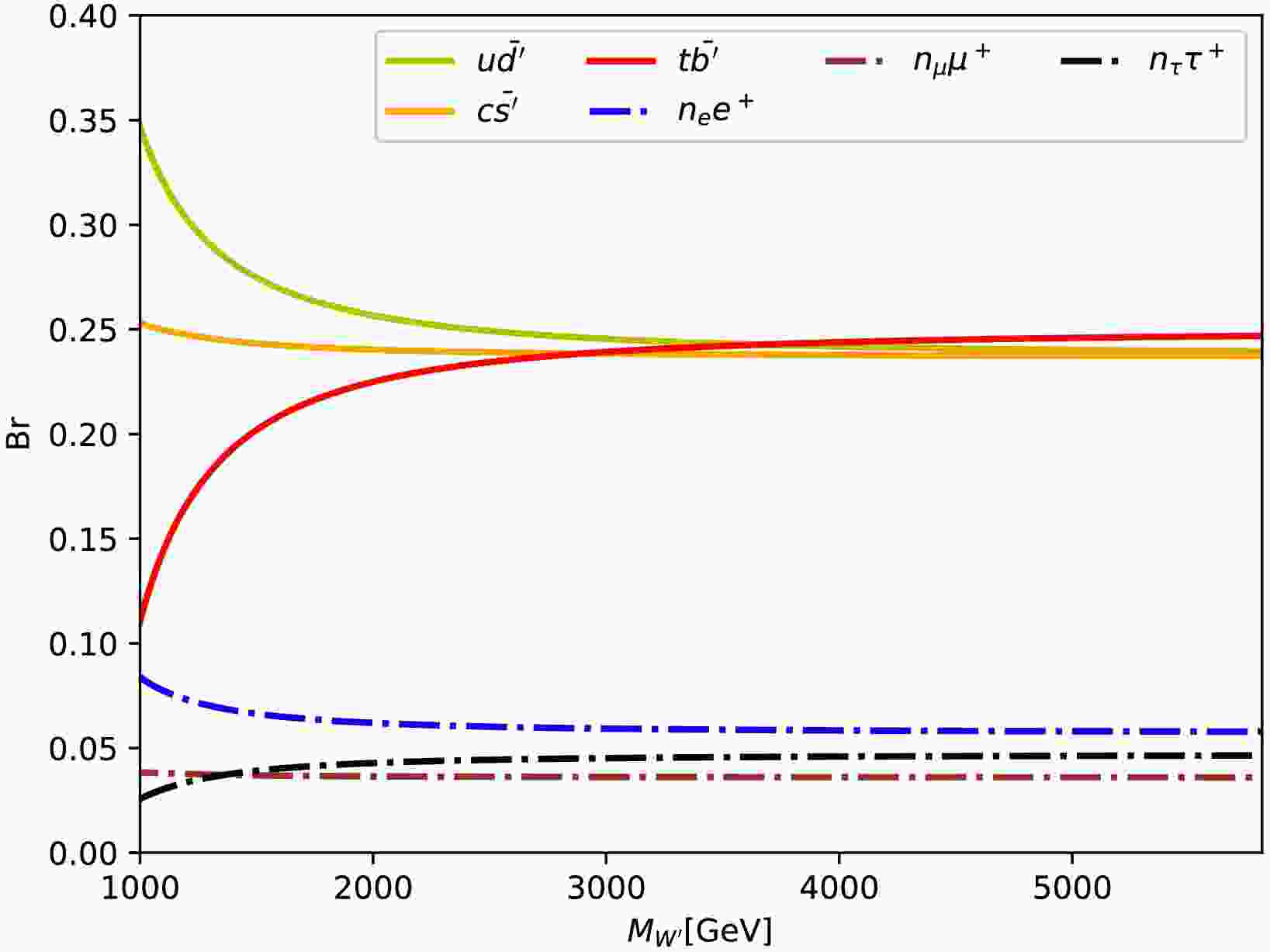










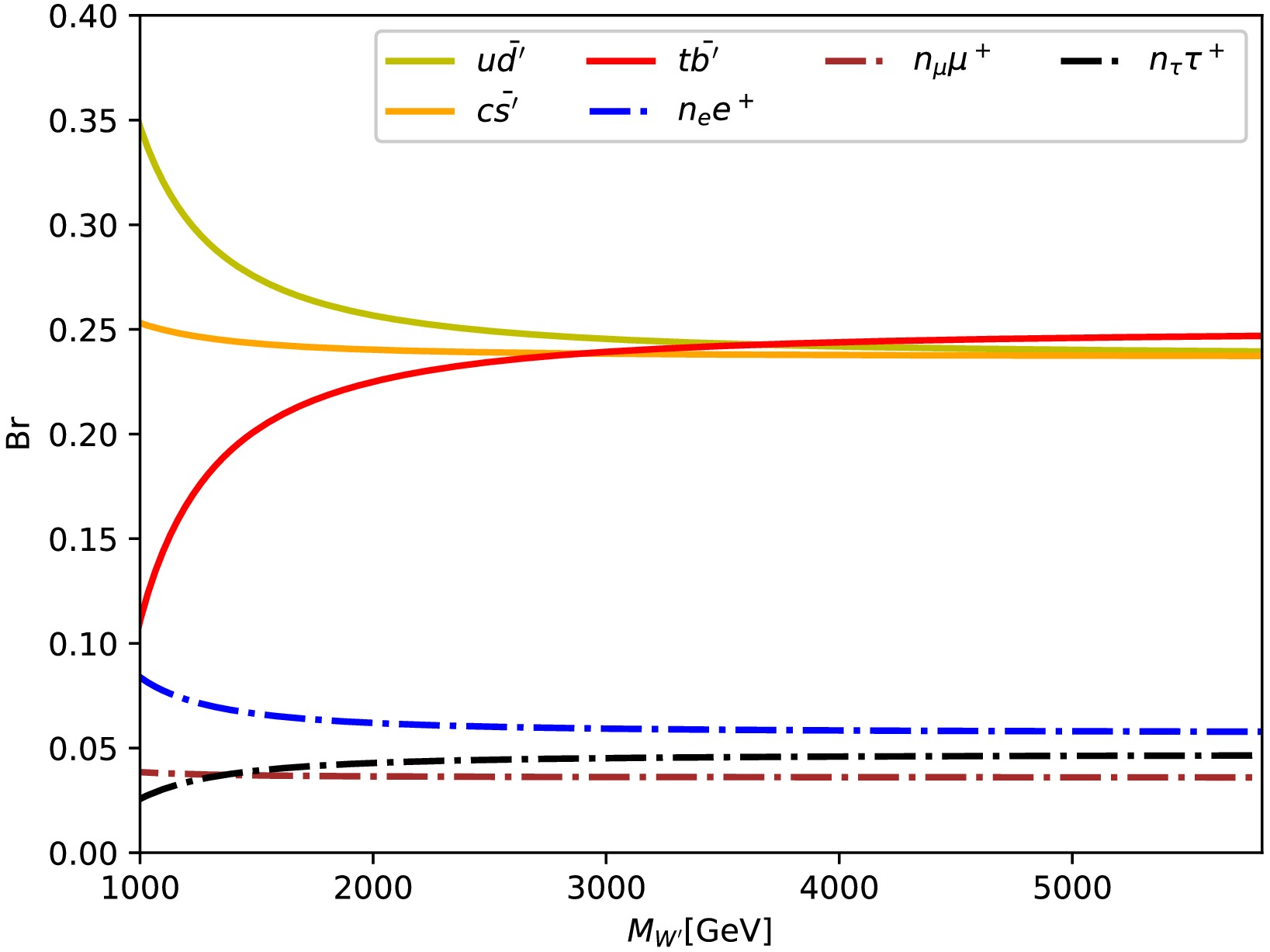



 DownLoad:
DownLoad: