Effect of electron–electron interaction on pair production in supercritical collisions of highly charged ions

Since the development of quantum electrodynamics (QED), considerable attention has been devoted to phenomena that occur in the non-perturbative regime of extremely strong electromagnetic fields. QED predicts that, when the strength of a static uniform electric field exceeds a critical threshold — on the order of 10¹⁶ V/cm — the vacuum becomes unstable and can spontaneously create electron-positron pairs. The experimental observation of this process is expected to provide a direct test of QED in the supercritical regime.

Despite significant advances in high-intensity laser technology (see, e.g., [1, 2]), field strengths achieved in laboratory conditions remain several orders of magnitude below the supercritical threshold. An alternative route to probing this regime is provided by the Coulomb field of superheavy nuclei with charge numbers exceeding a critical value, $ Z>Z_{\rm{cr}} $, where $ Z_{\rm{cr}}\approx 173 $. However, no such nuclei have been produced yet. Instead, heavy-ion collisions offer a means to achieve supercritical fields, which makes them a subject of theoretical interest for more than half a century. Early studies by Soviet and German physicists [3–14] demonstrated that, in collisions where the combined nuclear charge exceeds $ Z_{\rm{cr}} $ , the resulting Coulomb field can reach supercritical strength at sufficiently small internuclear distances $ R_{\rm{cr}} $. Under these conditions, the lowest unoccupied quasimolecular electronic state $ 1s\sigma_{1/2} $ may dive into the negative-energy continuum, which leads to the spontaneous creation of electron-positron pairs. The emitted positrons can escape and be detected, whereas the corresponding electrons remain bound, creating charged vacuum.

However, the direct observation of spontaneous vacuum decay in heavy-ion collisions faces significant challenges. In slow collisions ($ \sim 0.1c $, where $ c $ represents the speed of light), the supercritical field persists for only $ 10^{-21} $ s, which is two orders of magnitude shorter than the spontaneous resonance lifetime, which leads to a low probability of spontaneous pair production. In addition, spontaneous pair creation is strongly masked by the dynamical pair production induced by the time-dependent Coulomb field of moving nuclei. These two mechanisms interfere coherently and cannot be easily distinguished. Theoretical investigations by the Frankfurt group [13–21] suggested that spontaneous pair production can be observed only if the colliding nuclei form a quasi-bound state ("nuclear sticking"), which prolongs the supercritical phase and enhances the spontaneous channel. However, no experimental evidence for such sticking behavior with heavy ions has been found to date; this motivates the search for alternative approaches to detect vacuum decay in supercritical fields.

Over the past decade, the theoretical research group at Saint Petersburg State University has made significant progress in identifying possible experimental approaches for observing spontaneous vacuum decay in heavy-ion collisions. In the study reported in Refs. [22, 23], within the framework of the monopole approximation, a transition to the supercritical regime was detected in collisions where nuclei follow trajectories with a fixed minimal internuclear distance $ R_{\rm{min}} $ and varying energy parameter $ \varepsilon=E/E_0 $, where E and $ E_0 $ represent the collision energy and energy of the head-on collision, respectively. According to this approach, in supercritical collisions as $ \varepsilon $ decreases, the probability of pair production increases while the contribution of the dynamical mechanism diminishes because of the decreasing collision velocity. Further studies beyond the monopole approximation [24] confirmed signatures of the spontaneous pair production regime. Moreover, recent two-center calculations [25, 26] enabled an analysis of the angular distributions of emitted positrons, considering rotational coupling effects.

With the upcoming experimental facilities in Germany (GSI/FAIR) [27, 28], China (HIAF) [29], and Russia (NICA) [30], the study of pair production in heavy-ion collisions is becoming increasingly relevant. A key challenge in experimentally implementing the approach proposed in [22, 23] is the production of low-energy beams of fully stripped ions. In practice, partially stripped ions are more commonly available. In processes with such ions one has to account for the screening of the Coulomb field of the nuclei by the electron shells. The influence of the screening effect on the critical charge and critical distance is considered in Refs. [31, 32], which indicates that this effect changes the critical radius by approximately 10%–12%. The Frankfurt research group conducted extensive studies on electron and positron emission in subcritical and supercritical collision systems with filled lowest electron shells [17, 33–36]. Their results indicate that, in collisions involving partially ionized atoms, pair production probabilities are significantly suppressed due to Pauli blocking, with electron screening providing an additional reduction in the total probability.

In this study, we investigate the effect of electron-electron interaction on the signatures of spontaneous positron production in heavy-ion collisions within the supercritical regime. Calculations are performed for U–U, U–Cm, and Cm–Cm collision systems within the monopole approximation. The collisions of bare nuclei and of partially stripped ions with lowest filled shells are considered. The electron-electron interaction is included within two distinct mean-field approaches. The total positron creation probabilities as well as positron spectra are calculated and discussed.

Atomic units ($ \hbar=|e|=m_{e}=1 $) are used throughout the paper unless specified otherwise.

In our method, the collision of two heavy ions is described within the monopole approximation, which proves to provide an adequate description of the electron-positron pair production [24]. The electron-electron interaction in the initially occupied orbitals is treated using a mean-field approach, and therefore, we solve a set of one-electron time-dependent Dirac equations (TDDE) for independent electrons initially occupying the negative energy Dirac continuum and a number of bound-state orbitals (up to Fermi level $ F $)，

where $ \Psi({\boldsymbol{r}},t) $ represents a four-component one-electron orbital, and Hamiltonian $ H $ can be written as

where c is the speed of light, p is the momentum operator, and $ {\boldsymbol{\alpha}} $ and $ \beta $ are Dirac matrices.

Spherically symmetric potential $V_{ n}(r, t)$ in Eq. (2) represents an interaction with nuclei in the monopole approximation, and its dependence on time is caused by the variation in internuclear distance. The spherically symmetric mean-field potential $ V_{\rm{MF}}(r, t) $ is produced by electrons in initially occupied bound states. This potential is constructed by a self-consistent procedure before solving the time-dependent equation (1), and its time dependence is caused by the time evolution of the one-electron orbitals.

We use two different approaches to represent the mean-field potential $ V_{\rm{MF}}(r, t) $ and solve the TDDE (1). The first approach is based on the time-dependent density-functional theory (TDDFT). The mean-field potential $ V_{\rm{MF}}(r, t) $ comprises the Hartree electron-electron repulsion potential, exchange-correlation potential in the local-density approximation, and Fermi–Amaldi self-interaction correction. Eq. (1) is solved numerically using the generalized pseudospectral method, which has been extensively employed and discussed in earlier works [37–39]. The second approach employs a basis-set representation of the wave function in the TDDE (1) using $ B $-splines following the method implemented in earlier work [23]. The mean-field potential $ V_{\rm{MF}}(r, t) $ is calculated using the time-dependent Hartree–Fock–Slater (TDHFS) method, following the methodology developed by the Frankfurt group [33]. In both schemes described above, the Crank–Nicolson algorithm [40] is applied to perform the time evolution. Once ions collide and move apart, the positron creation probabilities and energy spectra are calculated by analyzing hole distributions in the negative-energy Dirac continuum. The pair-creation probabilities and positron spectra are calculated based on methods presented in Refs. [23, 25].

Total positron creation probabilities and energy distributions were computed within the monopole approximation for U–U, U–Cm, and Cm–Cm collisions. Nuclear trajectories were modeled as classical Rutherford trajectories, and the calculations were performed for both bare nuclei ($ F =0 $) and partially stripped ions. In the latter case, the first three $ s_{1/2} $ subshells and first three $ p_{1/2} $ subshells (i.e., subshells $ 1s_{1/2} $, $ 2s_{1/2} $, $ 3s_{1/2} $, $ 2p_{1/2} $, $ 3p_{1/2} $, and $ 4p_{1/2} $) were assumed to be occupied by electrons while all other electron orbitals were empty. We represented this occupation scheme as $ F=3 $. The case of $F=3 $ was extensively studied by the Frankfurt group [17, 33–36] because it closely modeled the GSI experiments [14]. Therefore, we selected the $F =3 $ occupation scheme in our calculations to compare our data with the previously published results. Further, we believe that the case of partially stripped ions with occupied inner subshells and empty outer subshells would be easier to implement experimentally than the case of the ions with pre-existing vacancies in the inner shells (e.g., collisions of bare nuclei with neutral atoms [23, 41]), although the latter case is more favorable for spontaneous positron creation. The numerical computations were performed on a pseudospectral radial grid consisting of 1600 points with 16384 time propagation steps. The spherically symmetric nuclear potential of the monopole approximation was obtained by averaging the two-center nuclear potential on a $ 80 $-point angular Gauss–Lobatto grid.

We validated the reliability of the employed methods by calculating the total positron creation probabilities for U–Cm and Cm–Cm collisions with $ F =3 $ at $ E \approx 748 $ and $ 781 $ MeV, respectively, including electron-electron interactions. Tables 1 and 2 compare the results obtained in this study with those from Ref. [36], wherein calculations are performed using the adiabatic TDHFS method. The computed probabilities exhibited good agreement with the previous results. Our TDDFT results for the total positron creation probabilities were slightly larger than the TDHFS results, which was not surprising because mean-field potentials were different in these two methods. Besides the exchange potential, the screening effect of the electron-electron repulsion was further reduced in the TDDFT method because of the Fermi–Amaldi self-interaction correction, which made the positron creation probabilities larger. However, the TDHFS results of Ref. [36] are even larger. The details of the numerical procedures in Ref. [36] are unavailable, and therefore, we cannot identify the cause for the small yet systematic difference between our results and those in Ref. [36].

We computed the total positron creation probabilities for U–U and Cm–Cm collisions at $ \varepsilon=1.0 $, $ 1.02$, and $ 1.05 $ with a minimum internuclear distance of $ R_{\rm{min}}=17.5 $ fm to investigate signatures of the spontaneous pair production regime. The results are presented in Table 3, where column 3 lists the probabilities for collisions of bare nuclei, while columns 4 and 5 provide the corresponding values for the ion collisions with the $ 1s_{1/2}-3s_{1/2} $ and $ 2p_{1/2}-4p_{1/2} $ subshells filled ($ F =3 $). For the positron creation probabilities in column 4, only the Pauli blocking effect is considered, and no screening is performed because of the electron-electron interaction. Thus, all electrons in the initially occupied bound and negative-energy continuum states are propagated in time independently under the influence of the time-dependent nuclear potential $V_{n}(r, t)$, with the mean-field potential $ V_{\rm{MF}}(r, t) $ discarded. The data in column 5 include the effect of electron-electron interaction through the potential $ V_{\rm{MF}}(r, t)$. The screening of the nuclear potential by the filled electron subshells results in an additional suppression of the positron production: the probabilities decrease by 17%– 18%.

Z	$ \varepsilon $	F=0	F=3	F=3
			No screening	With screening
92	1.00	1.12×10−2	3.63×10−4	2.98×10−4
	1.02	1.12×10−2	3.85×10−4	3.17×10−4
	1.05	1.12×10−2	4.19×10−4	3.48×10−4
96	1.00	3.87×10−2	9.24×10−4	7.62×10−4
	1.02	3.84×10−2	9.74×10−4	8.05×10−4
	1.05	3.79×10−2	1.05×10−3	8.72×10−4

Table 3.  Total positron creation probabilities for U–U and Cm–Cm collisions at $ R_{\rm{min}}=17.5 $ fm for different Fermi level configurations. Column 3 lists the results for bare nuclei, while columns 4 and 5 contain the probabilities for ions with $ F =3 $, without and with electron-electron interaction, respectively.

The bare nuclei results ($F=0 $) confirm that, for $ Z = 92, $ the probability remains nearly constant with increasing $ \varepsilon $, whereas it decreases for $ Z = 96$. This behavior is consistent with the supercritical regime discussed in Refs. [22, 23, 26]. When $ 1s_{1/2}-3s_{1/2} $ and $ 2p_{1/2}-4p_{1/2} $ shells are occupied ($F=3 $, columns 4 and 5), the absolute probability is 30 to 50 times smaller than that for the case with $F=0 $. For both $Z=92 $ and $96 $ collisions, the characteristic signatures of the supercritical regime observed for the bare nuclei disappear because the total probability increases with $ \varepsilon $, which is in contrast to the bare-nuclei case.

This behavior is readily understood: in collisions of bare nuclei, the $ 1s_{1/2} $ state serves as the primary destination for electrons created by the spontaneous pair-production mechanism when this state dives into the negative-energy continuum in the course of collision. Our previous calculations [42] revealed that the contribution of the spontaneous mechanism to the total positron creation probability in head-on collisions of bare nuclei with $ R_{\rm{min}}=17.5 $ fm comprised approximately 27% and 78% for the U–U and Cm–Cm collisions, respectively. However, in the $F=3 $ configuration, this state is initially occupied. If it remains occupied throughout the collision, the related channel of positron emission is closed because of the Pauli blocking effect. Actually, a vacancy can be created in the $ 1s_{1/2} $ state during the collision, which can open the spontaneous positron emission channel. However, the probability of such a process appears considerably small because the total probability of positron creation is 30 to 50 times less than that in the collisions of the bare nuclei ($F=0 $). Theoretical calculations presented in Ref. [33] suggest that, for U-U collisions with $E=4.7 $ MeV/u at $F=3 $, the $ 1s_{1/2} $ vacancy formation probability reaches values on the order only of a few percent. As a result, in the $F=3 $ case, positron creation is dominated by the transition of electrons from the negative-energy continuum to the higher-lying bound states, without diving into the negative-energy continuum during collision. Therefore, the signatures of the spontaneous positron creation mechanism are not observed. This holds true even when including the electron-electron interaction in the calculations. Accounting for the electron-electron interaction through the mean-field potential reduces the total positron-creation probabilities by 17%–18% without altering the overall trend.

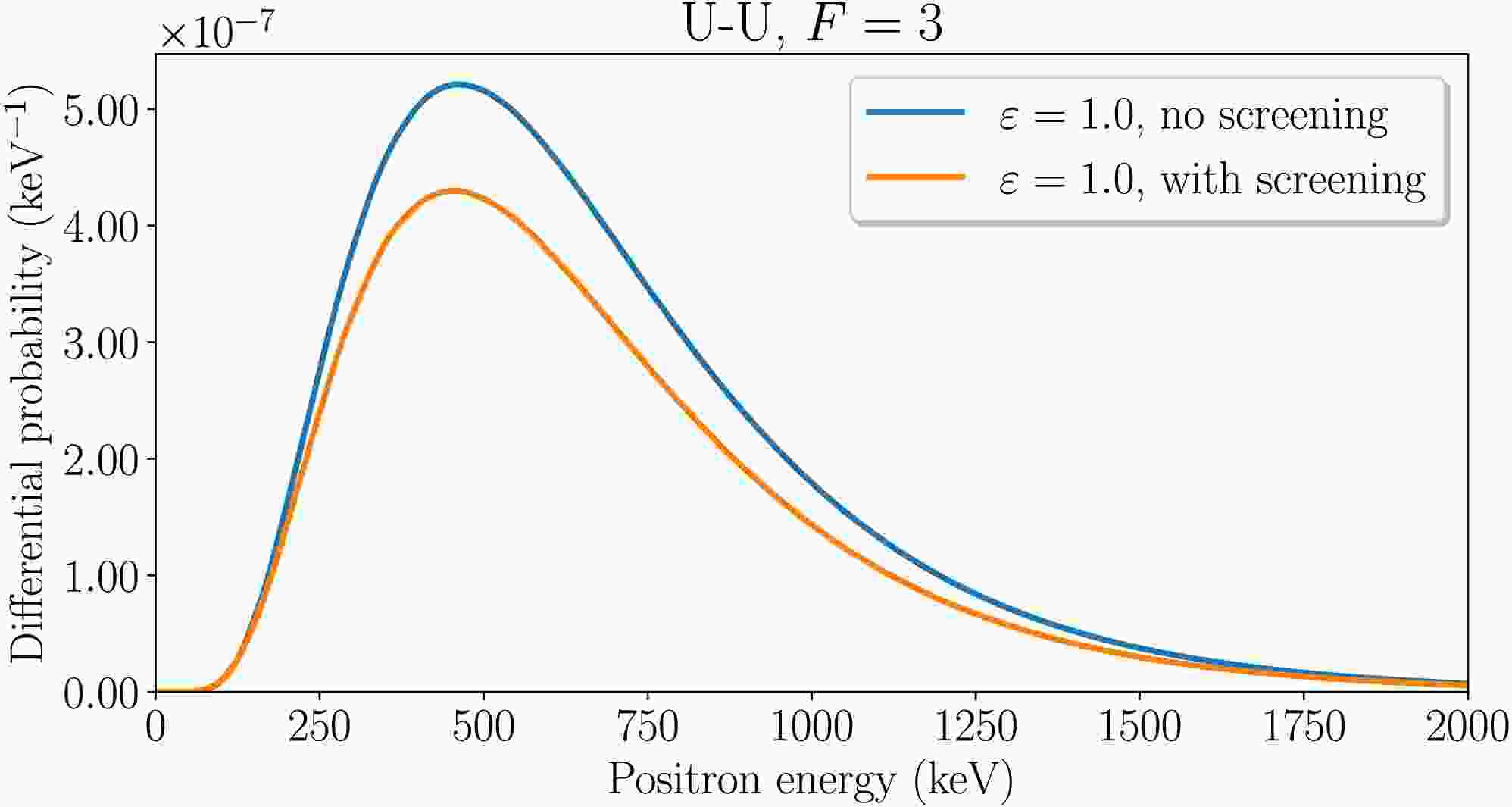
Our findings about the signatures of the supercritical positron creation regime are supported by calculations of the energy distributions of outgoing positrons. Figure 1 presents positron energy distributions for head-on U–U collisions with $ R_{\rm{min}}=17.5 $ fm at $F=3 $. The results obtained with and without considering the electron-electron interaction are presented. The inclusion of the electron-electron interaction in the calculations leads to an overall reduction in the spectra while leaving their qualitative behavior nearly unchanged.

Figure 1.  (color online) Energy spectra of positrons for the symmetric head-on collision of ions with $Z=92 $ and $F =3 $ at $ R_{\rm{min}}=17.5 $ fm with and without electron-electron interactions.

Figures 2 and 3 present the positron energy distributions for U–U and Cm–Cm collisions, respectively, at $ \varepsilon=1.0 $, 1.02, and 1.05 with $ R_{\rm{min}}=17.5 $ fm. The spectra were obtained for $ F = 3, $ including the electron-electron interaction. The final rotation angles of the internuclear axis for the scaled collision energies $ \varepsilon=1.02 $ and $1.05 $ are $ \chi_{\rm{max}}=31.9^{\circ} $ and $49.2^{\circ} $, respectively, for both U–U and Cm–Cm collisions.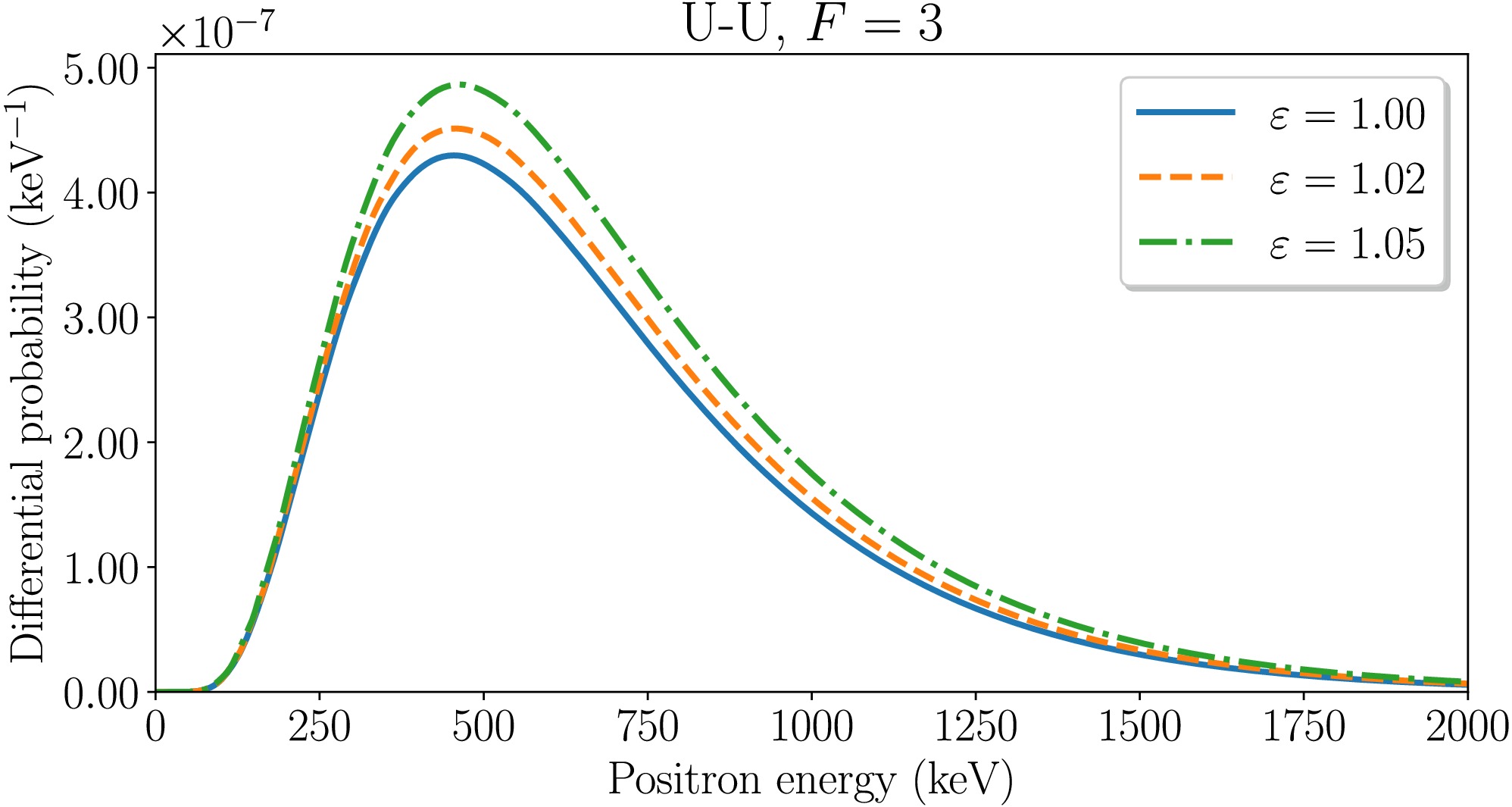

Figure 2.  (color online) Energy spectra of positrons for the symmetric collisions of nuclei with $Z=92 $ and $F=3 $ at $ R_{\rm{min}}=17.5 $ fm and $ \varepsilon=1.0 $, 1.02, and 1.05 with electron-electron interactions.

Figure 3.  (color online) Energy spectra of positrons for symmetric collisions of nuclei with $Z=96 $ and $F=3 $ at $ R_{\rm{min}}=17.5 $ fm and $ \varepsilon=1.0 $, 1.02, and 1.05 with included electron-electron interactions.

Increasing the scaled collision energy $ \varepsilon $ with the fixed minimum internuclear separation $ R_{\rm{min}} $ implies that the velocity of colliding ions increases and the time spent in the supercritical region (where the $ 1s_{1/2} $ energy level dives into the negative-energy continuum) decreases. Such changes are favorable for the dynamical positron production and unfavorable for spontaneous positron creation. Therefore, if the creation of positrons at the peak of the energy distribution is dominated by the spontaneous mechanism, it decreases with increasing $ \varepsilon $; otherwise, the differential probability of the positron creation would increase if the dynamical mechanism is dominant [23–26]. Figure 2 shows that the peaks of energy distributions increase with rising $ \varepsilon $. A similar trend is observed in Fig. 3 for Cm–Cm collisions. This behavior is in contrast with the U–U and Cm–Cm collisions of bare nuclei, where the distribution peaks decrease with an increase in $ \varepsilon$, which indicates the supercritical regime. In collisions involving filled lower shells with $F=3 $, the energy distribution peaks grow with increasing $ \varepsilon $, thereby indicating no characteristic signatures of the spontaneous vacuum decay. This observation supports conclusions drawn from the analysis of the total positron production probability.

In this study, we examined the effect of the electron-electron interaction on positron production in supercritical heavy-ion collisions. Within the monopole approximation, we calculated total positron creation probabilities and energy distributions for U–U, U–Cm, and Cm–Cm collision systems, considering both bare nuclei and ions with electronic states occupied up to $F=3 $. The electron-electron interaction was described using the TDDFT and TDHFS theoretical methods. The agreement of our results with previous studies confirms the reliability of the employed computational approaches.

Our analysis demonstrated that the presence of occupied electronic states leads to a substantial suppression of positron production as fully occupied lowest bound states cannot be filled with electrons created from the vacuum, and thus, they no longer contribute to positron production. Accordingly, the signatures of the spontaneous positron creation regime observed in the collisions of bare nuclei disappear for $F=3 $, and positron emission becomes predominantly driven by the dynamical rather than spontaneous mechanism. Considering the electron-electron interaction in calculations leads to a further 17%– 18% decrease in positron creation probabilities while the qualitative picture of the pair creation remains unchanged.

Our results indicate that the characteristic signatures of the transition to the supercritical regime, previously found in collisions of bare nuclei [22–26], are strongly suppressed in the collisions of partially stripped ions.