Fox-Wolfram moment of jet production in relativistic heavy-ion collisions

Quark-gluon plasma (QGP), a new state of QCD matter composed of deconfined quarks and gluons, has been a principal focus of contemporary research in high-energy nuclear physics for the past thirty years [1−4]. Highly energetic partons produced in the initial collision traverse the QGP medium, losing energy through interactions with the constituent partons of the medium. This phenomenon, known as jet quenching, serves as a powerful tool for investigating the properties of QGP [5−20]. Various observables have been developed to quantitatively investigate the phenomenon of jet quenching. Early studies focused on how the medium modifies hadron spectra and hadron correlations, including the suppression of leading hadron spectra, modifications of di-hadron correlations, and analyses of other hadronic observables [21−31]. With the continued operation of the Large Hadron Collider (LHC) and advances in theory, various jet-level observables have been developed. These observables focus on the production or correlation of inclusive jets [32−43], dijets [44−49], and tagged jets [50−66], with some also examining the structure and substructure of the aforementioned categories of jet events [67−84].

In addition to these commonly studied experimental observables, there is a category of measurements that capture the geometric shape of the entire jet event, known as jet-event shape observables [85−88]. Early studies of event-shape observables were primarily conducted in electron-positron collisions, deep inelastic scattering (DIS), and proton-antiproton collisions [89−98]. With extensive research in high-energy nuclear physics ongoing at the LHC, some theoretical studies involving jet-event shape observables in heavy-ion collisions have emerged in recent years [99−103]. These studies are of significant importance for understanding the properties of the nuclear medium [104−108] and elucidating the dynamics of extreme relativistic collisions [109, 110].

In this work, we extended the study of medium modifications of jet shapes in heavy-ion collisions to include Fox-Wolfram moments (FWMs), a distinctive set of event shape measurements characterized by expansions in terms of spherical harmonics [111]. The application of FWMs has been extensive in collider physics, particularly in high-energy physics domains, including Higgs physics [112, 113], top physics [114], and general investigations on $ e^+e^- $[115, 116] and hadron [117] collisions. This is the first theoretical attempt to calculate the medium modifications of the event-normalized distribution of the lower-order FWM, $ \text{FWM}_\text{1st}^\text{T} $ (denoted as $ H_1^T $ in this paper), for events with 2 jets and with $ > $ 2 jets, by comparing $ H_1^T $ distributions in p+p and Pb+Pb collisions at $ \sqrt{s} = 5.02 $ TeV. For events with $ 2 $ jets, the results reveal a suppression in the small $ H_1^T $ region and an enhancement in the large $ H_1^T $ region for the distribution in Pb+Pb collisions compared to p+p collisions. Meanwhile, for events with $ > $ 2 jets, there is a suppression of Pb+Pb collisions relative to p+p collisions in the large $ H_1^T $ region. Furthermore, when the jet multiplicity is unspecified, i.e., events with $ \ge $ 2 jets, the modifications resemble that of events with 2 jets. Computations regarding the relative contributions of both types of events with respect to $ H_1^T $elucidated the underlying reasons of these phenomena.

Our study on $ H_1^T $ serves as a valuable complement to other event shape observables in heavy-ion collisions such as jet broadening, $ B_{\rm tot} $, and transverse sphericity, $ S_{\perp} $, which have been investigated recently [99, 103]. The advantage of this study lies in the fact that, compared to $ B_{\rm tot} $, which gives no zero results only for events with jet number $ n_\text{jet} >2 $ [103], $ H_1^T $ covers the events both with jet number $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $. In addition, compared to transverse sphericity, which characterizes a pattern of energy flow [99] similar to that of FWMs, $ H_1^T $ may exhibit a larger magnitude of medium modification.

The paper is organized as follows. In Sec. II, we introduce FWMs and extract the specific observable of interest, along with a discussion of its physical interpretation in p+p collisions. In Sec. III, we present the results and a discussion about both p+p and Pb+Pb collisions, followed by a summary in Sec. IV.

Expressed as a superposition of spherical harmonics $ Y_\ell^m(\Psi_i) $, FWMs constitute a set of such observables [111]

FWMs are sensitive to the number, angular correlation, and energy distribution of jets. They systematically describe geometric correlations in terms of spherical harmonics. The inner sum is over the final state objects (in this case, jets). Various schemes exist for the construction of weight factors, $ W_{i}^o $, as previously reported [112, 117]. The 'o' here serves as a marker for a different scheme. It represents the individual components of momentum or the vector sum of different components, such as $ p_x $, $ p_y $, $ p_z $, $ p_T $, and $ |\vec{p}| $. The typical schemes are expressed as follows:

Given that the angular variable $ \Psi_i $ depends on the choice of axis, we reformulate Eq. (1) to achieve an axis-independent formulation by using the inherent relationship between spherical harmonics and Legendre polynomials. Specifically, the sum over spherical harmonics can be rewritten in terms of Legendre polynomials as

By substituting this relation into Eq. (1), we obtain the following simplified expression for FWMs:

This formulation expresses FWMs as a weighted sum over Legendre polynomials, making it more convenient for analyzing angular correlations in jet events while remaining independent of the reference axis.

According to different weight construction schemes, we can choose different angle schemes $ \Delta\Psi_{ij} $ to measure the distance between jets. Here, $ \Delta\Psi_{ij} $ can take values of $ \Delta\phi_{ij} $, $ \Delta\theta_{ij} $, and $ \Delta\Omega_{ij} $, which adhere to the following equation expressed in terms of spherical coordinates: $ \cos\Delta\Omega_{ij} = \cos\theta_i\cos\theta_j + \sin\theta_i\sin\theta_j \cos (\phi_i-\phi_j) $. The angles $ \phi_i $ and $ \theta_i $ represent the azimuth angle of jet and the angle between jet and beam directions, respectively, among which the latter satisfies the equation with jet rapidity $ \eta_i = -\ln(\tan\frac{\theta_i}{2}) $. Thus, it is straightforward to ascertain that $ \Delta\phi_{ij} $ and $ \Delta\theta_{ij} $ represent the azimuthal separation and the difference in rapidity between jets i and j, respectively. In addition, $ \Delta\Omega_{ij} $ represents the distance between them in a three-dimensional momentum space.

Given our emphasis on jet physics, the transverse momentum and azimuthal separation $ \Delta\phi_{ij} $ of jets were employed in the construction of the FWMs. The values of $ i,j (1, 2, 3, ...) $ represent jets ordered by descending transverse momentum. The marker 'o' changes to 'T':

Let us first analyze the toy model given by Eq. (5) when $ n_\text{jet} $ is equal to 2; it is shown in Fig. 1. For simplicity, we denote $ p_{T 2} = x\cdot p_{T 1} $, which simplifies the functional form of the weights $ W_{ij}^T $. Expanding the sum in the definition given by Eq. (5) with weights expressed by transverse momentum yields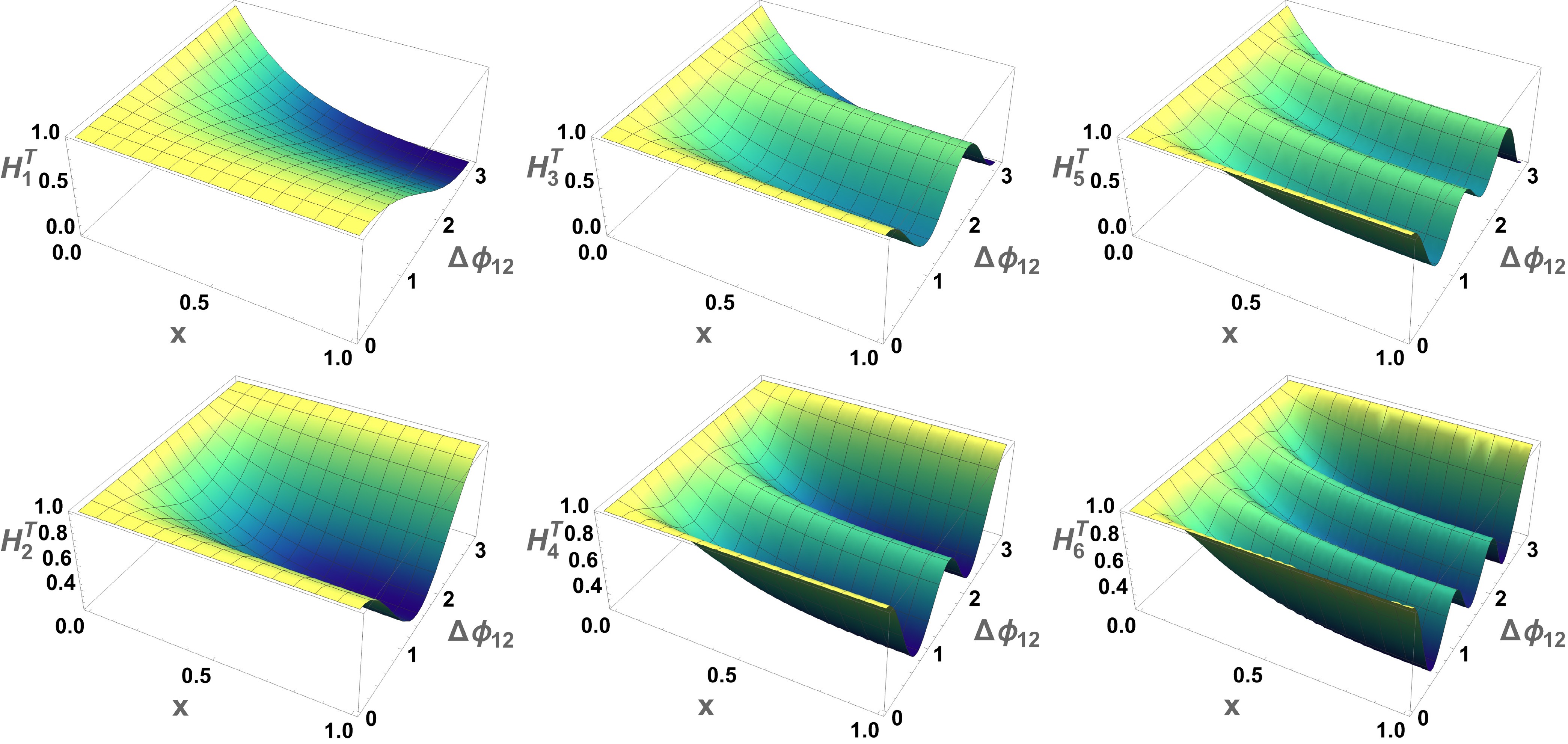

Figure 1.  (color online) Analytic results of the FWMs $ H_\ell^T $ ($ n_\text{jet} $ = 2) for $ \ell = 1,2,3,4,5,6 $.

If $ \ell = 0 $, then the Legendre polynomial $ P_0 = 1 $ results in $ H_0^T = 1 $, which is not meaningful for our study. Because of the properties of the Legendre polynomials, $ P_{\ell} $, the FWMs $ H_{\ell}^T $ exhibit strongly oscillatory behavior, as shown in Fig. 1; the larger the value of $ \ell $, the stronger the oscillatory behavior. This can be viewed as a change in the resolution with which the FWMs probe the structure of the QCD jet geometry [112]. For this reason, the study of FWMs of different orders was used to provide sufficient resolution to discriminate signals and backgrounds in Higgs and t$ \bar{\mathrm{t}} $ production studies [112, 114].

As $ \Delta \phi_{12} $ approaches π, $ H_{\ell}^T $ approaches 1 (even moments) or 0 (odd moments). All weights $ W_{ij}^T $ ensure that the range for the moments is $ 0 \le H_\ell^T \le 1 $ and preserve the different shapes of $ H_\ell^T $ for even or odd moments. As pioneers in the study of this observable in the field of jet quenching, we first focused on the monotonic relationship between the lower-order $ H_1^T $and azimuthal angle distance to investigate the jet-event shape. The definition is as follows:

This definition of $ H_1^T $ differs for events with different values of $ n_\text{jet} $. It is straightforward to see that for $ n_\text{jet} = 2 $ events, the definition of $ H_1^T $ is obtained by replacing $ P_\ell(\cos\Delta\phi_{12}) $ with $ \cos\Delta\phi_{12} $ in Eq. (6). However, owing to the increase in the number of variables, the definition of events $ n_\text{jet} = 3 $ is more complex; it is discussed in Appendix A.

In this study, jet productions in p+p collisions were simulated using a Monte Carlo event generator, SHERPA 2.2.11 [118], which performs NLO matrix-element calculations matched to the parton shower with several merging schemes. AMEGIC++ [119] and Comix [120] are built-in matrix-element generators of SHERPA that automatically calculate and integrate tree-level amplitudes, cooperating with their phase-space generator Phasic [119]. OpenLoops [121] programs were interfaced with SHERPA to provide virtual corrections. A method of MC@NLO-type was performed to match a fixed-order next-to-leading order (NLO) calculation with the resummation of the parton shower [122]. The parton distribution function (PDF) set 'NNPDF30_nlo' was loaded for beams [123, 124]. For high-transverse-momentum transfer processes and multi-jet production, LO calculations typically perform worse than NLO ones in describing experimental measurements of the azimuthal angle separation between jets [88]. In such cases, SHERPA, by directly incorporating higher-order matrix-element calculations, often provides a more accurate description of event kinematics than LO-precision generators [125]. Our calculations were performed at parton level for both p+p and Pb+Pb collisions.

The spatial structure of $ H_1^T $ is depicted in the top-left corner of Fig. 1. To gain further insights into the configuration structure of $ H_1^T $, we calculated the average azimuthal angle correlations for events with $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ in p+p collisions at a center-of-mass energy of $ \sqrt{s} $ = 5.02 TeV, considering three logarithmic intervals of $ H_1^T $, as presented in Table 1. The kinetic sets corresponding to this calculation are described in Sec. III. From Table 1, we observe that the azimuthal angle distance $ \langle\Delta\phi_{12}\rangle $ of $ n_\text{jet} = 2 $ events decreases with increasing $ H_1^T $. Additionally, for $ n_\text{jet} > 2 $ events, both $ \langle\Delta\phi_{12}\rangle $ and $ \langle\Delta\phi_{13}\rangle $ decrease while $ \langle\Delta\phi_{23}\rangle $ increases with $ H_1^T $. This indicates that the jet-event shape becomes broader as $ H_1^T $ increases for both $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ events. To present this geometric illustration more vividly, we provide visual schematic diagrams obtained from calculations in Fig. 2.

$\ln(H_1^T)$	$n_\text{jet} = 2$ events		$n_\text{jet} > 2$ events
	$\langle \Delta\phi_{12}\rangle$		$\langle\Delta\phi_{12}\rangle$	$\langle\Delta\phi_{13}\rangle$	$\langle\Delta\phi_{23}\rangle$
$\left [-10.0,-7.0 \right ]$	3.117		2.885	2.596	0.784
$\left [ -7.0,-3.0 \right ]$	3.026		2.849	2.560	0.831
$\left [ -3.0,0.0 \right ]$	2.573		2.520	2.198	1.138

Table 1.  Average azimuthal angle correlations calculated for $n_\text{jet} = 2$ and $n_\text{jet} > 2$ events in p+p collisions at $\sqrt{s}=5.02$ TeV over three $\ln(H_1^T)$ intervals.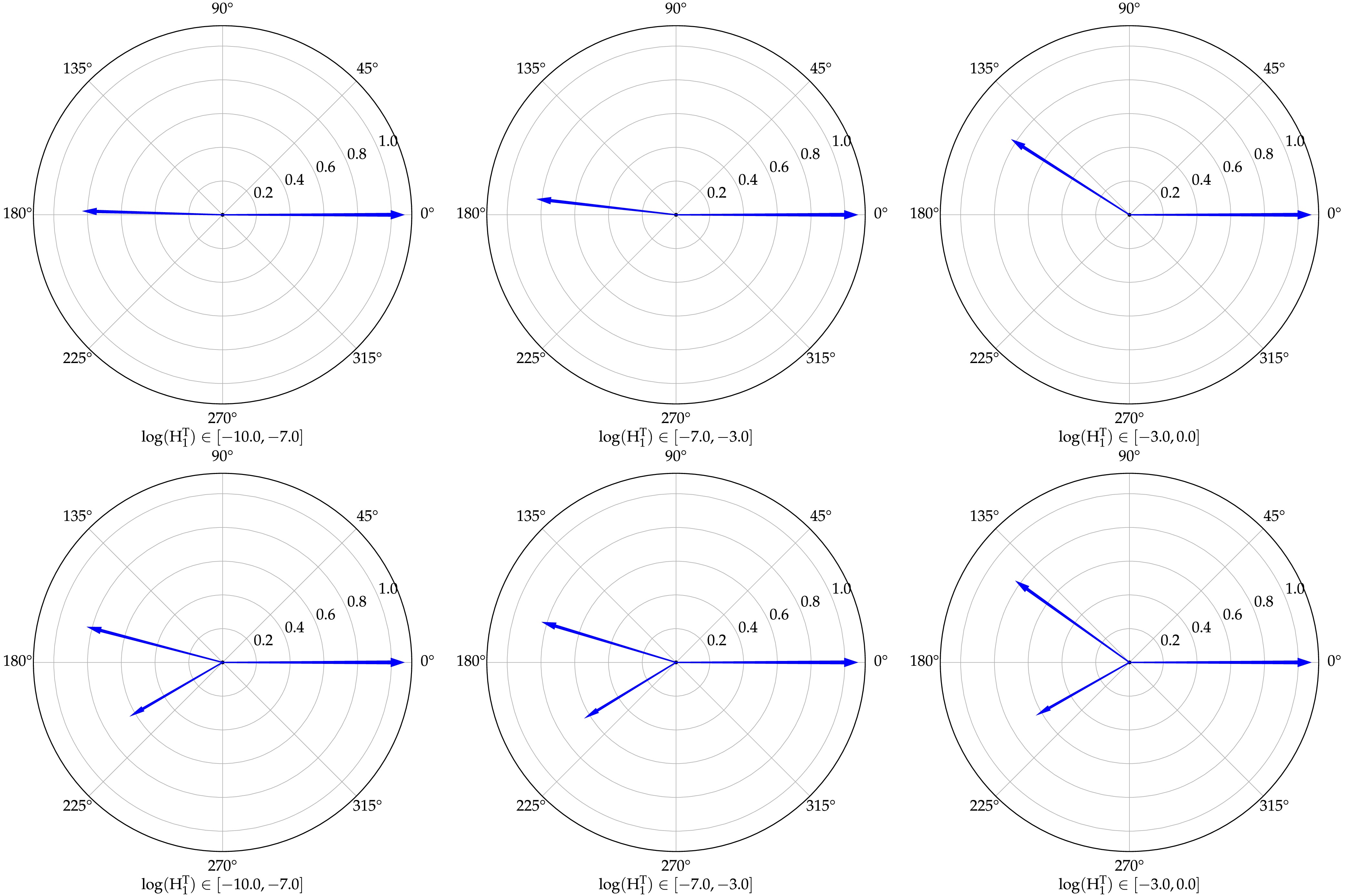

Figure 2.  (color online) Schematic diagrams in the transverse plane illustrating the spatial configurations of $ n_\text{jet} = 2 $ and $ n_\text{jet} = 3 $ events using polar coordinates over three consecutive $ H_1^T $ intervals.

Figure 2 shows schematic diagrams illustrating the spatial configurations of $ n_\text{jet} = 2 $ and $ n_\text{jet} = 3 $ events over three consecutive $ H_1^T $ intervals according to Table 1. These diagrams employ a scheme in which the direction of the leading jet is the polar axis of the polar coordinates. To achieve a better scheme of the geometric configuration of the jet events, we rescaled the transverse momentum of jets in a dimensionless interval from 0 to 1, preserving the relative proportionality between their transverse momentum magnitudes. These diagrams show that as $ H_1^T $ increases, both $ n_\text{jet} = 2 $ and $ n_\text{jet} = 3 $ event shapes become broader.

We used p+p data generated by the SHERPA event generator as a baseline to explore how the distribution of $ H_1^T $is modified after multiple scatterings with nuclear medium partons. We also used the linear Boltzmann transport (LBT) model [126−128] to simulate the physical process of multiple scatterings between jet and medium partons in QGP. The information of the bulk partons was provided by the (3+1)D CLVisc hydrodynamical model [129−133] with initial conditions simulated using a multi-phase transport (AMPT) model [134]. Both elastic and inelastic scattering processes were considered for the initial jet shower partons and thermal recoil partons.

In the LBT model, the $ 2 \rightarrow 2 $ elastic scattering process was simulated using the linear Boltzmann transport equation,

The inelastic scattering, termed as medium-induced gluon radiation in the LBT model, is described by the higher twist formalism [135−138],

We refer to [126−128] for an extensive discussion on the interpretation of various symbols and implementations of the elastic and inelastic scatterings of fast partons with the medium in Eqs. (8) and (9).

We generated p+p events with Sherpa + OpenLoops program packages and simulated the production of jets in Pb+Pb collisions at $ \sqrt{s_{NN}} = 5.02 $ TeV using the LBT model. Next, we present our results and analyze them. The anti-$ k_{\perp} $ algorithm was used to reconstruct jets with a cone size of R = 0.4 using the FastJet package [139]. The jet events were required to be at least two in this study. The kinematic sets were established for all jets as follows: transverse momentum of leading jet as $ p_T^\text{leading} > 110 $ GeV/c; threshold as $ p_T^\text{jet} > 30 $ GeV/c; and rapidity as $ |\eta| \le $ 2.5.

We started this investigation by studying the nuclear modifications of the $ H_1^T $ distributions for events with a fixed number of jets. The jet events were classified into two types, namely events with $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $.

Let us first focus on the event normalized spectrum of the $ H_1^T $ for $ n_\text{jet} = 2 $ events and its nuclear modification, as shown in the left panel of Fig. 3. This panel shows the results of the p+p (black line) and Pb+Pb (red line) collisions at $ \sqrt{s} = 5.02 $ TeV; the ratio of both, also known as the nuclear modification factor, is shown in the bottom panel. The distribution is apparently suppressed and enhanced separately in the small and large regions, taking approximately $ \ln(H_1^T) = -4.5 $ as a split. This medium modification means that the proportion of back-to-back jets, which are events with narrow shapes, is reduced. Therefore, the proportion of $ n_\text{jet} = 2 $ events is enhanced in regions characterized by large $ H_1^T $, where the event shapes are broader. The jet quenching effect indicates that the jet primarily loses energy through medium-induced gluon radiation. This results in a more diffuse distribution of total energy after traversing the medium, leading to the broadening of $ n_\text{jet} = 2 $ events.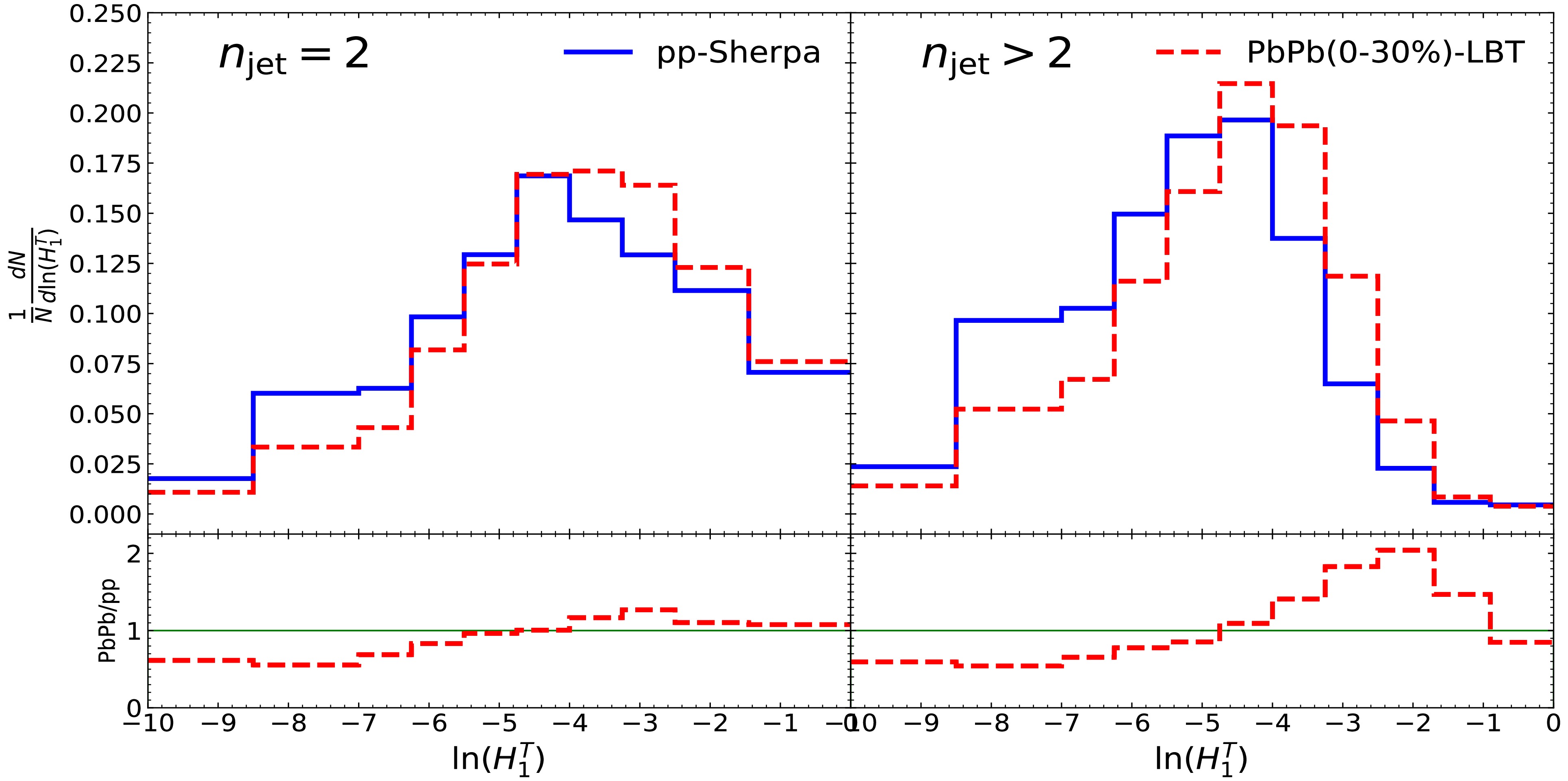

Figure 3.  (color online) Event normalized $ H_1^T $ distributions for $ n_\text{jet} = 2 $ (left panel) and $ n_\text{jet} > 2 $ (right panel) events in p+p and Pb+Pb collisions at $ \sqrt{s} = 5.02 $ TeV.

The event normalized $ H_1^T $ spectrum for $ n_\text{jet} > 2 $ events in p+p (black line) and Pb+Pb (red line) collisions and their nuclear modifications are shown in the right panel of Fig. 3. The distributions exhibit a significant enhancement in the bins where $ \ln(H_1^T) \in $ [–4.8,–0.9] by the medium, with suppressions observed in the other regions. The reason for the medium modification in the bins $ \ln(H_1^T) \in [-10, -0.9] $ is the same as that for $ n_{\text{jet}} = 2 $, as mentioned above: spread of momenta in the medium. Another aspect that should be considered is the jet-number reduction effect [140] when we focus on $ n_\text{jet} > 2 $ events (see Fig. 4). This causes the proportion of $ n_\text{jet} > 2 $ events to reduce significantly in the large region where $ \ln(H_1^T) \in $ [–0.9, 0].

Figure 4.  (color online) Histograms of the fraction of different numbers of jets in all jet events for p+p and Pb+Pb collisions at $ \sqrt{s}$ = 5.02 TeV.

To more intuitively reflect the medium modification of the event shape, we present the average azimuthal angle distance between jets for events with $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ over the entire $ \ln(H_1^T) $ statistical region in Table 2. It should be noted that we only consider the top three jets ranked by transverse momentum for $ n_\text{jet} > 2 $ events. Table 2 shows that the shape of $ n_\text{jet} = 2 $ events broadens, with the average azimuthal angle distance $ \langle \Delta\phi_{12} \rangle $ decreasing owing to medium modification. For $ n_\text{jet} > 2 $ events, both $ \langle \Delta\phi_{12} \rangle $ and $ \langle \Delta\phi_{13} \rangle $ decrease, while $ \langle \Delta\phi_{23} \rangle $ increases, indicating that the event shape is also broadened by medium modification.

$n_\text{jet} = 2$ events			$n_\text{jet} > 2$ events
p+p	Pb+Pb		p+p			Pb+Pb
$\langle \Delta\phi_{12}\rangle$	$\langle\Delta\phi_{12}\rangle$		$\langle\Delta\phi_{12}\rangle$	$\langle\Delta\phi_{13}\rangle$	$\langle\Delta\phi_{23}\rangle$	$\langle\Delta\phi_{12}\rangle$	$\langle\Delta\phi_{13}\rangle$	$\langle\Delta\phi_{23}\rangle$
2.946	2.922		2.829	2.539	0.847	2.816	2.465	0.934

Table 2.  Average azimuthal angle correlations calculated for $n_\text{jet} = 2$ and $n_\text{jet} > 2$ events in p+p and Pb+Pb collisions at $\sqrt{s}=5.02$ TeV over the entire $\ln(H_1^T)$ statistical region.

The histograms showing fractions of different numbers of jets in total jet events for p+p and Pb+Pb collisions at $ \sqrt{s} = 5.02 $ TeV are presented in Fig. 4. For Pb+Pb collisions, the change in the number of jets as a fraction of total jet events is significant compared to p+p collisions. The fraction of events with $ n_\text{jet} = 2 $ increases from 0.51 in p+p collisions to 0.56 in Pb+Pb collisions, and correspondingly, the total fraction of other events, i.e., $ n_\text{jet} > 2 $ events, decreases from 0.49 to 0.44. The decrease in the number of events is known as jet-number reduction effect. The reason for this is that some of the sub-leading jets experience energy loss in the medium, causing their transverse momentum magnitude to fall below our observational threshold of 30 GeV/c. As a result, the fraction of observed $ n_\text{jet} = 2 $ events increases in Pb+Pb collisions compared to p+p collisions.

Next, we analyze the $ H_1^T $ distribution for the combination of $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ events in proportion, as shown in Fig. 5. The nuclear modification factor exhibits a similar pattern to that of $ n_\text{jet} = 2 $ events, characterized by suppression at low $ H_1^T $ values and enhancement at high $ H_1^T $ values. To understand why the nuclear medium modification for total ($ n_\text{jet} \geq 2 $) events is as shown in Fig. 5, Fig. 6 presents the relative contributions of $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ events to $ H_1^T $ for both p+p and Pb+Pb collisions at $ \sqrt{s} = 5.02 $ TeV. In the low $ H_1^T $ region, $ n_\text{jet} > 2 $ events constitute a slightly larger proportion than $ n_\text{jet} = 2 $ events. As $ H_1^T $ increases, the percentage of $ n_\text{jet} = 2 $ ($ n_\text{jet} > 2 $) events gradually rises from approximately 40% (60%) in the low $ H_1^T $ region to approximately 90% (10%) in the high $ H_1^T $ region for p+p collisions. Similarly, the corresponding percentages transition from approximately 46% (54%) to approximately 89% (11%) for Pb+Pb collisions. The transition in the relative contributions between $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ events occurs at approximately $ \ln(H_1^T) = -4 $. The nuclear modification remains suppressed in the low $ H_1^T $ region, where both $ n_\text{jet} = 2 $ and $ n_\text{jet} > 2 $ events have similar fractions. In contrast, an enhancement effect is observed in the high $ H_1^T $ region, consistent with the behavior of $ n_\text{jet} = 2 $ events, which are dominant in this region.

Figure 5.  (color online) Top: event-normalized $H_1^T$ distribution of $n_\text{jet} \ge 2$ events in p+p and Pb+Pb collisions at $\sqrt{s}=5.02$ TeV; bottom: medium modification factor of event-normalized $H_1^T$ distribution of $n_\text{jet} \ge 2$ events.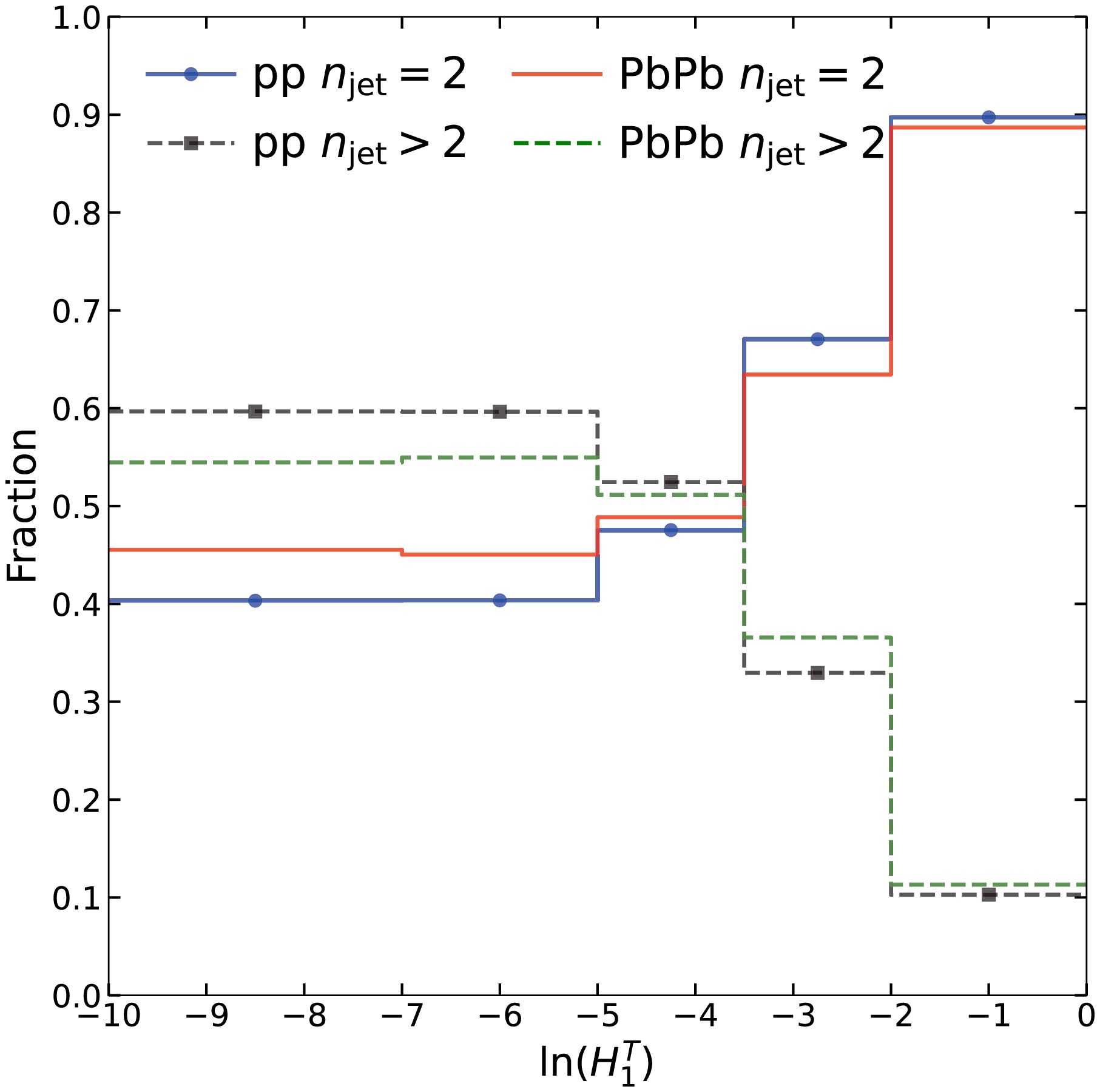

Figure 6.  (color online) Relative contribution fractions of $n_\text{jet} = 2$ and $n_\text{jet} > 2$ events from the distribution of $H_1^T$ normalized by the total number of events in p+p and Pb+Pb collisions at $\sqrt{s} =$ 5.02 TeV.

The focus of this study was put on the analysis of jet-event shapes described by $ H_1^T $ rather than by the transverse momentum or energy asymmetry. Nonetheless, the latter defines the former. We also studied the medium modification of the transverse momentum asymmetry for $ n_\text{jet} = 2 $ events (Appendix B).

We used the Monte Carlo event generator SHERPA to simulate jet production in p+p collisions. To incorporate virtual corrections, the OpenLoops programs were seamlessly integrated into the SHERPA environment. Additionally, we employed the LBT model to simulate the complex phenomenon of multiple scatterings between jets and the medium.

We investigated $ H_1^T $, which is the lower-order member of the set of FWMs related to QCD geometric patterns. We applied it to the field of jet quenching physics. This allowed us to examine how the medium modifies the jet-event shape for varying multiplicities ($ n_\text{jet} $). The results indicate that $ n_\text{jet} = 2 $ events undergo a pronounced broadening modification owing to the influence of nuclear matter. Meanwhile, the event shape for $ n_\text{jet} > 2 $ becomes broader owing to medium modification, except in the highest $ \ln(H_1^T) $ bin, where the jet-number reduction effect is significant. Additionally, we investigated the underlying reasons for the medium modification of $ H_1^T $ spectra for total jet events, without distinguishing between different multiplicities. This is achieved by analyzing the relative fraction of $ H_1^T $ between both types of events.

We extend our sincere gratitude to Jin-Wen Kang, Wei Dai, Shi-Yong Chen, Meng-Quan Yang, Sa Wang, and Shan-Liang Zhang for their invaluable discussions. We would also like to express our appreciation to the authors of the open-source software packages Sherpa [118], FastJet [139], HepMC2 [141], and ROOT [142].

The definition of $ H_1^T $ is complex when $ n_\text{jet} > 2 $ and is not discussed in detail in the main text. Here, we discuss the case of $ n_\text{jet} = 3 $ as an example:

Following Eq. (6), we denote $ p_{T 2} = y\cdot p_{T 1} $ and $ p_{T 3} = z\cdot p_{T 1} $, which simplifies the functional form of Eq. (A1). We obtain

The above simplification is intended to inform readers about a form similar to Eq. (6); however, owing to the increase in the number of variables, we did not conduct an in-depth analysis. Nonetheless, as discussed above, the physical interpretation of $ H_1^T $ in events with $ n_\text{jet} \geq 2 $ is that the event shape broadens as $ H_1^T $ increases.

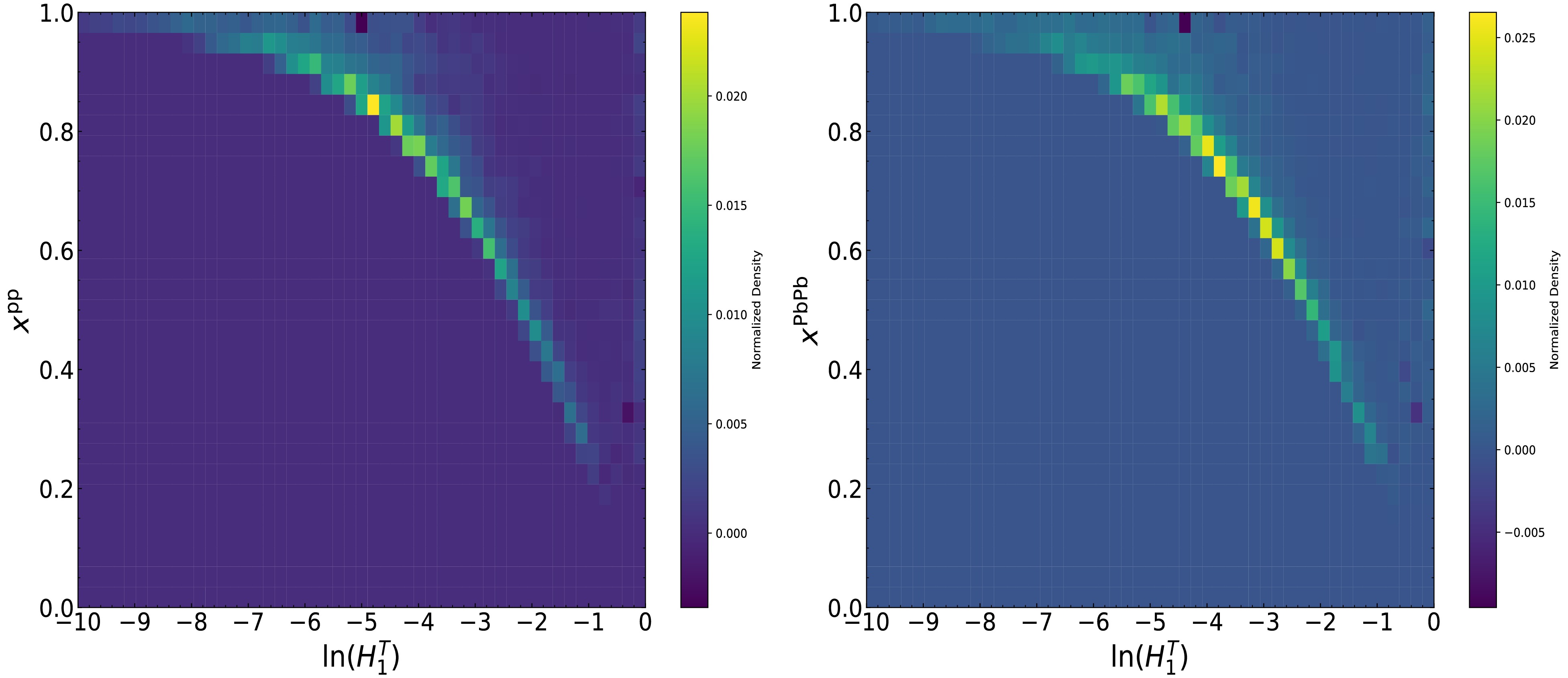
To further explore the factors responsible for the medium modification of the $ H_1^T $ distribution, we set $ n_\text{jet} = 2 $ events for correlation studies. The transverse momentum asymmetry is defined as $ x = p_{T 2}/p_{T 1} $. Figure B1 shows the distribution correlation between $ H_1^T $ and x for $ n_\text{jet} = 2 $ events in both p+p and Pb+Pb systems at $ \sqrt{s} $ = 5.02 TeV. Remarkably pronounced medium modification phenomena can be observed. It can be inferred that the medium modification of $ H_1^T $ exhibits moderate sensitivity to the transverse momentum imbalance between jets, which accentuates the transverse momentum asymmetry.

Figure B1.  (color online) Distribution correlation between $ H_1^T $ and x for $ n_\text{jet} = 2 $ events in p+p (left) and Pb+Pb (right) systems at $ \sqrt{s} = 5.02 $ TeV.