Influence of neutron-pair condensation on the difference in charge radii of mirror nuclei

As accurately measured quantities in terrestrial laboratories, charge radii are generally used to reflect nuclear structure phenomena, such as shape-phase transitions [1–6], shell quenching phenomena [7–13], and odd-even staggering (OES) effects [14–19]. Precise knowledge of nuclear size plays a key role in the study of nuclear physics and astrophysics [20]. Specifically, the difference in charge radii of mirror-paired nuclei, defined by exchanging the neutron number N and proton number Z while maintaining the same mass number $ A=N+Z $, is significantly associated with our understanding of fundamental interactions. A highly linear correlation between the difference in charge radii of mirror partner nuclei ($ \Delta{R_{{\rm{ch}}}} $) and the symmetry energy slope (L) was firstly proposed in Ref. [21]. Subsequently, numerous studies have verified that the differences in charge radii of mirror-pair nuclei are linearly correlated with the slope parameter of symmetry energy [22–31].

Owing to advances in experimental techniques, substantial data on the charge radii of nuclei far from the β-stability line have been accumulated [32, 33]. Generally, nucleus can be regarded as an incompressible liquid-drop, and its size can be described by the $ A^{1/3} $ or $ Z^{1/3} $ law [34–36]. However, the microscopic aspects, such as the information on proton density distributions and single particle levels, cannot be featured yet. The relativistic mean field theory [37, 38] and non-relativistic Skyrme Hartree-Fock-Bogoliubov (HFB) approach [39, 40] can also be used to describe the systematic evolution of nuclear charge radii; however, these fail to adequately capture local variations along long isotopic chains.

Fine structures of nuclear charge radii can be influenced by various underlying mechanisms [41]. By incorporating density gradient terms into the pairing interaction, the discontinuous behavior of charge radii can be effectively described [42]. As outlined in literature [27, 43], the correlations between the charge radii differences of mirror-pair nuclei and the slope parameter of symmetry energy are reduced by the pairing effects. Meanwhile, shape deformation also influences local variations in nuclear charge radii [1, 6]. As mentioned in Ref. [30], the quadrupole deformation correction has been considered in describing the charge radii difference of ³²Ar-³²Si; however, the overall influence of shape deformation is negligible. Additionally, recent studies suggest that the compression modulus of finite nuclei should not be ignored when determining the slope parameter of symmetry energy [43, 44].

Short-range correlations between neutrons and protons influence the charge density distributions near the Fermi surface [45–47]. Thus, neutron-proton correlations should be considered appropriately in describing the bulk properties of finite nuclei [48, 49]. Meanwhile, a strong coupling between neutron- and proton-pairing correlations (being α-clusters) [50] or a residual effective four-body force [51] is crucial in describing the local variations of the nuclear charge radii. Based on the relativistic mean-field model, a novel ansatz derived from the neutron- and proton-pair condensation around the Fermi surface has been incorporated into the root-mean-square (rms) charge radii formula [52]. This approach can reproduce the systematic evolution of nuclear charge radii, including the corresponding OES phenomena and shell closure effects [53–56], suggesting that the correlation between the neutron- and proton-pair condensation near the Fermi surface is crucial in describing the systematic trends of nuclear charge radii.

As previously described, the proton density distributions in mirror nuclei offer an alternative approach to ascertain the equation of state (EoS) of isospin asymmetric nuclear matter. Notably, studies analyzing the influence of neutron-pair condensation on determining the charge radii differences of mirror-paired nuclei remain scarce. Therefore, the effects of neutron-pair condensation on charge radii differences should also be further investigated using Skyrme energy density functionals (EDFs). In this study, the spherical HFB framework is employed, and the differential mean-square charge radii of Ni isotopes are used to test the validity of the developed model. Moreover, the charge radii differences of the mirror-pair nuclei ³²Ar-³²Si and ⁵⁴Ni-⁵⁴Fe are also applied to analyze the correlation between the charge radii difference of mirror pair nuclei and the slope parameter of nuclear symmetry energy.

The remainder of this paper is structured as follows. Section II presents the theoretical framework, while Sec. III outlines the numerical results and discussion. Finally, Sec. IV concludes the study and provides future perspectives.

The Skyrme density functional has achieved considerable success in describing various physical phenomena [39, 40, 57–59]. In this study, the Skyrme-like effective interaction is introduced as follows [60, 61]:

Here, $ {\bf{r}}={\bf{r}}_{1}-{\bf{r}}_{2} $ and $ {\bf{R}}=({\bf{r}}_{1}+{\bf{r}}_{2})/2 $ are naturally associated with the positions of two nucleons $ {\bf{r}}_{1} $ and $ {\bf{r}}_{2} $, $ {\bf{P}}= (\nabla_{1}-\nabla_{2})/2{\rm{i}} $ represents the relative momentum operator acting on the right, while its counterpart $ {\bf{P'}}= -(\nabla'_{1}-\nabla'_{2})/ 2{\rm{i}} $ denotes the complex conjugate acting on the left. $ {\bf{P_{\sigma}}}=(1+\vec{\sigma}_{1}\cdot\vec{\sigma}_{2})/2 $ represents the spin exchange operator, which is used to determine the relative strength of the $ S=0 $ and $ S=1 $ channels for a given term in the two-body interactions, with $ \vec{\sigma}_{1(2)} $ being the Pauli matrices. The last term features the spin-orbit force, where $ \sigma=\vec{\sigma}_{1}+\vec{\sigma}_{2} $. The quantities α, $ t_{i} $, $ x_{i} $ ($ i=0-3 $), and $ W_{0} $ represent the parameters of the effective forces used in this study.

The pairing correlations can be generally treated using either the Bardeen-Cooper-Schrieffer (BCS) method or the Bogoliubov transformation [37, 39, 40, 62–64]. In this study, the Bogoliubov transformation is used to treat the pairing correlations. The density-dependent zero-range pairing force is employed, defined as follows [65, 66]:

Here, $ \rho({\bf{r}}) $ is the baryon density distribution in coordinate space and $ \rho_{0}=0.16\; {\rm{fm}}^{-3} $ represents the nuclear saturation density. Generally, the values of η are set as $ 0.0 $, $ 0.5 $, or $ 1.0 $ for volume-, mixed-, or surface-type pairing interactions, respectively. As mentioned in Refs. [27, 43], the pairing correlations have an influence on determining the correlation between the charge radii difference of mirror-pair nuclei and the slope parameter of symmetry energy. Therefore, the mixed-type pairing force is selected in our calculations. The quantity $ V_{0} $ is adjusted by calibrating the empirical energy gaps with a three-point formula [65, 67]. The single-particle energy levels and wave functions of the constituent nucleons can be obtained by solving the HFB equations using the self-consistent iteration method [68].

The range of the proton matter distributions can be deduced from the wave functions of the constituent protons. The quantity of nuclear charge radius ($ R_{{\rm{ch}}} $) is defined as the rms radius of its proton distribution, which can be calculated using the following expression (in units of fm²) [55]:

The first term $ \langle{r_{{\rm{p}}}^{2}}\rangle $ represents the charge density distributions of point-like protons, while the second term is attributed to the finite size of protons [69]. For the third term, the expression $ \Delta{\cal{D}} $ is defined as $ \Delta{\cal{D}}=|{\cal{D}}_{n}-{\cal{D}}_{p}| $. The quantity of $ {\cal{D}}_{n} $ ($ {\cal{D}}_{p} $) is defined as follows:

where $ v_k^{n,p} $ is the amplitude of the occupation probability of the kth quasi-particle orbital for neutron or proton at the canonical basis, and $ u_k^2={1-v_k^2} $. Additionally, the quantity of $ {\cal{D}}_{n,p} $ can be used to measure the Cooper pairs condensation near the Fermi surface [70, 71]. The expression $ \Delta{\cal{D}} $ is used to measure the neutron- and proton-pair correlation near the Fermi surface [17, 52]. The parameter set $ a_{0}=0.561 $ is adjusted by reproducing the parabolic-like shape and odd-even oscillation behaviors in the charge radii of K and Ca isotopes [55]. The last term accounts for the correlation between simultaneously unpaired neutrons and protons. For mirror pair nuclei, the difference in charge radii ($ \Delta{R_{{\rm{ch}}}} $) can be obtained using Eq. (3). However, the last term is invalid because time-reversal symmetry is assumed in this study, restricting the analysis to even-even nuclei.

The influence of neutron-proton correlation, deduced from the neutron- and proton-pair condensation near the Fermi surface, has been incorporated into the rms charge radii formula based on the relativistic EDFs [52–56]. However, corresponding discussions are scarce within the Skyrme EDFs. First, the differential mean-square charge radii of Ni isotopes are employed to assess the validity of this theoretical model based on the Skyrme density functional model. A mixed-type pairing interaction is employed, with the pairing strength set to $ V_{0}=370.2 $ MeV fm³ by adjusting the empirical energy gap along the Ni isotopes. This approach is consistent with that described in Ref. [43]. Two pairs of mirror nuclei ³²Ar-³²Si and ⁵⁴Ni-⁵⁴Fe are used to examine the influence of neutron-proton correlations on determining charge radii differences in corresponding mirror-pair nuclei. For clarity, the results obtained using Eq. (3) are labeled as HFB^*, while those obtained without considering the influence of neutron- and proton-pair condensation are marked by HFB.

Shell closure effects of charge radii are generally observed across the entire nuclear chart [32, 33]. As mentioned in Ref. [72], Skyrme EDFs cannot effectively describe the shell closure effect in nuclear charge radii. The recently developed RMF (BCS)^* model can characterize the discontinuous behaviors of nuclear charge radii, especially the shell quenching phenomena [55]. Therefore, this method is well suited to evaluate the slope parameter of symmetry energy. The parameter sets of the effective forces used in this study, along with the corresponding values of the bulk properties of symmetric nuclear matter, are presented in Table 1. Under the specific incompressibility coefficients K, the slope parameter L and symmetry energy $ E_{{\rm{sys}}} $ at saturation density $ \rho_{0} $ span a wide range. The correlation between the charge radii differences of mirror partner nuclei and the slope parameter of symmetry energy can be influenced by the incompressibility coefficients of symmetric nuclear matter [43, 44]. Meanwhile, giant monopole resonances provide a measure of the isoscalar incompressibility $ K=230\pm10 $ MeV [73, 74]. Thus, the parameter sets s3032 and s4032, which have similar slope parameters but different incompressibility coefficients, are selected to describe the differential charge radii of Ni isotopes.

K /MeV	Sets	L /MeV	$ E_{{\rm{sys}}} $ /MeV
$ K\approx230 $ MeV	s3028	$ -11.2262 $	28
	s3030	22.8715	30
	s3032	36.2246	32
	s3034	56.1442	34
	s3036	71.5428	36
	s3038	87.6155	38
	s3040	106.0862	40
$ K\approx240 $ MeV	s4028	3.9774	28
	s4030	34.0735	30
	s4032	34.4283	32
	s4034	62.5884	34
	s4036	75.6679	36
	s4038	98.6522	38
	s4040	108.1741	40
$ K\approx250 $ MeV	s5028	33.0037	28
	s5030	30.0248	30
	s5032	43.5871	32
	s5034	60.3202	34
	s5036	80.1762	36
	s5038	97.4925	38
	s5040	112.2079	40

Table 1.  Saturation properties of the Skyrme parametrization sets used in this study [43], such as the incompressibility coefficients K (MeV), slope parameter L (MeV) and symmetry energy $ E_{{\rm{sys}}} $ (MeV) at saturation density $ \rho_{0} $ (fm^-3).

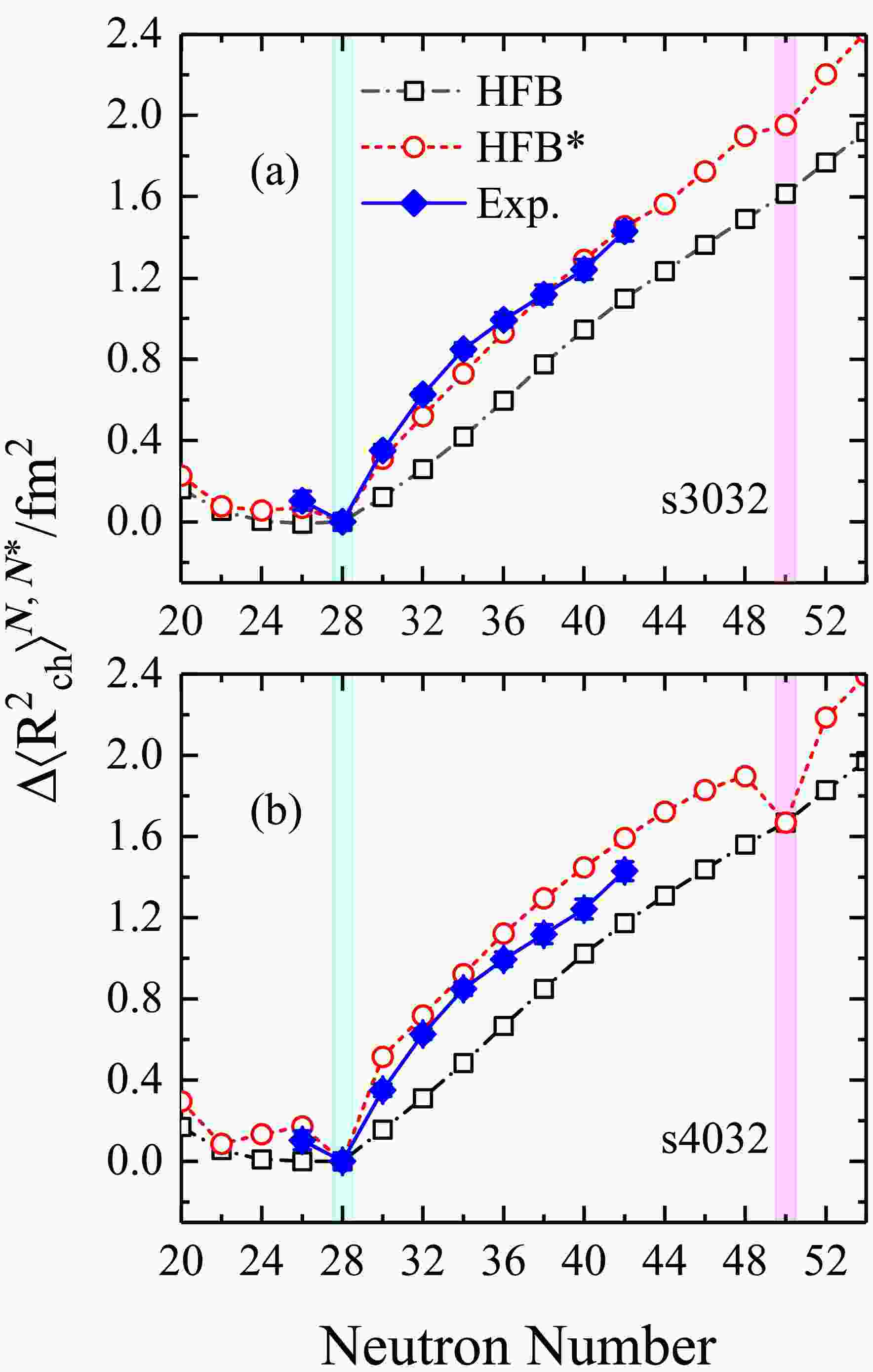
The charge radii of Ni isotopes have been measured accurately using the collinear laser spectroscopy technique [24, 72, 75]. The extracted results suggest that the shell quenching phenomenon in charge radii is pronounced near the fully filled $ N=28 $ shell. Moreover, across the neutron number $ N=28 $, the trend in charge radii changes is similar to that observed in the Ca isotopic chain. Notably, the systematic evolution of nuclear charge radii across $ N=28 $ exhibits a similar trend from K to Zn isotopic chains, indicating that this trend is almost independent of the atomic number [55, 76].

As shown in Fig. 1, the differential charge radii of Ni isotopes, relative to the reference nucleus ⁵⁶Ni, are depicted using the HFB and HFB^* methods with the effective forces s3032 and s4032, respectively. Notably, the HFB^* model can reproduce the trend in charge radii across the $ N=28 $ shell closure along Ni isotopic chain, as shown in Fig. 1 (a). Meanwhile, the decreased trend of charge radii from ⁵⁴Ni to ⁵⁶Ni can also be reproduced, resulting in a significantly observed kink phenomenon at the neutron number $ N=28 $. Notably, the charge radii values for isotopes ^60,62Ni are slightly underestimated when using the s3032 effective force. In contrast to the HFB^* model, the differential charge radii of Ni isotopes cannot be reproduced by the HFB model. Particularly, the rapid increase in charge radii is not effectively reproduced across the fully filled $ N=28 $ shell. The same scenario can be encountered around $ N=50 $, where the HFB model cannot represent the shrinking trend of charge radii. By contrast, shell quenching phenomenon in charge radii of Ni isotopes could be predicted at the neutron number $ N=50 $ using the HFB^* model.

Figure 1.  (color online) Mean-square charge radii differences of the even-even Ni isotopes relative to the ⁵⁶Ni nucleus obtained by the Skyrme EDFs with the parameter sets s3032 (a) and s4032 (b) are presented for HFB (open square) and HFB^* (open circle) methods. The experimental data are obtained from Refs. [24, 32, 33, 72, 75] (solid diamond). The shaded planes mark the neutron magic numbers $ N=28 $ (light blue) and $ N=50 $ (light pink), respectively.

An inverted parabolic-like shape of charge radii is observed between neutron numbers $ N=20 $ and $ N=28 $ along K and Ca isotopes [32, 33]. The HFB^* model reproduces the inverted parabolic-like shape of charge radii along Ni isotopic chain between the neutron numbers $ N=20 $ and $ N=28 $. However, this phenomenon cannot be reproduced by the HFB model. Particularly, the trend of change of charge radius for ⁵⁴Ni isotope cannot be effectively reproduced by the HFB model. Moreover, the inverted parabolic-like shape of charge radii obtained by the HFB^* model can also be found between the neutron numbers $ N=28 $ and $ N=50 $. Thus, additional experimental data are needed to support future research.

In Fig. 1(b), the results from the HFB and HFB^* models are based on calculations using the effective force s4032. The shell quenching effects of charge radii at the neutron numbers $ N=28 $ and $ N=50 $ can also be reproduced by the HFB^* model. However, the differential charge radii of ^66,68,70Ni isotopes obtained by the HFB^* model slightly deviate from the experimental data. The HFB model consistently underestimates the systematic trend in charge radii changes across the Ni isotopes. Significant deviations exist between the absolute values calculated with the effective force s3032 and experimental measurements, relative to those calculated by the effective force s4032. The stability of finite nuclei is mostly determined by the Coulomb force and the symmetry energy. A larger symmetry energy reflects stronger isospin interactions, which leads to broader charge density distributions [77]. In our calculations, the pronounced reduction in the differential charge radii at the neutron number $ N=50 $ can be obtained by the parameter set s4032 compared to the effective force s3032. This difference arises because the symmetry energy slopes are similar while the incompressibility coefficients are different. This is exemplified by the charge radius of ⁷⁸Ni, whose value calculated using the s3032 force is larger than that obtained using the effective force s4032 by approximately 0.02 fm. These results suggest that the effective force s4032 predicts more compact finite nuclei properties.

Accurate description of nuclear charge radii serves as a sensitive indicator to our understanding of fundamental interactions in exotic nuclei. As mentioned in Refs. [46, 49, 78], isospin interactions from the neutron-proton correlations should be properly considered when evaluating nuclear size. The greater ability of the HFB^* model to reproduce the differential charge radii of Ni isotopes is attributed to the neutron-proton correlations deduced from the neutron-pair and proton-pair condensation near the Fermi surface. This finding aligns with those from previous studies [79–81], where the neutron-proton interactions derived from the valence neutrons and protons accurately describe the local variations of nuclear charge radii along long isotopic chains. This finding further suggests that the neutron-proton correlations near the Fermi surface is crucial in determining the discontinuous variations of nuclear charge radii.

A highly linear correlation between the charge radii difference ($ \Delta{R}_{{\rm{ch}}} $) of mirror-pair nuclei and the slope parameter (L) of symmetry energy has been utilized to determine the isospin components in the EoS of asymmetric nuclear matter [21–31]. Therefore, it is theoretically essential to further investigate the influence of neutron-proton correlations on determining the values of $ \Delta{R}_{{\rm{ch}}} $ in a given pair of mirror nuclei. In our calculations, mirror nuclei with mass number $ A = 32 $ and 54 are employed to assess the influence of neutron-proton correlations on the charge radii difference. The corresponding experimental data are shown in Table 2.

A		$ R_{{\rm{ch}}} $ /fm	$ \Delta{R_{{\rm{ch}}}} $ /fm
32	Ar	3.3468(62)
	Si	3.153(12)	0.194(14)
54	Ni	3.7370(30)
	Fe	3.6880(17)	0.049(4)

Table 2.  Charge radii ($ R_{{\rm{ch}}} $) and charge radii difference ($ \Delta{R_{{\rm{ch}}}} $) databases for the $ A = 32 $ and 54 mirror pairs nuclei. The parentheses on the values of charge radii and the differences of charge radii are shown with systematic uncertainties [24, 30, 32, 33].

The theoretical results obtained from the HFB and HFB^* models are used to assess the correlation between $ \Delta{R}_{{\rm{ch}}} $ and L. As shown in Fig. 2, the results of $ \Delta{R}_{{\rm{ch}}} $ for mirror partner nuclei ⁵⁴Ni-⁵⁴Fe and ³²Ar-³²Si are presented as functions of the slope parameter L. The shaded planes indicate the systematic uncertainties of the charge radii difference between the corresponding mirror nuclei, including the ranges of $ 0.049(4) $ fm (⁵⁴Ni-⁵⁴Fe) and 0.194(14) fm (³²Ar-³²Si), respectively. The results obtained using the HFB and HFB^* models show the approximately linear correlation between $ \Delta{R}_{{\rm{ch}}} $ and L for both pairs of mirror nuclei. Generally, the uncertainty range of $ \Delta{R}_{{\rm{ch}}} $ covered by the fitted line is used to constrain the slope parameter L. Notably, the covered range of L changes significantly when using the HFB^* model.

Figure 2.  (color online) $ \Delta{R_{{\rm{ch}}}} $ of mirror partner nuclei ⁵⁴Ni-⁵⁴Fe (a) and ³²Ar-³²Si (b) obtained by the HFB (open circle) and HFB^* (solid pentagon) methods as a function of slope parameter L at saturation density $ \rho_{0} $. The experimental results are shown as horizontal light blue bands. The dot-dot-dashed lines indicate the corresponding theoretical linear fits.

In this study, the lower limit of L is constrained at $ 0.0 $ MeV. As shown in Fig. 2 (a), the coverd range of L obtained by the HFB model falls into $ 0.0\leq{L}\leq 38.11 \; (\pm5.07) $ MeV. By contrast, HFB^* model gives the range of $ 33.18\leq{L}\leq78.64\; (\pm3.58) $ MeV, consistent with finding from Ref. [24] where the deduced L value falls within the range $ 21\leq{L}\leq88 $ MeV. This indicates that the neutron-proton correlations around the Fermi surface can influence the determination of the values of $ \Delta{R}_{{\rm{ch}}} $. Moreover, a larger deviation can also be encountered in the mirror pair nuclei ³²Ar-³²Si. A range of $ 51.22\leq {L}\leq 97.87\; (\pm6.17) $ MeV can be extracted from ³²Ar-³²Si using the HFB method. Conversely, the HFB^* method yields a range of $ 62.21\leq{L}\leq111.59\; (\pm5.19) $ MeV. As demonstrated in Ref. [30], a relatively soft EoS is obtained, namely $ L\leq60 $ MeV. However, a stiffer EoS can be extracted from the charge radii difference of mirror pair nuclei ³²Ar-³²Si in our calculations. The results suggest that the HFB^* model yields a significantly stiffer EoS compared with the HFB model. These findings highlight the importance of properly accounting for neutron-proton correlations when constraining the slope parameter L. As mentioned in Refs. [43, 44, 82], the quantification arising from the incompressibility of nuclear matter is inevitable when evaluating the isospin components. As shown in Fig. 2, the influence of nuclear matter incompressibility coefficients cannot be clearly distinguished when analyzing the correlation between charge radii differences of mirror pair nuclei and the slope parameter of symmetry energy. This may lead to the relatively larger uncertainty ranges in evaluating the slope parameter L.

To facilitate the quantitative comparison under various incompressibility coefficients, the $ \Delta{R}_{{\rm{ch}}} $ for ⁵⁴Ni-⁵⁴Fe obtained by the HFB and HFB^* models is presented as a function of the slope parameter L, as shown in Fig. 3. The effective forces classified by various incompressibility coefficients K are used to examine the covered range of the slope parameters of symmetry energy. Notably, the ranges of the slope parameter L obtained using the HFB method differ significantly from those obtained using the HFB^* model for the mirror-pair nuclei ⁵⁴Ni-⁵⁴Fe. For the specific incompressibility coefficients, the covered lower and upper ranges of L are simultaneously enlarged with considering the neutron-proton correlations around the Fermi surface. However, for $ K=230 $ MeV and $ K=240 $ MeV, the covered ranges of L are almost similar for the HFB^* model. In contrast to $ K=230 $ MeV and $ K=240 $ MeV, the HFB^* model yields a relatively lower range of L when the effective forces classified by $ K=250 $ MeV are used.

Figure 3.  (color online) $ \Delta{R}_{{\rm{ch}}} $ of mirror-pair nuclei ⁵⁴Ni-⁵⁴Fe as a function of slope parameter L at the saturation density $ \rho_{0} $. The open circle represents the HFB calculations and the solid pentagon represents the results obtained by HFB^* model. The experimental data are depicted as the light blue shaded band. The dot-dot-dashed line indicates theoretical linear fits.

As previously described, the incompressibility coefficient influences the determination of the symmetry energy slope. As shown in Fig. 4, $ \Delta{R}_{{\rm{ch}}} $ for ³²Ar-³²Si as a function of L is also shown for both the HFB and HFB^* models. For parameter sets classified by various incompressibility coefficients, the upper and lower limit ranges of the slope parameter L obtained using the HFB^* model are systematically broader compared with those from the HFB method. For $ K=240 $ MeV and $ K=250 $ MeV, the covered ranges of L are almost similar for the HFB^* model. However, for $ K=230 $ MeV case, the upper range of L is approximately 20 MeV lower than that in the $ K=240 $ MeV and $ K=250 $ MeV cases. This further suggests that the correlation between the charge radii difference of mirror partner nuclei and the slope parameter of symmetry energy is influenced by the effective forces classified by various incompressibility coefficients. In Table 3, the charge radii of mirror partner nuclei ³²Ar-³²Si and ⁵⁴Ni-⁵⁴Fe are presented using various effective forces characterized by the incompressibility coefficients $ K\approx230 $, 240, and 250 MeV.

Figure 4.  (color online) Same as Fig. 3 but for mirror-pair nuclei ³²Ar-³²Si.

			HFB				HFB*
	Sets	32Si	32Ar	54Fe	54Ni	32Si	32Ar	54Fe	54Ni
$ K\approx230 $ MeV	s3028	3.1984	3.3471	3.7752	3.8215	3.2366	3.3829	3.7856	3.8225
	s3030	3.2275	3.3923	3.7893	3.8417	3.2346	3.3930	3.8002	3.8421
	s3032	3.2086	3.3906	3.7807	3.8344	3.2327	3.4054	3.7902	3.8356
	s3034	3.2101	3.4031	3.7847	3.8424	3.2331	3.4174	3.7945	3.8429
	s3036	3.2047	3.4080	3.7830	3.8438	3.2305	3.4248	3.7929	3.8441
	s3038	3.2027	3.4155	3.7844	3.8483	3.2298	3.4337	3.7944	3.8483
	s3040	3.2070	3.4263	3.7892	3.8569	3.2289	3.4402	3.7998	3.8577
$ K\approx240 $ MeV	s4028	3.2173	3.3667	3.7628	3.8100	3.2222	3.3682	3.7716	3.8110
	s4030	3.2590	3.4196	3.7828	3.8356	3.2638	3.4231	3.7921	3.8356
	s4032	3.1821	3.3612	3.7325	3.7843	3.2066	3.3763	3.7400	3.7869
	s4034	3.1996	3.3836	3.7528	3.8108	3.2078	3.3854	3.7624	3.8109
	s4036	3.1938	3.3857	3.7488	3.8091	3.2029	3.3884	3.7585	3.8094
	s4038	3.2043	3.4075	3.7641	3.8290	3.2131	3.4101	3.7741	3.8300
	s4040	3.1898	3.4001	3.7504	3.8166	3.2012	3.4049	3.7605	3.8177
$ K\approx250 $ MeV	s5028	3.1991	3.3578	3.7298	3.7774	3.2327	3.3893	3.7564	3.8045
	s5030	3.2018	3.3640	3.7388	3.7895	3.2110	3.3664	3.7457	3.7914
	s5032	3.1988	3.3738	3.7377	3.7902	3.2138	3.3811	3.7435	3.7933
	s5034	3.1984	3.3819	3.7402	3.7958	3.2127	3.3889	3.7463	3.7984
	s5036	3.2039	3.3992	3.7495	3.8085	3.2198	3.4076	3.7554	3.8110
	s5038	3.2040	3.4078	3.7524	3.8146	3.2194	3.4162	3.7587	3.8165
	s5040	3.1971	3.4099	3.7218	3.7870	3.2143	3.4198	3.7478	3.8063

Table 3.  Charge radii of mirror-pair nuclei ³²Ar-³²Si and ⁵⁴Ni-⁵⁴Fe (in units of fm) are presented with various effective forces classified by the incompressibility coefficients $ K\approx230 $, 240, and 250 MeV.

Generally, the neutron skin thickness of a heavy nucleus provides a valuable approach to constrain the EoS of isospin asymmetric nuclear matter. The difference in proton density distributions between mirror nuclei exhibits a strong correlation with the neutron skin thickness [25, 83]. This indicates that neutron skin thickness information can be derived directly from measured charge radii data. As demonstrated in Refs. [84, 85], the precise data on mirror charge radii cannot provide a strict constraint on the slope parameter L, as the correlation between the mirror charge radii differences $ \Delta{R}_{{\rm{ch}}} $ and the slope parameter L is weak. The bulk properties of finite nuclei cannot be adequately captured by effective forces deduced from infinite nuclear matter. This limitation arises from specific factors that influence the radii range of the proton density distributions, such as shell closure effect [11, 86] and isospin symmetry breaking [87–89]. Proton and neutron matter distributions influence each other. As discussed in this study, the neutron-proton correlations, deduced from the neutron-pair and proton-pair condensation around the Fermi surface, along with the compression modulus, significantly influence the determination of the charge radii differences of mirror nuclei. Therefore, these neutron-proton correlations and the compression modulus of symmetry nuclear matter must be considered when describing the nuclear charge radii [43, 55].

This is the first study to investigate the influence of the neutron-pair condensation near the Fermi surface on the determination of the symmetry energy slope based on Skyrme EDFs. The validity of the theoretical model is confirmed by reproducing the trend of changes of differential charge radii along Ni isotopes, which can be described well by this modified model. In particular, the model accurately captures the kink phenomenon in charge radii observed at the neutron number $ N=28 $. Meanwhile, the shell closure effect at $ N=50 $ is also evident in the charge radii of Ni isotopes. Notably, an inverted parabolic shape in charge radii is predicted between the neutron numbers $ N=20 $ and $ N=28 $. The same scenario can also be observed between $ N=28 $ and $ N=50 $; however, the amplitude is apparently weakened.

Notably, nuclear symmetry energy is crucial in various simulated codes [90–102]. Therefore, available density dependence of symmetry energy is required from multimessenger constraints. The correlations between the differences in charge radii of mirror pair nuclei ³²Ar-³²Si and ⁵⁴Ni-⁵⁴Fe and the slope parameters of symmetry energy can be influenced by neutron-proton correlations around the Fermi surface and the effective forces classified by various isoscalar incompressibility coefficients. A stiffer EoS can be obtained using the HFB^* model compared with results from the HFB method. The mean-square charge radius of a nucleus is naturally derived from its charge density distributions. Recent studies suggest that charge radii can be derived from the charge-changing cross section measurements of exotic nuclei [103, 104]. Moreover, the difference in charge-changing cross sections of mirror nuclei offers an alternative approach to evaluate the EoS of nuclear matter [105]. Thus, a unified model is required to accurately determine the slope parameter of symmetry energy using the charge radii difference of mirror-paired nuclei.