Thermodynamics of Schwarzschild-AdS black hole in non-commutative geometry

Non-commutative geometry is a theory of spacetime quantization [1−7], described by commutator $ \left[\hat{x}^{\mu},\hat{x}^{\nu}\right] = \mathrm{i}\hat{\Theta}^{\mu\nu} $, where $ \hat{x}^{\mu} $ and $ \hat{x}^{\nu} $ are spacetime coordinate operators, $ \hat{\Theta}^{\mu\nu} $ is an anti-symmetric constant tensor, Θ is a parameter with dimension of $ \left[\mathrm{L}^{2}\right] $ that represents the minimum spacetime scale, and $ \sqrt{\Theta} $ is a small quantity of the order of the Planck length $ \ell_{p} $ [1, 8]. Extensive research has been conducted to consider the effects of non-commutative fields in gravitational theories [9−16]. An interesting fact is that the commutator of coordinate operators being a nonzero constant Θ matrix is incompatible with Lorentz covariance [1], which potentially suggests a close relationship between non-commutative fields and the violation of Lorentz symmetry. This also provides a new insight into theories about the violation of Lorentz covariance [17−22]. Non-commutative geometry also provides a reasonable modification to Schwarzschild spacetime. Compared to the point-like mass distribution in the ordinary Schwarzschild spacetime, the mass distribution of a spherically symmetric star is altered to a Gaussian distribution $\rho = \dfrac{M}{\left(4\pi\Theta\right)^{{3}/{2}}}\exp\left(-\dfrac{r^{2}}{4\Theta}\right)$ and Lorentzian distribution $\rho = {M\sqrt{\Theta}}/[{\pi^{{3}/{2}}\left(r^{2}+\pi\Theta\right)^{2}}]$ spread throughout the entire space [23]. Unlike the Schwarzschild spacetime with singularities, these two distributions both lead to a regular de Sitter core at short distances. Many studies have investigated the properties of black holes (BHs) against the background of non-commutative geometry [9−12, 23−28]. In Ref. [9], the authors found that the evaporation endpoint of a Schwarzschild BH, corrected by a Gaussian distribution, is identified as a zero-temperature extremal BH, even in the case of electrically neutral and non-rotating objects. Moreover, there exists a finite maximum temperature that the BH can attain before eventually cooling down to absolute zero. The Schwarzschild BH with the Lorentzian distribution has also been extensively studied, including its gravitational lensing effects, quasinormal modes, BH shadows, and thermodynamic properties [25].

BH thermodynamics is a relatively young branch of BH physics. Since Hawking and Page made the groundbreaking discovery of phase transitions in Schwarzschild-AdS BHs in 1983 [29], this area has garnered significant attention, particularly concerning thermodynamics in anti-de Sitter (AdS) spacetime, which often yields more intriguing and profound conclusions. By correlating the BH's mass and the cosmological constant with enthalpy and pressure, researchers derived the first law of AdS-BH thermodynamics [30], laying the groundwork for a detailed exploration of this subject in AdS spacetime. A classic example is the Reissner-Nordström (RN)-AdS BH, whose thermodynamic properties were thoroughly researched in Ref. [31], revealing phase transitions akin to those of Van der Waals fluids, alongside critical points characterized by identical critical ratios and critical exponents. Additionally, the RN-AdS BH undergoes a Joule-Thomson process with inversion points, accompanied by a minimum critical mass [32]. Overall, extensive research indicates that BHs in AdS spacetime exhibit thermodynamic properties similar to those of Van der Waals systems [31, 33−39]. Notably, for a static spherically symmetric BH, if the energy-momentum tensor of the spacetime explicitly includes the BH's mass, the first law of thermodynamics for BHs requires modification [36, 37, 40], complicating the study of enthalpy and Gibbs free energy.

In this work, we investigate the thermodynamics of Schwarzschild-AdS BHs with Lorentzian distribution in non-commutative geometry. The remainder of this article is organized as follows. In Sect. II, we substitute the Lorentzian distribution into the Einstein equation with the cosmological constant to obtain the metric of a Schwarzschild-AdS BH in non-commutative geometry and discuss the existence of BH solutions. In Sect. III, we conduct detailed research on thermodynamics, including the revised first law, equation of state, behavior of phase transitions, and criticality. We also calculate the heat capacity and Gibbs free energy of the BH. In Sect. IV, we investigate the Joule-Thomson process. We study the inversion points and determine the conditions for their existence, specifically the minimum inversion temperature and minimum inversion mass. Finally, we summarize our findings and give a future outlook in Sect. V. Throughout this paper, the Planck units $ \hbar = k_{B} = G = c = 1 $ are used.

The Einstein equation with the cosmological constant Λ is

where $ R_{\mu}^{\nu} $ is the Ricci tensor, $ \delta_{\mu}^{\nu} $ is the Kronecker symbol, R is teh Ricci scalar, and $ T_{\mu}^{\nu} $ is the energy-momentum tensor. A spherically symmetric spacetime can be expressed as

By substituting the metric into the Einstein equation, one can obtain

The Lorentzian distribution ρ of mass density in non-commutative geometry is [9, 23−25]

where M is the mass of the BH, and Θ is a non-commutative parameter with dimension of $ \left[\mathrm{L}^{2}\right] $. The metric of Schwarzschild-AdS BH in non-commutative geometry is

It is clear that the correction of non-commutative geometry is of higher order.

To simplify the calculations, we introduce a parameter a with dimension $ \left[\mathrm{L}\right] $

where a and Θ are equivalent, as they can both be used to characterize the strength of the noncommutative geometry.

The metric of a Schwarzschild-AdS BH in non-commutative geometry is given by

To ensure the existence of a BH, it is necessary to satisfy $ f\left(r_{h}\right) = 0 $ ($ r_{h} $ is the radius of event horizon), $ M>0 $, and $ r_{h}>0 $. It is obvious that $ a>0 $. Meanwhile, AdS spacetime gives $ \Lambda<0 $. These conditions impose the following constraints:

The BH's mass, also regarded as its enthalpy, can be solved from $ f\left(r_{h}\right) = 0 $:

The temperature of the BH is defined by its surface gravity:

In the extended phase space of AdS BHs, the cosmological constant is related to the BH's pressure:

The BH's entropy satisfies the Bekenstein-Hawking relation:

where $ A = \int \int\sqrt{ g_{\theta\theta}g_{\phi\phi}}\mathrm{d}\theta\mathrm{d}\phi = 4\pi r_{h}^{2} $ is the surface area of the BH's event horizon. The above functions are helpful for deriving the thermodynamic first law. However, when the energy-momentum tensor $ T_{0}^{0} $ includes the BH's mass (as seen in Eq. 4), the conventional first law of thermodynamics $ \mathrm{d}M = T\mathrm{d}S+V\mathrm{d}P $ will be violated [36, 37, 40]. It is easy to verify that

The modified first law is written as

where W is the correction function,

Using the modified first law, one obtains

and the BH's thermodynamic volume

Here,

could be interpreted as "non-commutative potential". Treating the noncommutative parameter as a thermodynamic variable is not merely a formal requirement but also facilitates the derivation of the BH's Smarr relation.

For the BH's mass function $ M = M\left(S,P,a\right) $, performing a scale transformation $ r_{h}\rightarrow kr_{h} $ on the system, one can obtain

where $ d_{M} $, $ d_{S} $, $ d_{P} $, and $ d_{a} $ are scale dimensions of M, S, P, and a, respectively. Taking the derivative of both sides of the above equation with respect to k, one obtains

where $ M_{S} = \dfrac{\partial M}{\partial S} $. The same applies to P and a. One could set $ k = 1 $ and derive

According to Eqs. (5), (11), and (12), d_M = 1, $d_{S} =2,\;d_{P} = -2$, and $ d_{a} = 1 $. Thus, one finally obtains

With the help of Eqs. (16)−(18), one has

It is clear that when $ W = 1 $, the conventional Smarr relation appears. This relation is general. One only needs to fully consider quantities with scale dimensions and derive the Smarr relation using the same method. The general Smarr relation is as follows:

here, $ y^{i} $ represents the i-th thermodynamic variable other than entropy and pressure, $ d_{y^{i}} $ denotes its scale dimension, $ \Phi_{y^{i}} = W\dfrac{\partial M}{\partial y^{i}} $, and repeated indices imply summation.

Strictly speaking, according to Eq. (15), it should be considered that the first law of thermodynamics is only violated when the energy-momentum tensor of the spacetime outside the event horizon is affected by the BH's mass. In fact, the energy-momentum tensor of a Schwarzschild BH is also related to the BH's mass:

where $ \delta^{3}\left(x\right) $ is the Dirac delta function in three-dimensional space.

It should be noted that for the modified first law of thermodynamics, in general, Eq. (14) is not an exact differential form (see the proof in Appendix A). In other words, there does not exist a function $ {\cal{M}} $ satisfying Eq. (14). This issue will appear again when discussing the Gibbs free energy.

Now, we investigate the Smarr relation using the Komar integral [41, 42]. A Killing vector in a static spherically symmetric spacetime is given by $ \xi = \partial_{t} $, $ \xi^{\mu} = \left(1,0,0,0\right) $. To construct the Komar integral relation in the presence of a nonzero cosmological constant, it is necessary to introduce the Killing potential $ \omega^{\mu\nu} $ [30, 42−44], which satisfies

The Killing potential is not unique. In this work, we take the form

One could integrate the Killing equation $ \nabla_{\mu}\nabla^{\mu}\xi^{\nu} = -R_{\mu}^{\nu}\xi^{\mu} $ over a three-dimensional hypersurface Σ:

where $ \mathrm{d}\Sigma_{\nu} $ represents the surface elements of Σ. According to the Einstein equation (Eq. (1)),

In non-commutative Lorentzian spacetime, one could obtain

Thus, one has

By applying the Gauss theorem, one can derive

where $ \partial\Sigma $ is the boundary of Σ, and $ \mathrm{d}\Sigma_{\mu\nu} $ represents the surface elements of $ \partial\Sigma $. By choosing Σ as the entire space outside the horizon, $ \partial\Sigma = S^{2}_{r_{h}}\cup S^{2}_{\infty} $, where $ S^{2}_{r_{h}} $ represents the horizon sphere and $ S^{2}_{\infty} $ corresponds to the sphere at infinity. Specifically, for a standard Schwarzschild spacetime, no matter exists outside the horizon, which leads to the Komar integral relation in Refs. [30, 42]:

For a non-commutative Lorentzian BH, due to the influence of the noncommutative parameter a, the mass distribution of the BH can be regarded as a fluid distributed throughout the entire spacetime. Now, we proceed with the computation of the Komar integral. The area element of a two-dimensional sphere is given by $ \mathrm{d}\Sigma_{tr} = -\mathrm{d}\Sigma_{rt} = -r^{2}\mathrm{d}\Omega/2 $, where $ \mathrm{d}\Omega $ is the solid angle differential element. For the spherical surface at infinity, one has

One can calculate and obtain the nonzero components of $ \nabla^{\mu}\xi^{\nu} $

For the horizon sphere, the first term of Eq. (33) is

The second term of Eq. (33) is

The second term of Eq. (32) is exactly the charge associated with the conserved current $ J^{\mu} = T^{\mu\nu}\xi_{\nu} $. One could substitute in Eq. (4) and derive

Combining Eqs. (32), (34), and (36)−(38), we obtain

This conclusion is consistent with Eq. (23), because it is not difficult to verify

It is important to note that, unlike in the RN spacetime, the non-commutative parameter a is not suggested as an independent conserved charge, as it is coupled to the BH's mass M. In this case, the conserved charge of the spacetime is still more appropriately suggested as the energy of the gravitational field. From Eq. (34), it follows that the total energy of the gravitational field remains equal to the BH's mass M.

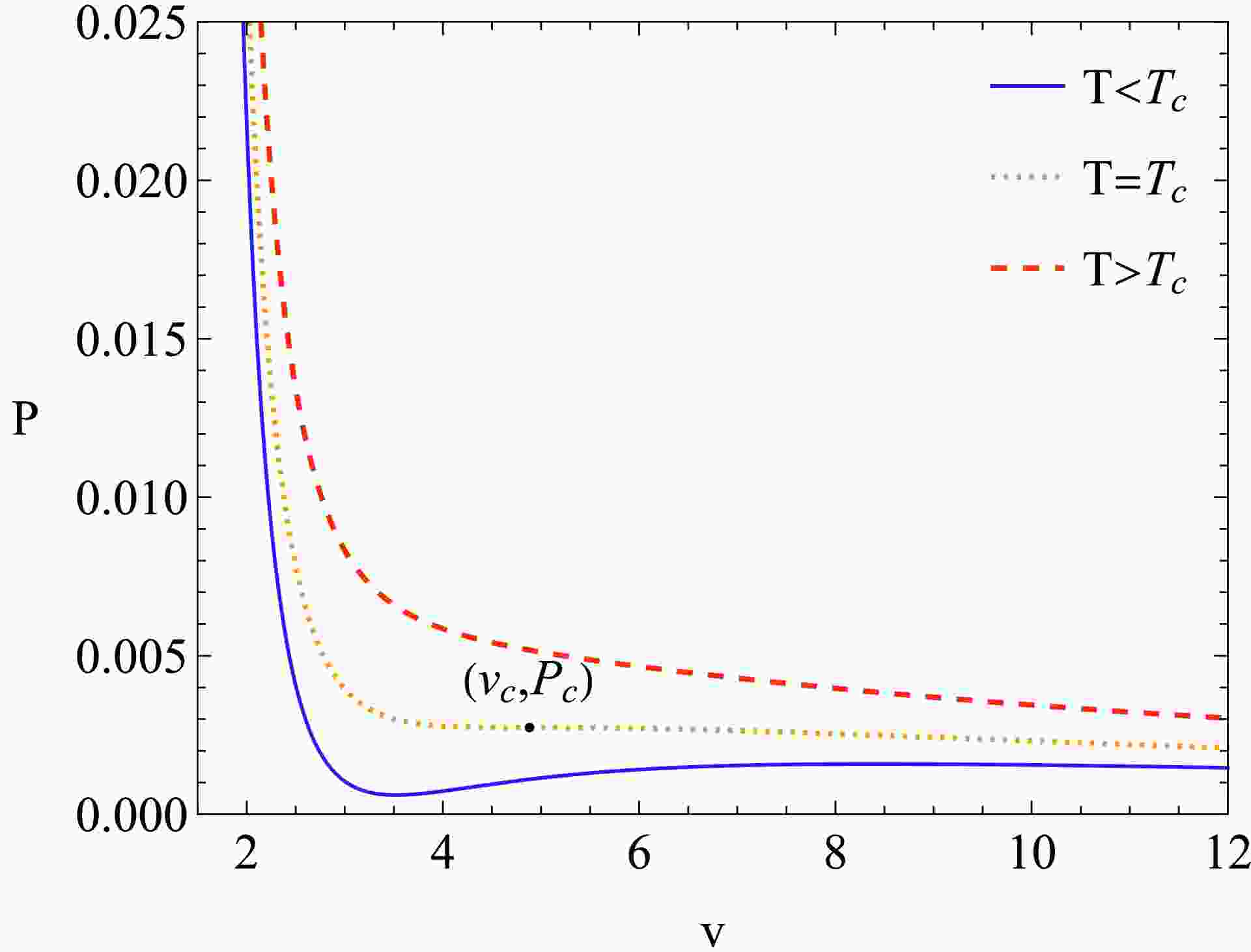
To investigate criticality, the specific volume $ v = 2r_{h} $ is introduced [31, 45]. By using this relation, Eqs. (10) and (11) will give the equation of state

The critical point meets

which leads to

The critical ratio is

This value is smaller than that of the Van der Waals system (0.375) [31]. The graph of $ P\left(v\right) $ is plotted in Fig. 1. As shown in the figure, there is only one critical point for a fixed parameter a. For an isothermal process $ T<T_{c} $, the small BH-large BH phase transition occurs. The part where the pressure increases is unstable, and a useful solution is to introduce an isobaric curve, which represents the process of the phase transition. The position of this isobaric curve is determined by Maxwell's area law [31, 36, 46, 47]: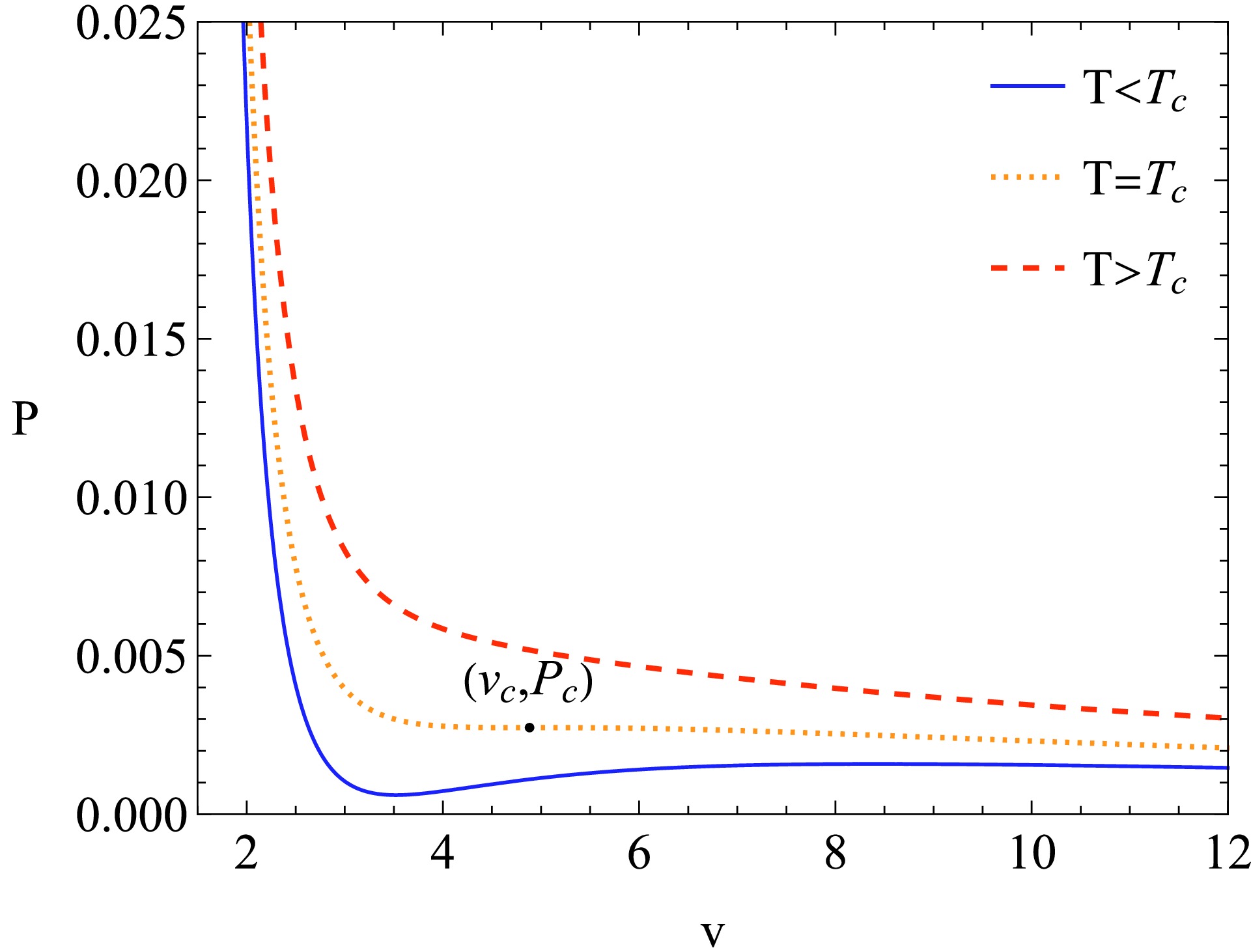

Figure 1.  (color online) Graph of $P\left(v\right)$ of Schwarzschild-AdS BH in non-commutative geometry. We set $a=1$ and plot $T=0.8T_{c}$, $T=T_{c}$, and $T=1.3T_{c}$. The black point is the critical point.

Figure 2 illustrates the result of Maxwell's area law. It is clear that with increasing temperature, the phase transition pressure also increases.

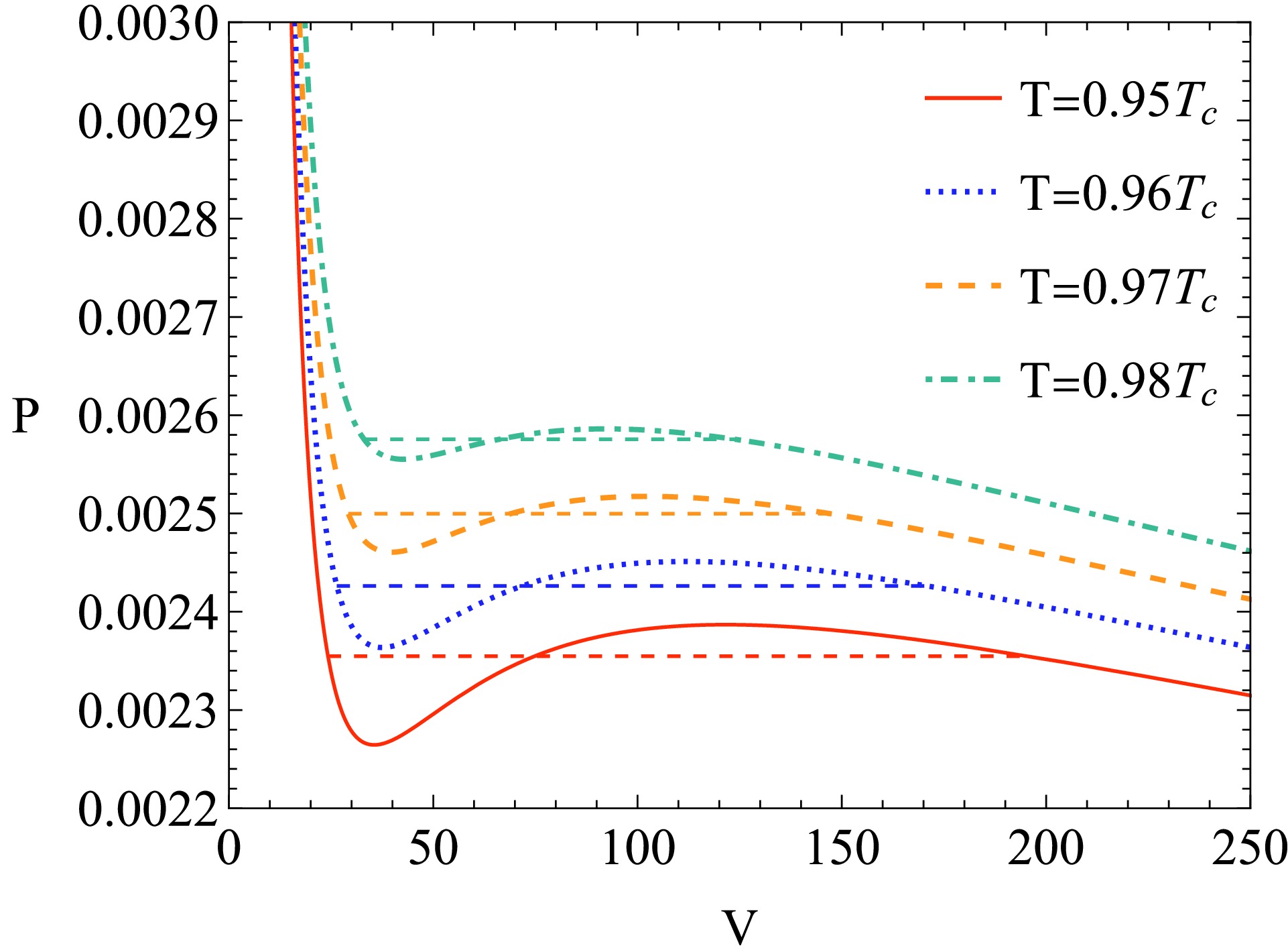
Figure 2.  (color online) Maxwell's area law in the $\left(V,P\right)$ phase graph. The dashed lines represent the phase transitions. We set $a=1$.

By defining

one could obtain the equation of corresponding state

where $ a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, a_{5} $ are nonzero constants. To calculate the critical exponents, a transformation is also performed:

After performing this transformation, the equation of state is expanded as a series, yielding

where $ c_{10}, c_{11}, c_{03} $ are nonzero constants.

There are four critical exponents [48]:

where $ C_{V} $ is the isochoric heat capacity. $ \Delta V $ is the phase transition volume, the change of the thermodynamic volume during the phase transition. $ \kappa_{T} $ is the isothermal compressibility. Eq. (53) describes the variation of the pressure with thermodynamic volume at the critical temperature $ T = T_{c} $.

Considering $ S = \dfrac{3^{2/3}\pi^{1/3}V^{2/3}}{4^{2/3}} $, the isochoric heat capacity is

which gives $ \alpha = 0 $.

To calculate the phase transition volume, Maxwell's area law is necessary. Eq. (45) yields

With the condition $ p\left(w_{1}\right) = p\left(w_{2}\right) $, the solution can be obtained as

This indicates $ \beta = \dfrac{1}{2} $.

Eq. (52) could be calculated as

which yields $ \gamma = 1 $.

When $ T = T_{c} $ ($ t = 0 $),

which shows that $ \delta = 3 $.

It is concluded that four critical exponents of the Schwarzschild-AdS BH in non-commutative geometry are the same as those of the Van der Waals system [31]. These four exponents conform to the Griffiths, Rushbrooke, and Widom functions [46, 48, 49]:

The isobaric heat capacity is

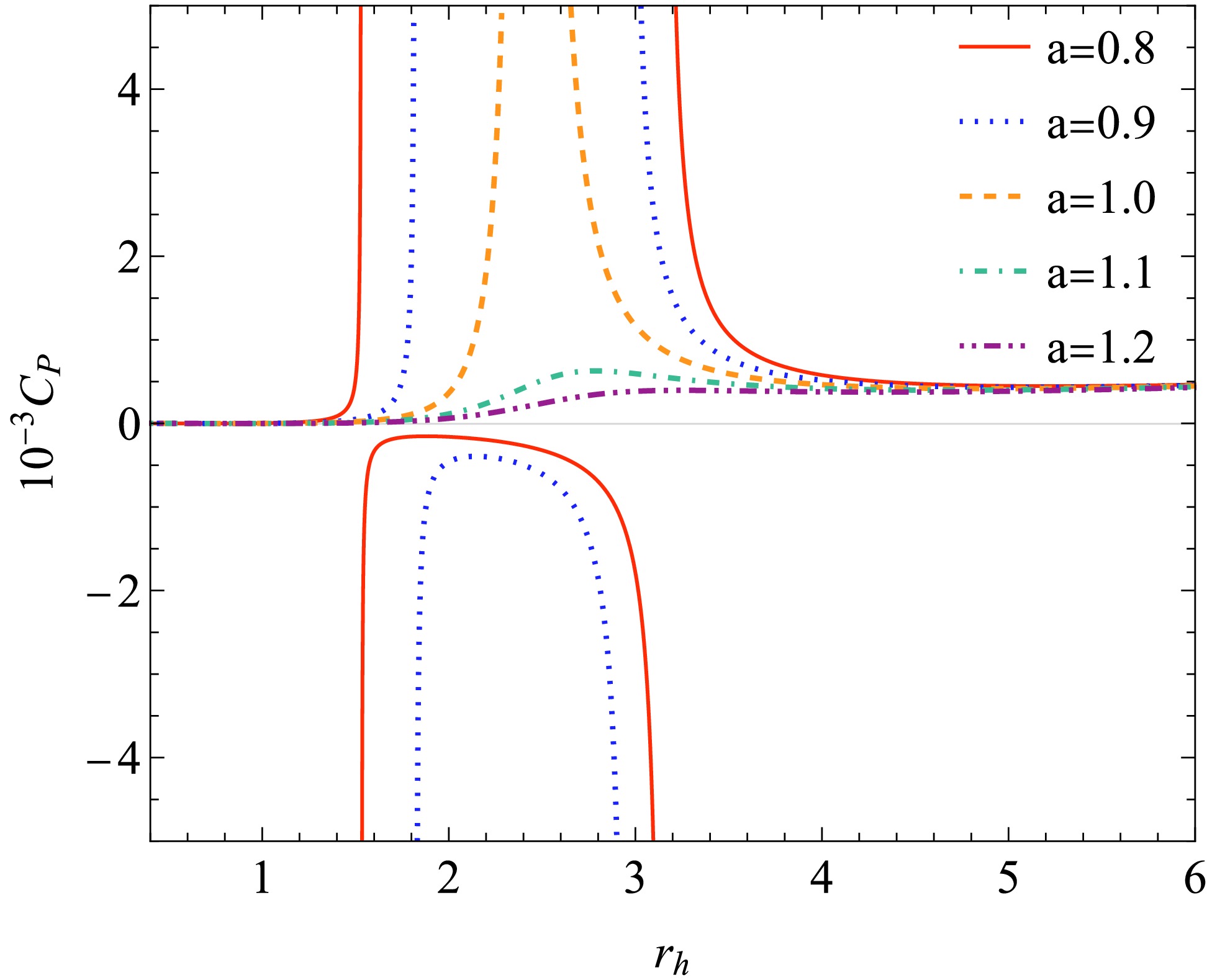
Figure 3 shows the heat capacity as a function of $ r_{h} $. When $ P<P_{c} $, there exist two different points satisfying $ \dfrac{\partial T}{\partial S} = 0 $ (marked by the dashed lines), resulting in the divergence of $ C_{P} $. Meanwhile, there is an unstable region with negative heat capacity (represented by the segments in Figs. 1 and 2 where P increases monotonically with V). As mentioned earlier, this unstable region can be eliminated using Maxwell's area law. As the pressure increases, phase transition points gradually combine into one at the critical point. At the critical point, the heat capacity still diverges to infinity, but the sign of the heat capacity no longer changes. It has also been shown that when the radius of the horizon is small, the heat capacity could also be negative. This interesting phenomenon is demonstrated in Fig. 4. This negative region is caused by the BH's temperature $ T<0 $. From a thermodynamic perspective, it indicates that an AdS-BH with an extremely small event horizon radius is unstable. This negative region is

Figure 3.  (color online) Heat capacity $C_{P}$ as a function of $r_{h}$. We set (a) $a=1, P=0.5P_{c}$, (b) $a=1, P=P_{c}$, and (c) $a=1, P=2P_{c}$.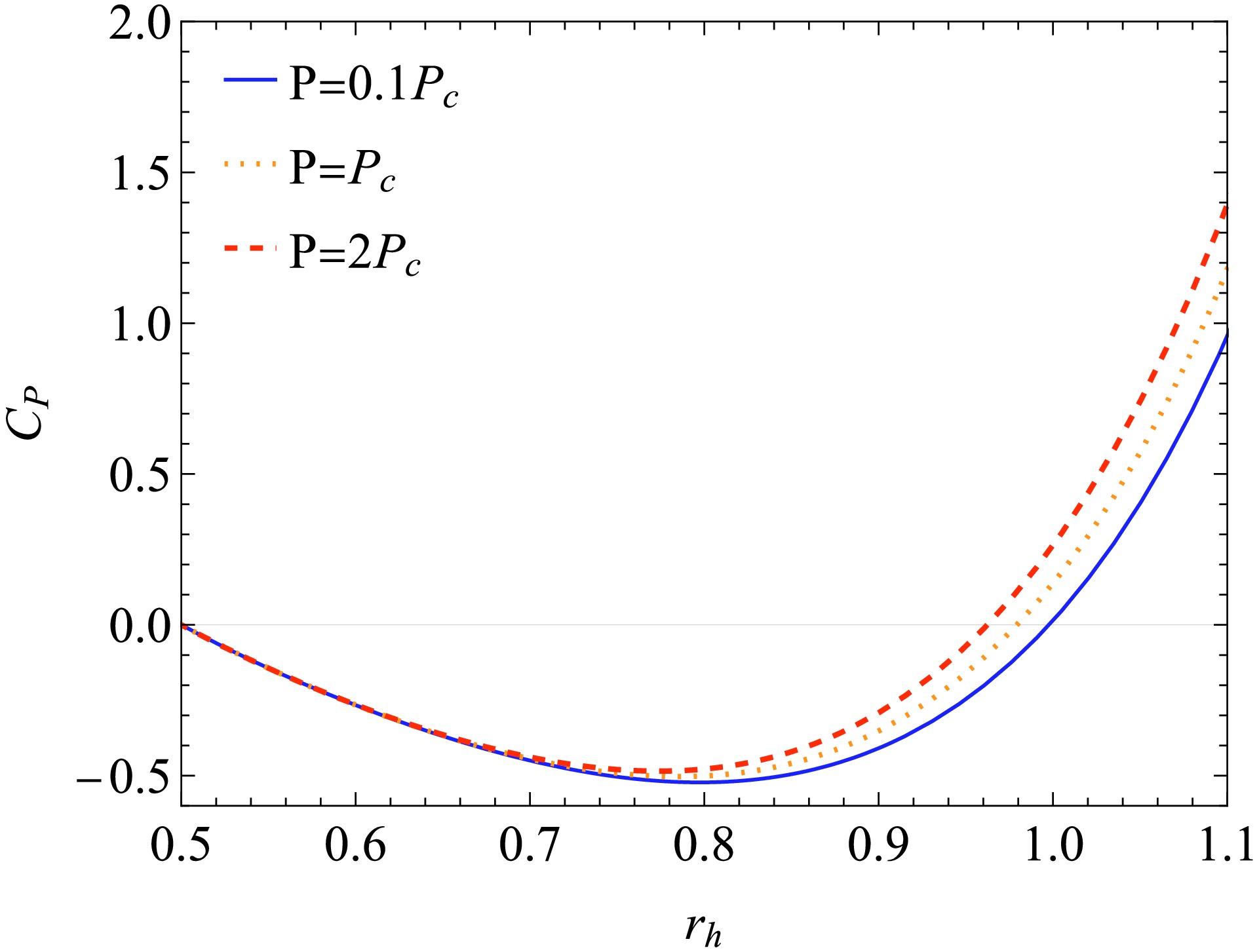

Figure 4.  (color online) Region where the heat capacity $C_{P}$ is negative when $r_{h}$ is too small. We set $a=1$.

where $r_{\rm min}$ is the positive root of the equation

We also investigated the influence of the non-commutative parameter a. As shown in Fig. 5, with increasing a, the distance between two phase transition points gradually shortens and they eventually converge at the critical point. As a continues to increase, the phase transition disappears.

Figure 5.  (color online) Heat capacity for different non-commutative parameters a. We set pressure $P=P_{c}\left(a=1\right)$.

In this section, we study the Gibbs free energy, defined as

It is well known in conventional thermodynamics that Gibbs free energy satisfies

For a constant pressure system, the change of the Gibbs free energy during a thermodynamic process is

Considering Maxwell's area law in the $ \left(S,T\right) $ coordinate system [39],

and that the first-order phase transition is an isothermal process, one obtains

The analysis of phase transitions for an isothermal system is similar. This implies that the Gibbs free energy of a thermodynamic system does not change before and after a first-order phase transition. More precisely, any isothermal and isobaric process that a system undergoes (which could be an irreversible process) must proceed in the direction of non-increasing Gibbs free energy. Specifically, for a reversible process occurring in an isothermal and isobaric system, the Gibbs free energy remains unchanged. However, for the Schwarzschild-AdS BH in non-commutative geometry, there is an issue in that $ T\mathrm{d}S+V\mathrm{d}P $ is not an exact form; it follows that $ -S\mathrm{d}T+V\mathrm{d}P $ is also not an exact form. In this case, the differential of G is

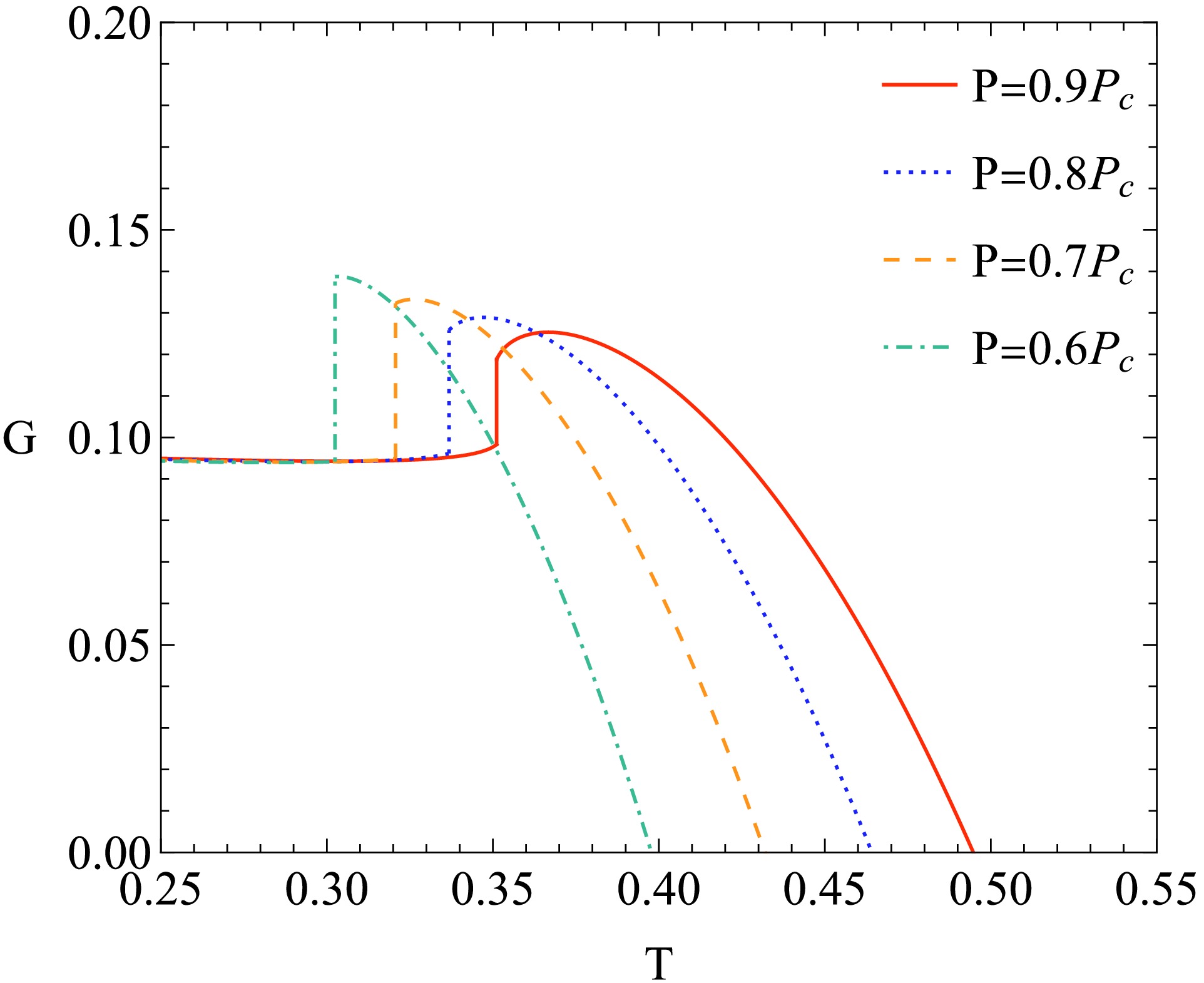
The Gibbs free energy is plotted in Fig. 6. In the locally monotonic region of $ G\left(T\right) $, the differential form of G can be rewritten as follows: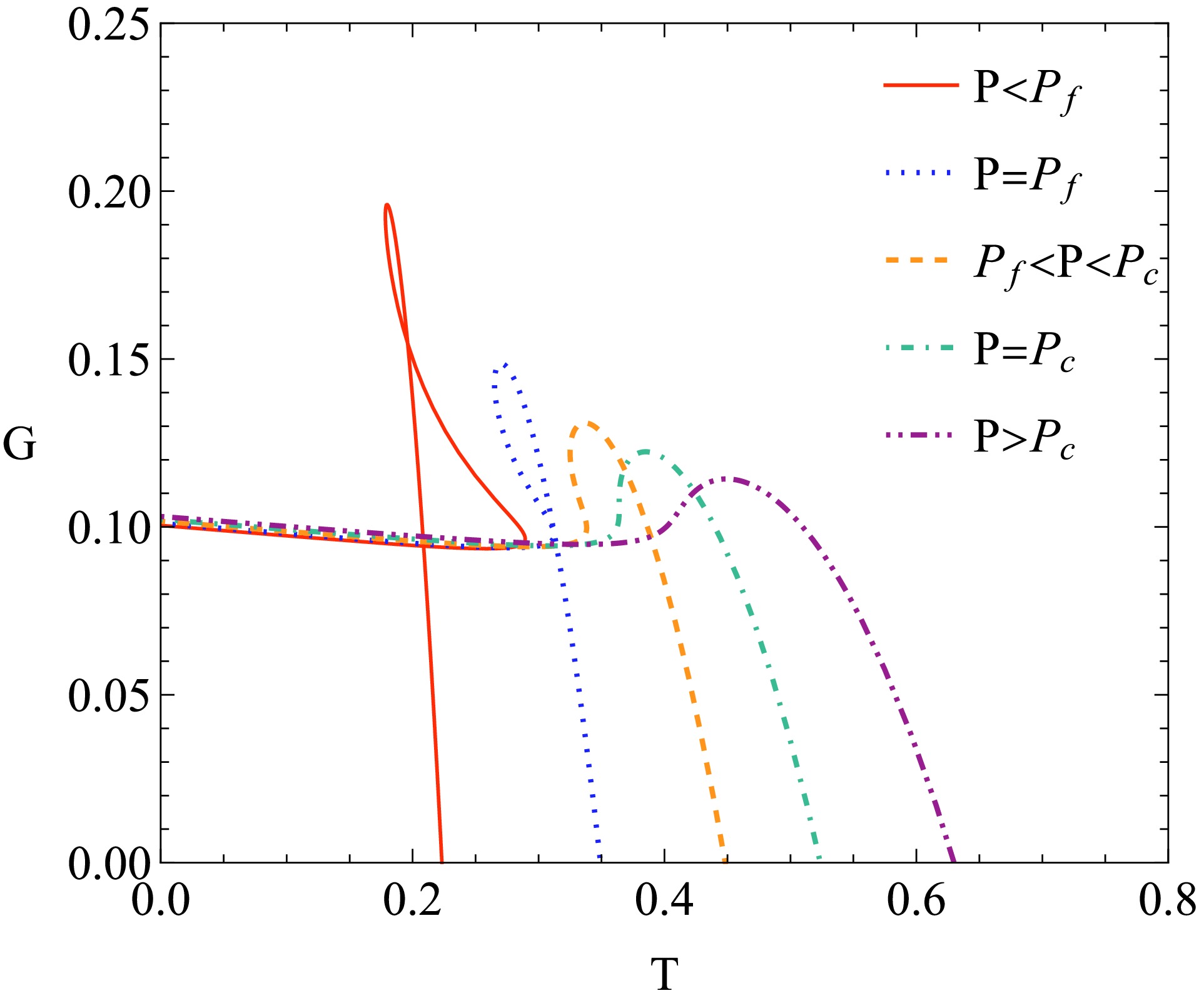

Figure 6.  (color online) Gibbs free energy for different pressure P. We set $a=0.1$ and $P=0.2P_{c},P_{f},0.75P_{c},P_{c},1.4P_{c}$.

which leads to

which is different from $ \dfrac{\partial G}{\partial T} = -S<0 $ in conventional thermodynamics, meaning that $ G\left(T\right) $ may exhibit a monotonic increasing region. When $ P<P_{c} $, because the function $ T\left(S\right) $ is not monotonic, the Gibbs free energy becomes locally multivalued. When $ P>P_{c} $, the Gibbs free energy becomes a single-valued function of T and P. Specifically, there exists a pressure $ P_{f} $ such that when $ P<P_{f} $, the $ G\left(T\right) $ curve exhibits self-intersection. It can be obtained that

which gives a dimensionless constant

However, unlike the thermodynamics of the Van der Waals system, the intersection points of the curve $ G\left(T\right) $ cannot be regarded as the phase transition points. This is because there is a change in Gibbs free energy before and after the transition. The location of the phase transition point should be determined by Maxwell's area law for the condition $ P<P_{c} $

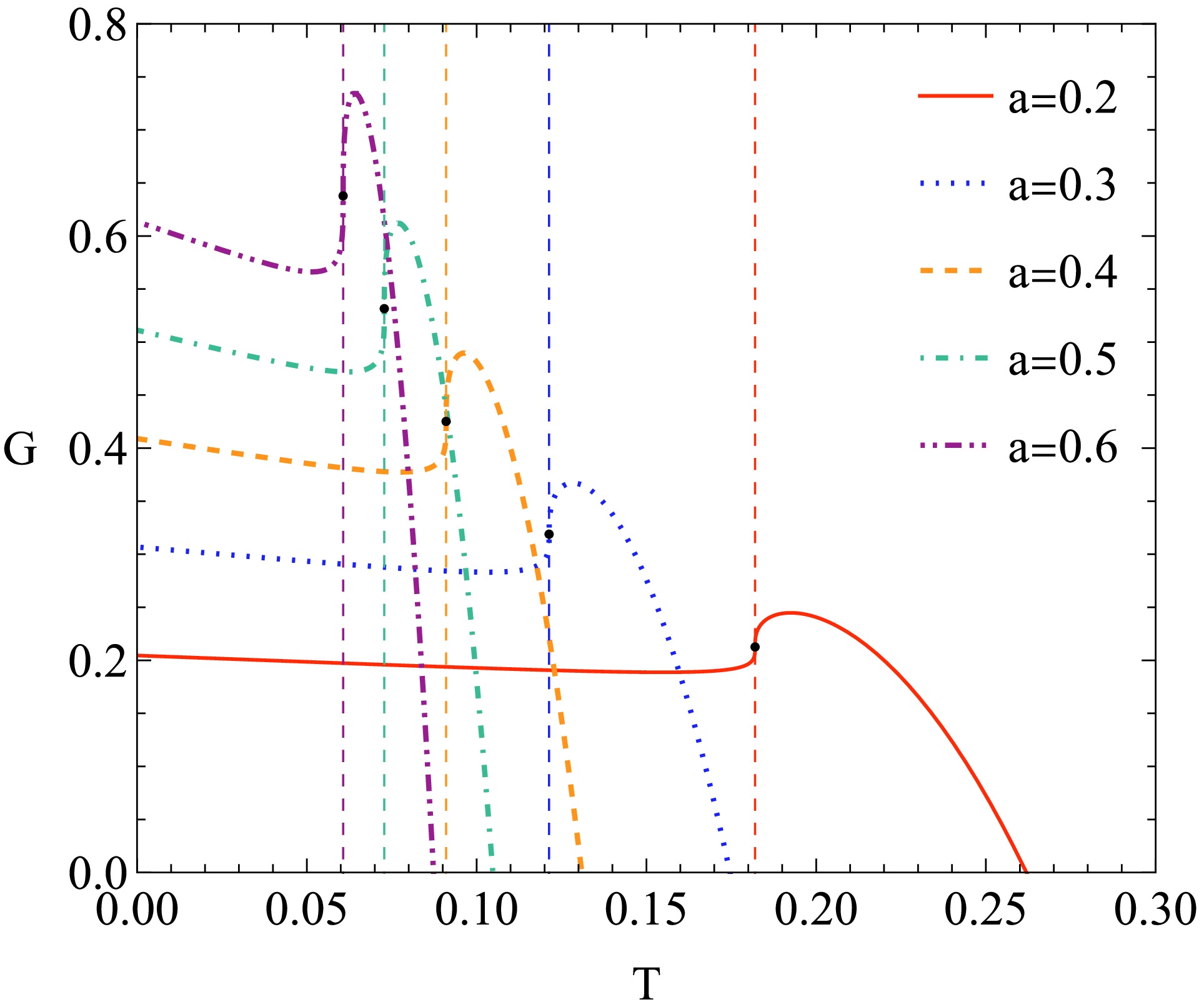
where $ S_{1} $ and $ S_{2} $ are the entropies of the initial and final states during the phase transition, respectively. The results are shown in Fig. 7. When considering Maxwell's area law, the Gibbs free energy is shown in Fig. 8. In this case, the Gibbs free energy for different pressures is plotted in Fig. 9. As shown in the figure, the vertical section of $ G\left(T\right) $ represents the phase transition. The change of the Gibbs free energy during a phase transition is given by Eq. (71).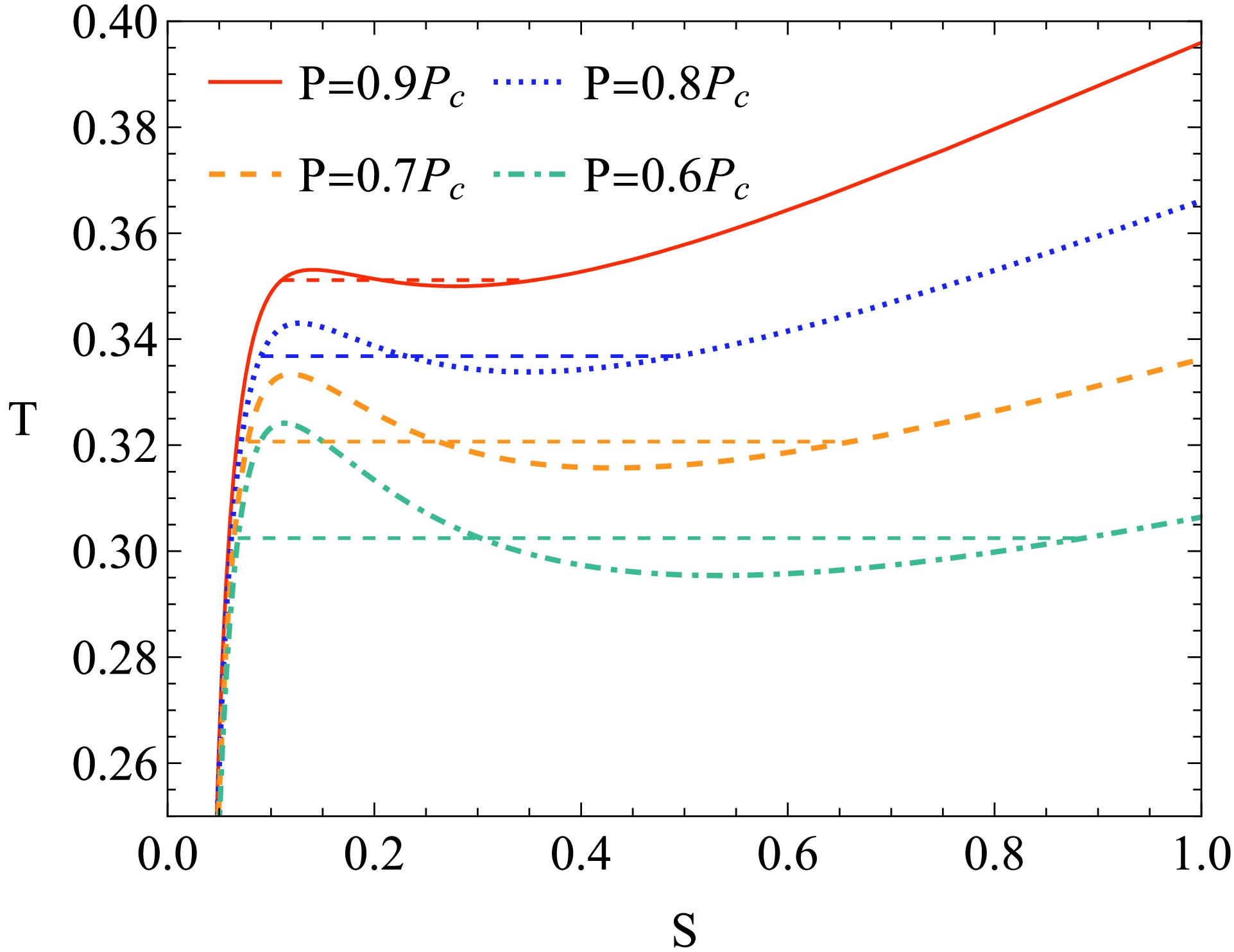

Figure 7.  (color online) Maxwell's area law in $\left(S,T\right)$ coordinate system. The dashed lines represent the phase transitions. We set $a=0.1$.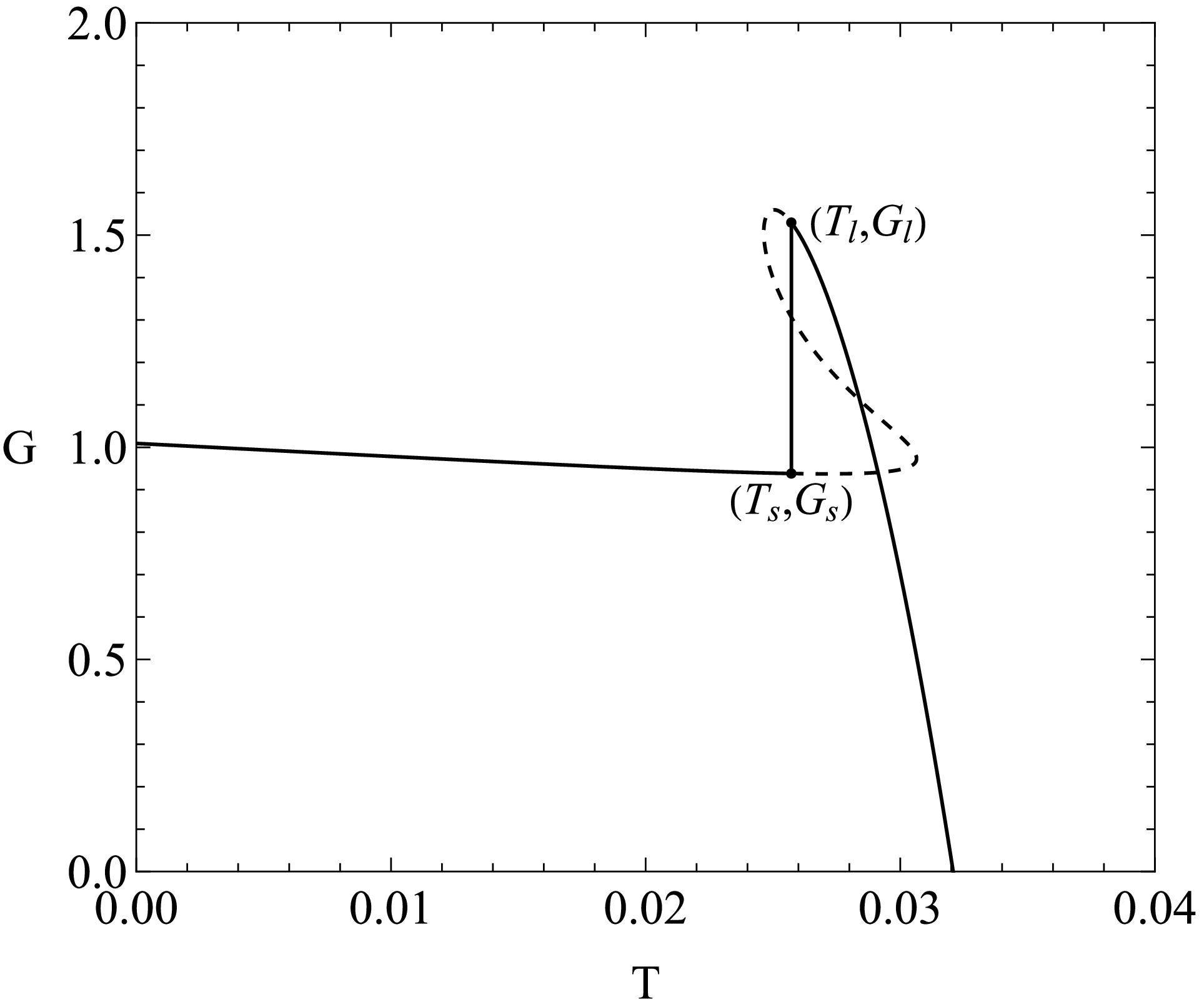

Figure 8.  Graph of Gibbs free energy $G\left(T\right)$ when considering Maxwell's area law. The points $\left(T_{s},G_{s}\right)$ and $\left(T_{l},G_{l}\right)$ represent the small BH and large BH, respectively. We set $a=1$ and $P=0.4P_{c}$.

Figure 9.  (color online) Gibbs free energy corrected by Maxwell's area law. We set $a=0.1$.

Here, a peculiar phenomenon occurs: according to Ehrenfest's classification of phase transitions, a discontinuous Gibbs free energy indicates the occurrence of a zeroth-order phase transition. The zeroth-order phase transition of BHs is a very intriguing phenomenon. Studies have shown that the dilaton-electromagnetic coupling interaction could lead to a zeroth-order phase transition [47, 50, 51]. However, unlike the physical mechanism that induces zeroth-order phase transitions, as described in Refs. [47, 50, 51], our research indicates that for a static, spherically symmetric AdS BH, the violation of the conventional first law of thermodynamics would lead to a change in the Gibbs free energy of a BH after undergoing a small BH-large BH phase transition.

At the critical point, $ G\left(T\right) $ is continuous, but the heat capacity $ C_{p} $ diverges to infinity, which results in

which indicates that the phase transition occurring at the critical point is a first-order phase transition. This phenomenon is shown in Fig. 10.

Figure 10.  (color online) At the critical points, the first-order phase transitions occur. The slope of the Gibbs free energy with respect to temperature diverges to infinity. The black points are the critical points.

The Joule-Thomson expansion in BH thermodynamics has been widely studied [32, 52−68]. The Joule-Thomson process is a thermodynamic system's throttling (constant enthalpy) expansion. As previously mentioned, the mass M of an AdS-BH is considered as its enthalpy. Although the first law has been modified, studying the constant mass process of BHs remains highly significant.

To study the constant mass process, we take M and $ r_{h} $ as variables and rewrite the BH's pressure and temperature:

The Joule-Thomson coefficient is

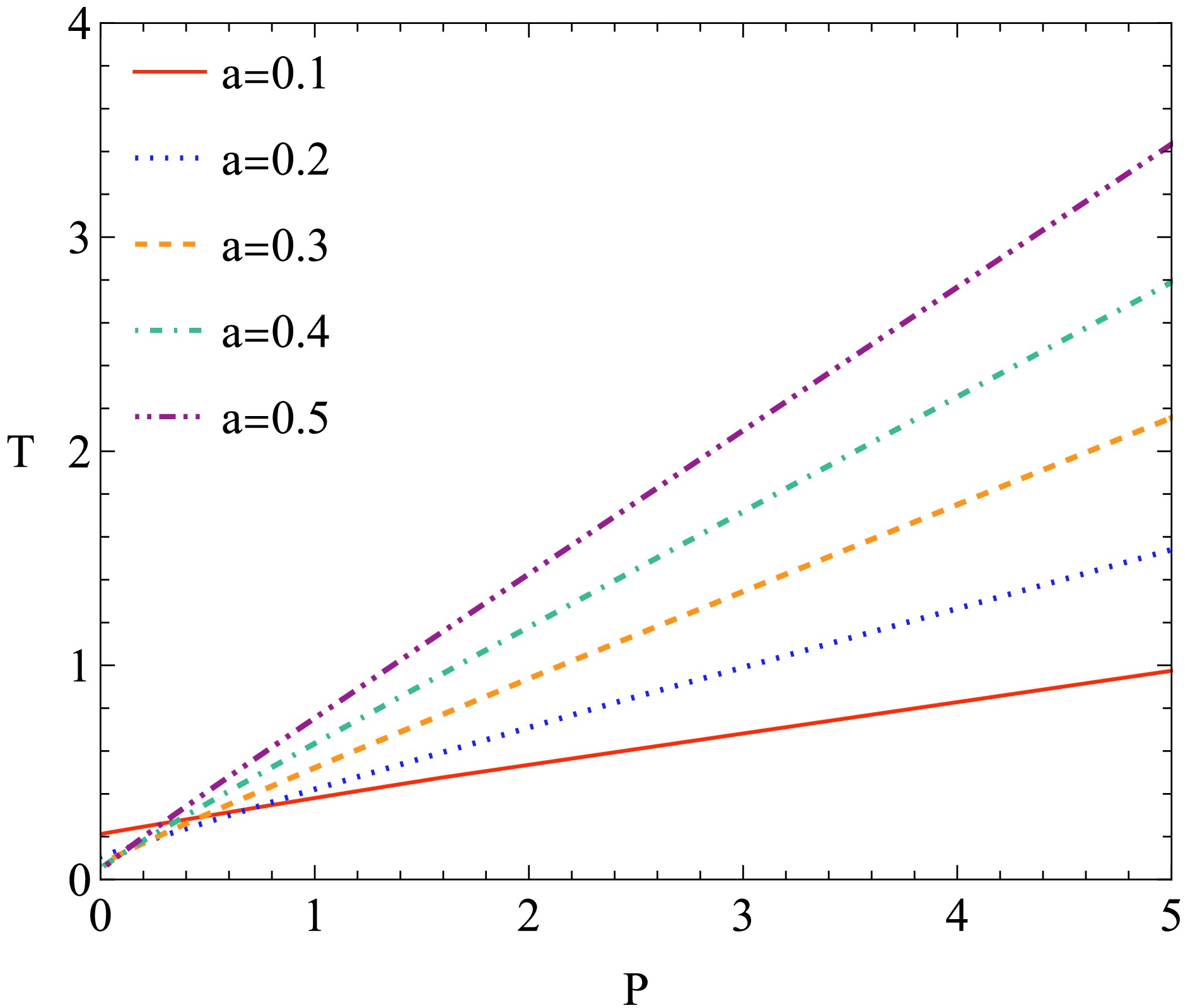
A process with $ \mu>0 $ is referred to as a cooling process, whereas a process with $ \mu<0 $ is called a heating process. The point where $ \mu = 0 $ is known as the inversion point.

The curve formed by all the inversion points in the $ \left(P,T\right) $ coordinates is called the inversion curve. As shown in Fig. 11, we plotted the inversion curves for different values of the parameter a. The figure clearly shows that as the inversion pressure $ P_{i} $ increases, the inversion temperature $ T_{i} $ also increases. Moreover, when $ P_{i} $ is not too small, $ T_{i} $ increases with increasing non-commutative parameter a. In the constant mass curves we will draw next, the inversion curve will divide the $ \left(P,T\right) $ phase space into two disconnected regions. The BH's cooling process is located in the upper left of the inversion curve, while the heating process is in the lower right.

Figure 11.  (color online) Inversion curves for different non-commutative parameters.

Specifically, when $ P_{i} = 0 $, one has the minimum inversion temperature

yielding a ratio that is independent of a:

This value lies between the results of the RN-AdS BH (0.5) and Van der Waals system (0.75). Interestingly, one study showed that the Joule-Thomson expansion of Van der Waals systems reveals the presence of a maximum inversion temperature $T_{i}^{\rm max}$ [32], whereas the BH we are studying does not exhibit this phenomenon.

Whether a BH undergoes an inversion point during its constant mass expansion depends on its mass M. It can be proven that under the conditions $ P>0 $, $ r_{h}>0 $, and $ M>0 $, the equation $ \mu = 0 $ has a solution if and only if

where $M_{i}^{\rm min}$ is the minimum inversion mass. Figure 12 shows the inversion curves and families of Joule-Thomson expansion curves for different parameters a. It can be clearly observed from the figure that BHs with mass less than $M_{i}^{\rm min}$ cannot experience an inversion point and will remain in the heating process throughout.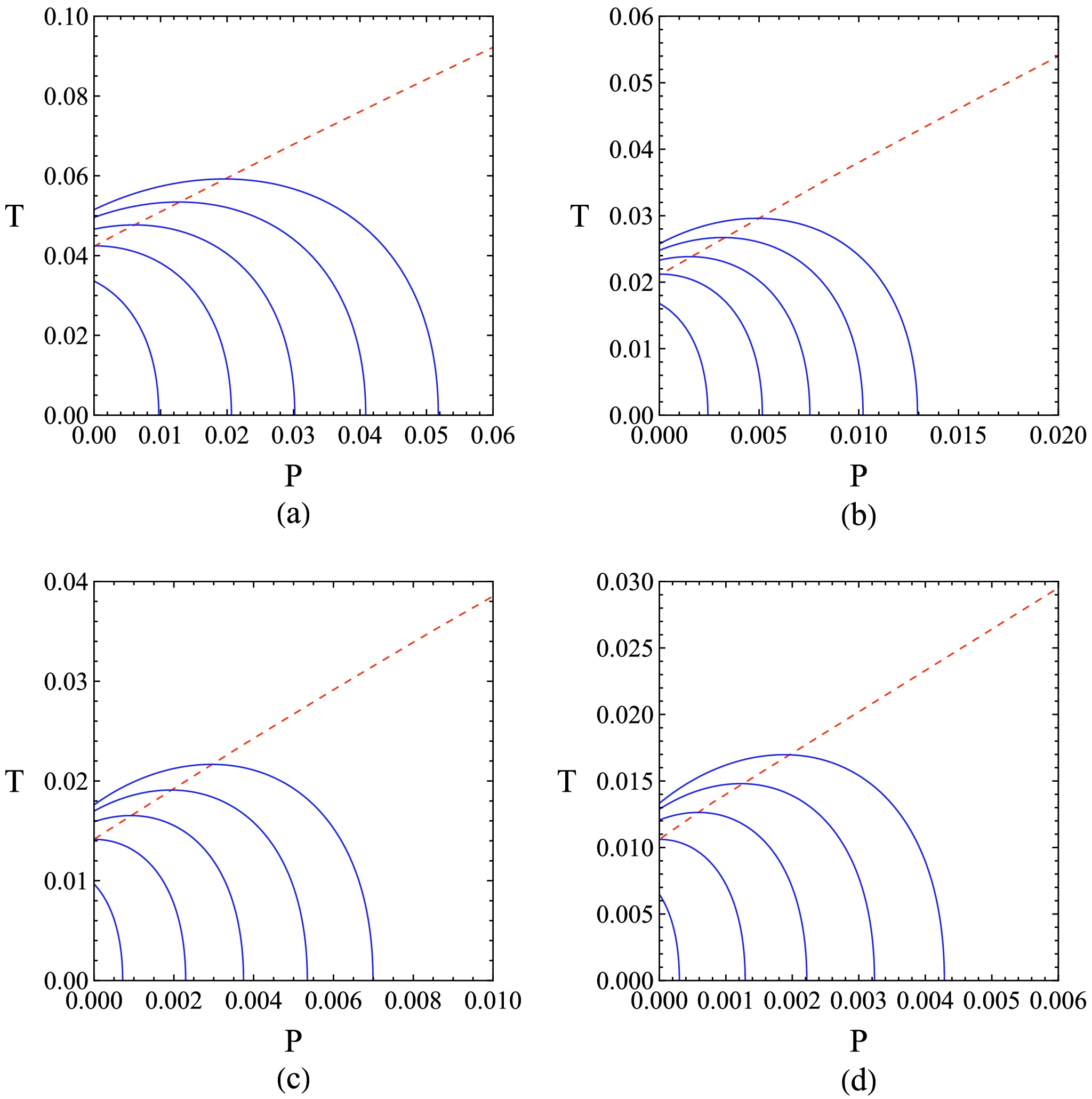

Figure 12.  (color online) C constant mass curves (blue solid lines) and inversion curves (red dashed lines) for different parameters a. The constant mass curves expand outward as the mass increases. We set (a) $a=0.5,M=0.51,M_{i}^{\rm min}\left(\simeq0.52\right),0.53, $$ 0.54,0.55$; (b) $a=1,M=1.02,M_{i}^{\rm min}\left(\simeq1.04\right),1.06,1.08,1.1$; (c) $a=1.5,M=1.52,M_{i}^{\rm min}\left(\simeq1.56\right),1.6,1.64,1.68$; (d) $a=2,M=2.02, $$ M_{i}^{\rm min}\left(\simeq2.08\right),2.14,2.2,2.26$.

In this paper, we investigated the thermodynamics of the Schwarzschild-AdS BH within the framework of non-commutative geometry. By solving the Einstein equation with a Lorentzian distribution and the cosmological constant, we derived a corrected Schwarzschild solution and studied its thermodynamics. Our analysis confirmed that the explicit inclusion of the BH's mass in the energy-momentum tensor disrupts the conventional first law of BH thermodynamics.

This study showed that the BH has a critical point, with a critical ratio of 0.36671. As the non-commutative parameter increases, the phase transition process shortens and eventually disappears after the critical point. Additionally, our calculation revealed that the BH exhibits the same critical exponents as those of the Van der Waals system, suggesting a deeper connection between BH thermodynamics and classical thermodynamic systems.

Furthermore, the violation of the conventional first law caused a sudden change of Gibbs free energy with respect to temperature during a small BH-large BH phase transition. This novel phenomenon indicated the occurrence of a zeroth-order phase transition.

Finally, we analyzed the Joule-Thomson expansion and identified the existence of inversion points, which depend on whether the BH's mass exceeds the critical minimum inversion mass. We also derived the minimum inversion temperature, adding to the understanding of BH thermodynamic behavior under non-commutative geometry. So far, there are no existing works systematically discussing the thermodynamic properties of Schwarzschild-AdS BHs with Lorentzian or Gaussian distributions, such as their first law, phase transitions and criticality, Joule-Thomson effect, etc. We hope that our work provides more valuable insights for the theoretical study of non-commutative geometry.

In future work, we aim to further investigate the higher-order effects of non-commutative geometry on the Schwarzschild spacetime, as Eq. (5) is an approximation retained up to the order of $ {\cal{O}}\left(a\right) $. Because the BH's mass explicitly appears in the energy-momentum tensor, the conventional first law of thermodynamics is violated, resulting in differential forms $ T\mathrm{d}S+V\mathrm{d}P $ and $ -S\mathrm{d}T+V\mathrm{d}P $ that are not exact forms. For thermodynamic quantities such as enthalpy and Gibbs free energy, there may be better ways to define these quantities, which would be a valuable topic for future research.

We want to thank Yu-Cheng Tang and Yu-Hang Feng for their useful suggestions.

The modified first law reads

Here, we have not explicitly written out the differential terms of the non-commutative parameter $ \mathrm{d}a $, as this does not affect the proof. This form is exact if and only if

By substituting

into Eq. (A2), one obtains

By using the chain rule for composite functions $ W\left(M,S\right) = W\left(M\left(S,P\right),S\right) $, the above formula gives

With the relation $ S = \pi r_{h}^{2} $, it is derived that

Meanwhile, W is

Thus, Eq. (A6) can be simplified as

However, this condition generally does not hold unless $ \dfrac{\partial T_{0}^{0}}{\partial M} = 0 $, that is, $ W = 1 $.

Thus, $ \mathrm{d}{\cal{M}} $ has been proven to not be an exact form. There is another method to prove this fact. If there is a scalar function $ {\cal{M}} $ satisfying Eq. (14), one could obtain its Smarr relation

Then, one could obtain

which leads to

Meanwhile, we require that $ \mathrm{d}{\cal{M}} = W\mathrm{d}M $, which gives

This does not hold unless W is a constant.

The form $ -S\mathrm{d}T+V\mathrm{d}P $ is not exact either because if there exists a function $ {\cal{G}} $ satisfying $ \mathrm{d}{\cal{G}} = -S\mathrm{d}T+V\mathrm{d}P $, then one can construct $ {\cal{M}} = {\cal{G}}+TS $ to meet $\mathrm{d}{\cal{M}} = T\mathrm{d}S+V\mathrm{d}P$, which causes a contradiction.