-
Many aspects of the neutrino are still ambiguous. They include its mass, flavor oscillation, weak mixing, and electromagnetic form factors. Most of the experiments to probe these properties have been performed via scattering of neutrinos on nuclei. To achieve quantitative answers to these questions, the errors (or uncertainties) arising from the nucleus have to be controlled below 2% [1]. To properly analyze numerous forthcoming neutrino-nucleus scattering data, models must be simultaneously consistent with the existing data and systematically improved so that one can increase the predictive power of theory. In addition, given that both the electron and neutrino are leptons, it is more desirable to satisfy the data of both electron-nucleus and neutrino-nucleus scattering simultaneously without adjusting to a specific process.
In the case of electron-nucleus scattering, the energy of the incident electrons can be experimentally controlled accurately. Thus, theoretical results can be easily compared with experimental data. In recent studies [2, 3], we showed that a nuclear structure model based on the effective field theory might be a candidate of ‘good nuclear model’, i.e., with no calibration with scattering data, the model exhibits excellent agreement with electron-nucleus scattering data. Moreover, we showed that the scattering cross sections are sensitive to the effective mass of the nucleon in the nuclear medium, and theoretical results with a large isoscalar effective mass should be favored to achieve better agreement with the data in both electron- [2, 3] and neutrino-nucleus [4] scattering.
However, more caution is needed concerning scattering with neutrinos. While the energy of the incident electrons is highly monochromatic, the neutrino energy is not determined accurately, so a certain amount of energy dispersion is inevitable. Concerning neutrino-nucleus scattering, models that reproduce the electron-nucleus data also show reasonable agreement with neutrino-nucleus data [4]; however, they are not as accurate as electron scattering models. In particular, model results always underestimate the experimental data with standard value of axial mass, MA = 1.032 GeV. If a good model for quasielastic (QE) electron scattering cannot describe the QE neutrino scattering as well as that of the electron, there must be additional contributions from channels other than the QE channel to neutrino scattering.
Many theoretical studies [4−16] have analyzed charged-current (CC) quasielastic experiments. Martini et al. [5, 6] calculated the contribution of the multiparticle-multihole (np-nh) to the ν−12C cross section for the interpretation of T2K, MiniBooNE, and SciBooNE data using the random phase approximation (RPA). In Refs. [7, 8], the CC total cross sections for νµ−12C and
$ \bar \nu_{\mu} - ^{12} $ C were compared with MiniBooNE and SciBooNE data by including a many-body expansion of the gauge boson absorption. Amaro and Arriola [9] calculated the double-differential and total cross sections to analyze MiniBooNE data with the relativistic Fermi gas (RFG) model by using axial-vector-meson dominance with axial mass MA = 1 GeV in the range$ 0.2 \lesssim Q^2 \lesssim 0.6 $ (GeV/c)$ ^2 $ . Using the extended superscaling approach (SUSAv2) including the meson exchange current (MEC), the experimental data from MiniBooNE, T2K, MINERνA, NOMAD, and SciBooNE were analyzed in a wide range of neutrino energies from hundreds of MeV to hundreds of GeV. It was shown that the contribution of 2p-2h is approximately 15% ~ 25%, depending on the kinematics [10].Within the framework of the QHD model, the roles of the strange axial form factor and axial mass were investigated for both neutral-current (NC) and CC quasielastic interactions off 12C, 40Ca, 56Fe, and 208Pb [11]. It was shown that the effect of the axial mass is not related to target nuclei and that of the strange axial form factor increases in heavier nuclei. In Ref. [12], the effects of the Pauli blocking and the distortion of the nucleon wave function in the final state were discussed for the single-pion production process. Both effects tend to improve the agreement with experimental data. Within a relativistic distorted wave impulse approximation (RDWIA), and taking into account the two-particle and two-hole MEC, the authors of Refs. [13, 14] calculated the CC νµ−12C and νµ−40Ar quasielastic scattering and then determined that 1 ≤ MA ≤ 1.20 GeV in comparison with MiniBooNE and MicroBooNE data. The authors of Ref. [4] calculated the CC quasielastic scattering with nonrelativistic nuclear energy density functionals. They concluded that the effect of isoscalar effective mass is dominant but that of isovector effective mass can be neglected. In Ref. [15], the contributions of np-nh and one-pion productions were studied for MicroBooNE and T2K data in absence of two-pion production and other inelastic processes; the theoretical results of this study achieved better agreement. For four relativistic nuclear models, namely QHD, nonlinear sigma, QMC, and chiral QMC, the theoretical cross sections for various kinematics were compared with MiniBooNE, MicroBooNE, T2K, and SciBooNE data. It was observed that the differences among nuclear models are sensitive to the kinematics [16].
Recent experiments of neutrino scattering on 40Ar nucleus conducted by the MicroBooNE Collaboration [17] posed a challenge for a 'good model'. To determine the sensitivity to the nuclear model, we employed models built on nonrelativistic frameworks. We considered four models: KIDS0 from the KIDS (Korea-IBS-Daegu-SKKU) energy density functional [18], and SLy4 [19], SkI3 [20], and MSk7 [21] from the Skyrme forces. The four models exhibit a similar saturation behavior in the symmetric nuclear matter and reproduce the nuclear properties at high accuracy. However, they critically differ in the density dependence of the symmetry energy and the effective mass of the nucleon. Comparison of the four models with experimental data for various kinematic conditions sheds lights on the significance of the effective mass and density dependence of the symmetry energy on the neutrion-nucleus scattering. These results will also guide us to improve the theoretical description and understanding of the lepton-neutrino scattering from elastic to deep inelastic regions.
In the present study, we calculated the QE cross sections for neutrino-nucleus scattering with the KIDS0 (detailed explanation about the model can be found in Ref. [2]), SLy4, SkI3, and MSk7 models and compared the results with experimental data. The wave functions of the continuum nucleons were generated with scalar and vector potentials obtained from the same potential used to describe the bound nucleons. This guarantees gauge invariance and current conservation. For Coulomb distortion of the outgoing muon, we used the approximation exploited by the Ohio group [22−25].
The paper is organized as follows. In Sec. II, basic formalism for the lepton-nucleus scattering is recapitulated. We present the results and discuss them in Sec. III. Finally, this study is summarized in Sec. IV.
-
To analyze inclusive QE CC
$ \nu({\bar \nu})-A $ scattering, we choose a coordinate system in which the target nucleus is placed at the origin. The four-momenta of the participating particles are denoted as piµ = (Ei, pi), pfµ = (Ef, pf), pAµ = (EA, pA), pA−1µ = (EA−1, pA−1), and pµ = (EN, p) for the incident neutrino, outgoing lepton, target nucleus, residual nucleus, and knocked-out nucleon, respectively. Within the laboratory frame, the inclusive cross section in the CC reaction is given by the contraction between lepton and hadron tensors:$ \begin{aligned}[b] {\frac {{\rm d}\sigma} {{\rm d}T_N}} = \;&4\pi^2{\frac {M_N M_{A-1}} {(2\pi)^3 M_A}} \int \sin \theta_l {\rm d}\theta_l \int \sin \theta_N {\rm d}\theta_N p f^{-1}_{\rm{rec}} \sigma^{W^{\pm}}_M \\ & \times [ v_L R_L + v_T R_T + h v_T' R_T' ], \end{aligned} $

(1) where
$ \theta_l $ denotes the scattering angle of the lepton,$ \theta_N $ is the polar angle of knocked-out nucleons,$ T_N $ is the kinetic energy of the knocked-out nucleon, and$ h=-1 $ $ (h=+1) $ corresponds to the intrinsic helicity of the incident neutrino (antineutrino). The$ R_L, R_T $ , and$ R^{'}_T $ are longitudinal, transverse, and transverse interference response functions, respectively. Detailed forms for the kinematical coefficients v and corresponding response functions R are given in Refs. [26, 27]. For the CC reaction, the kinematic factor$ \sigma^{W^\pm}_M $ is defined by$ \sigma^{W^\pm}_M = \sqrt{1 - {\frac {M^2_l} {E_f}}} \left ( {\frac {G_F \cos (\theta_C) E_f M_W^2} {2\pi (Q^2 + M^2_W)}} \right )^2, $

(2) where
$ M_W $ is the rest mass of the W-boson;$ M_l $ is the mass of an outgoing lepton;$ \theta_C $ represents the Cabibbo angle, given by$ \cos^2 {\theta_C} \simeq 0.9749 $ ; and$ G_F $ denotes the Fermi constant. The recoil factor$ f_{\rm{rec}} $ is expressed as$ f_{\rm{rec}} = {\frac {E_{A-1}} {M_A}} \left | 1 + {\frac {E_N} {E_{A-1}}} \left [ 1 - {\frac {{\bf q} \cdot {\bf p}} {p^2}} \right ] \right |. $

(3) For a free nucleon, the current operator of the CC reaction is composed of the weak vector and axial vector form factors:
$ \begin{aligned}[b] {\hat {\bf J}}^{\mu}=\;&F_{1}^V (Q^2){\gamma}^{\mu}+ F_{2}^V (Q^2){\frac {\rm i} {2M_N}}{\sigma}^{\mu\nu}q_{\nu} \\ &+ G_A(Q^2) \gamma^{\mu} \gamma^5+ {\frac {1} {2M_N}}G_P(Q^2) q^{\mu} \gamma^5. \end{aligned} $

(4) By conservation of the vector current (CVC) hypothesis, the vector form factors for the proton (neutron),
$ F_{i}^{V,\; p(n)} (Q^2) $ , are expressed as$ \begin{aligned}[b]& F^{V}_i (Q^2) = F^{p}_{i} (Q^2) - F^{n}_{i} (Q^2). \end{aligned} $

(5) The axial form factors for the CC reaction are given by
$ G_A (Q^2) = {\frac {-g_A} {(1+Q^2/M_A^2)^2}}, $

(6) with
$ g_A=1.262 $ ; the global value of the axial mass is$ M_A=1.032 $ GeV. The induced pseudoscalar form factor is parameterized by the Goldberger-Treimann relation,$ G_P(Q^2) = {\frac {2M_N} {Q^2+m^2_{\pi}}} G_A(Q^2), $

(7) where
$ m_{\pi} $ is the pion mass.As discussed in the introduction, the models were chosen to account for the uncertainties in the symmetry energy and effective mass of the nucleon. The density dependence of the symmetry energy is defined conventionally as
$ S(\rho) = J + {\frac {\rho - \rho_0} {3 \rho_0}}L + \cdots , $

(8) where ρ and
$ \rho_0 $ denote the baryon density and saturation density of the symmetric nuclear matter, respectively. Table 1 compares both similar ($ \rho_0 $ ,$ E_B $ ,$ K_0 $ ) and distint (J, L,$ \mu_s $ ,$ \mu_v $ ) behaviors of the model at the saturation density. The SkI3 and MSk7 models exhibit extreme behavior in both symmetry energy and effective mass. The values of L for both models differ by an order of magnitude, and the isoscalar effective mass of the SkI3 model is approximately half of the MSk7 model. By contrast, because the KIDS0 and SLy4 models are fitted to the same pure neutron matter equation of state in Ref. [28], the J and L values are similar to each other. However, they have very different values of$ \mu_s $ . Therefore, the comparison of both models can provide an evidence on the role of the isoscalar effective mass.$ \rho_0 $ 

$ E_B $ 

$ K_0 $ 

J L $ \mu_s $ 

$ \mu_v $ 

KIDS0 0.160 16.00 240.0 32.8 49.1 0.99 0.81 SLy4 0.160 15.97 229.9 32.0 45.9 0.69 0.80 SkI3 0.158 15.98 235.2 34.8 100.5 0.58 0.80 MSk7 0.157 15.80 231.2 28.0 9.4 1.05 1.05 Table 1. Nuclear matter properties of the models. Units are fm−3 for the saturation density
$ \rho_0 $ , MeV for the binding energy per nucleon$ E_B $ , incompressibility$ K_0 $ , and symmetry energy parameters J and L. The isoscalar and isovector effective mass ratios to the free nucleon mass$ \mu_s = m^*_s / M_N $ and$ \mu_v = m^*_v / M_N $ are dimensionless. -
By using the KIDS0, SLy4, SkI3, and MSk7 nuclear models, we calculated various differential and total cross sections for inclusive quasielastic neutrino-nucleus scattering from 40Ar and compared the theoretical results with MicroBooNE data. To include the final state interaction, the wave functions of the final nucleons were generated by the same potential as that of the bound nucleons. This assumption satisfies current conservation and guarantees gauge invariance. In neutrino experiments, the cross sections have to be averaged over the flux of the incident neutrino beam because the energy of incoming neutrinos cannot be fixed. Note that the whole cross sections in neutrino scattering were divided by the number of nucleons which are involved in the reaction. Moreover, the approximation proposed by the Ohio group [22−25] was applied to the Coulomb distortion of the lepton. In the figures presented next, the red solid curves represent the results for KIDS0, the black dashed curves represent those for SLy4, the blue dotted lines represent those for SkI3, and the sky blue dash-dotted lines represent those for MSk7.
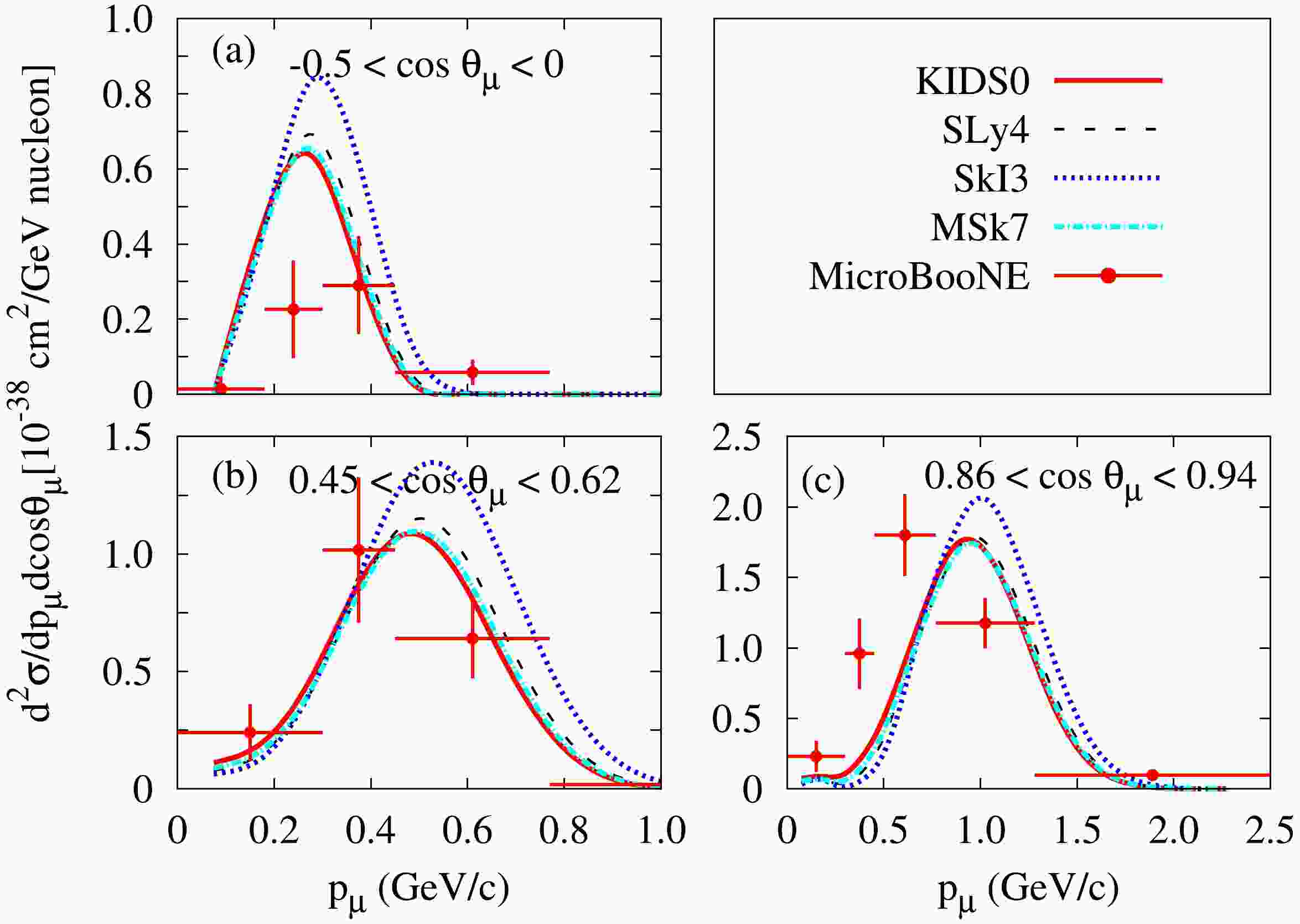
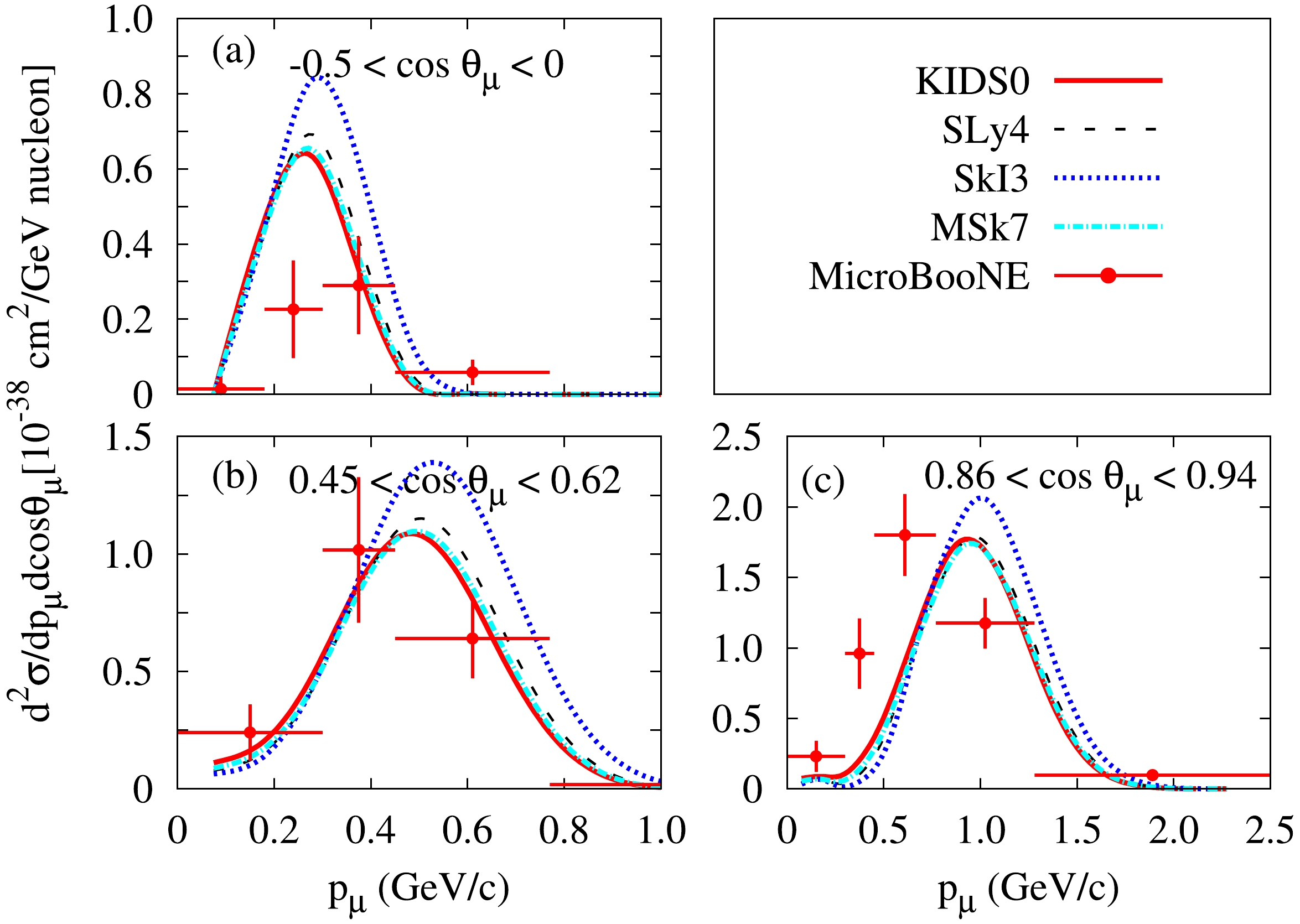
As shown in Fig. 1, the flux-averaged double-differential cross sections were calculated in terms of the momentum of the outgoing muon at fixed polar angles from 40Ar and compared with MicroBooNE data [29−31]. The positions of the peak shift toward large momentum with smaller angles were compared with the data. At the backward angle, the theoretical results overestimate the data. In particular, the cross sections of SkI3 are the largest ones and shift toward right side. The difference between the KIDS0 and MSk7 models is very small, that is, the effect of the symmetry energy hardly contributes to the double-differential cross section.
Figure 2 shows the fluxed-averaged single-differential cross section with respect to the energy transfer and the comparison with MicroBooNE data [17]. The theoretical results do not correctly describe the data at all because the various different reaction channels are entangled. The magnitude of SkI3 is the largest whereas that of KIDS0 and MSk7 is approximately consistent with the results shown in Fig. 1. In particular, although the peaks are located at the same position, the magnitude of SkI3 is larger than that of the other models by approximately 40%. This extremely large difference can be attributed to either the isoscalar effective mass, the symmetry energy parameter L, or both. However, the value of L for MSk7 also shows significant deviation from the KIDS0 and SLy4 models. In any case, the three models present similar results. The main effect of the magnitude difference might be caused by the isoscalar effective mass.
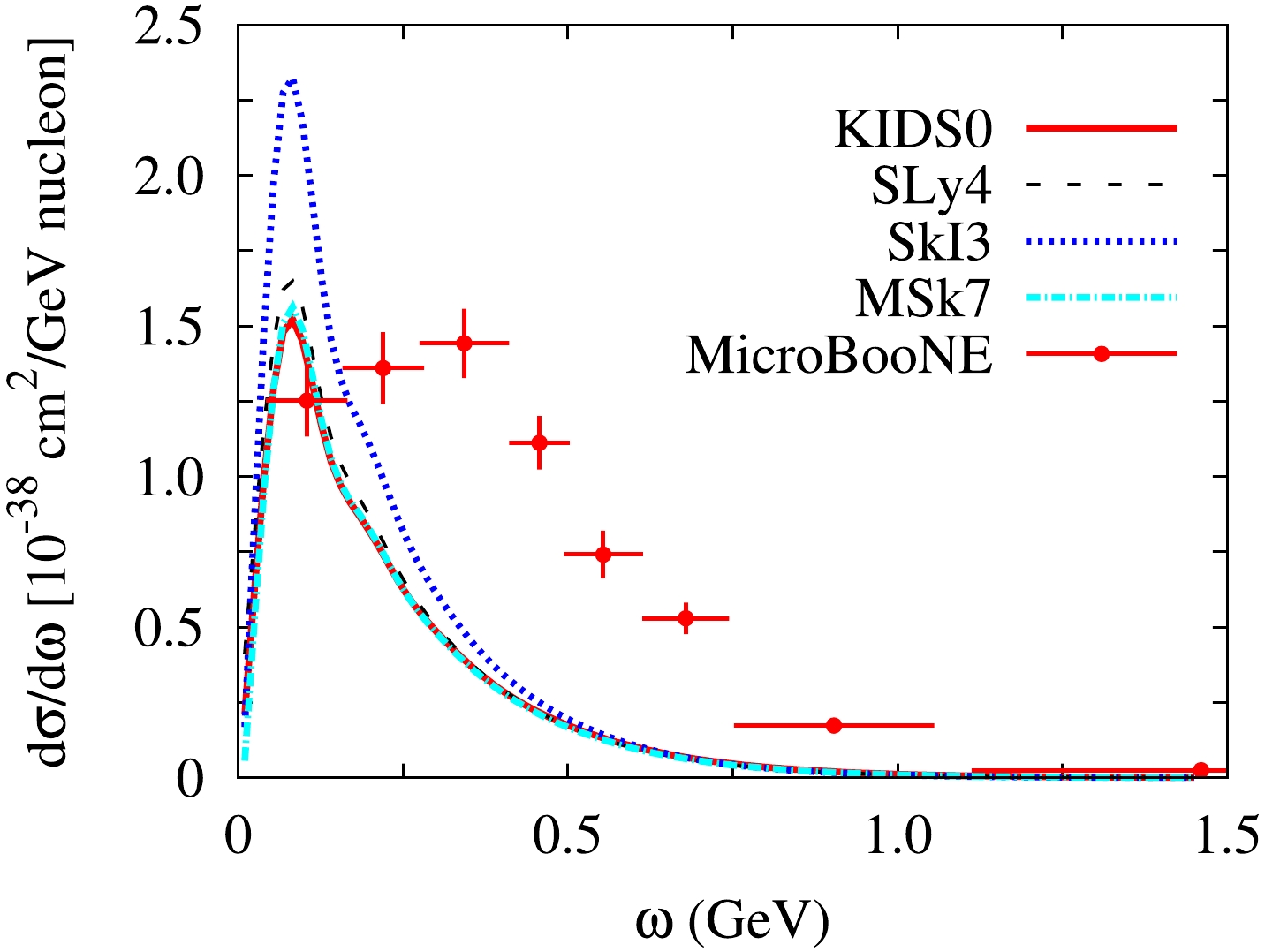
Figure 2. (color online) Flux-averaged single-differential cross sections in terms of the energy transfer from 40Ar. The data were measured by the MicroBooNE Collaboration [17].
In Fig. 3, the flux-averaged single-differential cross sections in terms of the energy of the outgoing muon from 40Ar are presented and compared with the MicroBooNE data [17]. The kinematics are similar to those of Fig. 2 owing to the relation of
$ E_{\mu}=\sqrt{p^2_{\mu} +m^2_{\mu}} $ after integrating the polar angle of the outgoing muon. SkI3 presents the largest values, similar to the above results. For this kinematics, only the QE process is dominant because the energy of the outgoing muon is fixed. Consequently, the theoretical shapes and positions of the peaks agree with the experimental data except for the magnitude. In particular, the results for SkI3 describe the experimental data very well; however, this might be an accidental good agreement.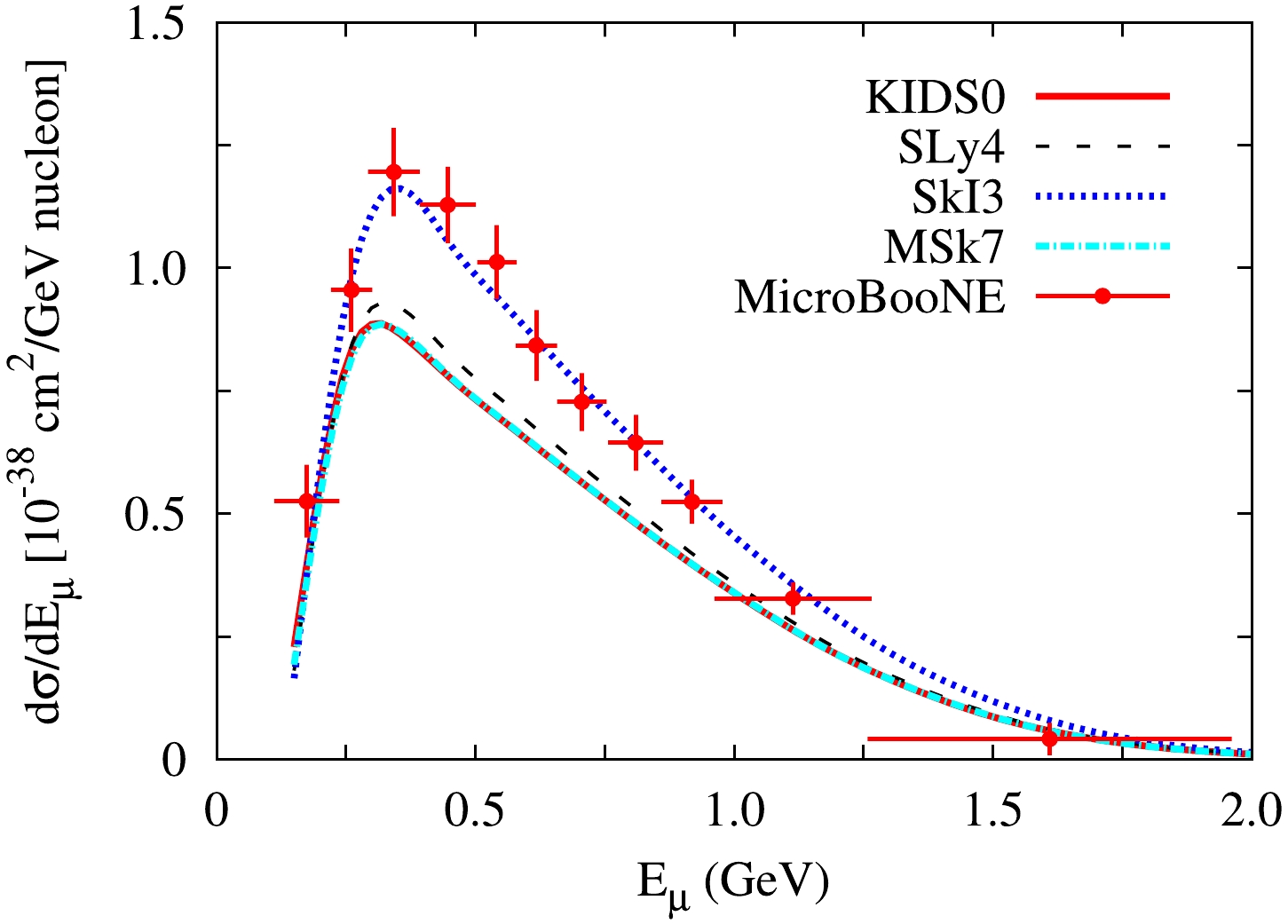
Figure 3. (color online) Flux-averaged single-differential cross sections in terms of the energy of the outgoing muon from 40Ar. The data were measured by the MicroBooNE Collaboration [17].
In Fig. 4, we present the scaled total cross sections in terms of the incident neutrino energy and their comparison with MicroBooNE [17] data. In the low energy region, the theoretical cross sections overestimate the data, and the cross section of SkI3 deviates from those of the other models at higher energy range. According to previous studies [4, 16], in the QE region, the theoretical total cross sections underestimate the MiniBooNE experimental data [32]. By contrast, in comparison with MicroBooNE data, the theoretical results overshoot experimental ones. Hence, this situation requires further analysis.
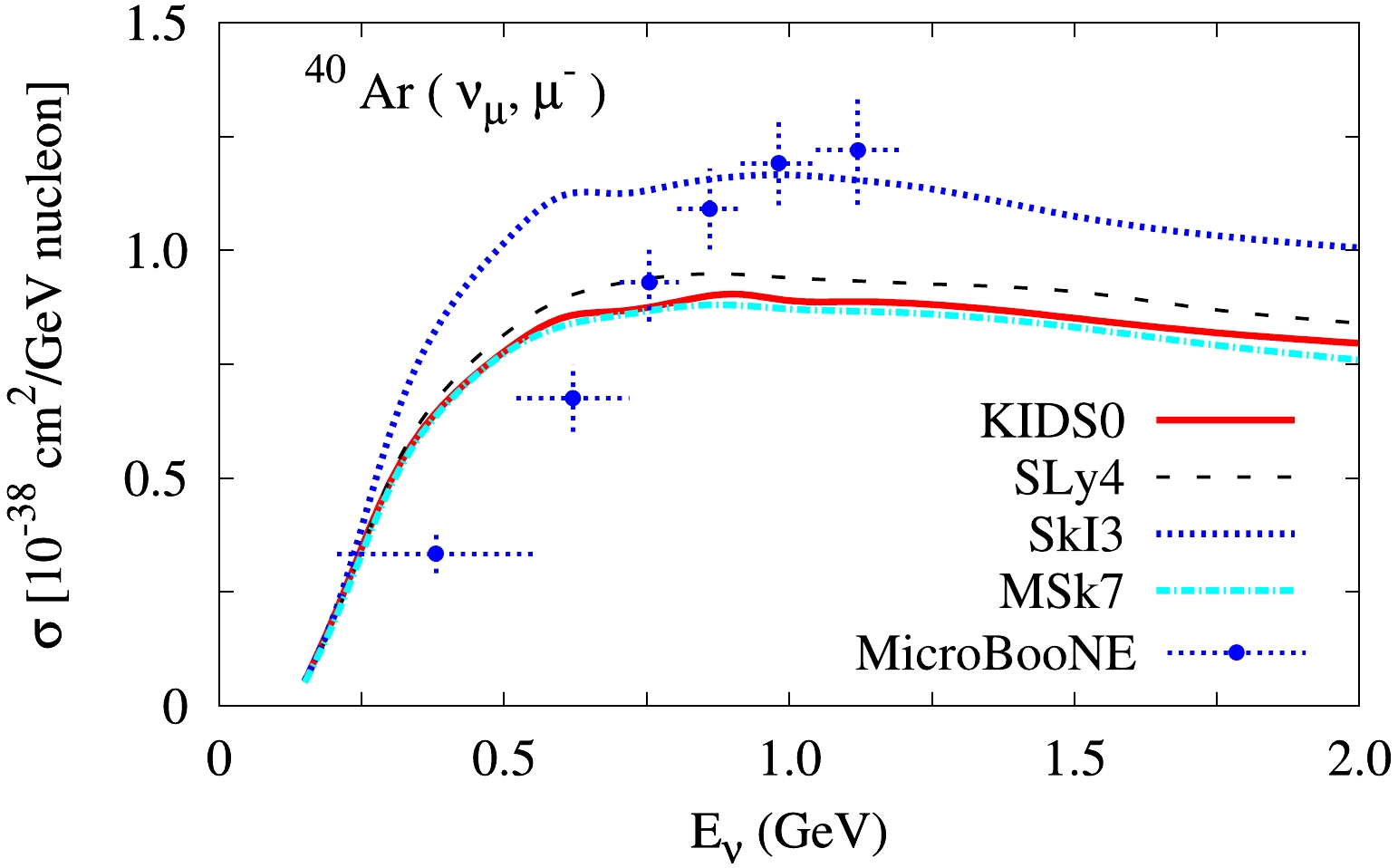
Figure 4. (color online) Scaled total cross sections in terms of the incident neutrino energy for the 40Ar
$ (\nu_{\mu}, \mu^-) $ reaction. The data were measured by the MicroBooNE Collaboration [17]. -
In the present study, we calculated the quasielastic neutrino-nucleus scattering off 40Ar with nonrelativistic nuclear models, and compared the theoretical results with MicroBooNE data. For the considered nonrelativistic models, the wave functions of the continuum and bound nucleons were generated by using the nonunitary transformation. Note that no parameters in the models were adjusted to the experimental data of neutrino-nucleus scattering, except for global values such as the axial mass in the electroweak operator. Moreover, we did not include inelastic processes such as particle-hole excitation and MEC.
The double-differential cross sections in the models do not provide the data reported from MicroBooNE. The cross sections agree with the data at forward angles but they do not agree with the data at backward angles. The single-differential cross sections were also calculated in terms of energy transfer and compared with the data measured from MicroBooNE. However, the theoretical results do not describe the data at all owing to the various entangled reaction channels. The theoretical cross sections of the SkI3 model agree with the MicroBooNE data for the outgoing muon energy relatively well, but the other models underestimate the data. Finally, the scaled total cross sections were calculated with respect to the incident neutrino energy. They overestimate the experimental data at lower incident energies but underestimate them at higher energies.
Comparison between theories shows more interesting and consistent trends. First, the results of the KIDS0 and MSk7 models are similar. Both models differ in the symmetry energy significantly. The similarity in the results can be interpreted as a signal for insensitivity to the symmetry energy. Second, for all the observables, KIDS0 and MSk7 are very similar, SLy4 presents slightly larger values than these two models, and SkI3 presents values exceeding those of the other three models. The KIDS0, SLy4, and SkI3 models present similar values of the isovector effective mass. Given the differences among these three models, this implies that the isovector effective mass is insensitive to the cross sections. By contrast, it was clearly observed that the results become larger with a smaller isoscalar effective mass. This can be summarized as follows: observable: KIDS0
$ \simeq $ MSk7 < SLy4 < SkI3,$ m^*_s $ : KIDS0$ \simeq $ MSk7 > SLy4 > SkI3. The results in the present study are consistent with those of precedent studies [2, 3, 4] in which we also observed that the isoscalar effective mass constitutes the dominant uncertainty that affects the lepton-nucleus scattering cross section in the quasielastic region.In conclusion, the differences among the KIDS0, SLy4, SkI3, and MSk7 nuclear models result from sensitivity to kinematics, and the cross sections from the models agree with the data relatively well at forward scattering angles for neutrino scattering. In particular, the cross sections of the SkI3 model deviate largely from those of the other models. It is necessary to improve the nuclear models and simultaneously include other processes such as MEC to describe experimental data more precisely.
Inclusive quasielastic neutrino-nucleus scattering with energy density functional nuclear models
- Received Date: 2024-03-19
- Available Online: 2024-08-15
Abstract: In this study, we calculated the inclusive charged-current neutrino-nucleus scattering from 40Ar in the quasielastic region. To explore the effect of uncertainties stemming from the nuclear structure, we used the KIDS (Korea-IBS-Daegu-SKKU) nuclear energy density functional and Skyrme force models, namely SLy4, SkI3, and MSk7. These models were selected to have distinct behavior in terms of the density dependence of the symmetry energy and the effective mass of the nucleon. In the charged-current neutrino scattering, the single- and double-differential cross sections were calculated for various kinematics. Total cross sections are reported as a function of the incident neutrino energy. The theoretical cross sections were compared with experimental data, and the roles of the effective mass and symmetry energy were investigated in terms of charged-current neutrino-nucleus scattering.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: