-
Studies on galaxy rotation curves, gravitational lensing, and the cosmic microwave background radiation suggest that a significant amount of "invisible" matter exists in the universe. [1]. By conducting theoretical and experimental research, current estimations suggest that the universe consists of 69.1% dark energy, responsible for universal expansion, 25.9% dark matter, which does not partake in electromagnetic interactions, and approximately 4.9% ordinary matter [2]. Numerous physicists dedicated significant efforts in identifying viable dark matter candidates beyond the Standard Model, with weakly interacting massive particles (WIMPs) that appear promising. In theory, WIMPs are electrically neutral particles with a mass range spanning from
${\rm GeV}/c^{2}$ to${\rm TeV}/c^{2}$ , and they interact with ordinary matter via weak interactions similar to those of neutrinos. WIMPs can be directly detected by observing the signals produced by the elastic scattering of the nucleus via atomic recoil on the detector ($ i.e. $ , nuclear recoil). Over the past two decades, a significant number of direct detection experiments for WIMPs have been proposed and executed.Inert gases, such as argon and xenon, are colorless, odorless, monatomic molecular gases with exceptionally low chemical reactivity. The chemical inertness of these elements renders them as safe media for detectors. Furthermore, liquid argon and liquid xenon are dense media characterized by substantial mass and minimal volume. These properties enable the construction of cost-effective, high-sensitivity liquid inert gas detectors with tonnage or even larger capacities, which are essential for detecting WIMPs due to the presumptively minuscule interaction cross-section between WIMPs and normal matter. The reserves of argon are very rich, and the content of noble gases in air is approximately 0.94%, [3] most of which is argon. The total content of other noble gases is less than one percent. Furthermore, relatively, argon is more suitable as a detection medium to build a super detector. Specifically, in southwestern Colorado, the gas argon will be extracted from a
$\rm CO_2$ well and separated onsite, with a production rate of$ 330 $ $\rm kg/day$ . Considering maintenance and downtime, this translates intro$ 90 $ $\rm tonne/year$ of underground argon (UAr) [4]. Construction of very large detectors using UAr is also quite possible (Darkside-20k is under construction) [5].The DEAP/CLEAN collaboration focuses on the direct detection of dark matter particles utilizing single-phase noble liquid detectors, including liquid argon or liquid neon [6]. The Argon Dark Matter (ArDM) experiment represents the first ton-scale two-phase liquid argon time projection chamber (TPC), while the WIMP Argon Program (WArP) [7] and DarkSide [8] both employ two-phase liquid argon TPCs for direct dark matter detection, yielding meaningful outcomes. Additionally, CRESST II utilizes$\rm CaWO_{4}$ as the absorber [9], ROSEBUD employs$\rm Al_{2}O_{3}$ as the absorber [10], CDMS II incorporates$\rm Ge/Si$ as the absorber [11], and EDELWEISS relies on$\rm Ge$ as the absorber [12], all in combination with phonon detectors. These experiments have also achieved notable results in direct dark matter detection.Argon-based detectors and phonon-mediated detectors are commonly utilized for direct detection of dark matter. Utilizing the beneficial properties of these complementary approaches in a single detector, an improved sensitivity to low-energy and low-mass dark matter interactions may be achieved. Specifically, a detector combining argon's low background and the excellent energy resolution afforded by phonon detection can exhibit a low energy threshold, high resolution, large active volume, and minimal background.
We propose a novel “argon phonon detector” that utilizes argon- and phonon-based detection techniques to maximize sensitivity for WIMPs of low mass. By merging argon's low background with phonon detectors' exceptional energy resolution, this proposed detector could extend exclusion contours in WIMP-parameter space to previously unexplored regions. Additionally, the newly optimized device allows next-generation dark matter detection experiments to explore new areas of WIMP theoretical space.
-
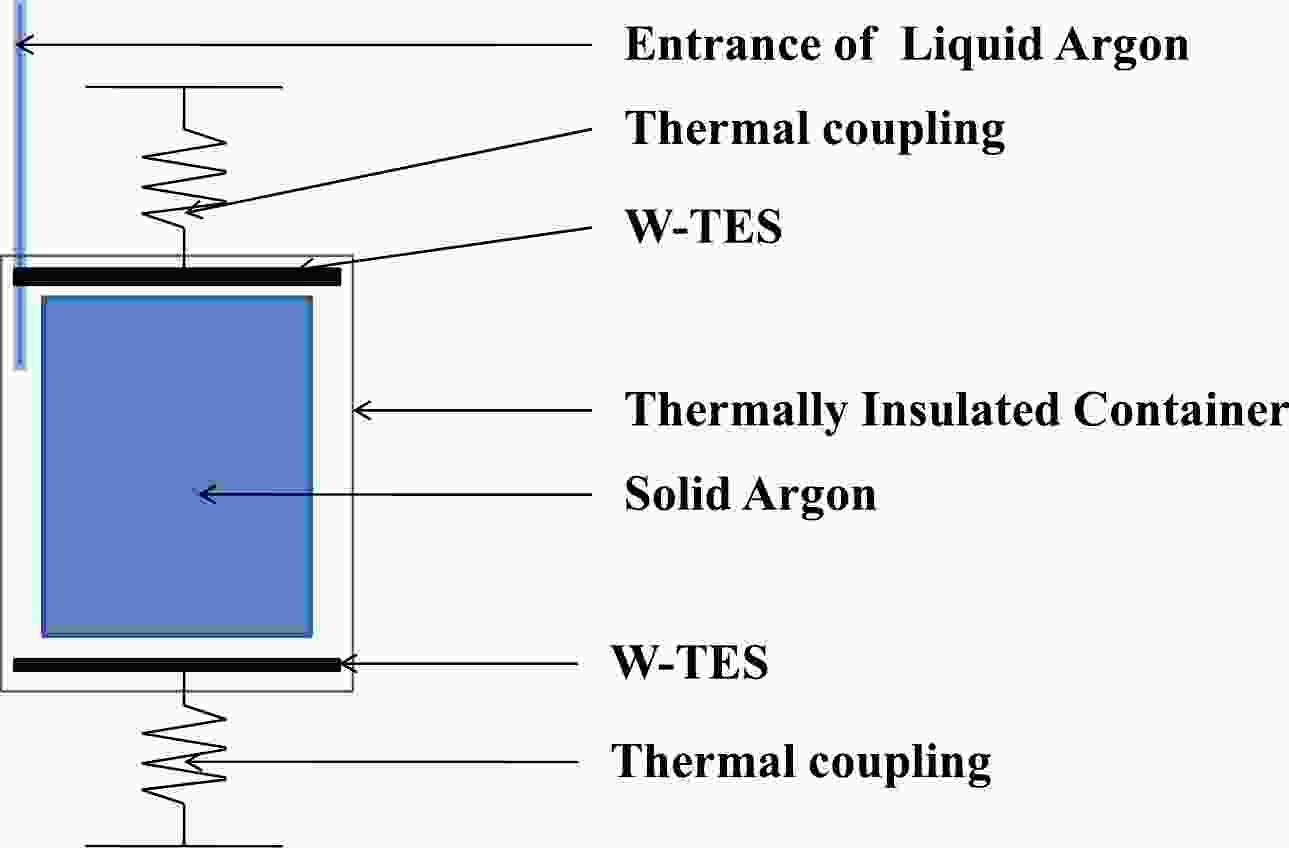
In this section, we present a theoretical analysis of the anticipated performance of solid-argon phonon detectors. Based on the fundamental structure of CRESST's phonon scintillation detector [13], a novel cylindrical solid-argon phonon detector model is constructed as shown in Fig. 1. The model is constructed with dimensions of
$ 3.44 $ cm in height and$ 3.44 $ cm in diameter, with a detector absorber mass of$ 32 $ g, and it utilizes tungsten transition edge sensors (W-TES) as temperature sensors. The density of solid argon at temperatures approaching$ 0 $ K is approximately 1.78 g/cm3 [14].
Figure 1. (color online) Schematic diagram depicting the module design for a phonon detector utilizing solid argon absorber.
In a phonon detector, a particle's interaction with the absorber transfers some or all of its kinetic energy, primarily producing phonons. These phonons are detected and transformed into an electrical signal. Their energy resolution is governed by the Poisson distribution's statistical fluctuations, which correlate with the number of phonons created for each energy deposition. The intrinsic energy resolution of the phonon detector depends on the heat capacity of the absorber and its operating temperature. The energy required to produce a single packet of thermal phonons is given by
$ \omega=K_bT $ , where$ K_b=8.617{\times}10^{-5} $ $\rm eV/K$ represents Boltzmann's constant and T denotes temperature in Kelvin.Assuming that 90% of the deposited energy can be converted into thermal energy [15], this becomes measurable energy (E) that can be detected by phonon detectors. The number of thermal phonons produced by incident particles with energy E can be expressed as
$ N=E/\omega $ . The energy resolution ($ \Delta{N} $ ) of the detector can be estimated using the root-mean-square fluctuation of the number of thermally generated phonons, which is given by$\Delta{N}= \sqrt{FN}=\sqrt{(FE/\omega)}$ , where F denotes the Fano factor. In this study, we assume$ F=1 $ [16]. The calculation of the detector's intrinsic resolution can be performed using the aforementioned Eq. (1),$ \begin{align} R= \frac{\Delta{E}_{\rm FWHM}}{E}=\frac{2.35\Delta{N}}{N}=2.35\sqrt{\frac{F\omega}{E}} .\end{align} $

(1) The energy resolution of a detector primarily depends on its operational state. Intrinsic energy resolution is significantly influenced by energy fluctuations in the absorber's surrounding environment and electronic noise. While the latter pertains to the performance of electronic components and is beyond this investigation's purview, our study centers on the effects of internal energy fluctuations at low temperatures on energy resolution. The internal energy
$ E' $ can be reasonably approximated by function$ E'\cong{N'K_b\cdot{T}}\cong{C\cdot{T}} $ . Hence, we can obtain Eq. (2) as follows:$ \begin{align} \Delta{E}'\cong{\sqrt{N'}K_bT}=\sqrt{N' K_b^{2}} T=\sqrt{C(T)K_b}T \end{align} $

(2) and then
$ \begin{align} \Delta{E}_{\rm FWHM}'=2.35\Delta{E}'\cong{2.35\sqrt{C(T)K_b}T}. \end{align} $

(3) The correlation between the intrinsic resolution of the phonon detector and quantity of solid argon crystals with respect to the operational temperature is depicted in Fig. 2. Based on Fig. 2, the intrinsic resolution of the phonon detector increases as the total crystal mass increases, and thereby, the operating temperature can easily be obtained.
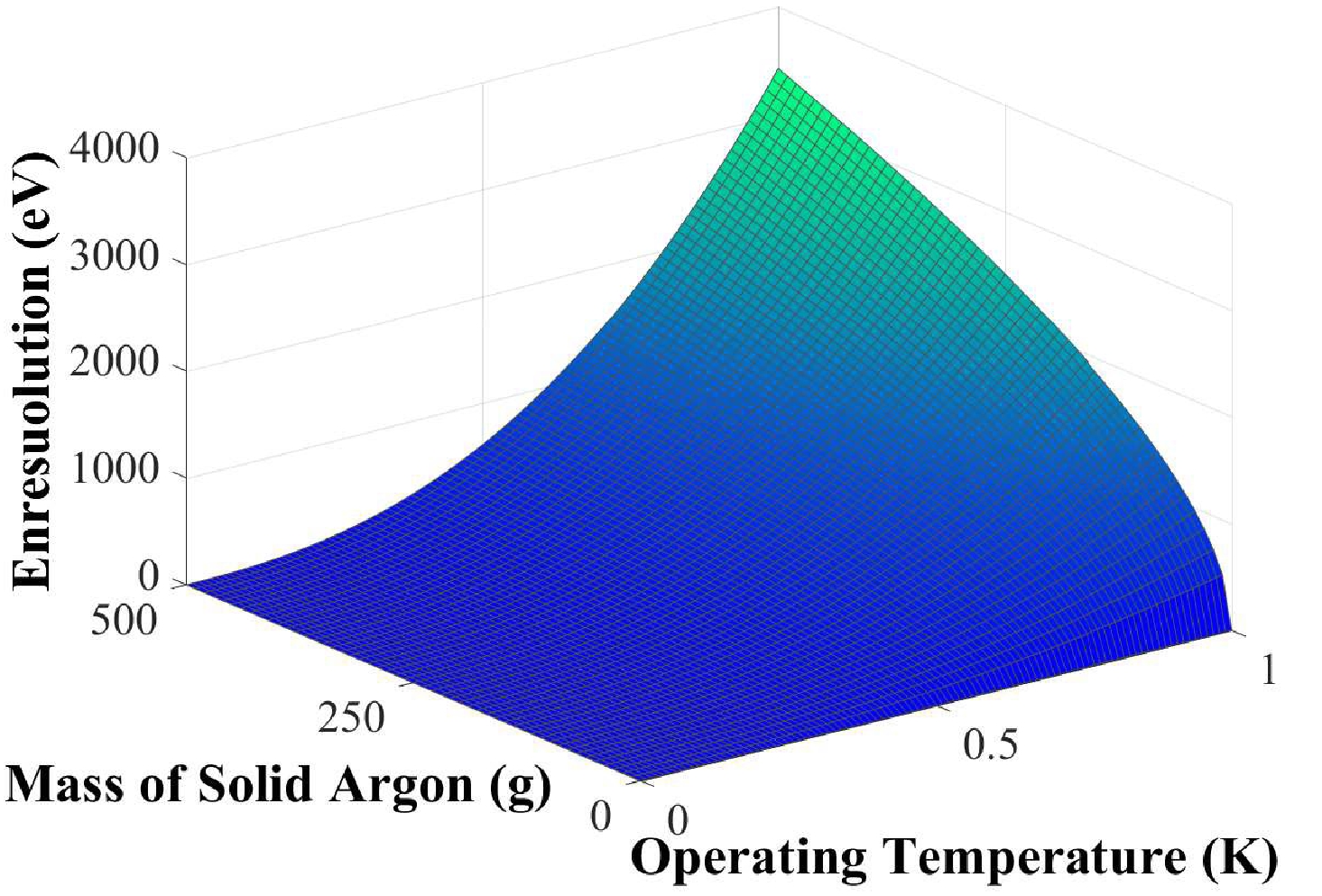
Figure 2. (color online) Correlation between the intrinsic resolution of the phonon detector, which arises from the internal energy fluctuations occurring at ultra-low temperatures, and the quantity of solid argon with respect to the operational temperature.
The resolution of a detector is directly proportional to the magnitude of temperature change induced by the deposition of the same amount of energy. Consequently, absorbers with smaller heat capacities tend to exhibit a higher resolution. Typically, the heat capacity of materials adheres to Debye's law at temperatures below the Kelvin level.
$ \begin{align} C_{V,m}=\frac{12}{5}{\pi}^{4}R{\frac{T}{{\theta}_{D}}}^3. \end{align} $

(4) It states that the heat capacity of a material is proportional to the cube of the absolute temperature (
$ T^{3} $ ) in the temperature regime below the Kelvin level [17].In Table 1, the values in the second column are obtained from specific heat measurements at moderately high temperatures (
$ T{\sim}\theta $ ), and the low-temperature value for$\rm Ar$ is extrapolated to$ 0 $ K from measurements at liquid helium temperatures [18]. By combining the Debye temperature obtained from Table 1 for several solid rare gases at$ 0 $ K and$ 0 $ pressure conditions, with the Debye law expressed in Eq. (4), it is straightforward to conclude that solid argon exhibits the lowest heat capacity under the same conditions. Hence, we opted for argon as the phonon detector absorber material among various rare gases.$ \theta_0=\frac{T_0+{\Delta}U_0}{\dfrac{9}{8}N_k} $ 

$\theta_0 ~\rm exp,~high$ 

$\theta_0 ~\rm exp,~low$ 

Ne 73 64 Ar 93 81 94 Kr 70 63 Xe 65 55 Table 1. Theoretical and experimental Debye temperatures of Solid
$\rm Ne $ ,$\rm Ar $ ,$\rm Kr $ , and$\rm Xe $ with$ \theta_{0} $ at$ 0 $ K and zero pressure.Based on the heat capacity data of solid argon presented in Table 2 at temperatures in the vicinity of a few Kelvin and utilizing Debye's law, it can inferred that the specific heat capacity of solid argon at
$ 15 $ mK is less than$ 1.97\times10^{-9} $ $\rm cal{\cdot}mole^{-1} K^{-1}$ [19]. Converted to appropriate units, this value is found to be below$ 2.06\times10^{-10} $ $\rm J{\cdot}g^{-1}{\cdot} K^{-1}$ . Comparing this with the empirical formula of sapphire heat capacity,$ C(T)=9.6\times10^{-5} T^3+1.7\times10^{-8} $ $\rm T{\cdot}J{\cdot}K^{-1}$ , which yields a heat capacity of$ 5.79\times10^{-10} $ $\rm J{\cdot}g^{-1} {\cdot}K^{-1}$ at$ 15 $ mK [20], it can be concluded that solid argon has a relatively low heat capacity. The performance of phonon detectors, in terms of resolution and threshold, is significantly influenced not only by the total heat capacity of the absorber but also by the temperature sensor employed:$T/\rm K$ 

$Cp(\rm cal~ mole^{-1} K^{-1})$ 

$T/\rm K$ 

$Cp(\rm cal~ mole^{-1} K^{-1})$ 

2 0.00468 8 0.4237 3 0.0161 10 0.7900 4 0.0417 12 1.227 5 0.0881 15 1.940 6 0.1651 20 2.990 Table 2. A partial specific heat capacity data of solid argon is presented.
$ \begin{align} \Delta{T}=\frac{\Delta{E}}{C(T)} {\rm e}^{-\frac{1}{\tau}}. \end{align} $

(5) The total heat capacity of the absorber is denoted by
$ C(T) $ , while$ \Delta{E} $ denotes the energy deposited within the absorber. Additionally, τ denotes a coefficient that is associated with the temperature sensor employed. The phonon detector's characteristic is the temperature increase of the absorber, measured by the temperature sensor. Thus, under consistent energy deposition, the detector's resolution is enhanced with a more distinct temperature shift. Specifically, Eq. (5) indicates that the intrinsic energy resolution of a phonon detector is directly related to the absorber's total heat capacity. Hence, it can be hypothesized that solid-argon detectors might display superior resolution when their quantity and component specifications align with those of sapphire detectors.In order to satisfy the stringent requirements of dark matter detection experiments concerning resolution and lower detection limits, W-TES are often utilized as temperature sensors due to their exceptional sensitivity. To enhance the sensitivity of W-TES sensors, a high-temperature evaporation process is typically employed to coat the W-TES material film onto the absorber's surface [21, 22]. However, given that the detector's absorber comprises solid argon, it cannot withstand high-temperature environments. To optimize the deposition of W-TES, an appropriate medium is chosen as the base. Subsequently, solid argon crystals are condensed onto the W-TES surface. Utilizing this method aids in avoiding potential damage to the absorber's crystal structure from high-temperature evaporation, which could otherwise compromise the detector's efficiency [23].
-
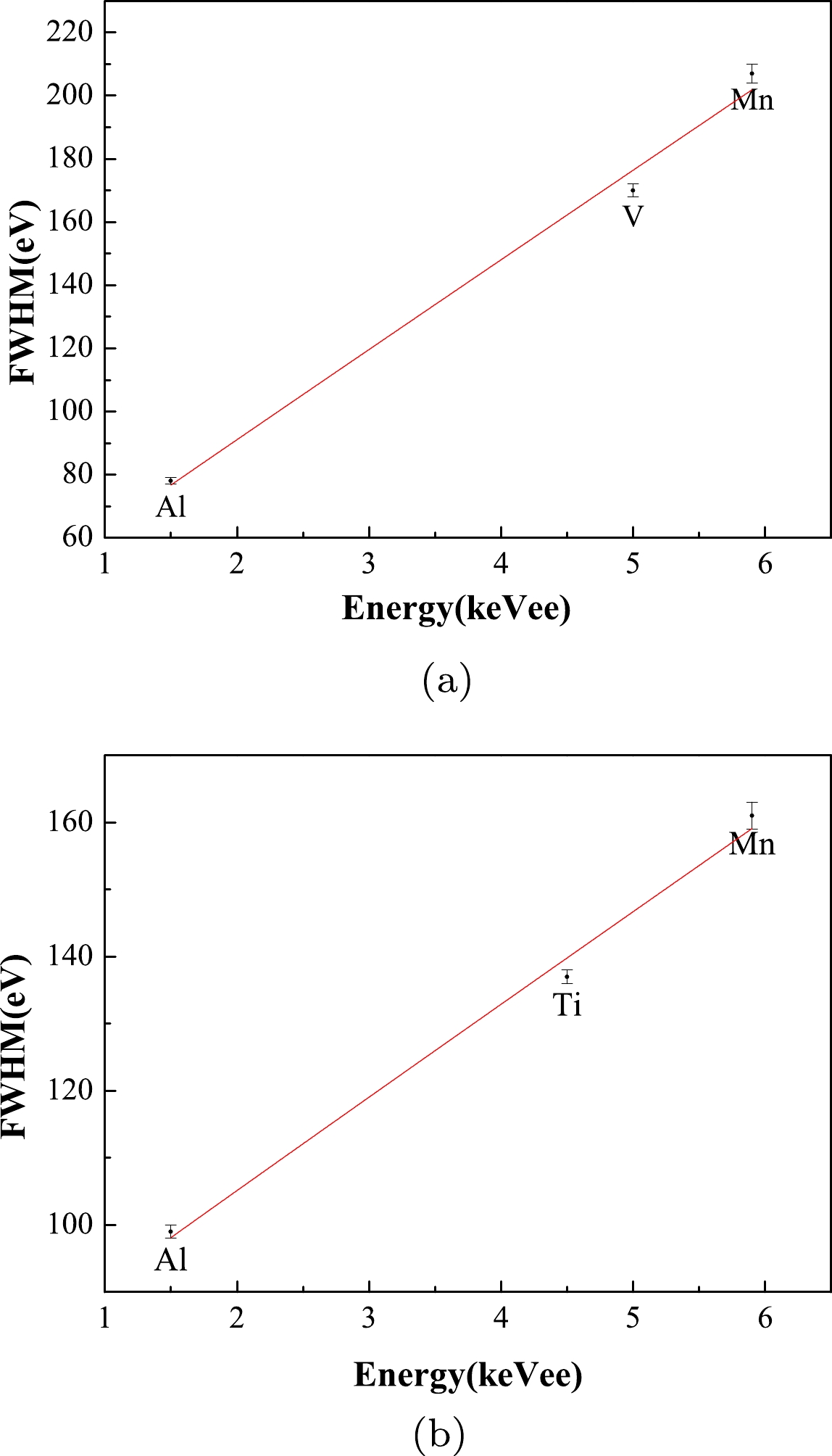
Phonon detectors featuring sapphire as the absorber demonstrate excellent detection performance. For instance, when the mass of sapphire, employed as the absorber, is
$ 4 $ g, the FWHM energy resolution is$ 78\pm1 $ eV at$ 1.5 $ keV,$ 170\pm2 $ eV at$ 5 $ keV, and$ 207\pm3 $ eV at$ 6 $ keV while the noise energy resolution at the baseline is$ 56 $ eV. When the mass of sapphire as the absorber is increased to$ 32 $ g, the FWHM energy resolution is$ 99\pm1 $ eV at$ 1.5 $ keV,$ 137\pm1 $ eV at$ 4.5 $ keV, and$ 161\pm2 $ eV at$ 6 $ keV, and the noise energy resolution at the baseline is$ 32 $ eV [24]. As the detector's resolution is influenced by a variety of factors, including statistical fluctuations and electronic noise, an optimized filter can be utilized to mitigate the impact of current-induced noise to enhance the energy resolution. The energy resolution of the detector is proportional to the square root of the energy due to the impact of statistical fluctuations, and the relationship between energy resolution and energy can be approximated as$ \begin{align} {\rm FWHM} (E)=2.36*(f_1+f_2 *\sqrt{E}+f_3*E), \end{align} $

(6) where
$ f_1 $ denotes the electronic noise,$ f_2 $ denotes the statistical fluctuation, and$ f_3 $ denotes the drift of the energy calibration over an extended period.Based on the aforementioned formula and resolution data of sapphire mentioned earlier, the energy resolutions of the sapphire detector for
$ 4 $ g and$ 32 $ g are fitted in Fig. 3(a) and Fig. 3 (b), respectively.Figure 3 displays the energy resolution of the sapphire detector experimental system with absorber masses of
$ 4 $ g and$ 32 $ g. The fitting results reveal that the relationship between the resolution and energy for a sapphire detector with an absorber mass of$ 4 $ g can be expressed as${\rm FWHM}(E)=2.36*(14.12+0.43*\sqrt{E}+11.99*E)$ , and the detector threshold is typically set to$ 5 $ times as much as the baseline noise, i.e.,$ 280 $ eV. Furthermore, the relationship between the resolution and energy for a sapphire detector with an absorber mass of$ 32 $ g can be represented as${\rm FWHM}(E)=2.36*(32.30+0.74*\sqrt{E}+5.69*E)$ , and the detector threshold is$ 160 $ eV.Considering factors such as the detector's size, performance, overall cost, and background level, a mass of 32 g was chosen as the ideal absorber mass for the solid argon phonon detector. The expected performance of this detector was calculated based on the sapphire phonon detector with an absorber mass of 32 g. The detector's main performance parameters are expected to exhibit a threshold of 160 eV, and the energy resolution is determined by the relationship
$\sigma(E) = 32.30 + 0.74\sqrt{E} + 5.69E$ , where${\rm FWHM}(E)= 2.36*\sigma(E)$ . -
Under the classical astrophysical premise, where the mass density of Weakly Interacting Massive Particles (WIMPs) is
$ 0.3 $ $\rm GeV/c^2{\cdot}cm^3$ , the most probable WIMP velocity relative to the galaxy is$ 220 $ $\rm km/s$ , and the Milky Way's escape velocity is$ 544 $ $\rm km/s$ , WIMPs and target nuclei are assumed to scatter elastically at a specific cross-section value [25]. Based on these assumptions, corrections are made in accordance with the experimental procedure, and the theoretically anticipated energy spectrum can be yielded. Considering the characteristics of elastic scattering and mass-energy assumptions for WIMPs, in addition to assuming that the target nucleus's velocity relative to the dark matter division is not zero and the Milky Way's escape velocity is finite, the counting rate of the nuclear recoil energy spectrum changes with the nuclear recoil energy as$ \begin{align} \frac{{\rm d} R(\nu_{E},\infty)}{{\rm d} E_R}=c_{1}\frac{R_0}{E_{0}r}{\rm e}^{\textstyle\frac{-c_{2}E_{R}}{E_{0}r}}. \end{align} $

(7) where R is the event rate per unit mass,
$ R_{0} $ the total event rate,$ E_R $ is the recoil energy, and$ E_{0} $ is the most probable incident kinetic energy of a dark matter particle of mass$ M_{D} $ , r is a kinematic factor$ 4M_{D}M_{T}/(M_{D}+M_{T})^2 $ for a target nucleus of mass$ M_{T} $ [26]. Among them,$ \nu_{E} $ ,$ c_1 $ , and$ c_2 $ all fluctuate periodically with the revolution of the earth, and the average values of$ \nu_{E}=244 $ $\rm km/s$ ,$ c_1= $ 0.786, and$ c_2=0.610 $ are taken here [27].Assuming an elastic collision between WIMPs and ordinary matter, and considering various astronomical parameters, we can compute and illustrate the differential energy spectra of recoil nuclei for different WIMP masses as shown in Fig. 4. By comparing the differential energy spectra of recoil nuclei for different target nuclei at varying WIMP masses, it is evident that argon exhibits a relatively high expected count rate in the high-energy region for large-mass WIMPs. Additionally, a comparatively high expected count rate can be realized for small-mass WIMPs by selecting an appropriate range within the low-energy region.
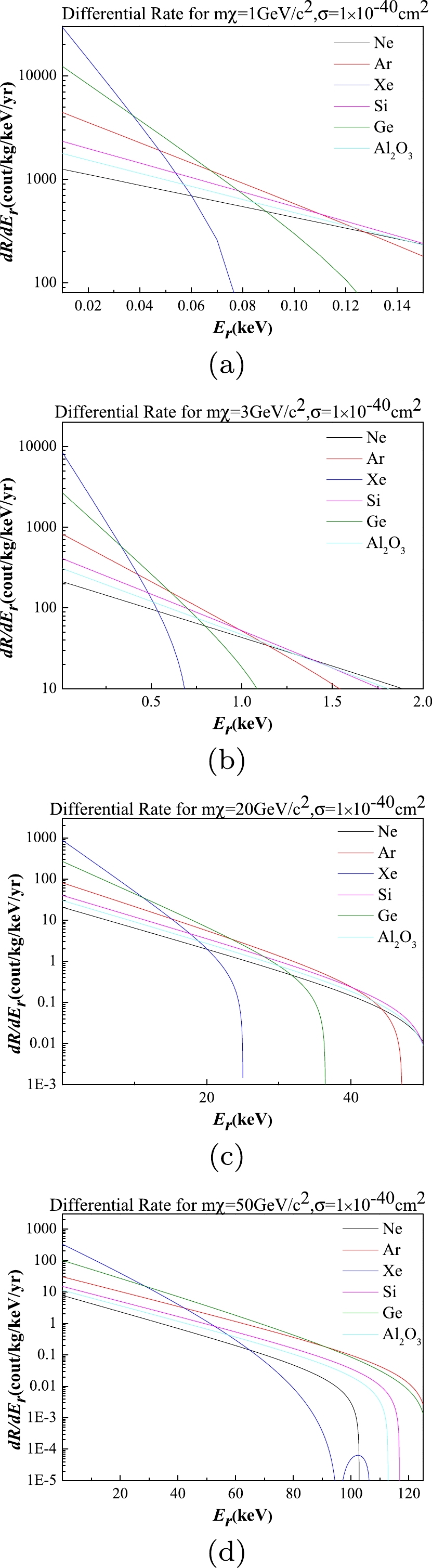
Figure 4. (color online) Expected differential energy spectra of nuclear recoils for various target nuclei interacting with WIMPs of different masses, with result of
$ 1 $ ${\rm GeV}/c^2$ presented in Fig. 4(a), result of$ 3 $ ${\rm GeV}/c^2$ presented in Fig. 4(b), result of$ 20 $ ${\rm GeV}/c^2 $ presented in Fig. 4(c), and result of$ 50 $ ${\rm GeV}/c^2 $ ) presented in Fig. 4(d). The nuclear recoil spectra for neon ($\rm Ne $ ), argon ($\rm Ar $ ), xenon ($\rm Xe $ ), silicon ($\rm Si $ ), germanium ($\rm Ge $ ), and Sapphire ($\rm Al_2O_3 $ ) targets are simulated using a standard halo model for galactic WIMPs.Statistical errors and noise in the detection process, as well as the detector and electronics, cause energy broadening in the experimental energy spectrum. The energy expansion of a single energy
$ E' $ follows the Gaussian function:$ \begin{align} \frac{{\rm d} N(E)}{{\rm d} E}=\frac{N}{(2{\pi})^{1/2}\sigma(E)}{\rm e}^{\textstyle-\frac{(E-E')^2}{2\sigma(E)^{2}}}. \end{align} $

(8) The Gauss broadening coefficient, obtained in Sec. II.B, is used to widen the nuclear recoil spectrum obtained in the solid argon detector, as shown in Fig. 5.
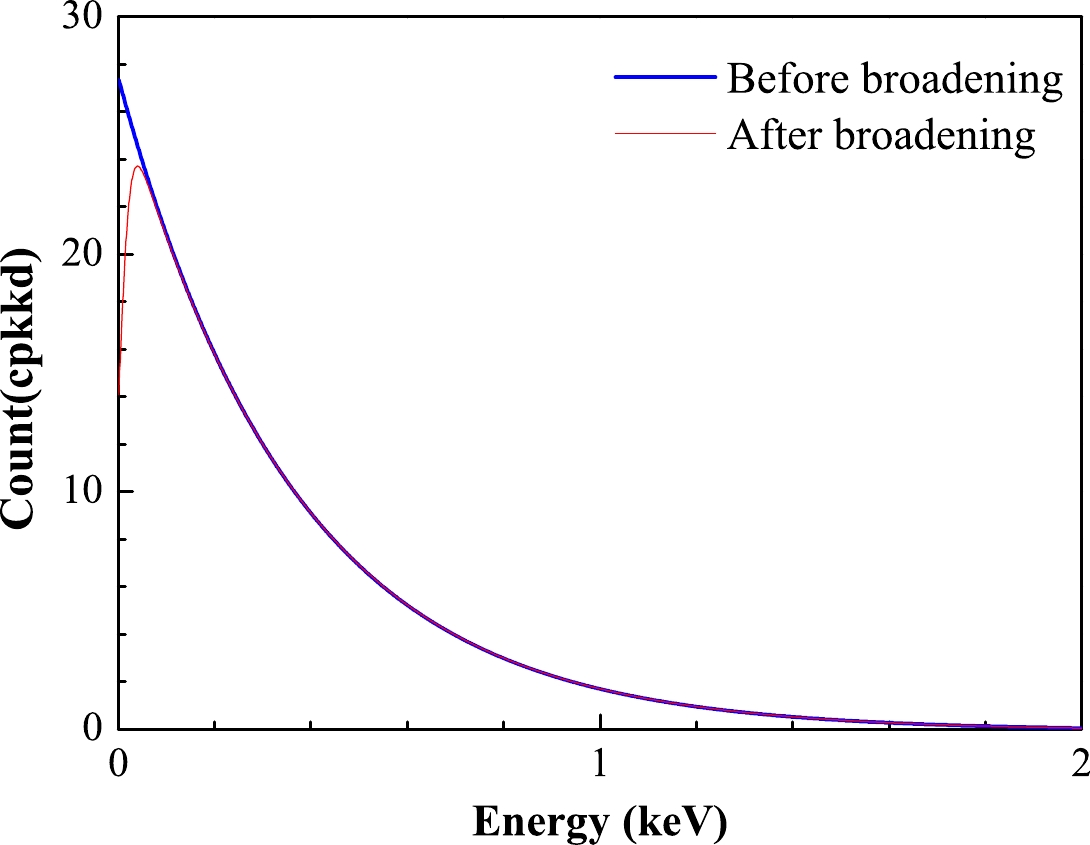
Figure 5. (color online) Expected energy spectrum of WIMPs events in a solid argon detector, based on the elastic scattering model. The energy spectrum is depicted in two stages: the blue curve represents the energy spectrum before broadening, while the red curve represents the energy spectrum after Gaussian broadening. The WIMPs in question exhibit a mass of
$ 3 $ ${\rm GeV}/c^{-2}$ and cross section of$ 10^{-40} $ $\rm cm^{2}$ . -
The event rate of reactions between dark matter and ordinary matter is extremely low, necessitating an environment with a very low radioactive background. Due to the random nature of the background contribution in the amplitude spectrum, direct subtraction is not feasible. This limitation significantly impacts the ability to detect cross-sections of interactions between dark matter and matter. To minimize the environmental background's impact on the event rate, the experiment is expected to be conducted at the China JinPing Underground Laboratory (CJPL). The vertical coverage depth of CJPL rocks is approximately
$ 2400 $ m (approximately$ 6720 $ m water equivalent depth), with cosmic ray flux at$ 61.7{\pm}11.7 $ $\rm m^{-2}{\cdot}y^{-1}$ , reaching the lowest level in the world. The specific activity of surrounding rock is$ 1.8{\pm}0.2 $ $\rm Bq{\cdot}kg^{-1}$ for$\rm ^{226}Ra$ , less than$ 0.27 $ $\rm Bq{\cdot}kg^{-1}$ for$\rm ^{232}Th$ , and less than$ 1.1 $ $\rm Bq{\cdot}kg^{-1}$ for$\rm ^{40}K$ [28]. As for the radiological contribution of the argon crystal itself, we calculated it via Monte Carlo simulation of the radioactivity of$\rm ^{39}Ar$ when evenly distributed among the solid argon crystal. Regarding the detector, the primary radioactivity present in solid argon is$\rm ^{39}Ar$ , with a specific activity of approximately$ 1 $ $\rm Bq{\cdot}kg^{-1}$ [29]. The specific activity of$\rm ^{39}Ar$ in argon without$\rm ^{39}Ar$ was assumed to be$ 0 $ $\rm Bq{\cdot}kg^{-1}$ for the calculations presented below.To summarize, the cosmic rays contribute less than
$ 10^{-3} $ count per kilogram per keV per day (cpkkd) to the energy spectrum of the detector. Similarly, the radioactivity from the surrounding rock and shielding contribute less than$ 10^{-3} $ cpkkd each. When considered together, the background contributes less than$ 10^{-2} $ cpkkd to the energy spectrum [30, 31]. In terms of the radiological contribution from the argon crystal, we utilized Monte Carlo simulation to calculate the radioactivity of$\rm ^{39}Ar $ when it is uniformly dispersed throughout the solid argon crystal.As demonstrated in Fig. 6, the radioactivity emanating from the solid argon crystal accounts for approximately
$ 10^{-2} $ cpkkd in the energy spectrum of the low-energy section (approximately$ 1 $ keV).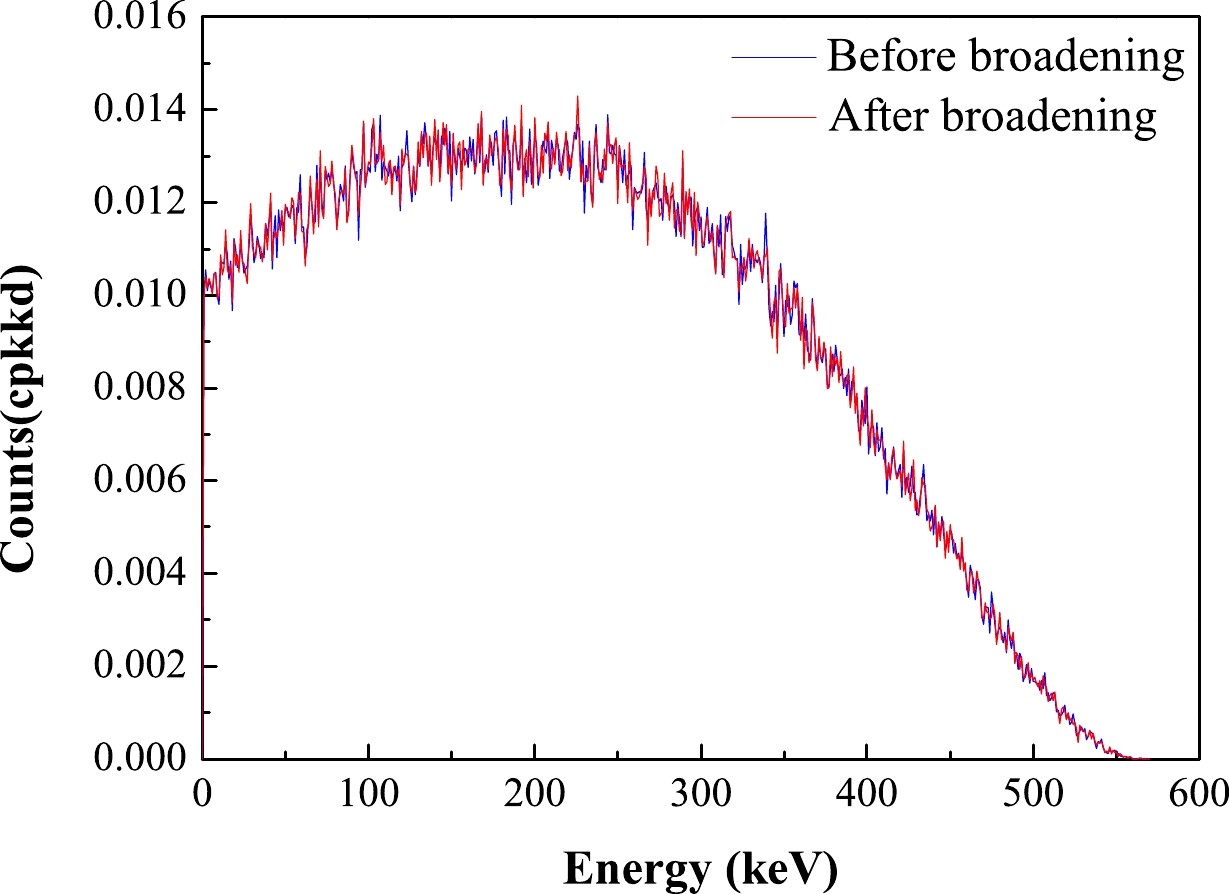
Figure 6. (color online) Monte Carlo simulation of the contribution of
$\rm ^{39}Ar$ in the energy spectrum with specific activity of$ 1 $ $\rm Bq{\cdot}kg^{-1}$ .The background count rate, derived from both external sources and the detector itself, has been determined, shedding light on the total event leakage rate. Once the event leakage rate in the energy spectrum was identified, we used the Binned Poisson method to enhance statistical analysis of the best intervals, enabling predictions of the argon detector's sensitivity to WIMPs based on a set exposure time and resolution [32, 33]. If the theoretically expected dark matter event rate is
$ dR_{ti}(\sigma) $ and the experimental measurement result is$ dR_{mi}(\sigma) $ , then the cross-sectional value σ satisfying the following equation under the confidence level$ (C.L.) $ will be excluded$ (dR_{ti}(\sigma) $ is considered as the expected value of the Poisson distribution):$ \begin{align} P[x>dR_{mi}{\mid}dR_{ti}(\sigma) ]{\geq}C.L. \end{align} $

(9) When the afor equation holds as an equality, the cross-section is denoted as
$ \sigma_{ex} $ , which is the smallest excluded cross-section. This method is used to determine the 90% confidence level upper limit for the unidentified signal [33].The results in Fig. 7 show that the lower limit of dark matter detection improves with increasing detection duration and decreasing energy threshold. These findings are of significant interest for the field of dark matter detection and offer new insights into the sensitivity limits of solid argon and sapphire crystals in the search for WIMPs.

Figure 7. (color online) Upper limit for WIMPs-nucleon scattering cross section at 90% confidence level in solid argon and sapphire crystals with a mass of
$ 5 $ kg, with and without$\rm ^{39}Ar$ background, are depicted. The study employs four different detection scenarios, characterized by different energy thresholds and durations:$ 500 $ days of continuous detection with an energy threshold of$ 0.2 $ keV (Fig. 7(a)),$ 1000 $ days of continuous detection with an energy threshold of$ 0.2 $ keV (Fig. 7(b)),$ 500 $ days of continuous detection with an energy threshold of$ 0.5 $ keV (Fig. 7(c)), and$ 1000 $ days of continuous detection with an energy threshold of$ 0.5 $ keV (Fig. 7(d)). Additionally, the upper limit from DarkSide-50 (purple line) and PandaX II [34] (black line) is displayed. -
By analogy with phonon detectors made from different materials, we discern the anticipated performance of solid argon phonon detectors in terms of energy threshold, energy resolution, and Gaussian broadening. By integrating these projected characteristics with classical astrophysical assumptions about massive weakly interacting particles, we derive exclusion limits based on specific exposure conditions. It is worth noting that even though energy resolution is a crucial aspect of the detector, it is often overlooked when estimating the exclusion limit. The detector's energy threshold, when relaxed to
$ 0.5 $ keV, has already reached the world's advanced level for direct dark matter detection (especially when the WIMPs mass scale is approximately$ 4.6 $ ${\rm GeV}/c^2$ ). Better results can be obtained when the detector's energy threshold reaches a lower value of$ 0.2 $ keV, with the WIMPs mass scale at$ 2.8 $ ${\rm GeV}/c^2$ . Compared to sapphire detectors of similar performance, solid argon detectors show notable advantages in a range where the WIMP mass is larger. For WIMP masses within$ 2 $ ${\rm GeV}/c^2$ , the advantage region of solid argon detectors with lower energy threshold becomes larger. By comparing the exclusion limit results for exposure times of$ 500 $ and$ 1000 $ days in Fig. 7, it can be observed that extending the exposure time has a significant effect on lowering the detection limit. Comparing the exclusion limit results for solid argon detectors, with and without$\rm ^{39}Ar$ , in Fig. 7, the superiority of$\rm ^{39}Ar$ -depleted detectors is evident. -
In general, extending the exposure time and amplifying the effective detection volume can significantly enhance prior prediction outcomes, leading to more optimal results. Based on the results mentioned, it is evident that choosing the right materials for the detector absorber, decreasing the detector's threshold, lengthening its exposure time, and minimizing surrounding background noise can contribute to effectively reducing the WIMP detection limit. Given that the results of Fig. 7(a) are consistent with a
$ 5 $ -kg detector, with a detection limit of$ 0.2 $ keV, exposed for$ 1000 $ days, it can be concluded that increasing the detector's effective mass can also significantly improve our predictive results. Targeted enhancements to the detector can further optimize the detection limit. When it comes to choosing the right materials for the target area, solid argon has already been identified as the absorber medium for the detector. However, according to Fig. 3, argon-based detectors do indeed exhibit higher detection limits in some energy ranges for detecting WIMPs of different masses. Lowering the detection threshold is a significant advantage for phonon detectors with over 90% absorption rate for nuclear recoil energy.For all types of detectors, the previous discussion can be utilised to reduce the upper limit of cross section detection, and argon phonon detectors exhibit their own unique advantages. First, the NUCLEUS experiment, based on the CRESST technique, utilized
$\rm Al_{2}O_{3}$ with a mass of$0.5~\rm g$ and aside length of$ 5 $ mm as an absorber. The results showed that it can reach the detection threshold of$E_{\rm th} =(19.7\pm0.9)$ eV via W-TES readout [22]. Therefore, if our detector uses a smaller mass of solid argon as the absorber, the detector resolution can be even higher, and the energy threshold can be even lower. Argon's ability to maintain long-term stability is a significant advantage, given its status as a rare gas element. Securing high-purity argon gas is straightforward, and creating high-purity solid argon crystals is similarly uncomplicated. This ease of preparation makes the production of large-mass solid argon phonon detectors viable. Furthermore, employing underground argon sources can mitigate potential background elevations due to substantial quantities of argon gas. Considering that the primary source of$\rm ^{39}Ar $ is cosmic ray spallation on$\rm ^{40}Ar $ , the concentration of$\rm ^{39}Ar $ should be lower in argon reservoirs that have been stored underground for a long time. Argon gas found in active$\rm CO_2 $ wells in southwestern Colorado has an extremely low concentration, with a radioactivity concentration of$ (1.4{\pm}0.2){\times}10^3 $ times lower than that of argon extracted from the atmosphere, reducing the contribution of$\rm ^{39}Ar $ radioactivity in the nuclear recoil energy spectrum [35, 36].Additionally, argon has very high light yield (irrespective of liquid or solid state) [37] and is a natural material for photo-phonon two-phase detector. The capability to acquire light signals in solid argon phonon detectors can be advanced, facilitating pulse discrimination and allowing for the exclusion of electron recoil events in the low-energy region.
After examining the performance criteria for dark matter detectors and the benefits of solid argon phonon detectors, it can be concluded that detectors based on solid argon have significant potential to deliver exceptional outcomes in upcoming dark matter detection initiatives.
Cryogenic phonon-detector model with solid argon for detecting dark matter
- Received Date: 2023-06-14
- Available Online: 2023-12-15
Abstract: Over the past few years, phonon detectors have emerged as a prevailing technology for detecting low-mass dark matter due to their low thresholds and high resolution. These detectors, which employ either dual-phase detectors combining phonon-light or phonon-electron interactions, have significantly advanced direct dark matter detection efforts. Argon, as a low-background and high-reserve detection medium, has also played a crucial role in this field. Both liquid-argon single-phase detectors and gas-liquid two-phase time projection chambers (TPCs) have contributed substantially to the direct detection of high-mass dark matter. By integrating these distinct detector types, the upper limits of the corresponding mass cross-section in dark matter detection can be lowered. We propose a phonon detector utilizing solid argon as the absorber, which combines the advantages of both aforementioned detector types. However, due to the requirement for an ultra-low temperature environment in the tens of millikelvin (mK) range, experimental investigations of solid argon phonon detector performance are currently constrained by technical limitations. Therefore, the performance analysis of the solid argon phonon detector presented in this study is only based on sapphire phonon detectors. Although there may be discrepancies between this approximation and the actual performance, the intrinsic characteristics of phonon detectors permit a qualitative evaluation of the solid argon phonon detector's potential capabilities.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: