-
The study of the low-lying excited
$ \Lambda^* $ and$ \Sigma^* $ hyperon resonances is one of the most important issues in hadron physics. In particular, since$ \Lambda(1405) $ was experimentally discovered [1, 2], its nature has garnered significant attention [3–8], and one explanation for$ \Lambda(1405) $ is the$ \bar{K}N $ hadronic molecular state [9–15]. In addition, for the isospin$ I=1 $ partner of$ \Lambda(1405) $ , the lowest$ \Sigma^{*}_{1/2^{-}} $ is crucial to understand light baryon spectra. At present,$ \Sigma^*(1620) $ with$ J^P = 1/2^{-} $ is listed in the latest version of the Review of Particle Physics (RPP) [16]. It should be emphasized that the$ \Sigma^*(1620) $ state is a one-star baryon resonance. Many studies indicate that the lowest$ \Sigma^*_{1/2^-} $ resonance is still far from being established, and its mass has been predicted to lie in the range$ 1380 \sim 1500 $ MeV [13, 17–20]. Thus, searching for the lowest$ \Sigma^*_{1/2^-} $ is helpful for understanding low-lying excited baryons with$ J^P=1/2^- $ and light flavor baryon spectra.The analyses of relevant data on the process
$ K^- p \to \Lambda \pi^+\pi^- $ suggest that a$ \Sigma^*_{1/2^{-}} $ resonance may exist with a mass of approximately 1380 MeV [17, 18], which is consistent with the predictions of unquenched quark model [21]. The analyses of$ K^{*}\Sigma $ photo-production also indicate that$ \Sigma^*_{1/2^{-}} $ is possibly buried under the$ \Sigma^*(1385) $ peak with a mass of 1380 MeV [22], and the search for$ \Sigma^*_{1/2^{-}} $ in the process$ \Lambda^+_c \to \eta\pi^+\Lambda $ has been proposed [23]. A more delicate analysis of CLAS data on the process$ \gamma p \to K \Sigma \pi $ [24] suggests that the$ \Sigma^*_{1/2^{-}} $ peak should be around 1430 MeV [13]. In Refs. [25, 26], we suggest searching for such a state in the processes$ \chi_{c0}(1P) \to \bar{\Sigma} \Sigma\pi $ and$ \chi_{c0}(1P)\to \bar{\Lambda}\Sigma\pi $ . In addition, in Ref. [27], one$ \Sigma^*_{1/2^{-}} $ state was found with a mass of approximately 1400 MeV by solving coupled channel scattering equations, and Ref. [28] suggests to search for this state in the photo-production process$ \gamma p \to K^{+} \Sigma^{*0}_{1/2^-} $ .It is worth mentioning that a
$ \Sigma^*(1480) $ resonance with$ J^P =1/2^- $ has been listed on the previous version of the RPP [29]. As early as 1970, the$ \Sigma^*(1480) $ resonance was reported in the$ \Lambda \pi^{+} $ ,$ \Sigma \pi $ , and$ p\bar{K}^{0} $ channels of$ \pi^+ p $ scattering in the Princeton-Pennsylvania Accelerator 15-in. hydrogen bubble chamber [30, 31]. In 2004, a bump structure around 1480 MeV was observed in the$ K^0_S p(\bar{p}) $ invariant mass spectrum of inclusive deep inelastic$ ep $ scattering by the ZEUS Collaboration [32]. Furthermore, a signal for a resonance at$ 1480 \pm 15 $ MeV with a width of$ 60 \pm 15 $ MeV was observed in the process$ pp \to K^{+}pY^{*0} $ [33].$ \Sigma^*(1480) $ has been investigated theoretically within different models [34–37]. In Ref. [37], S-wave meson-baryon interactions with strangeness$ S=-1 $ were studied within the unitary chiral approach, and one narrow pole with a pole position of$1468-{\rm i} \ 13 \ \rm MeV$ was found in the second Riemann sheet, which may be associated with the$ \Sigma^*(1480) $ resonance. However,$ \Sigma^*(1480) $ signals are insignificant, and the existence of this state still needs to be confirmed within more precise experimental measurements.Photo-production reactions have been used to study the excited hyperon states
$ \Sigma^* $ and$ \Lambda^* $ , and the LEPS [38] and CLAS [24] Collaborations have accumulated considerable relevant experimental data. For instance, with these data, we analyzed the process$ \gamma p\to K\Lambda^*(1405) $ to deepen our understanding of the nature of$ \Lambda^*(1405) $ in Ref. [39]. To confirm the existence of$ \Sigma^*(1480) $ , we propose to investigate the process$ \gamma N \to K\Sigma^*(1480) $ ① within the Regge-effective Lagrangian approach.Considering the
$ \Sigma^*(1480) $ signal was first observed in the$ \pi^+\Lambda $ invariant mass distribution of the process$\pi^+ p\to \pi^+K^+\Lambda$ , and the significance is approximately$ 3 \sim 4 \sigma $ [31], we search for charged$ \Sigma^*(1480) $ in the process$\gamma n \to K^{+}\Sigma^{*-}_{1/2^-}$ , which may also avoid the contributions of possible excited$ \Lambda^* $ states. We consider the t-, s-, and u-channel diagrams in the Born approximation by employing the effective Lagrangian approach, and the t-channel K/$ K^{*} $ exchanges terms within the Regge model. Then, we calculate the differential and total cross sections of the process$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ , which helps the experimental search for$ \Sigma^*_{1/2^-} $ .This paper is organized as follows. In Sec. II, the theoretical formalism for studying the
$ \gamma n \to K^+ \Sigma^{*-}(1480) $ reaction is presented. The numerical results of the total and differential cross sections and discussion are shown in Sec. III. Finally, a brief summary is given in the last section. -
The reaction mechanisms of the
$ \Sigma^*(1480) (\equiv \Sigma^*) $ photo-production process are depicted in Fig. 1, where we consider the contributions from the t-channel K and$ K^* $ exchange terms, s-channel nucleon pole term, u-channel Σ exchange term, and contact term.
Figure 1. Mechanisms of the
$ \gamma n \to K^+\Sigma^{*-}_{1/2^-} $ process. (a) t-channel K/$ K^* $ exchange terms, (b) s-channel nuclear term, (c) u-channel Σ exchange term, and (d) contact term.$ k_{1} $ ,$ k_{2} $ ,$ p_{1} $ , and$ p_{2} $ represent the four-momenta of the initial photon, kaon, neutron, and$ \Sigma^*(1480) $ , respectively.To compute the scattering amplitudes of the Feynman diagrams shown in Fig. 1 within the effective Lagrangian approach, we use the Lagrangian densities for the electromagnetic and strong interaction vertices, as in Refs. [28, 40–45],
$ \mathcal{L}_{\gamma K K} = -{\rm i} e\left[K^{\dagger}\left(\partial_{\mu} K\right)-\left(\partial_{\mu} K^{\dagger}\right) K\right] A^{\mu}, $

(1) $ \mathcal{L}_{\gamma K K^*}= g_{\gamma K K^*} \epsilon^{\mu \nu \alpha \beta} \partial_\mu A_\nu\partial_\alpha K_\beta^{*}K, $

(2) $ \mathcal{L}_{\gamma N N} = -e\bar{N}\left[ \gamma_{\mu}\hat{e} - \frac{\hat{\kappa}_{N}}{2M_{N}}\sigma_{\mu \nu}\partial^{\nu}\right]A^{\mu}N, $

(3) $ \mathcal{L}_{\gamma \Sigma \Sigma^{*}} =\frac{e\mu_{\Sigma \Sigma^{*}}}{2M_{N}}\bar{\Sigma}\gamma_{5}\sigma_{\mu \nu}\partial^{\nu}A^{\mu}\Sigma^{*}+ {\rm h.c.}, $

(4) $ \mathcal{L}_{K N\Sigma} = -{\rm i} g_{KN\Sigma}\bar{N}\gamma_{5}\Sigma K + {\rm h.c.}, $

(5) $ \mathcal{L}_{K^{*} N\Sigma^{*}} = {\rm i}\frac{g_{K^{*}N\Sigma^{*}}}{\sqrt{3}}\bar{K}^{*\mu}\bar{\Sigma}^{*}\gamma_{\mu}\gamma_{5}N + {\rm h.c.}, $

(6) $ \mathcal{L}_{K N\Sigma^{*}} = g_{KN\Sigma^{*}}\bar{K}\bar{\Sigma}^*N+{\rm h.c.}, $

(7) where
$ e(=\sqrt{4\pi\alpha}) $ is the elementary charge unit,$ A^{\mu} $ is the photon field, and$ \hat{e}\equiv (1+\tau_{3})/2 $ denotes the charge operator acting on the nucleon field.$ \hat{\kappa}_{N} \equiv \kappa_{p} \hat{e}+\kappa_{n}(1-\hat{e}) $ is the anomalous magnetic moment, and we take$ \kappa_{n}= -1.913 $ for the neutron [16].$ M_N $ and$ M_{\Sigma} $ denote the masses of the nucleon and the ground-state of the Σ hyperon, respectively. The strong coupling$ g_{KN\Sigma} $ is taken to be 4.09 from Refs. [46–48].$ g_{\gamma K K^{*}}=0.254\ \rm GeV^{-1} $ is determined from the experimental data of$\Gamma_{K^{*} \to K^+ \gamma}$ [16], and the value of$ g_{K^{*}N\Sigma^{*}}=-3.26-{\rm i}~0.06 $ is taken from Ref. [27]. In addition, the coupling$ g_{KN\Sigma^{*}}=8.74 $ GeV is taken from Ref. [37], and the transition magnetic moment$ \mu_{\Sigma\Sigma^*}=1.28 $ is taken from Ref. [28]②.In addition to the pseudoscalar coupling of Eq. (5), the vertex of
$ KN\Sigma $ may be described with the Lagrangian density of axial-vector coupling as follows [49, 50]$ \mathcal{L}_{KN\Sigma}=-\frac{g_{KN\Sigma}}{2M_N} \bar{N}\gamma_5\gamma_\mu (\partial^\mu K) \Sigma + {\rm h.c.}. $

(8) We discuss the difference between the two schemes in the next section. In this work, we perform the calculations with the Lagrangian density of Eq. (5) for the vertex of
$ KN\Sigma $ in the following.With the effective interaction Lagrangian densities given above, the invariant scattering amplitudes are defined as
$ \mathcal{M} =\bar{u}_{\Sigma^{*}}(p_{2},s_{\Sigma^{*}})\mathcal{M}^{\mu}_{h}u_{N}(k_{2},s_{p})\epsilon_{\mu}(k_{1},\lambda), $

(9) where
$ u_{\Sigma^{*}} $ and$ u_{N} $ represent the Dirac spinors,$ \epsilon_{\mu}(k_{1},\lambda) $ is the photon polarization vector, and the sub-index h corresponds to the different diagrams of Fig. 1. The reduced amplitudes$ \mathcal{M}^{\mu}_{h} $ are written as$ \mathcal{M}^{\mu}_{K^{*}} = \frac{g_{\gamma KK^{*}}g_{K^{*}N\Sigma^{*}}}{\sqrt{3}(t-M^2_{K^{*}})}\epsilon^{\alpha\beta\mu\nu}k_{1\alpha}k_{2\beta}\gamma_{\nu}\gamma_{5}, $

(10) $ \mathcal{M}^{\mu}_{K^-} = -2{\rm i} \frac{eg_{KN\Sigma^{*}}}{t-M^{2}_{K}}k_{2}^{\mu}, $

(11) $ \mathcal{M}^{\mu}_{\Sigma^-} = -{\rm i} \frac{e\mu_{\Sigma\Sigma^{*}}g_{KN\Sigma}}{2M_{n}(u-M^2_{\Sigma})}(\not q_{u}- M_{\Sigma})\sigma^{\mu \nu}k_{1\nu}, $

(12) $ \mathcal{M}^{\mu}_{n} = \frac{\kappa_{n}g_{KN\Sigma^{*}}}{2M_{n}(s-M_{n}^{2})} \sigma^{\mu\nu}k_{1\nu}(\not q_{s}+M_{n}). $

(13) To maintain gauge invariance in the full photoproduction amplitudes considered here, we adopt the amplitude of the contact term
$ \mathcal{M}^{\mu}_{c} = -{\rm i} eg_{KN\Sigma^{*}}\frac{p_{2}^{\mu}}{p_{2}\cdot k_{1}}, $

(14) for
$ \gamma n \to K^{+} \Sigma^{*-}_{1/2^-} $ .It is known that the Reggeon exchange mechanism plays a crucial role at high energies and forward angles [51–54]; thus, we adopt the Regge model when modeling the t-channel K and
$ K^{*} $ contributions by replacing the usual pole-like Feynman propagator with the corresponding Regge propagators as follows$ \begin{aligned}[b]& \frac{1}{t-M^{2}_{K}} \to \mathcal{F} ^{\rm Regge}_{K}\\ =& \left( \frac{s}{s_{0}^{K}}\right ) ^{\alpha_{K}(t)} \frac{\pi \alpha^{\prime}_{K}}{{\rm sin}(\pi \alpha_{K}(t))\Gamma(1+\alpha_{K}(t))}, \end{aligned} $

(15) $ \begin{aligned}[b]& \frac{1}{t-M^{2}_{K^{*}}} \to \mathcal{F}^{\rm Regge}_{K^{*}} \\= &\left( \frac{s}{s_{0}^{K^{*}}}\right ) ^{\alpha_{K^{*}}(t)-1} \frac{\pi \alpha^{\prime}_{K^{*}}}{{\rm sin}(\pi \alpha_{K^{*}}(t))\Gamma(\alpha_{K^{*}}(t))}, \end{aligned} $

(16) where
$ \alpha_{K}(t)=0.7\; {\rm GeV}^{-2}\times(t-M_{K}^{2}) $ and$\alpha_{K^{*}}(t)=1+ 0.83 {\rm GeV}^{-2}\times(t-M_{K^{*}}^{2})$ are the linear Reggeon trajectories. The constants$ s^{K}_{0} $ and$ s^{K^{*}}_{0} $ are determined to be 3.0 GeV$ ^{2} $ and 1.5 GeV$ ^{2} $ , respectively [55]. Here,$ \alpha'_K $ and$ \alpha'_{K^*} $ are the Regge-slopes.Then, the full photo-production amplitudes for the
$ \gamma n \to K^+ \Sigma^{*-}_{1/2^-} $ reaction can be expressed as$ \begin{aligned}[b] \mathcal{M}^{\mu} =& \left(\mathcal{M}_{K^-}^{\mu} + \mathcal{M}^{\mu}_{c}\right)\left(t-M_{K}^{2}\right) \mathcal{F} ^{\rm Regge}_{K}+ \mathcal{M}_{\Sigma^-}^{\mu}f_{u} \\ &+ \mathcal{M}_{K^{*}}^{\mu}\left(t-M_{K^{*}}^{2}\right) \mathcal{F}^{\rm Regge}_{K^*} +\mathcal{M}_{n}^{\mu}f_{s}, \end{aligned} $

(17) where
$ \mathcal{F} ^{\rm Regge}_{K} $ and$ \mathcal{F}^{\rm Regge}_{K*} $ represent the Regge propagators. The form factors$ f_{s} $ and$ f_{u} $ are included to suppress the large momentum transfer of the intermediate particles and describe their off-shell behavior because the intermediate hadrons are not point-like particles. For s-channel and u-channel baryon exchanges, we use the following form factors [40, 56]$ \begin{eqnarray} f_{i}(q_{i}^{2}) = \left[\frac{\Lambda_{i}^{4}}{\Lambda_{i}^{4} + (q_{i}^{2}-M_{i}^{2})^{2}}\right]^{2}, i=s,u \end{eqnarray} $

(18) where
$ M_{i} $ and$ q_{i} $ are the masses and four-momenta of the intermediate baryons, and$ \Lambda_{i} $ represents the cut-off values for the baryon exchange diagrams. In this study, we take$\Lambda_s= \Lambda_u=1.5$ GeV and discuss the results with different cut-offs.Finally, the unpolarized differential cross section in the center of mass (c.m.) frame for the
$ \gamma n \to K\Sigma^{*-}_{1/2^{-}} $ reaction reads as$ \begin{eqnarray} \frac{{\rm d}\sigma}{{\rm d}\Omega} = \frac{M_{N}M_{\Sigma^{*}}|\vec{k}_{1}^{\rm c.m.}||\vec{k}_{2} ^{\rm c.m.}|}{8\pi^{2}(s-M_{N}^{2})^{2}}\sum_{\lambda,s_{p},s_{\Sigma^{*}}}^{}|\mathcal{M}|^{2}, \end{eqnarray} $

(19) where s denotes the invariant mass square of the center of mass (c.m.) frame for
$ \Sigma^{*}_{1/2^{-}} $ photo-production, and${\rm d}\Omega = 2\pi {\rm d}{{\rm cos\theta} _{\rm c.m.}}$ , with$ \theta_{\rm c.m.} $ as the polar outgoing K scattering angle. Here,$ \vec{k}_1^{\rm c.m.} $ and$ \vec{k}_{2} ^{\rm c.m.} $ are the three-momenta of the photon and K meson in the c.m. frame,$ |\vec{k}_1^{\rm c.m.}| = \frac{s-M_N^2}{2\sqrt{s}}, $

(20) $ |\vec{k}_2^{\rm c.m.}| = \frac{\sqrt{\left[ s-(M_{\Sigma^*}+M_K)^2\right]\left[s-(M_{\Sigma^*}-M_K)^2\right]}}{2\sqrt{s}}. $

(21) -
In this section, we present our numerical results on the differential and total cross sections for the
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ reaction. The masses of the mesons and baryons are taken from the RPP [16], as given in Table 1. In addition, the mass and width of$\Sigma^*(1480)$ are$ M=1480\pm15 $ MeV and$ \Gamma=60\pm15 $ MeV, respectively [29].Particle Mass $/\rm MeV$ 

n 939.565 $ \Sigma^{-} $ 

1197.449 $ K^{+} $ 

493.677 $ K^{-} $ 

493.677 $ K^{*} $ 

891.66 Table 1. Particle masses used in this study.
First, we show the angle dependence of the differential cross sections for the
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ reaction in Fig. 2, where the center-of-mass energies$ W=\sqrt{s} $ varies from$ 2.0 $ to$ 2.8 $ GeV. The black curves labeled as "Total" are the results of all the contributions from the t-, s-, and u-channels and the contact term. The blue-dot and red-dashed curves represent the contributions from the u-channel Σ exchange and t-channel K exchange mechanisms, respectively. The magenta-dot-dashed and green-dot curves correspond to the contributions from the s-channel and t-channel$ K^{*} $ exchange diagrams, respectively, whereas the cyan-dot-dashed curves represent the contributions from the contact term. According to the differential cross sections, we find that the t-channel K meson exchange term plays an important role at forward angles for the process$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ , mainly because of the Regge effects of t-channel K exchange. The K-Reggeon exchange exhibits a steadily increasing behavior with$ {\rm cos}\theta_{\rm c.m.} $ and falls off drastically at very forward angles, which is consistent with the results of Ref. [28]. In the appendix, we show that the contribution from the t-channel K exchange is zero in the forward angle ($ \theta_{\rm c.m.}=0 $ ) and the backward angle ($ \theta_{\rm c.m.}=\pi $ ). In addition, the u-channel Σ exchange term mainly contributes to the backward angles. It should be emphasized that the contribution from the t-channel$ K^* $ exchange term is small and can be safely neglected for the process$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ , which is consistent with the results of Ref. [28].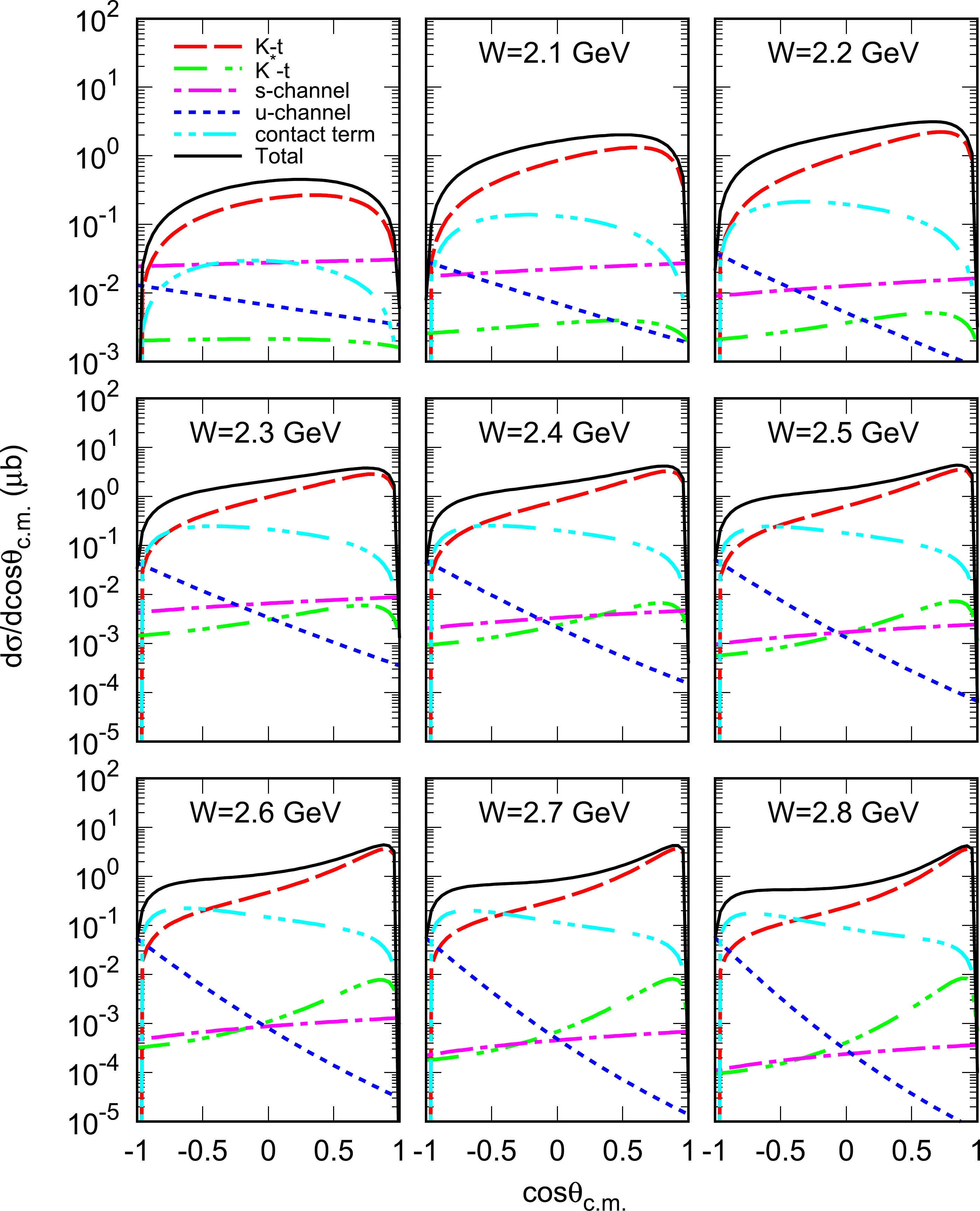
Figure 2. (color online)
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ differential cross sections as a function of$ \rm{cos \theta_{\rm c.m.}} $ are plotted for$ \gamma n $ -invariant mass intervals$ \left(\rm in\ \rm GeV \ units \right) $ . The black curve labeled as "Total" represent the results of all the contributions, including the t-, s-, and u-channels and the contact term. The blue-dot and red-dashed curves denote the contributions from the effective Lagrangian approach u-channel Σ exchange and t-channel K exchange mechanisms, respectively. The magenta-dot-dashed and green-dot-dashed curves represent the contributions of the s-channel and t-channel$ K^{*} $ exchange diagrams, respectively, whereas the cyan-dot-dashed curves represent the contributions of the contact term.As mentioned in Sec. II, in addition to the pseudoscalar coupling of Eq. (5), the vertex of
$ KN\Sigma $ may also be described with the Lagrangian density of axial-vector coupling [Eq. (8)]. We also present the contribution from the u-channel Σ exchange with the Lagrangian densities of Eqs. (5) and (8) in Fig. 3; we find that both of them contribute to the backward angles. Because the contribution from the u-channel is small, it is expected that either pseudoscalar coupling or axial-vector coupling for$ KN\Sigma $ does not affect our results significantly.
Figure 3. (color online)
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ differential cross sections with only the contribution from u-channel Σ exchange. The magenta-dot-dashed curves represent the results obtained with the axial-vector coupling of Eq. (8), and the blue-dotted curves represent the results obtained with the pseudoscalar coupling of Eq. (5).In addition to the differential cross sections, we also calculate the total cross section of the
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ reaction as a function of the initial photon energy. The results are shown in Fig. 4. The black curve labeled as "Total" represents the results of all the contributions, including the t-, s-, and u-channels and the contact term. The blue-dot and red-dashed curves represent the contributions from the u-channel Σ exchange and t-channel K exchange mechanisms, respectively. The magenta-dot-dashed and green-dot curves represent the contributions of the s-channel and t-channel$ K^{*} $ exchange diagrams, respectively, whereas the cyan-dot-dashed curve represents the contribution of the contact term. For the$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ reaction, its total cross section attains a maximum value of approximately$ 4.2 ~\mu $ b at$ E_{\gamma}=2.4 \ \rm GeV $ . It is expected that$ \Sigma^*(1480) $ can be observed by future experiments in the process$ \gamma n \to K^{+} \Sigma^{*-}\left(1480\right) \to \Sigma^{-}\pi^{0}/\Sigma^{0}\pi^{-}/\Sigma^{-}\gamma $ .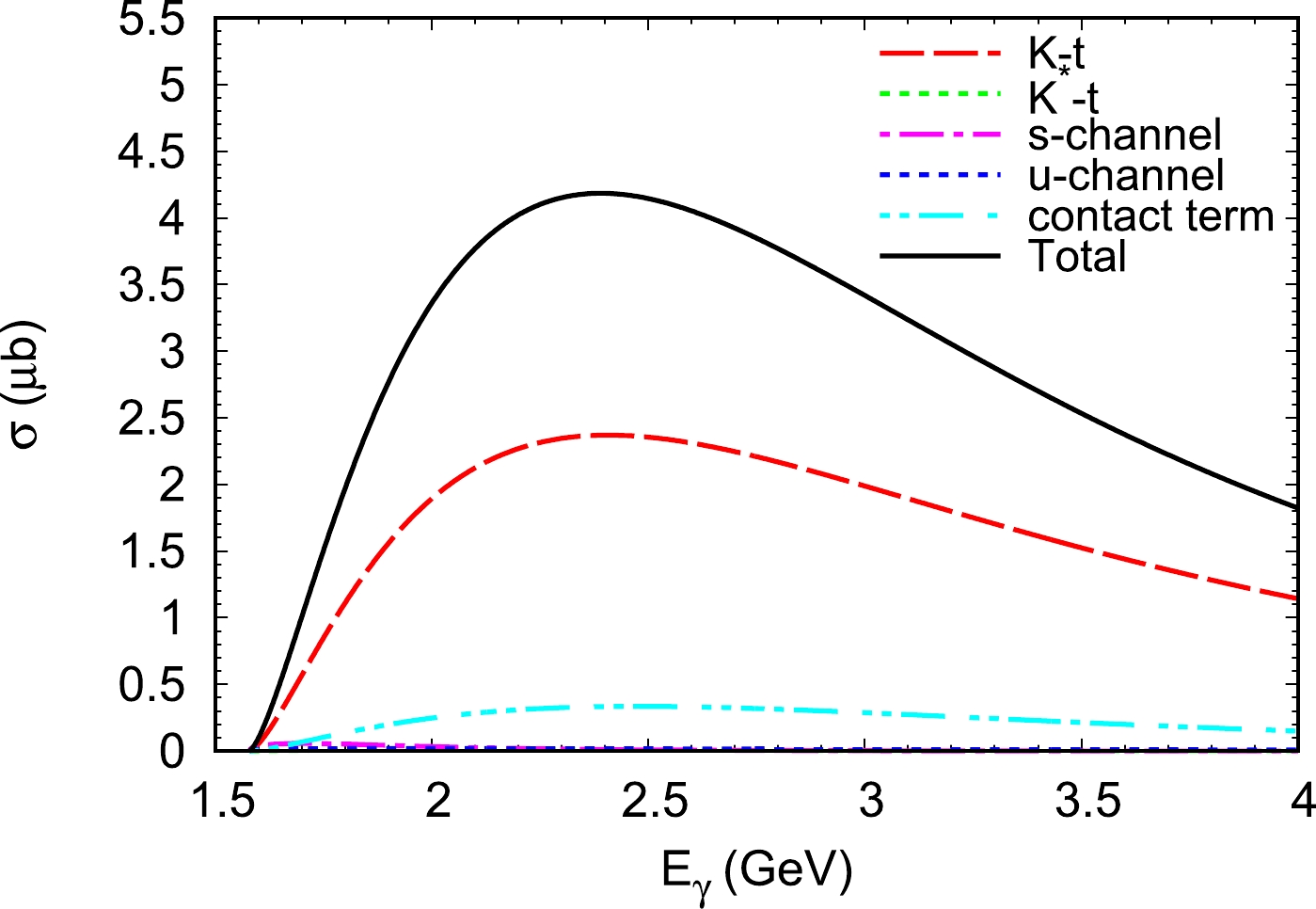
Figure 4. (color online) Total cross section for
$ \gamma n \to K^{+}\Sigma^{*}_{1/2^-} $ is plotted as a function of the lab energy$ E_{\gamma} $ . The black curve labeled as "Total" represents the results of all the contributions, including the t-, s-, and u-channels and the contact term. The blue-dot and red-dashed curves represent the contributions from the effective Lagrangian approach u-channel Σ exchange and t-channel K exchange mechanisms, respectively. The magenta-dot-dashed and green-dot curves represent the contributions of the s-channel nucleon term and t-channel$ K^{*} $ exchange diagrams, respectively, whereas the cyan-dot-dashed curve represents the contribution of the contact term.Finally, we show the total cross section for
$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ with the cut-off$ \Lambda_{s/u}=1.2 $ ,$ 1.5 $ , and$ 1.8 $ GeV in Fig. 5. We find that the total cross sections are weakly dependent on the value of the cut-off. Because the precise couplings of$\Sigma^*(1480)$ are still unknown, future experiments would benefit from constraining these couplings if the state$\Sigma^*(1480)$ is confirmed. -
The lowest
$ \Sigma^{*-}_{1/2^-} $ is far from established, and its existence is important to understand low-lying excited baryons with$ J^P=1/2^- $ . There are many experimental hints of$ \Sigma^*(1480) $ , as listed in the previous version of the RPP. We propose to search for this state in the photoproduction process to confirm its existence.Assuming that the
$ J^{P} = 1/2^{-} $ low lying state$ \Sigma^*\left(1480\right) $ has a sizeable coupling to$ \bar{K}N $ according to the study of Ref. [37], we phenomenologically investigate the$ \gamma n \to K^{+} \Sigma^{*-}_{1/2^-} $ reaction by considering the contributions from the t-channel$ K/K^* $ exchange term, s-channel nucleon term, u-channel Σ exchange term, and contact term within the Regge-effective Lagrangian approach. The differential and total cross sections for these processes are calculated with our model parameters. The total cross section of$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ is approximately$4.2 ~ \mu$ b around$ E_{\gamma}=2.4 \ \rm GeV $ . We encourage our experimental colleagues to further measure the$ \gamma n \to K^{+}\Sigma^{*-}_{1/2^-} $ process. -
In this appendix, we show that the contributions from the t-channel K exchange in the forward angle (
$ \theta=0 $ ) and backward angle ($ \theta=\pi $ ) are zero. In the c.m frame, the four-momenta of the outgoing K are$ k_2^0 = \frac{s+m^2_K-M^2_{\Sigma^*}}{2\sqrt{s}}, \tag{A1} $

$ k_2^1 = |\vec{k}_2^{\rm c.m.}| {\rm sin}\theta, \tag{A2}$

$ k_2^2 = 0, \tag{A3} $

$ k_2^3 = |\vec{k}_2^{\rm c.m.}| {\rm cos}\theta, \tag{A4} $

where
$ \vec{k}_2^{\rm c.m.} $ is the three-momentum of K [Eq. (21)]. The polarization vectors of the photon with momentum$ \vec{k}_1^{\rm c.m.} $ in the helicity basis are$ \epsilon (\vec{k}_1^{\rm c.m.}, \lambda=\pm 1) = \pm \frac{1}{\sqrt{2}}\left( \begin{array}{c} 0 \\ 1 \\ \mp {\rm i} \\ 0 \end{array} \right), \tag{A5}$

$ \epsilon (\vec{k}_1^{\rm c.m.}, \lambda=0) = 0. \tag{A6} $

We can easily find that
$ k_2^\mu \epsilon_\mu(\vec{k}_1^{\rm c.m.},\lambda=0,\pm 1)=0 $ for$\theta= 0,\pi$ , which implies that the amplitude of Eq. (11) for t-channel K exchange will be zero in the forward angle ($ \theta=0 $ ) and backward angle ($ \theta=\pi $ ).
Photo-production of lowest ${\boldsymbol\Sigma^{*}_{\bf 1/2^-}}$ state within the Regge-effective Lagrangian approach
- Received Date: 2023-01-20
- Available Online: 2023-05-15
Abstract: Because the lowest







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




























 DownLoad:
DownLoad: