-
In ultra-high energy collisions, the perturbative quantum chromodynamics predict a rapid increase in gluon density within the hadron with an increasing energy or decreasing momentum fraction due to the gluon splitting effects. However, the gluon density does not increase infinitely owing to the non-linear effect like that in gluon recombination. Consequently, the equilibrium between gluon splitting and recombination leads to the formation of saturated gluonic matter, which is also known as color glass condensate (CGC) [1]. Searching for the signal of CGC (gluon saturation) is one of the most crucial goals in high energy nuclear physics. In the experimental aspect, a large number of experiments have been devoted to finding substantial evidences for the existence of gluon saturation. For example, the H1 and ZEUS collaborations at HERA have measured the inclusive and diffractive structure functions. It has been shown that the structure function satisfies the geometric scaling effect [2], which provides strong evidence of the gluon saturation. On the theoretical side, there has been tremendous progress toward the deep understanding of higher-order corrections to the CGC evolution equations in the last fifteen years. The next-to-leading order (NLO) Balitsky-Kovchegov (BK) and JIMWLK equations were derived by considering quark loops [3, 4], gluon loops [5], Sudakov effects [6], and framework dependence [7, 8] (projectile or target rapidity representation).
Several NLO dipole amplitudes are obtained by solving the aforementioned NLO BK equations. These amplitudes allowed for rather successful applications to describe the small-x data at HERA [9–12], RHIC [13], and LHC [14, 15]. Unfortunately, it has been found that the DGLAP mechanism can also provide a similar description for the same group of data. For instance, the geometric scaling phenomenon, i.e., dipole amplitude
$ N(r,x) $ , is a function of a single variable$ rQ_s(x) $ instead of two independent variables r and x [16], which can be simultaneously explained by the CGC and DGLAP mechanisms [17]. Thus, it is very hard to distinguish the CGC evolution from the DGLAP evolution. It is useful to improve the precision of the CGC theory as much as possible, including the impact parameter dependence. We know that all the aforementioned dipole amplitudes do not include the impact parameter dependence, because the impact parameter is a non-perturbative effect and is impossible to take into account by analytically solving the BK equation. Meanwhile, obtaining the numerical solution to the impact parameter dependent BK equation is extremely time-consuming. Alternatively, the impact parameter dependence can be analyzed via modeling.There are two popular approaches to model the impact parameter dependence in the literature. First, the impact parameter is introduced into the dipole amplitude through the saturation scale
$ Q_s(x,b) $ , which is known as the b-CGC model [18]. Second, the dipole amplitude includes the impact parameter via a proton profile density function, which is called the IPSat model [19, 20]. It has been found that the impact parameter significantly improves the predictive power of the CGC theory. However, a recent study showed that an impact parameter dependent non-saturation (IPnonsat) model can give a similar quality description of a group of HERA data to the IPsat model [21]. We trace the reason back to the exponent of the dipole amplitude and find that the issue comes from the transition regime between dilute and dense areas. Inspired by the anomalous dimension improving the GBW and MV models in Ref. [22], we introduce the anomalous dimension into the IPSat model in order to improve the transition behavior of the dipole amplitude. The anomalous dimension improved impact parameter dependent model is applied to study the transverse momentum distribution of neutral and charged hadrons in high energy proton-proton (pp) collisions at LHC energies. The results indicate that our improved model agrees more closely with the data than the original IPSat model. Moreover, we study the nuclear modification factor ($ R_{pA} $ ) in proton-lead collisions in order to test the robustness of the improved model. The outcomes show that our anomalous dimension improved dipole amplitude becomes favorable by the$ R_{pA} $ data, see Sec. IV. -
In this section, we give a brief review of the
$ k_{t} $ factorization formalism to calculate the single inclusive hadron production in CGC effective field theory. For the single inclusive particle production process, the relationship between the longitudinal momentum fraction x and the rapidity y is$ x= (p_T/\sqrt{s_{NN}})\exp(\pm y) $ , where$ p_{T} $ is the transverse momentum of the produced particle and$ \sqrt{s_{NN}} $ is the collision energy per nucleon. At the LHC energies, when the particle is measured at the middle rapidity, the longitudinal momentum fraction for both the projectile and target is in the small-x range ($ x\leq 0.01 $ ). Thus, the$ k_{t} $ factorization formalism based on the CGC framework has prodigious superiority at LHC energies [14].According to the CGC
$ k_{t} $ factorization, to calculate the hadron production, one needs to know the gluon distribution produced through the hard process. The$ k_{t} $ factorization formalism of gluon production was first proposed in Ref. [23] and was extended in Ref. [24] by Kovchegov and Tuchin in the leading$ \log (1/x) $ and fixed coupling approximations. In recent years, many efforts have been made to describe the hadron production by using the$ k_{t} $ factorization approach [14, 25–27] (and the references therein). In particular, the$ k_{t} $ factorization has been improved significantly by including the higher order corrections [28]. In addition, the predictions calculated in the framework of the hybrid approach with the NLO corrections [29–31] can help our understanding of the inclusive hadron production in saturation physics. In terms of the$ k_{t} $ factorization, the number of inclusive gluons with transverse momentum$ p_T $ and y rapidity is given by [32–34]$ \begin{aligned}[b] \frac{ {{\rm{d}}} N^{A+B \rightarrow g+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}=&K\frac{2}{\sigma C_{F}} \frac{1}{p_{T}^{2}}\int {{\rm{d}}}^{2} \mathbf{b} {{\rm{d}}}^{2} k_{T} \frac{\alpha_{s}(Q)}{4}\\&\times \phi_{A}\left(\frac{\left|p_{T}+k_{T}\right|}{2}, x_{1}, \mathbf{R_T}\right)\\&\times \phi_{B}\left(\frac{\left|p_{T}-k_{T}\right|}{2}, x_{2}, \mathbf{R_T-b}\right), \end{aligned} $

(1) where
$ x_{1,2} = (p_T/\sqrt{s_{NN}})\exp(\pm y) $ and$ C_F = (N_c^2 - 1)/2N_c $ , with the number of colors being$ N_c=3 $ . In Eq. (1),$ \mathbf{b} $ is the impact parameter in an$ A+B $ collision, and$ \mathbf{R_T} $ is the impact parameter of the gluon relative to the center of the projectile A. In this paper, we focus on the$ pp $ and$p{\rm Pb}$ collisions. Thus, A denotes a proton, and B denotes a proton or lead. The σ is the effective interaction area, which is used to transfer the differential cross section to the multiplicity distribution. The$ k_{T} $ is the transverse momentum of the incoming parton inside the projectile, which interacts with the partons inside the target via gluon exchange and then produces the intermediate gluons with transverse momentum$ p_T $ .The factor K in Eq. (1) is a free parameter that accounts for the contributions from both the higher order corrections and all other possible dynamic effects [14]. Generally, one can obtain the K factor by fitting the experimental data. However, the remaining factors entering the
$ k_{t} $ factorization formalism affect the value of the K factor. In addition, the K value only changes the normalization and does not modify the shape of the$ p_{t} $ distribution. Therefore, we fix the K factor by matching the theoretical value with the experimental data at a fixed data point in this work.In Eq. (1),
$ \phi(k,x,\mathbf{b}) $ is the unintegrated gluon distribution (UGD), which reflects the density of gluons in the proton/nucleus. The$ \phi(k,x,\mathbf{b}) $ is a function of the longitudinal momentum fraction x, transverse momentum k, and impact parameter$ \mathbf{b} $ . We note that the UGD is a key ingredient for calculating the single inclusive hadron production, because it includes the information about the strong interaction between the color dipole (quark-antiquark pair) and target.It should be noted that the prescription for dealing with QCD coupling
$ \alpha_{s} $ in this work differs slightly from the formalism in Ref. [24]. In the original$ k_{t} $ factorization formalism,$ \alpha_{s} $ is a fixed constant. It is reasonable as the original$ k_{t} $ factorization formalism is at leading order accuracy. However, it is known that the running coupling effect, which is one of the next-to-leading order effects, is a dominant factor suppressing the evolution speed of the CGC system, which leads to rather good description of the HERA data [12]. This implies that the QCD coupling$ \alpha_{s} $ in Eq. (1) needs to be running with the scale Q. Furthermore, the QCD coupling in the UGDs has to be running with the scale Q. Following Ref. [14], the scale Q in$ \alpha_{s} $ is chosen to be run with the momentum$ Q = \max\{|p_T + k_T|/2, |p_T - k_T|/2\} $ . -
In this section, we introduce the key ingredients in the calculation of the single inclusive hadron production. First, we give a brief introduction of the UGDs. Then, we present an anomalous dimension improved IPSat model that will be used in the computation of the UGDs.
-
The UGD is a fundamental ingredient in the CGC factorization method. In the small-x region, the UGD can be used to describe many processes as it contains the most important information about strong interactions. There are two different proposals to define the UGD in the literature. The first one is the Weizs
$ \ddot{a} $ cker-Williams (WW) gluon distribution, which can be derived by using the WW approximation [35–37]. The other one is the dipole gluon distribution, which is defined as the Fourier transform of the dipole cross section [38, 39]. It should be noted that the WW gluon distribution can be interpreted as the number of gluons inside the target hadron, but the dipole gluon distribution has no clear partonic meaning. Which of these two gluon distributions is more relevant in a certain process has been a longtime puzzle that has been widely studied [32, 40, 41]. Refs. [40, 41] give a detailed description of the application of the gluon distribution for several processes. For the inclusive gluon production process, the probed gluon distribution is the dipole gluon distribution; thus, we shall use it as the UGD in our simulation. The dipole gluon distribution is given by [38, 39]$ \begin{equation} \phi(k,x,\mathbf{b})=\frac{C_{F}}{\alpha_{s}(k)(2 \pi)^{3}} \int {{\rm{d}}}^{2} \mathbf{r} {\rm e}^{-{\rm i} \mathbf{k} \cdot \mathbf{r}} \nabla_{\mathbf{r}}^{2} \mathcal{N}_{A}\left(r, x, \mathbf{b}\right), \end{equation} $

(2) where
$ \mathcal{N}_{A}\left(r, x, b\right) $ is the gluon dipole forward scattering amplitude in the adjoint representation of${S U}(3)$ . Generally,$ \mathcal{N}_{A}\left(r, x, b\right) $ can be found from the JIMWLK evolution equation. However,$ \mathcal{N}_{A}\left(r, x, b\right) $ does not need to come from the multiple rescatterings. In the large-$ N_c $ limit,$ \mathcal{N}_{A}\left(r, x, b\right) $ can be expressed in terms of the dipole amplitude in the fundamental representation [42, 43]:$ \begin{equation} \mathcal{N}_{A}(r, x, \mathbf{b})=2 \mathcal{N}(r, x, \mathbf{b})-\mathcal{N}^{2}(r, x, \mathbf{b}), \end{equation} $

(3) where
$ \mathcal{N}(r, x, \mathbf{b}) $ is the dipole scattering amplitude in the fundamental representation; in other words, it is a quark dipole amplitude. The relationship in Eq. (3) comes from the fact that a gluon dipole can be thought of as a pair of quark dipoles in the large-$ N_c $ limit [42, 43]. It should be noted that similar to Eq. (1), the QCD coupling$ \alpha_{s} $ in Eq. (2) is chosen to run with the momentum in order to achieve a consistent treatment of the running coupling in the$ k_t $ factorization formalism.From Eq. (2), one can see that the UGD is a two-dimensional Fourier transform of the gluon dipole scattering amplitude. Therefore, the description ability of the UGD depends on the accuracy of the dipole scattering amplitude. Usually, the dipole scattering amplitude in Eq. (3) can be obtained by solving the CGC evolution equations, such as the BK and JIMWLK equations. Unfortunately, the CGC evolution equations cannot be solved analytically [44]; in other words, one does not have the analytic dipole scattering amplitude. There are two ways to obtain the dipole scattering amplitude in the literature. The first one is to numerically solve the CGC evolution equation. However, this is quite complicated and extremely time-consuming because the CGC evolution is an integrated-differential equation. The second is to model the dipole amplitude inspired by the leading order BK equation, e.g., the GBW [45] and IIM [46] models. These two models significantly simplify the application of the CGC theory to describe the measurements at HERA, RHIC, and LHC energies. It is known that the GBW and IIM models can only give a qualitative description of the experimental data, as they are missing the higher order corrections and non-perturbation contributions. According to the GBW and IIM models, the impact parameter dependent models were established, i.e., the IPSat and b-CGC models, in order to include the non-perturbation effects. It has been shown that the impact parameter dependent CGC models improve the predictive power of the CGC theory, especially the IPSat model because of the DGLAP evolution included in it. In this work, we shall modify the IPSat model by including the anomalous dimension, which leads to a rather successful description of the experimental data. For details, see Sec. IV.
-
From the above description, we know that the dipole scattering amplitude is essential for calculating the single inclusive hadron production. In this subsection, we shall modify the original IPSat model by including the anomalous dimension, which leads to a significant improvement of the predictive power of the model.
As we know, obtaining the numerical solution of the impact parameter dependent CGC evolution equation is a challenge, as the computation is very complicated and time-consuming. However, some phenomenological models can effectively introduce the impact parameter dependence and achieve great success in describing the experimental data. One of these models is the IPSat model, which is a refined version of the GBW model [47] in which the DGLAP evolution effects are included. To show the reason why we modify the IPSat model, we first give a brief review of the development of the GBW model.
The GBW model is proposed to describe the saturation phenomenon in the inclusive and diffractive deep-inelastic scattering process. In the GBW model, the differential cross section of a quark dipole is given by [16, 45]
$ \begin{equation} \frac{ {{\rm{d}}}\sigma_{q\bar q}}{ {{\rm{d}}}^2 \mathbf{b}}=2\mathcal{N}(r, x)= 2\left[1-\mathrm{exp}\left(-r^2Q_s^2(x)/4\right)\right], \end{equation} $

(4) where the saturation scale is
$ Q_s^2(x) = (x_0/x)^{\lambda} $ GeV$ ^2 $ with two free parameters$ x_0 $ and λ. From Eq. (4), one can clearly see that the quark dipole amplitude$ N(r, x) $ approaches unity at a large dipole size$ r \gg 1/Q_s $ . The GBW model is a simple model but describes the physics in the deep saturation regions. Thus, it is widely used to describe the data in HERA energies. Moreover, the GBW model is normally used as the initial condition for numerically solving the evolution equations because of its simplicity. However, the GBW model has two grievous shortcomings. The first one is that the original GBW model only gives a better description for medium photon virtuality [18]. The other one is that the GBW model ignores the impact parameter dependence, which is essential for illustrating the physical phenomenon observed in the non-perturbation regions [10]. To solve the deviation at large photon virtuality, one can introduce the anomalous dimension γ into the quark dipole amplitude:$ \begin{equation} \mathcal{N}(r, x)= 1-\mathrm{exp}\left[-\left(r^2Q_s^2(x)/4\right)^{\gamma}\right]. \end{equation} $

(5) Here γ is a free parameter, which can be determined by fitting the experimental data. The original form will be recovered by setting
$ \gamma=1 $ . The anomalous dimension γ plays a special role in controlling the steepness of the fall-off trend of the quark dipole amplitude as the dipole size decreases [9]. It has been shown that the anomalous dimension improved GBW model together with the heavy quark contributions gives a reasonable description of the structure function data [22].The impact parameter dependence is, for the first time, introduced by assuming that the quark dipole differential cross section is a function of the transverse profile of the proton [19]:
$ \begin{equation} \frac{ {{\rm{d}}}\sigma_{q\bar{q}}}{ {{\rm{d}}}^2 \mathbf{b}} = 2\left[1-\exp\left(-\frac{\pi^2}{2N_c}r^2\alpha_s(\mu^2)xg(x,\mu^2)T(\mathbf{b})\right)\right], \end{equation} $

(6) where
$ T(\mathbf{b}) $ is the proton shape function. It is assumed that$ T(\mathbf{b}) $ has a Gaussian dependence on$ \mathbf{b} $ $ \begin{equation} T(\mathbf{b}) = \frac{1}{2\pi B_G}\mathrm{exp}\left(-\frac{b^2}{2B_G}\right), \end{equation} $

(7) where
$ B_G $ is a free parameter that represents the proton width. We would like to point out that Eq. (6) together with the Gaussian profile function of Eq. (7) is known as the IPSat model. In Eq. (6), the QCD coupling$ \alpha_{s} $ is chosen to run with the scale$ \mu^2 $ , which is related to the quark dipole size through$ \mu^2=4/r^2+\mu_0^2 $ , where$ \mu_0 $ is treated as a free parameter. Another component in the IPSat model is the gluon density$ xg(x,\mu^2) $ , which satisfies the leading order DGLAP evolution equation:$ \begin{equation} \frac{\partial xg(x,\mu^2)}{\partial\ln\mu^2} = \frac{\alpha_s(\mu^2)}{2\pi}\int_x^1 \frac{ {{\rm{d}}}{z}}{z}\;P_{gg}(z)xg\left(\frac{x}{z},\mu^2\right), \end{equation} $

(8) where
$ P_{gg}(z) $ is the splitting function of the gluon. Note that the gluon density in Eq. (8) has the same scale$ \mu^2 $ as the QCD coupling. To determine the quark dipole amplitude at a given dipole size, one needs to specify the initial gluon density at the start scale$ \mu_0^2 $ , which is given by the parameterized form$ \begin{equation} xg(x,\mu_0^2) = A_g\,x^{-\lambda_g}\,(1-x)^{5.6}, \end{equation} $

(9) where
$ A_g $ and$ \lambda_g $ are free parameters.The IPSat model achieves great improvement compared with the original GBW model because it includes the impact parameter dependence and DGLAP evolution effect. Therefore, the IPSat model is widely used to describe experimental data. For instance, it was used to study the single inclusive hadron production at RHIC and LHC [47, 48]. However, the IPSat model suffers a shortcoming in understanding the nuclear modification factor
$ R_{pA} $ . The authors in Ref. [48] used both the IPSat model and the running coupling Balitsky-Kovechegov (rcBK) equation to predict$ R_{pA} $ . They found that the results from the IPSat model increase unexpectedly fast when approaching unity compared with the results from the rcBK equation. This is because of the larger twist (anti-shadowing) contributions in the IPSat model, which disappear quickly at large momentum [48]. In the GBW case, it is known that the modification from the anomalous dimension makes the GBW model more favored by the experimental data at large photon virtuality. Inspired by the improvement of the GBW model, we propose that the quark dipole cross-section also has a dependence on the anomalous dimension:$ \begin{equation} \frac{ {{\rm{d}}}\sigma_{q\bar{q}}}{ {{\rm{d}}}^2 \mathbf{b}} = 2\left\{1-\exp\left[-\left(\frac{\pi^2}{2N_c}r^2\alpha_s(\mu^2)xg(x,\mu^2)T(\mathbf{b})\right)^{\gamma}\right]\right\}. \end{equation} $

(10) Now, the quark dipole cross-section, i.e., Eq. (10), includes both the impact parameter dependence and the anomalous dimension, which is called as IPSat-γ model in this work. Using Eq. (10), together with the
$ k_{t} $ factorization formalism, we can calculate the observables in the single inclusive hadron production processes at LHC energies. We find that the IPSat-γ model gives a better description of the experimental data than the IPSat model. -
In order to test the superiority of the IPSat-γ model, we calculate the single inclusive hadron production and compare it with the experimental data for
$ pp $ and$p{\rm Pb}$ collisions at LHC energies. First, we show the numerical results of the transverse momentum distributions in$ pp $ collisions at different energies and compare them with the experimental data. Then, we apply the anomalous dimension improved IPSat model to the$p{\rm Pb}$ collision cases and describe the single inclusive hadron production. Finally, we present results of the nuclear modification factor$ R_{pA} $ calculated via our IPSat-γ model. -
In this subsection, we present the results for the single inclusive hadron production in
$ pp $ collisions in the framework of$ k_T $ -factorization based on the IPSat-γ model. In order to obtain the hadron production from the gluon production in Eq. (1), we assume that the final charged hadron distribution is proportional to the gluon distribution:$ \begin{equation} \frac{ {{\rm{d}}} N^{p+p \rightarrow h+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}=\frac{2}{3} \kappa_g \frac{ {{\rm{d}}} N^{p+p \rightarrow g+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}, \end{equation} $

(11) where
$ \kappa_g $ is the gluon multiplication factor. In Eq. (11), the factor$ 2/3 $ is the proportion of the total hadrons that are final charged hadrons. Following Ref. [14],$ \kappa_g $ is set as a fixed value$ \kappa_g =5 $ .Alternatively, the transverse momentum distribution of hadron production can be calculated by using the fragmentation function (FF) approach. In this factorization formalism, the single inclusive hadron production is given by the convolution of the gluon production with the FFs:
$ \begin{equation} \frac{ {{\rm{d}}} N^{p+p \rightarrow h+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}=\int \frac{{\rm d} z}{z^{2}} D_{g}^{h}\left(z=\frac{p_{T}}{k_{T}}, Q\right) \frac{{\rm d} N^{p+p \rightarrow g+X}}{{\rm d} y {\rm d}^{2} k_{T}}, \end{equation} $

(12) where
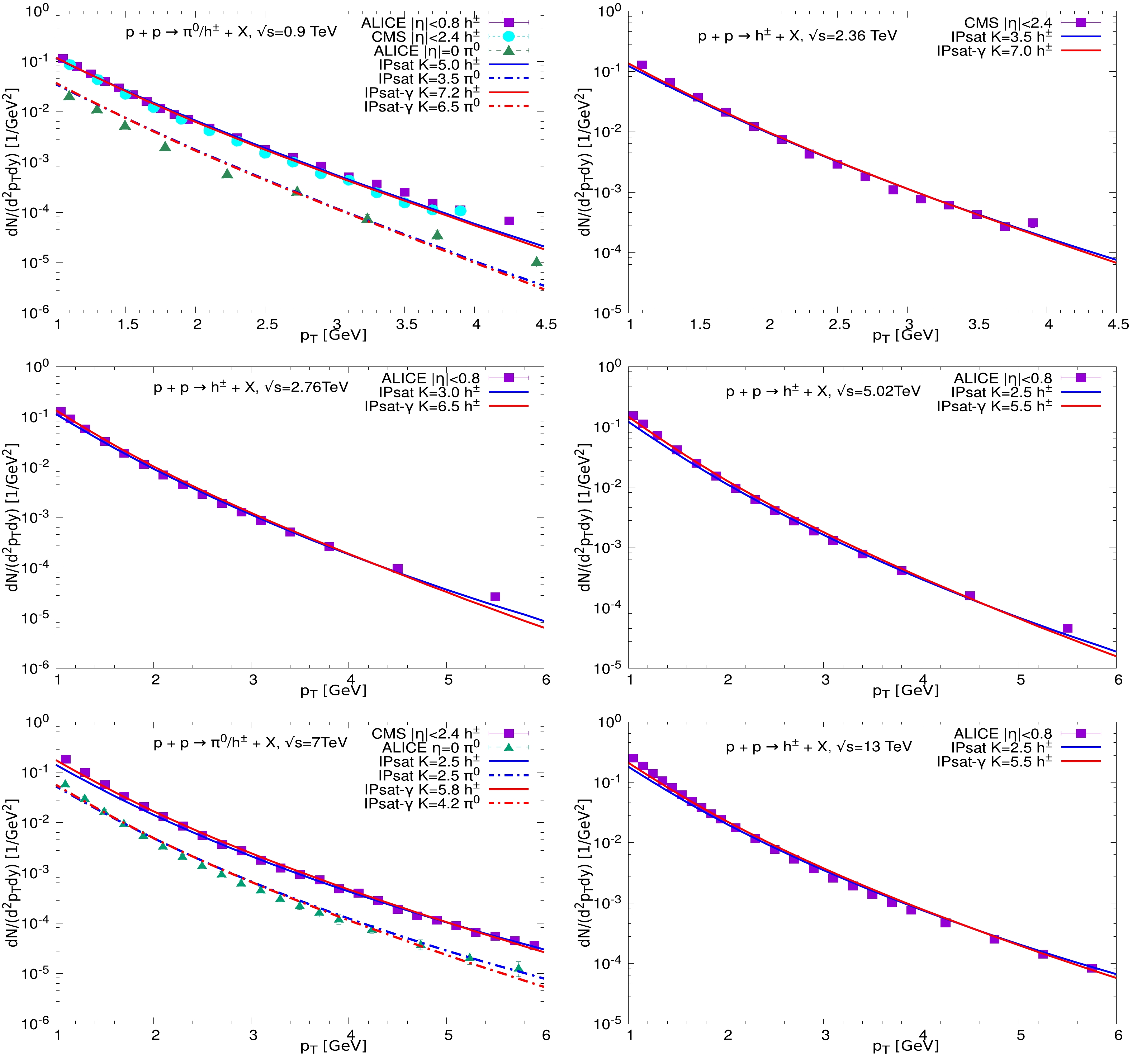
$ k_{T} $ and$ p_{T} $ are the transverse momenta of the gluon and the final hadron, respectively. The$ D_{g}^{h}\left(z=\dfrac{p_{T}}{k_{T}}, Q\right) $ is the fragmentation function, which describes the probability of a gluon splitting into a final hadron with longitudinal momentum fraction z.In Fig. 1, we show the transverse momentum distribution of charged hadrons and neutral pions in
$ pp $ collisions at$ \sqrt s = $ 0.9, 2.36, 2.76, 5.02, 7, and 13 TeV. The theoretical results are calculated using Eq. (11), and the experimental data are taken from ALICE and CMS collaborations [49–54]. Hereinafter, the anomalous dimension is set as$ \gamma=1.07 $ (we will discuss this in detail later). To demonstrate the significance of the anomalous dimension, we also give the results from the original IPSat model for comparison. In Fig. 1, the red curves denote the results calculated via IPSat-γ model, and the blue curves denote the results computed via the original IPSat model. The dashed curves represent the results for the neutral pion production. In the$ k_T $ -factorization formalism, there is a factor K in the hadron production; see Eq. (1). Following Ref. [14], we adjust the value of K to match the experimental data for the medium transverse momentum to simplify the simulation. Thus, the results from both models are in good agreement with the experimental measurements for the medium transverse momentum, as we can see in Fig. 1. We would like to note that the K factor is adjusted to match a fixed point of transverse momentum, which may lead to a slightly large K. Although one can fit the experimental data to obtain a suitable K factor, this is unnecessary, as the K factor only affects the normalization of the distribution and does not modify the shape. In addition, the NLO corrections can change both the shape and magnitude of the cross-sections. Because this paper is focused on the effects of the anomalous dimension, the contributions from both the higher order corrections and all other possible dynamic effects are absorbed into the K factor. From Fig. 1, we can see that the IPSat-γ model gives a better description of the data in low transverse momentum regions for all energies because the anomalous dimension provides effective control of the slope of the dipole scattering amplitude.It should be noted that both the anomalous dimension and the K factor will affect the prediction of the hadron distribution. As mentioned above, the anomalous dimension controls the shape of the distribution; however, the value of K only changes the normalization and does not modify the shape of the distribution. We confirmed that the distribution shape is very sensitive to changes in γ. A small shift in γ can lead to a large change in the distribution. In our simulation, K is a free parameter, and its value is adjusted to match the experimental data for the medium transverse momentum. Our main focus is to investigate the effect of the anomalous dimension on the hadron production. Therefore, it is better to set the anomalous dimension as a fixed value in order to verify the improvement of the ability to describe experimental data. We find that
$ \gamma=1.07 $ gives a global agreement with the experimental data.To test the fragmentation function dependence of the factorization formalism with the IPSat-γ dipole amplitude, we calculate the hadron production by using the two frequently-used FFs: KKP [55] and DSS [56]. It should be noted that the scale in the FFs can affect the spectra. Fortunately, this influence can be absorbed into the K factor. In this work, we set the transverse momentum as the scale of the FFs. Moreover, the low limit of the integral over the longitudinal momentum fraction z in Eq. (12) is restricted to
$ 0.05 $ in order to avoid the momentum sum rule violation.In Fig. 2, we show the transverse momentum distributions of charged hadrons in
$ pp $ collisions at the same energies as Fig. 1 but with two different FFs (KKP and DSS). The red and green curves denote the results calculated via IPSat-γ model with KKP and DSS FFs, respectively. At first glance, it seems that both the KKP and DSS can give a similarly good description for the charged hadron productions, which indicates that the IPSat-γ model is robust in the$ k_T $ -factorization framework despite different FFs. One of the key reasons is that the difference between the KKP and DSS can be absorbed into the K factor. However, if one takes a close-up view of Fig. 2, it can be seen that the results from the DSS FF are slightly more favored by the experimental data at large$ p_t $ , because the DSS FF is harder than KKP FFs. This outcome is consistent with the findings in Refs. [14, 57].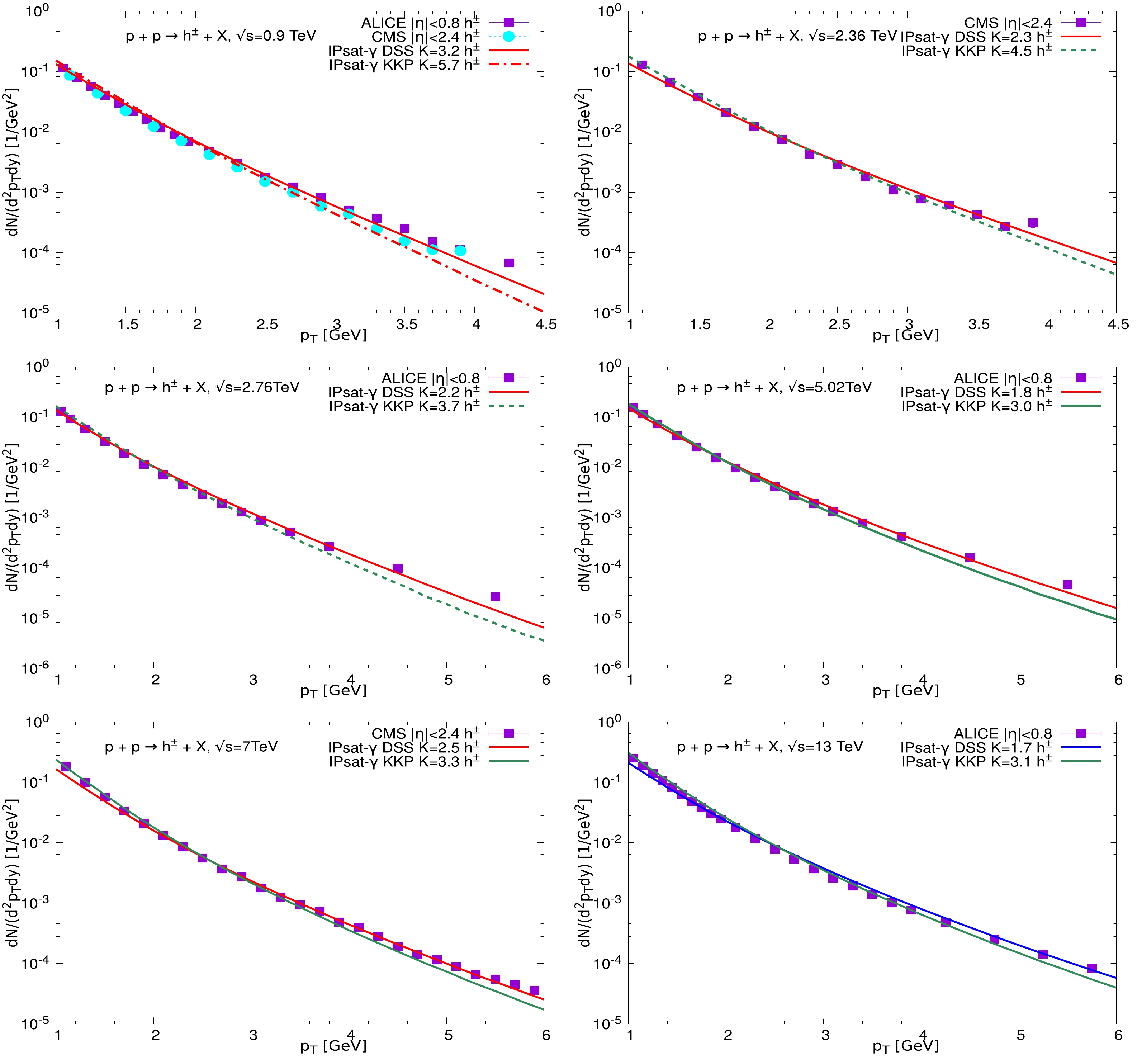
Figure 2. (color online) Transverse momentum distributions of charged hadrons based on the IPSat-γ model obtained using the FF approach for
$ pp $ collisions at$ \sqrt s = $ 0.9, 2.36, 2.76, 5.02, 7, and 13 TeV, respectively. The experimental data are taken from the ALICE and CMS collaborations [49–54]. -
At LHC energies, the observations from
$p{\rm Pb}$ collisions have also attracted considerable attention in both theoretical and experimental aspects. Therefore, we extend the$ k_T $ -factorization formalism mentioned above to the$p{\rm Pb}$ collisions. The main difference between the$ pp $ and$p{\rm Pb}$ collisions is the differential cross section. For a lead target, the differential cross section is given by$ \begin{equation} \frac{ {{\rm{d}}}\sigma^{p{\rm Pb}}_{q\bar{q}}}{ {{\rm{d}}}^2 \mathbf{b}} = 2\left\{1-\exp\left[-\frac{AT_{\rm Pb}(\mathbf{b})}{2}\sigma_{q\bar{q}}\right]\right\}, \end{equation} $

(13) where
$ A= 208 $ denotes the number of nucleons in a lead target. The$ \sigma_{q\bar{q}} $ is the quark dipole cross section and can be obtained by integrating Eq. (10) over the impact parameter. In Eq. (13), the thickness function$T_{\rm Pb}(b)$ is given by the Glauber model:$ \begin{equation} T_{\rm Pb}(\mathbf{b}) = \int_{-\infty}^{+\infty} {\rm d}z \rho (\sqrt{ \mathbf{b}^2 +z^2} ), \end{equation} $

(14) where ρ is the nucleon distribution in the lead. Note that the parameterized form of ρ satisfies the Woods-Saxon distribution [19].
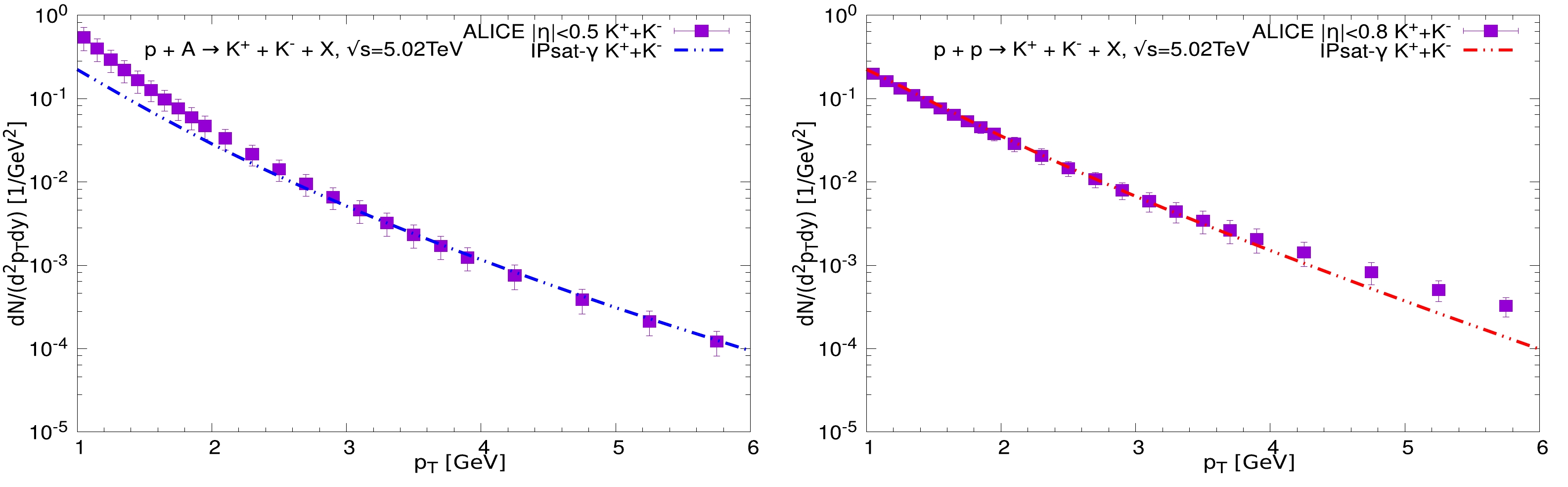
In Fig. 3, we study the transverse momentum distribution of charged kaons by using the
$ k_T $ -factorization formalism with the IPSat-γ model in$p{\rm Pb}$ collisions. For completeness, we also present the results for charged kaon production in$ pp $ collisions. We would like to point out that Fig. 3 gives the CGC$ k_T $ -factorization formalism, for the first time, to meet the charged kaon experimental data. From Fig. 3, one can see that the IPSat-γ model provides a reasonable description for both$ pp $ and$p{\rm Pb}$ collisions under certain uncertainties. In$ pp $ collisions, the IPSat-γ results are in good agreement with the experimental data for low and medium transverse momenta. Meanwhile, the IPSat-γ results are in good agreement with the experimental data for medium and high transverse momenta in the case of$p{\rm Pb}$ collisions. Generally, one can give a good description at any fixed transverse momentum by adjusting the K factor. However, this is unnecessary, as we hope that the K factor is at a fixed and reasonable value at the same energy for different collision systems. -
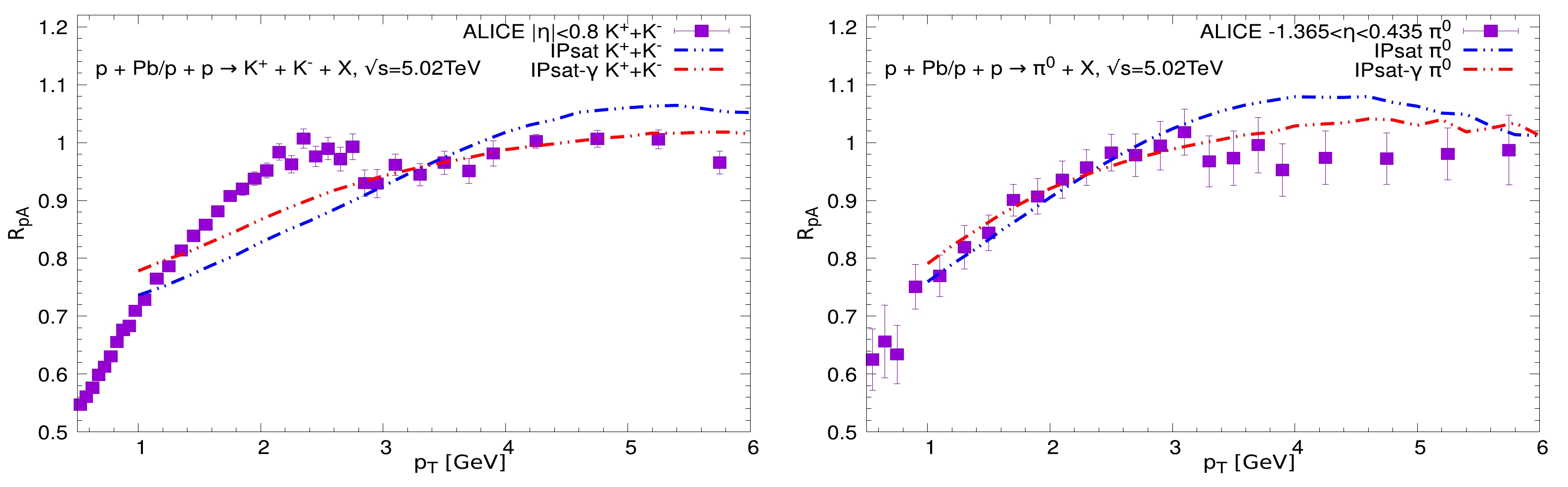
To further examine the robustness of the IPSat-γ model, we calculate the nuclear modification factor
$ R_{pA} $ by using the results for$ pp $ collisions and$p{\rm Pb}$ collisions. This observation reflects the gluon distribution in the initial state [60]. Therefore, the study of the nuclear modification factor gives us a new insight into the hadron production mechanisms. According to the Glauber model, the nuclear modification factor$ R_{pA} $ is defined as [61]$ \begin{equation} R_{pA}=\frac{1}{<N_{\rm coll}>}\frac{\dfrac{ {{\rm{d}}} N^{p+Pb \rightarrow h+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}}{\dfrac{ {{\rm{d}}} N^{p+p \rightarrow h+X}}{ {{\rm{d}}} y {{\rm{d}}}^{2} p_{T}}}, \end{equation} $

(15) where
$< N_{\rm coll} >$ is the average number of binary nucleon-nucleon collisions, which can be calculated via the Glauber model. From Eq. (15), we know that$ R_{pA} $ should be equal to unity in the absence of nuclear effects. We would like to note that$ R_{pA} $ is the ratio of the produced hadron multiplicities between$p{\rm Pb}$ collisions and$ pp $ collisions, and it is independent of the normalization factor. Therefore, the$ R_{pA} $ can provide a good perspective on the robustness of the IPSat-γ model.In Fig. 4, we show the nuclear modification factor of charged kaons and neutral pions calculated using the
$ k_T $ -factorization formalism with (red curves) and without (blue curves) the anomalous dimension. For both types of hadrons, we find that the$ R_{pA} $ increases with the transverse momentum. However, the$ R_{pA} $ is saturated to unity at large transverse momenta. From Fig. 4, we can clearly see that the results from the IPSat model deviate from the data points at large transverse momenta (3.5–6$ \mathrm{GeV} $ ), while the IPSat-γ model can give a relatively good description of the experimental data. It is worth pointing out that the values of$ R_{pA} $ obtained from the IPSat model exceed unity in some regions. These are reasonable outcomes for the following reasons. First, the longitudinal momentum fraction x increases with the transverse momentum at a fixed rapidity y. A larger x leads to an "anti-shadowing" enhancement of the UGD tail at large transverse momentum [14]. This shadowing is enhanced by Glauber fluctuation for a lead target as the UGD is not linear in the thickness function. Meanwhile,$< N_{\rm coll} >$ is linear in the thickness function. Second, the IPSat-γ model contains the anomalous dimension, which modifies the slope of the scattering amplitude in the transition from the dilute region to the saturation region. This modification has a similar role to the rcBK equation and leads to a low speed in approaching unity for the IPSat-γ model. -
In this paper, we proposed an approach to modify the saturation model by taking into account the anomalous dimension. Inspired by the prescription in the GBW model, we combine the impact parameter dependent IPSat model and the anomalous dimension to obtain an impact parameter and anomalous dimension dependent model (IPSat-γ). Using this new model, we calculate the transverse momentum distribution and nuclear modification factor of charged hadrons and neutral pions. The results from the IPSat-γ model are consistent with the measured transverse momentum distributions in
$ pp $ and$p{\rm Pb}$ collisions at LHC energies. Comparing the results obtained with and without the anomalous dimension, we find that the IPSat-γ model gives a more reasonable description of the nuclear modification factor than the original IPSat model. The increase in the nuclear modification factor is slowed by the anomalous dimension owing to its function of modifying the slope of the scattering amplitude in the transition from the dilute region to the saturation region. These numerical results indicate that the anomalous dimension plays a significant role in improving the predictive power of the dipole amplitude.
Single inclusive hadron production at the LHC with an improved impact parameter dependent saturation model
- Received Date: 2023-01-02
- Available Online: 2023-06-15
Abstract: To obtain a reasonable description of the hadron production at the LHC energies, the impact parameter dependent saturation model is modified by inclusion of an anomalous dimension γ, which controls the slope of the scattering amplitude in the transition from the dilute region to the saturation region. We calculate the transverse momentum distribution and nuclear modification factor of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: