-
The European Muon Collaboration (EMC) effect, a type of nuclear medium modification in the valence quark regime of
$ 0.3\lesssim x \lesssim 0.75 $ , refers to the noticeable deviation from unity of the structure-function ratio between the heavy nucleus ($ A>2 $ ) and the deuteron [1–9]. The deuteron is considered here as the reference nucleus, which is approximately regarded as a system of a free proton plus a free neutron. The EMC effect was first discovered in the muon-induced deep inelastic scattering (DIS) off the iron nucleus [1, 2]. Soon after this discovery, the EMC effect was confirmed by the electron-nucleus DIS data at SLAC [3, 4]. To date, many experimental measurements of the EMC effect have been reported on various nuclear targets.The EMC effect is surprising and attracts a signifiant amount of interest from theorists. The nuclear structure function is measured with the hard probe of momentum above GeV, while the per-nucleon binding energy inside the nucleus is approximately in the MeV scale. At the fundamental level of quarks and gluons, it is not clear how the relatively long-range nuclear force modifies the short-distance structure inside the nucleon. In the quark-parton model, the structure function is the incoherent summation of the quark distributions inside the nucleon. The discovery of the EMC effect implies that the quark distribution is evidently modified by the nuclear medium. If the quarks are completely confined inside the nucleon and do not play a role in the emergence of nuclear force, then the quark distribution should not be modified with the presence of surrounding nucleons. After decades of studies, many models have been constructed that properly describe the EMC effect, such as the off-shell correction [10, 11], x-rescaling model [12, 13], nucleon swelling and dynamical rescaling model [14–19], cluster model [20–27], point-like configuration suppression model [28, 29], and statistical model [30]. To differentiate the various models, more experiments and new observables beyond the
$ F_2 $ ratio are expected.It is speculated that the strength of the EMC effect depends on the local density instead of the global average density of the nucleus, according to the measurements of the very light nuclei
$ ^3 $ He and$ ^9 $ Be [31]. This interesting finding stimulates the physicists to imagine that the nuclear EMC effect emerges mainly from the local cluster structures inside the nucleus. The other hypothesis is that the EMC effect primarily results from the high-virtuality nucleons, which belong to the short-distance configurations of nucleons. This is supported by the unexpected linear correlation between the EMC effect and nucleon-nucleon short-range correlations (N-N SRC) [32, 33].The N-N SRC pairs are the temporary close-proximity fluctuations of two strongly interacting nucleons [34–37]. Experimentally, the N-N SRC pairs are identified as the nucleon pairs of high relative momentum between nucleons and small center-of-mass momentum of the pair [38–42]. The nucleons in SRC exhibit a much higher momenta than the nuclear Fermi momentum
$ k_{\rm F} $ . The abundance of N-N SRC pairs can be simply characterized by the probability of finding high-momentum nucleons [43–45]. These nucleons can form a close-proximity configuration and are also sensitive to the repulsive core of nucleon-nucleon interaction [46]. It is widely accepted that the intermediate-distance tensor force is the primary source of the formation of N-N SRC [46–49].Inspired by the observed linear correlation between the EMC effect and N-N SRC [32, 33], some nuclear physicists suggest that SRC pairs may be the underlying source of the EMC effect. This assumption is close to the traditional cluster model for the EMC effect [20–27]. The difference is that the cluster model is at the parton level with the six-quark bag picture, whereas the SRC explanation is based on the nucleon degrees of freedom, from which the properties of SRC nucleon are greatly modified. In a recent theoretical work, it was argued that the linear correlation between the EMC effect and N-N SRC is the natural result of the scale separation of the nucleon structure part (Λ-independent) and twist-four part (nuclear modification, Λ-dependent) of nuclear matrix elements [50]. It was demonstrated that the linear correlation between the EMC effect and N-N SRC can be derived in the effective field theory.
One key and intriguing question is whether there is causality between the EMC effect and SRC. Recently, the CLAS collaboration tested the SRC-driven EMC model with the simultaneous measurements of DIS and quasi-elastic inclusive process on the deuteron and heavier nuclei [45]. They extracted the modification function of the nucleon structure in SRC pairs and found that this modification function is nucleus-independent [45]. They showed that the EMC effect in all measured nuclei is consistent with the universal modification function of SRC pairs, and that the magnitude of the EMC effect in the nucleus can be described by the number of SRC pairs. In their view, the EMC effect is not the traditional static modification on all the independent nucleons but a strong dynamical effect for short time intervals of two strongly interacting nucleons fluctuating into a temporary high-local-density SRC pair [45]. The universal modification function of SRC was also carefully studied by J. Arrington and N. Fomin [51]. They found that there is almost no A-dependence of the universal modification function extracted with the Local-Density model, while there is weak A-dependence with the High-Virtuality model. The universal modification function resulting from data of various nuclei is consistent with a truly universal function, and the Local-Density hypothesis is favored [51].
A different approach has also been investigated and reported. Recently, in Ref. [52], the relationship between SRC and the EMC effect was further examined by incorporating the nuclear binding and nucleon off-shell effects. The authors argued that their analysis does not support the hypothesis that there is a causal connection between nucleons residing in SRCs and the EMC effect [52]. The EMC effect of the low-momentum and high-momentum nuclei are separately studied. The authors found that the Fermi motion effect is much stronger than the off-shell effect for SRC nucleons, with three different models for the off-shell effect [52]. Hence, they concluded that the SRC nucleons do not cause the dominant EMC effect [52]. This conclusion is contrary to what one expected in the past. It is worth further examining the relationship between the EMC effect and SRC from different viewpoints or theoretical models.
Currently, the approaches for describing the EMC effect can be classified into the following three categories: (i) all the nucleons are slightly modified when embedded in the nuclear medium; (ii) nucleons are unmodified most of the time but greatly modified when they fluctuate into N-N SRC; (iii) mean-field uncorrelated nucleons are slightly modified, and the nucleons are substantially modified for a short-time interval in the temporary SRC state. It is a prominent research topic to study whether the nuclear EMC effect entirely comes from the N-N SRC. Hence, in this work, we focus on the last two approaches to explain the EMC effect. In Sec. II, we illustrate the models we use to calculate the nuclear EMC effect. In Sec. III, we present the results of the EMC effect from SRC and mean-field nucleons. Finally, a short summary is provided in Sec. IV.
-
It is known that the traditional nuclear structure is almost irrelevant to the nuclear EMC effect. The nucleon momentum distribution leads to the Fermi motion effect around
$ x=1 $ . The per-nucleon nuclear binding energy is much smaller than the high-momentum virtual photon probe or nucleon mass. Nevertheless, the identity of nucleons inside nucleus is well established and it is the core of the traditional nuclear physics. The nucleon structure should be connected to the properties of the nucleon.In this study, we applied the x-rescaling model to evaluate the EMC effect, which is analyzed on the view that the nucleus is a sum of quasi-particles (bound nucleons). The mass is a fundamental property of the nucleon, and the change in the nucleon mass inside the nucleus should be taken into account for the nuclear medium effect. The nucleon effective mass in nucleus has been successfully used to describe the nuclear EMC effect [12, 13]. The Bjorken scaling variable is defined in terms of the free nucleon mass m as
$ x=Q^2/(2m\nu) $ . However, the struck nucleon in lepton-nucleus DIS could be far off-shell. The true scaling variable for nuclear DIS should be assumed to be$ x^{\prime}=Q^2/(2m^{*}\nu)=xm/m^{*}=x\eta $ , where$ m^{*} $ is the effective mass of the bound nucleon. Here,$ \eta=m/m^{*} $ is the rescaling factor of x, and the per-nucleon nuclear structure function$ F_2^{A} $ is given by$ \begin{array}{*{20}{l}} \begin{split} F_2^{A}(x, Q^2) = F_2^{N}(x\eta, Q^2), \end{split} \end{array} $

(1) where
$F_2^{N}$ is the free nucleon structure function. The rescaling of x is taken into account for the off-shell correction of the bound nucleon [12, 13, 53]. It was also pointed out that the exchanged virtual meson would take away a fraction of the nucleon momentum, thus resulting in the x-rescaling of the nuclear structure function [54].The nucleon effective mass in the x-scaling model is used to describe the off-shellness of the nucleon, with
$ E^2=p^2+m^{*2} $ [12, 13, 53]. The nucleon effective mass was also defined by Brueckner in 1950s within a non-relativistic many-body theory to account for the momentum-dependence of potential energy of a single particle, with$ E(k)=k^2/2m + V(0)+bk^2=k^2/2m^{*}+V(0), $ $ V(k)=V(0)+ bk^2+... $ , and$ m^{*}=m/(1+2bm) $ [55]. Therefore, the effective mass of the SRC nucleon in this study was different from Brueckner's definition. Brueckner's nucleon effective mass reflects leading effects of the space-time non-locality of the underlying nuclear interactions [56, 57], while the effective mass of SRC nucleon arises from the local interactions at short distance. The relations between these two effective masses should be investigated in the future. -
The intriguing question we aimed to answer through the present study is whether the N-N SRCs are totally responsible for the nuclear EMC effect. Therefore, we consider the first model, referred as model-A, for the convenience of discussion, in which only the short-range correlated nucleons are substantially modified while the uncorrelated nucleons are nearly unmodified. This model strongly relies on the causality between the SRC and the EMC effect, i.e., the N-N SRC is the primary source of the EMC effect. For model-A, the nuclear structure function
$F_2^{A}$ is decomposed as$ \begin{aligned}[b] F_2^{A}=&\left[n^{A}_{\rm SRC}F_2^{p\; {\rm in}\; {\rm SRC}}+n^{A}_{\rm SRC}F_2^{n\; {\rm in}\; {\rm SRC}}\right. \\ &\left.+(Z-n^{A}_{\rm SRC})F_2^{p}+(A-Z-n^{A}_{\rm SRC})F_2^{n} \right] /A, \end{aligned} $

(2) where
$n^{A}_{\rm SRC}$ is the number of proton-neutron SRC pairs in nucleus A,$F_2^{p\; {\rm in}\; {\rm SRC}}$ and$F_2^{n\; {\rm in}\; {\rm SRC}}$ are the modified nucleon structure functions in the SRC pair, and$F_2^{p}$ and$F_2^{n}$ are free nucleon structure functions. In Eq. (2), Z, N, and A are respectively the proton number, neutron number, and mass number. Here, the number of SRC pairs should be viewed as the time-averaged value for the dynamical system. Given that the deuteron is in the SRC configuration occasionally, the time-averaged number of SRC pairs in the deuteron is less than one, that is,$n^{d}_{\rm SRC} < 1$ .The SRC universality and isophobic property of N-N SRC pairs are the other two foundations of model-A. The universality of SRC can be described by a similar form of nuclear wave function at high nucleon momentum, which is confirmed by the experimental observations of the x-independence and the weak
$ Q^2 $ -dependence of the cross section ratio between two different nuclei in the region of$ 1.4\lesssim x \lesssim 2 $ [43–45]. Different experiments have revealed that most of the SRC pairs are the proton-neutron pairs [37, 39, 40, 42, 58, 59]. This isophobic property supports the point that the immediate tensor force is the primary source for the formation of N-N SRC pairs [46–49].For model-A, the number of SRC pairs in nucleus A and modified nucleon structure functions in SRC pair are key inputs. The number of SRC pairs in nucleus A is closely related to the measured SRC scaling ratio
$ a_2 $ (nucleus A over the deuteron) and number of SRC pairs in the deuteron, which is written as$ \begin{array}{*{20}{l}} n^{A}_{\rm SRC}=[A\times a_2(A)\times n_{\rm SRC}^{d}]/2. \end{array} $

(3) Note that the above relation (Eq. (3)) is a simplified assumption. The SRC scaling ratio
$ a_2 $ is measured using the high-energy electron inclusive scattering process off the nuclear targets [43–45], and the number of SRC pairs in the deuteron was determined in a previous analysis [60]. The free nucleon structure functions can be calculated with the parton distribution functions$ f_i(x,Q^2) $ , as$F_2^{N}(x,Q^2) = \sum_i e_i^{2} xf_i(x,Q^2)$ . In this study, the proton parton distribution functions were extracted from global analyses such as CT14 [61] and CJ15 [62]. The parton distributions of the free neutron are easily given by the parton distributions of the proton under the assumption of isospin symmetry, i.e.,$ u^{n}=d^{p} $ and$ d^{n}=u^{p} $ . By using the x-rescaling model, the structure function of the SRC nucleon is connected with the free nucleon structure function, which is expressed as$ \begin{aligned}[b]& F_2^{p\; {\rm in}\; {\rm SRC}}(x, Q^2) = F_2^{ p}(x\eta_{\rm SRC}, Q^2),\\ &F_2^{n\; {\rm in}\; {\rm SRC}}(x, Q^2) = F_2^{n}(x\eta_{\rm SRC}, Q^2),\\ \end{aligned} $

(4) in which
$ \eta_{\rm SRC} $ is the rescaling factor for the SRC nucleon;$ \eta_{\rm SRC} $ is directly connected with the effective mass of SRC nucleon as$ \eta_{\rm SRC}=m/m_{\rm SRC} $ , which is a universal factor among different nuclei. Given that the effective mass of SRC nucleon$ m_{\rm SRC} $ was extracted from a correlation analysis between the nuclear mass and SRC scaling ratio$ a_2 $ , the rescaling factor for SRC nucleon was computed to be$ \eta_{\rm SRC}=1.10 $ [60]. -
According to the nuclear shell model, the nucleons move independently in the mutual potential created by all the nucleons, which is usually approximated with the mean field. These mean-field nucleons are mainly governed by the long-range nuclear force. As revealed by a high energy electron probe, we know that nucleon-nucleon short-range correlations exist and they constitute an important microscopic structure of the nucleus. Although short-range correlated nucleons interact intensively, they are minorities in a temporary state. A more general hypothesis is that the structure function of mean-field nucleons is slightly modified, whereas the structure function of SRC nucleons is strongly modified. In other words, the N-N SRC may not generate the enough EMC effect.
For the second model, referred as model-B for the convenience of discussion, we propose that both the mean-field nucleons and SRC nucleons are modified by the nuclear medium or correlated partner nucleon. The nuclear structure function in model-B is decomposed as
$ \begin{aligned}[b] F_2^{A}=&\left[n^{A}_{\rm SRC}F_2^{p\; {\rm in}\; {\rm SRC}}+n^{A}_{\rm SRC}F_2^{n\; {\rm in}\; {\rm SRC}}\right. \\ &\left.+(Z-n^{A}_{\rm SRC})F_2^{p^*}+(A-Z-n^{A}_{\rm SRC})F_2^{n^*} \right] /A, \end{aligned} $

(5) where
$F_2^{p\; {\rm in}\; {\rm SRC}}$ and$F_2^{n\; {\rm in}\; {\rm SRC}}$ denote the structure functions of SRC nucleons, and$F_2^{p^*}$ and$F_2^{n^*}$ denote the structure functions of mean-field nucleons. Here, the number of SRC pairs$n^{A}_{\rm SRC}$ and structure functions of SRC nucleons are assumed to be the same as those of model-A. In model-B, the structure functions of mean-field nucleons are also calculated with the x-rescaling model, which is expressed as$ \begin{aligned}[b]& F_2^{p^*}(x, Q^2) = F_2^{p}(x\eta_{\rm MF}, Q^2),\\& F_2^{n^*}(x, Q^2) = F_2^{n}(x\eta_{\rm MF}, Q^2).\\ \end{aligned} $

(6) Different from the situation for SRC nucleons, we assume that the rescaling factor
$ \eta_{\rm MF} $ for the mean-field nucleon is nucleus-dependent, given that the effective mass of the mean-field nucleon depends on the nucleus. The nucleon densities of different nuclei are different. In this analysis, we let$ \eta_{\rm MF} $ be a free parameter for each nucleus. Note that the rescaling factor$ \eta_{\rm MF} $ for mean-field nucleons should be smaller than the rescaling factor$ \eta_{\rm SRC} $ for SRC nucleons. -
Figures 1 and 2 depict recent experimental measurements of the nuclear EMC effects in light and heavy nuclei, respectively. The predictions of model-A and model-B are also shown in the figures for the sake of comparison. The experimental data are extracted from the recent high-precision measurements by CLAS at JLab [45]. Note that the experimental data points are distributed in the valence quark region of x smaller than 0.6. Given that the data are far from the Fermi motion region near
$ x\sim 1 $ , the Fermi motion correction was neglected in this work.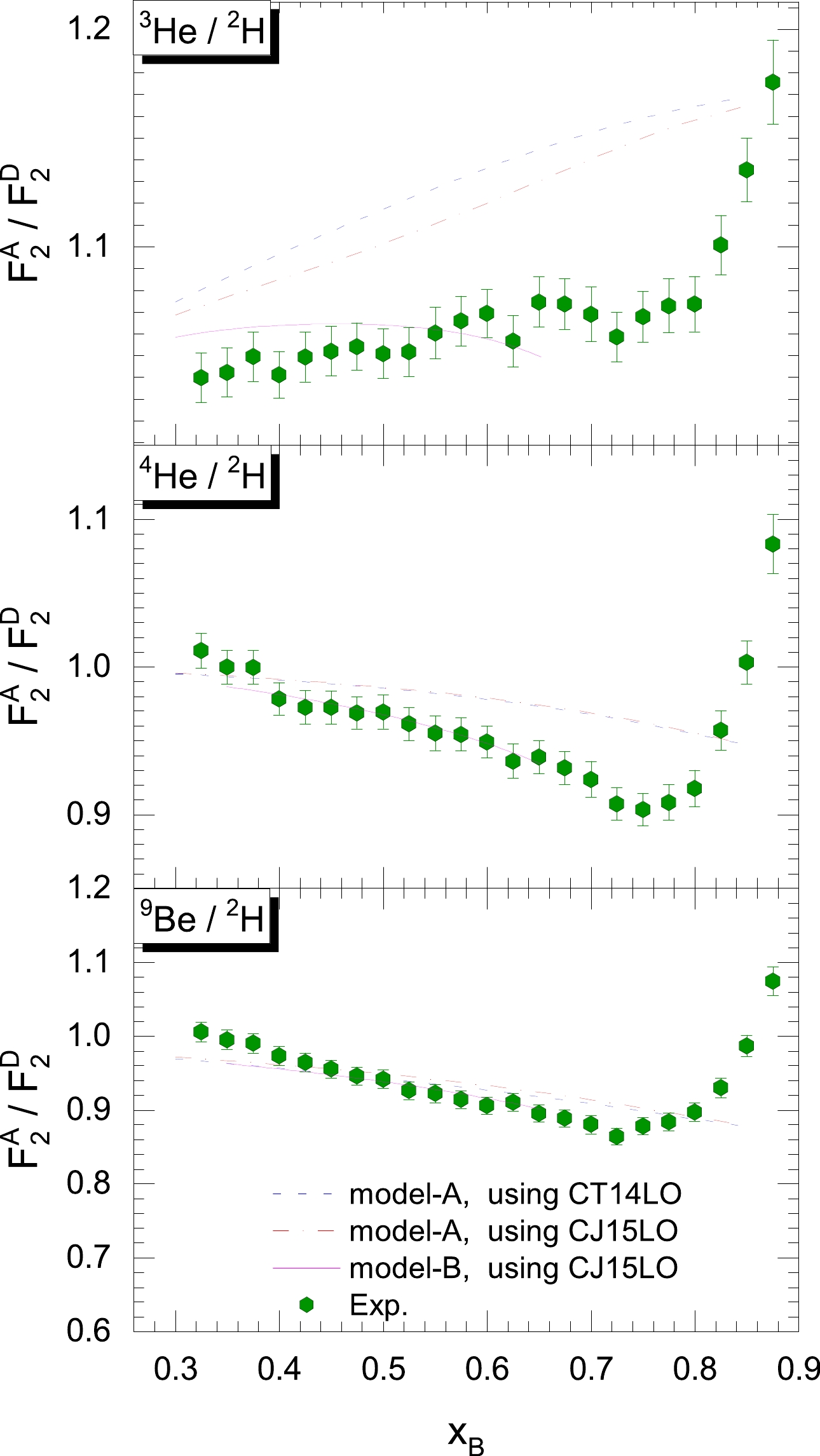
Figure 1. (color online) The predicted EMC ratios from the x-rescaling models are shown along with the experimental data (light nuclei). See the main text for details of the models. The experimental data are extracted from JLab Hall C [31].
$ Q^2 $ was set as 5.3 GeV$ ^2 $ in the model calculations to be consistent with the experiment.
Figure 2. (color online) The predicted EMC ratios from the x-rescaling models are shown with the experimental data (heavy nuclei). See the main text for details of the models. The experimental data are extracted from CLAS at JLab [45].
$ Q^2 $ was set to 2 GeV$ ^2 $ in the model calculations to be consistent with the experiment.We found that the EMC effect from model-A is much weaker than the experimental observations. For the calculations of structure function ratios in model-A, we used the parton distribution functions of CT14 and CJ15. Note that the dependence on the data set of parton distribution functions is weak. In conclusion, based on the x-rescaling model, only the nuclear modifications from short-range correlated nucleons are not enough to reproduce the nuclear EMC effect in experiments. We speculate that the valence distribution of mean-field nucleons is also modified, the modification of valence distribution in N-N SRC is not universal in different nuclei, or some other short-distance structures beyond N-N SRC exist with strong modifications on the inner nucleon structure, such as 3N-SRC and α clusters.
Note also that the number of proton-neutron SRC pairs in the deuteron is estimated to be
$n^{d}_{\rm SRC}=0.041$ by K. S. Egiyan et al. [43]; this value is much larger than the value from a previous analysis of ours [60]. In their analysis, the number of nucleons in N-N SRC pairs was defined as the number of nucleons of high momenta$ k>k_{\rm F}\approx 275 $ MeV/c [39, 43]. With this definition, a small fraction of mean-field nucleons may be misidentified as SRC nucleons, resulting in more SRC pairs than in our previous analysis. Nevertheless, Fig. 3 shows the predicted EMC ratios from model-A, taking the SRC$ a_2 $ data averaged from experiments [33, 45] and$n^{d}_{\rm SRC}=0.041$ [43]. The predicted EMC slopes are still smaller than the data by CLAS collaboration. Therefore, based on either our estimation on SRC numbers or the estimation by K. S. Egiyan et al., only the modifications on SRC nucleons are not enough to interpret the nuclear EMC effect. Then, we let the number of SRC pairs inside the deuteron be a free parameter. We found that, as the number of SRC pairs inside the deuteron increases by approximately 10%, the EMC effect can be explained only with the SRC nucleons. However, this high number of SRC pairs inside the deuteron is contradictory (much higher) with respect to the analysis based on the experimental data.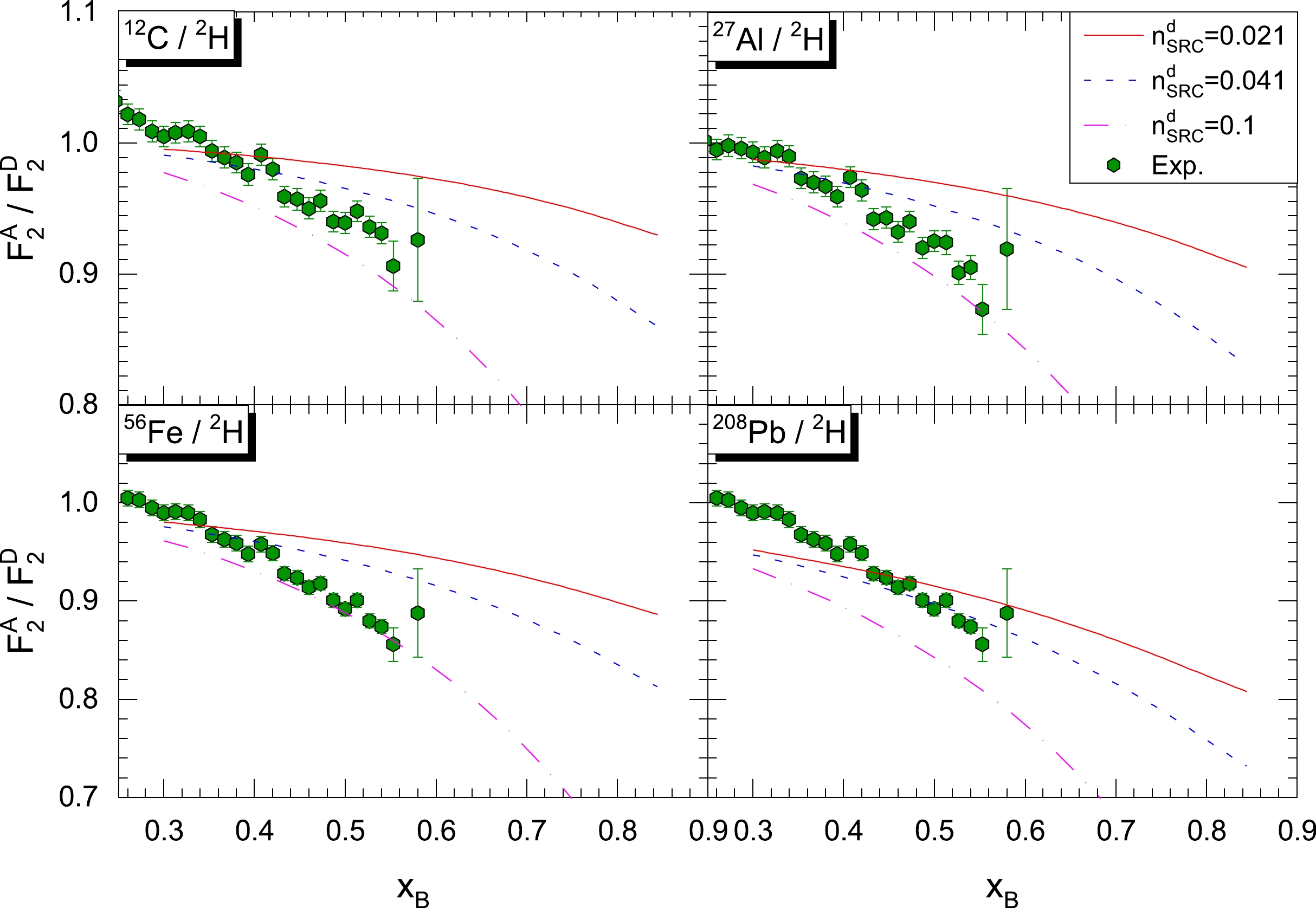
Figure 3. (color online) The predicted EMC ratios from a x-rescaling model (model-A) are shown along with the experimental data (heavy nuclei), with different input values for the parameter
$n^{d}_{\rm SRC}$ . See the main text for details of the model. The experimental data are extracted from CLAS at JLab [45].$ Q^2 $ was set to 2 GeV$ ^2 $ in the model calculations to be consistent with the experiment.In model-B, the mean-field nucleons are also modified, in addition to the SRC nucleons. We also assume in model-B that the rescaling factor
$ \eta_{\rm MF} $ is a free parameter and it depends on the nuclear medium. Thus, we performed the least square fit of model-B to the EMC ratio data in the range of$ 0.35<x_B<0.65 $ to find the optimal parameter$ \eta_{\rm MF} $ for each measured nucleus. The resulting values of$ \eta_{\rm MF} $ are listed in Table 1. In model-B,$\eta_{\rm MF}$ of the deuteron is simply one;$\eta_{\rm MF}$ of$ ^{208} $ Pb was determined to be 1.022$ \pm $ 0.002, which is a much smaller value than the rescaling factor for the SRC nucleon. Nevertheless, the mean-field nucleons in$ ^{208} $ Pb are evidently modified, judged by the obtained rescaling factor$\eta_{\rm MF}$ . By introducing the EMC effect of the mean-field nucleon, the model-B successfully explains the nuclear EMC effect.nucleus $ \eta_{\text{MF}} $ 

nucleus $ \eta_{\text{MF}} $ 

$ ^4 $ He

1.008 ± 0.001 $ ^9 $ Be

1.005 ± 0.002 $ ^{12} $ C

1.016 ± 0.002 $ ^{27} $ Al

1.021 ± 0.002 $ ^{56} $ Fe

1.027 ± 0.001 $ ^{208} $ Pb

1.022 ± 0.002 Table 1. The values of the fitted rescaling factor
$\eta_{\rm MF}$ for the mean-field nucleon are listed under the framework of model-B. In this model, modifications on both the SRC and mean-field nucleons lead to the observed nuclear EMC effect. The errors come only from the fits to the EMC effect data. The uncertainties of the parameters$n^{{d}}_{\text{SRC}}$ and$ a_2 $ are not included.Furthermore, let us analyze the nuclear dependence of the rescaling factor
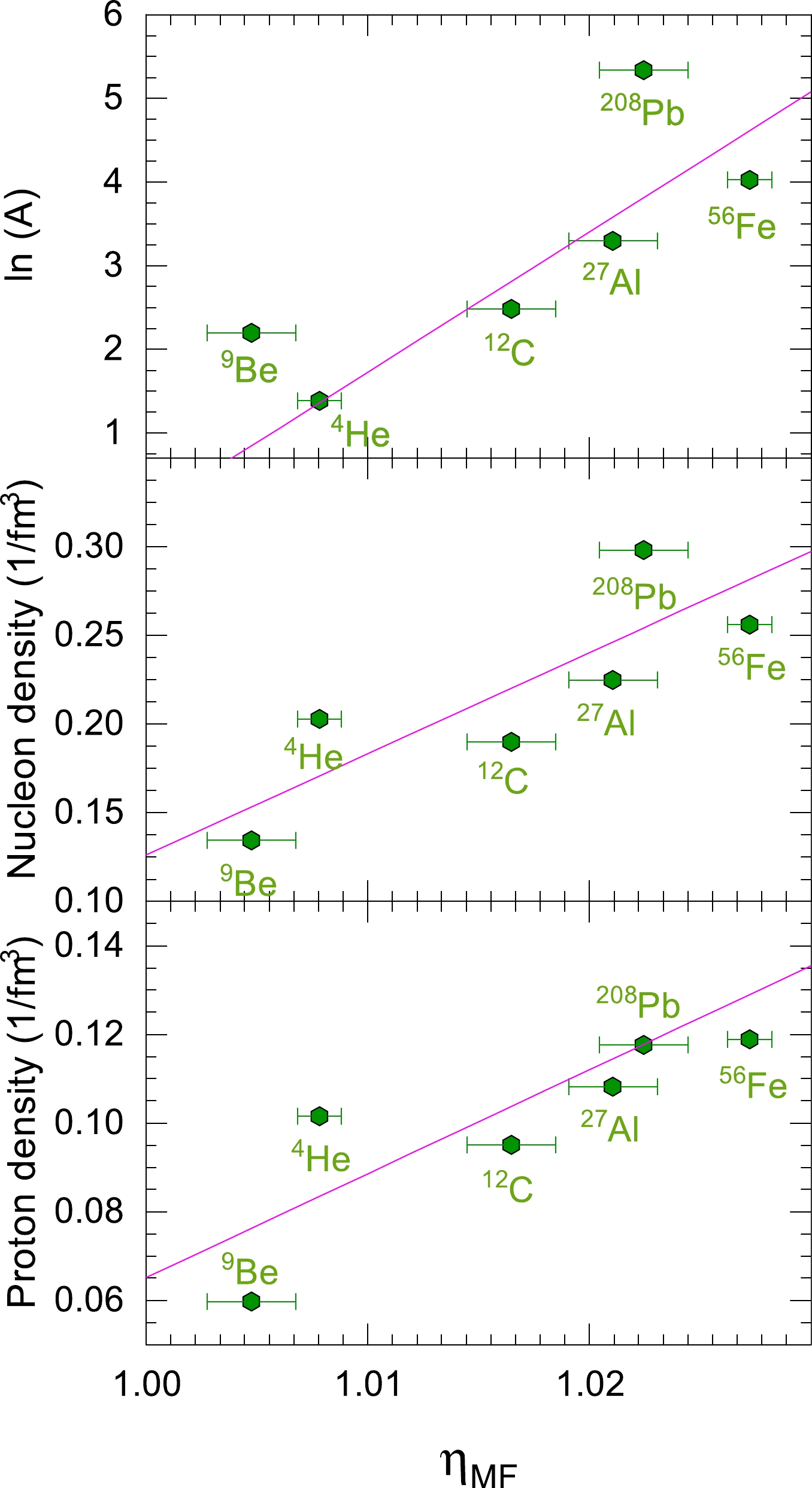
$\eta_{\rm MF}$ for the mean-field nucleon in model-B. The correlations between$\eta_{\rm MF}$ and$ \ln(A) $ ,$\eta_{\rm MF}$ and the nucleon density, and$\eta_{\rm MF}$ and the proton density are shown in Fig. 4. The nucleon density and proton density are calculated using$ A/(\frac{4}{3}\pi R^3) $ and$ Z/(\frac{4}{3}\pi R^3) $ , respectively, in which R is the charge radius of a nucleus. The data of nuclear charge radii are extracted from Ref. [63]. Given that the radius of the neutron distribution in the nucleus may not be the same as the charge radius, we also plot the correlation between$\eta_{\rm MF}$ and the proton density of the nucleus. Although the linear correlation is not perfect, the rescaling factor$\eta_{\rm MF}$ of the mean-field nucleon is more or less correlated with the nucleon density. The obtained rescaling factor of the mean-field nucleon is proportional to the average nuclear density. -
In the x-rescaling model, we tested the idea that N-N SRC is the dominant source for the nuclear EMC effect. The nuclear EMC effects of some nuclei were calculated within the x-re scaling model under the assumptions that the SRC nucleon is universal among different nuclei and that only the inner structure of short-range correlated nucleons are modified. The input mass of the N-N SRC pair and number of SRC pairs inside the deuteron are extracted from a previous analysis of the
$ a_2 $ data and nuclear mass [60]. We found that the nuclear medium correction on N-N SRC is not enough to explain the EMC effect observed in experiments, if the model applied in this study is correct. This conclusion is consistent with results analyzed with the off-shellness correction [52].If we assume that the rescaling factor
$ \eta_{\rm SRC} $ is A-dependent, Model-A can effectively describe the experimental data. However, this assumption breaks the universality of N-N SRC, which is basically supported by experimental observations [43–45] and some theoretical predictions [64, 65]. For Model-B, we found that the rescaling factor for uncorrelated nucleon is approximately linearly correlated with the nuclear density. This linear relation can be tested with further experimental measurements on more nuclear targets of different densities.We speculate that more origins of nucleon structure modifications beyond the short-distance configurations are needed, such as 3N SRC and α clusters. Other possible interpretations are that either the mean-field nucleon is significantly modified, or the N-N SRC pairs in different nuclei have different nuclear medium modifications. For a preliminary exploration, we show that the EMC effect can be explained if we just assume that the mean-field nucleon is also modified. Moreover, the nuclear modification on the mean-field nucleon scales with the density of the nucleus. In summary, we conclude that the SRC universality is wrong, the mean-field nucleon is also slightly modified, there are other sources beyond N-N SRC for the EMC effect such as the α cluster, or the applied x-rescaling model needs improvement.
Strong evidence of 3N SRC has not been found in the inclusive
$ ^4 $ He/$ ^3 $ He cross section ratio at JLab, and it is shown that isolating 3N SRC is much more challenging compared to isolating 2N SRC [66]. However, the theorists suggest that the scaling phenomenon from inclusive scattering on 3N SRC requires a high$ Q^2\gtrsim 3 $ GeV$ ^2 $ and the current experimental situation should be improved [67]. Within Model-A,$n^{d}_{\rm SRC}$ needs to increase from 0.021 to 0.1 to explain the experimental data of the EMC effect. Considering that the 3N SRC and α cluster also contribute to the EMC effect, the numbers of 3N SRC pairs and α clusters should be of the same order as N-N SRC if the structure-function modifications of N-N SRC, 3N SRC and α are similar. Given that there is no 3N SRC and α cluster in the deuteron and that the nuclear modifications inside 3N SRC and α could be stronger than that inside N-N SRC, the numbers of 3N SRC pairs and α clusters in heavy nuclei could be smaller than that of N-N SRC pairs, inferred from the current data of the EMC effect. More experimental measurements are needed for searching other short-distance structures beyond N-N SRC.
The European Muon Collaboration effect from short-range correlated nucleons in a x-rescaling model
- Received Date: 2022-10-11
- Available Online: 2023-04-15
Abstract: In this paper, we examine the hypothesis that the nuclear EMC effect arises merely from the N-N SRC pairs inside the nucleus and that the properties of the N-N SRC pair are universal among the various nuclei, using the conventional x-rescaling model for the EMC effect. With the previously determined effective mass of the short-range correlated nucleon and the number of N-N SRC pairs estimated, we calculated the EMC effect of various nuclei within the x-rescaling approach. According to our calculations, the nuclear EMC effect due to the mass deficits of the SRC nucleons is not sufficient to reproduce the observed EMC effect in experiments. We speculate that the internal structure of the mean-field single nucleon is also clearly modified. Alternatively, there can be more origins of the EMC effect beyond the N-N SRC configuration (such as the α cluster), or the universality of N-N SRC pair is significantly violated from light to heavy nuclei.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: