-
There are two types of
$ CP $ violation sources in the standard model (SM). The first is weak$ CP $ violation in the Cabibbo-Kobayashi-Maskawa (CKM) matrix [1, 2], and the second is strong$ CP $ violation related to topological charge in QCD vacuum [3–5]. Both have relations with Higgs Yukawa couplings. The CKM matrix originates from general Yukawa coupling matrices for three generations [6, 7], and the θ angle in QCD vacuum can rotate to the complex phase of the mass matrix via chiral transformation [8]. The SM Higgs boson is a$ CP $ -even scalar with$ CP $ -conserving interactions, whereas in new physics (NP) beyond the SM (BSM),$ CP $ violation usually relates to Higgs bosons. One reason for this is that there are often scalars and pseudoscalars instead of one single scalar in the SM. A mixture of scalars and pseudoscalars is natural. For example, in the two Higgs doublet model (THDM) [9], minimal supersymmetric SM (MSSM) [10], and composite Higgs model [11], pseudoscalars always appear and there are no simple rules forbidding a mixture between a scalar and pseudoscalar. Except for theoretical naturalness and generality, one practical motivation for a new$ CP $ violation source arises from the matter-antimatter asymmetry observed in our Universe [12–14]. In the electroweak baryogenesis mechanism [15],$ CP $ violation plus a sphaleron transition [16] may produce baryon and lepton number violation during an electroweak phase transition; however, the$ CP $ violation ratio in the SM is too small to achieve the quantity of the observed matter-antimatter asymmetry [17–19]. Therefore, a new$ CP $ violation source must be added to obtain electroweak baryogenesis.We choose two model-independent frameworks to study
$ CP $ violation: one is a traditional method using additional effective Lagrangian terms, whereas the other uses the on-shell scattering amplitude method to analyze amplitudes.Adding new
$ CP $ -violating terms to the Lagrangian offers a convenient effective description of new couplings BSM. The new terms can be$ CP $ conserved or$ CP $ violated but should obey Lorentz and gauge invariance. For a specific NP model, its new Higgs couplings can be simplified into these effective Lagrangian terms when other couplings are sufficiently small to be omitted. Therefore, constraints on these new Higgs couplings in the effective Lagrangian provide concrete limitations for model structures with certain gauge symmetries.The on-shell method is a novel tool to deal with amplitudes directly; not even a Lagrangian and Feynman diagram is required [20]. This method starts from on-shell particle states instead of field, sets up constraints, exploits analytical properties such as poles and branch cuts, and then obtains an available amplitude. Specifically, a
$ 3 $ -point massless (or one massive two massless) amplitude may be fixed via locality and little group scaling [20–22], and then an$ n+1 $ -point tree amplitude can be constructed from n-point amplitudes through recursion relations. In this way, all tree amplitudes can be obtained with clear mathematical structures.We focus on the
$ H\to \gamma \gamma $ ,$ H\to \gamma \ell \ell $ , and$ H\to 4\ell $ processes to analyze their BSM amplitudes. At the Large Hadron Collider (LHC), the$ H\to \gamma \gamma $ and$ H\to ZZ \to 4\ell $ processes are Higgs discovery channels [23, 24], which have the advantage of a clean background and relatively large signal. They are also golden channels for the precise measurement of Higgs properties [25–28]. In our previous research, we noticed that the$ CP $ violation phase could not be probed solely in the$ H\to \gamma \gamma $ or$ H\to \gamma \ell \ell $ process without interference from the background [29, 30]. Conversely, in the$ H\to ZZ \to 4\ell $ process,$ CP $ violation could be probed solely through its kinematic angles [28, 31–33]. These may be clearly explained at the amplitude level after we obtain a compact formula. In this paper, we explore the relations between these BSM amplitudes using the above two independent methods. A decomposition relation between these amplitudes is illustrated in an interesting diagrammatic way. Then, we calculate the same amplitude using the on-shell method (BCFW recursion relation), which can be regarded as a parallel proof of the decomposition relation. Meanwhile, the massive spinor formalism is applied to prove that it is also suitable for massive cases.This paper is organized as follows: In Sec. II, we show the amplitudes of the SM
$ HVV $ processes both at a proton-proton collider and$ e^+e^- $ collider. In Sec. III, we calculate BSM amplitudes in the effective Lagrangian description. The$ H\to \gamma \gamma $ ,$ H\to \gamma \ell \ell $ , and$ H\to 4\ell $ processes correspond separately to$ 3 $ ,$ 4 $ , and$ 5 $ -point amplitudes. In Sec. IV, we deduce decomposition relations for these amplitudes. In Sec. V, we reproduce these BSM amplitudes using the on-shell scattering amplitude approach. In Sec. VI, the BSM amplitudes from the on-shell scattering amplitude method are generalized to massive spinor cases. Finally, Sec. VII contains a summary and discussion. -
Experimentally, SM/BSM
$ HVV $ couplings can be measured/exploited at existing proton-proton colliders, such as the LHC, or future$ e^+e^- $ colliders, such as the Circular Electron Positron Collider (CEPC), International Linear Collider (ILC), and Compact Linear Collider (CLIC). To study BSM$ HVV $ couplings with$ CP $ violation, their interference with the corresponding SM process (including or not including Higgs) may become the dominant contribution because BSM couplings are generally assumed to be suppressed compared to the corresponding SM couplings. Before studying BSM amplitudes, the amplitudes of the SM$ HVV $ process and the main background process are introduced to show a global view of how amplitudes work for physics processes at colliders. Analyzing these amplitudes may unveil some mysteries that are not clear at the observable level. In the following, we take specific$ HZZ $ related processes as examples at a proton-proton collider and$ e^+e^- $ collider separately. For the example at the proton-proton collider, we focus on process-dependent amplitudes, show the amplitudes of the signal and background processes, and discuss how these amplitudes are used for experimental predictions. For the example at the$ e^+e^- $ collider, we focus on process-independent amplitudes, that is, the amplitudes with all external particles outgoing, which are related to process-dependent amplitudes via crossing symmetry. -
The
$ gg\to H \to ZZ \to 4 \ell $ process at the LHC is sensitive to BSM$ HVV $ couplings. The Feynman diagrams of this signal channel and its main background are shown in Fig. 1. In Fig. 1(a), the Higgs production process$ gg\to H $ is mediated by the top quark loop. Figure 1(b) represents the$ gg\to ZZ \to 4 \ell $ box process without Higgs, which is important in the off-shell Higgs region. Studying the interference between the signal and this continuum background in the off-shell Higgs region could provide a stringent bound on the Higgs width [34, 35] and also BSM$ HZZ $ couplings [31, 35]. In Fig. 1,$ \ell $ and$ \ell^\prime $ have different flavors. If we study the process of$ 4\ell $ with the same flavors, two more diagrams that describe another pairing of$ 4\ell $ should be added. Nevertheless, their amplitudes are similar [31].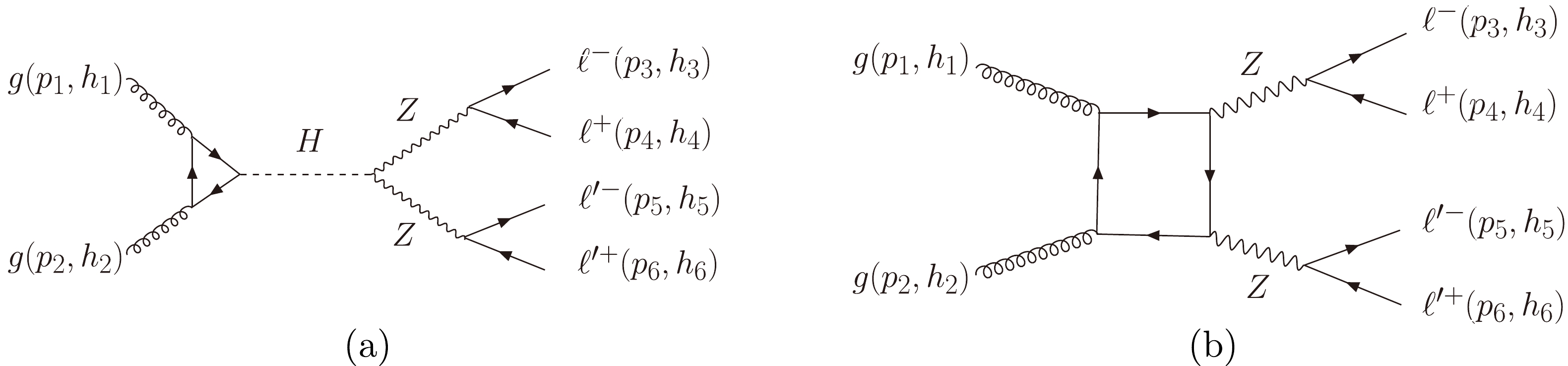
Figure 1. Feynman diagrams of the SM
$ HZZ $ related process and its main background with 4$ \ell $ final states at the LHC.The triangle top quark loop in
$ gg\to H $ may be integrated and described using an effective$ ggH $ coupling such that the helicity amplitudes of$ ggH $ are shown as [30]$ \begin{aligned}[b] \mathcal{M}^{gg\to H}(1^+_g,2^+_g)=&\frac{2c_g}{v}[12]^2 , \\ \mathcal{M}^{gg\to H}(1^-_g,2^-_g)=&\frac{2c_g}{v}\langle12\rangle^2 . \end{aligned} $

(1) Here,
$ \begin{aligned}[b] \frac{c_g}{v}=&\frac{1}{2}\sum\limits_f\frac{\delta^{a b}}{2}\frac{i}{16\pi^2}g^2_s4e \frac{m_f^2}{2M_W s_W}\frac{1}{M^2_H}\\&\times[2+s_{12}(1-\tau_H)C^{\gamma\gamma}_0(m_f^2)] , \end{aligned} $

(2) where
$ v=246 $ GeV is the vacuum expectation value of the Higgs,$a,~ b=1,2,...,8$ are$S U(3)_c$ adjoint representation indices for the gluons,$ \tau_H=4m_f^2/M^2_{H} $ , and the$ C^{\gamma\gamma}_{0}(m^2) $ function is a Passarino-Veltman three-point scalar function [36].$ \langle i j \rangle $ and$ [ij] $ follow the conventions in Refs. [37, 38]:$ \begin{aligned}[b] &\langle ij \rangle \equiv \langle i^-|j^+\rangle= \overline{u_-(p_i)} u_+(p_j),\\&[ ij ]\equiv \langle i^+|j^-\rangle = \overline{u_+(p_i)} u_-(p_j), \\ &\langle ij \rangle[ ji ] = 2 p_i \cdot p_j,\quad s_{ij} = (p_i+p_j)^2,\\& \epsilon_\mu^{\pm}(p_i,q)=\pm\frac{\langle q^{\mp}|\gamma_{\mu}|p_i^{\mp}\rangle}{\sqrt{2}\langle q^{\mp}|p_i^{\pm}\rangle}, \end{aligned} $

(3) where
$ p_i $ are the momenta of the external legs, q is the reference momentum that reflects the freedom of gauge transformation, and$\epsilon^{\pm}(p_i,~q)$ is for outgoing photons with$ \pm $ helicities. Notice that the gluons are incoming in Eq. (1). If we let them be outgoing, the amplitudes simply require an exchange between$ \langle\rangle $ and$ [] $ because of the crossing symmetry.The helicity amplitudes of
$ H\to ZZ \to 4\ell $ are [31]$ \begin{aligned}[b] \mathcal{M}^{H\to ZZ \to 4\ell}(3^-_{\ell^- },4^+_{\ell^+},5^-_{\ell^- },6^+_{\ell^+}) =&f\times l_e^2 \frac{M_W^2}{\cos^2{\theta_W}}\langle 35\rangle[46], \\ \mathcal{M}^{H\to ZZ \to 4\ell}(3^-_{\ell^- },4^+_{\ell^+},5^+_{\ell^- },6^-_{\ell^+}) =&f\times l_e r_e \frac{M_W^2}{\cos^2{\theta_W}}\langle 36\rangle[45],\\ \mathcal{M}^{H\to ZZ \to 4\ell}(3^+_{\ell^- },4^-_{\ell^+},5^-_{\ell^- },6^+_{\ell^+}) =&f\times l_e r_e \frac{M_W^2}{\cos^2{\theta_W}}\langle 45\rangle[36], \end{aligned} $

$ \begin{aligned}[b] \mathcal{M}^{H\to ZZ \to 4\ell}(3^+_{\ell^- },4^-_{\ell^+},5^+_{\ell^- },6^-_{\ell^+}) =f\times r_e^2 \frac{M_W^2}{\cos^2{\theta_W}}\langle 46\rangle[35], \end{aligned} $

(4) where the common factor f is defined as
$ f=-2i{\rm e}^3\frac{1}{M_W\sin\theta_W} P_Z(s_{34}) P_Z(s_{56}), $

(5) with
$ P_X(s)=\frac{1}{s-M^2_X+{\rm i}M_X\Gamma_X} $

(6) as the propagator of particle X. Hence, the total amplitude of
$ gg \to H \to ZZ \to 4\ell $ is$ \begin{array}{*{20}{l}} \mathcal{M}^{gg\to H\to ZZ \to 4\ell}= \mathcal{M}^{gg\to H}\times P_H(s_{12}) \times \mathcal{M}^{H\to ZZ \to 4\ell }\; . \end{array} $

(7) The amplitude of the box process
$ gg \to ZZ \to 4\ell $ in Fig. 1(b) is complicated owing to box loop integration. Its full analytical form can be found in Ref. [25], which is coded in the MCFM package [39]. We can perform phase space integration and obtain numerical cross sections in the MCFM package.When studying the observable effects of BSM
$ HVV $ couplings, we can add BSM amplitudes to the MCFM package and obtain total and partial cross section results. Because the analytical form of each amplitude is clear, each contribution for the cross section can be singly shown. For example, the interference contribution from the SM Higgs and BSM Higgs processes can be calculated by selecting the$ {\text {Re}}(\mathcal{M}^{SM}_H \mathcal{M}^{\ast{BSM}}_{H}) $ part in the code. In the Higgs off-shell region, the interference contribution between the continuum background and BSM process is also important; therefore,$ {\rm {Re}}(\mathcal{M}^{SM}_{\text {box}} \mathcal{M}^{\ast{BSM}}_{H}) $ must be solely focused on. More details can be found in Ref. [31]. -
At the
$ e^+e^- $ collider, the two main processes with the$ HZZ $ coupling are the$ ZH $ process and vector boson fusion process. Their Feynman diagrams are shown in Fig. 2. In these two processes,$ e^+e^- $ are incoming particles and$ b\bar{b} \ell^+\ell^- $ (or$ b\bar{b} e^+e^- $ ) are outgoing particles. Because crossing symmetry illustrates that an incoming particle can be replaced by an outgoing antiparticle and leave the S-matrix unchanged, we can first calculate the amplitude with all particles outgoing and then deduce the amplitude for the physics process just by relabeling the momenta, helicities, and particle properties. We do not go into detail about using crossing symmetry because it is trivial once the rules are set. Instead, we focus on how to express process-independent amplitudes with all external particles outgoing. Later, we maintain this convention for all BSM amplitudes. Therefore, the amplitudes we require are the same for Fig. 2(a) and Fig. 2(b) if$ \ell $ is assumed to be e or both are assumed to be massless. They may be written as$ \begin{aligned}[b] \mathcal{M}({1_b, 2_{\bar{b}}, 3_{e^-},4_{e^+},5_{l^-},6_{l^+}}) =& \mathcal{M}(1_b, 2_{\bar{b}}, I_H)\times P_H(s_{12}) \\&\times \mathcal{M}(I^\prime_H, 3_{e^-},4_{e^+},5_{l^-},6_{l^+} )\; , \end{aligned} $

(8) where
$ I_H $ and$ I^\prime_H $ represent the mediate H, which is broken into two parts and appears in each of the smaller amplitudes. The amplitude$ \mathcal{M}(I^\prime_H, 3_{e^-},4_{e^+},5_{l^-},6_{l^+}) $ is calculated using Eq. (4), except that the momentum of the Higgs boson is flipped to be outgoing. In fact, because the Higgs is a scalar, the amplitude will remain unchanged in this case. One new amplitude we should pay attention to is$ \mathcal{M}(1_b, 2_{\bar{b}}, I_H) $ , which is$ \begin{aligned}[b] \mathcal{M}(2^-_b,3^-_{\bar{b}})=&\frac{-i m_b}{v}\langle12\rangle, \\ \mathcal{M}(2^+_b,3^+_{\bar{b}})=&\frac{-i m_b}{v}[12]. \end{aligned} $

(9) The external b,
$ \bar{b} $ quarks are assumed to be massless in the high energy limit. The$ H b \bar{b} $ coupling is still fixed to be proportional to$ m_b $ . The amplitudes for massive particles are realized in the massive spinor formalism and require little group indices [22, 40, 41], which relate$ \langle12\rangle $ to the bolded$ \langle {12}\rangle $ , for example. We study these in Sec. VI. -
In this section, we first introduce BSM
$ HVV $ effective couplings and define the$ CP $ violation phase. Then, we calculate their amplitudes. Finally, we discuss the interference contribution from the BSM amplitudes. -
In SMEFT [42–44], the complete form of higher-dimensional operators can be written as
$ \mathcal{L}=\mathcal{L}_{\rm SM}+\frac{1}{\Lambda}\sum\limits_k C_k^{5}\mathcal{O}_k^{5} +\frac{1}{\Lambda^2}\sum\limits_k C_k^{6}\mathcal{O}_k^{6}+\mathcal{O}(\frac{1}{\Lambda^3})\; , $

(10) where Λ is the energy scale of new physics, and
$ C_k^{i} $ with$i=5,~6$ are Wilson loop coefficients.BSM
$ HVV $ (V represents γ,$ Z/W $ boson) vertices start from dimension-six operators$ \mathcal{O}_k^{6} $ . In the Warsaw basis [43], they are$ \begin{aligned}[b] \mathcal{O}^6_{\Phi D} =&(\Phi^{\dagger}D^{\mu}\Phi)^{\ast}(\Phi^{\dagger}D^{\mu}\Phi), \\ \mathcal{O}^6_{\Phi W}=& \Phi^\dagger \Phi W^{I}_{\mu\nu}W^{I\mu\nu},\; \; \mathcal{O}^6_{\Phi B}= \Phi^\dagger\Phi B_{\mu\nu}B^{\mu\nu},\\ \mathcal{O}^6_{\Phi WB}=& \Phi^\dagger \tau^I \Phi W^{I}_{\mu\nu}B^{\mu\nu}, \\ \mathcal{O}^6_{\Phi \tilde{W}}=& \Phi^\dagger\Phi \tilde{W}^{I}_{\mu\nu}W^{I\mu\nu}, \\ \mathcal{O}^6_{\Phi \tilde{B}}= &\Phi^\dagger\Phi \tilde{B}_{\mu\nu}B^{\mu\nu}, \\ \mathcal{O}^6_{\Phi \tilde{W}B}=& \Phi^\dagger \tau^I \Phi \tilde{W}^{I}_{\mu\nu}B^{\mu\nu}, \end{aligned} $

(11) where Φ is a doublet representation under the
$S U(2)_L$ group, the aforementioned Higgs field H is one of its four components, and$D_\mu=\partial_\mu-{\rm i} g W^{I}_{\mu}T^{I}-{\rm i}g^{\prime}YB_\mu$ , where g and$ g^\prime $ are coupling constants,$ T^{I}=\tau^{I}/2 $ , where$ \tau^{I} $ are Pauli matrices, Y is the$ U(1)_Y $ generator,$ W^{I}_{\mu\nu}=\partial_\mu W^{I}_{\nu}-\partial_\nu W^{I}_\mu- g\epsilon^{IJK}W^{J}_\mu W^{K}_\nu $ ,$ B_{\mu\nu}=\partial_\mu B_\nu-\partial_\nu B_\mu $ , and$ \tilde{X}_{\mu\nu}= \frac{1}{2}\epsilon_{\mu\nu\rho\sigma}X^ {\rho\sigma} $ .After spontaneous symmetry breaking, we obtain the
$ HVV $ effective interactions$ \mathcal{L}^{\rm int}=-\frac{c_{VV}}{v}HV^{\mu\nu}V_{\mu\nu} -\frac{\tilde{c}_{VV}}{v}HV^{\mu\nu}\tilde{V}_{\mu\nu}\; , $

(12) $ c_{VV} $ and$ \tilde{c}_{VV} $ are real numbers that originate from the Wilson loop coefficients, and V represents the vector boson. A detailed formula for$ c_{VV} $ ,$ \tilde{c}_{VV} $ , and the Wilson loop coefficients$ C_k^6 $ can be found in Ref. [31]. A standard analysis based on SMEFT should be a global study involving all dimension-6 operators. Here, we concentrate only on the new$ HVV $ terms.Dimension-6 operators can originate from loop momentum integration in loop diagrams with multi-outlegs. The virtual particles in the loop can be both SM particles and BSM new particles. The difference between the two cases is that the SM processes have definite dimension-6 coupling coefficients, whereas the dimension-6 coefficients in NP are still to be determined.
The
$ CP $ violation phase can be defined as$ \xi\; \equiv\; {\rm tan}^{-1}(\tilde{c}_{VV}/c_{VV})\; , $

when
$ {\rm{ Arg}}(\tilde{c}_{VV}/c_{VV})=0\; \; {\rm or}\; \; \pi\; , $

(13) where
$ \xi=0\; (\dfrac{\pi}{2}) $ represents a pure$ CP $ -even (-odd)$ HVV $ vertex.$ \xi\neq 0 $ indicates$ CP $ violation, and$ \xi=\dfrac{\pi}{2} $ corresponds to maximal$ CP $ violation if other Higgs vertices are supposed to be$ CP $ -even. In the amplitudes, we see that ξ appears as a phase, which changes sign under$ CP $ transformation. This is why we refer to it as the$ CP $ violation phase. Meanwhile,$ \begin{array}{*{20}{l}} c^S_{VV}\equiv\sqrt{c^2_{VV}+\tilde{c}^2_{VV}} \end{array} $

(14) can be defined as the amplitude modulus, which is proportional to signal strength in collider experiments.
-
In the following sections, for simplicity, we only take the amplitude of Higgs decay with the BSM
$ HVV $ vertex as an example to illustrate the decomposition relation. This is also the process-independent amplitude because the Higgs boson is a scalar and the amplitude is free of its incoming or outgoing. Full amplitudes with Higgs production and decay can be easily obtained by multiplying the BSM Higgs decay amplitudes with the partial amplitude of the Higgs production$ \mathcal{M}^{gg\to H} $ in Eq. (1) and a Higgs propagator in Eq. (6) at the proton-proton collider, or by multiplying it with the partial amplitude of$ H\to b\bar{b} $ Eq. (9) and a Higgs propagator in Eq. (6) at the$ e^+e^- $ collider, similar to Eq. (7) or Eq. (8), as discussed in Sec. II.Feynman diagrams with effective
$ HVV $ couplings are shown in Fig. 3. After several calculations, the helicity amplitudes are obtained as follows:
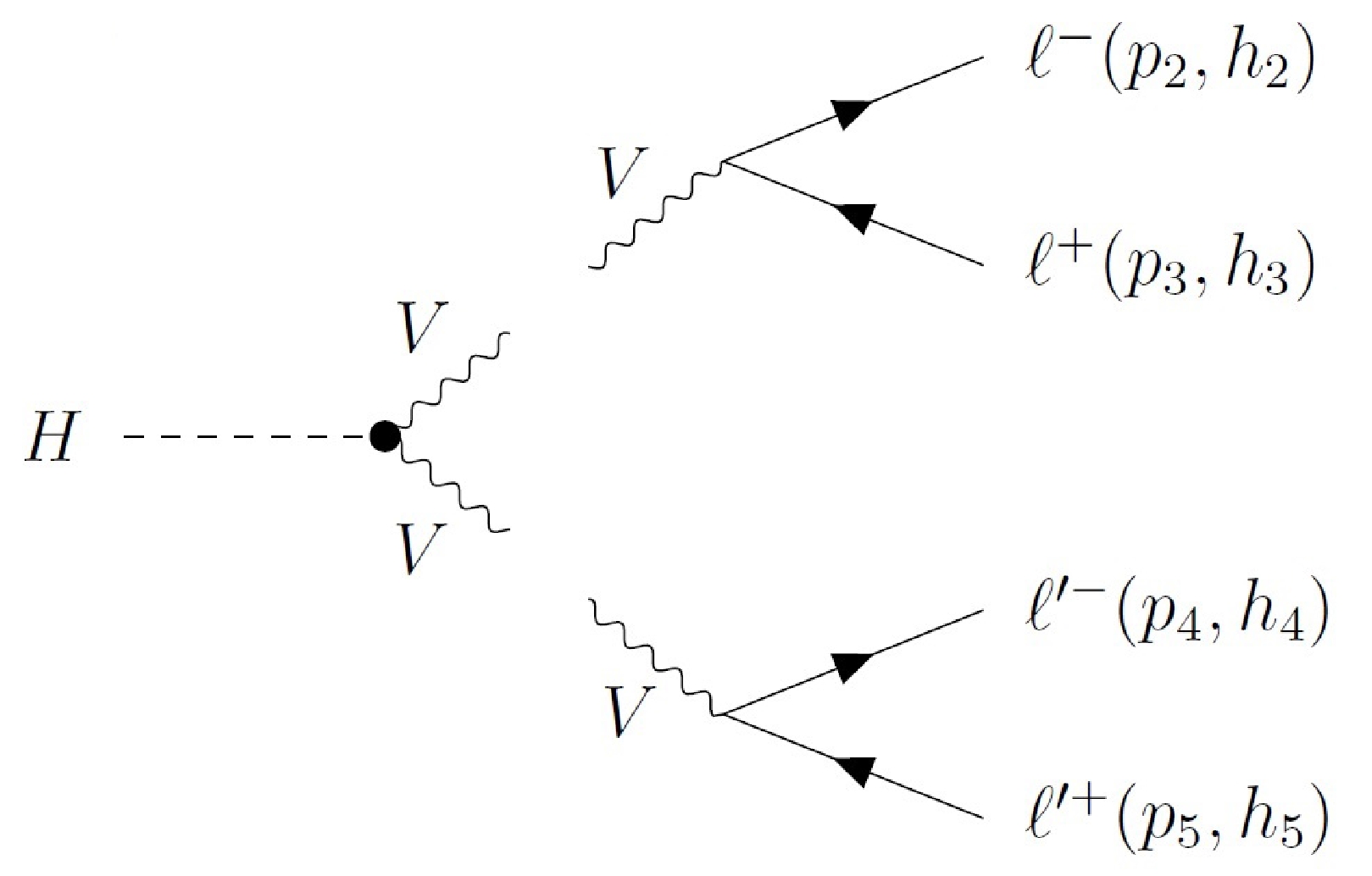
Figure 3. Feynman diagrams of
$ H\to \gamma \gamma $ ,$ H\to V \gamma\to \ell \ell \gamma $ , and$ H\to V V \to 2\ell 2\ell^\prime $ from left to right. Each$ HVV $ vertex is dotted as an effective coupling.● For the process
$ H\to\gamma \gamma $ ,$ \begin{aligned}[b] \mathcal{M}(2^+_\gamma,3^+_\gamma) =&\frac{2c^S_{\gamma\gamma}}{v}{\rm e}^{{\rm i}\xi}[23]^2\; , \\ \mathcal{M}(2^-_\gamma,3^-_\gamma) =&\frac{2c^S_{\gamma\gamma}}{v}{\rm e}^{-{\rm i}\xi}\langle23\rangle^2\; ,\\ \mathcal{M}(2^+_\gamma,3^-_\gamma)=&0\; , \\ \mathcal{M}(2^-_\gamma,3^+_\gamma)=&0\; , \end{aligned} $

(15) where we use
$\mathcal{M}(2_\gamma^{h_2},~3_\gamma^{h_3})$ to represent$\mathcal{M}(1_H^{h_1},~2_\gamma^{h_2},~3_\gamma^{h_3})$ because$ h_1 $ is trivially zero for all cases, and$ h_i $ are the helicities of the external legs with momentum outgoing. The results show that the helicities of the two photons should keep the same sign because the spin of the Higgs is zero and the total angular momentum is conserved. Under$ CP $ transformation,$\mathcal{M}(2^{+}_\gamma,~3^{+}_\gamma)$ changes to$\mathcal{M}(2^{-}_\gamma,~3^{-}_\gamma)$ . Analytically, this corresponds to$ \langle i j \rangle $ changing to$ [i j] $ . Thus, in Eq. (15), a general nonzero ξ represents$ CP $ violation.● For the process
$ H\to V \gamma\to \ell \ell \gamma $ ,$ \begin{aligned}[b] \mathcal{M}(2^-_{\ell^- },3^+_{\ell^+},4^-_\gamma) =&f^-_{V}(s_{23})\times \frac{2c^S_{\gamma V}}{v}{\rm e}^{-{\rm i}\xi}[23]\langle 24\rangle^2, \\ \mathcal{M}(2^-_{\ell^- },3^+_{\ell^+},4^+_\gamma) =&f^-_{V}(s_{23})\times \frac{2c^S_{\gamma V}}{v}{\rm e}^{{\rm i}\xi}\langle 23\rangle[34]^2, \\ \mathcal{M}(2^+_{\ell^- },3^-_{\ell^+},4^+_\gamma) =&f^+_{V}(s_{23})\times \frac{2c^S_{\gamma V}}{v}{\rm e}^{{\rm i}\xi}\langle 23\rangle[24]^2, \\ \mathcal{M}(2^+_{\ell^- },3^-_{\ell^+},4^-_\gamma) =&f^+_{V}(s_{23})\times \frac{2c^S_{\gamma V}}{v}{\rm e}^{-{\rm i}\xi}[23]\langle 34\rangle^2, \end{aligned} $

(16) where
$ s_{23}=(p_2+p_3)^2 $ ,$ f^-_{V}(s)=\sqrt{2}\; e\; l_VP_V(s) $ ,$ f^+_{V}(s)= -\sqrt{2}\; e\; r_VP_V(s) $ ,$ P_V(s)=\dfrac{1}{s-M^2_V} $ is the propagator of the gauge boson,$ l_V $ and$ r_V $ are theleft-handed and right-handed couplings between the vector boson and leptons, respectively, and leptons are supposed to be massless. The remaining helicity amplitudes are equal to zero and thus are not listed.● For the process
$ H\to V V \to 2\ell 2\ell^\prime $ ,$ \begin{aligned}[b] \mathcal{M}(2^-_{\ell^-},3^+_{\ell^+ },4^-_{\ell^{\prime -}},5^+_{\ell^{\prime +}}) =&f^-_{V}(s_{23})f^-_{V}(s_{45}) \frac{2c^S_{VV}}{v} \Big( {\rm e}^{{\rm i}\xi}\langle 23\rangle \langle 45\rangle [35]^2\\&+{\rm e}^{-{\rm i}\xi} [23][45]\langle 24\rangle^2 \Big), \\ \mathcal{M}(2^-_{\ell^-},3^+_{\ell^+ },4^+_{\ell^{\prime -}},5^-_{\ell^{\prime +}}) =&f^-_{V}(s_{23})f^+_{V}(s_{45}) \frac{2c^S_{VV}}{v} \Big( {\rm e}^{{\rm i}\xi}\langle 23\rangle \langle 45\rangle [34]^2\\&+{\rm e}^{-{\rm i}\xi} [23][45]\langle 25\rangle^2 \Big), \\ \mathcal{M}(2^+_{\ell^-},3^-_{\ell^+ },4^-_{\ell^{\prime -}},5^+_{\ell^{\prime +}}) =&f^+_{V}(s_{23})f^-_{V}(s_{45}) \frac{2c^S_{VV}}{v} \Big( {\rm e}^{{\rm i}\xi}\langle 23\rangle \langle 45\rangle [25]^2\\&+{\rm e}^{-{\rm i}\xi} [23][45]\langle 34\rangle^2 \Big), \\ \mathcal{M}(2^+_{\ell^-},3^-_{\ell^+ },4^+_{\ell^{\prime -}},5^-_{\ell^{\prime +}}) =&f^+_{V}(s_{23})f^+_{V}(s_{45}) \frac{2c^S_{VV}}{v} \Big( {\rm e}^{{\rm i}\xi}\langle 23\rangle \langle 45\rangle [24]^2\\&+{\rm e}^{-{\rm i}\xi} [23][45]\langle 35\rangle^2 \Big), \end{aligned} $

(17) where
$ VV $ can be$ \gamma\gamma $ ,$ ZZ $ ,$ \gamma Z $ , or$ W^+W^- $ . However, when it represents$ \gamma Z $ or$ W^+W^- $ , the original Lagrangian in Eq. (12) should be scaled by a factor of$ 2 $ overall to ensure a consistent formula. The remaining helicity amplitudes are equal to zero. -
Using the compact form of the amplitudes and the definition of
$ CP $ violation phases angle, it is interesting to compare the SM$ HVV $ amplitudes with BSM$ HVV $ amplitudes and then show how we can extract these BSM contributions in collider experiments.First, we compare the SM
$ H\gamma\gamma $ amplitudes with BSM$ H\gamma\gamma $ amplitudes. The SM$ H\gamma\gamma $ amplitudes can be obtained by replacing the coefficient$ C_g $ with$ C_\gamma $ in Eq. (1), where$ C_\gamma $ represents the triangle loop integral from both the top quark loop and W boson loop [45]. The BSM$ H\gamma\gamma $ amplitudes are shown in Eq. (15). Comparing Eq. (1) with Eq. (15), their spinor structures are the same, whereas the$ CP $ violation phase and coefficients are different. Therefore, for interference between these two amplitudes, the kinematic observables (such as the shape of the angular distribution of the external particles) will remain unchanged, except for an overall scale factor.Next, we compare the SM and BSM amplitudes in Eqs. (4) and (17) for the
$ H\to ZZ \to 4\ell $ processes. Their spinor structures are completely different, as each SM amplitude has two brackets (including both$ \langle\rangle $ and$ [] $ ) and one term, whereas the BSM amplitudes have four brackets and two summed terms. The two additional brackets in the BSM amplitudes originate from the partial derivatives in the dimension-6 operators, as shown in Eq. (12). Therefore, the extra momentum dependence of the BSM scattering amplitudes can be regarded as an indication of the momentum dependence of BSM couplings. It is obvious that this interference contribution between BSM and SM amplitudes, which is proportional to the momentum of the external particles, will be enhanced in the high energy region. In other words, the interference effects are expected to be searched for sensitively in the off-shell Higgs high energy region [31]. -
The amplitudes of
$ CP $ violation$ HVV $ processes in Eqs. (15), (16), and (17) have similar structures. In the$ H\to\gamma\gamma $ and$ H\to \ell\ell \gamma $ processes, there is only one term for each helicity amplitude. The$ CP $ violation phase exhibits as a global phase. However, in the$ H\to 4\ell $ process, two terms appear, and the$ CP $ violation phases have reverse signs. To explore how amplitudes change when external legs increase, we find a decomposition relation for a particular type of n-particle effective interaction. Then, we apply it to the$ HVV $ effective interactions and derive the corresponding amplitudes. -
Consider the amplitudes
$ M_{\mathrm{lower}} $ and$ M_{\mathrm{higher}} $ with m and more than m external lines, which both include m-particle effective interactions, for example, Fig. 4. In$ M_{\mathrm{higher}} $ , all propagators are vector bosons and are attached to the m-particle effective vertex. Therefore, vector bosons will be crucial in the construction of$ M_{\mathrm{higher}} $ . In this subsection, we assume that the vector bosons in$ M_{\mathrm{higher}} $ are massless to derive the decomposition relation. Because the contraction of the massless fermion current with the massless vector propagator is the same as that with massive vector bosons, the decomposition relations are valid for massive vector bosons. In the massive case, the vector bosons in$ M_{\mathrm{lower}} $ are still massless, but the vector bosons in$ M_{\mathrm{higher}} $ may be massive. For convenience, we relabel the momenta of$ M_{\mathrm{lower}} $ from$\{p_1,p_2,\cdots,~ p_m\}$ to$\{l_1,l_2,\dots,~l_{m-n};~k_1,k_2,\dots,~k_n\}$ , where k corresponds to the momenta of gauge bosons, and l corresponds to those of the others. Now, we express$ M_{\mathrm{lower}} $ in terms of the polarization$ \epsilon $ and vertex Γ,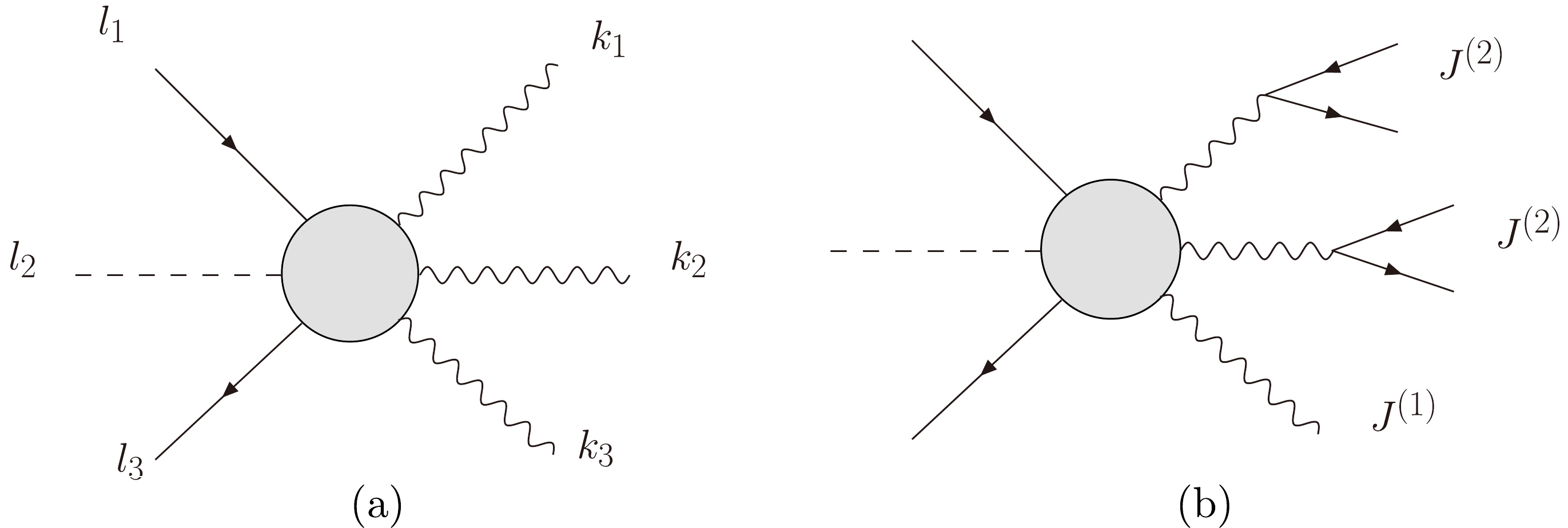
Figure 4. Diagram (a) and (b) are two examples of
$ M_{\mathrm{lower}} $ and$ M_{\mathrm{higher}} $ , where the circle represents the same effective interaction. In$ M_{\mathrm{lower}} $ ,$ k_i $ and$ l_i $ characterize vector bosons and other particles. In$ M_{\mathrm{higher}} $ , several external vector bosons are replaced with the current$ J^{(2)} $ , while the others are noted by$ J^{(1)} $ .$ \begin{aligned}[b]& M_{\mathrm{lower}}(l_1,\dots,l_{m-n};k_1^{h_1},\dots,k_n^{h_n})\\=&\Gamma^{\mu_1\cdots \mu_n}(k_1,\cdots,k_n)\prod\limits_i\epsilon^{h_i}_{\mu_i}(k_i,r_i)\; , \end{aligned} $

(18) where
$ h_i $ and$ r_i $ are the helicity and reference momentum of gauge boson i, respectively. Here, Γ is not the conventional vertex in SM Feynman diagrams.The decomposition relation is based on two key points. The first is that the BSM vertex Γ is multilinear to the momenta of vector bosons,
$ \begin{equation} \Gamma^{\mu_1\cdots \mu_n}(k_1,\dots,k_n)=\sum\limits_{j_1,\dots,j_n} \Gamma^{\mu_1\cdots \mu_n}(q_{1j_1},\dots,q_{nj_n})\; , \end{equation} $

(19) where
$ \begin{equation} k_i=\sum\limits_{j_i=1}^{n_i} q_{i j_i},\quad n_i = 1,2. \end{equation} $

(20) The second point is that the current
$ J_\mu $ is proportional to the polarization vector of a photon$ \epsilon_\mu $ . They can be written in uniform notation as$ \begin{equation} \begin{aligned} J^{(n_i)}_\mu(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}}) &=F^{(n_i)}_{q_{ij_i}}(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}})\epsilon_\mu^{H_{ij_i}}(q_{ij_i},r_{ij_i})\; , \end{aligned} \end{equation} $

(21) where
$ n_i $ is the number of external particles, and F is a factor. The helicity$ H_{ij_i} $ is a function of$ h_{ij_i} $ . When$ n_i=1 $ , it reduces to the polarization$ \epsilon_\mu $ and$ H_{i1}=h_{i1} $ . In this case, the reference momentum$ r_{ij_i} $ is arbitrary. When$ n_i=2 $ , it reduces to the current, whose expression will be given in the next subsection.Now, we express
$ M_{\mathrm{higher}} $ in terms of Γ and$ J^{(n_i)} $ . Combining Eqs. (19) and (21), it reduces to$ \begin{aligned}[b]\\ M_{\mathrm{higher}} &=\Gamma^{\mu_1\cdots \mu_n}(k_1,\dots,k_n)\prod\limits_i J^{(n_i)}_\mu(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}})=\sum\limits_{j_1,\dots,j_n} \Gamma^{\mu_1\cdots \mu_n}(q_{1j_1},\dots,q_{nj_n})\prod\limits_i F^{(n_i)}_{q_{ij_i}}(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}})\epsilon_\mu^{H_{i j_i}}(q_{ij_i},r_{ij_i})\\ &=\sum\limits_{j_1,\dots,j_n} F^{(n_i)}_{q_{ij_i}}(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}}) \Gamma^{\mu_1\cdots \mu_n}(q_{1j_1},\dots,q_{nj_n}) \prod\limits_i \epsilon_\mu^{H_{i j_i}}(q_{ij_i},r_{ij_i})=\sum\limits_{j_1,\dots,j_n} F^{(n_i)}_{q_{ij_i}}(q_{i1}^{h_{i1}},\dots,q_{in_i}^{h_{in_i}}) M_{\mathrm{lower}}(q_{i1}^{H_{ij_1}},\dots,q_{in_i}^{H_{ij_n}})\\ \end{aligned} $ 
(22) where we ignore the momenta l in
$ M_{\mathrm{lower}} $ . This is the decomposition relation for helicity amplitudes.Here, the multilinear property of the momentum dependence in the vertex Γ is crucial for the decomposition of helicity amplitudes. One may worry about the universality of this multilinear vertex, which may limit the usage of the decomposition relation. Our argument is that this multilinear momentum dependent vertex is widely observed in high dimensional couplings, both in the SM framework with loops and effective high dimensional operators. As shown in the next subsection, the momentum of the vector bosons in these vertices arises from the partial derivative of the vector boson in the Lagrangian, which is common, especially in higher dimensional operators.
-
Now, we aim to discover what types of effective interactions will give multilinear vertices. Because Γ is multilinear, each vector boson momentum should be linear in these vertices. This implies that there is no
$ D_\mu $ in the effective interactions. All momenta originate from the field strength tensor$ X_{\mu\nu} $ .In dimension-6 operators, there are only three types of effective operators,
$ \psi^2 X\varphi $ ,$ X^2\varphi^2 $ , and$ X^3 $ , fulfilling these conditions. The corresponding multilinear vertices are$ \begin{equation} \begin{aligned} (\bar{\psi}\gamma^{\mu\nu}\psi)\varphi X_{\mu\nu}&: &\Gamma^\mu(k_1)&=[l_1|k_1\gamma^\mu|l_2]+[l_1|\gamma^\mu k_1|l_2],\\ \varphi^2 X^{\mu\nu}X_{\mu\nu}&: &\Gamma^{\mu\nu}(k_1,k_2)&=k_1^\mu k_2^\nu-g^{\mu\nu}k_1\cdot k_2,\\ \mathrm{tr}(X^\mu_\nu X^\nu_\rho X^\rho_\mu )&: &\Gamma^{\mu\nu\rho}(k_1,k_2,k_3)&=k_1^\nu k_2^\rho k_3^\mu+\cdots.\\ \end{aligned} \end{equation} $

(23) The decomposition relation of Eq. (22) can be applied to these effective interactions.
From now on, we return to the
$ HVV $ vertex from Eq. (12) and use the label$\{p_1,p_2,\dots,p_m\}$ . This vertex is bilinear to the momenta of vector bosons, which is$ \begin{array}{*{20}{l}} \Gamma^{\mu\nu}(k,k^{\prime})= -i\frac{4}{v}[c_{VV}\; (k^{\nu} k^{\prime\mu}-k\cdot k^{\prime}g^{\mu\nu})+\tilde{c}_{VV}\; \epsilon^{\mu\nu\rho\sigma} k_{\rho}k^{\prime}_{\sigma} ]\; , \end{array} $

(24) where k,
$ k^{\prime} $ are the momenta of the two vector bosons. Hence, when$ k=p_2+p_3 $ or$ k^\prime=p_4+p_5 $ , or both, where$ p_i $ is the momentum of the external legs, we have$ \Gamma^{\mu\nu}(k,k^{\prime}) =\Gamma^{\mu\nu}(p_2+p_3,k^{\prime}) =\Gamma^{\mu\nu}(p_2,k^{\prime})+\Gamma^{\mu\nu}(p_3,k^{\prime}) $

(25) $ \begin{aligned}[b]&\quad\quad =\Gamma^{\mu\nu}(p_2+p_3,p_4+p_5) =\Gamma^{\mu\nu}(p_2,p_4)+\Gamma^{\mu\nu}(p_2,p_5) \\&\;\;\quad\quad+\Gamma^{\mu\nu}(p_3,p_4) +\Gamma^{\mu\nu}(p_3,p_5). \end{aligned} $

(26) However, we explicitly express the current
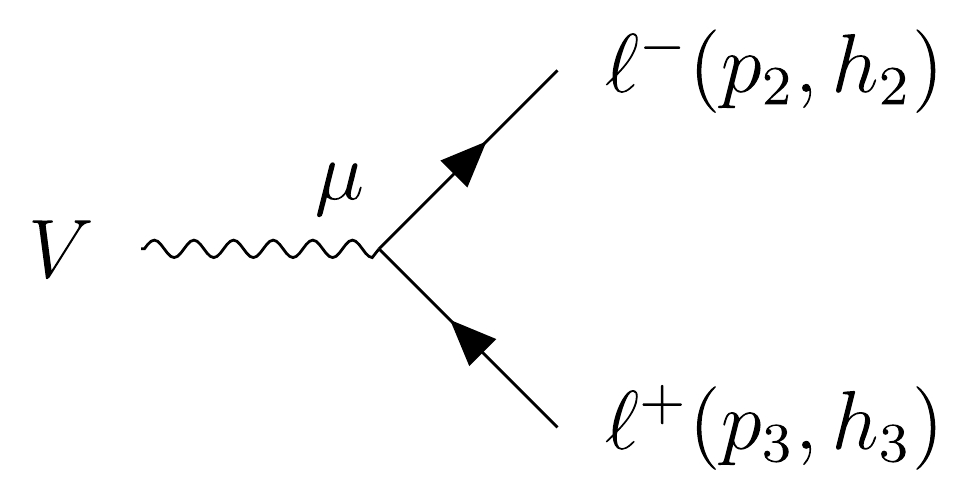
$ J_\mu $ of$ V\to\ell^+\ell^- $ in Fig. 5,$ J^{(2)}_\mu(p_2^{\mp\frac{1}{2}},p_3^{\pm\frac{1}{2}}) =\frac{f^{\mp}_V(s_{23})}{\sqrt{2}}\langle 2^\mp|\gamma_\mu| 3^{\mp}\rangle $

(27) $\quad\quad\quad\quad\quad =\pm f^{\mp}_V(s_{23})\langle2^\mp|3^\pm\rangle\epsilon_\mu^\pm(3,2) $

(28) $\quad\quad\quad\quad\quad =\pm f^{\mp}_V(s_{23})\langle2^\pm|3^\mp\rangle\epsilon_\mu^\mp(2,3), $

(29) where
$ \epsilon_\mu^\pm(3,2)\equiv\epsilon_\mu^\pm(p_3,p_2) $ can be considered a polarization vector of a photon with external momentum$ p_3 $ , and$ p_2 $ is the chosen reference momentum. Similarly,$ \epsilon_\mu^\pm(2,3) $ represents a photon with external momentum$ p_2 $ and reference momentum$ p_3 $ . In principle,$ J_\mu $ is a gauge-dependent quantity. Because we ignore the mass of leptons, it can be considered a gauge-independent quantity in our proof.According to Eqs. (28) and (29), we know that
$ H_{ij_i}=2h_{ij_i} $ , and the expressions of$ F^{(2)} $ are$ \begin{aligned}[b] F^{(2)}_{q_{i1}}(q_{i1}^{-\frac{1}{2}},q_{i2}^{+\frac{1}{2}}) &=f^-_V(k_i^2)[q_{i1}q_{i2}],\\ F^{(2)}_{q_{i2}}(q_{i1}^{-\frac{1}{2}},q_{i2}^{+\frac{1}{2}}) &=f^-_V(k_i^2)\langle q_{i1}q_{i2}\rangle,\end{aligned} $

$ \begin{aligned}[b] F^{(2)}_{q_{i1}}(q_{i1}^{+\frac{1}{2}},q_{i2}^{-\frac{1}{2}}) &=-f^+_V(k_i^2)\langle q_{i1}q_{i2}\rangle,\\ F^{(2)}_{q_{i2}}(q_{i1}^{+\frac{1}{2}},q_{i2}^{-\frac{1}{2}}) &=-f^+_V(k_i^2)[q_{i1}q_{i2}]. \end{aligned} $

(30) Based on these equations, we may decompose the amplitudes of
$ H\to V \gamma\to \ell \ell \gamma $ as$ \begin{aligned}[b] \mathcal{M}(2^-_{\ell^- },3^+_{\ell^+},4^-_\gamma) =&F^{(2)}_{p_2}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})\mathcal{M}(2_\gamma^-,4_\gamma^-)\\&+F^{(2)}_{p_3}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})\mathcal{M}(3_\gamma^+,4_\gamma^-)\\ =&f^l_V(s_{23})\times([23]\mathcal{M}(2_\gamma^-,4_\gamma^-)\\&+ \langle 23\rangle\mathcal{M}(3_\gamma^+,4_\gamma^-)), \end{aligned} $

(31) In the last step, the reference momenta of photons are different, which does not affect the form of
$ \mathcal{M}(\gamma,\gamma) $ because the vertex$ \Gamma^{\mu\nu} $ satisfies the Ward identity. The other helicity amplitudes of$ H\to V \gamma\to \ell \ell \gamma $ have a similar decomposition. An illustration of Eq. (31) is shown in Fig. 6. Each amplitude of$ H\to V \gamma\to \ell\ell\gamma $ is composed of two amplitudes of$ H\to \gamma \gamma $ , which degenerate to one term because the amplitude of$ H\to \gamma \gamma $ with reverse helicities is equal to zero. Therefore, the$ CP $ violation phase is maintained as a global phase in the$ H\to V \gamma\to \ell\ell\gamma $ process.Next, we prove that the decomposition relation is also suitable for the
$ H\to V V \to 4\ell $ process. That is,$ \begin{aligned}[b] &\mathcal{M}(2^-_{\ell^-},3^+_{\ell^+ },4^-_{\ell^{\prime -}},5^+_{\ell^{\prime +}})\\ =&F^{(2)}_{p_2}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})F^{(2)}_{p_4}(p_4^{-\frac{1}{2}},p_5^{+\frac{1}{2}})\mathcal{M}(2_\gamma^-,4_\gamma^-)\\ &+F^{(2)}_{p_2}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})F^{(2)}_{p_5}(p_4^{-\frac{1}{2}},p_5^{+\frac{1}{2}})\mathcal{M}(2_\gamma^-,5_\gamma^+)\\ &+F^{(2)}_{p_3}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})F^{(2)}_{p_4}(p_4^{-\frac{1}{2}},p_5^{+\frac{1}{2}})\mathcal{M}(3_\gamma^+,4_\gamma^-)\\ &+F^{(2)}_{p_3}(p_2^{-\frac{1}{2}},p_3^{+\frac{1}{2}})F^{(2)}_{p_5}(p_4^{-\frac{1}{2}},p_5^{+\frac{1}{2}})\mathcal{M}(3_\gamma^+,5_\gamma^+) \end{aligned} $

(32) $ \begin{aligned}[b] =& f^l_V(s_{23})f^l_V(s_{45})\times ( [23][45]\mathcal{M}(2_\gamma^-,4_\gamma^-) + [23]\langle 45\rangle\mathcal{M}(2_\gamma^-,5_\gamma^+)\\& + \langle 23\rangle [45] \mathcal{M}(3_\gamma^+,4_\gamma^-) + \langle 23\rangle\langle 45\rangle \mathcal{M}(3_\gamma^+,5_\gamma^+)\; ), \end{aligned} $

(33) where for the specific helicity states in Eq. (32), one term of
$ H\to 4\ell $ is decomposed into four terms. Furthermore, the four terms in Eq. (33) degenerate to two terms because reverse-sign$ H\to\gamma\gamma $ amplitudes are zero, as shown in Eq. (17). The diagrams are shown in Fig. 7.One may think it is ridiculous at first glance of the decomposition of the scattering amplitude of
$ H\to 4\ell $ into a combination of four$ H\to \gamma\gamma $ amplitudes because the final decay products of leptons are strangely changed into photons. We argue that this result is instructive and has a profound physical meaning. The amplitude of Higgs decay can be considered a function of the momentum of its decay products. Here, we simply find the form of the momentum dependence between the$ H\to 4\ell $ and$ H\to \gamma\gamma $ amplitudes. One can easily convert this result into similar processes obeying the two aforementioned key preconditions. Our results provide a new viewpoint for the amplitude of the multiple decays of the Higgs. -
From the decomposition relations, we see that the amplitudes of
$ H\to\gamma\gamma $ are the bases for other amplitudes. Because$ \mathcal{M}(+,-)=\mathcal{M}(-,+)=0 $ , the left bases are$ \mathcal{M}(+,+) $ and$ \mathcal{M}(-,-) $ .$ CP $ violation phases are reverse in the two bases. In the$ H\to\gamma\gamma $ and$ H\to V\gamma \to \ell\ell\gamma $ processes, the$ CP $ violation phase is a global phase in each amplitude. Therefore, generally, it is an unobservable phase if interference between this amplitude and background amplitudes is not considered [29, 30]. In the$ H\to 4\ell $ process, two bases coexist in each amplitude, and thus the$ CP $ violation phase appears as a physical observable. Moreover, this means that interference between the$ CP $ -even term and$ CP $ -odd term exists at the differential cross section level after squaring the amplitude. Therefore, the interference can be probed through kinematic angles [28, 31–33]. An obvious effect is a shift in the azimuthal angle caused by the interference between$ CP $ -even and$ CP $ -odd terms. Hence, we see the$ CP $ phase angle dependence clearly in$ HVV $ processes for the benefit of our amplitude decomposition relations. -
In the on-shell approach, the amplitude is not derived from Lagrangian and Feynman rules. Instead, it is constructed directly from on-shell particle states. In this section, we first introduce spinor variables for particles. We then show how the amplitudes of
$ H\gamma\gamma $ are represented and fixed. Finally, we obtain the amplitudes of$ H\gamma\ell\ell $ and$ H 4\ell $ through recursion relations. -
The right-handed and left-handed spinors in Eq. (3) have two-component versions [37, 38],
$ \begin{aligned}[b]& | i_\alpha \rangle \equiv \lambda_{i\alpha}\equiv u_+(p_i) \equiv |i^+ \rangle,\;\; |i^{\dot\alpha} ] \equiv \tilde\lambda^{\dot\alpha}_i\equiv u_-(p_i) \equiv |i^- \rangle, \\& \langle i^\alpha | \equiv \lambda_{i}^\alpha\equiv \overline{u_-(p_i)} \equiv \langle i^- |, \;\; [i_{\dot\alpha} | \equiv \tilde\lambda_{i\dot\alpha}\equiv \overline{u_+(p_i)} \equiv \langle i^+ |, \end{aligned} $

(34) where the spinor indices can be raised or lowered by the antisymmetric tensors
$ \epsilon^{\alpha\beta} $ and$ \epsilon_{\alpha\beta} $ ,$ \begin{array}{*{20}{l}} \lambda^\alpha=\epsilon^{\alpha\beta}\lambda_\beta,\quad \lambda_\alpha=\epsilon_{\alpha\beta}\lambda^\beta\; . \end{array} $

(35) In this notation,
$ \begin{array}{*{20}{l}} \langle i j \rangle \equiv \lambda_{i}^\alpha \lambda_{j\alpha}, \quad [ij] \equiv \tilde\lambda_{i\dot\alpha} \tilde\lambda^{\dot\alpha}_j\; . \end{array} $

(36) The on-shell momentum of a massless particle is represented as
$ \begin{array}{*{20}{l}} p_{\alpha\dot{\alpha}} \equiv p_\mu\sigma^{\mu}_{\alpha\dot{\alpha}} =\lambda_\alpha\tilde{\lambda}_{\dot{\alpha}}, \end{array} $

(37) where
$ \sigma^{\mu}=(1,\vec{\sigma}) $ , with$ \vec{\sigma} $ representing the Pauli matrices. -
A general three point amplitude with the interaction of one massive and two massless particles is shown in Fig. 8 [22], where
$ \alpha_i $ ,$ i=1,2,...,2S $ are the indices of spinors, S represents the spin of the massive particle, and$ h_2 $ ,$ h_3 $ are the helicities of the two massless particles.
Figure 8. General one massive and two massless particle interaction. The subscript S represents the spin of the massive particle, and
$ h_2 $ ,$ h_3 $ are the helicities of the two massless particles.For the amplitude of
$ H\gamma\gamma $ , because the massive particle H is a scalar with zero spin, we do not need to carefully consider its spinors, which makes the formula significantly simpler. The general ansatz is [22, 46, 47]$ \mathcal{M}_3(1_H,2_\gamma^{h_2},3_\gamma^{h_3})={\rm e}^{{\rm i}\xi^{h_2,h_3}}\frac{g}{m^{h_2+h_3-1}} [23]^{h_2+h_3}\; , $

(38) where
$\xi^{h_2,~h_3}$ represents a helicity-related phase, g represents an overall coupling constant, and m is the mass of the Higgs boson. Because$ \langle 23\rangle [32]=(p_2+p_3)^2=p_1^2=m^2 $ ,$ \langle 23\rangle =\dfrac{m^2}{[32]} $ . The little group scaling [20, 21] requires$ h_2+h_3=2h_2=2h_3 $ ; therefore,$\mathcal{M}(2_\gamma^{+},~3_\gamma^{-})= \mathcal{M}(2_\gamma^{-},~3_\gamma^{+})=0$ . The non-zero amplitudes are only$\mathcal{M}(2_\gamma^{+},~3_\gamma^{+})$ and$\mathcal{M}(2_\gamma^{-},~3_\gamma^{-})$ . Generality is not lost to require$ \xi^{+,+}= -\xi^{-,-}=\xi^\prime $ because their equal parts can be absorbed into the redefinition of g. The inequality of$|\mathcal{M}(2_\gamma^{+},~3_\gamma^{+})|\neq|\mathcal{M}(2_\gamma^{-},~3_\gamma^{-})|$ may also cause$ CP $ violation; however, this is not favored by physics assumptions. Specifically, from the Lagrangian in Eq. (12) we need$ C_{VV} $ and$ \tilde{C}_{VV} $ to be real to maintain the Lagrangian Hermitian conjugate so that it results in$|\mathcal{M}(2_\gamma^{+},~3_\gamma^{+})|=|\mathcal{M}(2_\gamma^{-},~3_\gamma^{-})|$ as in Eq. (15). From the above discussion, the nonzero amplitudes are$ \mathcal{M}_3(1_H,2_\gamma^+,3_\gamma^+)={\rm e}^{{\rm i}\xi^\prime}\frac{g}{m} [23]^2\; , $

(39) $ \mathcal{M}_3(1_H,2_\gamma^-,3_\gamma^-)={\rm e}^{-{\rm i}\xi^\prime}\frac{g}{m} \langle 23 \rangle^2\; , $

(40) which is equal to Eq. (15) as long as we require
$ \dfrac{g}{m}=\dfrac{2c^S_{\gamma\gamma}}{v} $ and$ \xi^\prime=\xi $ . -
The amplitudes of
$ H\to \gamma \ell \ell $ can be constructed from three point amplitudes using the recursion relations. For the amplitude of$ H\to \gamma \ell \ell $ , a factorization approach is$ H\to \gamma V, V\to \ell \ell $ . Figure 9 shows this factorization. The mediate particle is taken as γ to aviod the amplitudes of massive particles; its momentum is marked as "I." We shift the momenta of the$ 2,4 $ external particles according to the BCFW recursion relation approach [48–50]. That is,
Figure 9. Factorization of
$ H\to \gamma \ell \ell $ . We take the mediate particle as γ for simplicity.$ \begin{array}{*{20}{l}} |\hat{2}]=|2], \quad |\hat{4}]=|4]+z|2], \quad|\hat{4}\rangle=|4\rangle, \quad |\hat{2}\rangle=|2\rangle-z|4\rangle, \end{array} $

(41) where z is a complex number, and shifted momenta are hatted.
The corresponding analytical formula is
$ \begin{aligned}[b]& \mathcal{M}(1_{H},2^{h_2}_{\ell^- },3^{h_3}_{\ell^+},4^{h_4}_\gamma) \\=&P_\gamma(s_{23}) \mathcal{M}(1_H,\hat{4}^{h_4}_\gamma,-\hat{P}^-_{I\gamma}) \mathcal{M}(\hat{P}^+_{I\gamma},\hat{2}^{h_2}_{\ell^- },3^{h_3}_{\ell^+})\; \\ &+P_\gamma(s_{23}) \mathcal{M}(1_H,\hat{4}^{h_4}_\gamma,-\hat{P}^+_{I\gamma}) \mathcal{M}(\hat{P}^-_{I\gamma},\hat{2}^{h_2}_{\ell^- },3^{h_3}_{\ell^+})\; , \end{aligned} $

(42) where
$ \hat{p}_I=p_1+\hat{p}_4=-(\hat{p}_2+p_3 $ ) is the momentum of the mediate photon, and$ P_\gamma(s_{23})=1/s_{23}=1/(p_2+p_3)^2 $ is the propagator with unshifted momenta.The helicity amplitudes of
$ \gamma\ell^-\ell^+ $ are three point amplitudes with massless particles, which are fully fixed by little group scaling and dimension analysis,$ \mathcal{M}({1}^-_\gamma,{2}^-_{\ell^- },3^+_{\ell^+}) =\tilde{e}\frac{\langle 1 2\rangle^2}{\langle 23\rangle}\; , $

(43) $ \mathcal{M}({1}^-_\gamma,{2}^+_{\ell^- },3^-_{\ell^+}) =\tilde{e}\frac{\langle 1 3\rangle^2}{\langle 23\rangle}\; , $

(44) $ \mathcal{M}({1}^+_\gamma,{2}^-_{\ell^- },3^+_{\ell^+}) =\tilde{e}\frac{[ 1 3]^2}{[23]}\; , $

(45) $ \mathcal{M}({1}^+_\gamma,{2}^+_{\ell^- },3^-_{\ell^+}) =\tilde{e}\frac{[ 1 2]^2}{[23]}\; , $

(46) where
$ \tilde{e}=-\sqrt{2}e $ , Eqs. (43) and (44) correspond to the$ [23]=0 $ solution, and Eqs. (45) and (46) correspond to the$ \langle 23 \rangle=0 $ solution.After inserting Eqs. (40) and (43) into Eq. (42), we get
$ \begin{aligned}[b]& \mathcal{M}(1_{H},2^-_{\ell^- },3^+_{\ell^+},4^-_\gamma) \\=&\tilde{e}P_\gamma(s_{23})\times\frac{2c^S_{\gamma V}}{v}e^{-i\xi} \frac{\langle \hat{I} \hat{4} \rangle^2 [\hat{I}3]^2}{[\hat{2}3]}, \\ =&\tilde{e}P_\gamma(s_{23})\times\frac{2c^S_{\gamma V}}{v}e^{-i\xi} [23]\langle 24\rangle^2, \end{aligned} $

(47) where the last equation is because
$ \begin{aligned}[b] \langle \hat{4}\hat{I} \rangle [\hat{I} 3]=&\langle \hat{4}|\hat{p}_I |3] =\langle \hat{4}|\hat{p}_2+p_3 |3] \\=&\langle \hat{4}|\hat{p}_2 |3] =\langle \hat{4} \hat{2} \rangle [\hat{2} 3] =\langle 42 \rangle [23]\; , \end{aligned} $

(48) and an analytical continuum of
$ |-p\rangle = -|p\rangle $ ,$ |-p] = |p] $ is adopted. As a result, Eq. (47) is the same formula as the one derived in the effective Lagrangian calculation (see Eq. (16)). It is worth noting that because$ P_\gamma(s_{23})= \dfrac{1}{\langle 23 \rangle [32]} $ , Eq. (47) is proportional to$ \dfrac{\langle 24\rangle^2}{\langle 23 \rangle} $ and thus has a singularity when$ \langle 23 \rangle=0 $ .If we take the propagator V as a Z boson, we should consider a
$ H\gamma Z $ amplitude together with a$ Z\gamma\gamma $ amplitude. The$ H\gamma Z $ amplitude is an amplitude with two massive and one massless particle, and the$ Z\gamma\gamma $ amplitude is an amplitude with one massive and two massless particles. These are more complex than the$ H\gamma\gamma $ amplitude because the spin of Z is$ 1 $ . These two amplitudes should use bolded spinor variables [22, 46]. -
The amplitude of
$ H\to 4\ell $ is a five point amplitude, which can be factorized into two parts: a four point amplitude plus a three point amplitude. Each amplitude is split into four parts, as shown in Fig. 10.In a formula, it is
$ \begin{aligned}[b]& \mathcal{M}_5(1_{H},2^-_{\ell^- },3^+_{\ell^+},4^-_{\ell^{\prime-} }, 5^+_{\ell^{\prime+}}) \\=&P_\gamma(s_{23})\mathcal{M}(1_H,\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}},-\hat{P}^-_{I\gamma}) \mathcal{M}(\hat{P}^+_{I\gamma},\hat{2}^-_{\ell^- },3^+_{\ell^+}) \\ &+P_\gamma(s_{23})\mathcal{M}(1_H,\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}},-\hat{P}^+_{I\gamma}) \mathcal{M}(\hat{P}^-_{I\gamma},\hat{2}^-_{\ell^- },3^+_{\ell^+}) \\ &+ P_\gamma(s_{45})\mathcal{M}(1_H,\hat{2}^-_{\ell^- },3^+_{\ell^+},-\hat{P}^+_{I\gamma}) \mathcal{M}(\hat{P}^-_{I\gamma},\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}}) \\ &+ P_\gamma(s_{45})\mathcal{M}(1_H,\hat{2}^-_{\ell^- },3^+_{\ell^+},-\hat{P}^-_{I\gamma}) \mathcal{M}(\hat{P}^+_{I\gamma},\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}}) , \end{aligned} $

(49) which corresponds to diagrams A, B, C, and D, respectively. Diagrams A and B correspond to
$ (1,4,5)+(2,3) $ factorization, whereas diagrams C and D correspond to$ (1,2,3)+(4,5) $ factorization. We assume$ \ell\neq \ell^\prime $ for generality; hence, the factorizations of$ (1,2,5)+(3,4) $ and$ (1,3,4)+(2,5) $ are absent because of flavor symmetry. Next, we calculate these four diagrams separately.The formula for diagram A is
$ \begin{aligned}[b] &P_\gamma(s_{23}) \mathcal{M}(1_H,\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}},-\hat{P}^-_{I\gamma}) \mathcal{M}(\hat{P}^+_{I\gamma},\hat{2}^-_{\ell^- },3^+_{\ell^+}) \\ =&\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{-{\rm i}\xi}P_\gamma(s_{23}) P_\gamma(s_{\hat{4}5})[\hat{4}5]\langle \hat{4}\hat{I} \rangle^2 \frac{[\hat{I}3]^2}{[\hat{2}3]} \\ =& \frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{-{\rm i}\xi} P_\gamma(s_{23}) P_\gamma(s_{45}) [45][23]\langle 24\rangle^2\; , \end{aligned} $

(50) where in the last step we use
$ \begin{array}{*{20}{l}} \langle \hat{4}\hat{I} \rangle[\hat{I} 3]=\langle \hat{4}|\hat{p}_2+p_3|3] =\langle \hat{4}|\hat{p}_2|3]=\langle \hat{4}\hat{2} \rangle[\hat{2} 3] =\langle 42 \rangle[23] \end{array} $

(51) as in Eq. (48), and
$ P_\gamma(s_{\hat{4}5})[\hat{4}5]=\frac{-1}{\langle \hat{4}5 \rangle[\hat{4}5]} [\hat{4}5] =\frac{-1}{\langle 45 \rangle[45]} [45] =P_\gamma(s_{45})[45]\; , $

(52) $ \langle \hat{2}3\rangle=0 $ is chosen for the three-point amplitude, which is also required in diagram B.The formula for diagram B is
$ \begin{aligned}[b] &P_\gamma(s_{23}) \mathcal{M}(1_H,\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}},-\hat{P}^+_{I\gamma}) \mathcal{M}(\hat{P}^-_{I\gamma},\hat{2}^-_{\ell^- },3^+_{\ell^+}) \\ =&\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi}P_\gamma(s_{23}) P_\gamma(s_{\hat{4}5})\langle\hat{4}5\rangle[5\hat{I}]^2 \times\frac{\langle\hat{I}\hat{2}\rangle^2}{\langle\hat{2}3\rangle} \\ =&\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi} P_\gamma(s_{23})P_\gamma(s_{\hat{4}5})\langle\hat{4}5\rangle[5\hat{I}]^2\times 0 \\ =& 0, \end{aligned} $

(53) where the 3-point amplitude is equal to zero because
$ \langle\hat{2}3\rangle=\langle\hat{I}\hat{2}\rangle=0 $ .The formula for diagram C is
$ \begin{aligned}[b] &P_\gamma(s_{45})\mathcal{M}(1_H,\hat{2}^-_{\ell^- },3^+_{\ell^+},-\hat{P}^+_{I\gamma}) \mathcal{M}(\hat{P}^-_{I\gamma},\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}}) \\ =&\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi} P_\gamma(s_{45}) P_\gamma(s_{\hat{2}3}) \langle \hat{2}3\rangle [3\hat{I}]^2 \times\frac{\langle \hat{I}\hat{4}\rangle^2}{\langle \hat{4}5\rangle} \\ =&\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi} P_\gamma(s_{45}) P_\gamma(s_{23}) \langle 23\rangle \langle 45\rangle [35]^2\; , \end{aligned} $

(54) where
$ \begin{array}{*{20}{l}} [3\hat{I}]\langle \hat{I}\hat{4}\rangle=[35]\langle 5\hat{4}\rangle \end{array} $

(55) and
$ P_\gamma(s_{\hat{2}3})\langle \hat{2}3\rangle=\frac{-1}{\langle \hat{2}3 \rangle[\hat{2}3]} \langle \hat{2}3 \rangle =\frac{-1}{\langle 23 \rangle[23]} \langle 23\rangle =P_\gamma(s_{23}) \langle 23\rangle\; $

(56) are used.
$ [\hat{4}5]=0 $ is required.The formula for diagram D is
$ \begin{aligned}[b] &P_\gamma(s_{45})\mathcal{M}(1_H,\hat{2}^-_{\ell^- },3^+_{\ell^+},-\hat{P}^-_{I\gamma}) \mathcal{M}(\hat{P}^+_{I\gamma},\hat{4}^-_{\ell^{\prime-}},5^+_{\ell^{\prime+}}) \\ =&\frac{2c^S_{\gamma \gamma}}{v}e^{-i\xi} P_\gamma(s_{45}) P_\gamma(s_{\hat{2}3}) [\hat{2}3]\langle\hat{2}\hat{I}\rangle^2 \frac{[\hat{I}5]^2}{[\hat{4}5]} =0\; , \end{aligned} $

(57) where
$ [\hat{4}5]=[\hat{I}5]=0 $ makes the three point amplitude zero.After summing up the results of the four parts, that is, adding Eqs. (50), (53), (54), and (57) together, we get
$ \begin{aligned}[b]& \mathcal{M}(1_{H},2^-_{\ell^- },3^+_{\ell^+},4^-_{\ell^{\prime-} }, 5^+_{\ell^{\prime+}})\\=& \frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{-{\rm i}\xi} P_\gamma(s_{23}) P_\gamma(s_{45}) [45][23]\langle 24\rangle^2 \end{aligned} $

(58) $ +\frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi} P_\gamma(s_{45}) P_\gamma(s_{23}) \langle 23\rangle \langle 45\rangle [35]^2\; , $

(59) which has the same form as the one derived in the effective Lagrangian calculation (see Eq. (17)). Therefore, we obtain a consistent result from the on shell approach. The boundary contributions are assumed to be zero.
-
When the propagators are Z or W bosons, the massless on-shell method does not work, and we must use the little-group covariant massive spinor formalism [22, 40, 41]. In this section, we deduce
$ HVV $ amplitudes according to the presumed$ HVV $ vertex. A more general method starting from an ansatz is shown in Appendix 8. -
In the massive spinor formalism [22], a massive momentum is decomposed into two light-like vectors and thus two pairs of massless spinors,
$ \begin{aligned}[b]& {\boldsymbol{p}}_{\alpha \dot{\alpha}}=\lambda_\alpha^I \tilde{\lambda}_{I \dot{\alpha}}=\left|{\boldsymbol{p}}^I\right\rangle\Big[{\boldsymbol{p}}_I \mid, \quad \text { and } \quad\\& \overline{{\boldsymbol{p}}}^{\dot{\alpha }\alpha}=-\tilde{\lambda}^{I \dot{\alpha}} \lambda_I^\alpha=-\mid {\boldsymbol{p}}^I\Big]\left\langle{\boldsymbol{p}}_I\right|. \end{aligned} $

(60) Here,
$I=1,~2$ is the little-group index, and p is bolded to denote the massive momentum. The equation of motion reads as$ \begin{aligned}[b]& \left.\left.{\boldsymbol{p}} \mid {\boldsymbol{p}}^I\right]=m\left|{\boldsymbol{p}}^I\right\rangle, \quad \overline{{\boldsymbol{p}}}\left|{\boldsymbol{p}}^I\right\rangle=m \mid {\boldsymbol{p}}^I\right], \\&\left[{\boldsymbol{p}}^I \mid \overline{{\boldsymbol{p}}}=-m\left\langle{\boldsymbol{p}}^I\right|, \quad\left\langle{\boldsymbol{p}}^I\right| {\boldsymbol{p}}=-m\left[{\boldsymbol{p}}^I \mid\right.\right.. \end{aligned} $

(61) The polarized vector of a massive vector boson of momentum
$ {{\boldsymbol{p}}} $ and mass m is [51]$ \epsilon_\mu^{I J}({\boldsymbol{p}})=\frac{1}{\sqrt{2} m}\left\langle{\boldsymbol{p}}^I\left|\gamma_\mu\right| {\boldsymbol{p}}^J\right], $

(62) which corresponds to two transverse and one longitudinal mode,
$ \epsilon^+_\mu\equiv \epsilon^{11}_\mu,\quad \epsilon^0_\mu \equiv \frac{1}{2}(\epsilon^{12}_\mu+\epsilon^{21}_\mu),\quad \epsilon^-_\mu\equiv \epsilon^{22}_\mu\; . $

(63) -
According to the
$ HVV $ vertex in Eq. (24), the amplitude of$ HVV $ is$ \begin{array}{*{20}{l}} \mathcal{M}({\bf{1}}_H,{{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V)=\Gamma^{\mu\nu}({{\boldsymbol{p}}}_I,{{\boldsymbol{p}}}_J) \epsilon_\mu({{\boldsymbol{p}}}_I)\epsilon_\nu({{\boldsymbol{p}}}_J) \end{array} $

(64) Because
$ p_I^{\mu} p_J^{\nu} \epsilon_\mu(p_I)\epsilon_\nu(p_J)=0 $ , we may freely add this term in the amplitude formula and make the amplitude more symmetric.$ \begin{aligned}[b] \mathcal{M}({\bf{1}}_H,{{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V)=& -\frac{4}{v}[c_{VV}({{\boldsymbol{p}}}_I^{\mu} {{\boldsymbol{p}}}_J^{\nu}+ {{\boldsymbol{p}}}_I^{\nu} {{\boldsymbol{p}}}_J^{\mu}-{{\boldsymbol{p}}}_I\cdot {{\boldsymbol{p}}}_Jg^{\mu\nu})+\tilde{c}_{VV}\epsilon^{\mu\nu\alpha\beta} {{\boldsymbol{p}}}_{I\alpha}{{\boldsymbol{p}}}_{J\beta} ]\epsilon_\mu({{\boldsymbol{p}}}_I)\epsilon_\nu({{\boldsymbol{p}}}_J) \\ =&-\frac{1}{v}[c_{VV}{\rm tr}(\gamma^\mu\gamma^\alpha\gamma^\nu\gamma^\beta)+ {\rm i}\tilde{c}_{VV}{\rm tr}(\gamma^\mu\gamma^\nu\gamma^\alpha\gamma^\beta\gamma^5)]{{\boldsymbol{p}}}_{I\alpha}{{\boldsymbol{p}}}_{J\beta} \epsilon_\mu({{\boldsymbol{p}}}_I)\epsilon_\nu({{\boldsymbol{p}}}_J) \\ =&-\frac{1}{v}c^S_{VV}[{\rm e}^{-{\rm i}\xi}{\rm tr}(\sigma^\mu\bar{\sigma}^\alpha\sigma^\nu \bar{\sigma}^\beta)+ {\rm e}^{{\rm i}\xi}{\rm tr}(\bar{\sigma}^\mu{\sigma}^\alpha\bar{\sigma}^\nu \sigma^\beta)] {{\boldsymbol{p}}}_{I\alpha}{{\boldsymbol{p}}}_{J\beta} \epsilon_\mu({{\boldsymbol{p}}}_I)\epsilon_\nu({{\boldsymbol{p}}}_J)\; , \end{aligned} $ 
(65) where
$ \begin{array}{*{20}{l}} &&4(g^{\mu\alpha}g^{\nu\beta}-g^{\mu\nu}g^{\alpha\beta}+g^{\mu\beta}g^{\nu\alpha})={\rm tr}(\gamma^\mu\gamma^\alpha\gamma^\nu\gamma^\beta)= {\rm tr}(\sigma^\mu\bar{\sigma}^\alpha\sigma^\nu \bar{\sigma}^\beta)+{\rm tr}(\bar{\sigma}^\mu{\sigma}^\alpha\bar{\sigma}^\nu \sigma^\beta), \end{array} $

(66) $ \begin{array}{*{20}{l}} &&-4{\rm i}\epsilon^{\mu\nu\alpha\beta}= {\rm tr}(\gamma^\mu\gamma^\nu\gamma^\alpha\gamma^\beta\gamma^5) =-{\rm tr}(\gamma^\mu\gamma^\alpha\gamma^\nu\gamma^\beta\gamma^5)= -{\rm tr}(\sigma^\mu\bar{\sigma}^\alpha\sigma^\nu \bar{\sigma}^\beta)+{\rm tr}(\bar{\sigma}^\mu{\sigma}^\alpha\bar{\sigma}^\nu \sigma^\beta) \end{array} $

(67) are used. Eq. (65) shows a general formula for
$ HVV $ amplitudes, which constitutes two parts with opposite$ CP $ violation phases. If one part is zero, the$ CP $ violation phase degenerates to a trivial phase. After inserting Eqs. (61) and (63) into Eq. (65), we get$ \mathcal{M}({\bf{1}}_H,{{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V)= \frac{2c^S_{VV}}{v}[{\rm e}^{-{\rm i}\xi}\left\langle {{\boldsymbol{IJ}}}\right\rangle ^2+{\rm e}^{{\rm i}\xi} [ {{\boldsymbol{IJ}}}] ^2]\; . $

(68) When one vector boson is a massless photon, the amplitudes become
$ \begin{aligned}[b] \mathcal{M}({\bf{1}}_H,I^+_\gamma,{{\boldsymbol{J}}}_V)=& \frac{2c^S_{\gamma V}}{v}{\rm e}^{{\rm i}\xi} [ I{{\boldsymbol{J}}}] ^2\; , \\ \mathcal{M}({\bf{1}}_H,I^-_\gamma,{{\boldsymbol{J}}}_V)=& \frac{2c^S_{\gamma V}}{v}{\rm e}^{-{\rm i}\xi} \left\langle I{{\boldsymbol{J}}}\right\rangle ^2\; , \end{aligned} $

(69) where the compact form of a general amplitude decomposes into two parts, each with a trivial
$ CP $ violation phase. When both of the two vector bosons are massless photons, the amplitudes become$ \begin{aligned}[b]\\[-8pt] \mathcal{M}({\bf{1}}_H,I^+_\gamma,J^+_\gamma)=& \frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi} [ IJ] ^2\; , \\ \mathcal{M}({\bf{1}}_H,I^+_\gamma,J^-_\gamma)=& 0 \; , \\ \mathcal{M}({\bf{1}}_H,I^-_\gamma,J^+_\gamma)=& 0\; , \\ \mathcal{M}({\bf{1}}_H,I^-_\gamma,J^-_\gamma)=& \frac{2c^S_{\gamma \gamma}}{v}{\rm e}^{{\rm i}\xi}\left\langle IJ \right\rangle ^2\; . \\ \end{aligned} $

(70) Therefore, the general amplitude decomposes into four parts, each with a trivial global
$ CP $ violation phase, except for the zero ones.The amplitude of
$ Vl^- l^+ $ with massless leptons is$ \mathcal{M}\left({\boldsymbol{I}}_V, 2_{l^-}^-, 3_{l^+}^+\right)=e l_V\left\langle 2\left|\gamma^\mu\right| 3\right] \epsilon_\mu\left({\boldsymbol{p}}_I\right)=\sqrt{2} e l_V \frac{\langle 2 {\boldsymbol{I}}\rangle[3 {\boldsymbol{I}}]}{m_V}, $

(71) $ \mathcal{M}\left({\boldsymbol{I}}_V, 2_{l^-}^+, 3_{l^+}^-\right)=e r_V\left[2\left|\gamma^\mu\right| 3\right\rangle \epsilon_\mu\left({\boldsymbol{p}}_I\right)=\sqrt{2} e r_V \frac{[2 {\boldsymbol{I}}]\langle 3 {\boldsymbol{I}}\rangle}{m_V}, $

(72) $ \mathcal{M}({{\boldsymbol{I}}}_V,2^-_{l^-},3^-_{l^+})= \mathcal{M}({{\boldsymbol{I}}}_V,2^+_{l^-},3^+_{l^+}) =0. $

(73) -
We obtain the amplitude of
$ H\to VV \to 4\ell $ by simply gluing the amplitudes of$ H\to VV $ ,$ V\to \ell^+\ell^- $ , and$ V\to \ell^{\prime+}\ell^{\prime-} $ , as shown in Fig. 11.When a propagator goes on-shell, the amplitude factorizes into the tensor product of two subamplitudes.
$ \begin{equation} \lim\limits_{p^2\rightarrow m^2}\mathcal{M}=\frac{\mathcal{M}_L^{\{I_1... I_{2s}\}}\otimes \mathcal{M}_R^{\{J_1... J_{2s}\}}}{p^2-m^2}, \end{equation} $

(74) where
$ L,R $ represent left and right amplitudes for each gluing. For each propagator particle, the sign of its momentum is opposite in the left and right amplitudes, as shown explicitly in Eq. (42). An analytical continuum$ |-p\rangle = -|p\rangle $ ,$ |-p ] = |p ] $ is adopted. The gluing procedure is performed by choosing the singlet of the little-group for the on-shell propagator$ \begin{equation} \mathcal{M}_L^{\{I_1... I_{2s}\}}\otimes \mathcal{M}_R^{\{J_1... J_{2s}\}}=\mathcal{M}_{L,\{I_1... I_{2s}\}}\epsilon^{I_1J_1}...\epsilon^{I_{2s}J_{2s}} \mathcal{M}_{R,\{J_1... J_{2s}\}}. \end{equation} $

(75) Because the amplitude of
$ H\to VV \to 4\ell $ has two propagators,$ p_I $ and$ p_J $ , we take the limits$ p_I^2\rightarrow m^2_V $ and$ p_J^2\rightarrow m^2_V $ simultaneously,$ \begin{aligned}[b] \lim\limits_{p_I^2,p_J^2\rightarrow m^2_V} \mathcal{M}(1_{H},2^-_{\ell^- },3^+_{\ell^+},4^-_{\ell^{\prime-} },5^+_{\ell^{\prime+}}) =&f^-_V(s_{23}) f^-_V(s_{45})\mathcal{M}({{\boldsymbol{I}}}_V,2^-_{\ell^- },3^+_{\ell^+})\otimes\mathcal{M}({\bf{1}}_H,{{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V)\otimes\mathcal{M}({{\boldsymbol{I}}}_V,4^-_{\ell^{\prime-} },5^+_{\ell^{\prime+}})\\ =&\frac{2c^S_{VV}}{v}f^-_V(s_{23}) f^-_V(s_{45})\left[{\rm e}^{-{\rm i}\xi}\lim\limits_{p_I^2,p_J^2\rightarrow m^2_V}\mathcal{M}^a+{\rm e}^{{\rm i}\xi}\lim\limits_{p_I^2,p_J^2\rightarrow m^2_V}\mathcal{M}^b\right],\\ \end{aligned} $ 
(76) where
$ \mathcal{M}^a $ and$ \mathcal{M}^b $ in this limit are$ \begin{aligned}[b] \lim\limits_{p_I^2,p_J^2\rightarrow m^2_V}2\mathcal{M}^a =&\langle 2I^{I_1}\rangle\langle I_{I_1}J_{J_1}\rangle\langle J^{J_1}4\rangle[3I^{I_2}]\langle I_{I_2}J_{J_2}\rangle[J^{J_2}5]+\langle 2I^{I_1}\rangle\langle I_{I_1}J_{J_1}\rangle[J^{J_2}5][3I^{I_2}]\langle I_{I_2}J_{J_2}\rangle\langle J^{J_2}4\rangle\\ =&-\sqrt{p_I^2}\sqrt{p_J^2}\left(\langle 24\rangle[3|p_I p_J|5]+\langle 2|p_J|5]\langle3|p_I|4]\right),\\ \end{aligned} $

(77) $ \begin{aligned}[b] \lim\limits_{p_I^2,p_J^2\rightarrow m^2_V}2\mathcal{M}^b =&\langle 2I^{I_1}\rangle[I_{I_1}J_{J_1}]\langle J^{J_1}4\rangle[3I^{I_2}][ I_{I_2}J_{J_2}][J^{J_2}5]+\langle 2I^{I_1}\rangle[I_{I_1}J_{J_1}][J^{J_2}5][3I^{I_2}][I_{I_2}J_{J_2}]\langle J^{J_2}4\rangle\\ =&-\sqrt{p_I^2}\sqrt{p_J^2}\left(\langle 2|p_I p_J|4\rangle[35]+\langle 2|p_I|5]\langle3|p_J|4]\right),\\ \end{aligned} $

(78) and we use
$ \begin{array}{*{20}{l}} \left.\left|{\boldsymbol{p}}^I\right\rangle_\alpha\left\langle\left.{\boldsymbol{p}}_I\right|^\beta=-m \delta_\alpha^\beta, \quad\right| {\boldsymbol{p}}^I\right]^{\dot{\alpha}}\left[\left.{\boldsymbol{p}}_I\right|_{\dot{\beta}}=m \delta_{\dot{\beta}}^{\dot{\alpha}}\right.. \end{array} $

(79) When the propagators go off-shell, we should use
$ \begin{equation} \begin{aligned} p_I=p_2+p_3,\quad p_J=p_4+p_5,\quad \sqrt{p_I^2}=\sqrt{p_J^2}=m_V,\\ \end{aligned} \end{equation} $

(80) instead of
$ p_I $ and$ p_J $ . Now, we get$ \begin{equation} \begin{aligned} \mathcal{M}^a=m_V^2[45][23]\langle 24\rangle^2,\quad \mathcal{M}^b=m_V^2\langle 23\rangle \langle 45\rangle [35]^2. \end{aligned} \end{equation} $

(81) Consequently, the amplitude of
$ H\to VV \to 4\ell $ is$ \begin{aligned}[b]& \mathcal{M}(1_{H},2^-_{\ell^- },3^+_{\ell^+},4^-_{\ell^{\prime-} }, 5^+_{\ell^{\prime+}})\\=& \frac{2c^S_{VV}}{v} f^-_V(s_{23}) f^-_V(s_{45}) [{\rm e}^{-{\rm i}\xi}[45][23]\langle 24\rangle^2\\&+ {\rm e}^{{\rm i}\xi}\langle 23\rangle \langle 45\rangle [35]^2], \end{aligned} $

(82) which is the same as the previous result in Eq. (17).
In Eq. (75), the particles are all on-shell, especially for the propagator particles. In our specific process, before and after gluing,
$ s_{23}=s_{45}=m_V^2 $ should be required in the amplitude, except for the propagator factor. Therefore, Eq. (82) is the amplitude of$ H\to VV \to 4\ell $ in the on-shell limit. In contrast, Eq. (17) is obtained from the off-shell method and$ s_{23}\neq s_{45}\neq m_V^2 $ . Why are these two amplitudes the same? This is because the amplitude of$ H\to VV \to 4\ell $ is independent of the residue z. Eq. (48) illustrates this point explicitly, that is, the combined amplitude has no z dependence. -
Via the on-shell approach, we obtain a compact form to show that the
$ CP $ violation phase in the$ HVV $ amplitude is not a trivial phase because of the BSM$ HVV $ vertex. It degenerates to a trivial phase once the helicity of the vector boson is fixed, as in the$ H\gamma\gamma $ and$ H\to \gamma V $ cases. In contrast, using the off-shell method, we only observe the nontriviality of the$ CP $ violation phase in the$ H\to 4\ell $ amplitude. This is because we do not deal with the massive vector boson independently in the off-shell approach. Its full properties are exhibited indirectly in the four final states. -
The
$ HVV $ amplitudes with$ CP $ violation BSM are analyzed in two ways. The first is the off-shell method under the field theory framework. We decompose the helicity amplitudes of$ H\to \gamma V \to \gamma \ell\ell $ and$ H\to VV \to 4\ell $ into the helicity amplitudes of$ H\to\gamma\gamma $ . There are two preconditions for the decomposition relation. 1. The multilinear momentum dependence of the$ HVV $ vertexes, which allows us to decompose the vertexes of the overall momentum into a summation of the momenta of sub-processes. 2. The current of$ J_\mu $ in$ V\to\ell^+\ell^- $ is formally proportional to a photon's polarization vector, which allows us to replace such a sub-process by an equivalent photon. The second method is the on-shell scattering amplitude approach. For the massless propagator case, the 3-point amplitude of$ H\gamma\gamma $ is the starting point. Then, the 4-point amplitude of$ H \ell\ell \gamma $ and the 5-point amplitude of$ H 4\ell $ are obtained through recursion relations. For the massive propagator case, we adopt the little-group covariant massive-spinor formalism. This first expresses the$ HVV $ amplitude and then glues the$ V\ell\ell $ amplitudes to get final$ H\to VV \to 4\ell $ amplitudes. We obtain consistent results through the off-shell and on-shell methods.The
$ CP $ violation phase in the$ H\to VV \to 4\ell $ amplitude is a nontrivial phase, whereas in the$ H\to \gamma V \to \gamma \ell\ell $ and$ H\to\gamma\gamma $ amplitudes, it is a global trivial phase. In the off-shell approach, the decomposition relation shows that in the$ H\to VV \to 4\ell $ amplitude, it mixes$ H\to\gamma\gamma $ amplitudes with different helicities; hence, it mixes$ H\to\gamma\gamma $ amplitudes with different dependences on$ CP $ violation phases. In the on-shell approach, the nontriviality of the$ CP $ violation phase appears directly in$ HVV $ amplitudes, which is not a helicity amplitude but a compact massive-spinor amplitude. It degenerates to a trivial phase when the helicity of at least one vector boson is fixed, such as what occurs in the$ H\gamma V $ and$ H\gamma\gamma $ amplitudes. The decays of$ V\to \ell \ell $ maintain the nontriviality of the$ CP $ violation phase. The on-shell method supplies a simpler and clearer viewpoint for the$ CP $ violation phase in amplitudes. Our systematic analysis of a series of$ HVV $ process amplitudes reveals the dependence of the$ CP $ violation phase; therefore, it may be convenient for future$ CP $ violation searches in$ HVV $ couplings. -
We are grateful to Chih-Hao Fu and Kang Zhou for useful discussions on BCFW recursion relations. X.W. thanks Bo Feng for the Scattering Amplitude School 2021 in Hangzhou, China.
-
In Sec. VI.B, we derive massive
$ HVV $ amplitudes using the$ HVV $ vertex$ \Gamma^{\mu\nu} $ . Here, we construct them directly. Consider the three massive amplitudes$ \mathcal{M}({\bf{1}}_H, {{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V) $ . In this case, Ref. [22] showed that the spinor space is spanned by two tensors, the symmetric tensor$ \mathcal{O}_{\beta\gamma} $ and the antisymmetric tensor$ \varepsilon_{\beta\gamma} $ . We choose the first tensor$ \begin{aligned} \mathcal{O}_{\beta\gamma}=p_{2\{\beta\dot{\gamma}} p^{\dot{\gamma}}_{3\gamma\}}=|2_J\rangle_{\{\beta}[2^J 3^K]\langle 3_K|_{\gamma\}}+(\beta\leftrightarrow\gamma).\\ \end{aligned} \tag{A1}$

Therefore, the three massive amplitudes have the general form
$ \begin{aligned}[b] & \mathcal{M}({\bf{1}}_H,{{\boldsymbol{I}}}_V,{{\boldsymbol{J}}}_V)\\=&\lambda_2^{\beta_1 J_1}\lambda_2^{\beta_2 J_2}\lambda_3^{\gamma_1 K_1}\lambda_3^{\gamma_2 K_2}\sum\limits_{i=0}^1 g_{\sigma_i}(\mathcal{O}^{2-i}\varepsilon^i)_{\{\beta_1\beta_2\},\{\gamma_1\gamma_2\}}\\ =&\lambda_2^{\beta_1 J_1}\lambda_2^{\beta_2 J_2}\lambda_3^{\gamma_1 K_1}\lambda_3^{\gamma_2 K_2}\left(g_{\sigma_0}(\mathcal{O}\mathcal{O})_{\{\beta_1\beta_2\},\{\gamma_1\gamma_2\}}+g_{\sigma_1}(\mathcal{O}\varepsilon)_{\{\beta_1\beta_2\},\{\gamma_1\gamma_2\}}\right).\\ \end{aligned} \tag{A2} $

The second term
$ (\mathcal{O}\varepsilon) $ is$ \begin{aligned} \mathcal{O}_{\beta_1\gamma_1}\varepsilon_{\beta_2\gamma_2}+\mathcal{O}_{\beta_1\gamma_2}\varepsilon_{\beta_2\gamma_1} \rightarrow \langle\mathbf{2}\mathbf{3}\rangle[\mathbf{2}\mathbf{3}]. \end{aligned} \tag{A3} $

Because this term is symmetric between the angle and square brackets, it does not contribute to
$ CP $ violation. The first term$ (\mathcal{O}\mathcal{O}) $ can be parameterized as$ \begin{aligned}[b] &g_1\mathcal{O}_{\beta_1\beta_2}\mathcal{O}_{\gamma_1\gamma_2}+g_2(\mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}+\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1})\\ =&\frac{g_1}{2}(2\mathcal{O}_{\beta_1\beta_2}\mathcal{O}_{\gamma_1\gamma_2}-\mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}-\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1})\\ & +\frac{2g_2+g_1}{2}(\mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}+\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1})\\ =&\frac{g_1}{2}m^4_V(\varepsilon_{\beta_1\gamma_1}\varepsilon_{\beta_2\gamma_2}+\varepsilon_{\beta_1\gamma_2}\varepsilon_{\beta_2\gamma_1}) \end{aligned} $

$ \begin{aligned}[b] +\frac{2g_2+g_1}{2}(\mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}+\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1}), \end{aligned} \tag{A4} $

where we use the Schouten identity
$ \begin{aligned}[b] &2\mathcal{O}_{\beta_1\beta_2}\mathcal{O}_{\gamma_1\gamma_2}-\mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}-\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1}\\ =&\lambda^{J_1}_{2\{\beta_1}\lambda^{K_1}_{3\beta_2\}}\lambda^{J_2}_{2\{\gamma_1}\lambda^{K_2}_{3\gamma_2\}}([2_{J_1} 3_{K_1}][2_{J_2} 3_{K_2}]-[2_{J_1} 3_{K_2}][2_{J_2} 3_{K_1}])\\=&\lambda^{J_1}_{2\{\beta_1}\lambda^{K_1}_{3\beta_2\}}\lambda^{J_2}_{2\{\gamma_1}\lambda^{K_2}_{3\gamma_2\}}[2_{J_1} 2_{J_2}][3_{K_1}3_{K_2}]\\ \end{aligned} $

$ \begin{aligned}[b] =&m^2_V\lambda^{J_1}_{2\{\beta_1}\lambda^{K_1}_{3\beta_2\}}\lambda^{J_2}_{2\{\gamma_1}\lambda^{K_2}_{3\gamma_2\}}\varepsilon_{J_1 J_2}\varepsilon_{K_1 K_2}\\ =&m^4_V(\varepsilon_{\beta_1 \gamma_1}\varepsilon_{\beta_2 \gamma_2}+\varepsilon_{\beta_1 \gamma_2}\varepsilon_{\beta_2 \gamma_1}).\\ \end{aligned} \tag{A5}$

Therefore, the
$ (\mathcal{O}\mathcal{O}) $ term gives two independent structures that contribute to$ CP $ violation,$ \begin{aligned}[b] \mathcal{O}_{\beta_1\gamma_1}\mathcal{O}_{\beta_2\gamma_2}+\mathcal{O}_{\beta_1\gamma_2}\mathcal{O}_{\beta_2\gamma_1}&\rightarrow &[\mathbf{2}\mathbf{3}]^2,\\ \varepsilon_{\beta_1\gamma_1}\varepsilon_{\beta_2\gamma_2}+\varepsilon_{\beta_1\gamma_2}\varepsilon_{\beta_2\gamma_1}&\rightarrow &\langle\mathbf{2}\mathbf{3}\rangle^2.\\ \end{aligned} \tag{A6} $

Exploring HVV amplitudes with CP violation using decomposition and the on-shell scattering amplitude method
- Received Date: 2022-07-15
- Available Online: 2023-03-15
Abstract:






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















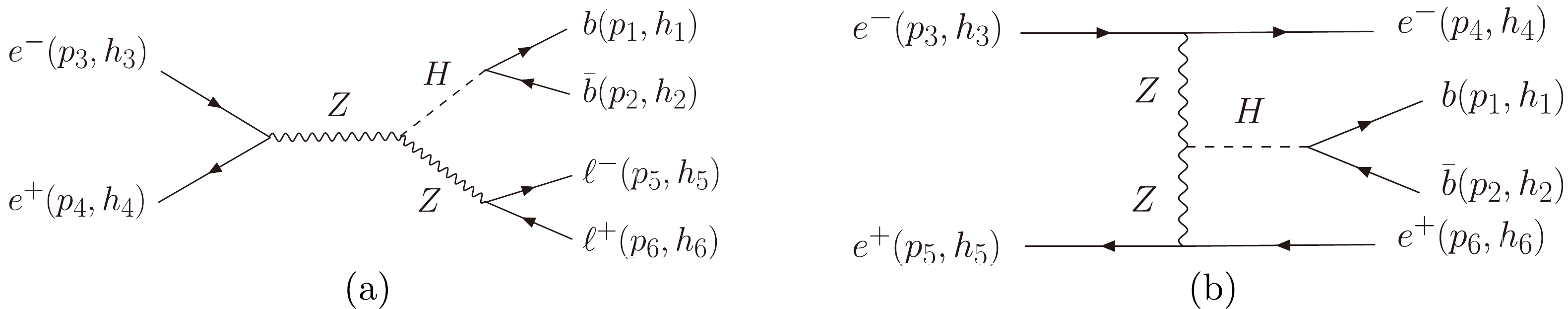






 DownLoad:
DownLoad: