-
Recent celestial observations such as supernovae, the CMB anisotropic parameter, and galaxy clustering strongly indicate that our Universe is spatially flat [1–6], and that there exists an exotic cosmic fluid called dark energy with negative pressure that constitutes about two-thirds of the total energy of the whole Universe [7, 8]. This cosmological component is characterized by its equation of state
$ {w} $ , which lies very close to$ -1 $ , or according to some recent data, below$ -1 $ [9, 10].Many candidates, including the cosmological constant, quintessence, phantom, quintom, and holographic dark energy, have been proposed to explain this mysterious component and its effects on the expansion of the Universe. However, scientists do not understand yet what dark energy is. Ever since the discovery of dark energy, cosmologists are confronted with two fundamental problems: (1) the coincidence problem and (2) the fine-tuning problem [11]. The coincidence problem states that the density of dark energy and matter evolves differently while the Universe expands and now they are comparable, which is an incredibly remarkable coincidence if there is no internal connection between them. The fine-tuning problem traces back to the simplest form of dark energy model, that is, the cosmological constant model introduced by Einstein. Although vacuum energy in quantum field theory has the same property, it is greater than the observed value by some
$ 123 $ orders of magnitude. Therefore, we need extreme fine-tuning of the vacuum energy. Both of these problems are solved through different models for dark energy (see e.g. [12–20]).Studying the black hole theory and string theory provides new relevant insight to resolve dark energy problems in a new way called holographic principle, which may provide some clues about dark energy properties. It is known that the entropy of a system scales not with its volume, but with its surface area in quantum gravity mediums [21–25]. Investigating Einstein's equation,
$ {G}_{\mu \nu }=8\pi {T}_{\mu \nu }+\mathrm{\Lambda }{g}_{\mu \nu } $ , shows that the cosmological constant$ \mathrm{\Lambda } $ is the inverse of some length squared,$ \left[\mathrm{\Lambda }\right]~{l}^{-2} $ . According to this fact, it is proposed in Refs. [26–28] that unknown vacuum energy proportional to the Hubble scale${l}_{H}\sim {H}^{-1}$ could be present. Consequently, the fine-tuning problem is solved by scaling the dark energy using the cosmological scale rather than the Planck length, and the coincidence problem is also alleviated. However, this model cannot explain the accelerated expansion of the Universe in late time wherein the effective equation of state for such vacuum energy is zero and the Universe is decelerating. Granda and Oliveros proposed another possibility: the length$ l $ is given by the average radius of the term$ {\left(\alpha {H}^{2}+\beta \dot{H}\right)}^{-1/2} $ in which$ \alpha $ and$ \beta $ are some constants of the model. Consequently, in their model, the energy density of dark energy$ {\rho }_{X}\propto \alpha {H}^{2}+\beta \dot{H} $ , which implies that the density of dark energy is proportional to the second Friedmann equation [29]. Different studies on this model were reported [30–33]. Recently, C. Gao et al. proposed a new version of dark energy that satisfies the holographic principle. The length$ l $ is given by the average radius of the Ricci scalar curvature,$ {R}^{-1/2} $ . Thus, one could obtain the dark energy density$ {\rho }_{X}\propto R $ . This model presents the dark energy model in two terms, one that evolves like non-relativistic matter$ ~{a}^{-3} $ and another that slowly increases with decreasing redshift [34]. This holographic dark energy model and its interacting versions are successful in fitting the current observations (see e.g. [35–38]). However, as shown in Ref. [34], the Ricci holographic dark energy, as one of the explicit cases of the Granda-Oliveros dark energy model, has some inconsistencies with the ages of some old objects. This problem was alleviated by considering Ricci dark energy as a viscous field .Alternatively, the particle horizon size
${l}_{PH}=a{\int }_{0}^{t}{\rm d}t/a$ could be used as the length scale [ 39], but as shown in Refs. [40–41], the equation of state for this dark energy model is greater than$ -1/3 $ . Therefore, it cannot describe the late-time accelerated expansion yet. In this study, we focused on the particle horizon to show how this parameter yields a new version of holographic dark energy. In this context, the acceleration of the particle horizon may be considered as the origin of the accelerated expansion of the Universe. Observations demonstrate that the Universe expands with an acceleration phase in late time and so the acceleration of the particle horizon evolves proportionally to this acceleration rate.$ {\ddot{l}}_{PH}=\dot{H}{l}_{PH}+{H}^{2}{l}_{PH}+H. $

(1) Checking the acceleration of the particle horizon shows that
$\left[{\ddot{l}}_{PH}\right]\sim {l}^{-1}$ . Consequently, rescaling Eq. (1) by the particle horizon$ {l}_{PH} $ yields$\left[{\ddot{l}}_{PH}/{l}_{PH}\right]\sim {l}^{-2}$ . Hence, assuming unknown vacuum energy, the energy density of dark energy could be proportional to$ {\ddot{l}}_{PH}/{l}_{PH} $ .In the next section, we describe this model and its cosmic equations. Sec. III is devoted to the model's structure formation and CMB anisotropic parameter. In Section IV, we summarize the results of the model.
Throughout this paper, we adopt the Planck units, i.e.,
$ c=\hslash =G=1 $ . -
In this paper, we assume that the Universe is homogenous, isotropic, and described by the Friedmann-Robertson-Walker metric,
$ {{\rm d}s}^{2}=-{{\rm d}t}^{2}+{a\left(t\right)}^{2}\left(\frac{{{\rm d}r}^{2}}{1-k{r}^{2}}+{r}^{2}{{\rm d}\theta }^{2}+{r}^{2}{\rm sin}^{2}\theta {{\rm d}\varphi }^{2}\right), $

(2) where
$ k=1, 0 $ , and$ -1 $ describe closed, flat, and open Universe, respectively. Different independent observations have confirmed that the observable Universe is spatially flat, i.e.,$ k=0 $ . Therefore, the first Friedmann equation is given by [1–6]$ {H}^{2}=\frac{8\pi }{3}\left({\rho }_{r}+{\rho }_{m}+{\rho }_{X}\right), $

(3) where
$ H\equiv \dot{a}/a $ is the Hubble parameter, with the overdot denoting the derivative with respect to the cosmic time$ t $ , and$ {\rho }_{r} $ ,$ {\rho }_{m} $ , and$ {\rho }_{X} $ are the energy density of radiation, non-relativistic matter, and dark energy, respectively.Following the holographic principle, we propose a new dark energy model in which the future event horizon area is proportional to the inverse of
$ {\ddot{l}}_{PH}/{l}_{PH} $ . Therefore, the energy density of dark energy is expressed as$ {\rho }_{X}=\frac{3\alpha }{8\pi }\left(\frac{{\ddot{l}}_{PH}}{{l}_{PH}}\right), $

(4) where
$ \alpha $ is the constant of the model and the factor$ 3/8\pi $ is used for convenience in the following calculations.To study a general holographic description, we assume the conventional formula for the Hubble rate [42],
$ H=\frac{\beta }{l}, $

(5) where
$ \beta $ is a positive constant for an expanding Universe and$ l $ denotes the cosmological length scale. For this scale, we use the particle horizon$ {l}_{PH} $ . Thus, from Eq. (5), we obtain the particle horizon as a function of the Hubble parameter,$ {l}_{PH}=\beta {H}^{-1}. $

(6) Note that this is the simplest assumption that we can apply here. If needed, this model can be expanded without this assumption. Substituting Eq. (6) into Eq. (4) when Eq. (1) is used yields
$ {\rho }_{X}=\frac{3\alpha }{8\pi }\left[\dot{H}+\left(1+\frac{1}{\beta }\right){H}^{2}\right]. $

(7) Setting
$ x=\mathrm{ln}a $ , we can express Eq. (3) as$ {H}^{2}=\frac{8\pi }{3}\left({\rho }_{m}{\rm e}^{-3x}+{\rho }_{r}{\rm e}^{-4x}\right)+\frac{\alpha }{\beta }\left[\left(1+\beta \right){H}^{2}+\frac{\beta }{2}\frac{{\rm d}{H}^{2}}{{\rm d}x}\right]. $

(8) With the scaled Hubble expansion rate
$ h=H/{H}_{0} $ , Eq. (8) becomes$ {h}^{2}={\mathrm{\Omega }}_{m0}{\rm e}^{-3x}+{\mathrm{\Omega }}_{r0}{\rm e}^{-4x}+\frac{\alpha }{\beta }\left[\left(1+\beta \right){h}^{2}+\beta h\frac{{\rm d}h}{{\rm d}x}\right], $

(9) where
$ {\mathrm{\Omega }}_{r} $ and$ {\mathrm{\Omega }}_{m} $ are the relative density of the radiation and non-relativistic matter in the present Universe, respectively.Solving Eq. (5), one obtains
$\begin{aligned}[b] {h}^{2}=&{\mathrm{\Omega }}_{m0}{\rm e}^{-3x}+{\mathrm{\Omega }}_{r0}{\rm e}^{-4x}+{c}_{0}{\rm e}^{-\frac{2\left(\left(\alpha -1\right)\beta +\alpha \right)}{\alpha \beta }x}\\&-\frac{\alpha \left(\beta -2\right){\mathrm{\Omega }}_{m0}}{\left(\alpha +2\right)\beta -2\alpha }{\rm e}^{-3x}-\frac{\alpha \left(\beta -1\right){\mathrm{\Omega }}_{r0}}{\left(\alpha +1\right)\beta -\alpha }{\rm e}^{-4x} ,\end{aligned}$

(10) where
$ {c}_{0} $ is an integration constant.Equation (10) shows that we can consider the last three terms as the energy density of dark energy,
$ {\rho }_{X}={c}_{0}{\rm e}^{-\frac{2\left(\left(\alpha -1\right)\beta +\alpha \right)}{\alpha \beta }x}-\frac{\alpha \left(\beta -2\right){\mathrm{\Omega }}_{m0}}{\left(\alpha +2\right)\beta -2\alpha }{\rm e}^{-3x}-\frac{\alpha \left(\beta -1\right){\mathrm{\Omega }}_{r0}}{\left(\alpha +1\right)\beta -\alpha }{\rm e}^{-4x}, $

(11) thus, the dark energy includes three terms; one of them slowly increases with decreasing redshift for
$ 0 < \alpha < \frac{\beta }{1+\beta }, $

(12) while another is proportional to the evolution of non-relativistic matter
$~{\rm e}^{-3x}$ and radiation$~{\rm e}^{-4x}$ . Observations have confirmed that the energy density of the dark energy grows with time, which implies that$ {c}_{0}\ne 0 $ .Equation (12) indicates that both constants
$ \alpha $ and$ \beta $ are positive while the second one is a necessary condition to have an expanded Universe.For conserved energy current, we obtain the pressure of dark energy as
$\begin{aligned}[b] {p}_{X}=&-{\rho }_{X}-\frac{1}{3}\frac{{\rm d}{\rho }_{X}}{{\rm d}x}=-\frac{\alpha }{3}\frac{\left(\beta -1\right){\mathrm{\Omega }}_{r0}}{\left(\alpha +1\right)\beta -\alpha }{\rm e}^{-4x}\\&-\frac{\left[\left(\alpha +2\right)\beta -2\alpha \right]{c}_{0}}{3\alpha \beta }{\rm e}^{-\frac{2\left(\left(\alpha -1\right)\beta +\alpha \right)}{\alpha \beta }x}. \end{aligned}$

(13) To have a more compact and convenient mathematical framework, Eqs. (12) and (13) can be expressed as
$ {\rho }_{X}={c}_{0}{\rm e}^{-\frac{2\left(\alpha \beta +\xi -\zeta \right)}{\alpha \beta }x}-\frac{\alpha \left(\beta -2\right){\mathrm{\Omega }}_{m0}}{\zeta }{\rm e}^{-3x}-\frac{\alpha \left(\beta -1\right){\mathrm{\Omega }}_{r0}}{\xi }{\rm e}^{-4x}, $

(14) $ {p}_{X}=-\frac{\alpha \left(\beta -1\right){\mathrm{\Omega }}_{r0}}{3\xi }{\rm e}^{-4x}-\frac{\zeta {c}_{0}}{3\alpha \beta }{\rm e}^{-\frac{2\left(\alpha \beta +\xi -\zeta \right)}{\alpha \beta }x}, $

(15) where we define
$ \zeta \equiv \left(\alpha +2\right)\beta -2\alpha, $

(16) $ \xi \equiv \left(\alpha +1\right)\beta -\alpha. $

(17) The equation of state
$ {\omega }_{X}={p}_{X}/{\rho }_{X} $ of dark energy is given by$ {\omega }_{X}=-1+\frac{\zeta }{3\alpha \beta }\left[\frac{{\alpha }^{2}\beta \left(\beta -1\right){\mathrm{\Omega }}_{r0}{\rm e}^{-4x}+\zeta \xi {c}_{0}{\rm e}^{-\frac{2\left(\alpha \beta +\xi -\zeta \right)}{\alpha \beta }x}}{\alpha \xi \left(\beta -2\right){\mathrm{\Omega }}_{m0}{\rm e}^{-3x}+\alpha \zeta \left(\beta -1\right){\mathrm{\Omega }}_{r0}{\rm e}^{-4x}-\zeta \xi {c}_{0}{\rm e}^{-\frac{2\left(\alpha \beta +\xi -\zeta \right)}{\alpha \beta }x}}\right]. $ 
(18) There are three constants, namely
$ \alpha $ ,$ \beta $ , and$ {c}_{0} $ , in the expressions of$ {\rho }_{X} $ and$ {p}_{X} $ . With the aid of current observational data, the values of these constants can be found. For example, we set$ {\omega }_{X0}\approx -1 $ ,$ {H}_{0}=67.4 $ ,$ {\mathrm{\Omega }}_{m0}\approx 0.315 $ , and$ {\mathrm{\Omega }}_{m0}\approx 8.1\times {10}^{-5} $ [43]. Thus, according to Eq. (9), in the current Universe,$ x=0 $ , and we have$ {c}_{0}=\frac{{\alpha }^{2}\left({\beta }^{2}-3\beta +2\right)}{\zeta \xi }+\frac{\left(2.37\alpha +1.37\right){\beta }^{2}-3.37\alpha \beta }{\zeta \xi } .$

(19) Furthermore, substituting Eq. (19) into Eq. (18) yields
$ \alpha $ expressed as$ \alpha \approx \frac{1.37\beta }{1.05\beta +2}. $

(20) Moreover, using Eq. (12), we obtain
$ 0 < \beta < 1.99. $

(21) Figure 1 shows the general behavior of the equation of state of dark energy in our model. Note that the evolution of the equation of state depends only on the value of
$ \beta $ ; for values of$ \beta $ near zero and less than 1, the dark energy evolves faster than for$ \beta > 1 $ and$ \beta \to 2 $ . However, regardless of the value of$ \beta $ , the dark energy in our model behaves as a phantom field in the near future and approaches$ {\omega }_{X}\approx -1 $ in the present time, while behaving nearly like matter for$ {\omega }_{X}\approx 0.33 $ .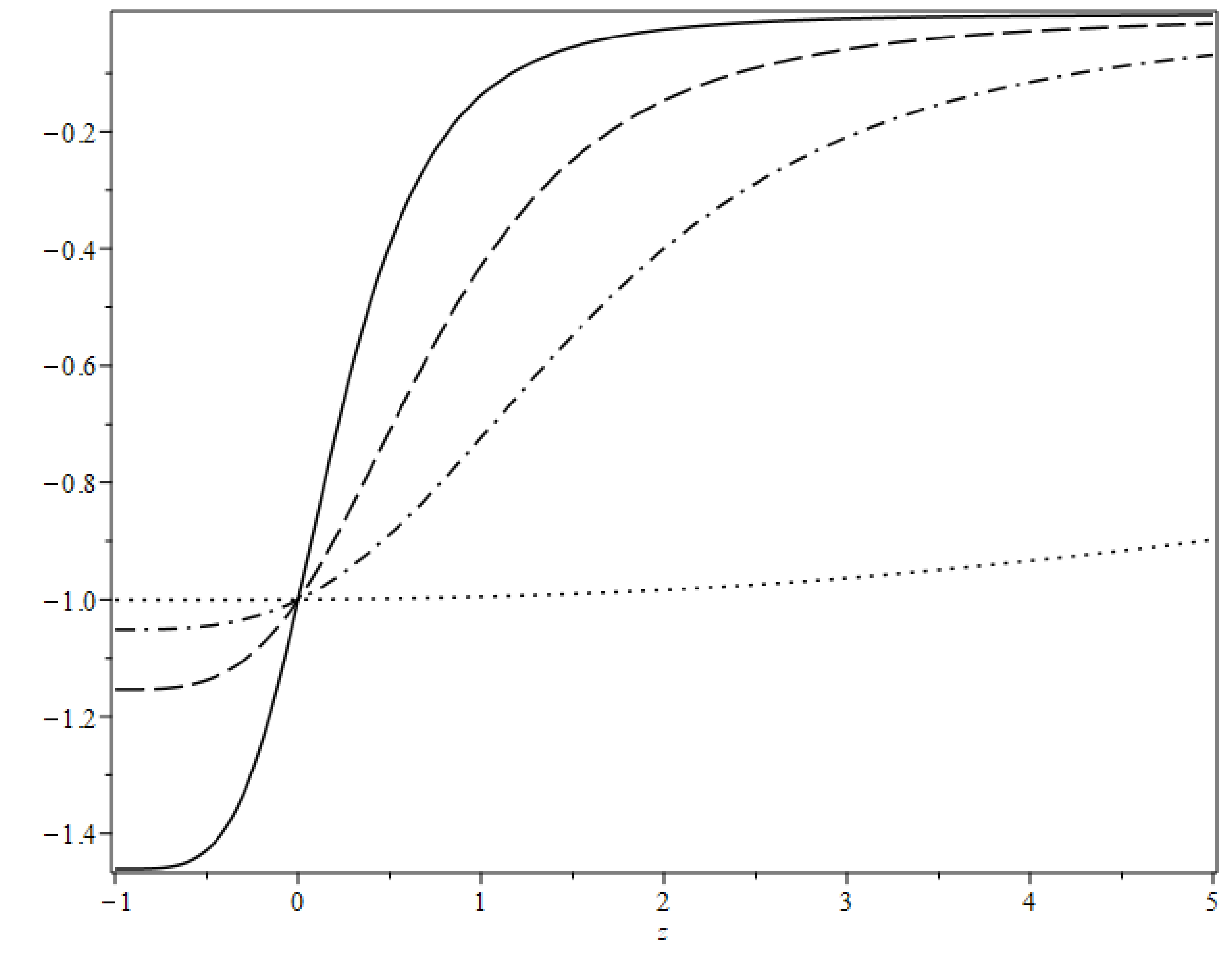
Figure 1. Evolution of the equation of state versus redshift for
$ \beta =0.5 $ (solid curve),$ \beta =1 $ (dashed curve),$ \beta =1.5 $ (dash-dotted curve), and$ \beta =1.99 $ (dotted curve).To find and constrain
$ \beta $ by observational data, plausible approaches to follow include the use of different sets of Supernovae Ia data and methods such as the Monte Carlo Markov chain algorithm [44]. In this study, we used the results of the joint analysis of SNe+CMB data and the$ \mathrm{\Lambda } $ CDM model, which suggests that the transition point occurs at$ {z}_{T}=0.52-0.73 $ [45].Hence, the set of constants
$ \{\alpha ,\beta \} $ is given by$ \alpha \approx 0.50-0.66, $

(22) $ \beta \approx 1.315-1.99, $

(23) where Eq. (20) is used. Note that setting
$ \beta =1 $ and$ 2 $ in Eq. (11) can cancel out the third and second terms, respectively. However, according to Eqs. (21) and (23), one finds the energy density of the dark energy in this model, which depends on matter and radiation. Thus,$ \beta =1 $ or$ 2 $ yields no valuable models.Figure 2 shows the evolution of the deceleration parameter of our model for
$ \beta =1.315, $ $ 1.657, $ and$ 1.99 $ .
Figure 2. Deceleration parameter as a function of redshift for
$ \beta =1.315 $ (solid curve),$ \beta =1.657 $ (dashed curve), and$ \beta =1.99 $ (dash-dotted curve).Figure 3 shows the age of the Universe as a function of redshift for
$ \beta =1.657 $ .$ t=\frac{1}{{H}_{0}}{\int }_{0}^{\frac{1}{1+z}}\frac{{\rm d}x}{h}. $

(24) Note that the age of the Universe is
$ \approx 13.8 $ Gyr, which satisfies recent observations [43].The three circles denote the ages of three old supernovae, LBDS 53W091 (
$ z=1.55 $ ,$ t=3.5 $ Gyr) [46], LBDS 53W069 ($ z=1.43 $ ,$ t=4.0 $ Gyr) [47], and APM 08279+ 5255 ($ z=3.91 $ ,$ t=2.1 $ Gyr) [48]. It shows that our model reduces errors in the age of these old supernovae under the Ricci holographic dark energy.Note also that our model yields a valuable equation of the state, deceleration parameter, and age of the Universe. Next, we compare our model with the Ricci holographic dark energy. From Eqs. (11) and (13), we can express the energy density and pressure of the dark energy in our model as
$ {\rho }_{X}\approx -15\times {10}^{-6}{\rm e}^{-4x}+0.021{\rm e}^{-3x}+0.66{\rm e}^{0.095x}, $

(25) $ {p}_{X}\approx -5.2\times {10}^{-6}{\rm e}^{-4x}-0.68{\rm e}^{0.095x}, $

(26) while the corresponding parameters in the Ricci dark energy are
$ {{\rho }_{X}}_{R}\approx 0.080{\rm e}^{-3x}+0.65{\rm e}^{0.348x} ,$

(27) $ {{p}_{X}}_{R}\approx -0.73{\rm e}^{0.348x}, $

(28) where we have made use of the Planck data [43].
The general behavior of the energy density and pressure in our model and their corresponding parameters in the Ricci dark energy are illustrated in Figs. 4 and 5. As shown in Fig. 4, the energy density of the Ricci dark energy is always larger than the energy density in our model; in the current Universe, they present a minimum deviation from each other,
$ \Delta \rho \approx 0.004 $ . The pressure in the Ricci scalar model goes to zero at infinity while this parameter in our model goes to negative infinity in high redshift. Therefore, this pressure can cancel the effects of the energy density of the dark energy in the past. The pressure of our dark energy coincides with the corresponding parameter in the Ricci dark energy at$ z\approx 0.02 $ , while their mutual deviation is approximately$ ~0.005 $ in the present Universe.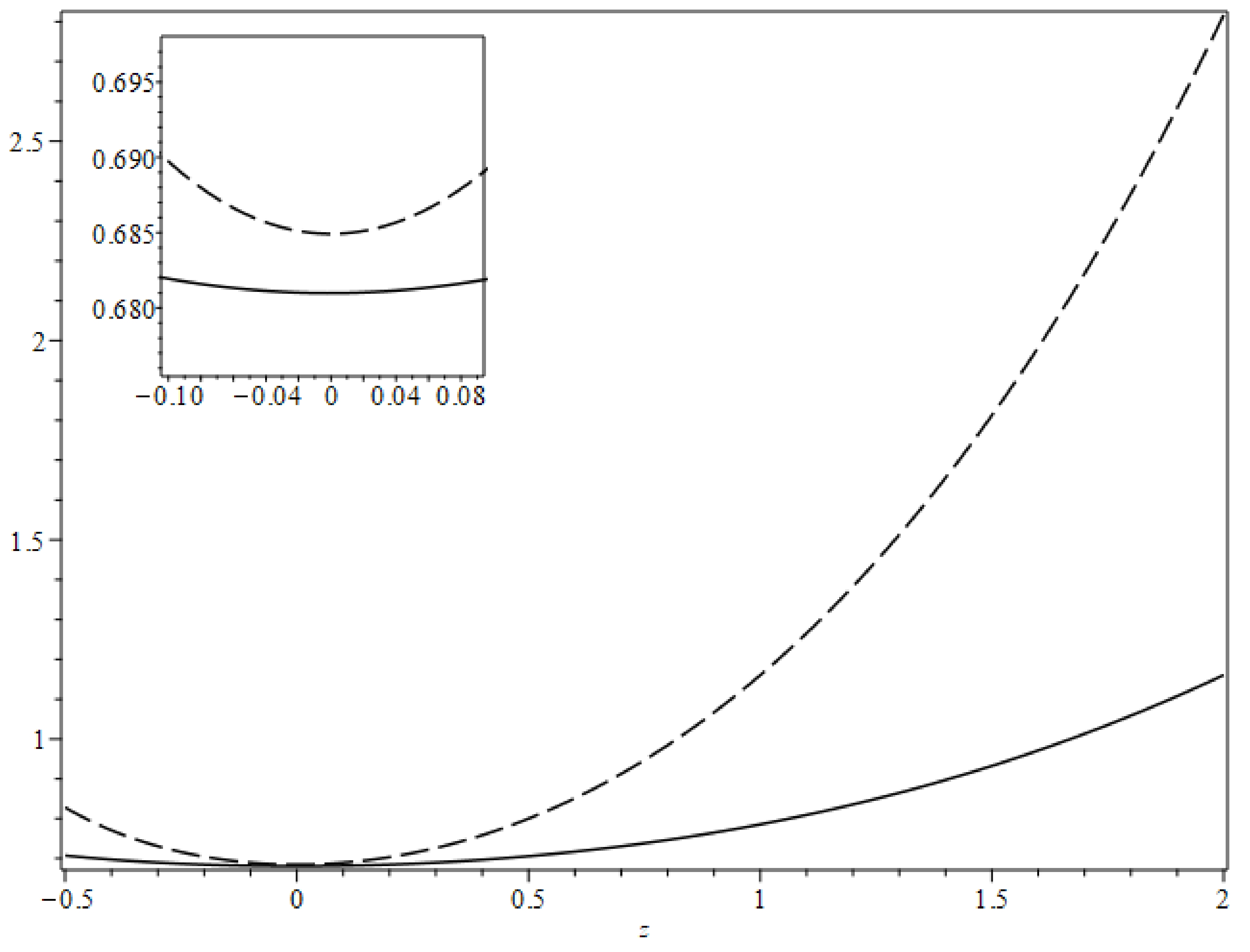
Figure 4. Energy density of our model (solid curve) compared with the corresponding parameter in the Ricci dark energy (dashed curve). We set
$ \beta =1.657 $ in our model.
Figure 5. Pressure of the dark energy in our model (solid curve) compared with the pressure in the Ricci dark energy (dashed curve) for
$ \beta =1.657 $ .In a final comparison between our model and Ricci dark energy, we investigated the evolution of different components using modifying COLOSSUS code [49]. Although both models coincide with observational data in the current Universe, our model makes smaller errors compared with the
$ \mathrm{\Lambda } $ CDM theory in high redshifts (approximately$ ~9{\text{%}} $ ). However, further consideration demonstrates that, for$ \beta \to 1.99 $ , the error in our model compared with the$ \mathrm{\Lambda } $ CDM theory is less than$ 1\% $ . This error in the Ricci dark energy model is approximately$ ~23{\text{%}} $ .So far, we have analyzed our model and compared its results with the Ricci dark energy model. In the next section, we study the structure formation in our model and a modified version of the CAMB code [50].
-
Our model, similar to the Ricci dark energy model, represents dark energy that behaves as matter in the past with a positive equation of state and positive pressure. Hence, our dark energy behaves like matter during most of the matter epoch. Therefore, in the early matter epoch, the matter component is greater than the corresponding component in the
$ \mathrm{\Lambda } $ CDM model. Given that dark energy in our model is described as a matter component with$ {\omega }_{X}\approx 0.33 $ during matter domination, the difference in matter component between our model and the$ \mathrm{\Lambda } $ CDM theory can be as large as approximately$ 33{\text{%}} $ . Therefore, it is necessary to consider structure formation during the matter-dominated epoch and explore how dark energy affects usual structure formation in our model .In Fig. 7, we compare the theoretical angular spectrum of CMB temperature anisotropy in our model with that of the
$ \mathrm{\Lambda } $ CDM model. To have a better insight, we calculated CMB TT, EE, and TE in Fig. 7. Note that they mostly differ from the standard model of cosmology at small scales; the experimental error bars are very large and thus the model is not in conflict with current CMB observations. The largest errors are approximately$ ~7\% $ for CMB TT , approximately$ ~14\% $ for CMB EE, and approximately$ ~40{\text{%}} $ for CMB TE when we set$ \beta =1.657 $ . The corresponding errors are less than$ 1{\text{%}} $ when$ \beta \to 1.99 $ . This demonstrates that the model agrees with the$ \mathrm{\Lambda } $ CDM model for the upper bound of constant$ \beta $ .
Figure 7. Theoretical CMB TT (top panel), EE (middle panel), and TE (bottom panel) for our model (dashed curves) compared with the corresponding parameters in the
$ \mathrm{\Lambda } $ CDM model. In this case, we set$ \beta =1.657 $ .We also studied the matter power spectrum of our model for
$ \beta =1.657 $ ; it is shown in Fig. 8. As expected, the radiation term in the energy density of the dark energy alleviates dust-like component effects. Therefore, the matter-radiation equality occurred at the same$ {a}_{eq} $ in the$ \mathrm{\Lambda } $ CDM model. By decreasing redshifts, the deviation between our model and the$ \mathrm{\Lambda } $ CDM model grows. However, these errors are not too large: at$ k={10}^{-1} $ , for$ z=0 $ , the error is less than$ 6\% $ ; at$ z=5 $ ,$ 10 $ , and$ 20 $ , the corresponding errors are less than$ 2\% $ ,$ 0.06\% $ , and$ 0.006\% $ , respectively. However, we expect that these errors will not be larger than$ 0.001\% $ for$ \beta \to 1.99 $ .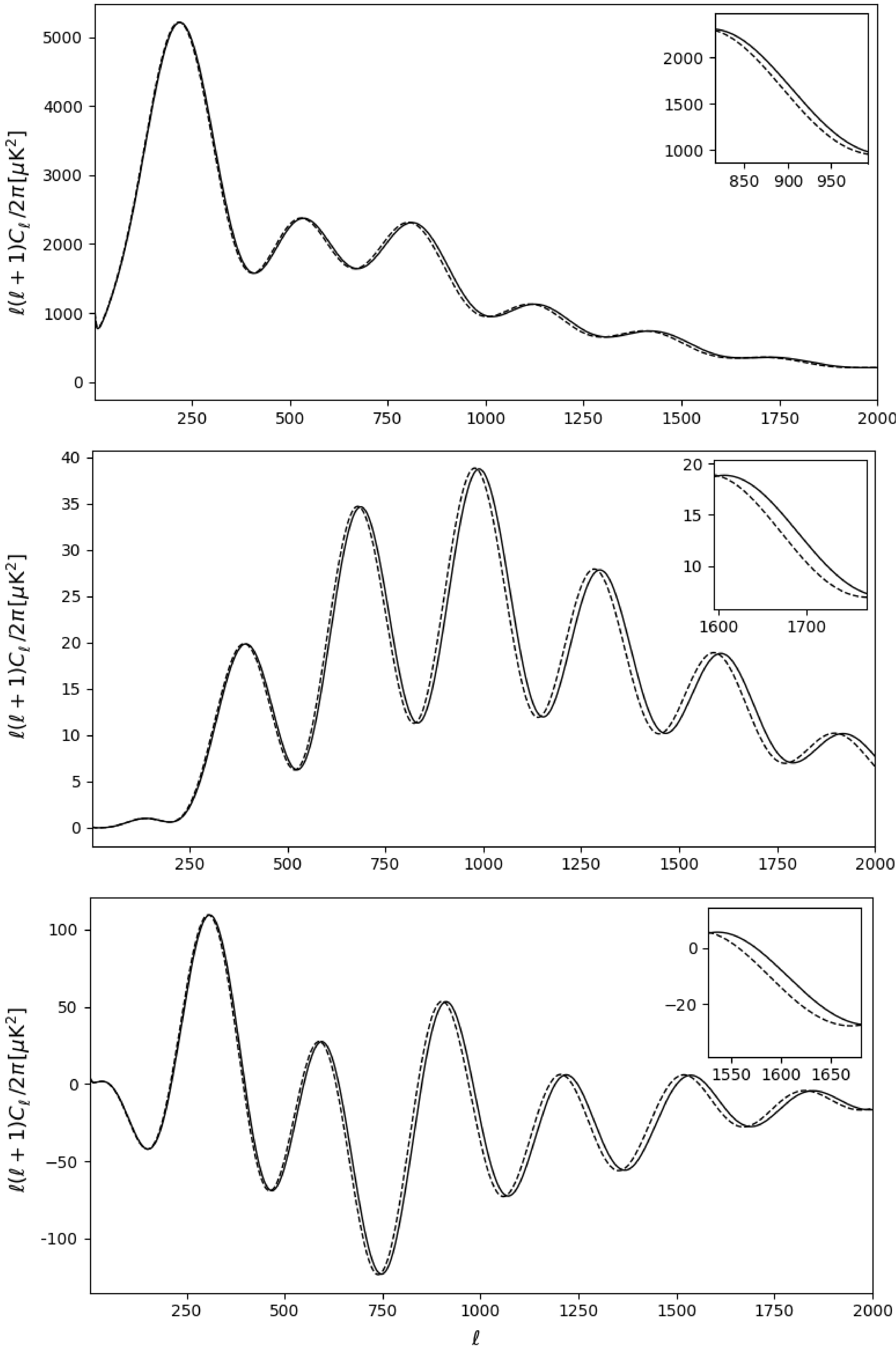
Figure 8. Matter power spectra for different redshifts of our model (dashed curves) compared to the
$ \mathrm{\Lambda } $ CDM model (solid lines). We set$ \beta =1.657 $ .The gravitational lensing of the CMB generates an observed polarization pattern. At the end of this study, we explored the lensing B-mode. This signal provides a measure of the projected mass distribution over the entire observable Universe and is considered a relevant instrument for the measurement of primordial gravity wave signals [51–52]. The largest difference between our model and the
$ \mathrm{\Lambda } $ CDM model is approximately$ ~4{\text{%}} $ around multipoles${{l}}\approx 880$ for default accuracy. This deviation for other lens-potential accuracies is approximately$ ~7{\text{%}} $ (Fig. 9). -
Dark energy as a dominant component in the late-time Universe is one of the robust unsolved problems in modern physics. The holographic principle proposes a set of dark energy models in which the dark energy density is inversely proportional to the area of the event horizon of the Universe. In this study, we reconsidered holographic dark energy such that the energy density of dark energy comes from the acceleration of the particle horizon. This model is similar to the Ricci dark energy model with different constants. Ricci dark energy presents two significant deviations compared with the
$ \mathrm{\Lambda } $ CDM model: in describing the age of old supernovae (Fig. 4 in Ref. [34]) and in the value of cosmic components in high redshifts (Fig. 6 in this study). These inconsistencies are alleviated in our model by fixing constant$ \beta $ . For$ \beta \to 1.99 $ , the behavior of most parameters, such as the evolution of components in high redshifts, matter power spectrum, and theoretical angular spectrum of CMB temperature anisotropy, coincides with the$ \mathrm{\Lambda } $ CDM theory with errors less than$ 0.1\% $ .
Figure 6. (color online) Evolution of different cosmic components in our model for
$ \beta =1.657 $ (dash-dotted curves),$ \beta =1.99 $ (dashed curves), and Ricci dark energy (dotted curves) compared with the$ \mathrm{\Lambda } $ CDM model (solid curves). Blue curves represent matter evolution in our model and Ricci dark energy, while orange curves represent dark energy evolution in these models.Constants in the model alleviate problems of the Ricci dark energy. Furthermore, consideration of structure formation parameters such as the angular spectrum of CMB temperature anisotropy and linear matter power spectrum demonstrates that our model agrees with observational data with small errors.
Similar to the Ricci dark energy model, the causality, fine-tuning, and coincidence problems are solved in our model. Given that our dark energy is determined by the locally observational particle horizon rather than by the future event horizon, the causality problem is solved. Furthermore, given that the energy density of dark energy in the current study is not associated with high-energy physics scales such as the Planck scale, the fine-tuning problem is solved. During the matter-dominated era, the energy density of dark energy becomes comparable to the Hubble parameter and to the size of the non-relativities matter. Thus, the coincidence problem in the late-time Universe is alleviated.
Holographic dark energy from acceleration of particle horizon
- Received Date: 2022-10-22
- Available Online: 2023-03-15
Abstract: Following the holographic principle, which suggests that the energy density of dark energy may be inversely proportional to the area of the event horizon of the Universe, we propose a new energy density of dark energy through the acceleration of the particle horizon scaled by the length of this parameter. The proposed model depends only on one free parameter:





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: