-
A precise knowledge of the equation of state of isospin asymmetry nuclear matter is essential to understand the physics of unstable finite nuclei and neutron stars [1–3]. The key quantity to describe asymmetric nuclear matter is the symmetry energy, which has been extensively studied by microscopic and phenomenological many-body approaches [4–9]. Symmetry energy in the nuclei leads to an increasing density distribution difference between neutrons and protons, resulting in the formation of a neutron skin or neutron halo in neutron-rich nuclei [10–16]. The neutron skin thickness
$ \Delta r_{np} $ , defined as the difference between the root-mean-square radii of the neutrons and protons, contains a considerable amount of inner structure information of nuclei [4]. The study of neutron distribution in nuclei is one of the hot topics in nuclear physics. Compared to the proton distribution, it is difficult to precisely measure the neutron distribution in nuclei experimentally since they are neutral particles [17–20]. A variety of experimental approaches have been attempted to extract the neutron skin thickness, since some experimental observables are sensitive to the density dependence of symmetry energy or the neutron skin thickness, such as parity violating electron scattering [21, 22], proton elastic scattering [23], and antiprotonic atoms [24]. In Ref. [25], the behaviors of nuclear density profiles of antiprotons annihilated on different targets were studied. It was found that the stiffness of symmetry energy varies significantly with the neutron-proton ratio in neutron-rich nuclei.Giant resonances are the collective motions of the protons and neutrons in the nucleus. It is well known that the properties of electric isovector multipole giant resonances are governed by the isovector part of the effective interactions. Hence, the electric pygmy resonances, dipole resonances, dipole polarizability, and isovector giant quadrupole resonance have been used to constrain the symmetry energy and to extract the neutron skin thickness [26–36]. There are also many other studies on extracting the neutron skin thickness using charge exchange excitations. It was shown that the isotopic dependence of the energy spacings between the Gamow-Teller resonance and isobaric analog state provides direct information on the evolution of neutron-skin thickness along the Sn isotopic chain in Ref. [37]. In Refs. [38–40], the energy difference between the anti-analog giant dipole resonance and the isobaric analog state in
$ ^{208} $ Pb was used to deduce the neutron skin and the density dependence of symmetry energy. It is known that the model-independent non-energy-weighted sum rule of charge exchange spin-dipole (SD) is directly related to the neutron skin thickness and has been suggested to measure the neutron skin thicknesses of unstable nuclei [41].Experimentally, the SD excitations were studied in
$ ^{90} $ Zr by the charge exchange reactions$ ^{90} $ Zr(p, n)$ ^{90} $ Nb and$ ^{90} $ Zr(n, p)$ ^{90} $ Y [42, 43] and in$ ^{208} $ Pb by the polarized protons for the charge exchange reaction$ ^{208} $ Pb(p, n)$ ^{208} $ Bi; each multipole component was successfully separated from the total strength [44]. The quenching problem for SD excitations was also discussed from the comparisons between RPA results and experimental data [45, 46]. The SD model-independent sum rule was extracted for$ ^{90} $ Zr in Ref. [47] using multipole decomposition analysis. For$ ^{208} $ Pb, the sum rule value is not yet available since the strength information in the counter experiment$ ^{208} $ Pb(n, p)$ ^{208} $ Tl is missing.In Refs. [47, 48], the authors used the experimental data of the model-independent non-energy-weighted sum rule to constrain the neutron skin of
$ ^{90} $ Zr; the theoretical calculations were performed in the proton-neutron random phase approximation (pn-RPA) with SLy4, SGII, and SIII interactions. To obtain more clean information on the neutron skin thickness and the density dependence of symmetry energy, one can use a family of effective interactions, such as SAMi-J interactions [49]. These effective interactions were built by fitting the parameters to specific observables of finite nuclei, such as binding energies, charge radii, and properties of infinite nuclear matter. The isovector part of the interactions is generated in such a way that the symmetry energy remains at a fixed value ($ \approx $ 26 MeV) at$ \rho\simeq $ 0.1 fm$ ^{-3} $ , so the interactions are characterized by different values of the symmetry energy at saturation density. In the fitting procedure, all isoscalar observables remain unchanged, e.g., the incompressibility coefficient almost equals 245 MeV. In this study, we first calculate the charge exchange SD strengths of$ ^{90} $ Zr and the model-independent sum rule values in the framework of Skyrme Hartree-Fock (HF) + pn-RPA with SAMi-J interactions; the calculated SD strengths are compared to the corresponding experimental data. We then extract the mean-square radii of the neutrons and the neutron skin thickness using the experimental sum rule value. With the restriction of the neutron skin, the estimated values for the symmetry energy J and its slope parameter L at saturation density are obtained.The paper is organized as follows. A brief report on the Skyrme HF and pn-RPA methods is presented in Sec. II. In Sec. III, we present the results and discussion. Finally, a summary and some remarks are given in Sec. IV.
-
The calculations are performed within the Skyrme HF and pn-RPA approaches; the detailed formulas for the theoretical models and matrix elements can be found in Refs. [50–53]. Here, we only give some information related to the subject of this paper. The operators of SD transitions are defined as
$ \hat{S}_{\pm}=\sum\limits_{im\mu} {t^{i}_{\pm} \sigma^{i}_{m} r_{i} Y_{1\mu} (\hat{r}_{i})}, $

(1) where the isospin operators t are expressed as
$ t_{3}=t_{z} $ and$ t_{\pm}=t_{x}\pm it_{y} $ ,$ \sigma_{m} $ is the spin operator,$ r_i $ is the radial dependence of the SD operators, and$ Y_{1\mu} $ is the spherical harmonics function. The sum on$ im\mu $ is for all the nucleons and all the magnetic quantum numbers. For the λ-pole SD operators, we have$ \hat{S}^{\lambda}_{\pm}=\sum_{i} {t^{i}_{\pm} r_{i} [\sigma \times Y_{1}(\hat{r}_{i})]^{\lambda}}, $

(2) which have three components
$ \lambda^{\pi}=0^{-}, 1^{-}, 2^{-} $ with the summation running over all nuclei i. The model-independent sum rule for the SD operator is derived as$ \begin{aligned}[b] \Delta S&=S_--S_+=\sum_{\lambda} (S^{\lambda}_--S^{\lambda}_+) \\ &=\sum_{\lambda} \frac{(2\lambda+1)}{4\pi} (N\langle r^{2} \rangle_{n} - Z\langle r^{2} \rangle_{p}) \\ &=\frac{9}{4\pi} (N\langle r^{2} \rangle_{n} - Z\langle r^{2} \rangle_{p}), \end{aligned} $

(3) It can be seen from Eq. (3) that the SD sum rule is directly related to the mean-square radii of the neutrons and the protons with the weights of neutron and proton numbers, which are denoted as
$ \langle r^{2} \rangle_{n} $ and$ \langle r^{2} \rangle_{p} $ , respectively. As we know that the root-mean-square (rms) charge radius of a nucleus can be measured experimentally at high precision, the rms proton radius$ \sqrt{\langle r^{2} \rangle_{p}} $ can be obtained from the charge radius after correcting from the proton form factor. Thus, the rms neutron radius$ \sqrt{\langle r^{2} \rangle_{n}} $ or the neutron skin thickness$ \Delta r_{np}=\sqrt{\langle r^{2} \rangle_{n}} -\sqrt{\langle r^{2} \rangle_{p}} $ can be derived from Eq. (3) if the sum rule value is fixed experimentally. -
The ground state properties of
$ ^{90} $ Zr are obtained using the Skyrme HF approach; a family of Skyrme interactions named SAMi-J is adopted in the calculations, where J = 27, 29, 31, 33, 35, which means the interactions have different symmetry energies and slope parameters at the saturation density, leading to different isovector properties of finite nuclei. The calculated rms radii of neutrons, protons, charge, and neutron skin thickness are listed inTable 1. Among the various radii, the rms charge radius can be determined accurately for many nuclei using electron scattering experiments. From Table 1, one can see that the calculated proton rms radii or charge radii are not affected very much from the adopted interactions; the experimental charge rms radius of$ ^{90} $ Zr is approximately 4.269 fm [54], and the data can be well described by the present calculations. After considering the effect of the finite size of the protons [55], one can obtain the proton rms radius of$ ^{90} $ Zr, which is approximately 4.209 fm. The calculated rms neutron radii and neutron skin thickness depend on the effective interactions, which increase gradually as shown inTable 1.SAMi-27 SAMi-29 SAMi-31 SAMi-33 SAMi-35 $r_n$ 

4.266 4.292 4.314 4.330 4.339 $r_p$ 

4.214 4.209 4.204 4.197 4.191 $r_c$ 

4.288 4.284 4.278 4.272 4.266 $r_n-r_p$ 

0.052 0.082 0.111 0.133 0.148 $S_--S_+$ 

136.9 146.5 155.4 162.1 166.5 Table 1. Various radii of
$^{90}$ Zr and neutron skin thickness calculated in Skyrme HF with SAMi-J effective interactions. The charge exchange SD sum rule$S_--S_+$ values calculated by the pn-RPA with SAMi-J effective interactions are also shown. The units for the radii and the SD sum rule are fm and fm$^{2}$ , respectively.Next, we investigate the SD
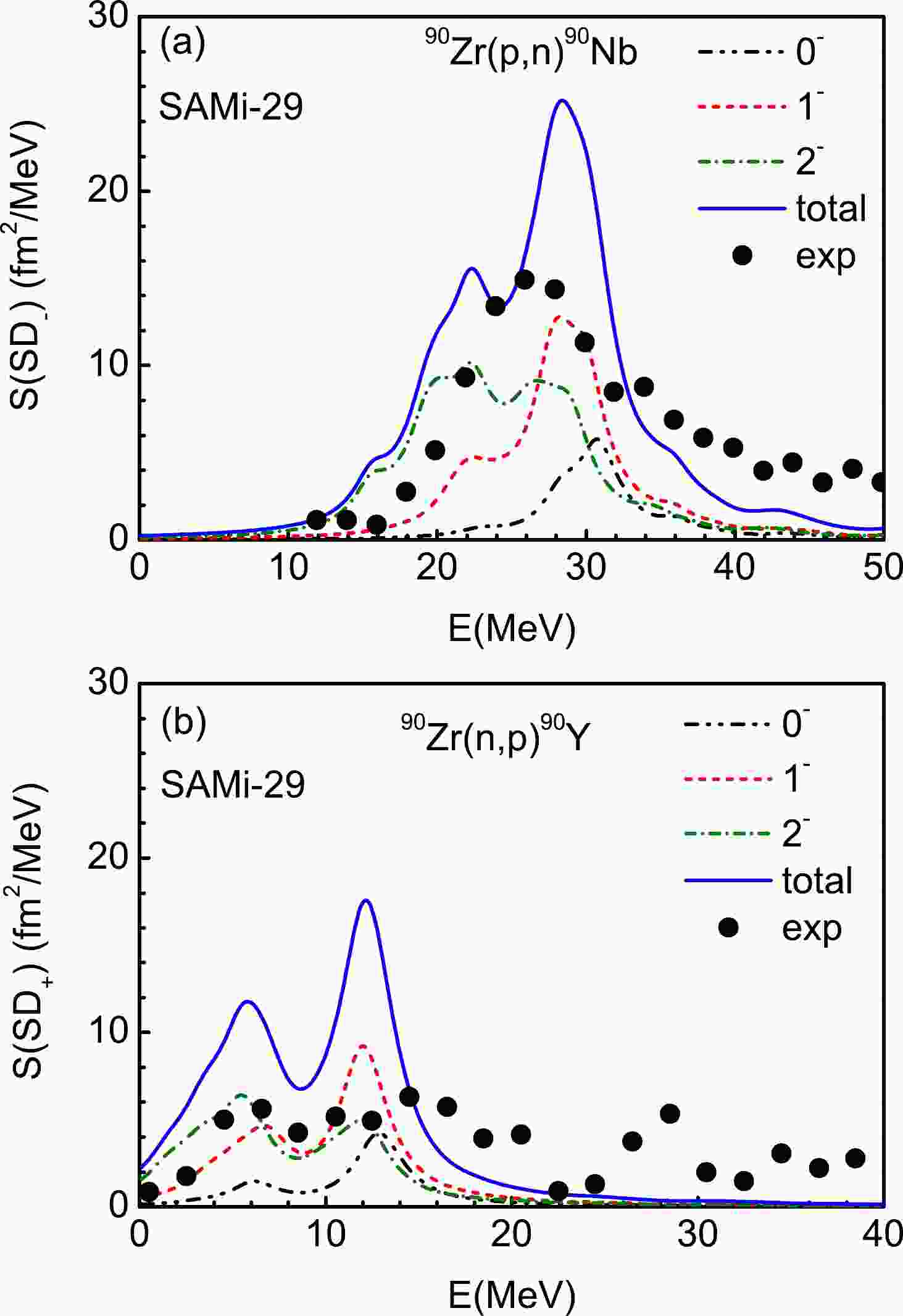
$ _\pm $ strengths calculated by the self-consistent pn-RPA [52, 53, 56, 57] to examine the theoretical model. The charge exchange SD$ _\pm $ strengths are calculated with the SAMi-J interactions. The SD$ _\pm $ total strengths and$\lambda^{\pi}=0^-,~1^-,~2^-$ components obtained with the SAMi-29 interactions are shown in Fig. 1 (a) and (b). The dashed-dotted-dotted, short-dashed, and short-dashed-dotted lines show the SD strengths of the$\lambda^{\pi}=0^-,~1^-,~2^-$ components, respectively, while the solid curves show the sum of the three multipoles. The experimental data from Refs. [42, 43] are also plotted in the figure. In Fig. 1 (a), the total experimental SD$ _- $ strength can be described well by the theoretical model; the main peak of the data appears at E$ _x \simeq $ 26.0 MeV, while the theoretical model predicts that the SD$ _- $ strength splits into two peaks: the pygmy one is located at E$ _x \simeq $ 22.4 MeV, and the stronger one is at E$ _x \simeq $ 28.0 MeV, which is very close to the experimental excitation energy. It can be seen clearly from Fig. 1 (a) that the pygmy total theoretical SD$ _- $ strength is formed mainly from the$\lambda^{\pi}=1^-,~2^-$ components, while the$\lambda^{\pi}=0^-,~1^-,~2^-$ components contribute to the main peak at E$ _x \simeq $ 28.0 MeV. From Fig. 1 (b), it is shown that the experimental SD$ _+ $ strength is very fragmented in the whole energy region, while the SD$ _+ $ strength is recognized experimentally at energy below 23.0 MeV in Refs. [43, 47]. The total theoretical result shows two peaks at E$ _x \simeq $ 5.7 MeV and E$ _x \simeq $ 12.2 MeV. The$\lambda^{\pi}=0^-,~1^-,~2^-$ components contribute to both peaks, but the contributions are mainly from the$\lambda^{\pi}=1^-,~2^-$ components.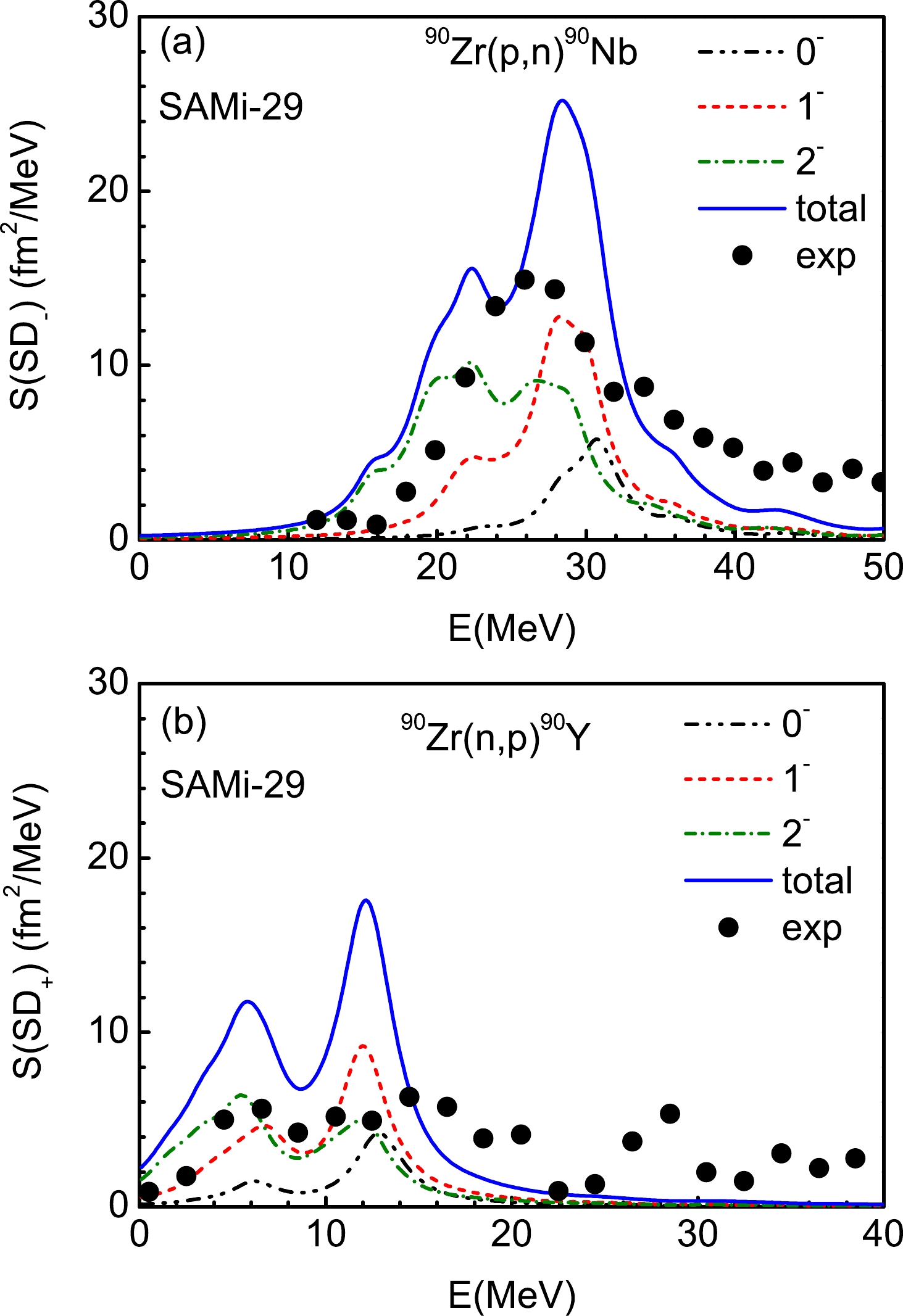
Figure 1. (color online) SD strength distributions for S(SD
$ _- $ ) (a) and S(SD$ _+ $ ) (b) calculated in the pn-RPA with SAMi-29 interactions. The$\lambda^{\pi}=0^-,~1^-,~2^-$ components and the total strengths are shown. The experimental data obtained from Refs. [42, 43] are shown as black symbols.When we obtain the total SD
$ _\pm $ strength distribution for each effective interaction, the integrated SD$ _\pm $ strength can be obtained by the following formula:$ \begin{array}{*{20}{l}} S_\pm=\int S(SD_\pm,E){\rm d}E. \end{array} $

(4) Since the experimental multipole decomposition (MD) analysis of the SD
$ _- $ (SD$ _+ $ ) channel becomes unstable when the excitation energy is over 40 MeV (23 MeV), as in Ref. [47], we integrate the SD$ _- $ strength up to an excitation energy of 40 MeV and the SD$ _+ $ strength up to 23 MeV. Consequently, we obtain the sum rule value$ S_–S_+ $ . The calculated values are listed in Table 1 for each adopted interaction. As discussed previously, the calculated proton rms radius of$ ^{90} $ Zr is almost constant for all effective interactions; we choose the experimental data 4.209 fm in the next investigation. Following the assumption, the model-independent sum rule of Eq. (3) is a linear function of the mean-square radii of the neutrons, which is well verified in Fig. 2, where the calculated sum rule values show a linear increase as the calculated mean-square radii of the neutrons increase. In Fig. 2, the red solid line shows the result of linear fitting; the gray short-dashed lines represent the experimental data. Its upper and lower limits are depicted by the shaded box, which reads as$S_--S_+$ = 147$ \pm $ 13 fm$ ^2 $ . It is clear that we can constrain the mean-square radii of the neutrons in the region of 18.147 to 18.697 fm$ ^2 $ as shown in the area marked by the box; we can then deduce the neutron skin thickness, which is approximately$ \Delta r_{np}=0.083 \pm 0.032 $ fm. The obtained neutron skin thickness is slightly larger than the values in Refs. [47, 48]. In previous investigations, the authors used several independent effective interactions in the calculations. Although the interactions have different behaviors of symmetry energy, the results may be affected by other factors, for example the incompressibility of nuclear matter. The interactions used in the present study are fitted in the same ansatz except for the different symmetry energies at the saturation density. The antiprotonic atoms experiment shows that the neutron skin thickness of$ ^{90} $ Zr is approximately$\Delta r_{np}= 0.09\pm 0.02\;\mathrm{fm}$ in Ref. [58]; our result for$ \Delta r_{np} $ is very close to the data.
Figure 2. (color online) Calculated
$S_--S_+$ values as a function of mean-square radii of the neutrons. The results are calculated with SAMi-J interactions and denoted as blue symbols.The neutron skin thickness is sensitive to the density dependence of the symmetry energy [59]; it is seen that the connection between
$ \Delta r_{np} $ and the slope parameter L of the nuclear symmetry energy is approximately linear. Using the relationship between the nuclear symmetry energy J (its slope parameter L) and the neutron skin thickness$ \Delta r_{np} $ extracted presently, we can further place restrictions on J (L). As seen in Fig. 3, the correlation between J and$ \Delta r_{np} $ is shown in the upper panel of the figure, while the lower panel presents the connection between L and$ \Delta r_{np} $ ; the gray short-dashed lines together with shaded boxes represent the constrained neutron skin thickness of$ ^{90} $ Zr. The fitting lines are shown as well. Many studies have discussed this kind of linear relationship, and it is also shown clearly in Fig. 3. The weighted average of J in Fig. 3 (a) is given as$J = 29.2 \pm 2.6\; \mathrm{MeV}$ . Compared with the symmetry energies obtained from other studies, the value of J in the present work is slightly smaller, but generally it still matches with other values.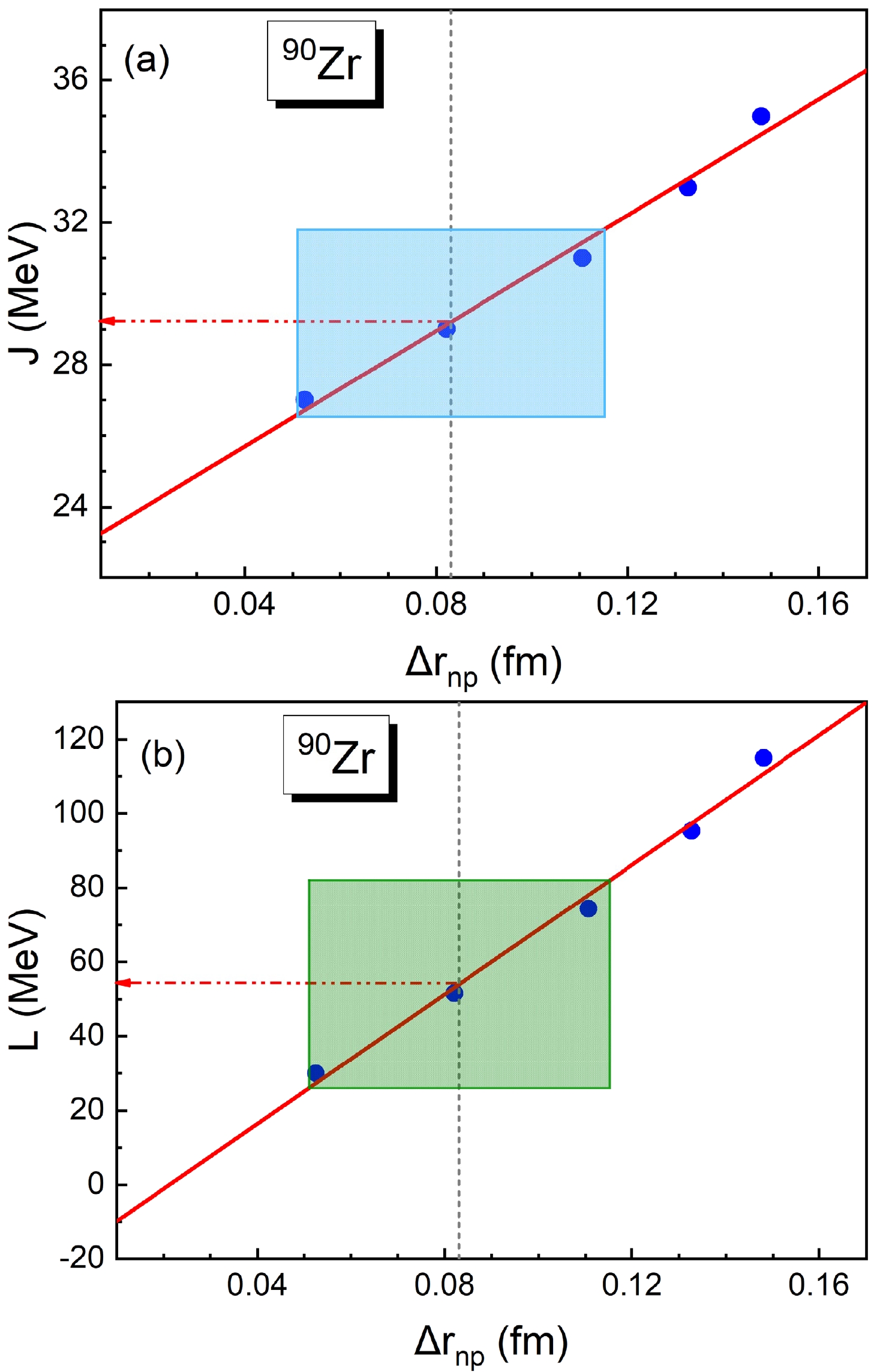
Figure 3. (color online) Correlations between the neutron skin thicknesses
$ \Delta r_{np} $ of$ ^{90} $ Zr and symmetry energies as well as the slope parameters given by SAMi-J interactions in this work.Finally, we discuss the slope parameter L. It can be found in Fig. 3 (b) that the correlation between L and
$ \Delta r_{np} $ is approximately linear. We also constrain the value of L by the present$ \Delta r_{np} $ of$ ^{90} $ Zr, so the slope parameter L is given as$L = 53.3 \pm 28.2\; \mathrm{MeV}$ . The L value is comparable with the results from other methods in the literature. The recent PREX-II experiment, measuring the parity violating asymmetry A$ _{PV} $ in$ ^{208} $ Pb, results in a neutron skin thickness of$ ^{208} $ Pb as$\Delta r_{np}^{208}=0.283\pm0.071 \;\mathrm{fm}$ [22]. The experimental data of PREX-II favor a stiff symmetry energy; the symmetry energy and the slope parameter can be constrained as$J=38.1 \pm 4.1 \;\mathrm{MeV}$ and$L=106 \pm 37 $ MeV [60], which systematically overestimate the current accepted limits$J=31.7 \pm 3.2\; \mathrm{MeV}$ and$L=58.7 \pm 28.1$ MeV [30, 61, 62]. Our results are consistent with the current accepted values. -
In summary, we have studied the SD
$ _\pm $ strengths of$ ^{90} $ Zr using the Skyrme HF plus pn-RPA with SAMi-J interactions. It is found that the present calculations can well reproduce the experimental SD$ _\pm $ strengths. We have also calculated the sum rule$S_--S_+$ values for each SAMi-J interaction. Employing the model-independent sum rule, we have constrained the mean-square radii of the neutrons and the neutron skin thickness$ \Delta r_{np} $ of$ ^{90} $ Zr, obtaining$ \Delta r_{np}=0.083 \pm 0.032 $ fm, which is consistent with the results of other studies; for example, the analysis of antiprotonic atoms gives$\Delta r_{np}=0.09 \pm 0.02\; \mathrm{fm}$ in Ref. [58]. Furthermore, the relationships between the neutron skin thickness$ \Delta r_{np} $ and nuclear symmetry energy J, as well as its slope parameter L, are used to extract information on J and L. The obtained$ \Delta r_{np} $ can place a constraint on the symmetry energy and slope parameter, giving values of$J=29.2 \pm 2.6\; \mathrm{MeV}$ and$L = 53.3 \pm 28.2 \mathrm{MeV}$ . To date, both the experimental SD$ _- $ and SD$ _+ $ strengths are known only for$ ^{90} $ Zr; if more experimental data for other nuclei are available in the future, more accurate information on the density dependence of symmetry energy can be obtained.
Neutron skin thickness of 90Zr and symmetry energy constrained by charge exchange spin-dipole excitations
- Received Date: 2022-09-28
- Available Online: 2023-02-15
Abstract: The charge exchange spin-dipole (SD) excitations of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: