-
The Einstein theory of gravity is so far the most accepted theory. It has been tested by observing the gravitational waves by the LIGO from a binary of BHs [1]. Other recent observations on the shadow of the supermassive BH at the center of the elliptical galaxy M87 and our own galaxy the Milky Way, reported by the EHT Collaboration [2, 3], have further confirmed the Einstein theory of gravity. These fascinating results on the gravitational waves produced from the collision of two merging BHs and the BH shadows have increased the interest of researchers in studying different BH solutions from different points of view and probing the fundamental physics of strong gravitational fields in the vicinity of BHs. The study of photon motion in spacetime surrounding a BH is essential for analyzing BH shadows and gravitational lensing. When light travels toward a gravitational source, according to the theory of general relativity, it deviates from its path due to the curvature produced by the source in its path. This bending of light by the gravitational source produces an effect very similar to that produced by an optical lens and is known as gravitational lensing (see, for example, [4]). In astrophysics, gravitational lensing can be used for observing distant objects in the Universe, such as galaxies lying in the line of sight of the gravitational source acting as the gravitational lens. Gravitational lensing can be categorized into two, namely (i) strong deflection gravitational lensing with a deflection angle much larger than 1 and (ii) weak deflection gravitational lensing with a deflection angle much less than 1. Weak deflection gravitational lensing can be further categorized into three: strong gravitational lensing, weak gravitational lensing, and micro gravitational lensing. In astronomy, strong gravitational lensing is mostly caused by galaxies and clusters of galaxies, and it may form multiple images and giant arcs. Strong gravitational lensing produces rings such as Einstein's rings and is used for observing the position and magnification of a BH [5]. Weak gravitational lensing is a result of some minor distortions with magnifications too small to be detected, unless their average is taken over a number of galaxies. Weak gravitational lensing is assumed to investigate the cause of the accelerated expansion of the observable Universe [6]. From astrophysical observations, the bending of light or photon beams and gravitational lensing observed so far are in the weak field limit, i.e., with very small deflection angles (or weak deflection angles) [7]. Strong deflection gravitational lensing will not be directly applicable in near future experiments because of its technological limitations, as it requires high resolution and magnification. For instance, the resolution of the relativistic image of the Sgr A* supermassive BH requires an angle of resolution of
$ 10^{-2} $ micro-arc-second, which is two orders better than the resolution that is attainable with the currently available technology [8]. Consequently, in the present study, we discuss the gravitational deflection angle caused by the charged-Kiselev BH (discussed in the next section) in the weak field limit. Further, in the close vicinity of a BH, the nearby passing light or photons move in circular orbits known as light rings. Because of these light rings, the central object, i.e., the BH, appears as a dark disk in the sky, which is called the shadow cast by the BH [9–11].The brightest objects in the Universe, quasars, were discovered in 1963, and after this discovery, gravitational lensing effects were studied with much greater interest [12]. The gravitational lensing effect of a quasar was observed for the first time in 1979 [13]. Gravitational lensing was first studied in the weak-field limit, and afterward, these studies were extended to the strong-field limit [14–17]. To analyze different spacetime parameters in BH spacetimes, gravitational lensing has been investigated by various studies [9, 18–21]. Bozza et. al have presented an analytical method for the study of gravitational lensing caused by the Schwarzschild BH [22]. After the proposal of this analytical technique for gravitational lensing of the Schwarzschild BH, it has been generalized for spherically symmetric static spacetimes [23]. Gravitational lensing for a spinning BH has also been studied by Bozza [24]. Virbhdra and Keeton have investigated gravitational lensing for both the Schwarzschild BH and the Janis-Newman-Winicour naked singularities [25]. Gibbons and Werner have proposed an alternate method to calculate the weak deflection angle of photons using the Gauss-Bonnet theorem (GBT) for asymptotically flat spacetimes [26]. Werner has applied it to stationary spacetimes using Finsler-Randers type geometry [27]. Ishihara et al. have extended the Gibbons and Werner method to non-asymptotically flat spacetimes using the finite distance corrections of the source and the receiver [28, 29]. Moreover, T. Ono et al. have shown that the method proposed by Gibbons and Werner can be applied to axisymmetric spacetimes [30]. Li et al. have studied the finite distance method for massive particles in the Jacobi-Maupertuis and Randers-Finsler metrics using the GBT [31, 32]. Crisnejo and Gallo have calculated the weak deflection angle caused by BHs in some plasma media using the GBT [33]. The study of gravitational lensing for charged BHs has also been carried out [34–64]. Other interesting works on strong deflection gravitational lensing have been presented for different BH spacetimes (for example, [65–69]). Another method for calculating the weak deflection angle is available in literature, which has already been applied for different BH spacetimes in modified theories of gravity [70–74].
Amongst the several proposals for estimating the spin of a rotating BH [75, 76], one proposal is that BH shadows might be helpful in placing constraints on the value of the spin parameters of BHs [77]. Falcke et al. were the first to introduce the idea of the observation of a BH shadow [78]. Virbhadra and Ellis obtained an equation for gravitational lensing that allows a large deflection of the light beam and therefore has been used for studying strong gravitational lensing by BHs [14]. They used their equation for studying gravitational lensing due to light deflection in the close vicinity of the photon sphere of the supermassive BH at the center of the galaxy. They theoretically found that, on both sides of the line joining the observer and the gravitational lens, there exists an infinite sequence of highly de-magnified images due to the photon sphere. They called these images relativistic images. Moreover, the recently released images, or more precisely, the relativistic images of the supermassive BHs in the center of the galaxy M87 and Milky Way, have opened a new window for researchers to constrain different BH parameters. Using the astronomical data provided by the EHT collaboration, free parameters for different ultra compact objects in the Einstein gravity and other alternative theories of gravity have been refined [79–84]. There are also several papers related to the observable shadow of a BH according to different theories of gravity [47, 54, 85–105].
One possible candidate to explain the current accelerated expansion of our Universe is the notion of dark energy. There are different models put forward for elaborating the nature of dark energy. These models include Chaplygin gas, the cosmological constant, K-essence, and quintessence. The quintessence model is the most accepted one and it has been proposed by some physicists as the fifth fundamental force in nature [106], for which the equation of state parameter is restricted as
$ -1<\omega_q< -1/3 $ . In the current study, we consider three different values of the parameter$ \omega_q $ , namely (i)$ \omega_q=-1 $ , which corresponds to the cosmological constant, (ii)$ \omega_q=-2/3 $ , which is considered for the pure quintessence dark energy, and (iii)$ \omega_q=-1/3 $ , which is taken for the frustrated cosmic strings network [107, 108], for which our Universe remains static (for further details, one may see Ref. [107]). In the astrophysical investigation of ultra compact objects, it is assumed that the quintessential dark energy produces gravitational effects on the gravitational deflection angle of photon beams (caused by a BH) coming from a distant star and may thus be taken into consideration in such a scenario. Therefore, it is of interest to have a BH solution in the quintessence environment. To obtain such a BH solution, Kiselev was the first to give a BH solution of the field equations of the general relativity for a spherically symmetric static source in the presence of quintessence [109]. He has also presented an electrically charged version of his BH solution with quintessence, which has been studied in different contexts including its shadow [110–114]. In literature, the correctness and validity of the Kiselev BH solution have been criticized (see, for example, [115, 116]). In this regard, Visser argued that the Kiselev BH solution does not represent the quintessence dark energy with an isotropic pressure [115]. Responding to the point of Visser, Sakti et al. [117] commented in a recent work that the Kiselev BH solution has been derived with the assumption of the isotropic averaging of the tensor components over the angles of space-like matter, where the equation of state is similar to that for the quintessence in cosmology. The Kiselev BH solution has also been generalized in the background of cloud of strings [118]. For the cloud of strings, it is assumed that they were formed during the early formation of structures in the Universe because of symmetry breaking [119]. The thermodynamics of the Kiselev BH with clouds of string have already been analyzed [120]. The time-like and null geodesics have also been investigated in the vicinity of the quintessential BH with clouds of strings [121].In the astrophysical scenario, mostly photons go through a plasma medium [122, 123]. Photons moving around BHs, surrounded by accretion disks consisting of plasma, may produce noticeable effects on the angular position of the image of the BH, resulting in various observable wavelengths [124]. Thus, the effects of plasma on the phenomenon occurring in the close vicinity of the horizon of BHs may provide extra understanding of the gravitational field of the charged-Kiselev BH in the string cloud background. This is one of the most promising reasons to investigate gravitational lensing and shadows of BHs in the presence of a plasma medium. Using the Synge method [125], the shadows of the Schwarzschild BH and Kerr BH have been analyzed in a plasma medium [126–129]. Kogan and Tsupko have shown that due to the dispersion properties of the nonuniform plasma, the gravitational deflection angle by the Schwarzschild BH depends on the frequency of the electromagnetic waves [130]. Er and Mao observed an extra deflection angle due to the presence of plasma in addition to the one produced by the gravitational source [131]. They further showed that the influence of a nonuniform plasma is greater than the influence of a uniform plasma medium on the BH shadow. The shadows of the Schwarzschild and Kerr BHs have been analyzed in the presence of plasma by taking into account the radial power-law density, and it was observed that the size and shape of the shadows for both of the BHs are changed due to the plasma effects [132]. The effects of a homogeneous plasma on gravitational lensing by a spherically symmetric static BH have been studied by Hakimov and Atamurotov [133]. In their work, Hakimov and Atamurotov analyzed the effects of the deformation parameter on the gravitational lens as well as the effects of the frequency of the plasma on the brightness of the source in the case of microlensing. The effects of plasma on the gravitational lensing and shadow cast by the charged-Kerr BH have been reported in literature [134]. The influence of a uniform plasma on weak gravitational lensing by a spherically symmetric BH in a modified gravity theory has been investigated in Refs.[135–146]. Some other recent interesting works relating the effects of plasma on the optical properties of BHs in Einstein gravity and other theories of gravity can be found in literature [147–152]. Inspired by the interesting results available in literature from the study of the optical properties of different BHs, in this work, we explore the optical properties such as the weak gravitational lensing and the shadow cast by the electrically charged and spherically symmetric static Kiselev BH in the string cloud background in the presence of plasma. In particular, we are keen on observing the effects of both uniform and nonuniform plasmas, along with the spacetime parameters, on the weak deflection angle and the shadow cast by the charged-Kiselev BH with clouds of strings.
We organize our paper as follows. In Sec. II, we provide the derivation of the spherically symmetric static spacetime metric of the charged-Kiselev BH in the presence of a cloud of strings. In Sec. III, we discus the photon motion in the spacetime of the charged-Kiselev BH in the string cloud background, for three different values of the equation of state parameter
$ \omega_q $ . In subsection A, we consider the case of$ \omega_q=-2/3 $ , which corresponds to the quintessence dark energy. In subsection B, we take$ \omega_q=-1 $ , which is the case of the cosmological constant, and in subsection C, we discuss the case of$ \omega _q=-1/3 $ , which corresponds to the frustrated network of cosmic strings. For all three values of the parameter$ \omega_q $ , we find that the radius of the photon sphere for the charged-Kiselev BH in the presence of string clouds increases with both the parameters γ and a, and it decreases with the charge Q of the BH. In Sec. IV, we analyze the photon motion in a uniform and nonuniform plasma medium in the vicinity of the charged-Kiselev BH with clouds of strings. In subsections A, B, and C, we consider the three different cases of the parameter$ \omega_q= -2/3 $ ,$ \omega_q=-1 $ , and$ \omega_q=-1/3 $ , respectively. In subsections D and E, the effects of uniform and nonuniform plasmas on the photon spheres are analyzed, respectively. For all three values of the parameter$ \omega_q $ , we observe that the radius of a photon sphere is larger in the presence of plasma compared with the radius of a photon sphere without plasma. In Sec. V, we study the weak deflection angle using the GBT. In subsection A, we consider a uniform plasma medium, and in subsection B we take into account a nonuniform plasma medium. We see that the uniform plasma increases the weak deflection angle, while the nonuniform plasma decreases it. In Sec. VI, subsection A, we investigate the effects of uniform plasma on the shadow cast by the charged-Kiselev BH in the presence of string clouds. We discuss the case of nonuniform plasma medium in subsection B. We observe that, with increasing values of the parameters γ and a, the radius of the shadow cast by the charged-Kiselev BH in clouds of strings increases, and it decreases with the charge Q of the BH. We also see that the presence of plasma shrinks the shadow size of the charged-Kiselev BH in the string cloud background. In the same section, we obtain upper values for the parameters γ and a, using the data released by the EHT collaboration. In Sec. VII, using the Sinc approximation (which is an approximation of a smooth function and widely used in literature; see, for example, [153, 154]), we calculate the the total absorption cross section at the eikonal limit for the charged-Kiselev BH in the string cloud background, where we observe that the absorption cross section decreases with the charge Q of the BH. In Sec. VIII, we present the conclusion of our work. Throughout this paper, we use a system of units in which$ G=1=c $ . -
In this section, we briefly present the derivation of the charged-Kiselev BH in the presence of string clouds. The detailed solution is already given in Refs. [118, 155].
The action for the spherically symmetric static and electrically charged Kiselev BH spacetime is given by
$ S=\frac{1}{2}\int{{\rm d}x^4\sqrt{-g}}(R-L_{F}+ L_{m}), $

(1) where g represents the determinant of the spherically symmetric static metric tensor
$ g_{\mu\nu} $ , R is the Ricci scalar, and$ L_{F} $ and$ L_{m} $ are responsible for the electromagnetic and matter parts of the action, respectively. Here, the matter part further consists of two parts, namely the cloud of strings and the quintessence, i.e.,$ L_m=L_s+L_q $ , defined below. In Eq. (1),$ L_{F}= \frac{1}{4}F_{\mu\nu}F^{\mu\nu}, $

(2) where the Maxwell tensor
$ F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu $ , and$ A_\mu $ is the potential term.The Lagrangian density for the cloud of strings is represented by [155]
$ L_s=-\frac{k}{2}\Sigma^{\mu\nu}\Sigma_{\mu\nu}, $

(3) where k is a constant related to the string tension and the bivector
$ \Sigma^{\mu\nu}=\epsilon^{\alpha\beta}\frac{\partial x^\mu}{\partial \lambda^{\alpha}}\frac{\partial x^\nu}{\partial \lambda^{\beta}}, $

(4) where
$ \epsilon^{\alpha \beta} $ is the two-dimensional Levi-Civita tensor, and$ \lambda^{\alpha} (\lambda^{\alpha}=\lambda^0, \lambda^1) $ gives a parameterization of the world sheet, which is described by the string with the following induced metric [155]:$ h_{\alpha \beta}=g_{\mu\nu}\frac{\partial x^\mu}{\partial \lambda^{\alpha}}\frac{\partial x^\nu}{\partial \lambda^{\beta}}. $

(5) The
$ \Sigma^{\mu \nu} $ respects the following three identities [155, 156]:$ \begin{array}{*{20}{l}} \Sigma^{\mu[\alpha}\Sigma^{\beta \sigma]}=0,\quad \nabla_\mu\Sigma^{\mu[\alpha}\Sigma^{\beta \sigma]}=0, \quad \Sigma^{\mu\alpha}\Sigma_{\alpha\sigma}\Sigma^{\sigma \nu}={\bf h} \Sigma^{\nu\mu}, \end{array} $

(6) where
$ {\bf h} $ stands for the determinant of$ h_{\alpha \beta} $ . From the variation of the Lagrangian density with respect to the metric tensor$ g_{\mu\nu} $ , one can obtain [156]$ T_s^{\mu\nu}=\rho_s\frac{\Sigma^{\mu\alpha}\Sigma^{\nu}_{\alpha}}{\sqrt{-\bf h}}, $

(7) where
$ \rho_s $ represents the density of the string cloud. The quantity$ {\rho_s}/{\sqrt{-\bf h}} $ is known as the gauge invariant density of the string cloud. Further, the quantity$ \rho_s $ is the function of r only as the spacetime taken here is spherically symmetric and static. With the utilization of the three identities given in (6), one can obtain$ \partial_\mu(\sqrt{-g}\Sigma^{\mu\alpha})=0 $ . Therefore, the non-zero components of the energy-momentum tensor for the spherically symmetric static spacetime with the string cloud background are [157]$ {T_s}_0^0 = {T_s}_1^1 = - \frac{a}{{{r^2}}},\quad {T_s}_2^2 = {T_s}_3^3 = 0,$

(8) where the constant a corresponds to the cloud of strings, and the line element in the Schwarzschild coordinates
$ (t, r, \theta, \phi) $ is given by [158]$ {\rm d}s^2=\left(1-a-\frac{2M}{r}\right){\rm d}t^2-\left(1-a-\frac{2M}{r}\right)^{-1}{\rm d}r^2 - r^2 {\rm d}\Omega^2. $

(9) Throughout,
${\rm d}\Omega^2={\rm d}\theta^2 + {\rm sin}^2\theta {\rm d}\phi^2$ and$ 0 < a < 1 $ [159]. In the case of$ a=0 $ , the line element (9) reduces to that for the Schwarzschild BH spacetime, where M represents the mass of the BH.For the quintessence we have [160]
$ L_q=-\frac{1}{2}g^{\mu\nu}\partial_\mu\phi \partial_\nu\phi-V(\phi), $

(10) where ϕ is the quintessence field and
$ V(\phi) $ is the potential term. For the matter fluid, the surviving components of the energy-momentum tensor for the Kiselev BH solution, which represents a spherically symmetric point gravitating source, are given by [118, 155]$ {T_q}_{0}^0={T_q}_{1}^1=\rho_{q}, \quad {T_q}_{2}^2={T_q}_{3}^3=-\frac{\rho_{q}}{2}(3\omega_q+1), $

(11) where
$ p_q $ and$ \rho_q $ stand respectively for the pressure and density of the quintessence matter and$ \omega_q $ is the equation of state parameter for the quintessence. The line element for the Kiselev BH without charge is$ \begin{aligned}[b] {\rm d}s^2=&-\left(1-\frac{2M}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2 \\ &+\left(1-\frac{2M}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, , \end{aligned} $

(12) where
$ \rho_{q}=-\frac{\gamma}{2}\frac{3\omega_q}{r^{3\omega_q+1}}\, , $

(13) and γ is the quintessence parameter, which depends on the equation of state parameter
$ \omega_q $ , the density of the quintessence matter, and the coordinate r. For instance, if$ \omega_q=-2/3 $ , then$ \gamma=\rho_q/r $ . Thus, the parameter γ varies directly with the density$ \rho_q $ and inversely with r and therefore goes to zero as r approaches infinity. The charged version of the Kiselev BH solution is given by [109]$ \begin{aligned}[b] {\rm d}s^2=&-\left(1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2\\ &+\left(1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, . \end{aligned} $

(14) The spherically symmetric static charged-Kiselev BH is then analyzed in the presence of a source that corresponds to the string clouds [118]. Under the assumption that the quintessence and cloud of strings are not interacting with each other, the non-zero components of the total energy-momentum tensor of the two matter-energy contents, for the Kiselev BH, are obtained as [118]
$ {T_{sq}}_{0}^0={T_{sq}}_{1}^1=\rho_{q}+\frac{a}{r^2}\, , $

(15) $ {T_{sq}}_{2}^2={T_{sq}}_{3}^3=-\frac{\rho_{q}}{2}(3\omega_q+1). $

(16) The line element for the spherically symmetric static Kiselev BH with a cloud of strings is obtained as [118]
$ \begin{aligned}[b] {\rm d}s^2=&-\left(1-a-\frac{2M}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2\\ &+\left(1-a-\frac{2M}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, . \end{aligned} $

(17) If the metric is also charged, then the charged-Kiselev BH with the string cloud background is given by [118]
$ {\rm d}s^2=-f(r){\rm d}t^2+\frac{1}{f(r)}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, , $

(18) with
$ f=1-a-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\gamma}{r^{3\omega_q+1}}. $

(19) In the metric given by (18), M and Q represent the mass and electric charge of the BH, respectively. The equation of state for the quintessence is given by
$ p_q=\omega_{q}\rho_q $ , with$ \omega_q\in(-1;-1/3) $ . The spacetime given by the metric (18) reduces to the metric for the Reissner-Nordstrom spacetime when$ a=0 $ and$ \gamma=0 $ . For the structure of the horizon of the metric represented by (18), one may see Ref. [118]. Here, we briefly discuss the horizon structure of the charged-Kiselev BH in the background of string clouds. According to the condition$ g_{00}=0 $ (or$ f=0 $ ), we plot the horizon orbits (see. Fig. 1). It is interesting to mention that the horizon depends on the parameters a, γ, and Q in the charged-Kiselev BH in the background of string clouds. -
To discuss the motion of photons in the charged-Kiselev BH in string clouds, we use the Hamiltonian [125]
$ \mathcal H(x^\alpha, p_\alpha)=\frac{1}{2} g^{\alpha \beta} p_\alpha p_\beta, $

(20) where
$ x^\alpha $ are spacetime coordinates. The four-momentum of the photon is defined by$ p_\alpha $ .The components of the four-velocity (equation of motion) of photons in the plane
$ \theta=\pi/2,\; (p_\theta=0) $ are [21, 127]$ \dot t\equiv\frac{{\rm d}t}{{\rm d}\lambda}= \frac{ {-p_{t}}}{f(r)} , $

(21) $ \dot r\equiv\frac{{\rm d}r}{{\rm d}\lambda}=p_r f(r) , $

(22) $ \dot\phi\equiv\frac{{\rm d} \phi}{{\rm d}\lambda}= \frac{p_{\phi}}{r^2}. $

(23) Here,
$ -p_{t}=\mathcal{E} $ and$ p_{\phi}=L $ are the specific energy and specific angular momentum of the particle, respectively. For a photon$ \mathcal H=0 $ , using this fact, we obtain the equation for the radial velocity as$ \begin{array}{*{20}{l}} \dot r^{2}=\mathcal{E}^{2}-V_{\rm eff}(r), \end{array} $

(24) where
$V_{\rm eff}(r)$ represents the effective potential and can be given as$ V_{\rm eff}(r)= \frac{L^2}{r^2}f(r). $

(25) -
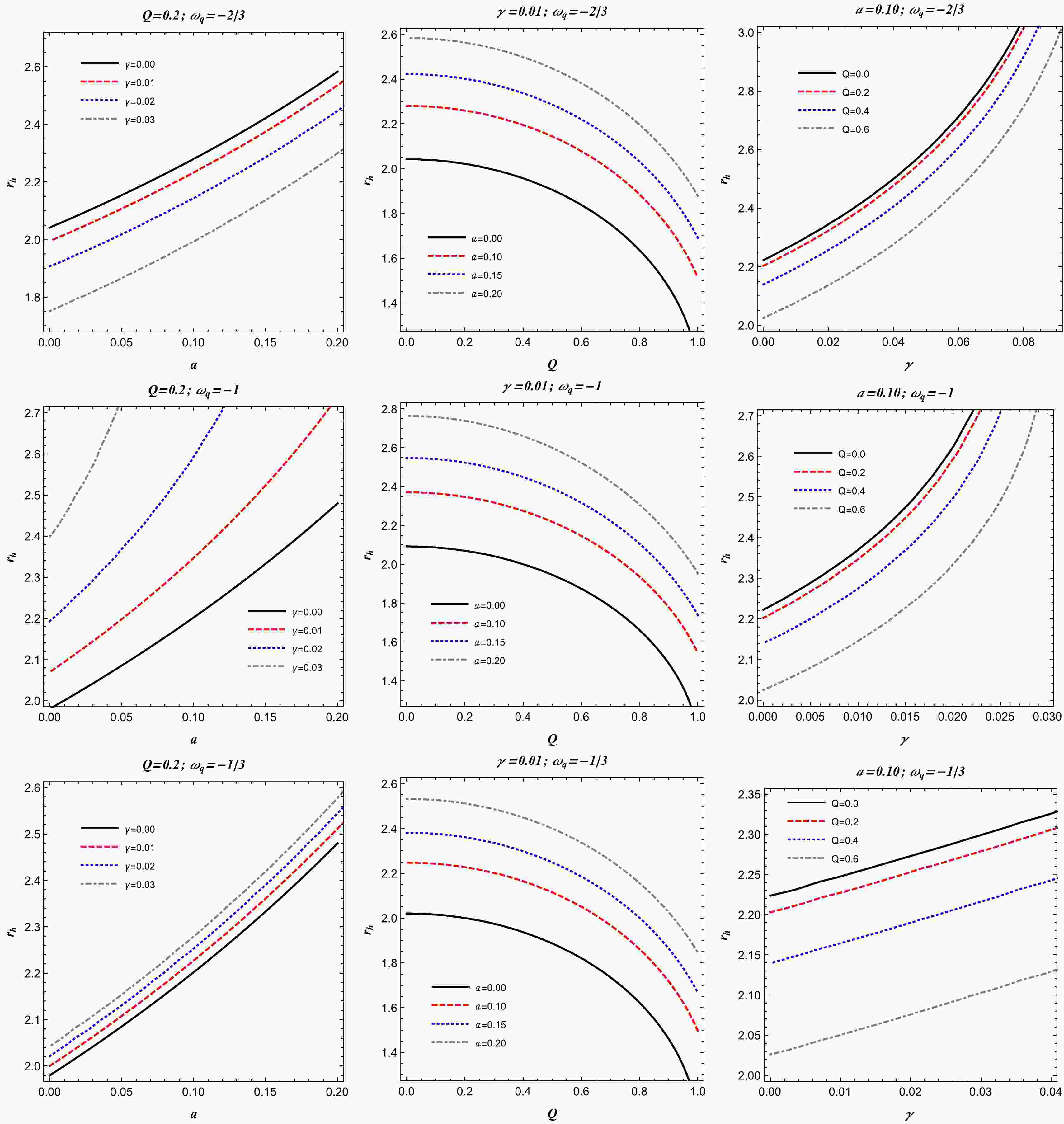
Here, we discuss the circular orbits of photons in the vicinity of the charged-Kiselev BH with clouds of strings for the equation of state parameter
$ \omega_q=-2/3 $ , which corresponds to the pure quintessence case. We would like to mention that the horizon structure and photon motion for the charged-Kiselev BH spacetime with clouds of strings for$ \omega_q=-2/3 $ have been discussed in a recent work [161]. However, we discuss it here for the sake of completeness. To obtain the circular orbits of photons, we use the equations$V_{\rm eff}'=0$ , where the prime denotes the derivative with respect to the radial coordinate r, and obtain$ \begin{array}{*{20}{l}} 4 Q^2-[r^2 (2 a+\gamma r-2)+6 M r]=0. \end{array} $

(26) The solution of Eq. (26) gives the radius of the photon orbit around the charged-Kiselev BH in the string cloud background. To gain more insight into the photon orbits, we plot them in Fig. 2 for different values of the spacetime parameters. It can be seen from this plot that, as the string cloud and quintessence parameters increase, the radius of the photon orbit increases, while the influence of the BH charge Q on the orbits of photons is just opposite to those of the parameters γ and a.
-
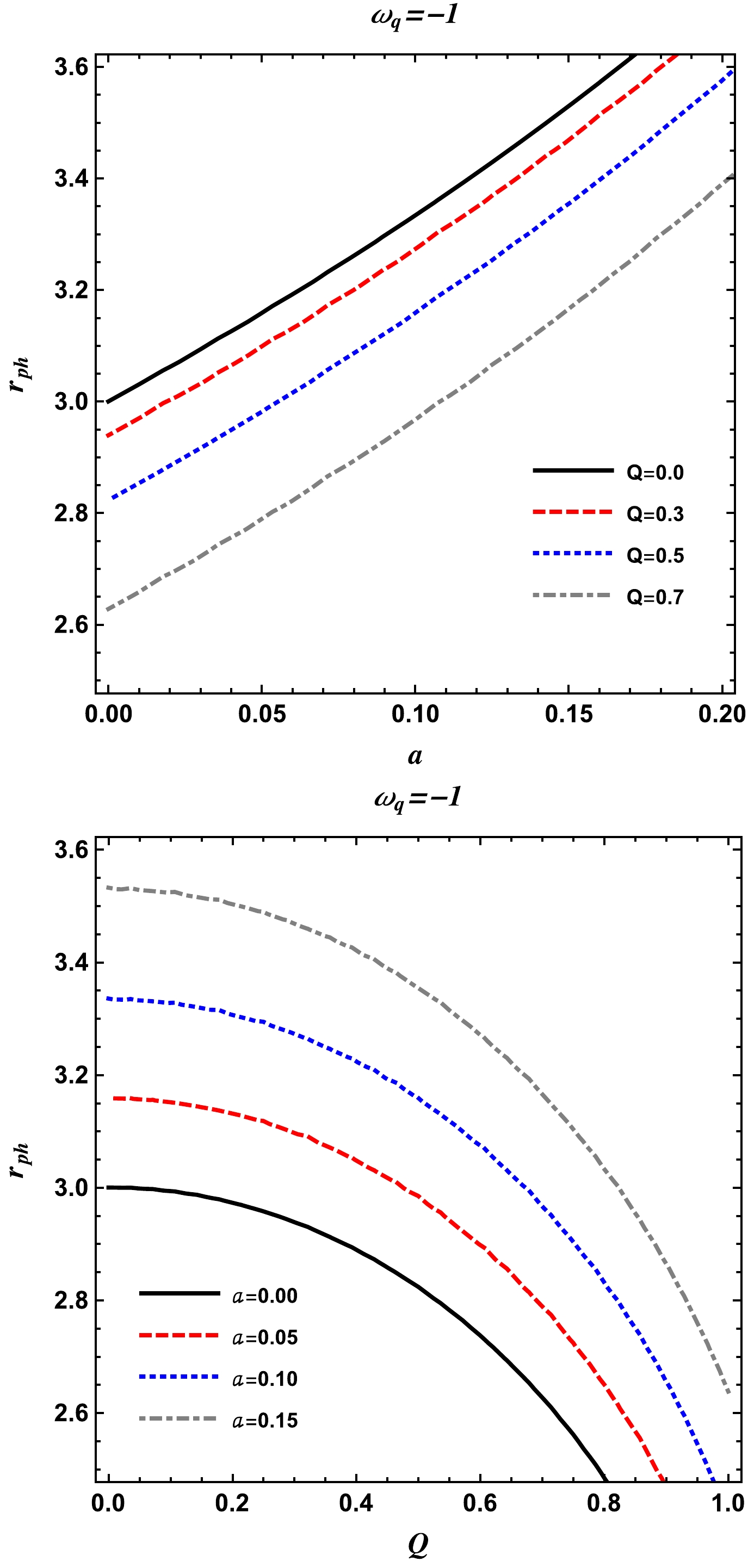
In this subsection we analyze the circular orbits of photons in the surroundings of the charged-Kiselev BH in the presence of clouds of strings when the equation of state parameter
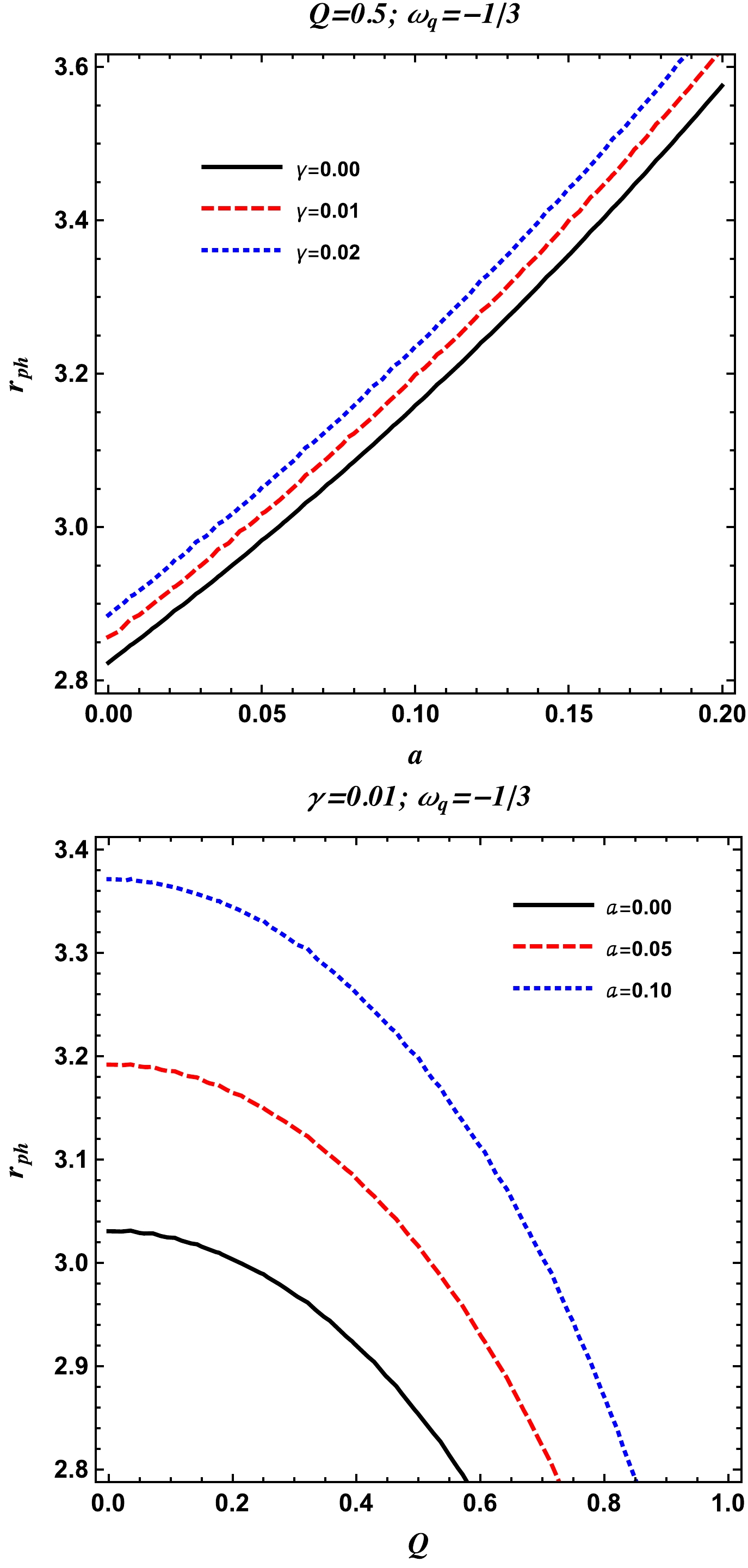
$ \omega_q=-1 $ , which corresponds to the case of the cosmological constant. Here, the radius$r_{\rm ph}$ of the photon orbit is given as$ r_{\rm ph}=\frac{-\sqrt{8 a Q^2+9 M^2-8 Q^2}-3 M}{2 (a-1)}. $

(27) In Fig. 3, the radius of the photon orbit is shown for different values of the parameters a and Q and
$ \omega_q=-1 $ . Here, we see that the radius of the photon orbit increases with the the parameter a and decreases with the parameter Q. From the same figure, it can also be seen that the radius of the photon orbit increases with the parameter γ. -
Here, we study the circular orbits of photon in the surrounding of the charged-Kiselev BH with string cloud background for the equation of state parameter
$ \omega_q=-1 $ , which corresponds to a network of cosmic strings. Here, the radius$r_{\rm ph}$ of the photon orbit is calculated as$ r_{\rm ph}=\frac{-\sqrt{8 a Q^2+8 \gamma Q^2+9 M^2-8 Q^2}-3 M}{2 (a+\gamma-1)}. $

(28) In Fig. 4, we notice that the radius of the photon orbit increases with the parameters γ and a for
$ \omega_q=-1/3 $ . Here, we can observe that with the charge Q of the BH, the radius of the photon decreases. For a detailed analysis on the photon orbits in the spacetime of the charged-Kiselev BH for the three different values of the parameter$ \omega_q $ , one may see Ref. [112]. -
In this section we study particle motion around the charged-Kiselev BH with string cloud background in the presence of plasma. The Hamiltonian in the presence of a plasma medium is given by [125, 127]
$ \mathcal{H}=\frac{1}{2}g^{\alpha\beta}p_{\alpha}p_{\beta}+\frac{1}{2} \omega^2_{\text{p}}. $

(29) Here,
$ \omega^2_{p}=4 \pi e^2 N(r)/m_e $ is the plasma frequency ($ m_e $ and e are the electron mass and charge, respectively, and$ N(r) $ is known as the number density of the electrons around a compact object). The four-velocity components for photons around a BH in the equatorial plane are [21, 127]$ \dot t\equiv\frac{{\rm d}t}{{\rm d}\lambda}= \frac{ {-p_t}}{f(r)} , $

(30) $ \dot r\equiv\frac{{\rm d}r}{{\rm d}\lambda}=p_r f(r) , $

(31) $ \dot\phi\equiv\frac{{\rm d} \phi}{{\rm d}\lambda}= \frac{p_{\phi}}{r^2}, $

(32) where the relationship
$ \dot x^\alpha=\partial \mathcal{H}/\partial p_\alpha $ is taken into account. From (31) and (32), we obtain the equation of the phase trajectory for photons around a compact object as$ \frac{{\rm d}r}{{\rm d}\phi}=\frac{r^2 f(r) p_r}{p_{\phi}}. $

(33) With the use of the constraint
$ \mathcal H=0 $ for photons, the above equation for the trajectory of a photon can be written as follows [21, 127]:$ \frac{{\rm d}r}{{\rm d}\phi}=\sqrt{r^2 f(r)}\sqrt{h^2(r)\frac{\omega^2_0}{p_\phi^2}-1}, $

(34) where we define
$ h^2(r)=r^2\Bigg(\frac{1}{f(r)}-\frac{\omega^2_p(r)}{\omega^2_0}\Bigg). $

(35) Here,
$ \omega_0 $ is the frequency of a photon. -
Here, we investigate the circular orbits of photons in the spacetime of the unit mass charged-Kiselev BH with the string cloud background in the presence of plasma for the equation of state parameter
$ \omega_q=-2/3 $ . In this case, the radius of the photon orbit$ r_{\text{ph}} $ can be obtained by solving the equation given as [21, 127]$ \frac{{\rm d}(h^2(r))}{{\rm d}r}\bigg|_{r=r_{\text{ph}}}=0. $

(36) The substitution of (35) into (36) gives the algebraic equation for the radius
$ r_{\text{ph}} $ of the photon sphere around the BH in the plasma medium as$ \begin{aligned}[b]& -\frac{r_{\text{ph}}^2 \left(r_{\text{ph}} (r_{\text{ph}} (2 a+\gamma r_{\text{ph}}-2)+6 M)-4 Q^2\right)}{\left(Q^2-r_{\text{ph}} (r_{\text{ph}} (a+\gamma r_{\text{ph}}-1)+2 M)\right)^2} \\=&2\Bigg[\frac{\omega^2_{\text{p}}(r_{\text{ph}})}{\omega^2_0}+\frac{r\omega'_{\text{p}}(r_{\text{ph}}) \omega_{\text{p}}(r_{\text{ph}})}{\omega^2_0}\Bigg]. \end{aligned} $

(37) Here,
$ ' $ is the derivative with respect to the coordinate r. The last equation cannot be solved analytically and we give graphical analysis for the$ r_{\text{ph}} $ in Fig. 5 for different values of the involved parameters. Here, we see that, for increasing values of the uniform plasma parameter, the radius of the photon orbit also increases. -
Here, we calculate the circular orbits of photons in the vicinity of the charged-Kiselev BH with the string cloud background in the uniform plasma medium for the equation of state parameter
$ \omega_q=-1 $ . In this case, we have$ \begin{aligned}[b]& -\frac{2 r_{\text{ph}}^2 \left(r_{\text{ph}} ((a-1) r_{\text{ph}}+3 M)-2 Q^2\right)}{\left(Q^2-r_{\text{ph}} \left(r_{\text{ph}} \left(a+\gamma r_{\text{ph}}^2-1\right)+2 M\right)\right)^2} \\=&2\Bigg[\frac{\omega^2_{\text{p}}(r_{\text{ph}})}{\omega^2_0}+\frac{r_{\text{ph}}\omega'_{\text{p}}(r_{\text{ph}}) \omega_{\text{p}}(r_{\text{ph}})}{\omega^2_0}\Bigg]. \end{aligned} $

(38) In Fig. 6, for different values of the uniform plasma, we plot the radius of the photon orbit for fixed values of the charge Q and parameter γ against the parameter a. As in the case of
$ \omega_q=-2/3 $ , here, the radius of the photon orbit also increases with the uniform plasma parameter. -
Here, we study the circular orbits of photons in a plasma medium in the spacetime of the charged-Kiselev BH with string clouds for the equation of state parameter
$ \omega_q=-1/3 $ . Here, we have$ \begin{aligned}[b]& -\frac{2 r_{\text{ph}}^2 \left(r_{\text{ph}} (r_{\text{ph}} (a+\gamma-1)+3 M)-2 Q^2\right)}{\left(Q^2-r_{\text{ph}} (r_{\text{ph}} (a+\gamma-1)+2 M)\right)^2} \\=&2\Bigg[\frac{\omega^2_{\text{p}}(r_{\text{ph}})}{\omega^2_0}+\frac{r_{\text{ph}}\omega'_{\text{p}}(r_{\text{ph}}) \omega_{\text{p}}(r_{\text{ph}})}{\omega^2_0}\Bigg]. \end{aligned} $

(39) From Fig. 7, it is evident that the radius of the photon orbits increases when the uniform plasma parameter increases. We see that, for all te three values of the parameter
$ \omega_q $ , the photon sphere expands with an increase in the value of the uniform plasma parameter. -
In this subsection, we look at the effects of the uniform plasma, when
$ \omega _p^2= \text{const.} $ , on the circular orbits of photons in the vicinity of the charged-Kiselev BH in string clouds. We use Eqs. (35) and (36) to obtain results in the case of the uniform plasma with a constant value of the parameter. From Fig. 8, we see that the radii of photon spheres around the charged-Kiselev BH in clouds of strings increase with the uniform plasma for$\omega _p^2= \text{const}$ . -
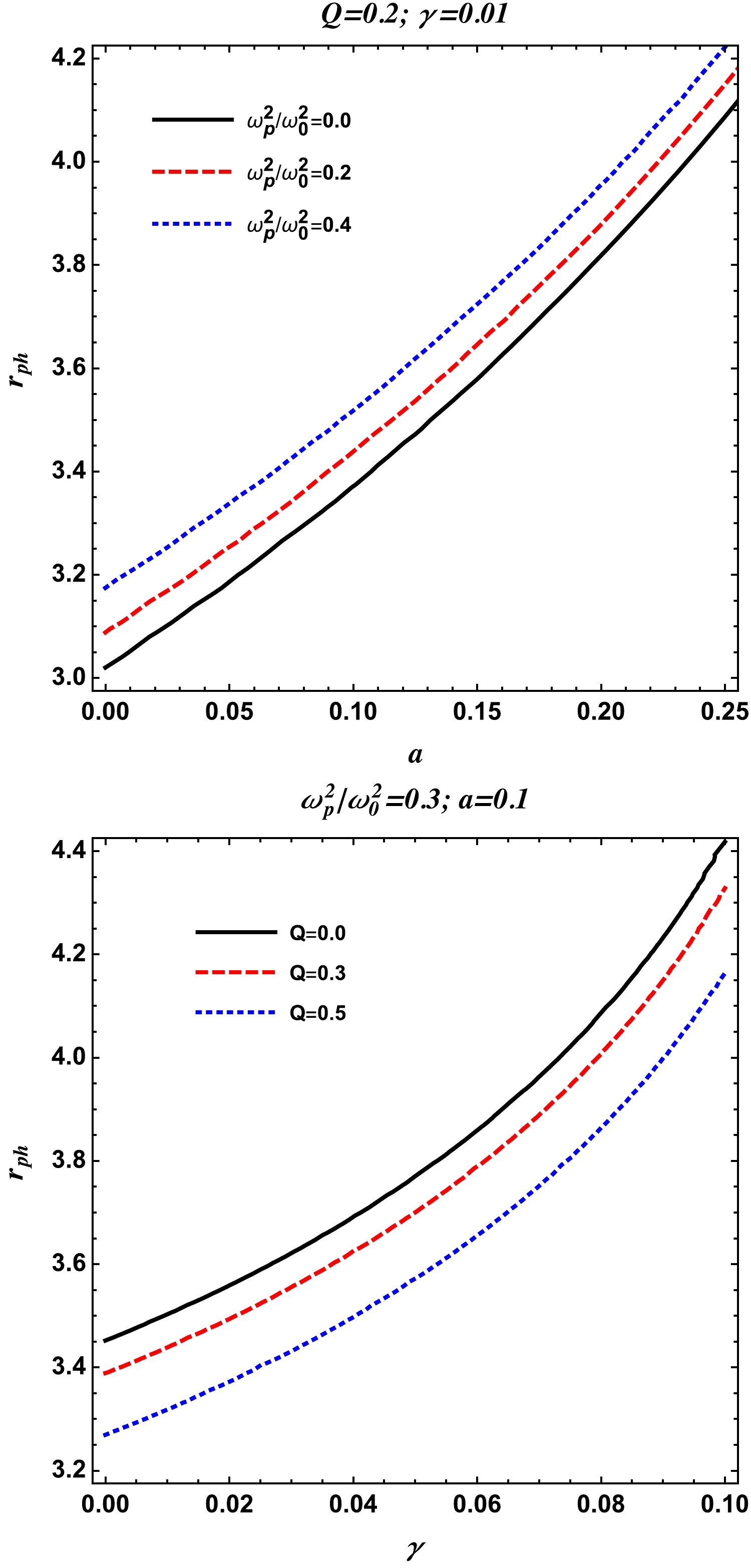
Now, we study the effects of nonuniform plasma on the radii of photon spheres in the vicinity of the charged-Kiselev BH in the background of clouds of strings. Here, we take a simple power-law of the following form for the frequency of the plasma [21, 162]:
$ \omega^2_{p}(r)=\frac{z_0}{r^q}, $

(40) where
$ q>0 $ and$ z_0 $ are two free parameters [162]. For the analysis of the main features of the above power-law model, we take$ q=1 $ and$ z_0 $ as a constant [162]. Using Eqs. (37) and (40), the radius of the photon sphere$r_{\rm ph}$ in the nonuniform plasma medium is shown for different values of the charge Q of the charged-Kiselev BH in the string cloud background, string cloud parameter a, and quintessence parameter γ in Fig. 9.
Figure 9. (color online) Radius of the photon sphere versus the string cloud parameter a (top panel) and quintessence parameter γ (bottom panel) for fixed values of the nonuniform plasma parameter and BH charge Q.
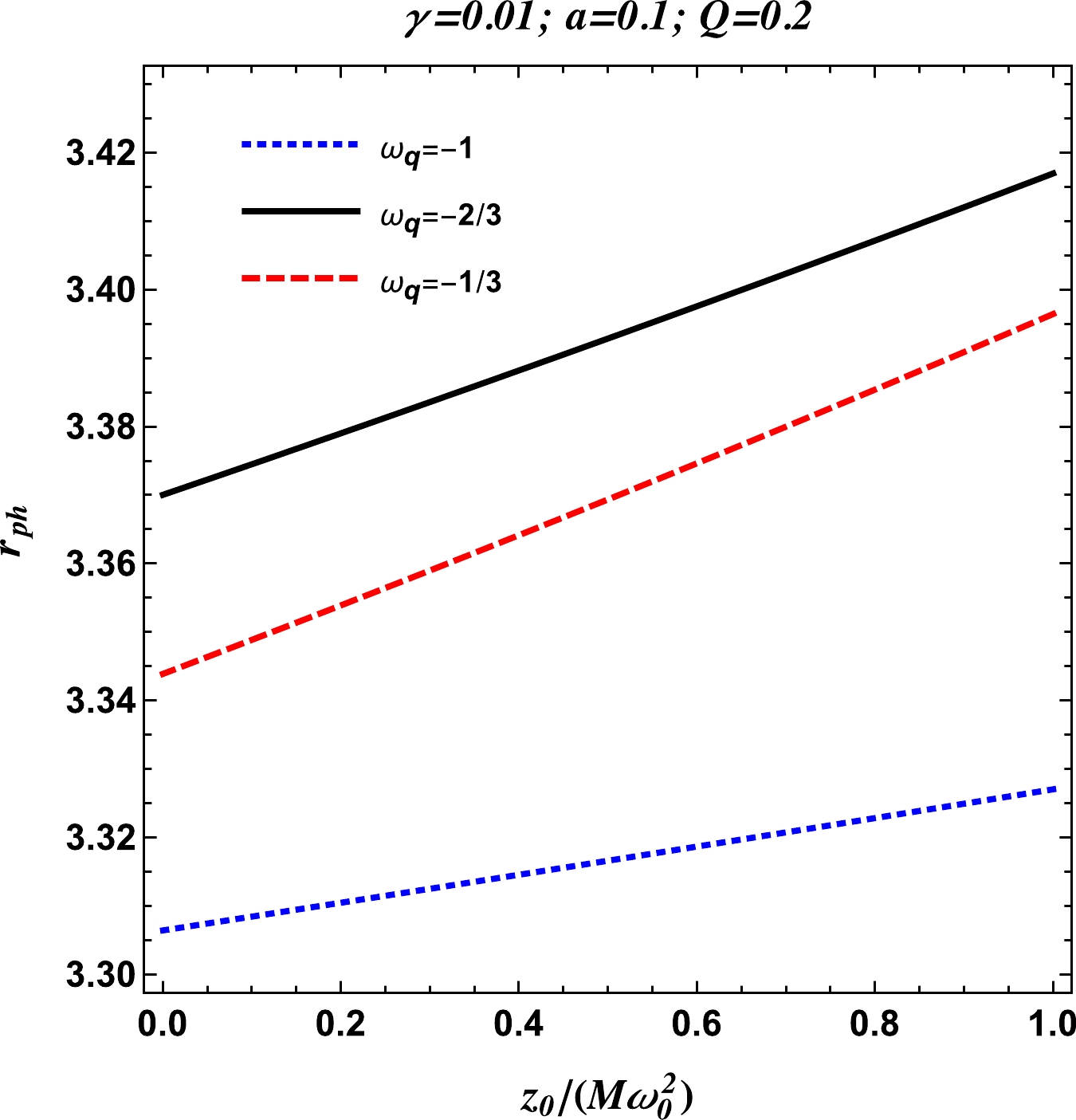
In Fig. 10, we see the behavior of the radius of the photon sphere for the three different values of the parameter
$ \omega_q $ , while keeping the parameters γ, a, and Q fixed. Here, we see that the radius of the photon sphere increases with the plasma parameter. From Fig. 10 we also notice that the radius$r_{\rm ph}$ is the largest for the pure quintessence case, i.e., for$ \omega_q=-2/3 $ , and$r_{\rm ph}$ is the smallest when$ \omega_q=-1 $ , which corresponds to the case of the cosmological constant. -
In this section, we study the effects of a plasma medium on the weak deflection angle by the charged-Kiselev BH with string cloud background. For this purpose, we use the refractive index of the plasma medium
$ n(r) $ for different cases of frequencies such as uniform plasma with$ \omega _p^2(r)= \text{const.} $ and nonuniform plasma with$ \omega^2_{p}(r)= z_0/r^q $ .The charged-Kiselev BH with string cloud background can also be written as [118]
$ \begin{aligned}[b] {\rm d}s^2=-&\left(1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2\\ &+\left(1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + l^2r^2 {\rm d}\Omega^2\, , \end{aligned} $

(41) where the cloud of string parameter
$ l^2=1-a $ is obtained from the coordinate transformations used in Refs. [163–165].First, we obtain the corresponding optical metric for the charged-Kiselev BH with the string cloud as follows:
$ {\rm d} \sigma ^ { 2 } = g _ { i j } ^ { \mathrm { opt } } {\rm d} x ^ { i } {\rm d} x ^ { j } =\frac{n^{2}(r)}{F(r)}\left(\frac{{\rm d} r^{2}}{F(r)}+l^2r^2 {\rm d} \varphi^{2}\right), $

(42) where
$ F=\left(1-\dfrac{2M}{r}+\dfrac{Q^2}{r^2}-\dfrac{\gamma}{r^{3\omega_q+1}}\right) $ and$ i, j = 0,1,2,3. $ Note that the refractive index$ n(r) $ is$ n^{2}(r)=1-\frac{\omega_{\mathrm{p}}^2(r)}{\omega^2(r)}, $

(43) with
$ \omega(r)=\dfrac{\omega_{0}}{\sqrt{f(r)}}, \quad \omega_{0}=\rm { const } $ , and plasma frequency$ \omega_p $ . -
Using the uniform plasma with
$ \omega _p^2(r)= \text{const.} $ , we calculate the Gaussian curvature for the above optical metric as follows:$ \begin{aligned}[b]\\ \mathcal{K}\approx &\frac{30 \gamma M Q^2 \omega _p^2 \omega _q}{r^6 \omega _0^2}-\frac{96 \gamma M Q^2 \omega _p^2 \omega _q \log (r)}{r^6 \omega _0^2}+\frac{30 \gamma M \omega _p^2 \omega _q}{r^4 \omega _0^2}-\frac{36 \gamma M \omega _p^2 \omega _q \log (r)}{r^4 \omega _0^2}+\frac{32 \gamma M Q^2 \omega _p^2}{r^6 \omega _0^2}\\&+\frac{12 \gamma M \omega _p^2}{r^4 \omega _0^2}+\frac{6 \gamma M \omega _q}{r^4}-\frac{9 \gamma M \omega _q \log (r)}{r^4}+\frac{3 \gamma M}{r^4}-\frac{15 \gamma Q^2 \omega _p^2 \omega _q}{r^5 \omega _0^2}+\frac{39 \gamma Q^2 \omega _p^2 \omega _q \log (r)}{r^5 \omega _0^2}\\&-\frac{15 \gamma \omega _p^2 \omega _q}{2 r^3 \omega _0^2}+\frac{9 \gamma \omega _p^2 \omega _q \log (r)}{2 r^3 \omega _0^2}-\frac{13 \gamma Q^2 \omega _p^2}{r^5 \omega _0^2}-\frac{3 \gamma \omega _p^2}{2 r^3 \omega _0^2}-\frac{3 \gamma Q^2 \omega _q}{2 r^5} \\& +\frac{9 \gamma Q^2 \omega _q \log (r)}{r^5}-\frac{9 \gamma \omega _q}{2 r^3}+\frac{3 \gamma \omega _q \log (r)}{r^3}-\frac{3 \gamma Q^2}{r^5}-\frac{ \gamma}{r^3}-\frac{26 M Q^2 \omega _p^2}{r^5 \omega _0^2}\\&-\frac{3 M \omega _p^2}{r^3 \omega _0^2}-\frac{6 M Q^2}{r^5}-\frac{2 M}{r^3}+\frac{5 Q^2 \omega _p^2}{r^4 \omega _0^2}+\frac{3 Q^2}{r^4},\\ \end{aligned} $ 
(44) Note that there is no contribution from the cloud of strings. At very large R,
$ C_{R}:=r(\varphi)=R=const $ (for more details, see [26, 33]).We also have
$ \frac{{\rm d}\sigma}{{\rm d}\varphi}\bigg|_{C_{R}}= n ( R ) \left( \frac { l^2 r^2 } { F ( R ) } \right) ^ { 1 / 2 }, $

(45) which has the following limit of the geodesic curvature
$ \kappa_g $ :$ \lim\limits_{R\to\infty} \kappa_g\frac{{\rm d}\sigma}{{\rm d}\varphi}\bigg|_{C_R}=l\,. $

(46) At spatial infinity,
$ R\to\infty $ , and by using the straight light approximation$ r=b/\sin\varphi $ with the impact parameter b, the Gauss-Bonnet theorem reduces to [26, 33]$\begin{aligned}[b]& \lim\limits_{R\to\infty} \int^{\pi+\alpha}_0 \left[\kappa_g\frac{{\rm d}\sigma}{{\rm d}\varphi}\right]\bigg|_{C_R}{\rm d}\varphi \\=&\pi-\lim\limits_{R\to\infty}\int^\pi_0\int^R_{\frac{b}{\sin\varphi}}\mathcal{K} {\rm d}S, \end{aligned} $

(47) where
${\rm d}S=\sqrt{{\rm det} \sigma}{\rm d}r {\rm d}\varphi$ .We calculate the weak deflection angle α in the weak field limit approximation as follows:
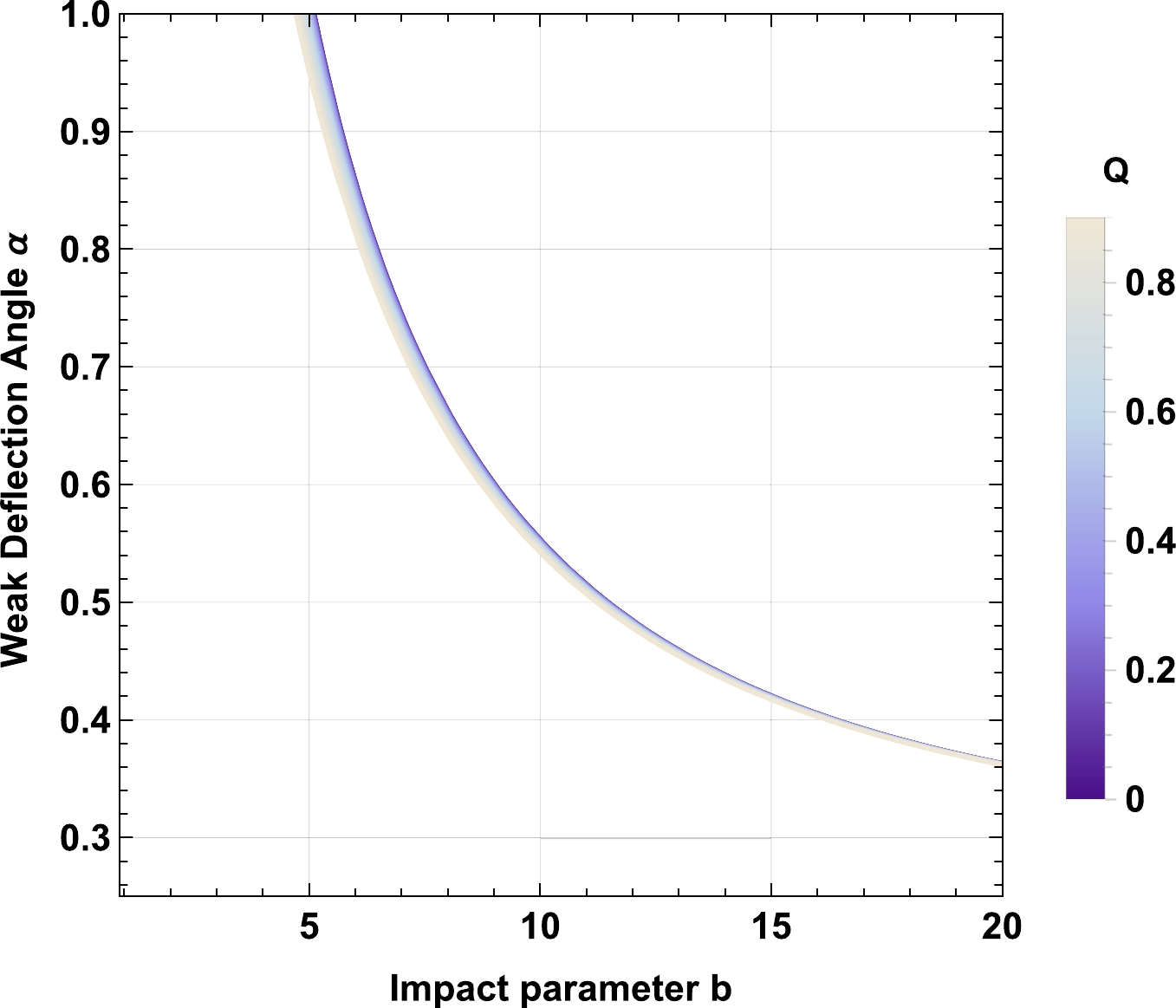
$ \begin{aligned}[b] \alpha \approx & \pi a+\frac{4 M}{b}-\frac{3 \pi Q^2}{4 b^2}-\frac{15 \pi \gamma M \omega _p^2 \omega _q}{2 b^2 \omega _0^2}+\frac{9 \pi \gamma M \log (b) \omega _p^2 \omega _q}{b^2 \omega _0^2}+\frac{3 \pi \gamma M \log (64) \omega _p^2 \omega _q}{2 b^2 \omega _0^2}-\frac{3 \pi \gamma M \omega _p^2}{b^2 \omega _0^2}-\frac{3 \pi \gamma M \omega _q}{2 b^2} \\&+\frac{9 \pi \gamma M \log (2 b) \omega _q}{4 b^2}-\frac{3 \pi \gamma M}{4 b^2}-\frac{5 \pi Q^2 \omega _p^2}{4 b^2 \omega _0^2}-\frac{3 \gamma \omega _p^2 \omega _q}{b \omega _0^2}+\frac{3 \gamma \log (8) \omega _p^2 \omega _q}{b \omega _0^2}-\frac{9 \gamma \log (b) \omega _p^2 \omega _q}{b \omega _0^2}\\& +\frac{3 \gamma \omega _p^2}{b \omega _0^2}-\frac{3 \gamma \omega _q}{b}-\frac{6 \gamma \log \left(\frac{b}{2}\right) \omega _q}{b}+\frac{2 \gamma}{b}+\frac{6 M \omega _p^2}{b \omega _0^2}. \end{aligned} $

(48) Here, we show that the photon rays move in a medium of homogeneous plasma. Note that
$ \omega_p\to 0 $ , removing the effect of the plasma on the deflection angle obtained in Eq. (48). As a result, the string cloud parameter a, the quintessence parameter γ, and the plasma parameter increase the deflection angle α. In contrast, the charge parameter Q decreases the deflection angle α, shown in Figs. 11 and 12.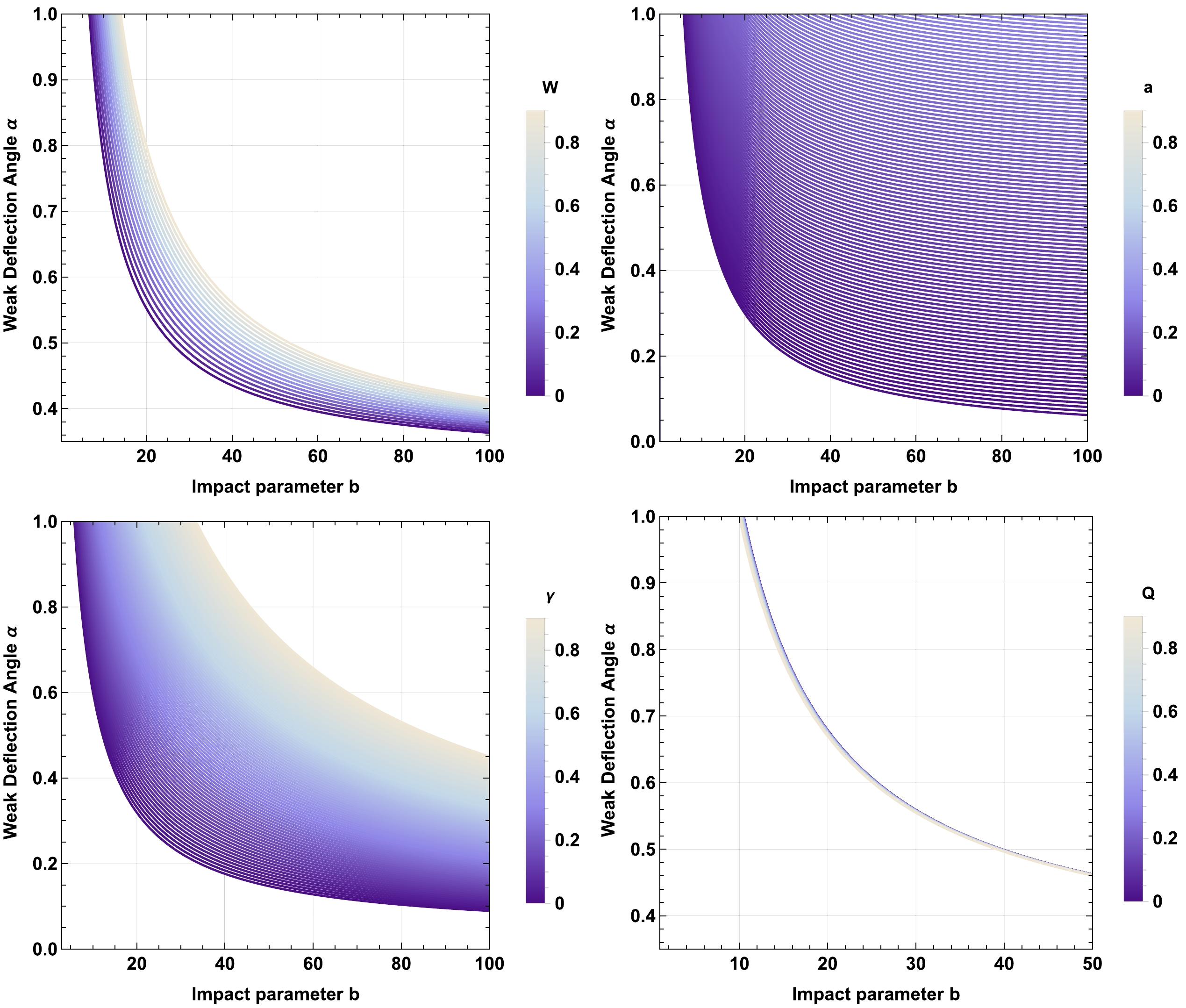
Figure 11. (color online) The first figure shows the behavior of weak deflection angle α of the charged-Kiselev BH in the cloud of strings in the presence of uniform plasma
$ W=\frac{\omega_p^2}{\omega_0^2} $ for fixed values of$ \gamma=0.01 $ , BH mass$ M=1 $ , charge$ Q=0.5 $ ,$ \omega_q=-1 $ , and string cloud parameter$ a=0.1 $ . The second figure shows α with uniform plasma$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ \gamma=0.01 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ , and variable a. The third figure shows α with$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ ,$ a=0.1 $ , and variable γ. The fourth figure shows α in the presence of uniform plasma for fixed values of$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ M=1 $ ,$ W=0.5 $ ,$ \omega_q=-1 $ ,$ a=0.1 $ , and variable Q.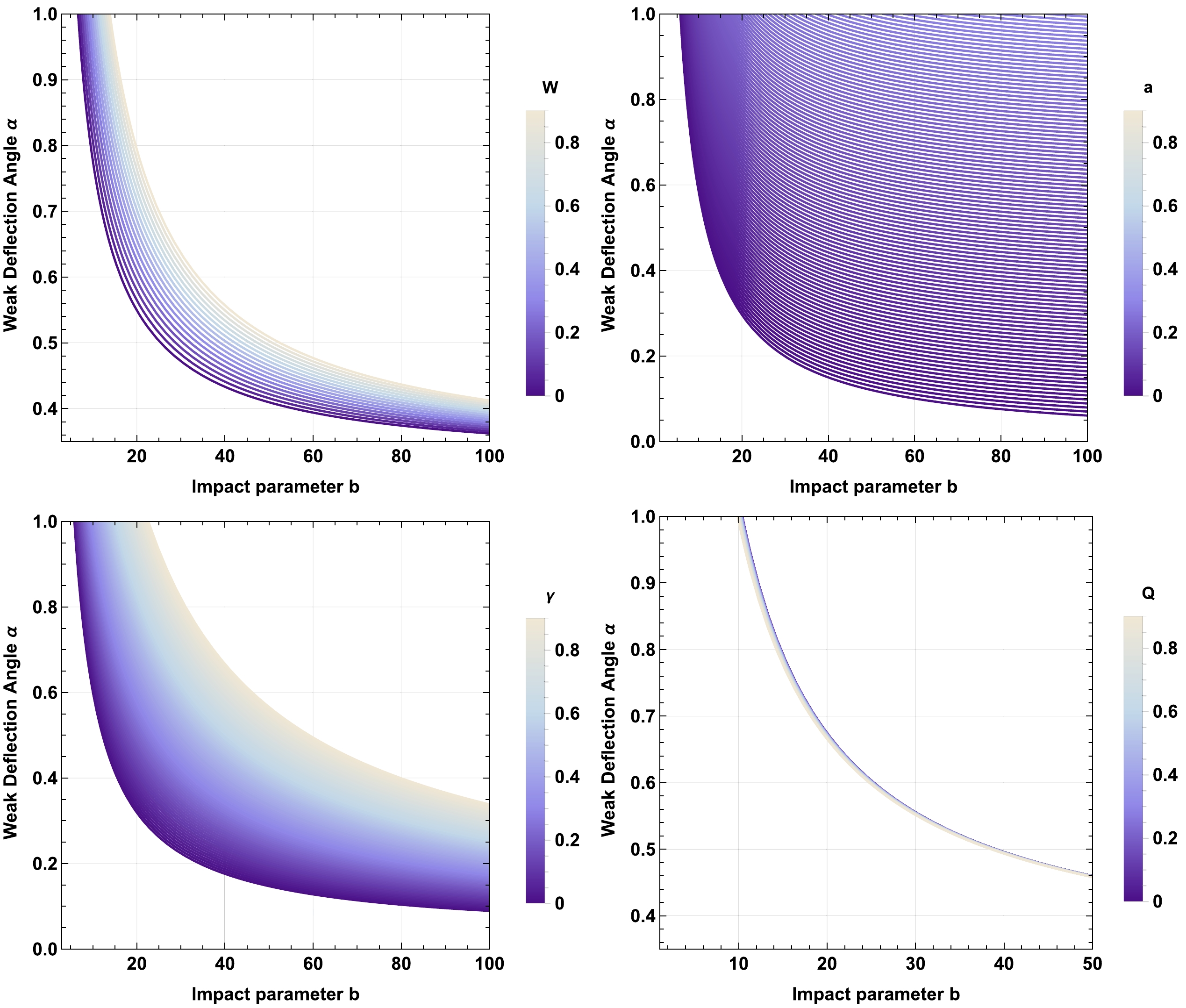
Figure 12. (color online) The first figure shows the weak deflection angle α with uniform plasma
$ W=\frac{\omega_p^2}{\omega_0^2} $ for fixed values of$ \gamma=0.01 $ , BH mass$ M=1 $ , charge$ Q=0.5 $ ,$ \omega_q=-2/3 $ , and string cloud parameter$ a=0.1 $ . The second figure shows the angle α with uniform plasma for fixed values of$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ \gamma=0.01 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-2/3 $ , and variable a. The third figure shows α with the uniform plasma for fixed values of$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-2/3 $ ,$ a=0.1 $ , and variable γ. The fourth figure shows the angle α with uniform plasma for fixed values of$ W=\frac{\omega_p^2}{\omega_0^2}=0.3 $ ,$ M=1 $ ,$ \gamma=0.5 $ ,$ \omega_q=-2/3 $ ,$ a=0.1 $ , and variable Q. -
Now, we use the nonuniform plasma with
$ \omega^2_{p}(r)= z_0/r^q $ to calculate the Gaussian curvature for the optical metric given above. Please check the appendix for details of the Gaussian curvature, for the optical metric A (1) and for the weak deflection angle A (2).Here, we investigate the motion of photons in a nonuniform plasma medium. Note that, if
$ z_0 \to 0 $ , the effect of the plasma on the deflection angle obtained in Eq. (59), vanishes. For$ \omega_q=-1 $ , a decrease in the nonuniform plasma parameter$ z_0 $ increases the deflection angle α, shown in Fig. 13. Moreover, the cloud of strings parameter a increases the deflection angle α, shown in Fig. 14, while decreasing the value of the parameter γ makes the deflection angle smaller, shown in Fig. 15. As expected, increasing the value of the charge Q of the BH decreases the deflection angle, which can be seen in Fig. 16. When$ \omega_q=-2/3 $ , the impact of the spacetime parameters on the deflection angle remains the same as it was in the case of$ \omega_q=-1 $ , compared in Figs. 17, 18, 19, and 20.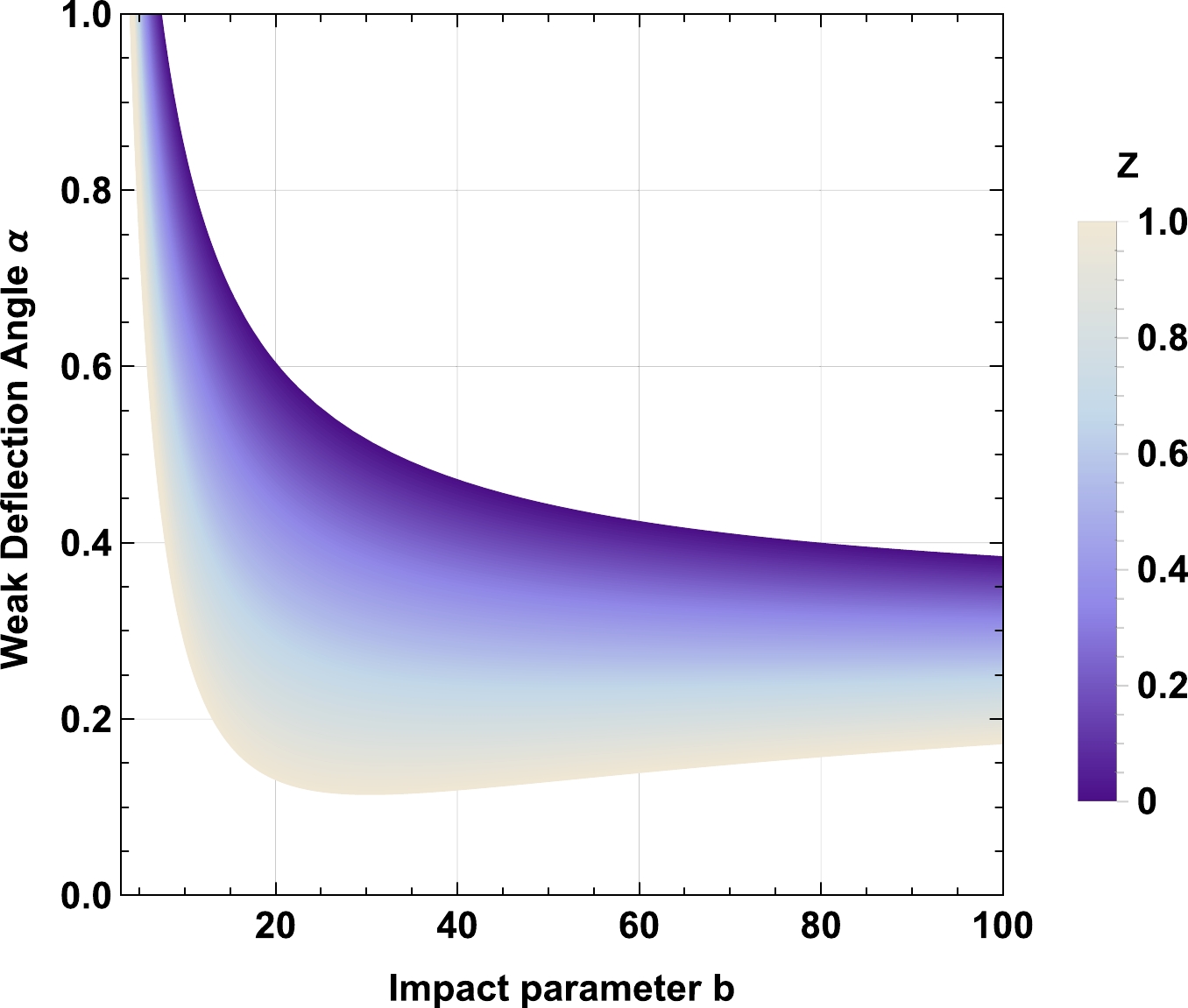
Figure 13. (color online) Behavior of the weak deflection angle α of the charged-Kiselev BH with
$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ , and$ a=0.1 $ .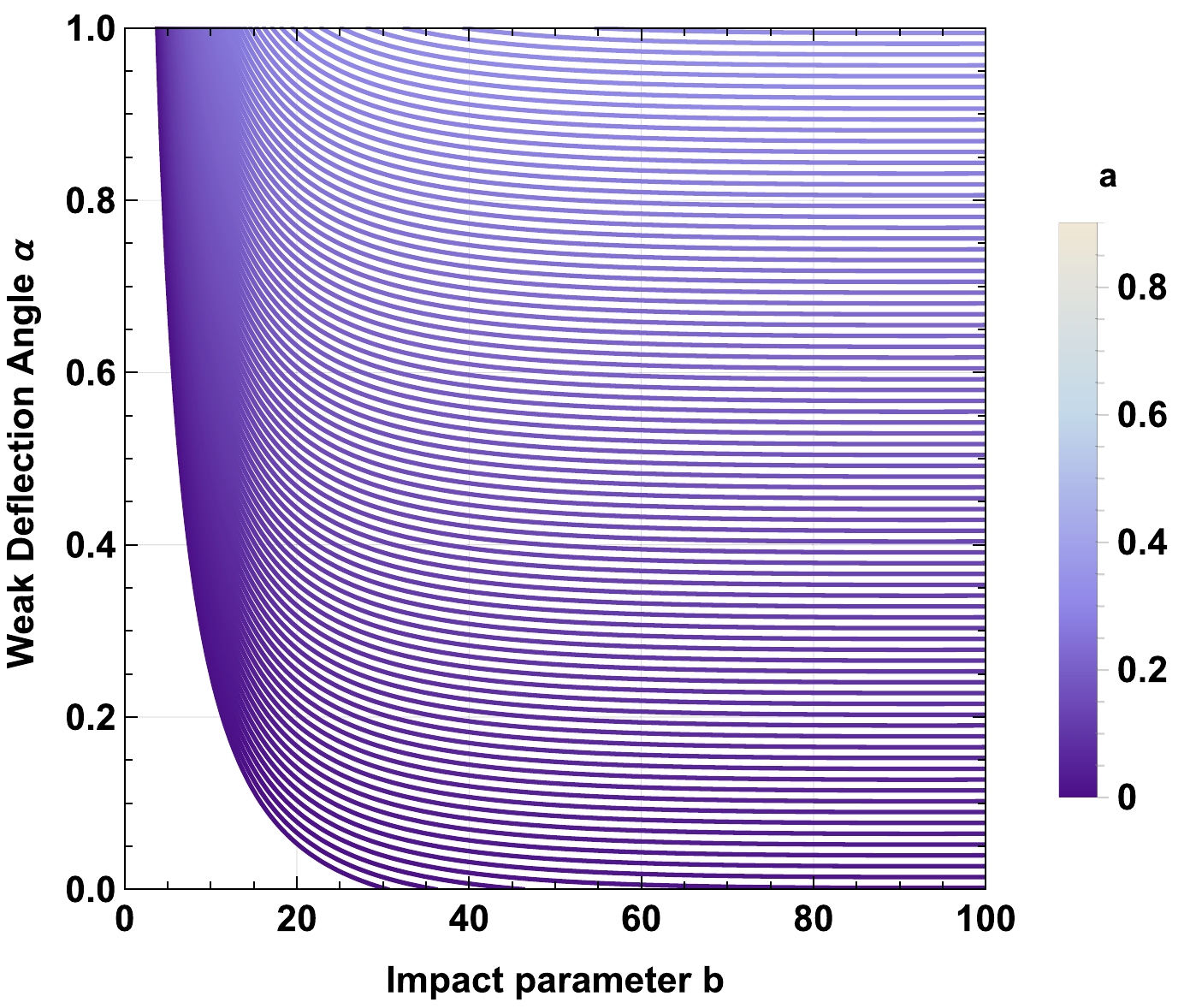
Figure 14. (color online) Behavior of the weak deflection angle α of the charged-Kiselev BH in a cloud of strings in the presence of nonuniform plasma for fixed values of
$ Z=\frac{z_0^2}{\omega_0^2}=0.5 $ ,$ \gamma=0.01 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ , and string cloud parameter$ a=0.1 $ .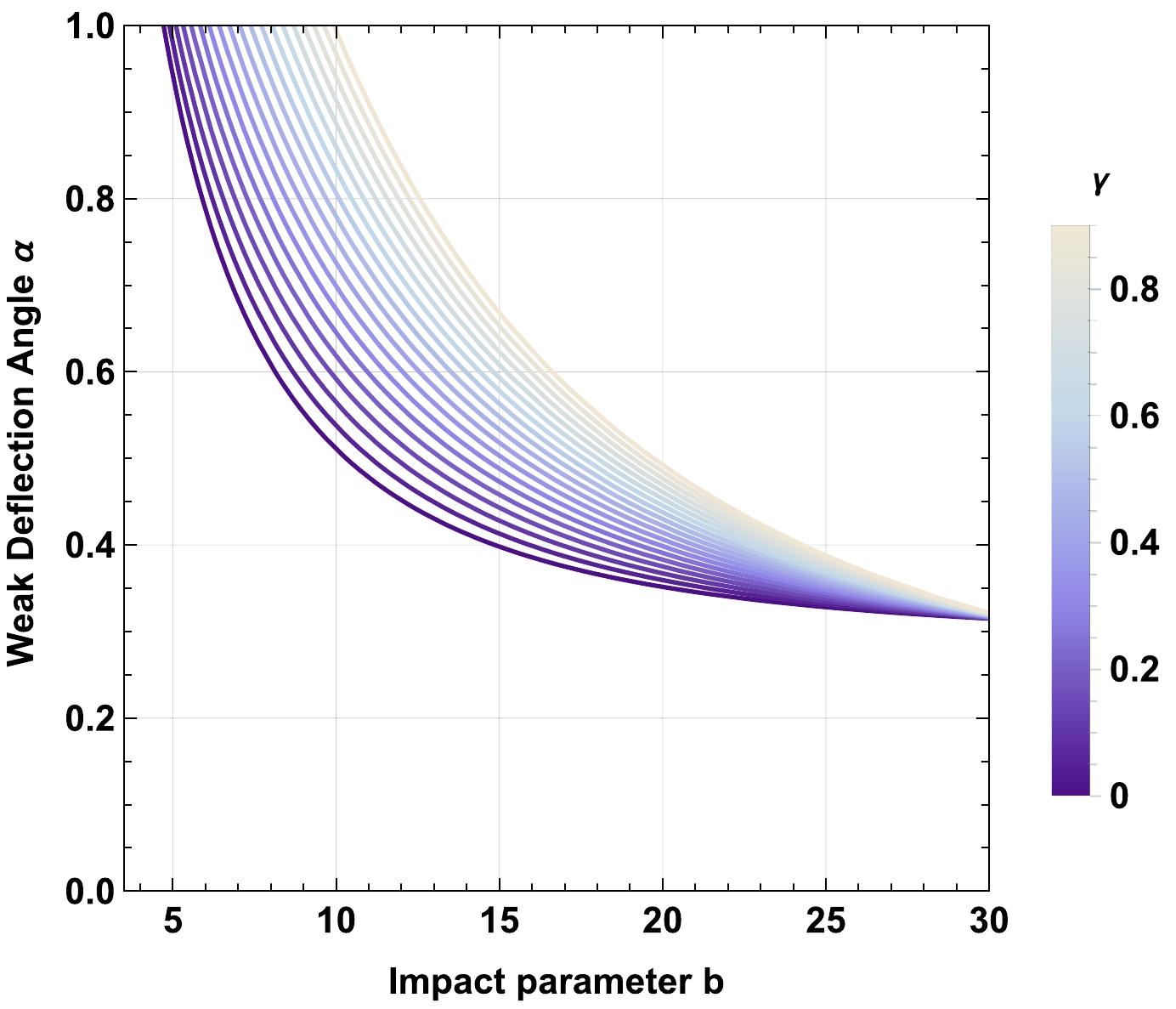
Figure 15. (color online) Behavior of the weak deflection angle α of charged-Kiselev BH in a cloud of strings in the presence of nonuniform plasma for fixed values of
$ Z=\frac{z_0^2}{\omega_0^2}=0.5 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ ,$ a=0.1 $ , and variable γ.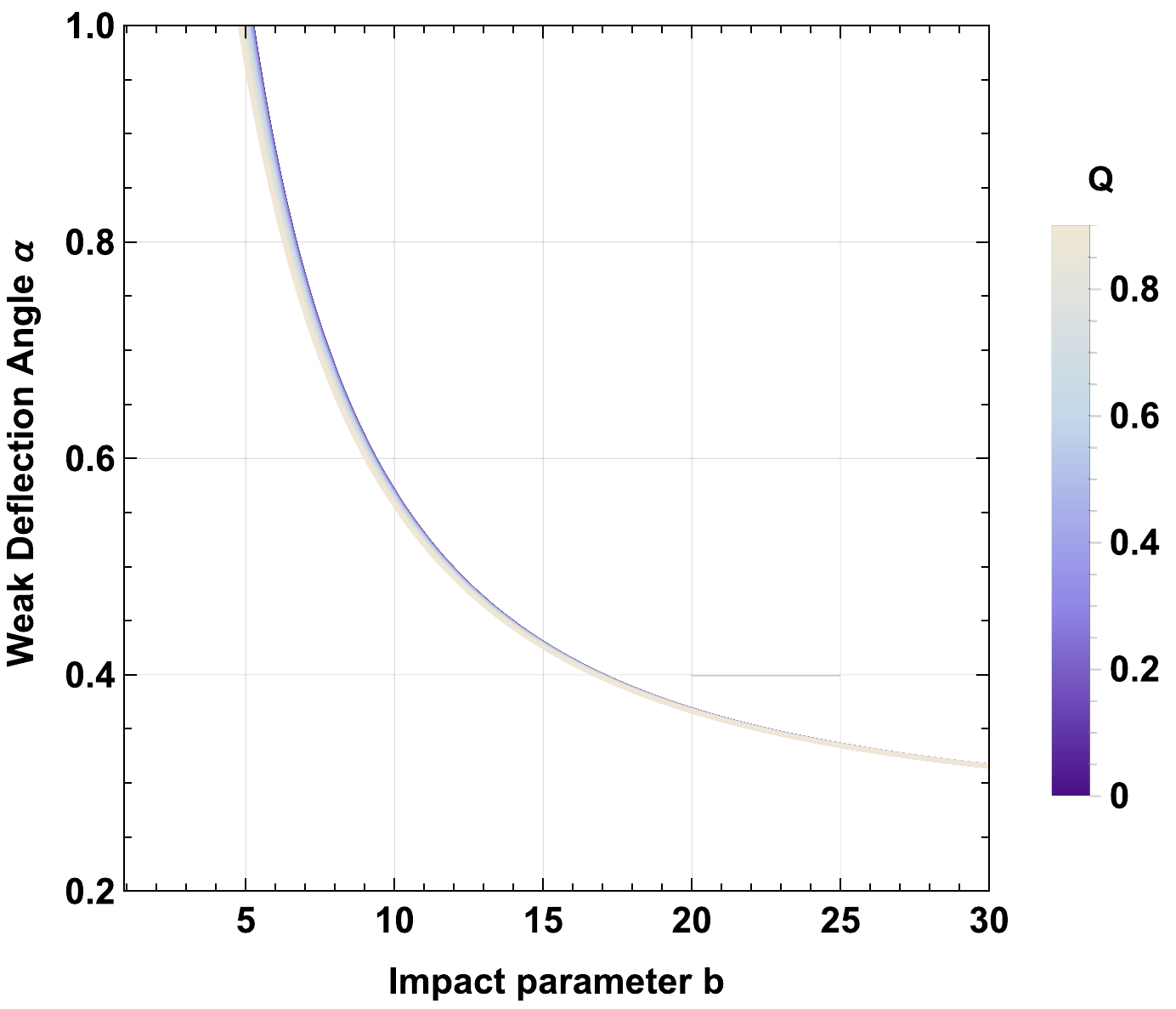
Figure 16. (color online) Behavior of the weak deflection angle α of the charged-Kiselev BH in a cloud of strings in the presence of nonuniform plasma for fixed values of
$ Z=\frac{z_0^2}{\omega_0^2}=0.5 $ ,$ M=1 $ ,$ \gamma=0.5 $ ,$ \omega_q=-1 $ ,$ a=0.1 $ , and variable Q.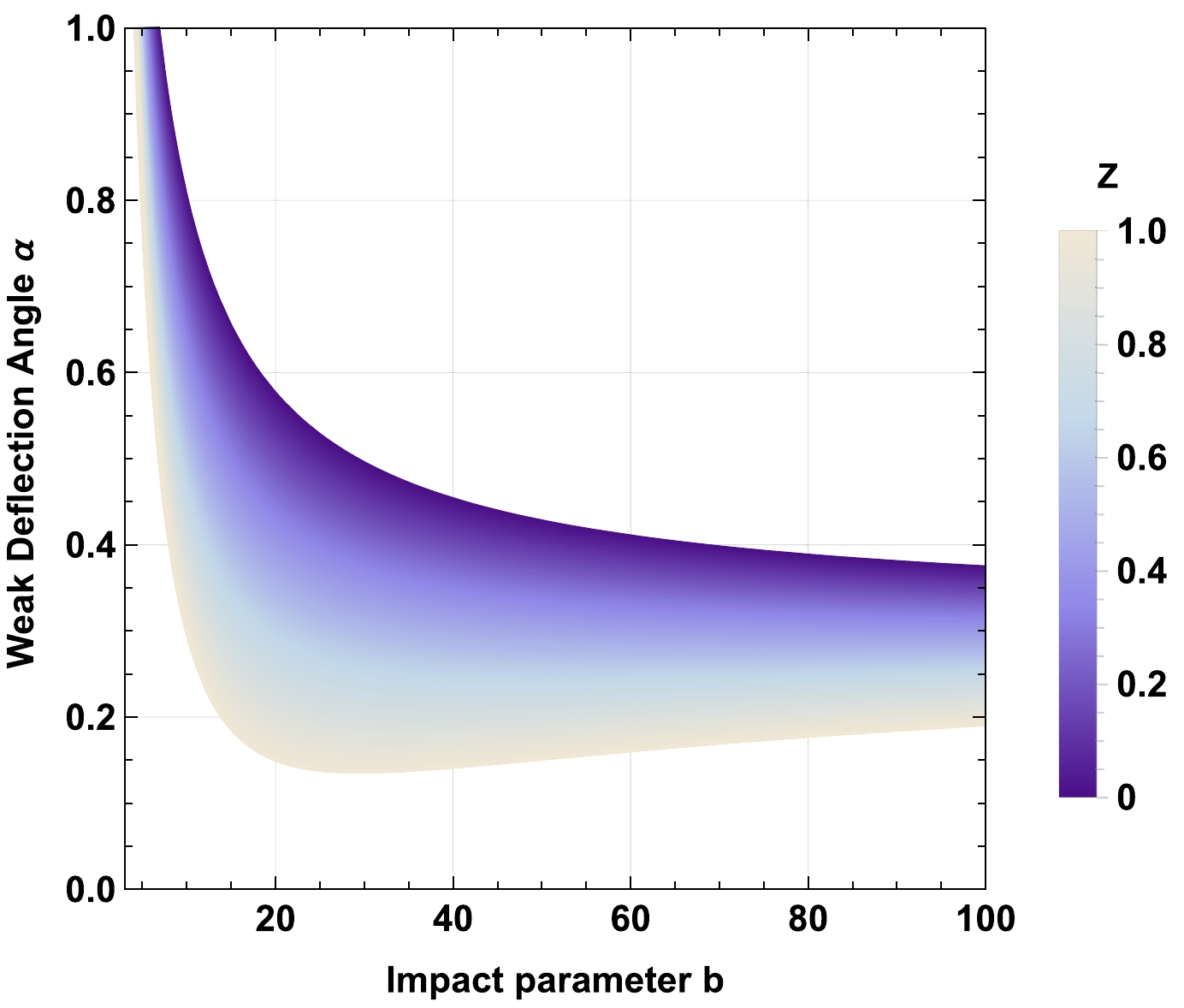
Figure 17. (color online) Behavior of the weak deflection angle α of the charged-Kiselev BH in a cloud of strings in the presence of nonuniform plasma
$ Z=\frac{z_0^2}{\omega_0^2} $ for fixed values of$ \gamma=0.01 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-2/3 $ , and$ a=0.1 $ .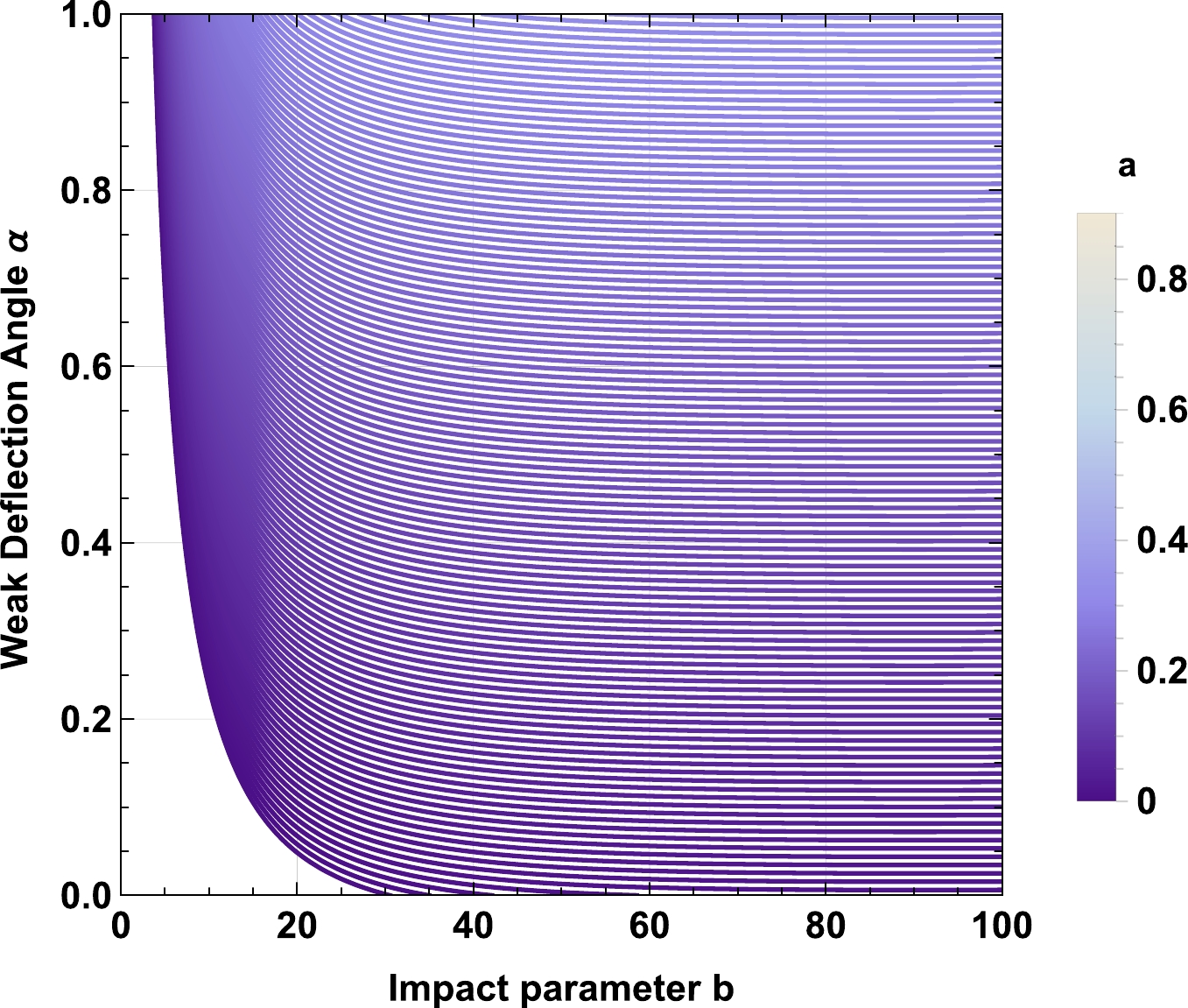
Figure 18. (color online) Behavior of the weak deflection angle α of the charged-Kiselev BH in cloud of strings in the presence of nonuniform plasma for fixed values of
$ Z=\frac{z_0^2}{\omega_0^2}=0.5 $ ,$ \gamma=0.01 $ ,$ M=1 $ ,$ Q=0.5 $ ,$ \omega_q=-1 $ and$ a=0.1 $ . -
In this section, we study the shadow of the charged-Kiselev BH in the background of string clouds. For the angular radius of the BH shadow, we explore [86, 166]
$ \sin^2 \alpha_{\rm sh}=\frac{h(r_{\rm ph})^2}{h(r_{\rm obs})^2}, $

(49) with
$ h(r)^2=\frac{r^2}{f(r)}, $

(50) where
$ h(r) $ was introduced in Sec. IV (see. Eq. (35)).$\alpha_{\rm sh}$ is the angular radius of the BH shadow, and$r_{\rm obs}$ is the observer distance, which is very large but finite at$r_{\rm obs}=D\simeq8.3$ kpc for Sgr A* or$r_{\rm obs}=D\simeq16.8$ Mpc for M87*. It is worth noting that, in an astrophysical realistic scenario, the quintessential field parameter γ is supposed to be constant in the Universe and extremely small, and thus the cosmological horizon is supposed to be located at large distances. The quantity$r_{\rm ph}$ is the radius of the photon sphere, as mentioned previously.We now combine Eqs. (49) and (50), and for a distant observer, Eq. (49) takes the following form:
$ \sin^2 \alpha_{\rm sh}=\frac{r_{\rm ph}^2}{f(r_{\rm ph})}\frac{f(r_{\rm obs})}{r^2_{\rm obs}}. $

(51) One can find the radius of the BH shadow for an observer at a large distance using Eq. (51) as [166]
$ R_{\rm sh}\simeq r_{\rm obs} \sin \alpha_{\rm sh} \simeq \frac{r_{\rm ph}}{\sqrt{f(r_{\rm ph})}}{\sqrt{f(r_{\rm obs})}}. $

(52) The variation of the radius of the shadow of the charged-Kiselev BH in string clouds with the parameters γ, a,
and Q can be seen in Fig. 21. From this figure, we can see that the influences of the string cloud parameter a and quintessence parameter γ increase the size of the BH shadow, and the BH shadow decreases with an increase in the BH charge Q. Thus, the presence of the string clouds and quintessence increases the intensity of the spherically symmetric gravitational field due to the Reissner-Nordstrom BH. 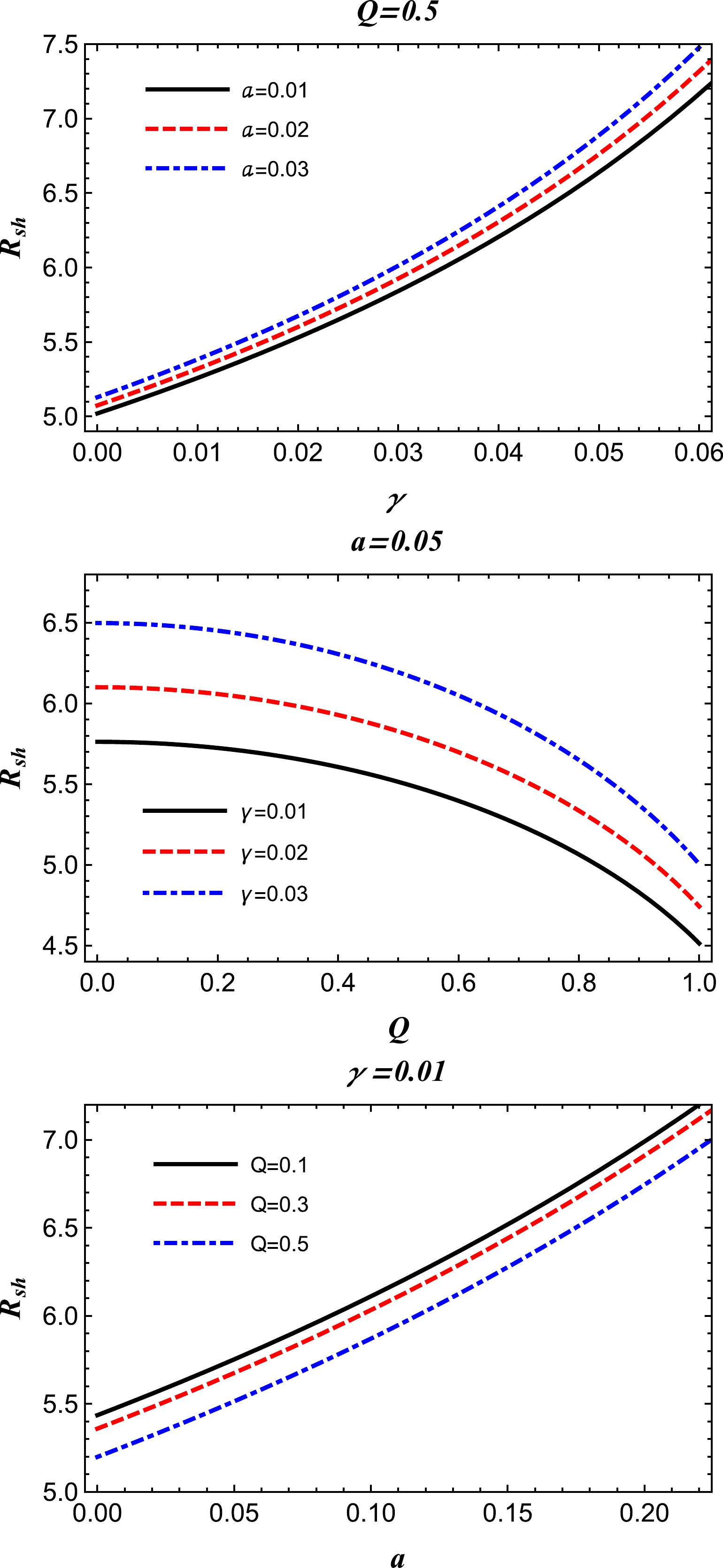
Figure 21. (color online) Radius of the shadow of the charged-Kiselev BH in a cloud of strings for different values of the quintessence parameter γ, the BH charge Q, and the string cloud parameter a, where
$ \omega_q=-2/3 $ and$ M=1 $ .In Fig. 22, the radius of the shadow of the charged-Kiselev BH in the string cloud background is plotted against the parameter γ for the three different values of the parameter
$ \omega_q $ and for fixed values of the parameters a and Q. From the plots, we observe that the radius of the shadow cast by the BH increases with the parameter γ for all three values of the parameter$ \omega_q $ , and it is maximum for$ \omega_q=-1 $ and minimum for$ \omega_q=-2/3 $ .
Figure 22. (color online) Radius of the BH shadow versus quintessence parameters for different values of
$ \omega_q $ and$ M=1 $ .Here, we take the assumption that the supermassive BHs M87* and Sgr A* are spherically symmetric static and electrically charged, surrounded by the quintessence and clouds of strings, although the observation made by the EHT collaboration does not support the assumption made here. However, here we theoretically explore the upper limits on the parameters γ and a, using the data provided by the EHT collaboration. To constrain these two parameters, we use the observational data released by the EHT collaboration for the shadows of the supermassive BHs M87* and Sgr A*. The angular diameter of the shadow, the distance from Earth, and the mass of of the BH at the center of the galaxy M87 are
$ \theta_\text{M87*} = 42 \pm 3 \:\mu $ as,$ D = 16.8 \pm 0.8 $ Mpc, and$ M_\text{M87*} = 6.5 \pm 0.7 \times $ $ 10^9 \: M_\odot $ , respectively [2]. For Sgr A*, the data recently provided by the EHT collaboration are$ \theta_\text{Sgr A*} = 48.7 \pm 7 \:\mu $ ,$ D = 8277\pm9\pm33 $ pc, and$ M_\text{Sgr A*} = 4.297 \pm 0.013 \times $ $ 10^6 \: M_\odot $ (VLTI) [167]. Based on these data, we calculate the diameter of the shadow cast by the BH per unit mass from the following expression [103, 168]:$ d_\text{sh} = \frac{D \theta}{M}\,. $

(53) We can then obtain the diameter of the shadow from the expression
$ d_\text{sh}^\text{theo} = 2R_\text{sh} $ . Thus, the diameter of the shadow image is$ d^\text{M87*}_\text{sh} = (11 \pm 1.5)M $ for M87* and$ d^\text{Sgr A*}_\text{sh} = (9.5 \pm 1.4)M $ for Sgr A*. Using the data provided by the EHT collaboration, we obtain the upper limits on the parameters γ and a for the supermassive BHs at the centers of the galaxies M87 and Sgr A*. We present our results obtained here in Table 1. We notice that the upper limit of the parameter γ decreases when the parameter a grows. This suggests that the effect of the string cloud is slightly larger on the spacetime geometry compared to that of the quintessence.Parameters Estimated values of parameters for M87* BH $Q=0 $ 

$Q=0.5 $ 

$Q=1.0 $ 

a $0.01000\;\;\;\;0.05000\;\;\;\;0.10000$ 

$0.01000\;\;\;\;0.05000\;\;\;\;0.10000$ 

$0.01000\;\;\;\;0.05000\;\;\;\;0.10000$ 

γ $0.03295\;\;\;\;0.02400\;\;\;\;0.01340$ 

$0.04110\;\;\;\;0.03140\;\;\;\;0.02000$ 

$0.07680\;\;\;\;0.06320\;\;\;\;0.04476$ 

Parameters Estimated values of parameters for Sgr A* BH $Q=0 $ 

$Q=0.5 $ 

$Q=1.0 $ 

a $0.01000\;\;\;\;0.03000\;\;\;\;0.04700$ 

$0.01000\;\;\;\;0.05000\;\;\;\;0.08500$ 

$0.01000\;\;\;\;0.05000\;\;\;\;0.10000$ 

γ $0.00800\;\;\;\;\;$ 

$0.00358\;\;\;\;0.00000$ 

$0.01700\;\;\;\;0.00800\;\;\;\;\;$ 

$0.00000$ 

$0.05800\;\;\;\;0.04430\;\;\;\;0.02850$ 

Table 1. Upper values of γ and a for the supermassive BHs in the galaxies M87 and Sgr A. Note that we set
$M=1$ .We now investigate the radius of the shadow of the charged-Kiselev BH with the background of string clouds in a plasma medium. The radius of the BH shadow in plasma can be given as [21, 127]
$ R_{\text{sh}}\simeq\sqrt{r_{\text{ph}}^2\bigg[\frac{1}{f(r_{\text{ph}})}-\frac{\omega^2_p(r_{\text{ph}})}{\omega^2_0}\bigg]f(r_{obs})}. $

(54) In the vacuum case
$ \omega_{\text{p}}(r)\equiv0 $ , we recover the radius of the shadow of the charged-Kiselev BH in the string cloud background without the plasma medium. -
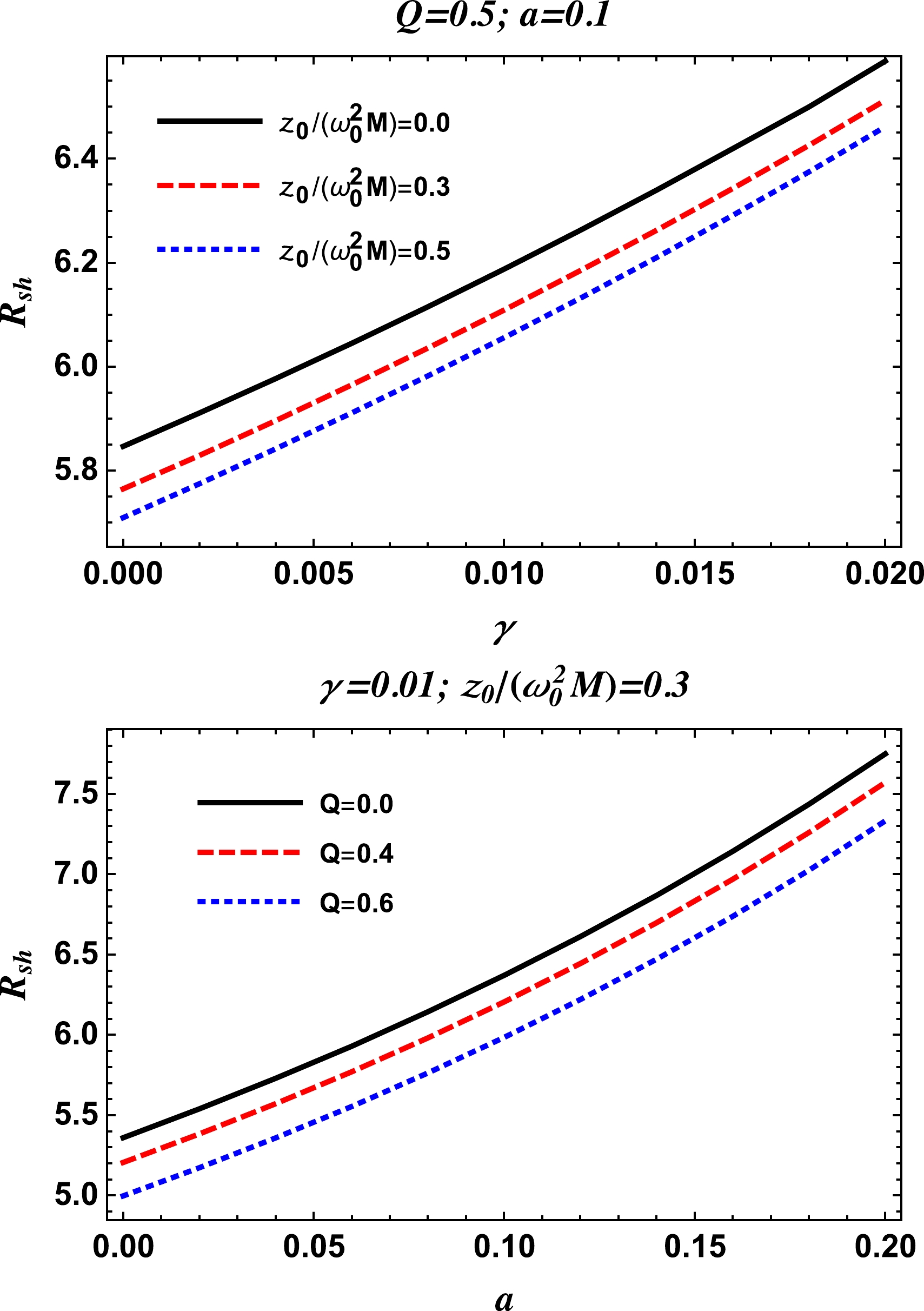
Now, we study the radius of the shadow for the charged-Kiselev BH with the string cloud background in the presence of a uniform plasma
$ \omega _p^2= \text{const.} $ . From the combination of (54) and (37), we can numerically obtain the radius of the BH shadow for different values of the spacetime parameters, as shown in Fig. 23. From Fig. 23, we see that the radius of the shadow increases with the parameters γ and a, and it decreases with the charge Q of the BH. We also see that the radius of the shadow cast by the charged-Kiselev BH in the string cloud background decreases with an increase in the value of the uniform plasma parameter. -
Here, we analyze the size of the shadow of the charged-Kiselev BH with string clouds in the presence of a nonuniform plasma. In this case, the frequency of the plasma is required to obey the following power-law form [162]:
$ \omega^2_{p}(r)=\frac{z_0}{r}. $

(55) We can now obtain the radius of the shadow cast by the charged-Kiselev BH in the background of the cloud of strings, for the involved spacetime parameters in the presence of the nonuniform plasma. The dependence of the BH shadow on the different spacetime parameters is shown in Fig. 24. Here, we see that, for the nonuniform plasma, the behavior of the radius of the shadow of the charged-Kiselev BH in string clouds is the same as it was in the case of the uniform plasma, as discussed above.
-
The absorption cross section oscillates around the constant geometric-optics value for a BH, which is related to the photon sphere. It increases monotonically with increasing frequency for an ordinary material sphere [169]. The cross section of the photon sphere is related to the impact parameter at critical value, and it limits the value of the absorption cross section, the BH characteristic properties at low energies, where the cross section equals to the BH area [170, 171], and also at high energies [155], using the geometrical cross section of the photon sphere. Using the Regge pole techniques, Decanini et al. [155] showed that the oscillatory pattern of the high energy absorption cross section is related to a Sinc(x) function included photon sphere.
The absorption cross section for high frequency waves is approximately the so-called classical capture cross section of null geodesics, given by
$\sigma_{\rm geo} = \pi b_c^2$ , where$ b_c $ is the critical impact parameter. In the eikonal limit, the oscillatory part of the absorption cross section can be written as [155]$ \sigma_{\rm osc} = - 4 \pi \frac{\lambda b_c^2}{w} {\rm e}^{-\pi \lambda b_c} \sin\frac{2 \pi w}{\Omega_c}, $

(56) where we use
$ \operatorname{sinc}(x)=\dfrac{\sin x}{x} $ , and λ is known as the Lyapunov exponent$ \lambda = \sqrt{\frac{f(r_c)}{2 r_c^2} \big(2f(r_c)-r_c^2f''(r_c)\big)}, $

(57) and
$ \Omega_c = \sqrt{\dfrac{f(r_c)}{r_c^2}} $ , where$ r_c $ is the radius of the photon sphere. The Sinc approximation then states that the total absorption cross section at the eikonal limit is$\sigma_{\rm abs} \approx \sigma_{\rm osc} + \sigma_{\rm geo}$ [154, 169, 172]. In Fig. 25, we plot the total absorption cross section for various values of Q. -
In this study, we investigated shadow and gravitational weak lensing by the charged-Kiselev BH in the background of clouds of strings, in the presence of plasma. First, we studied photon spheres in the spacetime of the charged-Kiselev BH in the string cloud background without any plasma and noticed the impact of the quintessence parameter γ, the string cloud parameter a, and the BH charge Q on the radii of such spheres. It can be seen from Fig. 2 that the radius of a photon sphere in the vicinity of the charged-Kiselev BH with string clouds increases with the parameters γ and a and decreases with the charge Q of the BH. Next, we analyzed the effects of both uniform and nonuniform plasmas on the radii of the photon spheres of the charged-Kiselev BH in string clouds, as shown in Figs. 5 and 9. We observed that the radii of the photon spheres in the presence of plasma are larger than the radii of the photon spheres without plasma.
We also calculated the weak deflection angle using the GBT to probe the effects of the cloud of strings parameter a, the quintessence parameter γ, and the charge Q of the BH and of the plasma medium on the weak deflection angle α. Therefore, we considered the photon rays moving in a medium of homogeneous plasma. Note that
$ \omega_p\to 0 $ , removing the effect of the plasma on the deflection angle obtained in Eq. (48). As a result, the string cloud parameter a, the quintessence parameter γ, and the uniform plasma parameter increase the deflection angle α, while increasing the charge Q of the BH decreases the deflection angle α, shown in Figs. 11 and 12. Moreover, for the case of$ \omega_q=-1 $ , decreasing the nonuniform plasma parameter$ z_0 $ increases the deflection angle, as seen in Fig. 13. In addition, the string cloud parameter a increases the deflection angle α, as seen in Fig. 14, while decreasing the value of the parameter γ decreases the deflection angle, as seen in Fig. 15. As expected, increasing the value of the charge Q of the BH decreases the deflection angle, as seen in Fig. 16. Similarly, when$ \omega_q=-2/3 $ , the behaviors of the deflection angle remain the same as in the previous case of$ \omega_q=-1 $ for the spacetime parameters and the plasma parameter, shown in Figs. 17, 18, 19, and 20. The effect of plasma on the deflection angle is that the uniform plasma increases it while the nonuniform plasma decreases it. In this study, we have seen that weak gravitational lensing cannot provide sufficient bounds on the spacetime parameters. The study of timelike geodesics in the spacetime of the charged-Kiselev BH with clouds of strings may be useful in placing constraints on the different spacetime parameters. Some studies have already been conducted in this direction [74, 173–175].Subsequently, we studied the effects of uniform and nonuniform plasmas on the shadow cast by the charged-Kiselev BH with clouds of strings and noticed the dependence of the parameters γ, a, and Q on the shadow of the BH in the presence of plasma. We saw that, with increasing values of γ and a, the radius of the shadow of the charged-Kiselev BH in a cloud of strings increases, and it decreases with the charge Q of the BH, as shown in Figs. 21, 23, and 24. Further, we noticed that the presence of plasma reduces the radius of the shadow of the charged-Kiselev BH in the string cloud background. Interestingly, we obtained upper values for the parameters γ and a using the data provided by the EHT collaboration and presented these values in Table 1. We also calculated the high energy absorption cross section using the Sinc approximation, shown in Fig. 25 for different values of the charge Q and for fixed values of the other spacetime parameters. We observed that the absorption cross section decreases with the frequency ω and also with the charge Q of the BH.
We saw that the existence of quintessence and clouds of strings enhances the size of the shadow cast by the charged-Kiselev BH with the string cloud background; therefore, the combined effect of the cloud of strings and quintessence increases the intensity of the gravitational field of the BH.
-
We would like to thank the referee for their useful comments, which have considerably improved this paper. F.A. acknowledges the support of Inha University in Tashkent. G.M. is thankful to Prof. Gao Xianlong from the Department of Physics, Zhejiang Normal University, for his kind support and help during this research. A.{Ö}. would like to acknowledge the contribution of the COST Action CA18108 - Quantum gravity phenomenology in the multi-messenger approach (QG-MM).
-
For the nonuniform plasma with
$ \omega^2_{p}(r)=z_0/r^q $ , the Gaussian curvature for the optical metric is calculated as follows:$ \begin{aligned}[b] \\[-8pt] \mathcal{K}\approx & \frac{9 \gamma \log (r) \omega _q Q^2}{r^5}+\frac{39 \gamma \log (r) z_0^2 \omega _q Q^2}{r^5 \omega _0^2}+\frac{75 \gamma q \log (r) z_0^2 \omega _q Q^2}{r^5 \omega _0^2}+\frac{192 \gamma M q \log ^2(r) z_0^2 \omega _q Q^2}{r^6 \omega _0^2}+\frac{30 \gamma M z_0^2 \omega _q Q^2}{r^6 \omega _0^2} \\&+\frac{30 \gamma M q z_0^2 \omega _q Q^2}{r^6 \omega _0^2}+\frac{3 Q^2}{r^4}-\frac{3 \gamma Q^2}{r^5}-\frac{6 M Q^2}{r^5}-\frac{3 \gamma \omega _q Q^2}{2 r^5}+\frac{5 q z_0^2 Q^2}{r^4 \omega _0^2}-\frac{10 q \log (r) z_0^2 Q^2}{r^4 \omega _0^2}+\frac{5 z_0^2 Q^2}{r^4 \omega _0^2}-\frac{13 \gamma z_0^2 Q^2}{r^5 \omega _0^2}\\&-\frac{26 M z_0^2 Q^2}{r^5 \omega _0^2}-\frac{15 \gamma q z_0^2 Q^2}{r^5 \omega _0^2}-\frac{30 M q z_0^2 Q^2}{r^5 \omega _0^2}+\frac{26 \gamma q \log (r) z_0^2 Q^2}{r^5 \omega _0^2}+\frac{52 M q \log (r) z_0^2 Q^2}{r^5 \omega _0^2}-\frac{78 \gamma q \log ^2(r) z_0^2 \omega _q Q^2}{r^5 \omega _0^2} \\&-\frac{15 \gamma z_0^2 \omega _q Q^2}{r^5 \omega _0^2}-\frac{15 \gamma q z_0^2 \omega _q Q^2}{r^5 \omega _0^2}+\frac{32 \gamma M z_0^2 Q^2}{r^6 \omega _0^2}+\frac{40 \gamma M q z_0^2 Q^2}{r^6 \omega _0^2}-\frac{64 \gamma M q \log (r) z_0^2 Q^2}{r^6 \omega _0^2}\\&-\frac{96 \gamma M \log (r) z_0^2 \omega _q Q^2}{r^6 \omega _0^2}-\frac{180 \gamma M q \log (r) z_0^2 \omega _q Q^2}{r^6 \omega _0^2}+\frac{3 \gamma \log (r) \omega _q}{r^3}+\frac{6 \gamma M \omega _q}{r^4}+\frac{9 \gamma \log (r) z_0^2 \omega _q}{2 r^3 \omega _0^2} \\&+\frac{45 \gamma q \log (r) z_0^2 \omega _q}{2 r^3 \omega _0^2}+\frac{72 \gamma M q \log ^2(r) z_0^2 \omega _q}{r^4 \omega _0^2}+\frac{30 \gamma M z_0^2 \omega _q}{r^4 \omega _0^2}+\frac{30 \gamma M q z_0^2 \omega _q}{r^4 \omega _0^2}-\frac{\gamma}{r^3}-\frac{2 M}{r^3}-\frac{9 \gamma \omega _q}{2 r^3}+\frac{3 \gamma M}{r^4} \\&-\frac{9 \gamma M \log (r) \omega _q}{r^4}-\frac{3 M z_0^2}{r^3 \omega _0^2}-\frac{5 M q z_0^2}{r^3 \omega _0^2}+\frac{3 \gamma q \log (r) z_0^2}{r^3 \omega _0^2}+\frac{6 M q \log (r) z_0^2}{r^3 \omega _0^2}-\frac{9 \gamma q \log ^2(r) z_0^2 \omega _q}{r^3 \omega _0^2} \\ &-\frac{3 \gamma z_0^2}{2 r^3 \omega _0^2}-\frac{5 \gamma q z_0^2}{2 r^3 \omega _0^2}-\frac{15 \gamma z_0^2 \omega _q}{2 r^3 \omega _0^2}-\frac{15 \gamma q z_0^2 \omega _q}{2 r^3 \omega _0^2}+\frac{12 \gamma M z_0^2}{r^4 \omega _0^2}+\frac{20 \gamma M q z_0^2}{r^4 \omega _0^2}-\frac{24 \gamma M q \log (r) z_0^2}{r^4 \omega _0^2} \\& -\frac{36 \gamma M \log (r) z_0^2 \omega _q}{r^4 \omega _0^2}-\frac{120 \gamma M q \log (r) z_0^2 \omega _q}{r^4 \omega _0^2} \end{aligned}\tag{A1} $ 
The weak deflection angle in the nonuniform plasma is then found:
$ \begin{aligned}[b] \alpha \approx & -\frac{3 \pi Q^2}{4 b^2}+\frac{5 \pi q \log (b) z_0^2 Q^2}{2 b^2 \omega _0^2}-\frac{5 \pi q z_0^2 Q^2}{4 b^2 \omega _0^2}+\frac{5 \pi q \log (4) z_0^2 Q^2}{4 b^2 \omega _0^2}-\frac{5 \pi z_0^2 Q^2}{4 b^2 \omega _0^2}+\frac{2 \gamma}{b}+\frac{4 M}{b}+\frac{3 \gamma \log (4) \omega _q}{b}\\&+\frac{3 \gamma M \pi \log (8) \omega _q}{4 b^2}+\frac{9 \gamma M \pi \log (b) \omega _q}{4 b^2}+\frac{18 \gamma q \log ^2(2) z_0^2 \omega _q}{b \omega _0^2}+\frac{18 \gamma q \log ^2(b) z_0^2 \omega _q}{b \omega _0^2}+\frac{33 \gamma q z_0^2 \omega _q}{b \omega _0^2}+\frac{9 \gamma \log (2) z_0^2 \omega _q}{b \omega _0^2}\\&+\frac{27 \gamma q \log (b) z_0^2 \omega _q}{b \omega _0^2}+\frac{12 \gamma M \pi q \log (2) z_0^2 \omega _q}{b^2 \omega _0^2}+\frac{9 \gamma M \pi \log (2) z_0^2 \omega _q}{b^2 \omega _0^2}+\frac{9 \gamma M \pi q \log (4) z_0^2 \omega _q}{b^2 \omega _0^2}+\frac{30 \gamma M \pi q \log (b) z_0^2 \omega _q}{b^2 \omega _0^2}\\&+\frac{9 \gamma M \pi \log (b) z_0^2 \omega _q}{b^2 \omega _0^2}+\frac{3 \gamma M \pi q z_0^2 \omega _q}{2 b^2 \omega _0^2}-\frac{3 \gamma \omega _q}{b}-\frac{6 \gamma \log (b) \omega _q}{b}-\frac{3 \gamma M \pi \omega _q}{2 b^2}-\frac{3 \gamma M \pi }{4 b^2}+\frac{3 \gamma z_0^2}{b \omega _0^2}\\&+\frac{6 M z_0^2}{b \omega _0^2}-\frac{7 \gamma q z_0^2}{b \omega _0^2}-\frac{14 M q z_0^2}{b \omega _0^2}+\frac{\gamma q \log (64) z_0^2}{b \omega _0^2}+\frac{2 M q \log (64) z_0^2}{b \omega _0^2}-\frac{6 \gamma q \log (b) z_0^2}{b \omega _0^2} \\&-\frac{12 M q \log (b) z_0^2}{b \omega _0^2}-\frac{3 \gamma z_0^2 \omega _q}{b \omega _0^2}-\frac{27 \gamma q \log (2) z_0^2 \omega _q}{b \omega _0^2}-\frac{9 \gamma \log (b) z_0^2 \omega _q}{b \omega _0^2}-\frac{9 \gamma q \log (16) \log (b) z_0^2 \omega _q}{b \omega _0^2}-\frac{3 \gamma \pi ^2 q z_0^2 \omega _q}{2 b \omega _0^2} \\&-\frac{5 \gamma M \pi q z_0^2}{b^2 \omega _0^2}+\frac{\gamma M \pi q \log (64) z_0^2}{b^2 \omega _0^2}+\frac{6 \gamma M \pi q \log (b) z_0^2}{b^2 \omega _0^2}-\frac{3 \gamma M \pi z_0^2}{b^2 \omega _0^2}-\frac{18 \gamma M \pi q \log ^2(b) z_0^2 \omega _q}{b^2 \omega _0^2} \\&-\frac{6 \gamma M \pi q \log (64) \log (b) z_0^2 \omega _q}{b^2 \omega _0^2}-\frac{9 \gamma M \pi q \log ^2(4) z_0^2 \omega _q}{2 b^2 \omega _0^2}-\frac{3 \gamma M \pi ^3 q z_0^2 \omega _q}{2 b^2 \omega _0^2}-\frac{15 \gamma M \pi z_0^2 \omega _q}{2 b^2 \omega _0^2}+a \pi. \end{aligned} \tag{A2}$

Weak deflection angle and shadow cast by the charged-Kiselev black hole with cloud of strings in plasma
- Received Date: 2022-09-15
- Available Online: 2023-02-15
Abstract: In this study, the gravitational deflection angle of photons in the weak field limit (or the weak deflection angle) and shadow cast by the electrically charged and spherically symmetric static Kiselev black hole (BH) in the string cloud background are investigated. The influences of the BH charge Q, quintessence parameter γ, and string cloud parameter a on the weak deflection angle are studied using the Gauss-Bonnet theorem, in addition to studying the influences on the radius of photon spheres and size of the BH shadow in the spacetime geometry of the charged-Kiselev BH in string clouds. Moreover, we study the effects of plasma (uniform and non-uniform) on the weak deflection angle and shadow cast by the charged-Kiselev BH surrounded by the clouds of strings. In the presence of a uniform/nonuniform plasma medium, an increase in the string cloud parameter a increases the deflection angle α. In contrast, a decrease in the BH charge Q decreases the deflection angle. Further, we observe that an increase in the BH charge Q causes a decrease in the size of the shadow of the BH. We notice that, with an increase in the values of the parameters γ and a, the size of the BH shadow increases, and therefore, the intensity of the gravitational field around the charged-Kiselev BH in string clouds increases. Thus, the gravitational field of the charged-Kiselev BH in the string cloud background is stronger than the field produced by the pure Reissner-Nordstrom BH. Moreover, we use the data released by the Event Horizon Telescope (EHT) collaboration, for the supermassive BHs M87* and Sgr A*, to obtain constraints on the values of the parameters γ and a.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: