-
With the advent of the concept of isospin quantum number, the proton and neutron have been manifested as two states of the nucleon in view of the strong interaction, formalizing the charge symmetry or charge independence of the nuclear interaction [1]. A pair of mirror nuclei is then a natural laboratory for testing isospin symmetry, which leads to the existence of isobaric multiplets and analog states or resonances [2, 3]. Another conjecture, used in the present study, is that, if the nuclear interaction is charge independent, the mass differences of mirror nuclei would be dominantly determined by the Coulomb interaction [4, 5]. By employing the conventional liquid drop mass formula, this point can be readily verified through available experimental data on nuclear mass. Of course, there are still residual mass differences (RMDs) for mirror pairs after excluding the Coulomb interaction, which may be attributed to the broken isospin symmetry [6–8].
In turn, once the above RMDs can be effectively described for a better evaluation of the mass differences (MDs) of mirror nuclei, one of their masses can be predicted based on the other [9–11]. For many decades, this idea has been actualized in the prediction of the masses of proton-rich nuclei owing to the abundance of binding energy (BE) data in the partner (neutron-rich) side, especially in the recent years [12, 13, 14]. The MDs of mirror nuclei are also used in the modifications of mass formulas, such as in the Weizsäcker-Skyme (WS) model [15] and a combination of the Kelson-Garvey relationship [16]. The treatment of MDs in mirror nuclei can be classified into two main groups, namely, the refined Coulomb interaction energy [12, 13, 17] and empirical RMDs [10, 11, 14, 18]. Besides the traditional liquid drop model (LDM), density functional theory has been employed to improve the former quantity [12, 13]. As for the RMD case, a popular idea is based on the shell effect correction [14, 18], in which the differences between the proton and neutron mean-field approximations are considered along with their spin-orbit interactions. Within the valence correlation scheme (VCS), the (modified) valence nucleon product and the linear form of valence nucleon number have been used to reveal the remarkable similarity generated from complicated nuclei [1, 19]. With these in mind, this study aims to introduce the VCS into the RMD curve of mirror nuclei, serving as a more reasonable evaluation of the MDs of a mirror pair and the subsequent masses of involved nuclei.
Let us begin with a macroscopic-microscopic type mass formula,
$ \begin{aligned}[b] B(Z,N)=&B_{{\rm LDM}}+B_{\mathrm{mic}}\\ =&a_{{\rm V}}A+a_{{\rm S}}A^{2/3}+a_{{\rm C}}\frac{Z^2}{A^{1/3}}+a_{I}\frac{(N-Z)^2}{A}\\ &+a_{{\rm P}}\frac{(-1)^Z+(-1)^N}{\sqrt{A}}+B_{\mathrm{mic}}. \end{aligned} $

(1) Here, the macroscopic part corresponds to the conventional LDM, which is comprised of the volume, surface, Coulomb, symmetry, and pairing energies. Clearly, these terms, except the Coulomb energy, satisfy the charge independence of nuclear interactions, that is, their values are unchanged if the neutron and proton numbers are exchanged. The
$ B_{\mathrm{mic}} $ part is only considered in terms of the shell correction in this study. This is consistent with the treatment in WS-type mass models [15], which also include the mirror nuclei constraint. Before proceeding to the VCS shell correction for mirror nuclei, it is interesting to check the validity of the MDs of mirror nuclei in the sole Coulomb energy.As a starting point, the MD of a pair of mirror nuclei, namely, (
$ Z,N $ ) and ($ N,Z $ ), is expressed via the BE,$ \begin{equation} \Delta B(Z,N)= B(Z,N)-B(N,Z), \end{equation} $

(2) where the convention of
$ N>Z $ is used in this study. Following the traditional Bethe-Weizsäcker mass formula, i.e., the above$B (Z,N)$ equation, the$\Delta B (Z,N)$ value is determined by the Coulomb displacement energies,$ \begin{equation} \Delta B(Z,N)=a_{{\rm C}}\frac{Z^2-N^2}{A^{1/3}}=-a_{{\rm C}}\Delta Z A^{2/3}, \end{equation} $

(3) where
$ \Delta Z=N-Z $ . Therefore, it is interesting to check the validity or reliability of the above formula, which is also somewhat related to the Nolen-Schiffer anomaly [17, 20]. By collecting the 106 pairs of mirror nuclei in the AME16 compilation [21], the quantity$ \Delta B/\Delta Z $ is plotted against$ A^{2/3} $ in Fig. 1. As expected, a linear relationship between the two former quantities is obtained, and the fixed$a_{{\rm C}}$ value is –0.715 MeV, which is comparable with the commonly-accepted value [9–11]. However, there is a sizable intercept for this linear line, which is beyond the capability of Eq. (3) (the expected value is zero). Of course, the aforementioned formula for Coulomb energy originates from the assumption of a uniformly charged nuclear sphere. If one considers the diffuseness modification, proton form-factor correction, and other effects [20, 22, 23], the Coulomb energy should be rewritten. Nonetheless, these corrections appear to not have the ability to reproduce the non-zero intercept value. Moreover, they cannot clearly enhance the accuracy of the evaluation of the Coulomb displacement energy, as shown in Ref. [18]. This unexpected deviation may contribute to the quantal correction to the empirical Coulomb energy via the so-called exchange energy [23, 24]. It is simply stated that the exchange (xC) term can be expressed as$E_{{\rm xC}}=\sum_{a,b}\langle ab|{\rm e}^2/r_{12}|ab-ba\rangle$ , in which the double summation covers all single-proton states in the Fermi sea. The exchange term is then found to be proportional to$Z^2/\Omega k_{{\rm F}}^2$ within the Fermi gas model [25]. Because the Fermi momentum is related to the volume parameter via$k_{{\rm F}}\sim (Z/\Omega)^{1/3}$ and$ \Omega\sim A $ , the Coulomb exchange potential is fixed as$a_{{\rm xC}}^{'}Z^{4/3}/A^{1/3}$ . Through Taylor expansion to the first order, the total Coulomb displacement energy can be expressed as$\Delta B(Z,N)/\Delta Z= a_{{\rm C}}A^{2/3}+(2^{5/3}/3)a_{{\rm xC}}'=$ $a_{{\rm C}}A^{2/3}+a_{{\rm xC}}$ , where the final constant is responsible for the non-zero intercept in Fig. 1. Moreover, it is found that the MDs of mirror nuclei can be reproduced more accurately after the introduction of exchange Coulomb energy. In addition, the Coulomb displacement energy should be responsible for the energy differences between isobaric states in mirror nuclei. As mentioned in Ref. [24], the fixed values of$a_{{\rm C}}$ and$a_{{\rm xC}}$ would be different from this case of MDs in mirror nuclei. This is worth further investigation and may be related to the Nolen-Schiffer anomaly.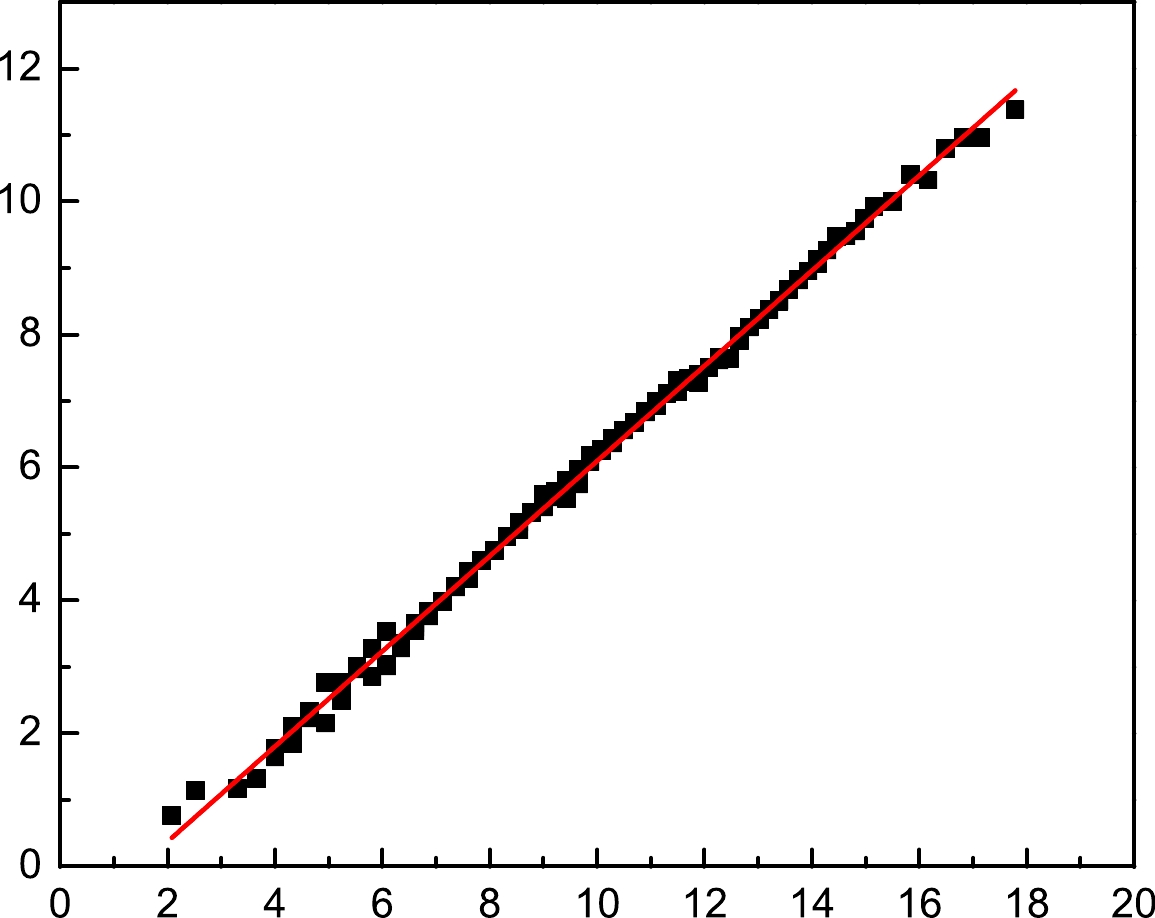
Figure 1. (color online) Binding energy difference between mirror nuclei (divided by the difference in their proton numbers) versus the mass number quantity
$A^{2/3}$ . Despite the linear relationship, there is an intercept value at approximately –1.053 MeV, which is consistent with the analysis in Ref. [24].Now, we investigate the RMDs between mirror nuclei after excluding the Coulomb displacement energy. As mentioned before, the RMDs are attributed to the shell correction in this case via the valence nucleon scheme. In the VCS, there are three types of Casten plots [1, 19, 26, 27], namely,
$N_p N_n$ ,$\frac{N_ pN_n}{N_p+N_n}$ , and$\alpha N_ p+\beta N_ n$ , in which$N_ p$ ($N_ n$ ) is the difference between the proton (neutron) number and the nearest magic number for one given nucleus. The two former quantities have been widely used in the description of structural factors, such as the ratio of excitation energies$ E_{4_{1}^{+}}/E_{2_{1}^{+}} $ [1, 19], empirical shell corrections [24], and preformation probability of clustering in heavy nuclei [28–31]. However, these two quantities would be identical, even if the proton and neutron numbers are exchanged for mirror nuclei, implying that they are not suitable for mapping the RMDs of mirror pairs. In comparison, the last Casten factor,$\alpha N_ p+\beta N_ n$ , would change for mirror nuclei. Moreover, this factor has shown its effectiveness in the evaluation of nucleon separation energies and decay energies [26, 27].Keeping this in mind, the MDs of mirror nuclei can be expressed as
$ \begin{equation} \Delta B(Z,N)=(-a_{{\rm C}}A^{2/3}+a_{{\rm xC}})\Delta Z+\alpha N_ p+\beta N_ n, \end{equation} $

(4) where the first term is the Coulomb displacement energy, and the residual terms correspond to the shell correction. By fitting the available experimental MDs in 106 pairs of mirror nuclei (
$ 1\leq\Delta Z\leq5 $ ) from AME16 [21], the parameters are obtained as$a_{{\rm C}}=-0.7267$ ,$a_{{\rm xC}}=-1.207$ ,$ \alpha=0.0374 $ , and$ \beta=-0.0134 $ , with the standard deviation between theory and experiment$ \sigma=0.291 $ MeV. This fitting procedure is performed using the Levenberg-Marquardt iteration algorithm to obtain the parameters simultaneously. Better insight into the validity of the above formula can be found in Fig. 2. As shown, the deviation between the calculated$ \Delta B $ value and the measured value is generally in the range$ -0.75\sim 0.5 $ MeV, except for the pairs (1, 3) and (5, 10) with extreme neutron-proton ratios. As shown in Ref. [10], it is worth noting that, if mirror nuclei are divided into five groups according to the$ \Delta Z $ value and the respective fitting process for each group, the standard deviation σ would be clearly reduced for Eq. (4).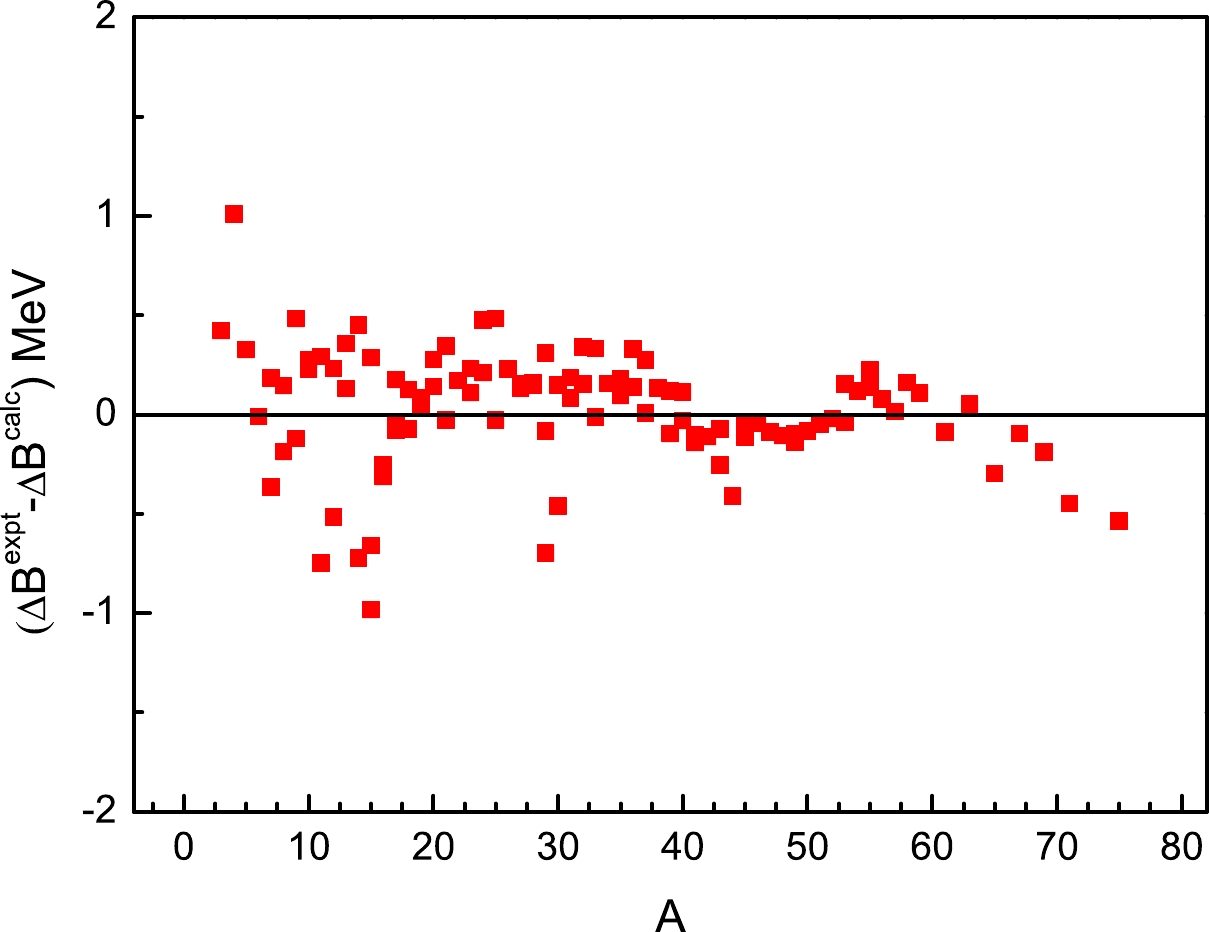
Figure 2. (color online) Difference between the experimental
$\Delta B$ value of mirror nuclei and the calculated value via Eq. (4) versus the mass number A. The zero line is to guide the eye.However, the accuracy of the above formula appears to increase with increasing mass number, which corresponds to the different regions in the shell-model text, as discussed in Refs. [14, 32]. In fact, after these mirror pairs are classified into four groups via the magic number, that is, (
$ 2 \sim 8 $ ), ($ 8 \sim 20 $ ), ($ 20 \sim 28 $ ), and ($ 28 \sim 50 $ ), the standard deviation of Eq. (4) is 0.315 MeV, 0.206 MeV, 0.093 MeV, and 0.098 MeV for these four regions, respectively, implying a decrease in the general σ value (0.291 MeV) and an improvement in the present approach. Of course, there are still clear fluctuations in the difference$ \Delta B^{\mathrm{expt}}-\Delta B^{\mathrm{calc}} $ in Fig. 2, which may correspond to the residual shell or another structural effect due to the few-body character for light nuclei. In this sense, the$\alpha N_ p+\beta N_ n$ term or its higher order term is not fully capable of covering the RMDs$\Delta B^{\mathrm{expt}}(Z,N)- (-a_{{\rm C}}A^{2/3}+ a_{{\rm xC}})\Delta Z$ , although this VCS term is good at describing the separation energies and decay energies of heavier nuclei [26, 27]. This deserves further investigation, possibly from the perspective of nucleon-nucleon interactions. Moreover, the mass relationship between mirror nuclei introduces a possible method of predicting the BE of unknown nuclei. There are six new pairs of mirror nuclei with measured masses in the AME20 table [33] when compared to AME16 [21]. This provides us with a good opportunity to test the present formula for the MDs of mirror nuclei. Table 1 presents the predicted results for these new mirror pairs, where the deviation between the calculation and measurement is listed in the last column. Encouraged by these small deviations for mirror nuclei from both the AME16 and AME20 tables, the$ \Delta B $ formula, namely, Eq. (4), is applied to predict the BEs of several unknown proton-rich nuclei near the dripline.Z N A $\Delta B^{{\rm expt}}$ /MeV

$\Delta B^{{\rm calc}}$ /MeV

δ /MeV 24 20 44 31.177 31.346 0.169 25 21 46 32.472 32.486 0.014 26 22 48 33.615 33.611 −0.004 27 23 50 34.765 34.721 −0.044 28 24 52 35.989 35.817 −0.172 37 36 73 11.321 11.665 0.344 Table 1. Detailed results of the six new pairs of mirror nuclei from AME20 [33]. The proton, neutron, and mass numbers are listed in columns one to three, respectively, and the experimental and evaluated
$\Delta B$ values are shown in the fourth and fifth columns, respectively, along with their deviations in the last column.By combining Eqs. (2) and (4), we find that, once the BE of one nucleus is obtained, the BE value of its pair can be readily found using
$ B(N,Z)=B(Z,N)-\Delta B(Z,N) $ . Owing to the abundance of data on$ B(Z,N) $ ($ N>Z $ ) in AME20 [33], we predict the BEs of 47 proton-rich nuclei in the ranges$ \Delta Z\leq 4 $ and$ A\leq 90 $ , as displayed in Table 2. For comparison, other theoretical results from the finite-range droplet model (FRDM) [23] and WS type nuclear mass model [34] are listed in the last two columns of this table, indicating the consistency between our evaluations and these other results. Encouraged by this, it is hoped that the present formula for MDs in mirror nuclei and the corresponding predictions will be useful for future experiments.Z N A $BE {\rm pred}$ /MeV

$BE$ [23] /MeV

$BE$ [34] /MeV

19 15 34 261.400 260.47 260.845 21 17 38 295.083 295.55 294.640 23 19 42 328.862 330.39 328.978 30 26 56 454.493 454.04 453.505 30 27 57 469.609 469.12 469.477 31 27 58 468.137 467.25 468.102 31 28 59 486.080 485.68 485.697 31 29 60 500.078 498.77 499.433 32 28 60 487.179 486.45 485.767 32 29 61 501.501 500.08 500.568 32 30 62 517.745 516.37 516.983 33 29 62 499.845 498.48 498.654 33 30 63 516.333 515.52 515.408 33 31 64 530.259 529.23 529.267 34 30 64 517.424 516.52 515.862 34 31 65 531.386 530.51 530.468 34 32 66 547.888 547.09 547.727 35 31 66 529.516 529.15 528.139 35 32 67 546.019 547.97 545.482 35 33 68 560.034 559.90 559.381 36 32 68 547.153 546.97 545.923 36 33 69 561.080 561.11 560.733 36 34 70 577.933 577.98 578.011 37 34 71 575.747 576.48 576.162 37 35 72 589.934 590.57 590.122 38 35 73 590.884 591.42 591.701 38 36 74 608.076 608.68 609.167 39 36 75 606.206 607.29 607.094 39 37 76 621.100 621.78 621.302 39 38 77 637.394 638.12 637.758 40 37 77 621.336 622.53 622.315 40 38 78 638.649 639.75 639.567 40 39 79 652.477 653.22 652.961 41 39 80 651.481 652.11 651.293 41 40 81 667.360 667.97 667.829 42 39 81 651.482 652.34 652.081 42 40 82 668.883 669.06 669.469 42 41 83 682.607 682.34 682.731 43 40 83 666.396 667.23 666.965 43 41 84 681.403 681.62 680.950 43 42 85 697.666 698.02 698.024 44 42 86 699.264 699.47 699.641 44 43 87 713.011 713.16 713.703 45 43 88 711.770 712.05 711.897 45 44 89 728.857 728.35 728.869 46 44 90 729.934 730.18 730.807 To summarize, the MDs between mirror nuclei are initially ascribed to the Coulomb displacement energy by considering the charge-independent nucleon-nucleon interaction. After the systematic analysis of the experimental data of MDs for 106 pairs of mirror nuclei from AME16, the exchange Coulomb term is reconfirmed as essential for the reasonable description of Coulomb displacement energy in terms of both accuracy and physics. The RMDs of mirror pairs are then dependent on the valence nucleon number in the VCS picture. Considering the request of broken isospin symmetry, the linear formula of the valence proton (neutron) number, i.e.,
$\alpha N_{ p}+\beta N_{ n}$ , is selected to obtain the MD formula for mirror nuclei. Besides the satisfactory agreement between theory and evaluation for AME16, the experimental MDs are well reproduced for six new pairs of mirror nuclei in AME20. A number of predictions are then made on the BEs of proton-rich nuclei using the available BE values of relatively neutron-rich nuclei from AME20 for use in future measurements.
Binding energies of proton-rich nuclei determined from their mirror pairs
- Received Date: 2022-07-27
- Available Online: 2023-01-15
Abstract: In addition to the Coulomb displacement energy, the residual differences between the binding energies of mirror nuclei (a pair of nuclei with the same mass number plus interchanged proton and neutron numbers) contribute to the shell effect via the valence scheme in this study. To this end, one linear combining type of valence nucleon number, namely,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: