-
It is well-known that the mass of a nucleus is crucial in various aspects of nuclear physics and astrophysics [1]. Via experimental research, approximately 3200 nuclei have been observed [2], among which the masses of approximately 2500 nuclei have been measured and evaluated in the "Atomic Mass Evaluation" (AME) [3]. In a recent calculation, it was demonstrated that more than 9000 nuclei can be bound [4]. Among the unmeasured nuclei, several are of great importance for nuclear astrophysics, e.g., the heavy neutron-rich nuclei involved in the rapid neutron capture process of nucleosynthesis, which contain more neutrons than the heaviest measured isotope. It is believed that measurement of these nuclei is unlikely in the near future. As a result, a theoretical mass model is the only solution for obtaining their properties.
In early theoretical studies, macroscopic models [5] that neglects microscopic effects were developed. It is not surprising that systematic deviations were observed for nuclei close to shell closures or those with large deformations when applying these models. Currently, global mass models roughly fall into two categories: (1) microscopic mass models with the concept of the mean field, such as the Skyrme or Gogny Hartree-Fock-Bogoliubov (HFB) approaches [6–9] and the relativistic mean field (RMF) model [4, 10–13]; (2) macroscopic-microscopic mass models, such as the finite-range droplet model (FRDM) [14], extended Thomas-Fermi plus Strutinsky integral (ETFSI) model [15], Koura-Tachibana-Uno-Yamada (KTUY) model [16], extended Bethe-Weizsäcker (BW2) formula [17], and Weizsäcker-Skyrme (WS) mass models [18–22]. Based on the Strutinsky energy theorem [23, 24], the binding energy in these macroscopic-microscopic mass models can be decomposed in two parts, smoothing macroscopic energy and oscillating microscopic shell correction energy, representing quantal shell effects. The root-mean-square (rms) deviations between the theoretical calculations and data are a convenient accuracy indicator. For microscopic mass models, an rms deviation of approximately 0.6 MeV is achieved with the HFB approach [6, 7], whereas more than 1 MeV is obtained using RMF models [4, 10–13]. These values are approximately 2.2, 1.4, and 1.1 MeV in the mass tables of the TMA [10], PC-PK1 [11], and DD-MEB [12] density functionals, respectively. It should be noted that not all nonrelativistic approach parameterizations yield small deviations, e.g., 1.4 to 1.9 MeV for the even-even UNEDF mass table [8]. In the case of macroscopic-microscopic models, an rms deviation of approximately 0.7 MeV is typical. With some empirical considerations for residual corrections, an rms deviation of 0.335 MeV was obtained with the third Weizsäcker-Skyrme (WS3) model [20]. In the fourth Weizsäcker-Skyrme (WS4) model, the surface diffuseness correction has been further considered, and the rms deviation has been dramatically reduced to below 0.3 MeV [22]. In the Duflo-Zuker (DZ) mass model [25], the rms deviation can be as small as 0.36 MeV, with which reliable mass predictions can be made. Besides these global models, Garvey-Kelson (GK) relations [26, 27], the isobaric multiplet mass equation (IMME) [28], and residual proton-neutron interactions [29] are used to check the consistency of nuclear mass predictions.
Inspired by the WS4 mass model, where the shell correction energy is evaluated using single particle levels obtained in a Woods-Saxon potential, it is interesting to consider replacing the single particle levels with the those obtained in a relativistic potential. RMF theory has received widespread attention owing to its successful description of numerous nuclear phenomena across the nuclear chart over several decades. The basic advantage of RMF theory is the natural introduction (inclusion) of spin-orbit terms [30]. It was demonstrated that relativistic models give a reasonable description of spin-orbit splitting, whereas non-relativistic Skyrme interactions produce an incorrect trend [31]. Moreover, the origin of the pseudo-spin symmetry of the single particle levels can be explained as relativistic symmetry [32–34]. For these reasons, RMF theory is a good candidate for providing a good single-particle spectrum description. Its successful applications include superheavy nuclei [35–39], pseudospin symmetry [40–42], single-particle resonances [43, 44], hypernuclei [45–51], thermal shape transitions [52–54], and shell correction [55–58].
In this paper, the microscopic energy is based on single-particle levels acquired in RMF theory. The total macroscopic-microscopic energies of even-even nuclei with proton numbers from 8 to 110 are evaluated and compared with available mass data. In Sec. II, the relativistic Weizsäcker framework along with RMF theory are briefly introduced. In Sec. III, calculated nuclear masses are presented and compared. Some possible improvements are also discussed. Finally a summary is given in Sec. IV.
-
In the relativistic Weizsäcker mass model, the total energy of the nucleus is the sum of the macroscopic deformed liquid-drop energy and the microscopic energy
$ \Delta E_{\rm{micro}} $ .$ \begin{aligned}[b] E(A,Z,\beta) =&E_{\rm LD}(A,Z)\prod\limits_{k\geqslant2}(1+b_k\beta_k^2)\\ &+\Delta E_{\rm{micro}}(A,Z,\beta). \end{aligned} $

(1) The macroscopic energy part is the same as that in the WS4 mass model [22] with axial deformation inputs taken from the RMF calculations. A modified Bethe-Weizsäcker mass formula [22, 59] describes the spherical liquid-drop energy
$ E_{\rm LD}(A, Z) $ as$ \begin{aligned}[b] E_{\rm LD}(A,Z) =& a_vA+a_sA^{2/3}+E_c+a_{\rm{sym}}I^2Af_s\\ &+a_{\rm{pair}}A^{-1/3}\delta_{np}+\Delta W, \end{aligned} $

(2) where
$ I=(N-Z)/A=(A-2Z)/A $ is the convenient isospin asymmetry. The first three terms on the right side of Eq. (2) correspond to the volume, surface, and Coulomb energies, respectively. More specifically,$ E_c=a_c Z^2/ A^{1/3}(1- 0.76Z^{-2/3}) $ . In the fourth term, the symmetry energy coefficient$ a_{\rm sym} $ is related to the model parameters$ c_{\rm sym} $ , κ, and ξ via$ a_{\rm{sym}}=c_{\rm{sym}}\left(1-\frac{\kappa}{A^{1/3}} +\xi\frac{2-\left\lvert I\right\rvert }{2+\left\lvert I\right\rvert A}\right) $

(3) whereas the correction factor
$ f_s $ is expressed with an additional model parameter$ \kappa_s $ owing to the surface diffuseness$ f_s=1+\kappa_s \epsilon A^{1/3} $ with$ \epsilon=(I-I_0)^2-I^4 $ , where the isospin asymmetry of the nuclei along the β-stability line is expressed as$ I_0=0.4A/(A+200) $ . The intermediate parameter$ \epsilon $ is also used in the factor with the shell correction energy.$ \delta_{np} $ in the fifth pairing term is expressed as$ \delta_{np} = (2-|I|-I^{2}) 17 / 16 $ for the even-even nuclei discussed here. Finally, the sixth term is the Wigner-like term$ \Delta W=c_W ({\rm e}^{\left\lvert I\right\rvert }-{\rm e}^{-\left\lvert \eta \right\rvert }) $

(4) where η denotes the effective distance from a nucleus to the shell stability line described by
$ N = 1.37Z + 13.5 $ .The contribution of nuclear deformations (namely,
$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ ) to the macroscopic energy is represented by the factors$ \prod\limits_{k=2,4,6}(1+b_k\beta_k^2) $ multiplied to the spherical$ E_{\rm LD}(A,Z) $ . All three$ b_k $ coefficients (namely,$ b_2 $ ,$ b_4 $ , and$ b_6 $ ) depend on the model parameters$ g_1 $ and$ g_2 $ via the relation$ \left({k}/{2}\right)g_1A^{1/3}+\left({k}/{2}\right)^2g_2A^{-1/3} $ . The ground state deformations$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ are extracted from the RMF calculation.Owing to the surface diffuseness, a correction factor
$ f_d =1+\kappa_d\epsilon $ is introduced to the microscopic energy term via$ \Delta E_{\rm{micro}}=c_1 f_d E_{\rm{sh}} $ , where$ E_{\rm{sh}} $ is the shell correction energy. Because the majority of the mirror nuclei of the even-even nuclei with measured mass go beyond the drip-line, the shell energy term of the mirror nuclei$ E'_{\rm{sh}} $ is not introduced here. To obtain the shell correction energy$ E_{\rm{sh}} $ , the order of the Gauss-Hermite polynomials is set to$ p = 2M = 6 $ , and the smoothing parameter is set to$ \gamma=1.3 \hbar \omega_0 $ with$ \hbar \omega_0 = 41 A^{-1/3} \left(1\pm \dfrac{1}{3}\dfrac{N-Z}{A}\right) $ MeV, where the plus (minus) sign holds for neutrons (protons). This parameter setting is consistent with previous relativistic calculations [55, 56, 58] and slightly different from the WS4 settings$ \gamma=1.2 \hbar \omega_0 $ with$ \hbar \omega_0 = 41 A^{-1/3} $ MeV. Further details can be found in the references therein.To summarize this macroscopic-microscopic framework, the spherical liquid-drop energy requires nine parameters
$ a_v $ ,$ a_s $ ,$ a_c $ ,$ c_{\rm{sym}} $ , κ, ξ,$ \kappa_s $ ,$ a_{\rm{pair}} $ , and$ c_W $ , while the deformation factors depend on$ g_1 $ and$ g_2 $ . In contrast, the microscopic energy has two model parameters$ c_1 $ and$ \kappa_d $ . The ground state properties are first obtained by unconstrained axial deformed RMF calculation. Then, the single particle levels are extracted in the evaluation of the shell correction energy. Compared with the WS4 mass model, residual corrections, which typically include the mirror nucleus effect, residual pairing correction, and influence of triaxial (or tetrahedral) deformation, are not considered.For RMF theory, the starting point is the Lagrangian density, which contains the degrees of freedom associated with the nucleon ψ and interacting mesons, including isoscalar scalar σ- and vector ω-mesons, isovector vector ρ-mesons, and the photon A field. The Dirac equation for the nucleon
$ \psi_k $ ,$ \begin{array}{*{20}{l}} [\gamma_\mu({\rm i}\partial^\mu-V^\mu)-(m+S)]\psi_k=0, \end{array} $

(5) can be obtained using the conventional variation principle, where the scalar S and vector potential
$ V^\mu $ are calculated in terms of the densities and currents, which are related back to$ \psi_k $ itself. Consequently, the self-consistent potentials, densities, and currents are obtained iteratively. Further details can be found in Refs. [30, 60–62] and related calculations [58]. Additionally, pairing correlations are considered using the δ-force BCS method with a smooth cutoff factor to simulate the effect of finite range [63, 64].There are numerous ways of fitting model parameters. In this study, the Levenberg-Marquardt method [65, 66] is employed. This algorithm can be regarded as a regularization of the Gauss-Newton method. Every iteration updates a regularization parameter to indirectly control the step size and produce global convergence. This method has been widely used in density functional fitting in RMF theory [67, 68].
-
The density functional for RMF theory is chosen as DD-LZ1 [69]. The spurious shell closure at 58 and 92, which commonly appears in previous density functionals, is partially cured by applying a different form of density-dependent meson-nucleon coupling strength. Taking the isotope
$ ^{244} $ Cm, which is close to$ Z=92 $ , as an example, the proton single-particle levels obtained using different density functionals are demonstrated in Fig. 1. The result obtained using another density functional PC-PK1 [68] is compared side by side. The spurious shell gap at spherical$ Z=92 $ is significantly larger than that at$ Z=82 $ with a ratio of$ 3.7 / 1.6 \approx 2.3 $ for the density functional PC-PK1, whereas such a gap ratio reduces to$ 3.2 /2.2 \approx 1.5 $ for the density functional DD-LZ1. It is well accepted that the sizable structural change of spherical shell gaps affects not only the properties of spheroidal nuclei but also the properties of neighboring deformed nuclei. For example, on the prolate side of this figure, the crossings of the upward levels belonging to$ 1h_{9/2} $ and the downward levels belonging to$ 1i_{13/2} $ move from large deformations for PC-PK1 to small deformations for DD-LZ1. The first crossing is at ($ \beta_2=0.14, \;E_{\rm{s.p.}}=-5.10 $ MeV) for PC-PK1, and the corresponding crossing is located at ($ \beta_2=0.11, E_{\rm{s.p.}}=-5.45 $ MeV) for DD-LZ1. Thus, the ground states of nuclei near$ Z=92 $ , along with gaps enclosed by upward and downward single-particle levels, will be substantially altered. Another treatment for spurious shell closures is related to the Lorentz tensor ρ-field in relativistic Hartree-Fock theory [70] with high computational cost.In the RMF calculations, a large major shell number
$ N_f=20 $ of the harmonic-oscillator basis is adopted to achieve convergence over the nuclear chart. For pairing correlation, the pairing strengths$ V_q $ of the δ pairing force$ V({\boldsymbol{r}})=V_q\delta({\boldsymbol{r}}) $ are taken from the density functional PC-PK1 to be$ -349.5 $ and$ -330.0 $ MeV$ \cdot $ fm$ ^3 $ for neutrons and protons, respectively [68].Taking the well-known prolate deformed nucleus
$ ^{156} $ Dy as an example, the neutron and proton shell correction energies as well as the binding energy as functions of quadrouple deformation$ \beta_2 $ are plotted in Fig. 2. For the shell correction energies, a valley of several MeV in depth is localized near$ \beta_2 \approx 0.2 $ and$ \beta_2 \approx 0.4 $ for neutrons, whereas a flat plain between$ \beta_2 \approx 0.35 $ and$ \beta_2 \approx 0.5 $ can be found for protons. Consequently, the total shell correction energy curve has a minimum at$ \beta_2=0.39 $ , which is similar to the potential energy curve with a close minimum at$ \beta_2=0.35 $ . The (total) shell correction energy$ E_{\rm{sh}} $ , as a quantitative quantity representing shell effects, normally has a minimum near the ground state on the potential energy curve. In the following calculation, the shell correction energies are based on the single-particle levels taken from the ground states obtained in axial deformed RMF theory.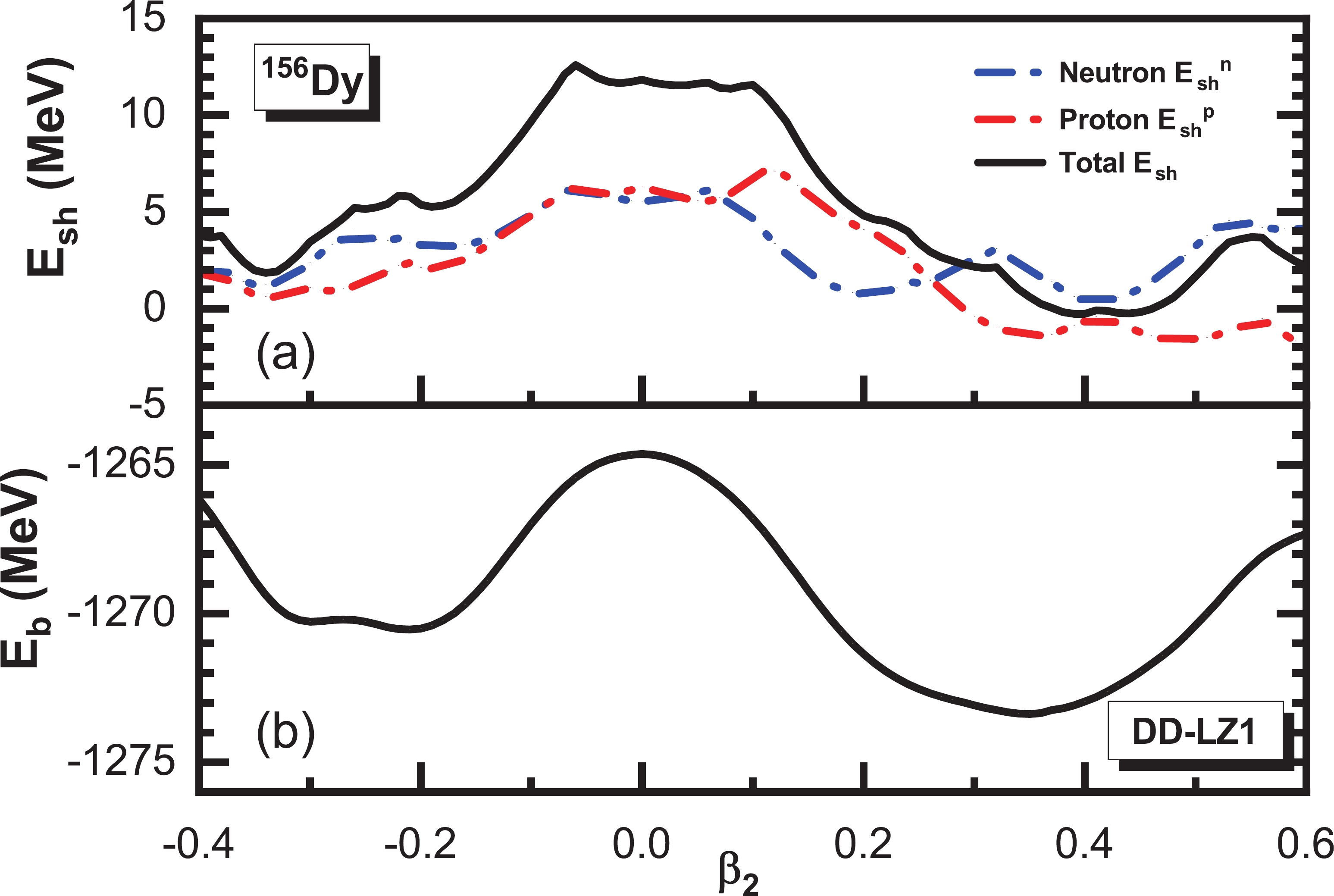
Figure 2. (color online) Neutron, proton, and total shell correction energy (upper) and binding energy (lower) as functions of deformation for the nucleus
$ ^{156} $ Dy, obtained via relativistic mean field calculations using the density functional DD-LZ1 [70].There are 642 even-even (N and
$ Z \geqslant 8 $ ) measured nuclear masses$ M_{\rm{exp}} $ in the AME2020 [3]. The absolute values of the ground state deformations of these nuclei, obtained with axial deformed RMF code, along with the available 252 experimental deformations [71] are shown in Fig. 3 as functions of neutron number. It is clear that the nuclear shapes evolve from one shell closure to another systematically, and the RMF calculation has good consistency with the data. The deformation energy, which is the energy difference between the spherical and predetermined equilibrium shapes, for the current model is also compared with those of WS4 [72] in this figure. It can be seen that the deformation energy and absolute deformation share several common behaviors. The results of the current model are typically larger than those of the WS4 model for light and intermediate nuclei and smaller than those of the WS4 model for heavy nuclei.
Figure 3. (color online) Upper: Absolute ground state deformations of 642 even-even nuclei, obtained via relativistic mean field calculations using the density functional DD-LZ1 [69], along with available experimental data [71]. Lower: Deformation energy in MeV obtained using the current model compared with the corresponding WS4 results.
Next, the neutron (proton) shell correction energy as a function of neutron (proton) number is plotted in Fig. 4. The shell correction energies demonstrate a valley at exactly each magic number. This is also the reason for using shell correction energy as an indicator for magic numbers in Ref. [35]. The neutron shell correction energies exhibit wide spreading, while the proton counterparts are narrow.

Figure 4. (color online) Neutron (proton) shell correction energy as a function of neutron (proton) number for 642 even-even nuclei, obtained via relativistic mean field calculations using the density functional DD-LZ1 [69].
Figure 5 shows the total shell correction energy obtained using WS4 and the current calculation, denoted as WR1. For the WS4 mass model,
$ E_{\rm{sh}} $ is tightly packed with certain valleys at the magic numbers. Consistent with the previous figure (Fig. 4),$ E_{\rm{sh}} $ for light nuclei is sparsely populated, exhibiting a combined dependence on neutron number as well as uncharted proton number. This behavior leads to large spreading for microscopic energy$ \Delta E_{\rm{micro}} $ and is responsible for the large rms deviation between the theoretical mass and experimental data.Table 1 shows the fitted model parameters along with the corresponding rms deviation for WS4 and WR1. The first three parameters
$ a_v $ ,$ a_s $ , and$ a_c $ do not change considerably. The obtained symmetry energy$ c_{\rm{sym}} $ is smaller than the extracted value ($ J \approx $ 30–32 MeV) using various approaches [73–78]. Two parameters are associated with$ E_{\rm{sh}} $ : the first parameter$ c_1 $ decreases, whereas the second,$ \kappa_d $ , increases considerably.$ a_v /{\rm{MeV}}$ 

$ a_s /{\rm{MeV}}$ 

$ a_c /{\rm{MeV}}$ 

$ c_{\rm{sym}} /{\rm{MeV}}$ 

κ ξ $ \kappa_s $ 

WS4 −15.5181 17.4090 0.7092 30.1594 1.5189 1.2230 0.1536 WR1 −15.8743 18.2666 0.7395 24.5632 0.1421 0.4122 −0.0638 $a_{\rm{pair}}/{\rm{MeV}}$ 

$c_W/{\rm{MeV}}$ 

$g_1$ 

$g_2$ 

$c_{1}$ 

$\kappa_d$ 

$\sigma_{\rm rms}/{\rm{MeV}}$ 

WS4 −5.8166 1.0490 0.0104 −0.5069 0.6309 5.0086 0.295 WR1 4.9927 2.1458 −0.0025 −0.0002 0.4347 28.0047 1.353 Table 1. Parameters of the mass models WS4 [22] and WR1.
Although the obtained coefficients for
$ g_1 $ and$ g_2 $ in Table 1 are almost zero, the contribution from the macroscopic part may be reasonable for heavy nuclei because the absolute value of the spherical liquid-drop energy$ E_{\rm LD} $ is large for heavy nuclei. If$ g_1 $ and$ g_2 $ are removed, the corresponding rms deviation increases by 0.437 MeV. Moreover, if we use the deformations from WS4 to constrain the RMF calculation, the rms deviation decreases from 1.353 to 1.307 MeV, whereas the other parameters do not change significantly. This may suggest that the ground state deformations for the Skyrme interaction and DD-LZ1 interaction agree well.The rms deviation σ is defined as
$ \sigma^{2}=\dfrac{1}{N} \sum\bigg[M_{\rm{exp}}^{(i)}- M_{\rm{the}}^{(i)}\bigg]^{2} $ , and the deviation between the theoretical mass$ M_{\rm{the}} $ and experimental data$ M_{\rm{exp}} $ for the FRDM, WS4, and WR1 models are shown in Fig. 6. Compared with FRDM and WS4, the deviation is typically overbinding for open-shell nuclei and underbinding near the magic numbers. Note that the scales of the three mass models are different.If we take the AME2016 version of the experimental data [79], similar parameters are obtained, and the deviations between the theoretical mass and experimental data are generally within 2 MeV for new nuclei appearing in AME2020.
One possible way to reduce the rms deviation is to treat neutron shell correction and proton shell correction separately. It turns out that their coefficients are 0.4298 and 0.4949, respectively, which differ slightly from the original typical
$ c_1 $ , 0.4347. The corresponding rms deviation decreases slightly to 1.327 MeV. This may imply that the neutron single-particle levels are as good (bad) as the proton counterparts.It is clear that the substantial difference between WR4 and WR1 originates from the single-particle levels. Returning to the fitting procedure of DD-LZ1, it is adjusted based on the binding energies and charge radii of ten selected nuclei with spherical symmetry. It should be noted that the binding energy directly obtained in the RMF calculation, which is used for fitting, is not used in our mass model. The single-particle levels incorporated in our model are actually not optimized during the fitting of DD-LZ1. Thus, a density functional in RMF theory offering a better description of single-particle levels is in great need. This is not an easy task, an obvious reason being the lack of abundant experimental single-particle levels.
Another reliable source of single-particle levels may be found from the deformed relativistic Hartree-Bogoliubov theory in the continuum (DRHBc) mass table [13], which recently finished even-even nuclei calculations. The pairing correlation of Bogoliubov transformation is crucial in the description of open-shell nuclei, and it may serve as a remedy for the description of single-particle levels between magic numbers. The density functional of this DRHBc mass table is chosen as PC-PK1, which may suffer spurious shell closures. Nevertheless, the integration of single-particle levels from the even-even DRHBc mass table is worth attempting in the near future.
In exotic nuclei, the Fermi surface is close to the continuum threshold, and owing to pairing correlations, valence nucleons are likely scattered to the single-particle resonant states in the continuum. Thus, extending the current Strutinsky procedure to include the contribution from the single-particle resonant states becomes important for nuclei far from the stability line. It has been demonstrated that Green's function method is an efficient tool for studying single-particle resonant states [43, 44]. In the further development of the relativistic Weizsäcker mass model, this extension may guarantee good extrapolation toward the drip-line.
-
In summary, a relativistic Weizsäcker mass model is proposed based on the single-particle levels and ground state deformations obtained in RMF theory. The density functional of RMF theory is chosen as DD-LZ1, which partially removes spurious shell closures. The shell correction energies exhibit wide spreading compared with the Skyrme values. After fitting, the rms mass deviation is found to be 1.353 MeV. Therefore, a relativistic density functional with more reliable single-particle levels is in great need. For exotic nuclei, an extended Strutinsky procedure that incorporates Green's function method for the resonate states is in progress.
A Global Weizsäcker mass model with relativistic mean field shell correction
- Received Date: 2022-03-03
- Available Online: 2022-10-15
Abstract: A relativistic Weizsäcker mass model is proposed based on the single-particle levels and ground state deformations obtained in axial deformed relativistic mean field theory. The density functional of relativistic mean field theory is chosen as DD-LZ1, which can partially remove spurious shell closures. Compared with the fourth Weizsäcker-Skyrme mass model, the proposed model provides shell correction energies that exhibit wide spreading, and the root-mean-square mass deviation is 1.353 MeV. Further improvement is in progress.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: