-
The physics of low-mass neutron star (NS), the supernovae explosion, and the formation of new elements are governed by the same set of parameters, which predict the properties of finite nuclei, especially the neutron-skin thickness (
$ \Delta R_{np} $ ) [1, 2]. Since the proton is a charged particle, precise measurement of its radius$ R_p $ is possible. However, an accurate determination of the neutron distribution inside a finite nucleus suffers significant uncertainties [3–5]. The exact measurement of neutron radius$ R_n $ and/or neutron-skin thickness$ \Delta {R_{np}}=R_n-R_p $ is helpful to calibrate many theoretical models in terms of the quantity directly related to isospin asymmetry. The symmetry energy J and its slope parameter L are crucial entities to understand the equation of state (EoS). A lot of attempts have been initiated to fix their values and their correlations with other physical quantities [6–11]. For example, the strong correlations of neutron-skin thickness in 208Pb nucleus with various neutron star properties within the relativistic mean-field (RMF) models have been described either in terms of the coupling of the isovector–vector ρ- meson with the nucleons [12] and/or the cross-coupling of isoscalar–vector ω- with the isovector–vector ρ- mesons [13–15].The pressure of the neutron-rich matter normally drives the surface tension in the atomic nucleus and plays the same role against gravity in a neutron star. Even though their magnitudes differ on a large scale, they share a common origin, which is sensitive to the equation of state (EoS). Precise measurement of the neutron radius
$ R_n $ is supposed to be possible using the parity-violating weak neutral interaction at Thomas Jefferson National Accelerator Facility (JLab) termed as the Lead Radius Experiment (PREX) [16, 17]. Based on this principle, the PREX-I result for$ R_n $ of 208Pb is reported in Ref. [4] with$ R_n=5.78^{+0.16}_{-0.18} $ fm and a neutron-skin thickness of$ \Delta{R_{np}}= R_n-R_p = 0.33^{+0.16}_{-0.18} $ fm. To reduce the uncertainty further, the PREX-2 result was published with the neutron-skin thickness as$ \Delta{R_{np}=0.283\pm{0.071}} $ fm [1] and the point neutron distribution radius$ R_n=5.727\pm{0.071} $ fm (knowing the precise value of the point proton distribution radius as$ R_p=5.444 $ fm [18, 19] with the corresponding charge radius$ R_{ch}=5.501 $ fm [20]). The hadron scattering data by Kłos et al. [21] and Zenihiro et al. [22] are also in competition with the recent PREX-2 range. Also, recently, a new method has been introduced by Kurasawa et al. [23] and Naito et al. [24] to extract the neutron distribution radius$ R_n $ even using the normal electron scattering data, while its feasibility is still under discussion. All these recent precise measurements of$ R_n $ (or$ \Delta R_{np} $ ) allow the refitting of the relevant parameters with the theoretical models to reproduce the properties of finite nuclei and in parallel to describe the properties of the neutron star.The PREX-2 measurements of the neutron-skin thickness of 208Pb [1] with
$ \sim $ 1% uncertainty allows us to revisit the isospin-dependent interaction terms of the existing nuclear models. In this direction, Reed et al. [2] employed the property of strong correlation of neutron-skin thickness$ \Delta{R}_{np} $ with the slope parameter of symmetry energy L and constrained its value to$ L = 106 \pm 37 $ MeV [9, 10, 25, 26]. Also, the symmetry energy J is fixed to be in the range$ J=38.1\pm{4.7} $ MeV by using specific sets of relativistic mean-field (RMF) parametrizations. These values of L and J are surely larger than the presently settled values obtained either from theoretical models or from various experimental measurements [27–34]. The precise measurement of the neutron-skin thickness of 208Pb by Adhikari et al. [1] and the new constraint on nuclear matter observables from Reed et al. [2] motivate us to revisit the recent RMF parameter sets, namely, G3 and IOPB-I, by tuning the essential couplings that (rarely) affect the global properties of infinite nuclear matter and finite nuclei. These two forces are reasonably good at reproducing the experimental data for finite nuclei, including superheavy nuclei and highly isospin-asymmetric systems including neutron stars. These forces are also able to generate the constraint associated with the gravitational waves strain in binary neutron star merger GW170817 events [35–37] and references therein. Here we have focused on two couplings of the RMF Lagrangian, namely,$ \Lambda_{\omega} $ and$ g_{\rho} $ , and tuned to reproduce the recent experimental$ R_n $ for 208Pb without affecting the other bulk properties of finite nuclei and infinite nuclear matter. The detailed procedure is highlighted in the subsequent sections.The paper is arranged as follows: after a brief introduction in Section I, a short description of the relativistic mean-field formalism is given in Section II. Since RMF is already a standard theory, we only outline the essential ingredients needed for these discussions. Section III describes the fitting procedure of the parameter sets. In Section IV, we discuss our results and compare them with the empirical and/or experimental data. Finally, concluding remarks are given in Section V.
-
The nonlinear relativistic mean-field Lagrangian density is constructed by the interaction of nucleons with the well-known
$ \sigma- $ ,$ \omega- $ ,$ \rho- $ ,$ \delta- $ and photon fields, generated by$ \sigma- $ ,$ \omega- $ ,$ \rho- $ ,$ \delta- $ mesons and protons, respectively. The self and cross-couplings among the mesons are also included in the extended relativistic mean-field (E-RMF) theory, which has evolved in the framework of effective field theory motivated by naive dimensional analysis (NDA) and the naturalness concept. Taking into account this E-RMF, NDA, and naturalness criteria, the G3 and IOPB-I force parameters are designed, and the E-RMF Lagrangian density is written as [36–41]:$ \begin{aligned}[b] {\cal{E}}({r})=& \sum\limits_\alpha \varphi_\alpha^\dagger({r}) \Bigg\{ -{\rm i} {\bf{\alpha}} \cdot {\bf{\nabla}} + \beta \left[M - \Phi (r) - \tau_3 D(r)\right]+ W({r})+ \frac{1}{2}\tau_3 R({r}) \frac{1+\tau_3}{2} A ({r}) - \frac{{\rm i} \beta{\bf{\alpha}}}{2M} \cdot \left (f_\omega {\bf{\nabla}} W({r}) + \frac{1}{2}f_\rho\tau_3 {\bf{\nabla}} R({r})+\lambda {\bf{\nabla}} A \right)\\ & +\frac{1}{2 M^2} (\beta_\sigma+\beta_\omega \tau_3)\Delta A \Bigg\} \varphi_\alpha (r) + \left ( \frac{1}{2} + \frac{\kappa_3}{3!}\frac{\Phi({r})}{M} + \frac{\kappa_4}{4!}\frac{\Phi^2({r})}{M^2}\right ) \frac{m_s^2}{g_s^2} \Phi^2({r}) - \frac{\zeta_0}{4!} \frac{1}{ g_\omega^2 } W^4 ({r}) + \frac{1}{2g_s^2}\left( 1 + \alpha_1\frac{\Phi({r})}{M}\right) \left( {\bf{\nabla}}\Phi({r})\right)^2 \\ & - \frac{1}{2g_\omega^2}\left( 1 +\alpha_2\frac{\Phi({r})}{M}\right) \left( {\bf{\nabla}} W({r}) \right)^2 - \frac{1}{2}\left(1 + \eta_1 \frac{\Phi({r})}{M} + \frac{\eta_2}{2} \frac{\Phi^2 ({r})}{M^2} \right) \frac{m_\omega^2}{g_\omega^2} W^2 ({r}) -\frac{1}{2e^2} \left( {\bf{\nabla}} A({r})\right)^2 - \frac{1}{2g_\rho^2} \left( {\bf{\nabla}} R({r})\right)^2 - \frac{1}{2} \left( 1 + \eta_\rho \frac{\Phi({r})}{M} \right) \\ &\times \frac{m_\rho^2}{g_\rho^2} R^2({r}) - \frac{\eta_{2\rho}}{4 M^2}\frac{{m_\rho}^2}{{g_\rho}^2}\left(R^{2}(r)\times W^{2}(r)\right) +\frac{1}{2 g_{\delta}^{2}}\left( {\bf{\nabla}} D({r})\right)^2 +\frac{1}{2}\frac{{m_{\delta}}^2}{g_{\delta}^{2}}\left(D^{2}(r)\right) - \frac{1}{2 e^2}({\bf{\nabla}}A)^2+\frac{1}{3 g_\gamma g_\omega} A \Delta W +\frac{1}{g_\gamma g_\rho}A\Delta R.\; \end{aligned} $ 
(1) Here
$ \Phi = g_s\sigma $ ,$ W = g_\omega \omega $ , R = g$ _\rho\vec{\rho} $ and$ D=g_\delta\delta $ are the redefined fields, with their coupling constants$ g_\sigma $ ,$ g_\omega $ ,$ g_\rho $ and$ g_\delta $ and their masses$ m_\sigma $ ,$ m_\omega $ ,$ m_\rho $ and$ m_\delta $ , respectively, for σ, ω, ρ, and δ mesons, and$ \frac{e^2}{4\pi} $ is the photon coupling constant. By including the self and cross-couplings in the model, it behaves as a flexible model to produce the various properties associated with the finite nuclei as well as neutron stars. It is also known that the cross-couplings regulate the systematic behaviour of the equation of state of pure neutron matter. The effects of various self and cross-couplings are explained further in Section III. From the effective-RMF energy density [Eq. (1)], a set of coupled differential equations for finite nuclei (equation of motion) and the expression for pressure and energy (equation of state) for infinite nuclear matter are obtained using the Euler–Lagrange equation and the energy–momentum tensor, respectively [37]. The scalar and vector densities are$ \rho_s(r)=\sum\limits_\alpha \varphi_\alpha^\dagger({r})\beta\varphi_\alpha({r}), $

(2) $ \rho_v(r)=\sum\limits_\alpha \varphi_\alpha^\dagger({r})\varphi_\alpha({r}) , $

(3) respectively. A detailed numerical evaluation is available in Refs. [13, 35, 37, 42]. The terms having
$ g_\gamma, \; \lambda, \; \beta_\sigma $ and$ \beta_\omega $ in Eq. (1) are responsible for the effects associated to the electromagnetic structure of the pion and nucleon [39].To replicate the magnetic moments of the nuclei, we must obtain the constant λ which is defined by$ \lambda=\frac{1}{2}\lambda_p (1+\tau_3)+\frac{1}{2}\lambda_n (1-\tau_3) $

(4) with
$ \lambda_p=1.793 $ and$ \lambda_n=-1.913 $ the anomalous magnetic moments for the proton and neutron, respectively [39]. The parameters$ \beta_\sigma $ and$ \beta_\omega $ , as well as$ f_\rho $ , were then chosen to match the nucleon's observed charge radii. -
In open-shell nuclei, the pairing correlation plays a crucial role [43, 44]. When the pairing interaction
$ v_{\rm pair} $ includes non-zero matrix elements, the nucleons pairs are invariant under time reversal symmetry:$ \langle \alpha_2 \overline{\alpha_2} \vert v_{\rm pair}\vert\alpha_1 \overline{\alpha_1}\rangle = -G , $

(5) where
$ \alpha=\vert nljm\rangle $ and$ \overline{\alpha}=\vert nlj-m\rangle $ (with$ G>0 $ and$ m>0 $ ) are the quantum states. Here a constant force method is used within the BCS approach [45–47], where a constant value of G for pairings of the active pair shell, the seniority type interaction is employed. The constant force G is connected with the pairing energy$E_{\rm pair}$ as:$ E_{\rm pair}= -{G}\left[\sum\limits_{i>0}{u_iv_i}\right]^2, $

(6) where
$ u_i $ and$ v_i $ are termed the occupation probabilities:$ u_i^2= 1 - v_i^2. $

(7) The variation with respect to the occupation numbers
$ v_i^2 $ provides the BCS equation$ 2\epsilon_i u_iv_i - \Delta (u_i^2 - v_i^2) = 0, $

(8) with
$ \Delta = {G}\sum_{i>0}{u_iv_i} $ . This is the well known BCS equation and the densities are contained within the occupation number$ n_i $ ,$ n_i = v_i^2 = \frac{1}{2}\left[ 1 - \frac{\epsilon_i - \lambda} {\sqrt{ (\epsilon_i - \lambda)^2 + \Delta^2}} \right], $

(9) where λ is the chemical potential and
$ \epsilon_i $ is the single-particle energy of the nucleus. The values of G ($ G_n $ for neutron and$ G_p $ for proton) are fixed by reproducing the binding energies and charge radius of 120Sn and 160Sn within the one harmonic oscillator shell above and below the Fermi level. Further details can be found in references [13, 42, 48]. -
The inception of the relativistic mean-field model was in 1955 when it was proposed as a classical field theory with the relativistic formulation of nuclear force [49, 50]. Later on, a proper mathematical formulation was given to the model by Miller and Green [51] and Brockmann [52], assuming a scalar and vector interaction potential. Finally, Walecka [53], Serot and collaborators [54, 55] extended the formalism to the various domains of finite and infinite nuclear systems. Each extension in the model shows that every interaction corresponds to a particular property of the nuclear potential. For example, the
$ \sigma- $ meson is mainly responsible for the strong attraction at the intermediate range of the nuclear force, but the self-interaction of this scalar meson produces a weak repulsion at long-range [56, 57]. Furthermore, the self-interaction of the$ \sigma- $ meson allows the constraint of the incompressibility of nuclear matter at nuclear saturation to the updated empirical range$ K_{\infty} = 240 \pm 20 $ MeV [58–60]. The$ \omega- $ meson is responsible for the strong hard-core repulsion of the nuclear potential and its self-interaction generates attraction at a concise range and makes the nuclear equation of state (EoS) softer [45, 61, 62]. Detailed discussion on the influence of various interactions can be found in Refs. [42, 57].At present, it is clear that each interaction in the Lagrangian density leads to a physical property, of either the finite nuclear and/or infinite nuclear matter system. Thus, effective field theory with the NDA and naturalness approach added to E-RMF formalism parallels all possible self- and cross-couplings in the interactions. In this way, the G1 and G2 parameter sets are proposed in Refs. [38, 39]. In the G1 parameter set [39], the considered Lagrangian density has only the contributions of the isoscalar–isovector cross-coupling, which has a greater implication for the neutron radius and equation of state (EoS) of asymmetric nuclear matter. Similarly, the G2 parameter set [39], based on the (E-RMF) approach, is very successful in reproducing the NM properties including the structure of NS as well as of finite nuclei. However, the
$ \delta- $ meson and cross-coupling of ω and$ \rho- $ are not considered here, which support the study of nuclear and neutron matter properties including neutron stars. More details can be found in Ref. [15]. Further, the effects of the$ \delta- $ meson on the nuclear potential are realised in [63, 64]. The$ \delta- $ meson interaction along with the couplings of G1 and G2 is the product of the G3 set [36]. Another version of the parameter set known as IOPB-I is designed specially to successfully describe the nuclear matter properties at sub- and supra-saturation density [37].The fitting of parameters for the nuclear energy functional is a delicate procedure because of the resultant of the kinetic and potential energies and the vector and scalar fields. There are various correlations between the different parameters and various observable for finite and infinite nuclear matter systems. Thus, one assumes that it is impossible to find a physically meaningful fit by keeping nearly all the parameters fixed and changing only a few of them. However, this is not the case in the present context. This is because we are providing the readjustment and/or reconstruction of the recently developed parameter sets by adopting the recent constraint from PREX-2 measurements. In other words, we are only fine-tuning the parameter sets, which were not properly tuned for the neutron radius of the finite nucleus due to inadequate information while designing.
Currently, the PREX-2 results with precise measurement of the neutron radius of 208Pb allow us to revisit our successfully fitted parameters, namely, G3 and IOPB-I. It is well-known that the existence of strong correlations of neutron-skin thickness in the 208Pb nucleus with various isospin-dependent properties of infinite nuclear matter and neutron stars build upon the isovector–vector ρ- and isoscalar–vector ω-meson within the relativistic mean-field (RMF) models [12–15, 63, 64]. In other words, the isospin-dependent quantities of finite and/or infinite nuclear matter, including neutron stars will be described either in terms of the coupling of the isovector–vector ρ- meson with nucleons [12, 63, 64] and/or the cross-coupling of isoscalar–vector ω- with isovector–vector ρ- mesons [13–15]. It has also been verified that the changes in the cross-coupling of ω- with ρ- meson hardly affect the bulk nuclear properties of finite nuclei except for the isospin-dependent quantities, for example, neutron radius. Hence, it is crucial and also interesting to constrain the recently developed G3 and IOPB-I parameter sets with the PREX-2 data for neutron-skin thickness
$ \Delta R_{np} $ . In other words, the G3 and IOPB-I parameter sets are readjusted by considering the PREX-2 data and applying these modified parameterizations for the structural analysis of finite nuclei and the properties of infinite nuclear matter, including neutron stars. -
The cross-coupling of ρ-mesons with
$ \sigma- $ and$ \omega- $ mesons allows for varying neutron-skin thickness in a heavy mass nucleus like 208Pb [14, 65, 66]. This coupling$ \Lambda_{\omega} $ also matters a lot for the giant resonances, like monopole and quadrupole [67]. The density dependence of the symmetry energy can be changed regularly by modifying the$ \omega\text{–}\rho $ coupling$ \Lambda_{\omega} $ , without hampering the EoS of symmetric matter. Higher values of$ \Lambda_{\omega} $ represent the soft nature density dependences of the symmetry energy and vice versa. Again the excitation energy used in studying the giant resonances is higher than the softness of symmetry energy [67]. The ρ-meson coupling takes care of the neutron–proton asymmetry in the system. Therefore, the apparent choice for the minimal tuning of parameters is$ \Lambda_{\omega} $ and$ g_{\rho} $ . For example, the binding energy of an asymmetric system increases with the$ \Lambda_{\omega} $ coupling, whereas$ g_{\rho} $ decreases the binding energy. On the other hand, the neutron distribution radius$ R_n $ decreases with the increase of$ \Lambda_{\omega} $ , while$ R_n $ remains almost unchanged with$ g_{\rho} $ . Hence, the fine-tuning of these two parameters is needed to constrain the neutron-skin thickness of 208Pb using the recent PREX-2 observation data. It is worth mentioning that here we have considered the recently fitted parameters G3 and IOPB-I, which are constrained based on various empirical nuclear matter values and experimental data for finite nuclei. This implies that the tuning of these two parameters, namely,$ \Lambda_{\omega} $ and$ g_{\rho} $ , is acceptable for satisfying the experimental constraint on neutron-skin thickness without substantial change in other bulk properties of finite nuclei. Table 1 lists the original (O) and modified (M) values of the G3 and IOPB-I parameter sets. Note that only the values of$ \Lambda_{\omega} $ and$ g_{\rho} $ are revised, and the effects on various properties of finite and infinite nuclear systems are analysed.Parameter G3(O) G3(M) IOPB-I(O) IOPB-I(M) $ m_{s}/M $ 

0.559 0.559 0.533 0.533 $ m_{\omega}/M $ 

0.832 0.832 0.833 0.833 $ m_{\rho}/M $ 

0.820 0.820 0.812 0.812 $ m_{\delta}/M $ 

1.043 1.043 0.0 0.0 $ g_{s}/4 \pi $ 

0.782 0.782 0.827 0.827 $ g_{\omega}/4\pi $ 

0.923 0.923 1.062 1.062 $ g_{\rho}/4 \pi $ 

0.962 0.872 0.885 0.803 $ g_{\delta}/4 \pi $ 

0.160 0.160 0.0 0.0 $ k_{3} $ 

2.606 2.606 1.496 1.496 $ k_{4} $ 

1.694 1.694 −2.932 −2.932 $ \zeta_{0} $ 

1.010 1.010 3.103 3.103 $ \eta_{1} $ 

0.424 0.424 0.0 0.0 $ \eta_{2} $ 

0.114 0.114 0.0 0.0 $ \eta_{\rho} $ 

0.645 0.645 0.0 0.0 $ \Lambda_{\omega} $ 

0.038 0.021 0.024 0.015 $ \alpha_{1} $ 

2.000 2.000 0.0 0.0 $ \alpha_{2} $ 

−1.468 −1.468 0.0 0.0 $ f_\omega/4 $ 

0.220 0.220 0.0 0.0 $ f_\rho/4 $ 

1.239 1.239 0.0 0.0 $ \beta_\sigma $ 

−0.087 −0.087 0.0 0.0 $ \beta_\omega $ 

−0.484 −0.484 0.0 0.0 Table 1. Masses and coupling constants for original G3(O) [36] and IOPB-I(O) [37] and their modified sets G3(M) and IOPB-I(M). The mass of nucleon M is 939 MeV. The dimension of
$ k_3 $ is fm$ ^{-1} $ , and all other coupling constants are dimensionless. (O) and (M) stand for original and modified parametrizations, respectively.The effects of
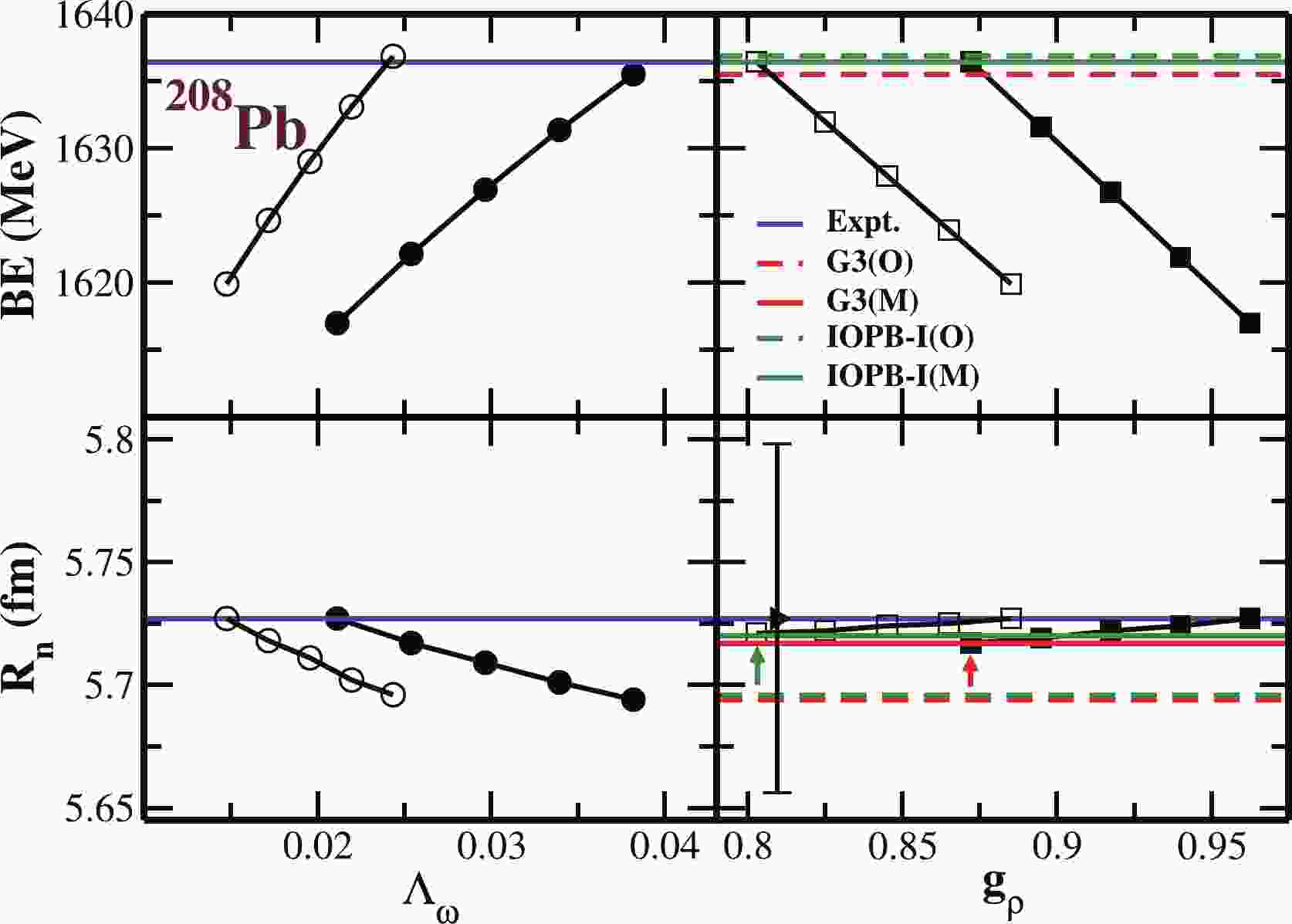
$ \Lambda_{\omega} $ and$ g_{\rho} $ on binding energy and$ R_n $ with$ \Lambda_{\omega} $ and$ g_{\rho} $ are shown in Fig. 1. We calculate the binding energy (BE) and radius$ R_n $ with variation of$ \Lambda_{\omega} $ from 0.038 to 0.021 without changing$ g_{\rho} $ for the G3 parameter set. As stated above, we find the increase of binding energy with$ \Lambda_{\omega} $ . Then, we change the values of$ g_{\rho} $ from 12.094 to 10.961 to bring back the binding energy, which is a standard procedure for tuning the parameter sets. It is worth mentioning that the binding energy decreases with the increase of$ g_{\rho} $ , without affecting$ R_n $ . The experimental binding energy (blue line) [68] is shown for comparison. By fixing the experimental values of BE and$ R_n $ , we calibrate the$ \Lambda_{\omega} $ and$ g_{\rho} $ combination as 0.021 and 10.961, which is termed as G3(M) parameter set, as tabulated in Table 1. We follow the same procedure for the IOPB-I parameter set and found the modified values of$ \Lambda_{\omega} $ and$ g_{\rho} $ are 0.014 and 10.090 respectively. The results for binding energy and neutron distribution radius are also shown in Fig. 1.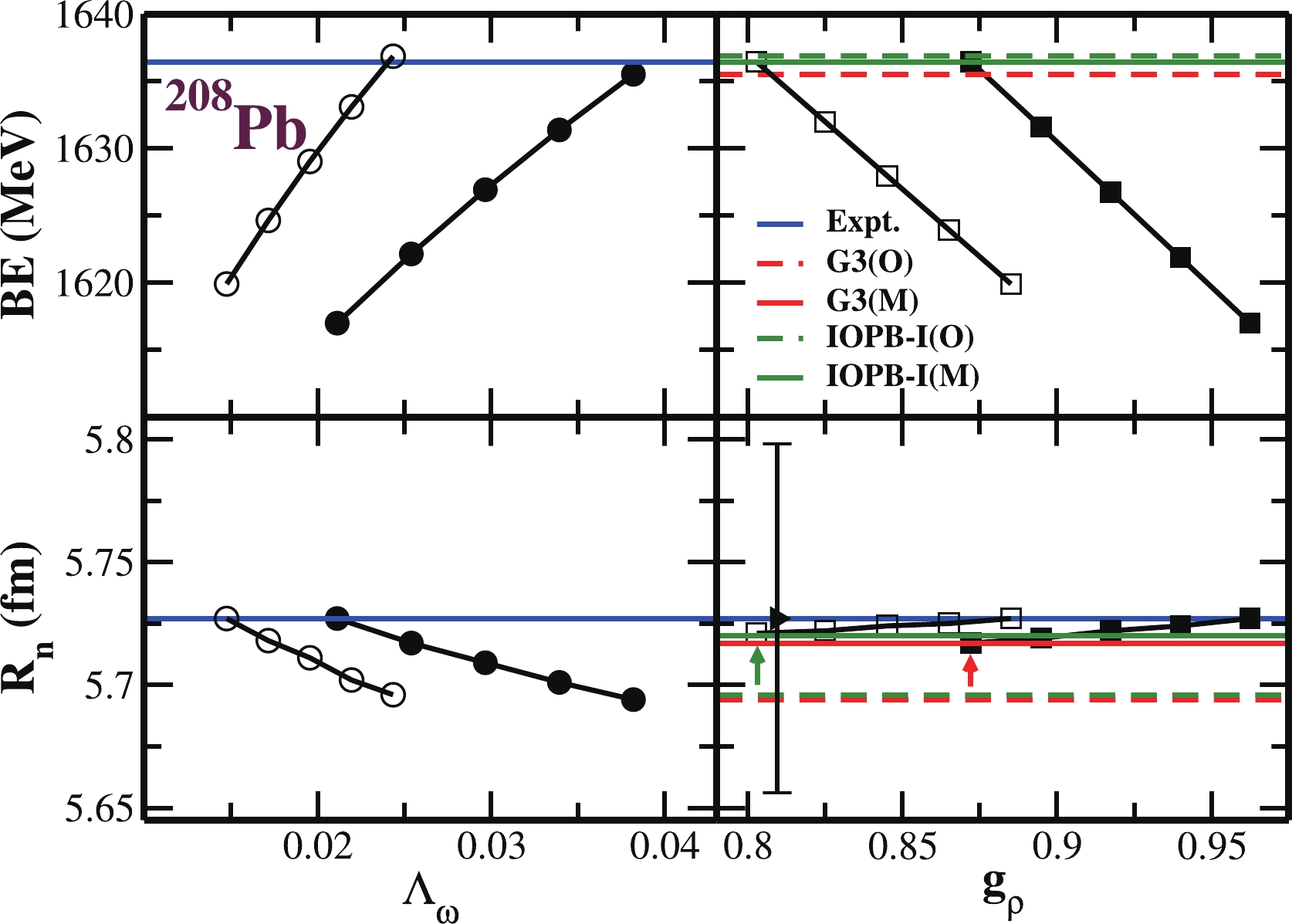
Figure 1. (color online) Binding energy (upper panels) in MeV and neutron distribution radius
$ R_n $ (lower panels) in fm with original G3(O) (dashed red) and G3(M) (solid red) parameter sets for 208Pb as a function of ω–ρ field coupling constant$ \Lambda_{\omega} $ . Similarly, for ρ-meson coupling$ g_{\rho} $ , IOPB-I(O) and IOPB-I(M) are in dashed green and solid green lines, respectively. The changes of BE (circle) and$ R_n $ (square) correspond to both G3(M) (solid) and IOPB-I(M) (empty), respectively. The experimental data with error bars [1,68] are given for comparison. The single arrow is for the better visibility of$ R_n $ . -
After constraining the values of
$ \Lambda_{\omega} $ and$ g_{\rho} $ to the recent PREX-2 data of$ R_n $ and the binding energy for 208Pb, we calculate the bulk properties of even–even spherical nuclei. The calculated binding energy, root-mean-square (rms) neutron and charge radius for a few well-known nuclei are listed in Table 2 along with the experimental data [1, 22, 68–74]. Here we have used the traditional formula$ R_{ch} = \sqrt{R_{p}^2 + 0.64} $ as the G3 and IOPB-I forces have already included the spin–orbit interaction self-consistently [55, 75-77]. In both original and modified G3 and IOPB-I, the constants$ \beta_\sigma $ and$ \beta_\omega $ , as well as$ f_\rho $ , are responsible for the determination of charge radii (see Sec. II). Also, the spin–orbit interaction contributes to charge radius without coupling as explained in Ref. [78]. This originates from the magnetic form factors of nucleons. Here the charge radius of the nucleus ($ R_{ch} $ ) comes from the electromagnetic size of the nucleon and can be expressed as$ R_{ch} = \sqrt{R_{p}^2 + r_{p}^2} $ , where$ R_{p} $ is the point proton radius and$ r_{p} $ represents the charge radius of a single proton [78]. At the time of construction of the original G3 and IOPB-I parameters [36, 37], we have taken the available value of$ R_n $ , however a more precise value has arisen recently by the Parity violating experiment by the PREX collaboration, which needs to be included by modifying the original G3 and IOPB-I forces. Although the original G3 and IOPB-I forces produce the neutron distribution radius$ R_n $ within the range of error bars, we are considering G3(M) and IOPB-I(M) taking the more precise value of$ R_n $ . However in some cases, there are some uncertainties; for example, in the case of$ ^{116,132} $ Sn, the value situates outside the precise range. Hence it is crucial to test the whole nuclear chart using these modified parameter sets.Nucleus Force BE $ R_{ch} $ 

$ R_{n} $ 

$ R_p $ 

16O G3(M) 128.59 2.706 2.613 2.641 G3(O) 128.59 2.706 2.612 2.641 IOPB-I(M) 127.63 2.704 2.575 2.602 IOPB-I(O) 127.63 2.705 2.575 2.602 Expt. 127.62 2.699 — 2.577 40Ca G3(M) 342.46 3.458 3.351 3.401 G3(O) 342.46 3.458 3.351 3.401 IOPB-I(M) 343.07 3.457 3.322 3.371 IOPB-I(O) 343.07 3.458 3.321 3.371 Expt. 342.05 3.477 $ 3.306_{-1.0}^{+0.05} $ [69,72]

3.383 48Ca G3(M) 416.99 3.461 3.621 3.434 G3(O) 416.18 3.466 3.613 3.439 IOPB-I(M) 415.04 3.436 3.593 3.377 IOPB-I(O) 414.62 3.441 3.583 3.381 Expt. 415.96 3.477 $ 3.499_{-0.05}^{+0.05} $ [69,72]

3.383 90Zr G3(M) 783.25 4.271 4.319 4.239 G3(O) 782.91 4.275 4.312 4.243 IOPB-I(M) 782.25 4.249 4.297 4.194 IOPB-I(O) 782.23 4.253 4.289 4.197 Expt. 783.81 4.269 $ 4.283_{-0.02}^{+0.02} $ [69,72]

4.193 116Sn G3(M) 985.67 4.630 4.715 4.587 G3(O) 985.67 4.634 4.704 4.591 IOPB-I(M) 986.65 4.615 4.701 4.547 IOPB-I(O) 986.85 4.621 4.688 4.552 Expt. 988.66 4.625 $ 4.692_{-0.05}^{+0.05} $ [70]

4.555 132Sn G3(M) 1105.43 4.725 4.970 4.699 G3(O) 1103.54 4.731 4.948 4.705 IOPB-I(M) 1103.06 4.699 4.965 4.648 IOPB-I(O) 1102.42 4.705 4.941 4.654 Expt. 1102.72 4.709 $ 4.880_{-0.04}^{+0.04} $ [70]

4.641 208Pb G3(M) 1636.43 5.567 5.717 5.510 G3(O) 1635.51 5.541 5.694 5.514 IOPB-I(M) 1636.42 5.516 5.721 5.470 IOPB-I(O) 1636.87 5.521 5.696 5.474 Expt. 1636.43 5.501 $ 5.727_{-0.071}^{+0.071} $ [1]

5.444 304120 G3(M) 2131.41 6.336 6.487 6.313 G3(O) 2131.02 6.338 6.460 6.314 IOPB-I(M) 2134.37 6.327 6.507 6.286 IOPB-I(O) 2135.71 6.329 6.478 6.287 Expt. — — — — Table 2. Binding energy (BE in MeV) and neutron distribution radius (
$ R_n $ in fm) for selected spherical nuclei with G3(M) and IOPB-I(M) parameter sets. The predictions for G3(O) and IOPB-I(O) are listed for comparison.The charge radius$ R_{ch} $ is obtained by adopting the finite size effect of the nucleon, i.e.,$ R_{ch} = \sqrt{R_{p}^2 + 0.64} $ fm. Experimental data are taken from Refs. [1, 22, 69–73] and references therein. See text for more details.As expected, the BE and
$ R_n $ remain unchanged for symmetric nuclei where the number of neutrons is equal to the number of protons, i.e., N =Z nuclei, for example, 16O and 40Ca. The neutron distribution radius changes moderately for all other nuclei, with a minute influence on the binding energy. To examine the applicability of these two modified parameters within the relativistic mean-field approach, we calculate the binding energies and charge radii of 195 even–even nuclei within the range 8 $ \leq Z \leq $ 92 with 14$ \leq A \leq $ 232. The differences between the calculated values and the experimental data for binding energy$ \Delta E $ as a function of mass number is displayed in Fig. 2. The red and green colours are assigned for the G3(M) and IOPB-I(M) parameter sets, respectively. From the figure, one notices the deviations in binding energies for most of the considered nuclei are broadly reproduced within$ \pm 3 $ MeV, barring a few exceptions. The overall rms deviation in binding energy$ \Delta E = BE_{\rm expt.} - BE_{\rm cal} $ for G3(M), and IOPB-I(M) are 3.751973 and 3.5698173 MeV, respectively. These values are consistent with the original version of the parameter sets and a little overestimate the corresponding rms deviations obtained with well-calibrated non-relativistic effective interactions [79–83]. To avoid similarity we have not given the figure with original sets, which can be found in Fig. 1 of Ref. [36]. This is because the region of preference and the numbers of nuclei considered in the present studies are in the intermediate-mass region of the nuclear chart, where the nuclei are deformed in their ground state and our present calculation is limited to spherical coordinates. For describing the ground-state properties of open-shell nuclei, in these calculations, the pairing correlations are treated at the quasi-BCS level, which is a well-known procedure adopted in various studies [13, 36, 37, 42]. Similarly, the rms deviation ($ \delta r $ ) for charge radii for these nuclei are calculated for the available experimental data and found to be 0.023278 for G3(M) and 0.021237 for IOPB-I (M).The radial dependence of the density distributions for protons and neutrons for 48Ca and 208Pb are displayed in the left and right panels of Fig. 3, respectively. The red and green colours are assigned for G3 and IOPB-I forces respectively. The choice of the density distributions of asymmetric nuclei is due to analysis of the effect of coupling constants
$ \Lambda_{\omega} $ and$ g_{\rho} $ , which are crucial for the isospin asymmetry of the system. The corresponding experimental charge density [84] is displayed for comparison. From the figure, one notices that the agreement between the calculation and the charge density from experiments is reasonably good and exactly overlap at the surface. In the interior of the nucleus, the quantal oscillations shown by the proton densities are, in general, well averaged, which may further be correlated with the shell effect.
Figure 3. (color online) Proton (p) and neutron (n) density distributions of 48Ca and 208Pb for the original G3(O) and IOPB-I(O) and modified G3(M) and IOPB-I(M) parameter sets, compared with experimental data [84].
In the preceding paragraph, we have given predictions of G3(M) and IOPB-I(M) within relativistic mean-field theory for the ground-state energies and radii which agree well with experimental values. Hence, it is interesting to examine the isotopic shift in Pb-nuclei. The isotopic shift of charge radii is defined as
$\Delta R_{ch}^2 = R_{ch}^2 (^A{\rm Pb}) - R_{ch}^2 (^{208}{\rm Pb})$ . The calculated isotopic shift for G3(M), and IOPB-I(M) are displayed in Fig. 4 along with the original G3(O) and IOPB-I(O) predictions. The comparison is also made for the semi-realistic effective interaction M3Y-P6a parameter set [85]. From the figure, both parameter sets lie quite close to the experimental values [86] and the shift at N = 126 is reasonably well reproduced. Comparing both parameter sets with the experimental data, one can find that G3 (original and modified) has a relatively better match to experimental data than IOPB-I. Furthermore, comparing the original and modified parameter sets for both G3 and IOPB-I cases, we did not find any substantial difference in the isotopic shift of Pb nuclei. As the odd–even staggering effect is taken into account by H. Nakada et al., the predictions with M3Y-P6a parameter data follows a slightly zig-zag pattern, which is absent in the case of original and modified versions of the G3 and IOPB-I sets. Here in the Pb- isotopic series, in the case of odd-N nuclei, the neutron pairing density is reduced, which directly affects the proton density and as result, the charge radius decreases [87]. More information regarding the isotopic shift can be found in our previous work Ref. [88] and in the works of Perera et al. [89]. The development of this shift for a magic neutron over an isotopic chain can be correlated with the occupation of the neutron single-particle energy levels [90, 91] and is discussed in the subsequent paragraph.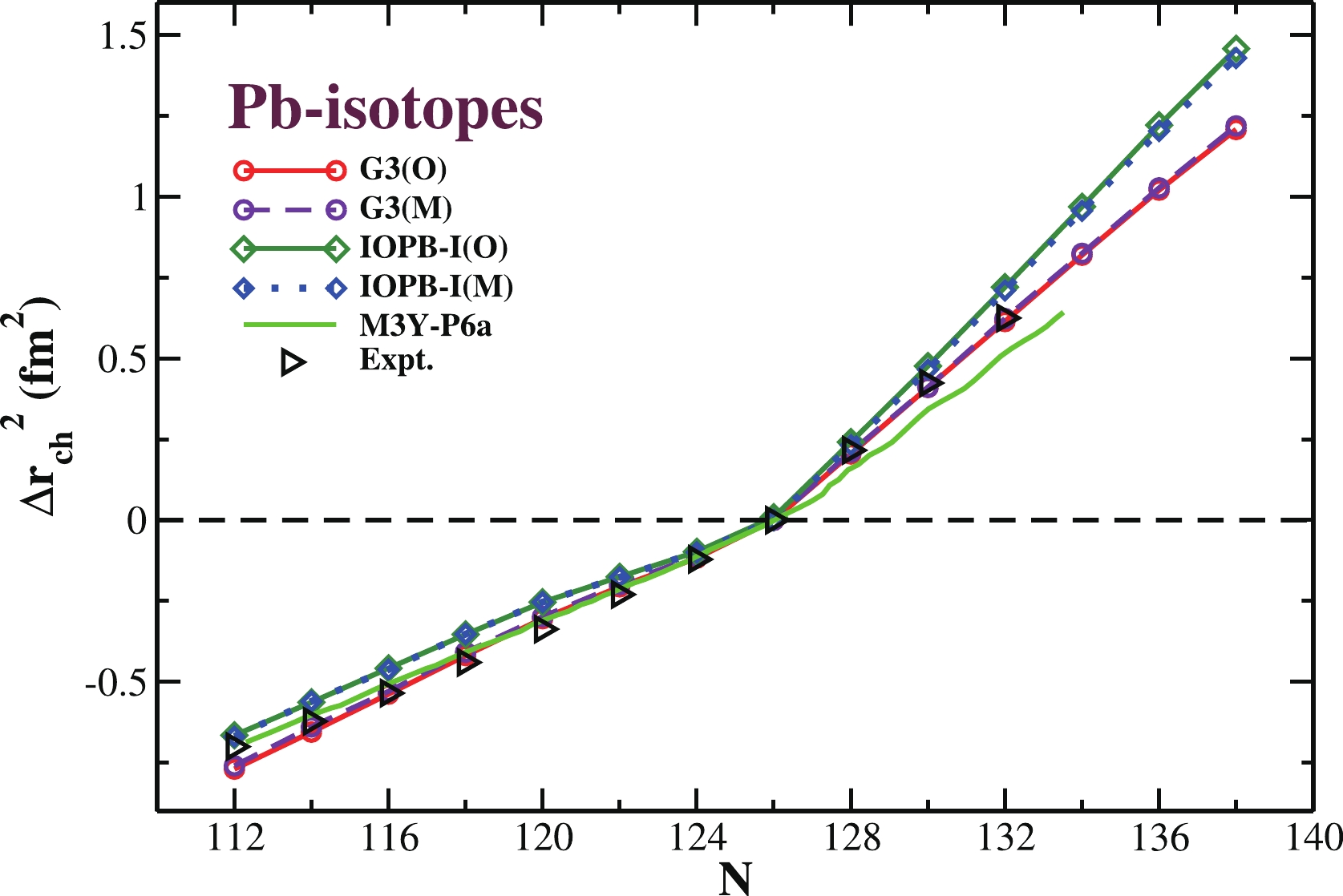
Figure 4. (color online) Isotopic shift
$ \Delta R_{ch}^2 $ in charge radius$ R_{ch} $ for Pb-isotopes for G3(M) and IOPB-I(M) compared with the G3(O) and IOPB-I(O) predictions, the experimental data [86], and the predictions from the semi-realistic effective interaction M3Y-P6a parameter set [85].The pairing is important and also crucial to a certain extent for the open-shell nuclei. To gain more insight into the pairing properties, we have calculated the average pairing gap for the isotopic chain of Sn-nuclei. The results are shown in Fig. 5 for both original (O) and modified (M) G3 and IOPB-I parameter sets and compared with Gogny-D1S HFB prediction, along with the SIII
$ ^{\delta} $ and SkP interactions [92]. From the figure, we found that the RMF with G3(M) and IOPB-I(M) are following the pattern of Gogny-D1S Hartree–Fock–Bogoliubov (HFB) predictions [92]. The strength of the gap obtained for G3 and IOPB-I (both original and modified) are in agreement with the SIII$ ^{\delta} $ and SkP interactions, while underestimated by the Gogny-D1S HFB values. The reason is, in both the G3 and IOPB-I parameter sets, we have used the BCS pairing method and here we have compared it with the Bogoliubov pairing approach. The simple BCS approach is an appropriate formalism for nuclei near the stability line. It is also known that, when we are moving away from the$ \beta- $ stability line, towards the drip line region, the Bogoliubov pairing approach is producing the pairing energy reasonably compared to the BCS approach. Again, if we compare the G3 and IOPB-I (both original and modified) data with the SIII$ ^{\delta} $ and SkP interactions, one can notice the magnitudes of the pairing gaps are nearly equal. The uncertainties at these neutron numbers N = 58, 62, 112 indicate the correlation with the shell/sub-shell closure, which is force-dependent. A similar trend is also found for N = 62 for SIII$ ^{\delta} $ in Ref. [92]. More systematic studies by choosing different pairing forces may provide the answer to these uncertainities at different neutron numbers within mean-field models [12, 92, 93].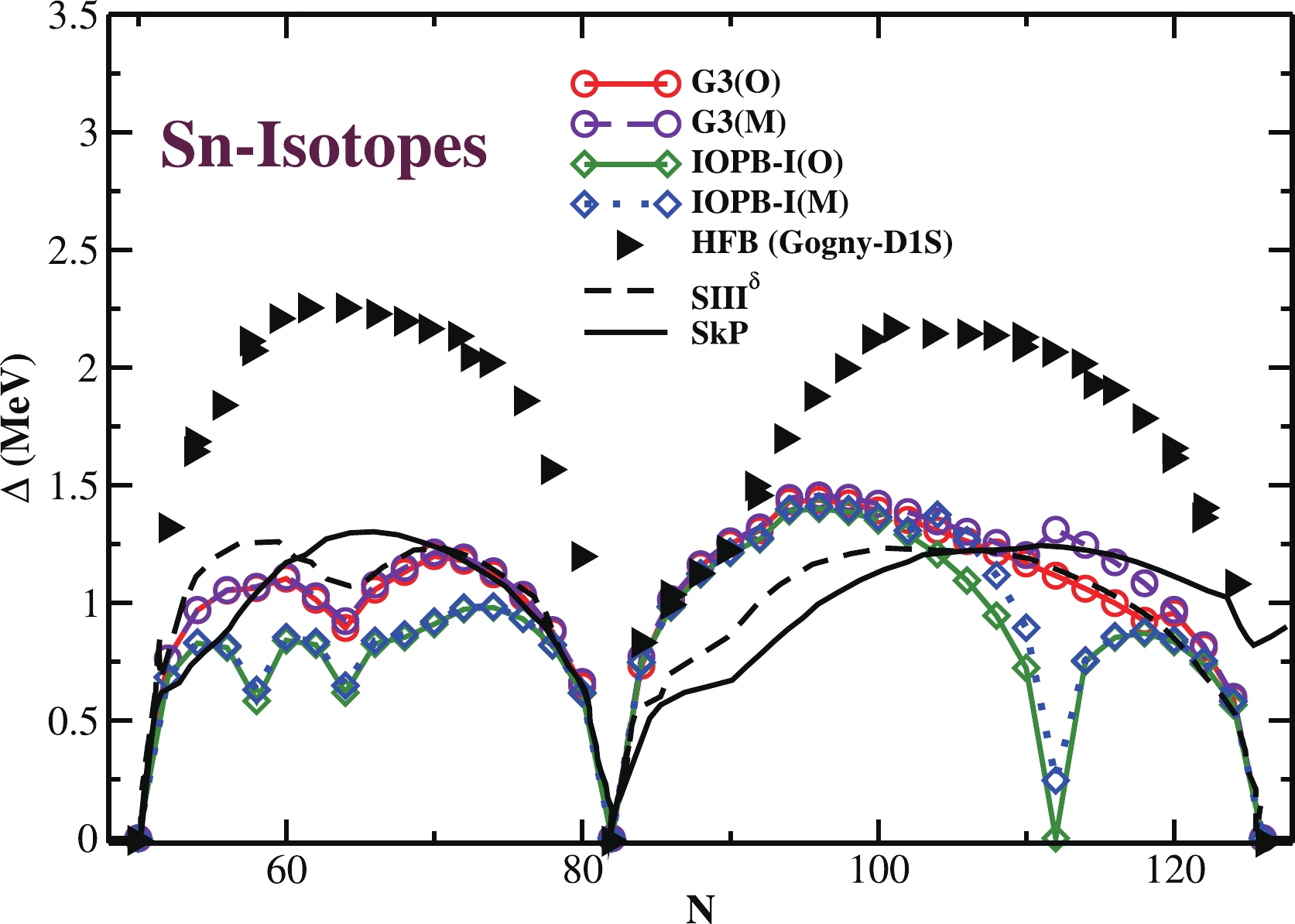
Figure 5. (color online) Average pairing gap Δ (in MeV) for Sn-isotopes for modified G3(M) and IOPB-I(M), along with G3(O) and IOPB-I(O) values. The HFB prediction for Gogny (D1S) and Skyrme SIII
$ ^{\delta} $ and SkP interactions [92] are given for comparison.The ordering of the particle and hole levels for neutrons in 208Pb from the RMF approach for both original and modified G3 and IOPB-I parameter sets are shown in Fig. 6, along with the experimental data [94, 95]. From the figure, notice that the single-particle levels are consistent with the experimental data except for the neutron
$ 2f_{5/2} $ level, which lies below the$ 3p_{1/2} $ level. A similar case is also found for$ 2g_{9/2} $ . However, this is a common fact in many mean-field models [96–98]. The magnitude of level spacing from RMF for all the parameter sets is larger than the experimental data, which is another issue in mean-field models [99]. The difference may be improved by modifying the effective mass and adopting particle vibration into the Lagrangian. At present, this is beyond the scope of the relativistic mean-field model. As mentioned above, the single-particle spacing and the occupancies play a crucial role in the isotopic shift at neutron shell/subshell closure over an isotopic chain. In this context, here one can notice that the$ 1i_{11/2} $ level lies close to$ 2g_{9/2} $ , and the same happens for heavier Pb isotopes (not shown here). Upon calculating the gap between$ 2g_{9/2} $ and$ 1i_{11/2} $ levels along the isotopic chain of Pb, the gap is found to be about 1 MeV below N = 126 and suddenly decreases to 0.6 MeV as soon as N = 126 is reached. Therefore, one can expect a relatively large occupation of the$ 1i_{11/2} $ state in Pb isotopes with more than 126 neutrons, and as a result, an appearance of the kink/shift at N = 126 (see Fig. 4) [88]. -
Nuclear matter quantities such as binding energy per particle for symmetric nuclear matter (E/A), the isospin-dependent observable symmetric energy J, slope parameter L, surface symmetric energy coefficient
$ K_{\rm sym} $ , skewness parameter$ Q_{\rm sym} $ , and incompressibility$ K_{\infty} $ have been calculated using the modified G3(M) and IOPB-I(M) parameter sets. Furthermore, we can expand the asymmetric nuclear matter (NM) incompressiblity$ K(\xi) $ in terms of asymmetry parameter$ (\xi) = \frac{(\rho_n - \rho_p)}{(\rho_n + \rho_p)} $ as,$ \begin{equation} K(\xi)=K+K_\tau \xi^2+{\cal{O}}(\xi^4), \end{equation} $

(10) where K is the incompressibility at the saturation density and
$ K_\tau $ can be expressed as,$ \begin{equation} K_\tau= K_{\rm sym.}-6L-\frac{Q_0 L}{K}, \end{equation} $

(11) where
$ Q_0=27\rho^3\dfrac{\partial^3 \cal{E}}{\partial {\rho}^3} $ in symmetric NM at saturation density [37]. The incompressibility of asymmetric nuclear matter coefficient$K_{\rm asy}$ , isospin asymmetric coefficient$ K_{\tau} $ , central density$ \rho_0 $ , incompressibility of second-order at saturation density$K_{\rm sat2}$ and slope of incompressibility$ M_0 $ are also calculated for the modified G3(M) and IOPB-I(M) parameter sets. The calculated nuclear matter (NM) properties along with neutron star (NS) properties from the modified G3(M) and IOPB-I(M) are listed in Table 3, along with the original G3(O), and IOPB-I(O) estimates. The experimental/empirical values are also listed with the ranges and/or error bars for comparison. More details on the nuclear matter saturation properties, symmetry energy, its coefficients, and their empirical/experimental ranges can be found in Refs. [58-60, 100–105].NM G3 G3 IOPB-I IOPB-I Expt. NS (O) (M) (O) (M) J 31.842 33.063 33.355 34.831 33.4–42.8 [2] L 49.317 65.530 63.700 78.947 69–143 [2] $ K_{\rm sym} $ 

−106.07 −113.99 −36.60 −61.46 − (174–31) [100] $ Q_{\rm sym} $ 

915.47 525.46 859.90 559.57 — $ K_{\infty} $ 

243.97 243.97 222.33 222.33 220– 260 [58–60,101] $ K_{\rm asy} $ 

−401.98 −507.17 −418.80 −535.14 — $ Q_0 $ 

−466.61 −466.61 −96.67 −96.67 — $ K_{\rm tau} $ 

−307.65 −381.84 −391.10 −500.81 − (840–350) [102–104] $ \rho_{0} $ 

0.148 0.148 0.149 0.149 0.148–0.185 [105] $ K_{\rm sat2} $ 

−307.65 −381.84 −391.10 −500.81 — $ M_0 $ 

2460.98 2460.98 2571.31 2571.31 — E/A −16.024 −16.024 −16.105 −16.105 − (15.0–17.0) [105] M 1.99 1.99 2.14 2.14 $ 1.97_{-0.04}^{+0.04} $ [106],

$ 2.14_{-0.09}^{+0.10} $ [107],

$ 2.01_{-0.04}^{+0.04} $ [108]

R 10.81 10.87 11.80 11.85 $ 13.02_{-1.06}^{+1.24} $ ,

$ 12.71_{-1.19}^{+1.14} $ [109]

Λ 464.63 498.23 689.62 727.43 70–580 [110–112] $ \lambda_2 $ 

2.61 2.81 3.87 4.11 — $ k_2 $ 

0.09 0.09 0.11 0.11 — Table 3. Nuclear matter (NM) properties (in MeV) at saturation density (
$ \rho_0 $ in fm$ ^{-3} $ ) and neutron star (NS) properties, such as maximum mass (M in solar mass unit) and radius (R km), obtained using the original G3(O) and IOPB-I(O) and the modified G3(M) and IOPB-I(M) parameter sets. The tidal Love number$ k_2 $ , tidal deformability ($ \lambda_2 $ ) and dimensionless tidal deformability$ (\Lambda $ ) at 1.4 solar mass are also presented. The experimental values for both NM and NS quantities are given for comparison, wherever available.Constraining the
$ \Lambda_{\omega} $ and$ g_{\rho} $ parameters with respect to the PREX-2 result of$ R_n $ , we find the J and L values roughly as per the limit of Reed et al. [2], i.e.,$33.063 \lt J \lt 34.831$ MeV and$65.530 \lt L \lt 78.947 $ MeV. Comparing J and L from G3(M) and IOPB-I(M), one can see that the IOPB-I(M) set is a better fit with the prediction of Ref. [2]. Further, smooth improvements can observed for G3(M) and IOPB-I(M) for these nuclear matter observables. Upon the analysis of J, L and$ K_{\infty} $ , we find a significant enhancement in the symmetric energy coefficient J and the slope parameter L, while not affecting the nuclear matter incompressibility. This is because the chosen parameters$ \Lambda_{\omega} $ and$ g_{\rho} $ do not strike the symmetric nuclear matter EoS. The symmetric energy coefficient is defined as$ J(\rho)=\dfrac{1}{2}\left[\dfrac{\partial^2 {e}(\rho, \alpha)} {\partial \alpha^2}\right]_{\alpha=0} $ , where$ e(\rho,\alpha) $ is the energy density obtained from the EoS and$ \alpha=\left(\dfrac{\rho_n-\rho_p}{\rho_n+\rho_p}\right) $ , with$ \rho_n $ and$ \rho_p $ the neutron and proton density distributions. Practically, the value of J at saturation density is obtained from the energy difference between the pure neutron matter (PNM) and the symmetric nuclear matter (SNM). Although the EoS of SNM does not depend on the ρ-meson coupling, it highly relies on the asymmetric nuclear matter EoS.In Fig. 7, we have shown the behaviour of nuclear matter parameters J and L with the change of paramaters
$ \Lambda_{\omega} $ and$ g_{\rho} $ . In the process of tuning the G3(M) and IOPB-I(M) from the original G3(O) and IOPB-I(O), here the values of symmetry energy J decrease with the increase of$ \Lambda_{\omega} $ and increase with the increase of$ g_{\rho} $ . Similar behaviour is found for slope parameter L with$ \Lambda_{\omega} $ , except the trend with$ g_{\rho} $ , which is decreasing with increasing values of$ g_{\rho} $ . Fig. 8 shows the variation of pressure with baryon density for both original and modified G3 and IOPB-I sets for symmetric nuclear matter (SNM). The empirical flow data [113] is given for comparison. The G3 parameter set has excellent agreement with the heavy-ion collisions (HIC) data. Fig. 8 In comparison to G3(O), IOPB-I(O) has a stiffer EoS, although it still matches with the empirical HIC data. Similarly, G3(M) and IOPB-I(M) overlap exactly over the original G3(O) and IOPB-I(O) parameters and exhibit the same nature.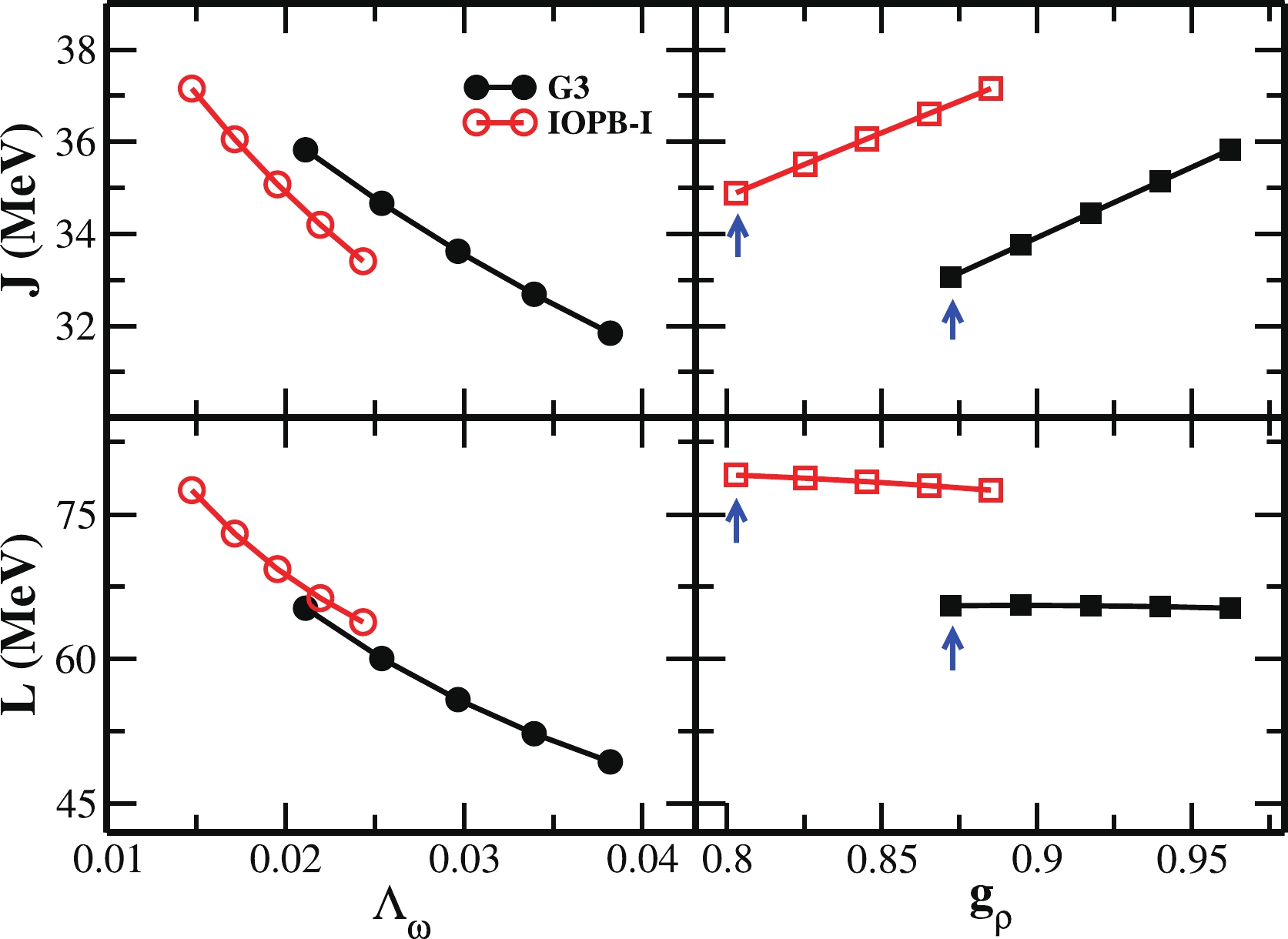
Figure 7. (color online) Symmetry energy J (upper panels) and slope parameter L (lower panels) for G3 (black solid shapes) and IOPB-I (red open shapes) parameter sets as a function of
$ \Lambda_{\omega} $ (left panels, circles) and$ g_{\rho} $ (right panels, squares). The single arrow is for better visibility of the values of modified G3(M) and IOPB-I(M).
Figure 8. (color online) Calculated pressure with the variation of baryon density. The results for G3(O), IOPB-I(O), G3(M) and IOPB-I(M) are compared with HIC data [113] for symmetric nuclear matter.
The nuclear EoS plays a crucial role in studying neutron star properties. In Fig. 9, the EoS of original and modified G3 and IOPB-I forces are presented along with the extracted recent GW170817 observational data. The shaded regions are deduced from GW170817 data with 50% (grey) and 90% (orange) credible limit [112]. Both the original and modified versions of G3 and IOPB-I fit on top of the empirical data, having some differences in lower as well as higher energy density regions. However, these undulations are very marginal between the original G3(O) and IOPB-I(O) and modified G3(M) and IOPB-I(M), respectively. The modified forces G3(M) and IOPB-I(M) are further applied to neutron star matter to determine mass M and radius R. The M–R profile with the original and the modified forces are shown in Fig. 10 and also in Table 3 as earlier discussed. The experimental observations for mass and possible radius [106, 107] are also shown in the figure. It is interesting to note that the overall results for both modified and original parameter sets are unchanged. The calculated mass and radius obtained for both the original and modified parameter sets are compiled in Table 3. The values of M and R for all the parameter sets are well within the recent measurements [106–109].

Figure 9. (color online) Equations of states of
$ \beta- $ equilibrated matter for G3(O), IOPB-I(O), G3(M) and IOPB-I(M) parameter sets. The shaded regions are for 50% (grey) and 90% (orange) posterior credible limits given by the GW170817 data [112].Finally, we have calculated the highly-discussed binary neutron star merger properties [111, 112, 114] such as the Love number
$ k_2 $ , quadrupole tidal deformability$ \lambda_2 $ and the dimensionless tidal deformability Λ for the modified G3(M) and IOPB-I(M) parameter sets listed in Table 3. Figure 11 shows the effect of the considered tuning parameters$ \Lambda_{\omega} $ and$ g_{\rho} $ on tidal deformability ($ \lambda_2 $ )($ 10^{36} $ gm cm$ ^2 $ sec$ ^2 $ ) and dimensionless tidal deformability$ (\Lambda $ ) at maximum solar mass in the conversion from original G3(O) and IOPB-I(O) to modified G3(M) and IOPB-I(M) parameters. One can notice from the figure the effect of$ \Lambda_{\omega} $ over tidal deformability ($ \lambda_2 $ ) is almost negligible, while on the other hand for the G3 parameter set the values are decreasing with the increase of$ g_{\rho} $ . The pattern is the reverse for the IOPB-I set. In the case of the tidal deformability Λ, for the G3 parameter, it firstly decreases and then increases slightly with the variation of both$ \Lambda_{\omega} $ and$ g_{\rho} $ , while the opposite trend is followed by IOPB-I parameter set. From Figs. 7 and 11 we conclude that the dependency on$ \Lambda_{\omega} $ and$ g_{\rho} $ is significant for J and L, but nominal for tidal properties such as$ \lambda_2 $ and Λ. From the above analysis, we find the modified version of G3 and IOPB-I can reproduce all the nuclear matter quantities and neutron star properties, including neutron star mergers, and compete with the original version along with the current PREX-2 constraint on neutron-skin thickness. More systematic analysis of various regions of the nuclear chart with systematic study of nuclear and star matter quantities will be communicated soon.
Figure 11. (color online) Tidal deformability (
$ \lambda_2 $ (upper panels, units$ 10^{36} $ gm cm$ ^2 $ sec$ ^2 $ ) and dimensionless tidal deformability$\Lambda $ (lower panels) at maximum solar mass for G3 (black solid shapes) and IOPB-I (red open shapes) parameter sets as a function of$ \Lambda_{\omega} $ (left panels, circles) and$ g_{\rho} $ (right panels, squares). The single arrow is for better visibility of the values of modified G3(M) and IOPB-I(M). -
In summary, we have revisited the relativistic mean-field forces for G3 and IOPB-I parameter sets, applying the currently reported constraint on the neutron radius of 208Pb by PREX-2. It is worth demonstrating that the precise measurement of the neutron distribution radius discriminates various theoretical predictions. Hence it provides an opportunity to modify the force parameter or readjust the model with the implication of new interactions in the model. In this context, we have performed a minimal modification to the relevant couplings of recently developed G3 and IOPB-I parameter sets with E-RMF without compromising the predictions for finite nuclei and infinite nuclear matter. We carried out fine-tuning of the
$ \omega-\rho $ cross-coupling$ \Lambda_{\omega} $ along with the coupling of isovector–vector-meson ($ g_{\rho} $ ) to reproduce the recent experimental$ R_n $ . The updated values of$ \Lambda_{\omega} $ and$ g_{\rho} $ are 0.021 and 0.872 for G3, and 0.014 and 0.803 for IOPB-I, respectively. The modified parameter sets reproduce the neutron distribution radius as 5.717 and 5.721 (in fm) for G3(M) and IOPB-I(M) respectively, which both meet the present experimental demand of$ R_{n}^\text{Expt.} = 5.727 \pm 0.071\,\text{fm}$ .The modified forces have been used to calculate ground-state properties such as binding energies, root-mean-square charge distribution radii
$ R_{ch} $ , nuclear density distributions, pairing gap parameters, and single-particle energies for a few even–even nuclei. Further, we have considered 195 even–even nuclei to estimate the root-mean-square (rms) deviation in binding energy with respect to the experimental data, and the results compare favourably with the well-calibrated effective interactions of Skyrme, Gogny and other RMF parametrizations. The rms deviation has also been calculated for the charge radius using the available experimental data. We found a reasonable value for the rms deviation consistent with other theoretical calculations, with binding energy 3.751973 and 3.5698173 MeV and charge radii 0.023278 and 0.021237, respectively for the G3(M) and IOPB-I(M) parameter sets. We have also performed the same for G3(O) and IOPB-I(O), where the mean deviation of BE is found to be 2.69674 and 2.3537 MeV. We have also verified the pairing gap for Sn-isotopes and found a pattern match to the Hartree–Fock–Bogoliubov predictions. The isotopic shift and the single-particle energy spacing is also examined for 208Pb, which match reasonably with the experimental data. Comparing the original version of G3 and IOPB-I parameter sets with the modified version, we did not find any substantial difference in the nuclear bulk properties except the neutron radial distribution, i.e., the skin-thickness.Subsequently, the density and isospin-dependent nuclear matter parameters, such as symmetry energy J, slope L, and other specific observables, have also been estimated, significantly favouring the experimental or other theoretical predictions. Furthermore, the dependence on
$ \Lambda_{\omega} $ and$ g_{\rho} $ for J, L,$ \lambda_2 $ , Λ have been estimated. We noticed that the changes in NM quantities J, L are significant, but changes are nominal for NSM quantities. For example, the value of symmetry energy is 31.842 MeV for original G3(O), and after the modification, modified G3(M) produces the value of J as 33.063 MeV. Similarly, the J values are 33.355 and 34.831 MeV for IOPB-I(O) and IOPB-I(M), respectively. For both the parameter sets, the new values are closer to the limit set up by Reed et al. [2]. The EoS for symmetric NM and neutron star matter was briefly discussed. We noticed that both the original and modified G3 and IOPB-I forces are in good agreement with the empirical data. Further, the forces are applied to calculate the properties of high isospin asymmetry dense systems such as neutron star matter have been tested to validate the constraint from GW170817 binary neutron star merger events [111, 112]. We find better predictions in the modified version of G3 and IOPB-I compared to the original version for finite and infinite nuclear matter systems. Hence, recalibration of the parameters is essential for theoretical studies in parallel with the PREX-2 constraint on neutron radius of 208Pb. -
We thank H. C. Das and Ankit Kumar for fruitful discussions, and JAP thanks the Institute of Physics, Bhubaneswar for providing computer facilities during the work.
Constraining the relativistic mean-field models from PREX-2 data: effective forces revisited
- Received Date: 2022-02-17
- Available Online: 2022-09-15
Abstract: Based on the current measurement of the neutron distribution radius (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: